针对推力吸附爬壁机器人的研究主要分为2种:纵列式和共轴式. 纵列式推力吸附爬壁机器人主要有Sukvichai等 [ 3] 提出的纵列式双旋翼爬壁机器人、苏黎世迪士尼研究中心和ETH合作开发的VertiGo [ 4] 、Adarsh等 [ 5] 提出的MTMUR、Liang等 [ 6] 设计的推力吸附机器人等. 纵列式的推力吸附机构由2个前后排列、双叶片的旋翼组成,旋翼旋转平面可以调整,提供与墙面法线方向垂直、墙面法线方向平行的推力. 共轴式推力吸附爬壁机器人主要有Alkalla等 [ 7- 8] 提出的EJBot-Ⅰ、EJBot-Ⅱ. 共轴式的推力吸附机构由2个同轴排列、双叶片的旋翼组成,旋翼旋转平面不可以调整,提供与墙面法线方向平行的推力. 纵列式推力吸附爬壁机器人控制复杂,既要控制推力吸附机构的旋翼旋转速度、旋翼旋转平面,还要控制机器人行走方向. 共轴式推力吸附爬壁机器人的控制相对简单,只需控制推力吸附机构的旋翼转速与行走,与纵列式相比其负重能力更强.
EJBot-Ⅱ是在EJBot-Ⅰ基础上的更新,但EJBot-Ⅱ只对机架进行简单的拓扑优化,并未进行详细的参数设计,未分析流场. 本研究在EJBot-Ⅱ的基础上,结合桥梁壁面安全隐患排查的实际需求,介绍共轴式推力吸附爬壁机器人,采用控制变量法对不同气动参数下的推力吸附机构进行气动建模和流场仿真分析,比较仿真结果对推力吸附机构进行优化设计;基于拓扑优化,分别用构件响应面优化和直接优化对机器人机架进行结构参数优化设计;分别在室内和室外,对样机性能试验测试.
1. 总体设计
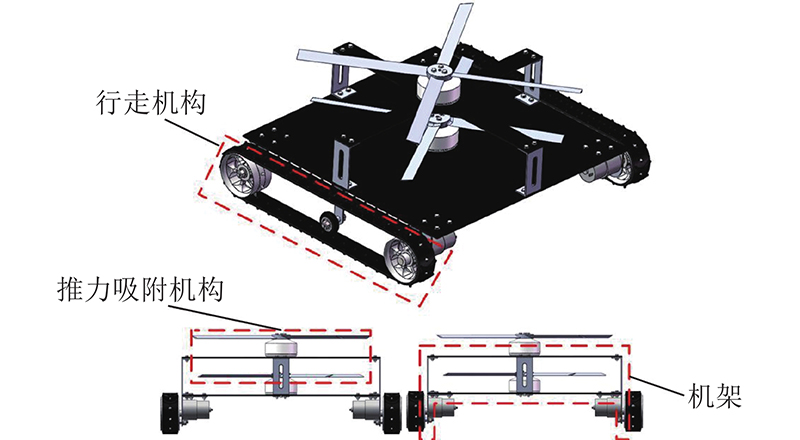
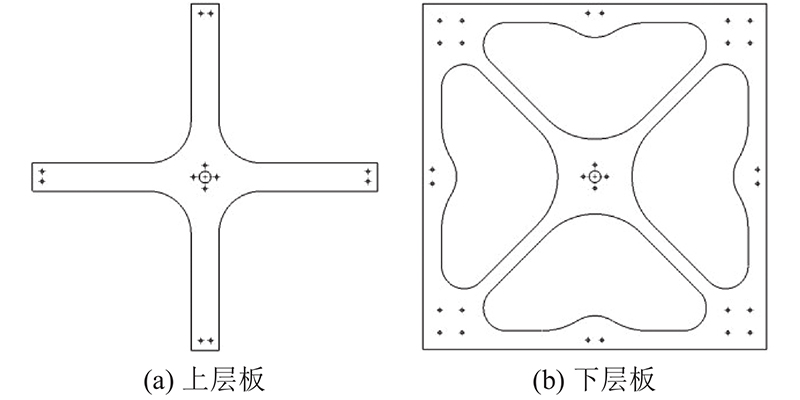
共轴式双旋翼推力吸附方案能有效地控制机器人的结构尺寸,减轻机器人自重,相对地增大机器人的负载能力. 推力吸附机器人具备在混凝土壁面上攀爬和负载的能力,主要由推力吸附机构、行走机构、机架组成,如 图1所示.
图 1
推力吸附机构主要作用是为机器人提供正压力,由与旋转中心轴共线、半径为0.175 m、转速相等、转动方向相反的2层旋翼构成。推力吸附机构的桨叶翼型选用NACA4 412. 机架由上、下层板及支座组成,连接和固定着各个功能部件. 上、下层板作为机架的主体,主要作用是固定旋翼驱动电机和传递旋翼驱动电机产生的荷载. 行走机构位于机器人下层,采用履带式行走方式,通过支座与下层板连接,直接与壁面接触. 行走机构既能实现基本的行走功能,又能抵消上、下层旋翼产生的扭矩.
本研究通过流场仿真、优化算法优化推力吸附机构、机架. 推力吸附机构优化能够增强单位功率下机器人推力吸附机构推力,机架优化在满足使用条件后能够减轻机器人质量,对两者进行优化的目的是增强负载能力、降低能耗、增加续航时间.
2. 推力吸附机构优化设计
采用控制变量法控制旋翼的叶片数、桨叶安装角、间距比,分别对机器人气动模型进行仿真求解;比较不同气动参数值下机器人的气动性能,以优化单位功率的机器人推力为目标进行综合分析,确定气动参数;在不同转速下,分析机器人的推力、扭矩、所需功率、旋翼上下表面压力、速度矢量等气动性能,为机器人样机的研制提供理论支撑.
2.1. 推力及所需功率
式中: K ⊥为垂直吹风增重系数,
在悬停状态下,单旋翼所需功率主要包含型阻功率、诱导功率及有效功率等:
式中: N n为单旋翼所需功率, ξ为功率损失系数, m k为功率系数, K P0为型阻修正系数, J 0为诱导功率修正系数, C X7为型阻系数. 分别以旋翼推力、所需功率表示旋翼转速,得到在悬停状态下,单旋翼所需功率与推力的关系为
定义参数 γ来描述推力吸附机构旋翼所需功率与旋翼推力间的关系,表达式为
由式(3)、(4)可知,单位功率下, γ越小,机器人提供的推力越大.
2.2. 推力吸附机构结构参数优化
2.2.1. 叶片数
保持气动参数不变,分别建立 k=2、3、4、5、6的机器人气动模型. 流场仿真求解相应 γ与 k关系如 表1所示. 表中 γ u为上层旋翼 γ, γ d为下层旋翼 γ, γ s为双旋翼 γ. 可知,当 k=3或4,上、下层旋翼共同作用时, γ s最小. 叶片数越多,旋翼实度(旋翼桨叶面积与桨盘面积之比)越大;在达到同等大小的推力时,旋翼实度越大,所需的转速越低,旋翼可靠性能越好. 即当 k=4时,转速更低,机器人的整体性能更优越.
表 1 推力吸附机构的叶片数与 γ的关系
Tab.1
| k/片 | γ u | γ d | γ s |
| 2 | 36.32 | 22.02 | 19.74 |
| 3 | 36.74 | 21.04 | 19.19 |
| 4 | 39.37 | 20.37 | 19.19 |
| 5 | 40.41 | 20.77 | 19.64 |
| 6 | 43.52 | 20.70 | 20.13 |
2.2.2. 桨叶安装角
保持气动参数不变,建立上、下层旋翼安装角( θ u, θ d)如 表2所示的机器人气动模型. 可知,随着安装角增大, γ趋于稳定;当( θ u, θ d)=(14°,13°)时, γ s最小.
表 2 推力吸附机构的安装角与 γ的关系
Tab.2
| θ u/(°) | θ d/(°) | γ u | γ d | γ s |
| 6 | 5 | 111.12 | 23.55 | 27.64 |
| 7 | 6 | 42.11 | 22.13 | 20.80 |
| 8 | 7 | 39.37 | 20.37 | 19.19 |
| 9 | 8 | 36.09 | 19.59 | 18.16 |
| 10 | 9 | 34.08 | 19.01 | 17.43 |
| 11 | 10 | 32.32 | 18.74 | 16.92 |
| 12 | 11 | 31.27 | 18.61 | 16.64 |
| 13 | 12 | 30.37 | 18.65 | 16.48 |
| 14 | 13 | 29.87 | 18.84 | 16.47 |
| 15 | 14 | 29.50 | 19.40 | 16.69 |
| 16 | 15 | 29.70 | 19.28 | 16.66 |
2.2.3. 间距比
保持气动参数不变,定义 H为上、下层旋翼间距, D为旋翼直径,如 表3所示分别建立旋翼间距比 H/ D的机器人气动模型. 可知, γ s随着间距比增大而减小;当 H/ D≥0.19时, γ s变化不大且较为稳定. 由于 H越大,机器人重心越高,稳定性越差,综合考虑,取 H/ D=0.2.
表 3 推力吸附机构的间距比与 γ的关系
Tab.3
| H/ D | γ u | γ d | γ s |
| 0.10 | 47.12 | 31.77 | 27.19 |
| 0.15 | 32.82 | 22.52 | 19.02 |
| 0.18 | 30.80 | 20.36 | 17.43 |
| 0.19 | 29.43 | 19.91 | 16.92 |
| 0.20 | 29.26 | 19.64 | 16.74 |
| 0.23 | 28.96 | 19.37 | 16.55 |
| 0.25 | 29.47 | 19.03 | 16.49 |
| 0.30 | 29.87 | 18.84 | 16.47 |
综上所述,当 k=4、( θ u, θ d)=(14°,13°)、 H/ D=0.2时,机器人的气动性能较好,单位功率下能够产生更大的推力.
2.3. 机器人气动性能
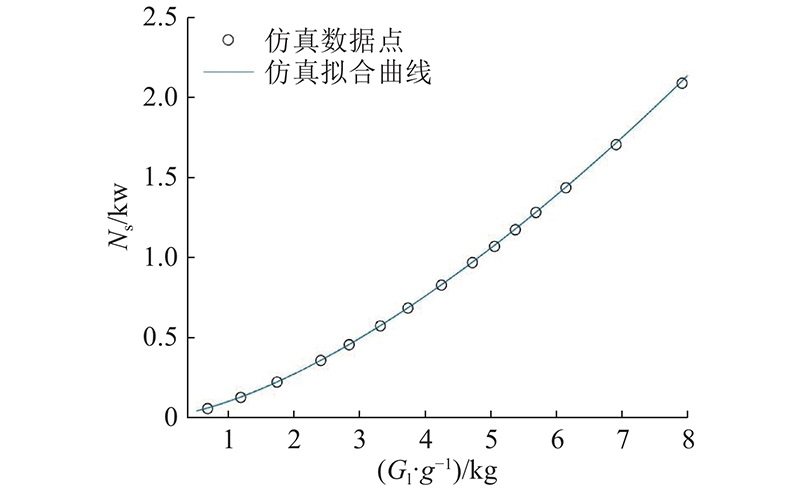
确定推力吸附机构结构并建立气动仿真模型,控制旋翼转速,求得在不同转速下,机器人所需功率 N s与产生的推力关系,如 图2所示. 可知,随着功率的增长,推力增长趋势随之减弱. 根据式(3),以 f( x)= ax 1.5对仿真数据点进行拟合得到
图 2
图 2 推力吸附爬壁机器人的仿真功率与推力
Fig.2 Simulated power and thrust of thrust adsorption wall-climbing robot
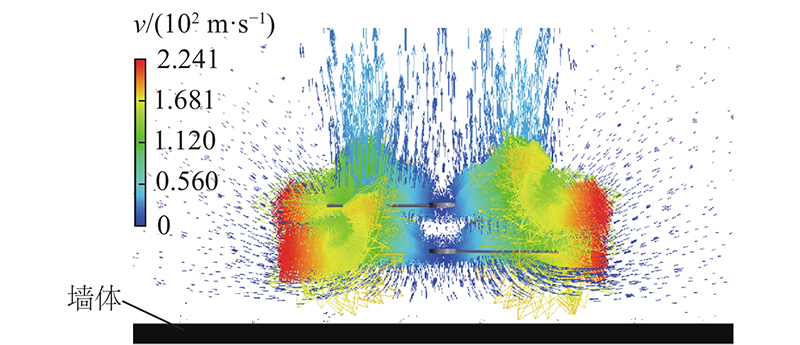
当机器人上、下层旋翼转速为8 500 r/min时,空气速度 v矢量图如 图3所示. 图中,旋翼下端矩形为部分墙体的截面,旋翼提供的推力将机器人压在壁面上;空气由机器人四周流入,由垂直与壁面方向流出;越靠近上、下层旋翼桨尖位置, v越大;从旋翼流出的气体又流回旋翼,导致上、下层旋翼流场相互干扰,特别是下层旋翼的流场,其对上层旋翼的流场造成了严重干扰.
图 3
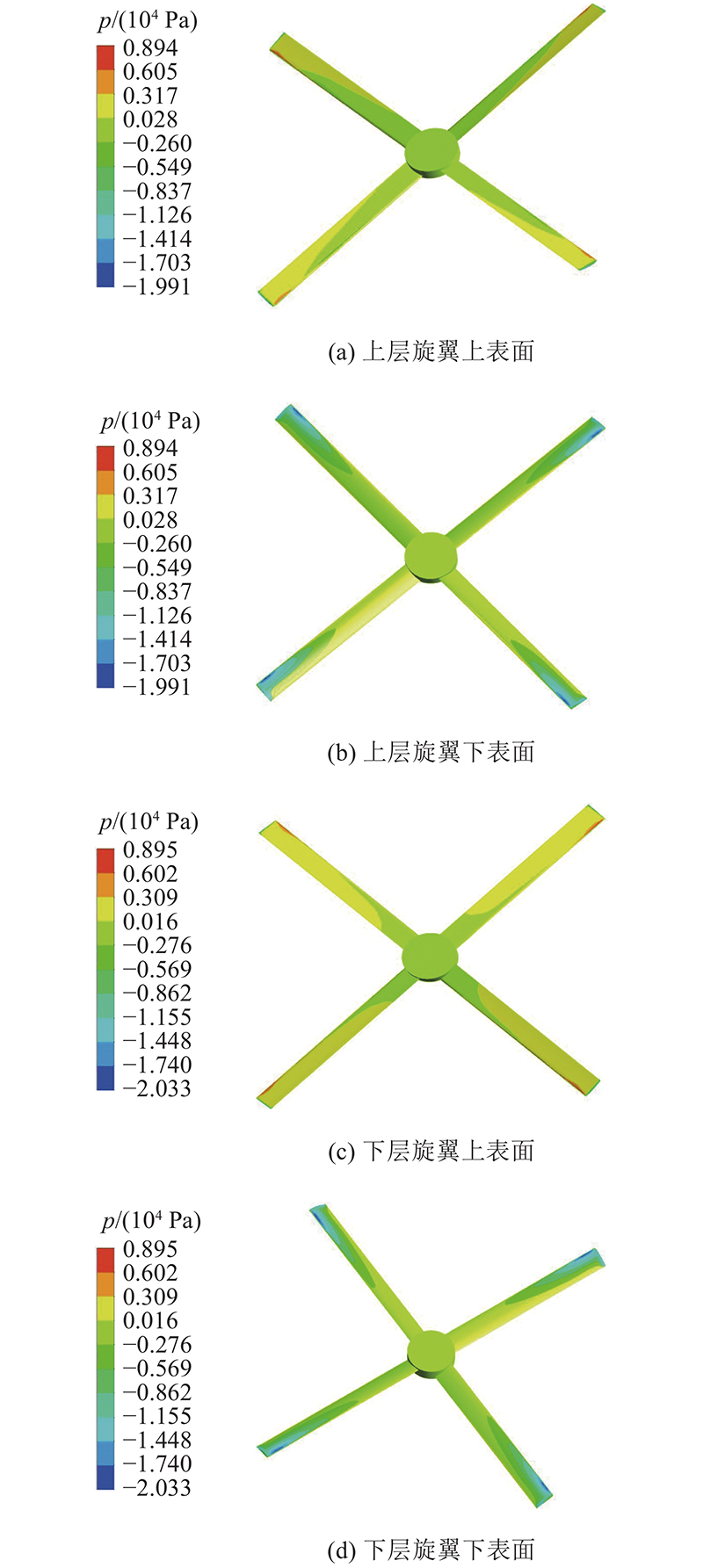
上、下层旋翼推力可由上、下层旋翼上、下表面压差与旋翼截面计算得出. 如 图4所示为机器人上、下层旋翼转速为8 500 r/min时旋翼的压力云图. 可知,旋翼截面压力分布与截面曲率大小成反比;旋翼上表面压力大于下表面;越靠近桨尖,旋翼上、下表面压差越大;上、下层旋翼压力云图限值不相等,下层旋翼压力云图略大于上层旋翼,即下层旋翼推力大于上层旋翼推力.
图 4
3. 机架优化
优化机架结构将针对上、下层板进行. 在完成上、下层板拓扑优化的基础上,进行参数优化;综合考虑机架材料属性和加工工艺,进行上、下层板结构设计 [ 11] . 优化算法采用多目标遗传优化算法(multi objective genetic algorithm, MOGA)和单目标自适应优化算法(adaptive single-objective,AS-O). MOGA用于连续输入变量,可以在目标空间中找到1组分布较好的帕累托最优解,求解精度较高,可以优化多个目标,即能构建响应面优化又能直接优化. AS-O用于连续输入变量,所需样本点数目少,容错能力强,只能优化1个目标,且只能用于直接优化 [ 12- 13] .
3.1. 拓扑前结构分析
3.1.1. 荷载及约束
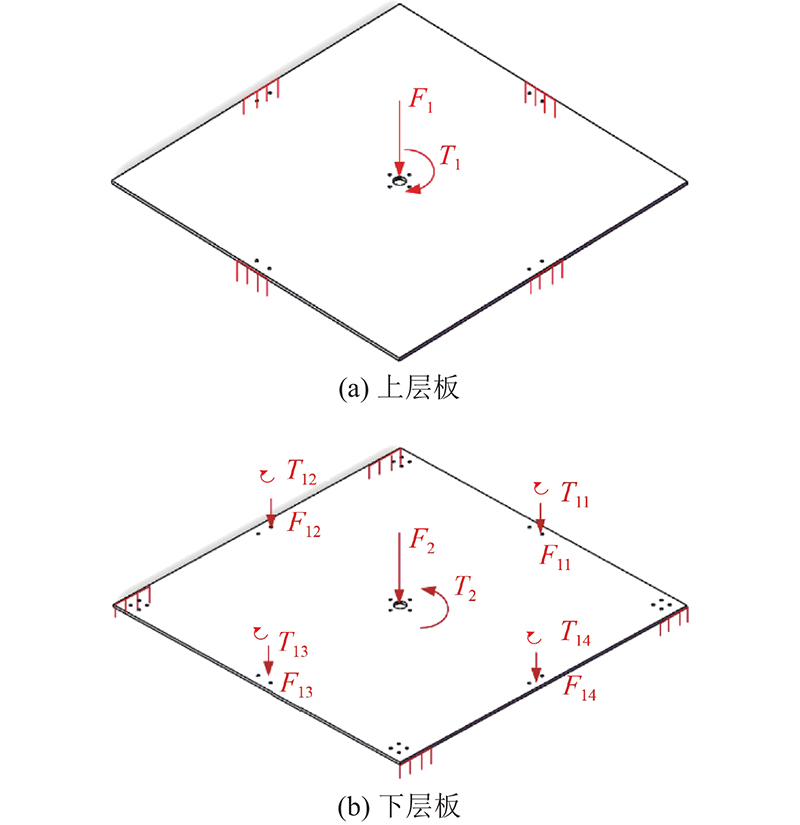
当机器人停留在壁面上时,上层板由与下层板连接支座固定支撑,主要受上层旋翼系统的推力及扭矩;下层板由与行走系统连接支座固定支撑,主要受上层旋翼系统的推力、扭矩及下层旋翼系统的扭矩、推力;上层旋翼系统的推力、扭矩由支座传递到下层板底边中心处. 如 图5所示,对上、下层板的受力情况进行简化,上层板在底边中心处固定,正中心处受荷载作用;下层板在4个边固定,分别在正中心和底边中心共5处受荷载作用. 图中,当旋翼转速为8 500 r/min时, T 1 、F 1分别为上层旋翼的扭矩和推力, T 2 、F 2分别为下层旋翼正中心的扭矩和推力, T 11、 T 12、 T 13、 T 14、 F 11、 F 12、 F 13、 F 14分别为下层旋翼4个边中心的扭矩和推力, T 1为 T 11、 T 12、 T 13、 T 14的和, T 11、 T 12、 T 13、 T 14与 T 2方向相反, F 11、 F 12、 F 13、 F 14的大小相等且它们的和等于 F 1.
图 5
3.1.2. 材料力学性能
上、下层板采用特制的新型轻质材料,密度为1.6 g/
3.1.3. 静力学及模态分析
拓扑前上层板最大变形为0.053 mm,最大应力为10.56 MPa;下层板的最大变形为0.16 mm,最大应力为41.89 MPa. 如 表4所示为拓扑前上、下层板前6阶的固有频率 f u和 f d.
参考旋翼电机的测试数据,旋翼电机转速小于8 500 r/min,则振源的最高频率小于141.67 Hz,为了避开旋翼驱动电机的激振频率,上、下层板的固有频率大于200 Hz.
表 4 拓扑前机架上、下层板的前6阶固有频率
Tab.4
| Hz | ||||||
| 阶数 | f u | f d | 阶数 | f u | f d | |
| 1 | 360.9 | 225.8 | 4 | 368.2 | 433.9 | |
| 2 | 364.0 | 391.7 | 5 | 447.6 | 666.9 | |
| 3 | 368.2 | 391.8 | 6 | 843.4 | 885.1 | |
3.2. 拓扑优化
采用相对密度法,以机架上、下层板的最小柔度 λ( x )为优化目标,设定保留体积比为约束条件,对机架上、下层板进行拓扑优化设计,其数学模型为
式中: x 为机架上、下层板单元相对密度向量, U 为机架上、下层板系统位移列阵, K 为机架上、下层板结构总刚度矩阵, R v为机架上、下层板保留体积比, V 0为机架上、下层板初始结构体积,
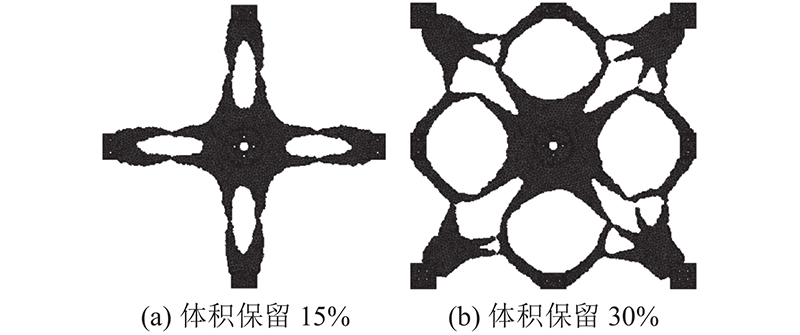
由于上、下层板受力情况不同,且固定位置不同,上、下层板的优化目标分别为体积减小到原体积的15%、30%,拓扑优化网格图如 图6所示.
图 6
3.3. 初始结构设计
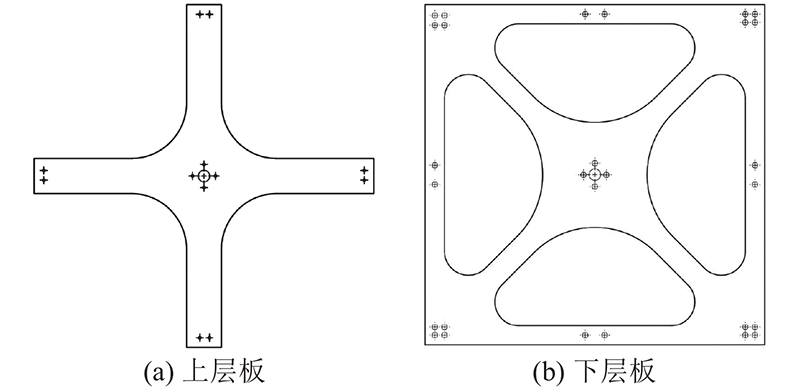
确定上、下层板主要尺寸为参数优化设计初始值,其结构设计俯视图如 图7所示.
图 7
3.4. 静力学及模态分析
初始结构设计的上层板最大变形为0.091 mm,最大应力为13.56 MPa;下层板的最大变形为0.33 mm,最大应力为44.34 MPa. 如 表5所示为上、下层板的前6阶固有频率. 可知,第一阶固有频率最小,固有频率随阶数依次增大.
表 5 初始设计时机架上、下层板的前6阶固有频率
Tab.5
| Hz | ||||||
| 阶数 | f u | f d | 阶数 | f u | f d | |
| 1 | 425.9 | 220.3 | 4 | 1793.0 | 468.6 | |
| 2 | 1057.2 | 466.8 | 5 | 2456.4 | 502.3 | |
| 3 | 1057.4 | 468.6 | 6 | 2876.1 | 600.6 | |
3.5. 参数优化
与拓扑前相比,初始结构设计上、下层板的最大变形、最大应力相应增大;上层板前6阶的固有频率波动较大,相应增大;下层板前6阶的固有频率波动较小,各有增减.
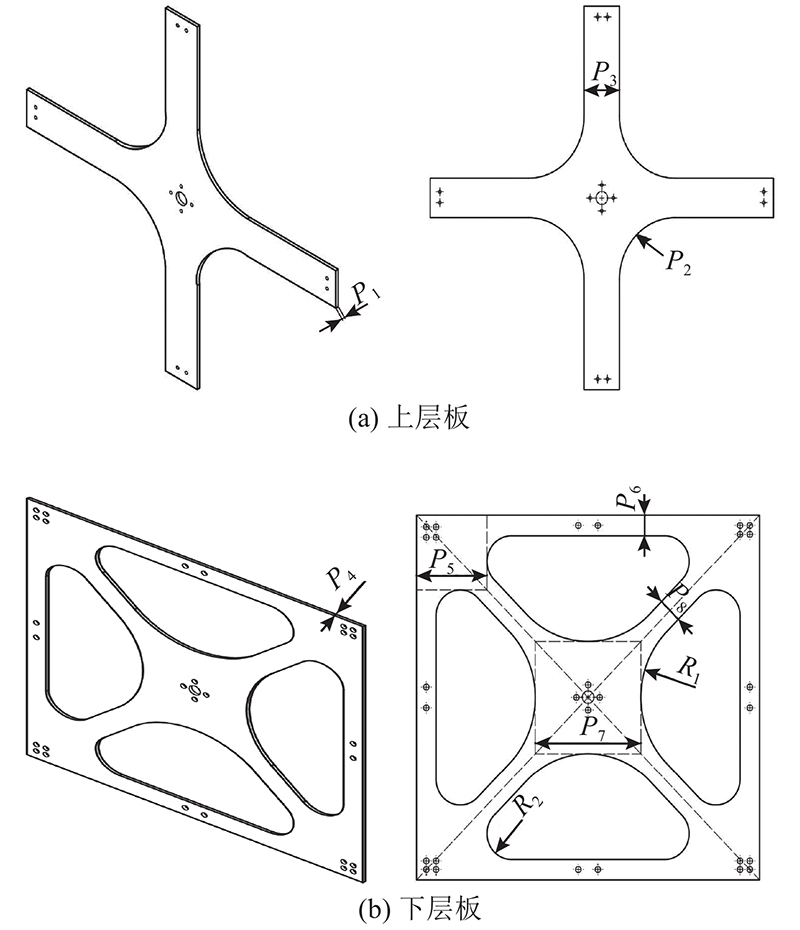
3.5.1. 结构参数化
图 8
表 6 机架上、下层板的参数变化范围
Tab.6
| P 1 | P 2 | P 3 | P 4 | P 5 | P 6 | P 7 | P 8 | |
| mm | ||||||||
| 初始值 | 3.0 | 60.0 | 38.0 | 3.0 | 76.0 | 21.0 | 114.0 | 25.5 |
| 上限 | 4.0 | 80.0 | 50.0 | 4.0 | 80.0 | 28.0 | 120.0 | 30.0 |
| 下限 | 1.5 | 10.0 | 30.0 | 1.5 | 50.0 | 20.0 | 51.0 | 8.0 |
| 取值 | 2.0 | 45.0 | 30.0 | 3.0 | 65.0 | 20.0 | 80.0 | 15.0 |
3.5.2. 优化模型
对上、下层板进行尺寸参数优化,使上、下层板满足使用要求后,总质量最轻. 对上、下层板的使用要求主要有3个方面:强度、变形、固有频率. 选用的轻质材料强度大,且最大变形与最大应力正相关,为了减小计算量,把最大等效应力小于许用应力作为隐藏约束条件. 故以结构质量 m作为目标优化函数,第一阶固有频率 、最大变形量作为约束条件,建立优化设计数学模型:
式中: P h、 P 1为尺寸变量的上、下限, d为变形量, d 0=0.6 mm, f min为最小一阶固有频率, f 0=200 Hz.
3.5.3. 参数优化结果分析
图 9
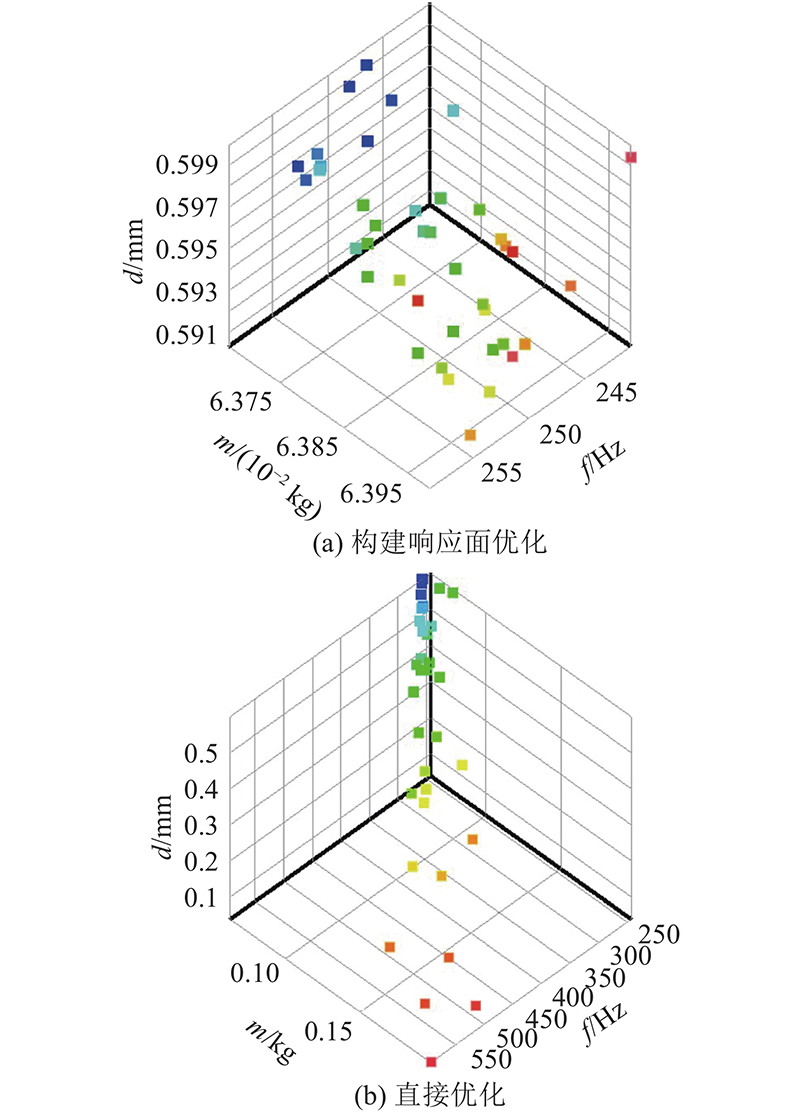
图 9 上层板的优化Pareto解集分布图
Fig.9 Distribution diagram of optimal Pareto solution set for upper plate
图 10
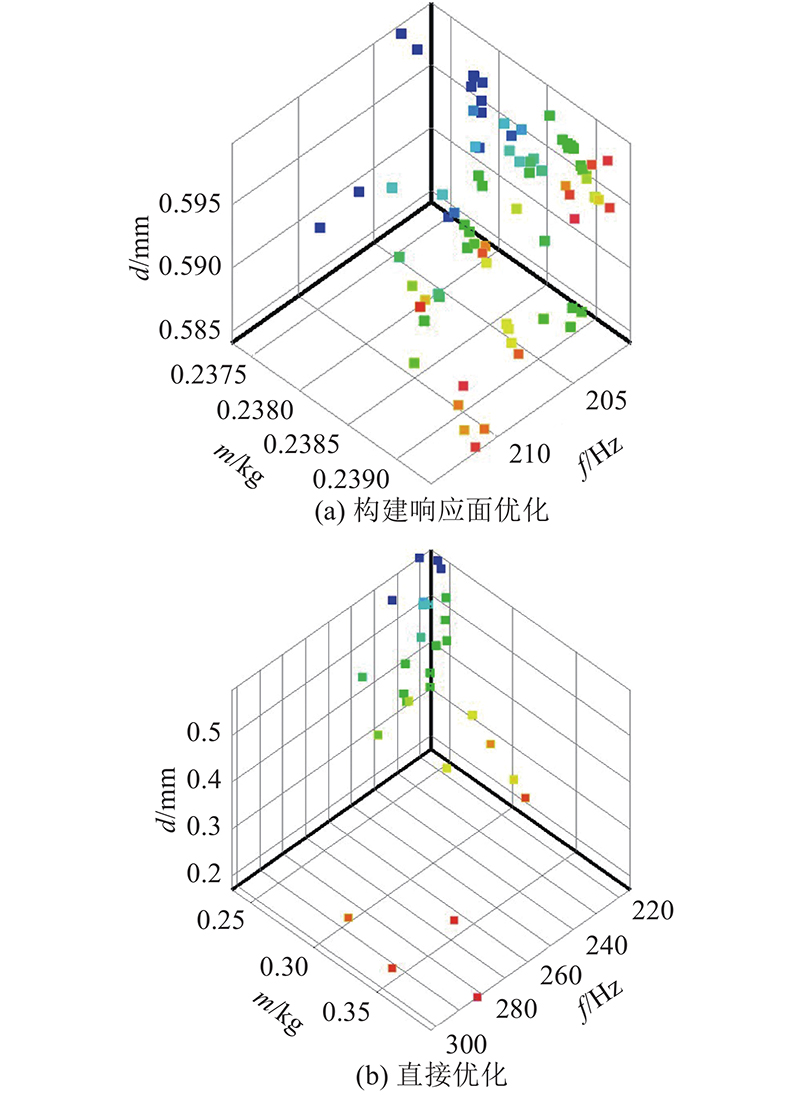
图 10 下层板的优化Pareto解集分布图
Fig.10 Distribution diagram for optimal Pareto solution set for lower plate
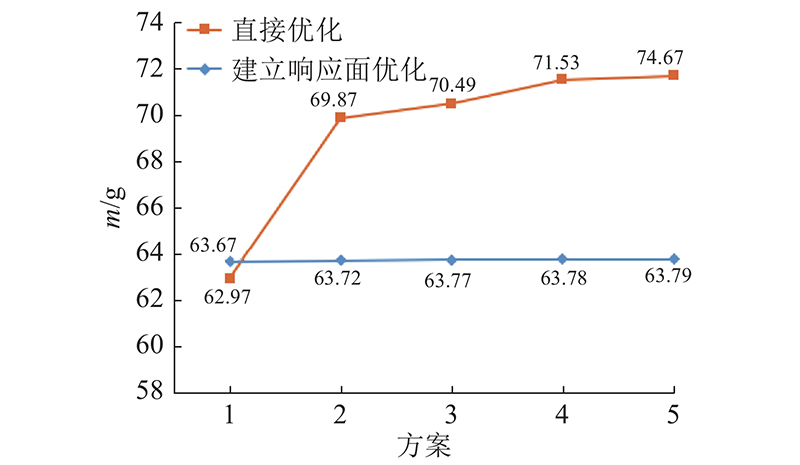
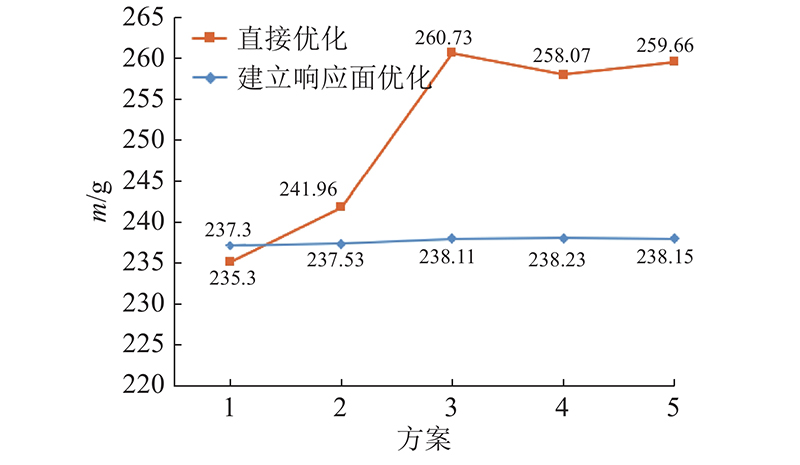
为了进一步比较AS-O直接优化和构建响应面MOGA优化的差异,分别提取上、下层2种方法优化后的5组候选点如 表7~ 10所示,上、下层2种方法优化后的质量对比如 图11、 12所示. 可知,与响应面优化相比,直接优化获得的结果范围更大,构建响应面优化获得的结果更集中; P 1、 P 4的变化(即板厚变化)对最大变形量、一阶固有频率、整体质量的影响都比较大;上、下层板构建响应面优化获得的最轻结构质量分别集中在63.70、238.00 g附近,直接优化获得的最轻结构质量分别在62~72 g、235~261 g;在2种优化方法的优化结果中,上、下层板最轻结构质量分别为62.97、235.30 g,与初始质量相比分别减小78.91、80.09 g,降低55.62%、25.39%.
表 7 上层板的直接优化结果
Tab.7
| 方案 | P 1/mm | P 2/mm | P 3/mm | d/mm | f/Hz | m/g |
| 1 | 1.80 | 30.25 | 30.00 | 0.60 | 257.49 | 62.97 |
| 2 | 1.91 | 23.18 | 32.01 | 0.50 | 274.86 | 69.87 |
| 3 | 1.81 | 42.08 | 32.50 | 0.50 | 261.50 | 70.49 |
| 4 | 1.88 | 27.88 | 33.01 | 0.49 | 271.75 | 71.53 |
| 5 | 2.03 | 25.49 | 30.56 | 0.43 | 290.58 | 71.67 |
| 初始值 | 3.00 | 60.00 | 38.00 | 0.09 | 425.90 | 141.88 |
表 8 上层板的构建响应面优化结果
Tab.8
| 方案 | P 1/mm | P 2/mm | P 3/mm | d/mm | f/Hz | m/g |
| 1 | 1.75 | 43.80 | 30.05 | 0.60 | 248.04 | 63.67 |
| 2 | 1.79 | 35.99 | 30.01 | 0.60 | 255.64 | 63.72 |
| 3 | 1.73 | 47.61 | 30.03 | 0.60 | 244.55 | 63.77 |
| 4 | 1.76 | 43.73 | 30.04 | 0.60 | 248.59 | 63.78 |
| 5 | 1.79 | 37.90 | 30.02 | 0.60 | 254.21 | 63.79 |
| 初始值 | 3.00 | 60.00 | 38.00 | 0.09 | 425.90 | 141.88 |
表 9 下层板的直接优化结果
Tab.9
| 方案 | P 4/mm | P 5/mm | P 6/mm | P 7/mm | P 8/mm | d/mm | f/Hz | m/g |
| 1 | 2.80 | 68.56 | 20.00 | 78.56 | 15.09 | 0.60 | 220.27 | 235.30 |
| 2 | 2.97 | 69.04 | 20.43 | 71.83 | 11.98 | 0.57 | 235.89 | 241.96 |
| 3 | 2.93 | 63.58 | 22.14 | 61.93 | 24.35 | 0.57 | 222.89 | 260.73 |
| 4 | 2.81 | 75.57 | 20.86 | 80.09 | 18.34 | 0.51 | 232.28 | 258.07 |
| 5 | 3.02 | 75.14 | 21.06 | 65.17 | 13.74 | 0.52 | 258.75 | 259.66 |
| 初始值 | 3.00 | 76.00 | 21.00 | 114.00 | 25.50 | 0.33 | 220.05 | 315.39 |
表 10 下层板的构建响应面优化结果
Tab.10
| 方案 | P 4/mm | P 5/mm | P 6/mm | P 7/mm | P 8/mm | d/mm | f/Hz | m/g |
| 1 | 2.93 | 60.86 | 20.12 | 84.66 | 13.85 | 0.60 | 203.19 | 237.30 |
| 2 | 2.92 | 59.41 | 20.21 | 82.54 | 15.47 | 0.60 | 203.60 | 237.53 |
| 3 | 2.93 | 60.86 | 20.28 | 84.96 | 13.81 | 0.60 | 203.03 | 238.11 |
| 4 | 2.96 | 60.86 | 20.04 | 83.23 | 13.45 | 0.59 | 206.02 | 238.23 |
| 5 | 2.93 | 60.86 | 20.34 | 84.66 | 13.81 | 0.60 | 203.22 | 238.15 |
| 初始值 | 3.00 | 76.00 | 21.00 | 114.00 | 25.50 | 0.33 | 220.05 | 315.39 |
图 11
图 11 上层板直接优化与建立响应面优化的质量对比
Fig.11 Comparison of direct optimization results for upper plate and response surface optimization results
图 12
图 12 下层板直接优化与建立响应面优化的质量对比
Fig.12 Comparison of direct optimization results for lower plate and response surface optimization
3.5.4. 优化设计
通过对比2种优化方法对上、下层板的优化结果,结合加工成本和加工工艺,上、下层板参数见 表6.
图 13
4. 试验测试及分析
4.1. 室内试验
如 图14所示,测试装置为天平秤与恒压源. 天平秤:精度为1 g、量程为10 kg. 恒压源:输入电压为220 V交流,输出电压为24 V直流,输出功率为3 000 W.
图 14
4.1.1. 试验结果
在室内,通过试验测试平台测得样机瞬时推力及瞬时电流. 对测得的数据进行整理,推力单位转换为kg,电流乘以恒压转换为电功率,所有测得数据点位置关系,如 图15所示. 以 f( x)= ax 1.5对试验功率与推力数据点进行拟合,试验输入功率与推力关系为
图 15
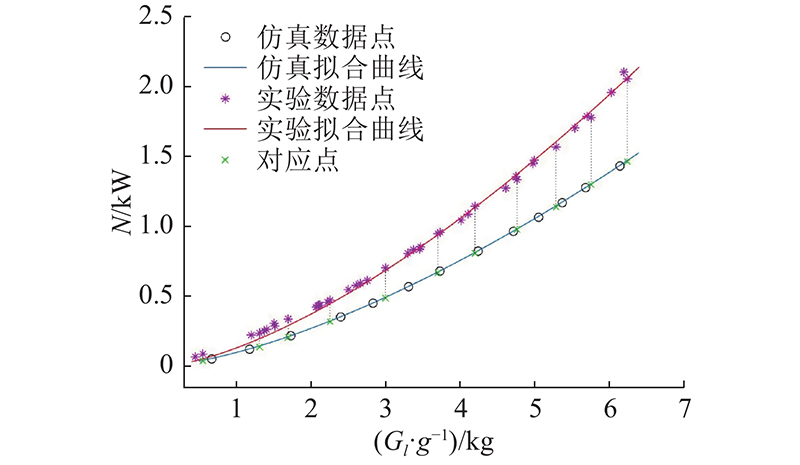
图 15 推力吸附爬壁机器人功率和推力的试验与仿真结果对比
Fig.15 Comparison of experiment and simulation results on power and thrust for thrust adsorption wall-climbing robot
比较仿真数据点拟合曲线和测试数据点拟合曲线,试验拟合曲线上同等推力在仿真拟合曲线上的对应点. 由 图15可以看出,在同推力下,样机试验比仿真耗费更多的功率. 即同等功率下,样机产生的推力小于仿真结果.
为了研究推力吸附机构性能,比较单位功率下旋翼所产生的推力 ψ的试验值 ψ t与仿真值 ψ s. 气动仿真所需功率由转速结合扭矩求得,即输出功率 N s,结合电机最大效率电流模拟仿真电机输入功率
表 11 旋翼推力、功率的试验值和仿真值
Tab.11
| G l / kg | N t / kw | ψ t/ (g · w −1) | N s / kW | N I / kW | ψ s/ (g · w −1) | R ψ | |
| 0.557 | 0.091 | 6.121 | 0.039 | 0.049 | 11.283 | 0.542 | |
| 1.310 | 0.243 | 5.391 | 0.141 | 0.178 | 7.340 | 0.734 | |
| 1.701 | 0.338 | 5.033 | 0.209 | 0.265 | 6.430 | 0.783 | |
| 2.256 | 0.478 | 4.720 | 0.319 | 0.404 | 5.587 | 0.845 | |
| 3.000 | 0.706 | 4.249 | 0.489 | 0.619 | 4.847 | 0.877 | |
| 3.702 | 0.953 | 3.885 | 0.671 | 0.849 | 4.359 | 0.891 | |
| 4.201 | 1.144 | 3.672 | 0.811 | 1.027 | 4.092 | 0.897 | |
| 4.765 | 1.338 | 3.561 | 0.980 | 1.241 | 3.841 | 0.927 | |
| 5.283 | 1.570 | 3.365 | 1.143 | 1.447 | 3.651 | 0.922 | |
| 5.758 | 1.784 | 3.228 | 1.301 | 1.647 | 3.496 | 0.923 | |
| 6.240 | 2.056 | 3.035 | 1.468 | 1.858 | 3.358 | 0.904 |
4.1.2. 安装误差
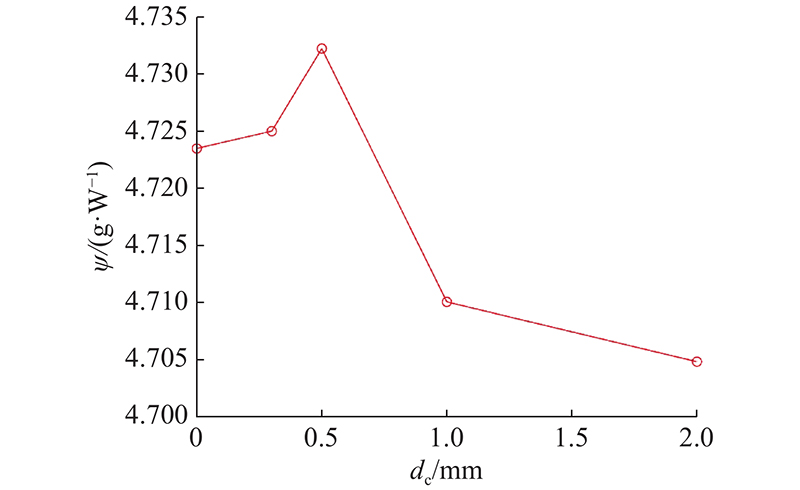
对上、下层旋翼旋转中心轴偏差 d c进行微量变化,比较变化前后仿真模型 ψ, 如 图16所示. 可知, d c与推力吸附机构性能密切相关. 当上、下层旋翼旋转中心轴不共线、存在微量偏差, ψ增大;随着 d c增大, ψ减小.
图 16
当对机器人推力吸附机构旋翼进行组装时,注意上、下层旋翼旋转中心对中,避免由于安装误差而影响推力吸附机构的 ψ. 对其他因素(如翼型变形)造成的 ψ影响,由于翼型改变,上、下层旋翼流场变化过于复杂,本文不展开讨论.
4.2. 室外测试
4.2.1. 工况分析
机器人在不同壁面倾角下的受力情况如 图17所示. 图中, G为机器人自重, β为机器人吸附壁面相对地面的倾角, μ为摩擦系数, F t1、 F t2、 F t3、 F t4分别为不同工况下推力吸附机构提供的推力, f 1、 f 2、 f 3、 f 4分别为个分图中壁面对机器人在点 O 2处的反作用力; l为机器人与墙面接触长度的一半, d为机器人重心距墙距离, l > d.
图 17
图 17 不同倾角状态下的推力吸附爬壁机器人
Fig.17 Thrust adsorption wall-climbing robot under different tilt angles
由于橡胶与混凝土面的摩擦系数不大于0.85,经计算得, F t4最大. F t为推力吸附机构提供的推力;将壁面对机器人的反作用力进行简化,机器人分别在点 O 1 、O 2处受壁面的反作用力. 以 O 1为参考点对机器人力矩情况进行分析:
机器人不发生倾覆,壁面对机器人的反作用力不小于零, f 1 、f 2 、 f 3 、f 4分别不小于零,即:
由式(11)可知,当 β=0°,所需 F t最大, F t≥ G. 当 F t与 F t4值相等时, F t > G , 机器人不发生倾覆. 即当机器人在竖直壁面上时,需推力系统提供的推力最大,竖直壁面是机器人最难停留的倾角壁面.
4.2.2. 试验验证
为了验证样机具备在壁面上的攀爬能力,选竖直壁面验证样机攀爬能力,样机在竖直壁面攀爬,如 图18所示. 可知,样机具备壁面攀爬能力.
图 18
5. 结 论
(1) 介绍共轴式推力吸附爬壁机器人,该机器人由共轴双旋翼提供推力、履带式行走,对推力吸附机构和机架进行优化设计,增强机器人负载能力、降低能耗、增加续航时间.
(2) 完成机器人推力吸附机构优化设计,发现上、下层旋翼流场相互干扰,特别是上层旋翼被下层旋翼严重干扰,当间距比为0.2时,上、下层旋翼流场相互干扰趋于稳定. 当叶片数为4、安装角为(14°,13°)、间距比为0.2时,机器人推力吸附机构综合气动性能相对较好.
(3) 结合流场仿真,求解旋翼表面压力. 旋翼截面压力分布与截面曲率大小成反比;旋翼上表面压力大于下表面;越靠近桨尖,旋翼上、下表面压差越大;下层旋翼推力大于上层旋翼推力.
(4) 完成机器人机架结构的上、下层板参数优化设计,与构建响应面参数优化相比,直接参数优化获得的上、下层板尺寸解集点更分散,全局性更好,分布范围更广,构建响应面参数优化解集点较更集中. 通过参数优化设计,上、下底板整体质量与拓扑结果相比分别降低48.64%、16.98%.
(5) 结合旋翼电机最大效率电流模拟推力吸附机构输入功率,计算并比较 ψ的试验值与仿真值,发现其最大比值接近1,即气动仿真结果可靠. 同时,建立上、下层旋翼旋转中心轴偏差模型,发现中心轴偏差与推力吸附机构 ψ密切相关.
(6) 对在不同倾角壁面上的机器人进行力学分析,机器人在竖直壁面上时所需推力最大;在竖直壁面上对机器人样机性能进行测试,机器人样机具备壁面攀爬能力.
(7) 采用的是相对简单的矩形桨,只对双旋翼的翼型、叶片数、安装角、半径长、上下旋翼间距进行了初步探讨. 对样机进行测试时,当机器人推力吸附机构的旋翼转动后,样机噪声较大且衍生风场较强. 计划对机器人推力吸附机构旋翼桨叶外形进行更深入的研究,选取恰当的旋翼桨叶气动外形,提高机器人推力吸附机构旋翼效能并降低其工作噪声.
参考文献
我国桥梁安全与健康检测监测新技术的发展与应用: 访在役长大桥梁安全与健康国家重点实验室主任张宇峰
[J].DOI:10.3969/j.issn.1672-9889.2020.06.001 [本文引用: 1]
Development and application of new inspection and monitoring technology for bridge safety and health in China: interview with Zhang Yufeng, director of the state key laboratory of safety and health for in-service long span bridge
[J].DOI:10.3969/j.issn.1672-9889.2020.06.001 [本文引用: 1]
Multi-terrain multi-utility robot
[J].DOI:10.1016/j.procs.2018.07.100 [本文引用: 1]
Design and stability analysis of a wall-climbing robot using propulsive force of propeller
[J].DOI:10.3390/sym13010037 [本文引用: 1]
Tele-operated propeller-type climbing robot for inspection of petrochemical vessels
[J].DOI:10.1108/IR-07-2016-0182 [本文引用: 1]
EJBot-II: an optimized skid-steering propeller-type climbing robot with transition mechanism
[J].DOI:10.1080/01691864.2019.1657948 [本文引用: 1]
共轴刚性旋翼非定常气动特性初步试验研究
[J].DOI:10.3969/j.issn.1673-1220.2017.01.003 [本文引用: 1]
Preliminary experimental research on unsteady aerodynamic characteristics of coaxial rigid rotor
[J].DOI:10.3969/j.issn.1673-1220.2017.01.003 [本文引用: 1]
重载机器人横梁结构静动态特性分析与优化
[J].
Static and dynamic characteristic analysis and structure optimization for crossbeam structure of heavy-duty truss robot
[J].
Multi-objective optimization using genetic algorithms: a tutorial
[J].