路径规划作为NP-hard(non-deterministic polynomial-time hard)优化问题,常使用启发式算法来解决[4],其中遗传算法(genetic algorithm, GA)是一种经典的优化算法,在移动机器人领域得到广泛应用. 例如,徐兴等[5]提出引入灾变策略的改进遗传算法,并在移动机器人路径规划中寻找最优路径. Tsai等[6]提出并行精英遗传算法和迁移算子,具有保持种群多样性、抑制过早收敛和保持并行性的优点. 在静态环境下,上述算法能够有效地找到最优路径. 然而,上述算法灵活性不足,移动机器人存在须在不同模式之间切换的情况,如停止、旋转和重新启动,以便沿着多边形线移动. 这种模式切换过程耗时且能量消耗大,并且对于某些任务,平滑运动也是必要的[7]. 因此,除了距离约束外,仍须考虑耗时、节能、机器人速度和路径平滑等优化约束[8-9].
目前应用在移动机器人路径规划问题中的路径平滑技术主要有Bezier曲线、B样条曲线和非均匀有理B样条曲线. 许多学者也提出其他考虑路径平滑性的规划方法,如基于圆弧[10]、杜宾曲线和回旋曲线[11]等. 其中,Bezier曲线、B样条曲线常应用于平滑路径规划问题[12-13]. B样条曲线具有局部控制性质,比Bezier曲线更加灵活,是机器人路径平滑最常用的数学工具. 张伟明等[14]采用B样条曲线对搜索到的路径进行平滑处理,成功消除了路径的折线问题. 刘景森等[15]将蝙蝠算法与三次样条曲线插值实现了规划路径的二阶导的连续性(C2). Li等[16]利用五次B样条曲线生成沿每个坐标轴的运动轨迹,实现C4连续(即四阶连续可导). 通过以上研究分析可以看出,B样条技术在实现路径连续性上具有显著优势,但上述研究并没有考虑路径最短及安全性问题. Song等[17]提出GABE算法,利用GA算法以路径长度最短为目标搜索最优点作为分段Bezier曲线的控制点来生成平滑路径,但规划出的路径仅满足G1连续(即曲线在公共连接点处具有公共的单位切矢). 此外,Tsai等[6,18]用三次B样条技术对规划器生成的初始可行路径进行平滑处理,构造无碰撞连续路径,但都未考虑机器人的移动距离. Li等[19]提出IPSO-SP算法,在粒子群算法的基础上结合三次样条曲线插值实现了规划路径的二阶导的连续性(C2),但规划的平滑路径紧贴障碍物,并不是最安全的. 综上,目前关于通过B样条技术生成平滑路径既满足C2连续还兼顾安全性和最短性的研究并不多,且对于如何避障规划出最短路径也并未给出明确的方法.
为了进一步探索适用于移动机器人实际场景的平滑路径规划方法,本研究提出B样条技术与GA融合的全局路径规划方法,以满足最短路径、安全路径和C2连续性的要求. 本研究的主要创新和贡献如下:1)改进初始种群生成方法,生成具有多样性的初始种群,避免算法在早期陷入局部最优;2)构建带安全距离和路径长度多约束的适应度函数,以引导算法的进化过程;3)设计基于C2连续的三次B样条曲线的路径表示方法,以提高机器人的行驶稳定性.
1. 相关理论
1.1. B样条曲线
B样条曲线(B-spline curve)是基于节点向量和控制点的光滑曲线表示方法,具有较强的曲线表示能力. 其曲线定义[20]如下:
式中:
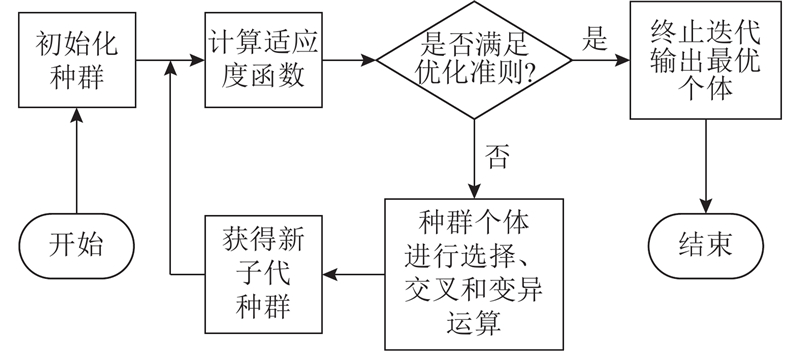
1.2. GA算法
图 1
2. B样条与GA融合的路径规划方法
2.1. 问题表示与编码
提出基于B样条技术的静态区域路径规划方法,其中使用遗传算法来搜索最合适的点作为B样条曲线的控制点P.
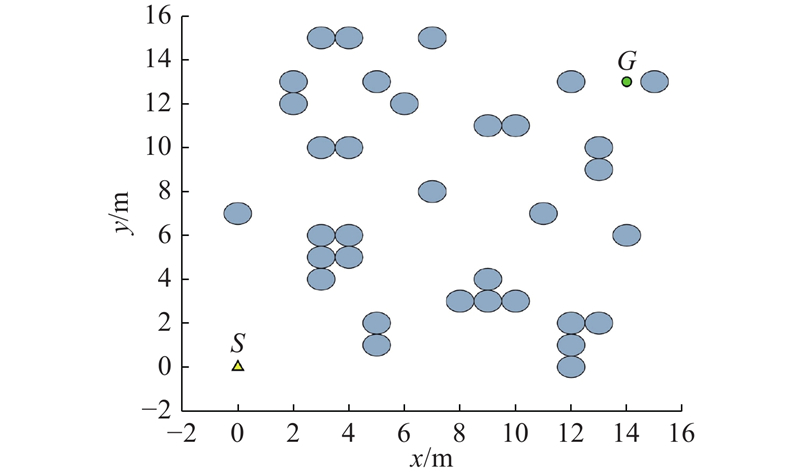
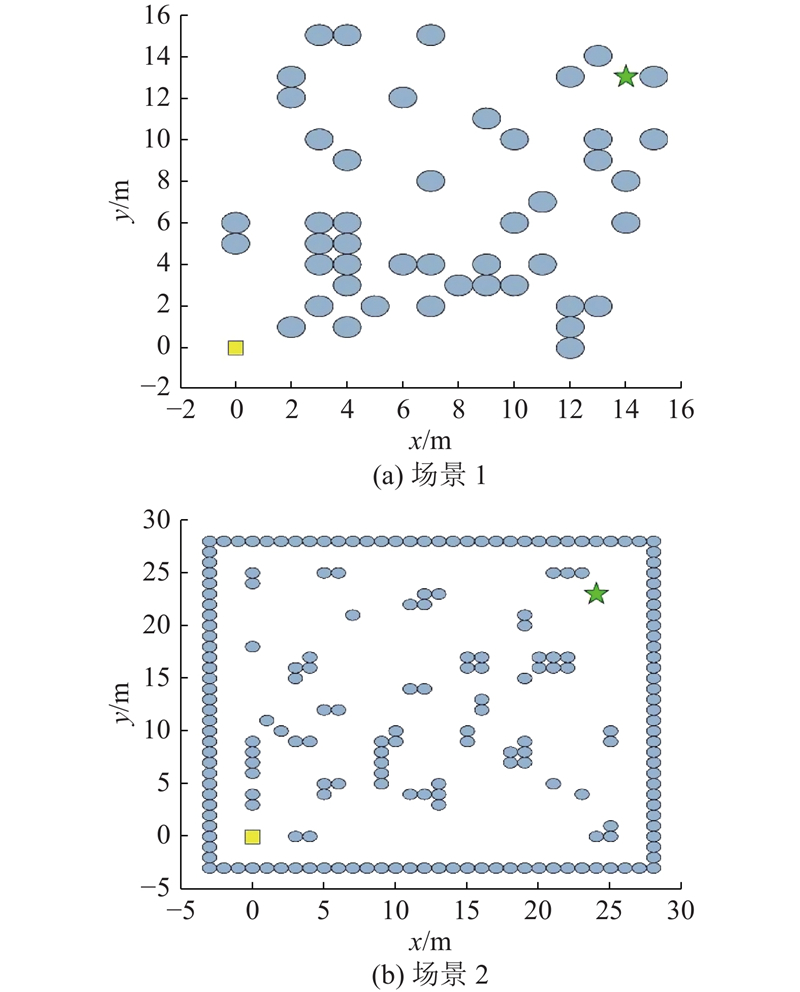
为了给移动机器人导航提供可靠的环境信息并模拟在真实场景中的环境信息,采用二维连续地图对实际场景进行建模,如图2所示. 图中,将真实场景抽象为一个二维平面,并在平面表示各种地理特征和障碍物. 路径规划算法的目标是在不碰撞的前提下,优化起始点S和终点G之间的距离.
图 2
采用实数编码方式,将每个坐标点的x和y坐标作为实数基因. 每条染色体可以表示为一个实数数组,其中每个基因都是一个实数. 上述映射关系如下:
式中:S为坐标数组,I为实数数组,m为矩阵的列向量数,flen( )为矩阵长度计算函数,gres( )为改变矩阵维数函数,[ ]表示指定行向量数.
设一条路径的控制点坐标数组S为一条染色体,记
2.2. 改进初始种群方法
2.2.1. 多目标A*算法
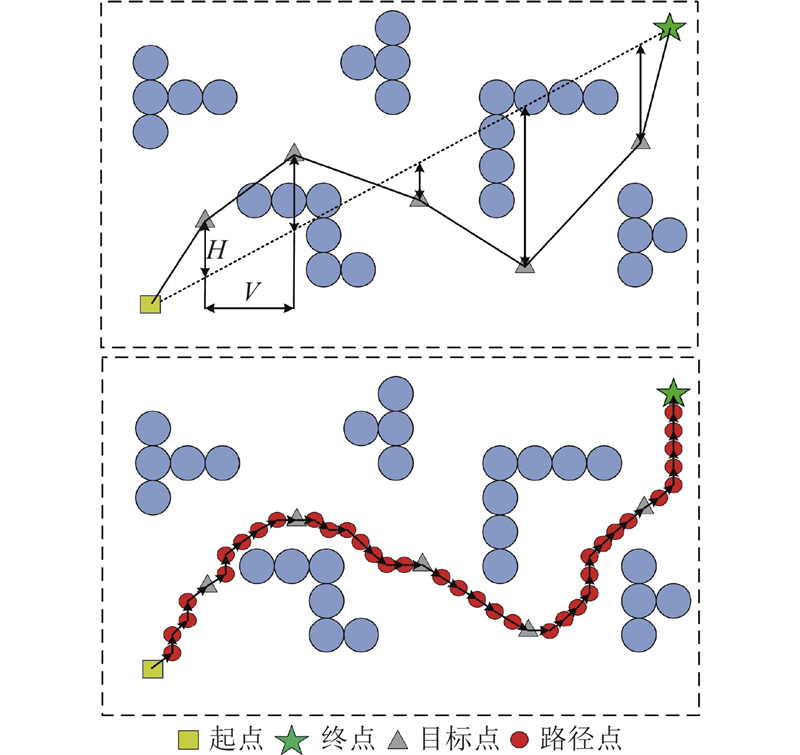
图 3
图 3 基于多目标A*算法生成路径型值点的示意图
Fig.3 Schematic diagram of path-type value points generation based on multi-objective A* algorithm
通过多目标A*生成路径型值点,具体步骤如下:
1)确定路径的起点、终点和基准线. 根据最大纵向范围
2)根据纵向随机范围H和横向随机范围V确定区域,并选择分布在基准线两侧的目标点.
3)采用多目标A*算法[4]联接多个目标点,表达式如下:
式中:Vi、Hi分别为目标点的横、纵坐标;
2.2.2. 生成初始种群
合适的初始化策略可以缓解算法在早期阶段陷入局部最优解. 初始种群缺乏多样性,极易导致进化过程过早收敛到局部最优解附近. 因此,为了增加种群个体的多样性,提高算法初始种群的质量,通过多目标A*算法产生路径型值点. 移动机器人适用于连续的工作环境,而多目标A*算法生成的是一系列离散的从起始状态到目标状态之间的路径点,须重构路径轨迹.
为了便于研究复杂环境中机器人路径轨迹规划的方法,将一条路径轨迹定义为k次B样条曲线. 在已知控制点Pi和节点矢量U=[0,···,0, uk+1, ···, un, 1, ···, 1]的情况下,通过式(1)可以计算曲线上的对应点. 但是,在机器人复杂环境中的路径轨迹规划中,通常只能在二维模型上获取离散的路径型值点,须通过控制点Pi来构成B样条曲线,以便完成后期的算法进化之类的过程.
由于高次插值曲线将带来更多难以给出的边界条件之类的问题,基于实际工程问题需要,在实践中广泛采用三次B样条曲线作为插值曲线,即取k=3,节点矢量端点重复度为4[24]. 因此有u0=u1=u2=u3=0,un+1=un+2=un+3=un+4=1,再确定定义域的内节点值. 在复杂坏境中由多目标A*算法规划出的路径轨迹中会出现按弦长分布不均匀的情况,因此选用积累弦长参数化法对n−1个路径型值点qi(i=0,1,···,n−2)进行参数化,则B样条节点矢量参数如下:
将曲线定义域
式(9)共含n−1个方程和n+1个未知控制顶点. 对于三次B样条曲线,因节点矢量中首末节点取四重节点,则首末控制顶点与首末型值点相重,即
式中:系数矩阵中首行非零元素b1、c1、a1与右端列阵中矢量e1,表示首端点边界条件;末行非零元素cn−1、an−1、bn−1与右端列阵中矢量en−1,表示末端点边界条件. 其余各行元素ai、bi、ci以及右端矢量元素ei (i=2, ···, n−2)满足如下方程:
利用切矢条件构建附加方程系数与右端矢量:
式中:
求解式(10)~(12)便可以得到全部控制顶点.
2.3. 适应度函数设计
综合考虑路径的安全性、最短性和易行性,以达到更加全面和实用的结果. 基于三次B样条设计的路径轨迹具有连续的二阶导数,使得机器人能够平滑地跟随路径,保证了路径的易行性,因此,本研究最优准则应主要考虑路径的安全性和最短性. 这样的综合考虑可以确保所规划的路径不仅具备高度安全性,还能够尽可能地减少行驶距离,提高效率.
根据上述问题,以路径长度和路径安全作为评判指标,建立适应度函数评估种群中个体的优劣. 所提适应度计算方法如下:
式中:Ffit1为路径长度,Ffit2为安全性惩罚函数,w1、w2为权值系数. Ffit1越大,路径个体表现越好.
1)Ffit1采用如下弧长公式计算:
式中:(x(u),y(u))为以u为参数的曲线.
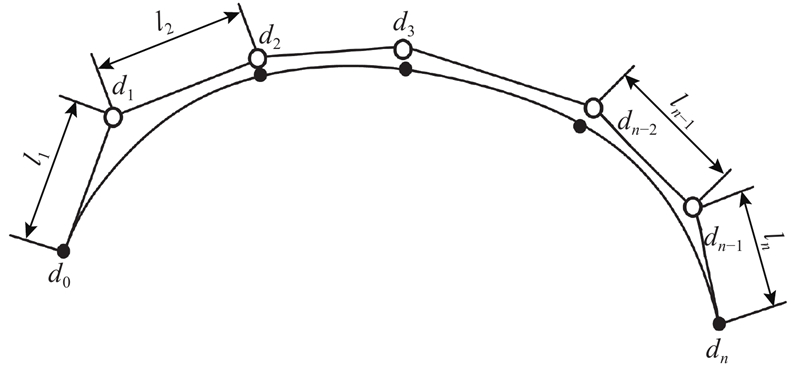
为了计算Ffit1还须确定节点矢量U= [u0, u1, ···, un+k+1]中具体的节点值,采用积累弦长参数化法. 令控制多边形的各边长依次为li=|di−di−1|,i=1, 2, ···, n. 总边长为
图 4
图 4 k次B样条曲线分段连接点与控制多边形的对应关系
Fig.4 Correspondence between k-times B-spline segment connectors and control polygons
2)为了使规划的路径具备安全性,将避障作为适应度函数中的关键因素之一,以优化路径. 为此,构造指数函数将距离映射到实数集R内,定义如下安全性惩罚函数:
式中:Dsafe为安全阈值参数,dmin为路径轨迹与障碍物的最近距离.
式中:x(u)、y(u)由式(1)确定,O为机器人空间的障碍物集合,
2.4. 遗传算子
遗传算子是遗传算法中的重要组成部分,用于模拟生物进化中的遗传操作. 它们通过模拟自然选择、交叉和突变等过程,对种群中的个体进行操作和变换,实现对问题空间的搜索和优化.
1)选择算子. 选择算子筛选出具有更好适应性的个体,提高种群整体的适应度水平. 若个体的选择概率大,则有机会被多次选中,则其遗传基因就会在种群中扩大;优秀基因使得下一代种群具备更优秀的性状,并逐步趋向目标解. 通过不断迭代,优秀基因逐渐累积,种群的适应度逐渐提高,进化过程得以推进. 本研究采用轮盘赌法,其中个体被选择的概率为
式中:
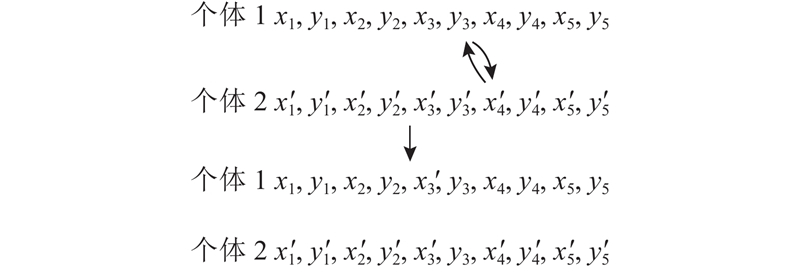
2)交叉算子. 交叉算子是遗传算法中的重要操作,通过引入新的基因组合,打破个体之间的相似性,帮助算法跳出局部最优解,避免陷入早熟状态. 在交叉操作中,采用单点交叉方式,其过程如图5所示. 图中,灰色圈圈是障碍物,正方形是起点,五角星是终点. 交叉点选择2条路径的控制顶点,发生交叉的个体会从基因序列中随机位置对配对的染色体进行基因位变换. 染色体的编码为
图 5
图 5 基于单点交叉方式的交叉过程示意图
Fig.5 Schematic diagram of crossover process based on single-point crossover approach
3)删除算子. 为了缩短染色体的长度L和算法运行时间,新增删除算子. 其主要思想如下:
(a)使用随机数生成器生成一个介于[3, L−2]范围内的随机数r(起点和终点除外).
(b)判定染色体的长度大于设定的阈值,否则结束. 直接执行下一个变异算子.
(c)执行判定随机数r是奇数,否则删除位点r−1和位点r的基因.
(d)删除位点r和位点r+1的基因.
4)变异算子.为了防止遗传算法在优化过程中陷入局部最优解,在搜索过程中,须对个体进行变异. 变异算子采用单点变异法. 对种群个体执行两两配对操作,随机设置一个位置为变异点,如图6所示. 在个体内部交换2个基因的值,最终生成2个新的子代个体.
图 6
图 6 基于单点变异方式的变异操作示意图
Fig.6 Schematic diagram of mutation operation based on single-point mutation approach
2.5. 自适应策略
在传统GA中,交叉概率Pc和变异概率Pm在迭代过程中是定值,当在算法初始阶段设置较大的交叉概率Pc和变异概率Pm时,可以加快淘汰适应度较差个体的速度. 然而,在种群进化的后期,如果保持固定的Pc和Pm,可能会导致算法陷入随机搜索的情况,因为适应度函数值趋向于平均值,并且没有新的个体生成. 因此,本研究引入自适应策略来调整Pc和Pm[25],以提高算法的收敛速度和性能. 自适应策略可以根据种群的适应度情况动态地调整Pc和Pm. 交叉概率Pc和变异概率Pm表达式分别如下:
式中:k1,k2∈[0.3, 1.0],k1<k2;k3,k4∈[0.001,0.100],k3<k4;Fc表示交叉操作父本的适应度,Fmax表示最大适应度,Favg表示平均适应度,Fm表示变异操作父本的适应度.
2.6. 所提算法流程
本研究提出的B样条与遗传算法融合的路径规划算法流程图如图7所示.
图 7
3. 实验结果与分析
图 8
表 1 各算法参数设置
Tab.1
| 方法 | 参数 | 数值 |
| GABE算法/本研究方法 | 种群大小 | 100 |
| 交叉概率 | 0.9 | |
| 变异概率 | 0.1 | |
| 迭代次数 | 200 | |
| IPSO-SP算法 | 种群大小 | 150 |
| 惯性权重 | 0.8 | |
| 个体学习因子c1 全局学习因子c2 | 0.5 | |
| 迭代次数 | 200 |
3.1. 种群生成方法对比
不同初始种群生成方法在4种环境中的规划路径参数比较如表2所示. 表中,t为消耗时间. 从消耗时间可以看出,在小规模地图中,随机法具有一定的优势;随着地图规模的增加,本研究初始化方法的优势逐渐凸显. 从适应度参数来看,本研究初始化方法表现始终最优. 综上,本研究种群初始化方法能够显著提高适应度,缩短消耗时间,并加快算法的收敛速度. 因此,本研究种群初始化方法在路径生成中具有明显的优势.
表 2 不同初始种群生成方法的性能对比
Tab.2
| 地图 | NUM | 随机法 | 随机法+筛选步骤 | 本研究方法 | |||||
| Favg | t/s | Favg | t/s | Favg | t/s | ||||
| 10×10 | 80 | 45 | 125 | 70 | |||||
| 20×20 | 80 | 219 | 297 | 225 | |||||
| 30×30 | 80 | 428 | 510 | 389 | |||||
| 40×40 | 80 | 620 | 713 | 519 | |||||
3.2. 仿真实验1
图 9
图 9 不同算法在场景1的路径规划结果对比
Fig.9 Comparison of path planning results of different algorithms in scenario 1
表 3 各算法在18×18地图上的实验结果对比
Tab.3
| 方法 | Lavg/m | Navg | Pavg | 连续性 |
| GABE算法 | 21.39 | 46 | 0.07 | G1 |
| IPSO-SP算法 | 19.98 | 29 | 0.03 | C2 |
| A*-DWA算法 | 20.73 | — | — | C0 |
| 本研究方法 | 19.59 | 31 | 0.01 | C2 |
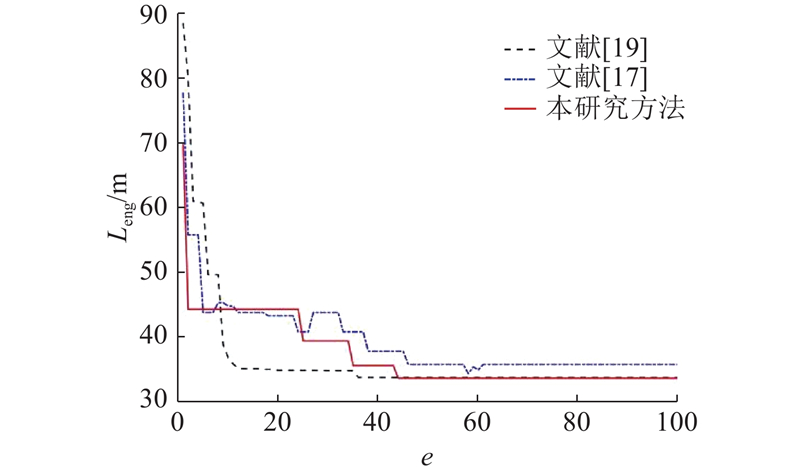
如图10所示为本研究方法与GABE算法、IPSO-SP算法的路径长度变化曲线. 图中,e为迭代次数,Leng为路径长度. 可以看出,GABE算法的平均收敛次数最高,且早熟概率也高,易导致路径质量严重下降. IPSO-SP算法相比GABE算法平均收敛次数减少36.95%,而本研究方法相比GABE算法平均收敛次数减少32.61%. IPSO-SP算法平均收敛次数最低,但早熟率较高. 采用本研究所设计的自适应策略来调整交叉和变异概率能大幅提高算法的收敛速度和性能,并且有效避免算法陷入局部最优解. 至于路径长度方面,本研究算法寻优的路径最短,仅为19.59 m,而GABE算法的平均路径长度比本研究方法长8.42%,同时,A*-DWA算法和IPSO-SP算法比本研究方法的平均路径长度分别长5.50%和1.95%,可以看出,本研究算法的全局寻优能力比IPSO-SP算法强. 本研究方法能在搜索到最短路径的同时减少收敛次数,在多次规划时能有效降低算法早熟概率,且保证路径具有C2连续.
图 10
图 10 场景1下不同算法的路径长度随迭代次数变化曲线对比
Fig.10 Comparison of path length variation curves with iteration number for different algorithms in scenario 1
3.3. 仿真实验2
图 11
图 11 不同算法在场景2的路径规划结果对比
Fig.11 Comparison of path planning results of different algorithms in scenario 2
图 12
图 12 场景2下不同算法的路径长度随迭代次数变化曲线对比
Fig.12 Comparison of path length variation curves with iteration number for different algorithms in scenario 2
表 4 各算法在35×35地图上的实验结果对比
Tab.4
| 方法 | Lavg/m | Navg | Pavg | 连续性 |
| GABE算法 | 61 | 0.22 | G1 | |
| IPSO-SP算法 | 39 | 0.16 | C2 | |
| A*-DWA算法 | — | — | C0 | |
| 本研究方法 | 44 | 0.02 | C2 |
尽管地图场景变大了,4种算法都能规划有效路径. GABE算法最容易陷入局部最优解,且平均收敛次数最高,而本研究方法平均收敛次数为44,相比GABE算法平均收敛次数减少27.87%. IPSO-SP算法具有较高的收敛速度,但同时也伴随着高早熟率的问题,易导致生成的路径质量大幅下降. 本研究设计的交叉和变异算子能有效提高算法的求解速度,同时搜索得到全局最优解. 在路径长度方面,本研究方法求解的平均路径长度最短,仅仅33.82 m,而A*-DWA算法的平均路径比本研究方法长1.89%,同时IPSO-SP算法比本研究方法的平均路径长度长0.38%,再一次验证了本研究方法优异的全局搜索能力.
在连续性方面,A*-DWA算法并不能满足规划出的路径具有C2连续,GABE算法也仅能满足路径的G1连续. 虽然IPSO-SP算法规划的路径具有C2连续,但该方法没有考虑安全问题,易与障碍物碰撞. 而本研究方法能在保证安全性(避障)和路径连续(C2连续)的条件下,使得路径最短.
3.4. 实物实验
图 13
图 13 实验室前期搭建的麦克纳姆轮小车
Fig.13 Mecanum wheel robot constructed in early stage of laboratory
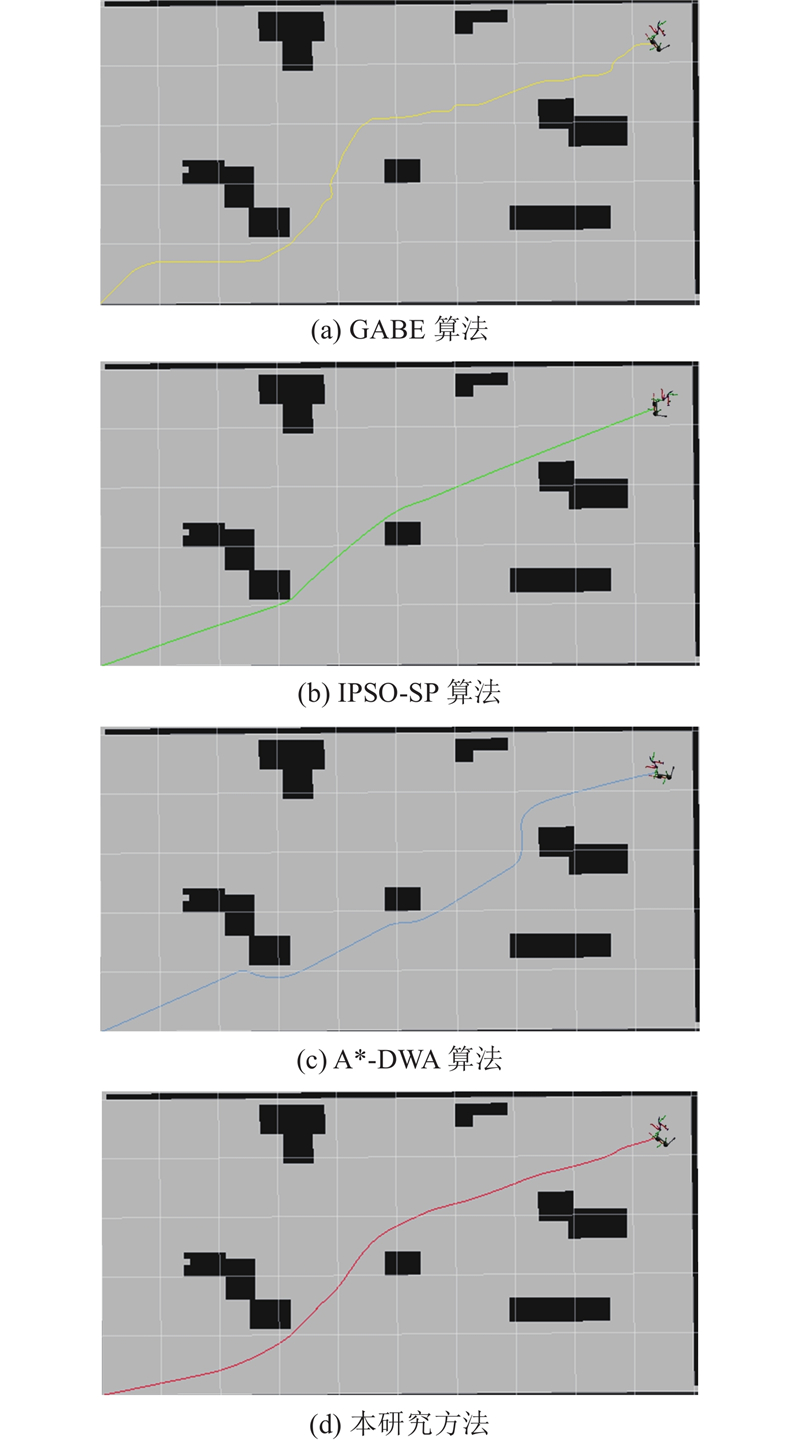
所使用的地图为小车通过激光雷达扫描室内场景,再利用GIMP(GNU Image Manipulation Program)软件修正,存储为.pgm格式的地图. 如图14(a)~(d)所示为所提算法和对比算法的路径规划结果在Rviz(Robot Visualization)上的可视化结果. 可见,通过所提方法和对比方法,小车均能找到一条全局路径,使得车辆能够在规避障碍物的同时抵达目的地. 从路径结果可以看出,GABE算法所规划的路径包含较多冗余部分,会增加导航的复杂性;IPSO-SP算法的路径则过于靠近障碍物,会显著降低导航的安全性,导致机器人与障碍物发生碰撞;A*-DWA算法,没有充分考虑路径的长度和连续性,会降低导航的效率. 与上述方法相比,本研究路径规划可以保证在满足安全距离条件下路径最优且C2连续,有助于提高导航的安全性和效率.
图 14
图 14 4种算法在ROS机器人上的路径可视化结果
Fig.14 Visualization results of four algorithms on ROS robot for path planning
4. 结 语
高效安全的路径规划算法是移动机器人领域的重要技术基础. 针对机器人在复杂障碍物环境中的路径规划问题,提出B样条技术与GA融合的路径规划方法. 设计基于多目标A*算法生成路径型值点以及反求控制点的方法,以增加个体多样性生成优质初始种群,提高算法早期的收敛速度;将安全性和最短路径作为适应度函数的评价指标,来实现起点和终点之间最小化移动距离的连续、安全路径;在进行交叉和变异操作前引入自适应策略调整概率,提升算法的收敛速度和性能,防止算法在进化过程中过早收敛到局部最优解附近. 实验结果表明,在不同类型障碍物环境下,本研究方法相比现有方法收敛更快、不易陷入早熟,规划的路径更短又连续安全,便于移动机器人的运动控制. 所提方法能够有效求解复杂障碍物静态环境中的移动机器人路径规划问题. 未来的工作将着重改进局部搜索过程,解决动态避障问题,并在真实的复杂动态环境中进行更多实验以评估和改进模型的性能.
参考文献
基于改进蚁群算法的移动机器人路径规划
[J].
Mobile robot path planning based on improved ant colony algorithm
[J].
Many-objective evolutionary algorithm based agricultural mobile robot route planning
[J].DOI:10.1016/j.compag.2022.107274
Novel planning methodology for energy stations and networks in regional integrated energy systems
[J].DOI:10.1016/j.enconman.2019.112441 [本文引用: 1]
Research on intelligent disinfection-vehicle system design and its global path planning
[J].DOI:10.3390/electronics12071514 [本文引用: 3]
基于改进遗传算法的移动机器人全局路径规划
[J].
Global path planning for mobile robots based on improved genetic algorithm
[J].
Parallel elite genetic algorithm and its application to global path planning for autonomous robot navigation
[J].DOI:10.1109/TIE.2011.2109332 [本文引用: 2]
Bezier curve based smooth path planning for mobile robot
[J].
基于人工蜂群-自适应遗传算法的仓储机器人路径规划
[J].
Path planning for warehouse robot based on the artificial bee colony-adaptive genetic algorithm
[J].
A new fuzzy Bezier curve modeling by using fuzzy control point relation
[J].
Three-dimensional autonomous obstacle avoidance algorithm for UAV based on circular arc trajectory
[J].
Path smoothing techniques in robot navigation: state-of-the-art, current and future challenges
[J].DOI:10.3390/s18093170 [本文引用: 1]
满足曲率约束的B样条曲线连续路径平滑方法
[J].
Continuous path smoothing method of B-spline curve satisfying curvature constraint
[J].
A continuous RRT*-based path planning method for non-holonomic mobile robots using B-spline curves
[J].DOI:10.1007/s12652-021-03625-8 [本文引用: 2]
基于改进RRT~*算法的移动机器人路径规划
[J].
Mobile robot path planning based on improved RRT* algorithm
[J].
基于改进蝙蝠算法和三次样条插值的机器人路径规划
[J].
Robot path planning based on improved bat algorithm and cubic spline interpolation
[J].
An approach for smooth trajectory planning of high-speed pick-and-place parallel robots using quintic B-splines
[J].DOI:10.1016/j.mechmachtheory.2018.04.026 [本文引用: 1]
A new genetic algorithm approach to smooth path planning for mobile robots
[J].DOI:10.1108/AA-11-2015-094 [本文引用: 2]
Collision-free and smooth trajectory computation in cluttered environments
[J].DOI:10.1177/0278364912453186 [本文引用: 1]
Genetic algorithms
[J].DOI:10.1038/scientificamerican0792-66 [本文引用: 1]
改进链式多种群遗传算法的防空火力任务分配
[J].
Air defense firepower task assignment based on improved chainlike multi-population genetic algorithm
[J].
基于改进多目标自适应遗传算法的机器人路径规划
[J].
Robot path planning based on improved multi-objective adaptive genetic algorithm
[J].
Local corner smoothing transition algorithm based on double cubic nurbs for five-axis linear tool path
[J].DOI:10.5545/sv-jme.2016.3525 [本文引用: 2]
Optimal reactive power dispatch using an adaptive genetic algorithm
[J].DOI:10.1016/S0142-0615(98)00016-7 [本文引用: 1]