非确定性多项式时间困难(nondeterministic polynomial-time hard)问题是指在多项式时间内无法找到最优解,但可以在多项式时间内验证任何一个解是否正确的问题[4]. 多UAV协同路径规划属于NP-Hard问题中的一种,该问题需要在有限的计算能力和较优的路径之间寻求平衡. 启发式优化算法内在的并行能力和随机性特点使其在这种平衡中展现了优秀的寻优能力,一系列的启发式优化算法已经被证明可用于处理复杂多约束路径规划问题. Zhang等[5]提出改进的果蝇优化算法(ө-MAFOA)来解决UAV规划问题,采用突变适应机制增强果蝇算法在开发阶段和探索阶段之间的平衡,利用基于相位角的编码策略实现快速收敛. Qu等[6]针对UAV路径规划问题,结合简化的灰狼算法(SGWO)和改进的共生生物搜索算法(MSOS),提出新的混合算法(HSGWO-MSOS). 该算法加快了收敛速度,保持了种群探索能力,提高了算法的开发能力. Duan等[7]提出将蚁群算法(ACO)和差分进化算法(DE)混合的算法(ACODE),解决无人作战飞行器的三维路径规划问题,该算法在加快全局收敛速度的同时,保证了蚁群算法的鲁棒性.
黏菌算法(slime mould algorithm,SMA)具有原理简单、调节参数少、便于实现、寻优效率高等优点,但原始的SMA存在易陷入局部最优以及开发和探索阶段之间不平衡的局限性[8]. 针对上述问题,本文提出基于SMA的改进黏菌蜂群混合算法(ISMABC),对原始SMA存在的局部最优及不平衡问题进行优化.
1. 路径规划问题的描述
1.1. 路径规划原理
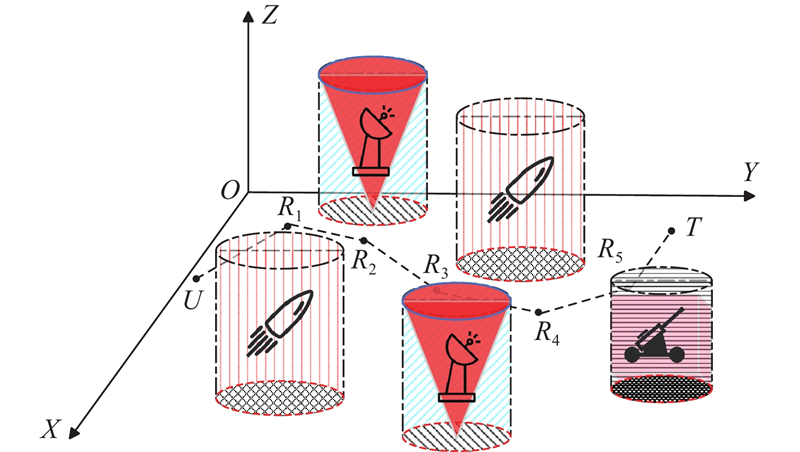
本文的目的是在战场仿真环境中规划出可供多架无人机飞行的路径. 通过对威胁源和地形进行仿真建模,构建基本的战场环境. 战场环境由基本的雷达、火炮、导弹等威胁源构成. 上述3种威胁源的威胁原理均不相同,但其影响范围可以分别近似为圆锥体、圆柱体和正方体. 将上述3种威胁源统一处理为具有不同半径的圆柱体,这种处理方式既保留了威胁源的基本特性,又极大简化了建模的复杂性. 路径规划的定义是指在已知的环境内规划出一条从出发点U到目标点T的最优路径. 采用离散的路径点表示轨迹,通过将路径点(U, R1, R2,
图 1
1.2. 约束条件和适应度函数
为了规划出可供无人机飞行的高质量路径,需要建立合适的适应度函数,考虑各种飞行约束条件. 在静态三维全局路径规划中,主要包含2个部分:第一部分是适应度函数;另一部分是各种约束条件,如偏航角、俯仰角和安全距离等.
1.2.1. 路径长度、飞行高度
路径长度是由一系列路径点组成的,UAV的路径长度适应度函数定义为
式中:
UAV在穿越战场环境时,可以利用地形作为掩护,降低被防空系统发现的概率. 对飞行高度进行积分,使UAV倾向于低空航路. UAV的路径高度约束定义为
式中:
1.2.2. 禁飞区域、地形威胁
在战场环境中,禁飞区可以表示为被雷达、导弹、火炮等覆盖的区域. 使用半径不同的圆柱体来表述上述威胁源. 将UAV禁飞区的适应度函数定义为
式中:
当UAV与地形发生碰撞时,付出的代价是极其高昂的. 将UAV受到地形威胁的适应度函数定义为
若路径点不与地形碰撞,则该约束代价为0,否则代价为
1.2.3. 路径平滑
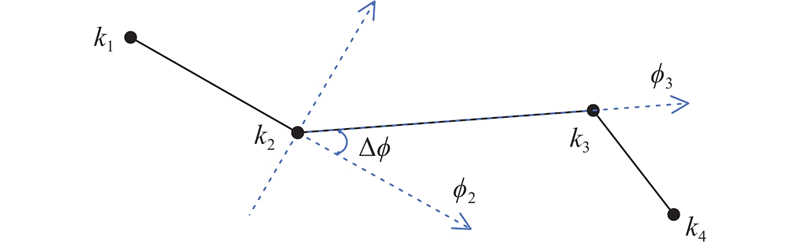
由于UAV自身性能的限制,需要对俯仰角、航向角加以限制. 当UAV飞行姿态变化时,UAV的能量消耗会明显增加. 为了减小能量损耗,对UAV的俯仰角和偏航角约束如下.
式中:
式中:
图 2
1.2.4. 协同约束
在多UAV协同路径规划中,空间约束要求每架UAV之间的距离在安全范围内. 假设
式中:
多UAV协同意味着每架UAV到达目标点所需的时间应满足一定的条件. 假设每架UAV同时到达目标点,则说明在分别考虑了每个UAV的速度变化范围和飞行距离后,每架UAV可以同时到达. 假设UAV
这说明只有当每架UAV的到达时间间隔重叠时,多UAV协同才可以实现.
综上所述,UAV的总体路径成本为
式中:
对于多UAV协同路径规划,采用ISMABC优化算法求解代价函数,使得路径满足飞行限制约束及UAV性能约束. 建立的模型如下:
式中:
2. 多无人机协同路径规划问题的求解
2.1. 黏菌算法
黏菌算法是由Li等[9]提出的新型仿生优化算法. 该算法的数学模型主要包括2个阶段:探索阶段和开发阶段.
2.1.1. 探索阶段
黏菌可以根据空气中的气味接近食物,其收缩模式描述如下:
式中:
其中
式中:
2.1.2. 开发阶段
即使黏菌找到了更好的食物来源,它们仍然会分离一些个体探索其他区域,试图寻找更高质量的食物来源. 黏菌种群更新位置的数学模型为
式中:
2.2. 改进的黏菌蜂群混合算法
采用佳点集对SMA算法的初始种群进行重新分布,有利于扩大搜索范围,提高算法的精度. 为了提高算法的收敛速度,引入非线性反馈因子. 在利用精英反向学习策略寻找到全局最优后,考虑到人工蜂群算法(artificial bee colony,ABC)[10]具有强大的搜索能力,引入全局最优位置引导,提高算法的开发能力.
许多启发式优化算法都是在搜索空间内随机生成种群位置,导致在迭代后期存在个体多样性减小的问题. 佳点集可以在搜索空间中均匀取点,有助于避免个体之间的交叉或重叠,提高种群的多样性. 本文采用佳点集初始化种群.
反馈因子
式中:
针对反向学习策略生成的反向解不一定比当前搜索空间更容易搜索到全局最优解这一问题,Yildiz等[11]提出精英反向学习(elite opposition-based learning,EOBL). 该策略对当前种群中的精英个体构造反向种群,增加种群的多样性,从当前种群和反向种群构成的新种群中选取最优个体作为新一代个体,进入下一次迭代. 本文计算并比较所有个体的适应度,针对全局适应度最好的个体采用精英反向策略,提高种群质量和全局收敛速度.
针对黏菌算法易陷入局部最优的特点,引入人工蜂群算法,并对其作出改进. 基本的人工蜂群搜索策略的数学模型如下:
式中:
式中:
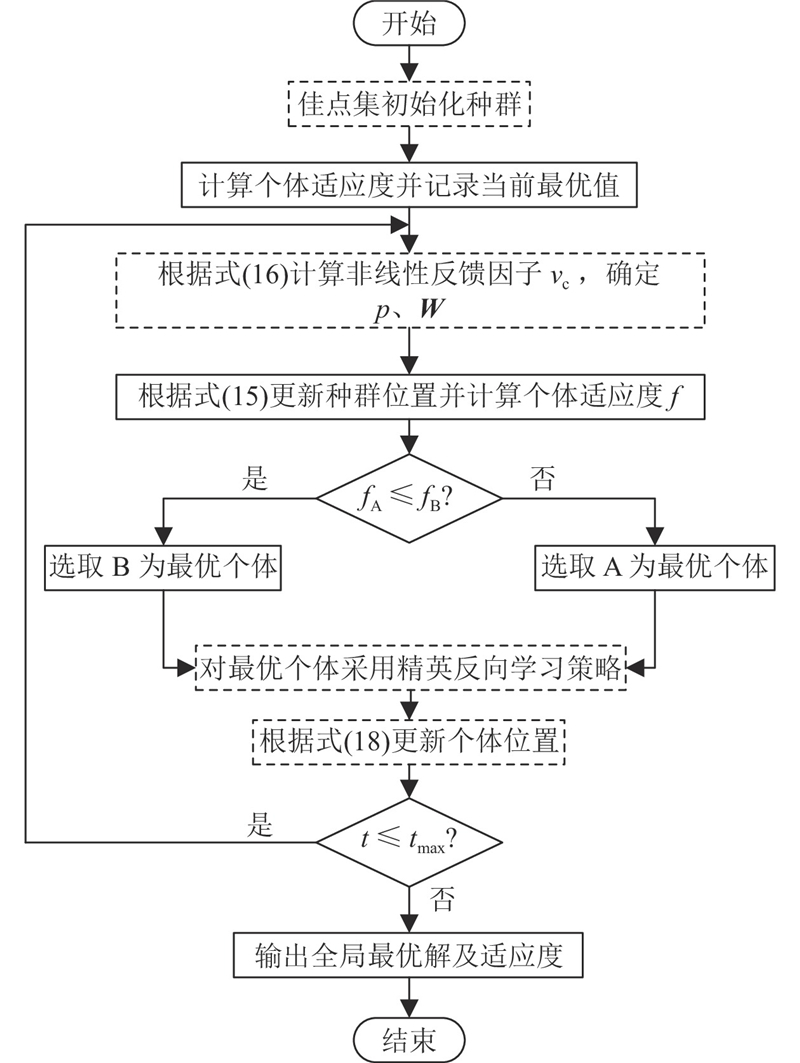
2.3. 利用ISMABC求解多无人机协同路径规划的流程
利用ISMABC算法求解多UAV协同路径规划问题,流程如图3所示. 图中,虚线框表示本文改进的内容. 流程归纳为如下步骤.
图 3
1)利用佳点集初始化黏菌种群. 确定搜索空间的黏菌数量及最大迭代次数
2)计算黏菌种群中每只黏菌个体的适应度
3)利用式(16)计算非线性收敛因子
4)通过式(15)更新黏菌种群的位置.
5)计算并比较个体适应度
6)对最优个体采用精英反向学习策略,提高种群多样性和种群质量.
7)根据式(18)更新种群位置,跳出局部最优.
3. 算法验证与仿真实验
3.1. 算法验证
为了验证ISMABC算法的有效性与优越性,选择SMA[9]、ABC[10]、HHO[12]、GWO[13]、WOA[14]、SSA[15]6种算法进行对比分析. 为了保证公平,在相同的实验平台上,所有的算法迭代次数设置为300,种群规模设置为30,各算法参数与原文献保持一致. 取23个基本测试函数[13]中的单峰测试函数
表 1 单峰函数的测试结果
Tab.1
| 算法 | 函数 | 最优值 | 平均值 | 方差 | 耗时均值/s |
| HHO | 4.21×10−75 | 3.49×10−58 | 1.16×10−113 | 3.07×10−2 | |
| 1.95×10−39 | 3.49×10−31 | 3.33×10−60 | 3.09×10−2 | ||
| 3.67×10−70 | 8.87×10−43 | 7.78×10−83 | 0.151 | ||
| 4.22×10−39 | 9.78×10−31 | 2.44×10−59 | 3.76×10−2 | ||
| 1.23×10−5 | 2.55×10−4 | 7.59×10−8 | 6.01×10−2 | ||
| ABC | 2.65×10−22 | 1.51×10−18 | 1.43×10−69 | 0.192 | |
| 2.20×10−22 | 2.77×10−19 | 3.43×10−42 | 0.197 | ||
| 2.22×10−29 | 2.35×10−25 | 2.21×10−54 | 0.304 | ||
| 2.99×10−18 | 7.12×10−15 | 3.32×10−39 | 0.199 | ||
| 0.212 | 0.577 | 2.82×10−2 | 0.208 | ||
| GWO | 5.09×10−17 | 4.35×10−15 | 4.33×10−29 | 4.02×10−2 | |
| 2.05×10−10 | 4.19×10−9 | 2.25×10−14 | 4.09×10−2 | ||
| 5.69×10−4 | 0.615 | 2.30×10−2 | 8.93×10−2 | ||
| 5.53×10−5 | 8.75×10−4 | 3.44×10−7 | 4.01×10−2 | ||
| 9.95×10−4 | 3.60×10−3 | 2.40×10−6 | 4.63×10−2 | ||
| WOA | 5.21×10−53 | 2.36×10−41 | 4.39×10−80 | 1.44×10-2 | |
| 1.12×10−35 | 2.77×10−29 | 2.57×10−40 | 1.52×10-2 | ||
| 3.04×104 | 6.45×104 | 2.73×108 | 6.36×10-2 | ||
| 3.60×102 | 52.3 | 7.00×102 | 1.44×10-2 | ||
| 7.07×10−5 | 5.80×10−3 | 4.50×10−5 | 2.07×10-2 | ||
| SSA | 0 | 1.09×10−69 | 1.16×10−136 | 9.31×10−2 | |
| 0 | 1.26×10−34 | 1.60×10−66 | 9.49×10−2 | ||
| 0 | 1.38×10−59 | 1.29×10−116 | 0.191 | ||
| 0 | 2.13×10−32 | 2.25×10−62 | 9.28×10−2 | ||
| 1.50×10−5 | 4.18×10−4 | 1.05×10−7 | 0.105 | ||
| SMA | 0 | 7.77×10−222 | 0 | 0.120 | |
| 1.00×10−196 | 6.40×10−99 | 4.75×10−190 | 0.120 | ||
| 0 | 8.09×10−239 | 0 | 0.170 | ||
| 4.21×10−216 | 9.06×10−112 | 8.21×10−221 | 0.120 | ||
| 7.77×10−5 | 2.74×10−4 | 4.81×10−8 | 0.129 | ||
| ISMABC | 0 | 0 | 0 | 0.113 | |
| 0 | 0 | 0 | 0.115 | ||
| 0 | 0 | 0 | 0.216 | ||
| 0 | 0 | 0 | 0.113 | ||
| 2.01×10-7 | 8.65×10-5 | 5.52×10-9 | 0.127 |
表 2 多峰函数的测试结果
Tab.2
| 算法 | 函数 | 最优值 | 平均值 | 方差 | 耗时均值/s |
| HHO | −1.26×104 | −1.25×104 | 2.92×105 | 6.25×10−2 | |
| 0 | 0 | 0 | 5.10×10−2 | ||
| 8.88×10−16 | 8.88×10−16 | 0 | 5.22×10−2 | ||
| 0 | 0 | 0 | 6.22×10−2 | ||
| ABC | −6.28×103 | −4.84×103 | 1.50×105 | 2.21×10−2 | |
| 1.94×102 | 2.42×102 | 2.70×102 | 0.211 | ||
| 3.90 | 5.31 | 0.513 | 0.211 | ||
| 1.43 | 2.08 | 0.121 | 0.219 | ||
| GWO | −8.42×103 | −5.85×103 | 8.44×105 | 4.77×10−2 | |
| 2.05×10−12 | 6.97 | 28.2 | 4.30×10−2 | ||
| 2.25×10−9 | 1.15×10−8 | 4.08×10−17 | 4.33×10−2 | ||
| 2.66×10−15 | 6.00×10−3 | 1.19×10−4 | 4.81×10−2 | ||
| WOA | −1.26×104 | −1.01×104 | 3.32×106 | 2.14×10−2 | |
| 0 | 1.00×10−2 | 1.10×10−2 | 1.67×10−2 | ||
| 8.88×10−16 | 6.32×10−15 | 1.13×10−29 | 1.76×10−2 | ||
| 0 | 1.40×10−2 | 4.00×10−3 | 2.18×10−2 | ||
| SSA | −1.26×104 | −8.64×103 | 6.05×106 | 0.106 | |
| 0 | 0 | 0 | 9.66×10−2 | ||
| 8.88×10−16 | 8.88×10−16 | 0 | 9.83×10−2 | ||
| 0 | 0 | 0 | 0.106 | ||
| SMA | −1.26×104 | −1.26×104 | 2.27 | 0.131 | |
| 0 | 0 | 0 | 0.124 | ||
| 8.88×10−16 | 8.88×10−16 | 0 | 0.126 | ||
| 0 | 0 | 0 | 0.130 | ||
| ISMABC | −1.26×104 | −1.26×104 | 3.70×10−2 | 0.132 | |
| 0 | 0 | 0 | 0.117 | ||
| 8.88×10−16 | 8.88×10−16 | 0 | 0.119 | ||
| 0 | 0 | 0 | 0.128 |
表 3 固定维度函数的测试结果
Tab.3
| 算法 | 函数 | 最优值 | 平均值 | 方差 | 耗时均值/s |
| HHO | 0.998 | 1.56 | 1.52 | 4.02×10−1 | |
| −1.03 | −1.03 | 2.90×10−16 | 3.68×10−2 | ||
| −10.1 | −5.23 | 0.837 | 4.92×10−2 | ||
| −10.3 | −5.27 | 0.892 | 5.53×10−2 | ||
| −5.13 | −4.99 | 0.360 | 6.28×10−2 | ||
| ABC | 0.998 | 1.01 | 7.00×10−3 | 0.519 | |
| −1.03 | −1.03 | 5.09×10−13 | 0.192 | ||
| −10.2 | −9.45 | 2.70 | 0.210 | ||
| −10.4 | −10.2 | 0.713 | 0.218 | ||
| −10.5 | −10.5 | 3.86×10−8 | 0.227 | ||
| GWO | 0.998 | 4.84 | 17.6 | 0.159 | |
| −1.03 | −1.03 | 3.19×10−15 | 1.36×10−2 | ||
| −10.2 | −9.04 | 5.54 | 1.98×10−2 | ||
| −10.4 | 10.4 | 0.826 | 2.25×10−2 | ||
| −10.5 | −1.02×101 | 2.21 | 2.53×10−2 | ||
| WOA | 0.998 | 3.26 | 10.3 | 0.158 | |
| −1.03 | −1.03 | 7.56×10−17 | 1.28×10−2 | ||
| −10.2 | −7.70 | 7.74 | 1.72×10−2 | ||
| −10.4 | −7.24 | 8.81 | 2.00×10−2 | ||
| −10.5 | −6.63 | 10.3 | 2.28×10−2 | ||
| SSA | 0.998 | 9.24 | 22.6 | 0.320 | |
| −1.03 | −1.03 | 7.08×10−17 | 2.99×10−2 | ||
| −10.2 | −9.93 | 1.00 | 4.33×10−2 | ||
| −10.4 | −10.3 | 0.658 | 4.85×10−2 | ||
| −10.5 | −10.5 | 0.282 | 5.47×10−2 | ||
| SMA | 0.998 | 0.998 | 3.29×10−23 | 0.206 | |
| −1.03 | −1.03 | 6.22×10−17 | 5.79×10−2 | ||
| −10.2 | −10.2 | 3.85×10−7 | 6.85×10−2 | ||
| −10.4 | −10.4 | 8.64×10−7 | 7.13×10−2 | ||
| −10.5 | −10.5 | 3.25×10−7 | 7.45×10−2 | ||
| ISMABC | 0.998 | 0.998 | 2.18×10−28 | 0.359 | |
| −1.03 | −1.03 | 2.65×10−20 | 6.03×10−2 | ||
| −10.2 | −10.2 | 7.85×10−9 | 7.64×10−2 | ||
| −10.4 | −10.4 | 3.61×10−9 | 8.12×10−2 | ||
| −10.5 | −10.5 | 9.01×10−9 | 8.77×10−2 |
表 4 CEC2017测试集算法的比较结果
Tab.4
| 函数 | WOA | SSA | HHO | SMA | ISMABC | |||||||||
| 平均值 | 标准差 | 平均值 | 标准差 | 平均值 | 标准差 | 平均值 | 标准差 | 平均值 | 标准差 | |||||
| CEC01 | 1.73×1010 | 5.77×109 | 1.23×1010 | 5.78×109 | 2.19×107 | 2.40×107 | 5.38×106 | 1.56×107 | 5.98×102 | 7.72×102 | ||||
| CEC03 | 6.81×104 | 9.62×103 | 4.62×104 | 1.79×104 | 6.41×104 | 1.58×104 | 4.58×104 | 9.99×103 | 2.02×104 | 2.56×103 | ||||
| CEC06 | 6.06×102 | 6.51 | 6.93×102 | 1.21 | 6.39×102 | 18.6 | 6.24×102 | 8.63 | 6.13×102 | 1.57×10−13 | ||||
| CEC07 | 1.53×103 | 62.3 | 1.73×103 | 50.3 | 1.98×102 | 51.6 | 9.42×102 | 51.9 | 7.69×102 | 1.85 | ||||
| CEC12 | 9.31×108 | 1.95×109 | 1.16×109 | 1.86×109 | 1.99×106 | 1.31×106 | 1.13×106 | 9.47×105 | 4.21×105 | 2.05×105 | ||||
| CEC14 | 1.29×106 | 1.97×106 | 2.37×104 | 2.76×104 | 3.14×104 | 3.79×104 | 4.74×104 | 5.67×104 | 1.39×105 | 6.21×104 | ||||
| CEC19 | 1.09×107 | 1.13×107 | 1.45×106 | 1.92×106 | 8.65×103 | 7.32×103 | 9.73×103 | 1.97×104 | 3.91×103 | 1.85×103 | ||||
| CEC26 | 6.13×103 | 6.25×102 | 7.18×103 | 1.64×103 | 5.48×103 | 1.23×103 | 2.89×103 | 79.5 | 3.31×103 | 2.17×102 | ||||
| CEC28 | 3.92×103 | 2.99×102 | 4.48×103 | 4.27×102 | 3.46×103 | 39.1 | 3.27×103 | 1.29×103 | 3.20×103 | 13.9 | ||||
| CEC30 | 4.86×107 | 3.66×107 | 1.44×107 | 8.41×106 | 2.94×104 | 3.83×104 | 1.23×105 | 2.67×105 | 7.16×103 | 1.49×103 | ||||
从表4可知,当求解单峰CEC01、CEC03函数时,ISMABC算法相对于其他4种对比算法表现优秀. 当求解简单多峰函数CEC06、CEC07、CEC012时,ISMABC算法均优于对比算法. 当求解混合函数CEC14时,ISMABC不如SSA算法. 当求解组合函数CEC26时,ISMABC算法的表现不如SMA算法. 当求解CEC28、CEC30时,ISMABC算法的平均值和标准差均优于对比算法. 综上所述,当利用ISMABC算法求解测试函数时,在大多数测试函数中得到的结果相比于其他算法更优,表明ISMABC算法相对于其他算法具有更高的寻优能力及收敛速度.
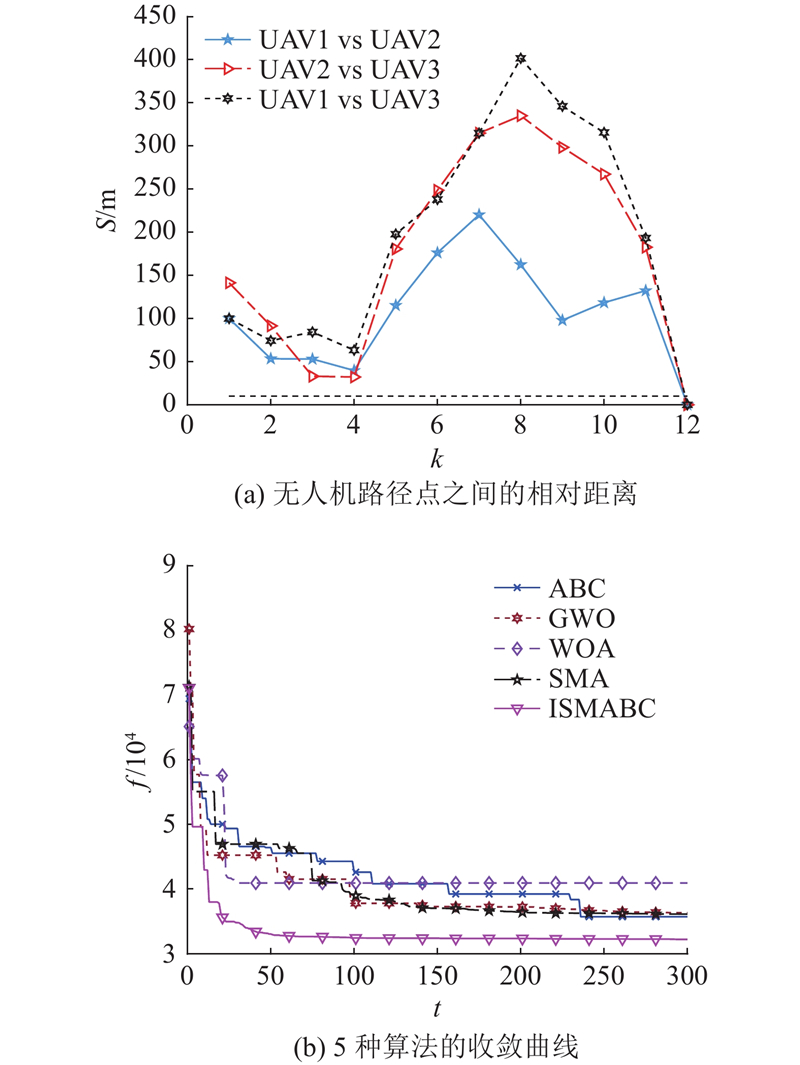
为了对ISMABC的收敛性能进行验证,利用7种算法独立求解
图 4
图 4 ISMABC 及6种对比算法的收敛曲线
Fig.4 Convergence curve of ISMABC and six comparison algorithms
3.2. 仿真实验
在MATLAB上构建三维仿真环境,开展路径规划实验. 将算法的迭代次数均设置为300,种群规模设置为30,各算法的参数与原文献保持一致. 在3个场景下进行仿真实验. 其中一个是地形环境(场景1),第2个是在稀疏禁飞区环境下(场景2),第3个是在密集禁飞区环境下(场景3). 仿真规划面积为
表 5 UAV起点和目标点
Tab.5
| UAV | 起点坐标 | 目标点坐标 |
| UAV1 | (50, 150, 50) | (900, 900, 50) |
| UAV2 | (150, 150, 50) | (900, 900, 50) |
| UAV3 | (150, 50, 50) | (900, 900, 50) |
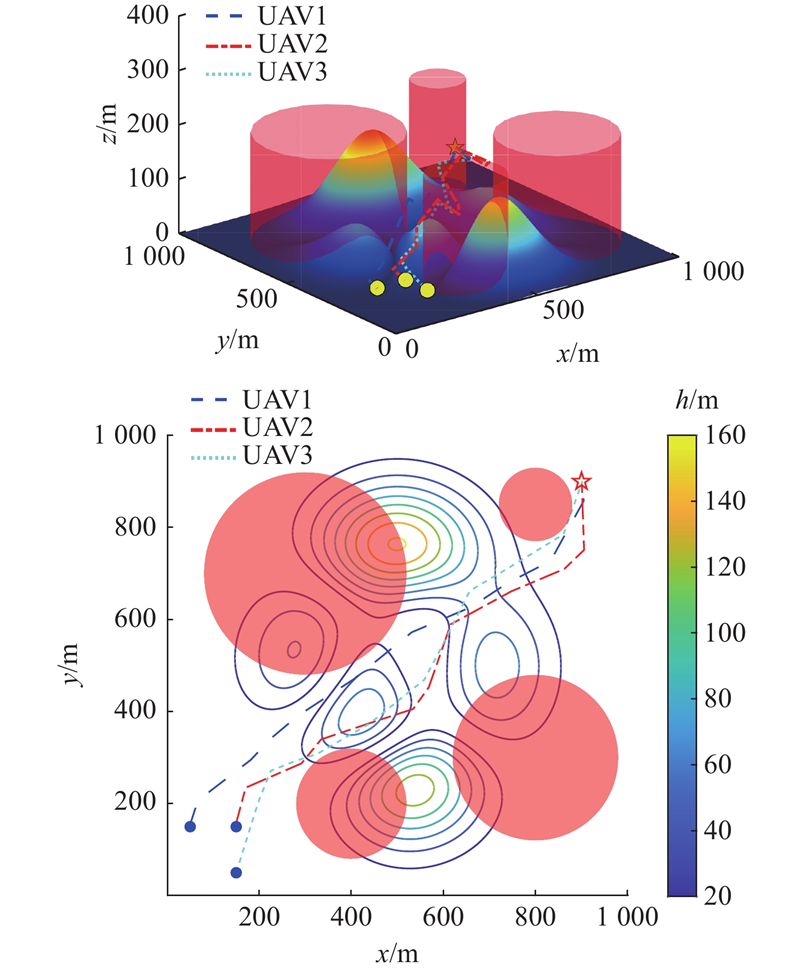
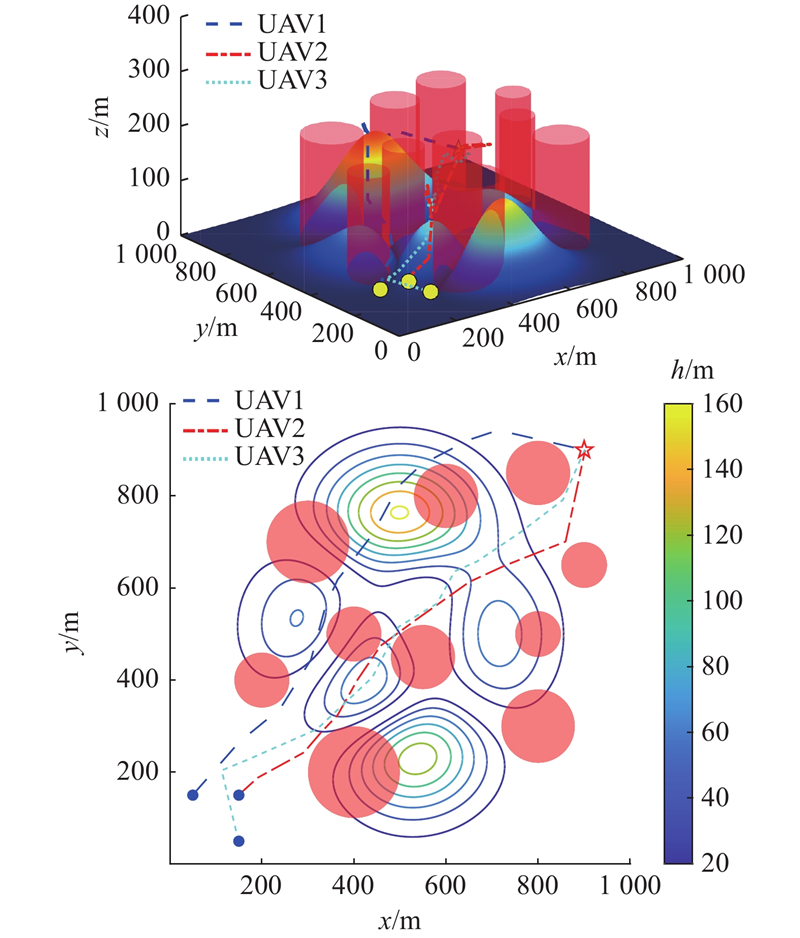
表 6 威胁源的参数
Tab.6
| 环境 | 威胁 | 位置坐标 | r | h |
| 场景2 | 1 | (800, 300) | 180 | 200 |
| 2 | (400, 200) | 120 | 200 | |
| 3 | (300, 700) | 220 | 200 | |
| 4 | (800, 850) | 80 | 200 | |
| 场景3 | 1 | (400, 500) | 60 | 200 |
| 2 | (800, 300) | 80 | 200 | |
| 3 | (400, 200) | 100 | 200 | |
| 4 | (300, 700) | 90 | 200 | |
| 5 | (800, 850) | 70 | 200 | |
| 6 | (200, 400) | 60 | 200 | |
| 7 | (800, 500) | 50 | 200 | |
| 8 | (600, 800) | 70 | 200 | |
| 9 | (900, 650) | 50 | 200 | |
| 10 | (550, 450) | 70 | 200 |
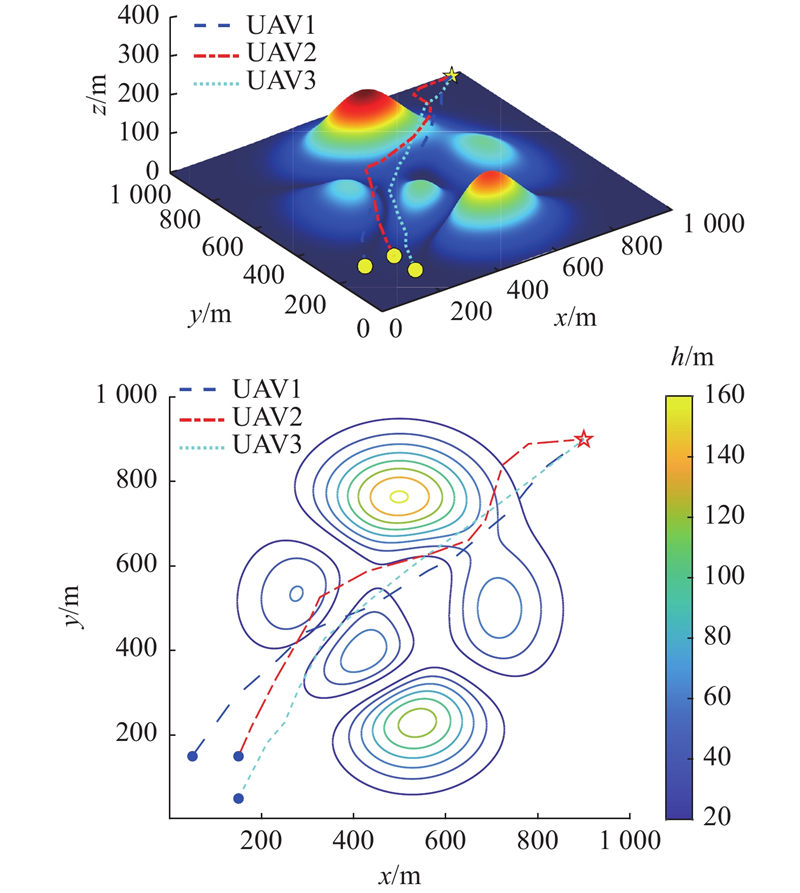
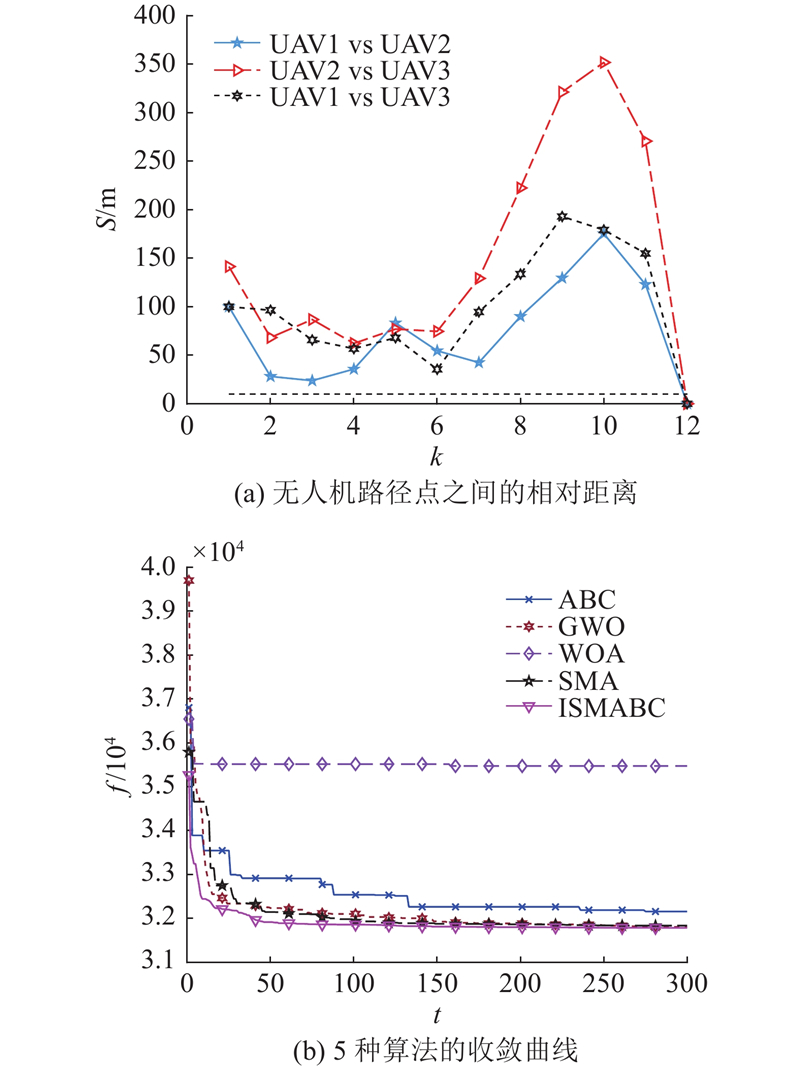
3.2.1. 场景1
图 5
表 7 场景1的路径长度和到达时间
Tab.7
| 场景1 | l/m | T/s |
| UAV1 | 1 174.3 | [58.715, 117.43] |
| UAV2 | 1 202.8 | [60.14, 120.28] |
| UAV3 | 1 172.9 | [58.645, 117.29] |
图 6
3.2.2. 场景2
图 7
表 8 场景2的路径长度和到达时间
Tab.8
| 场景2 | l/m | T/s |
| UAV1 | 1 235.6 | [61.78, 123.56] |
| UAV2 | 1 235.5 | [61.775, 123.55] |
| UAV3 | 1 235.7 | [61.785, 123.57] |
图 8
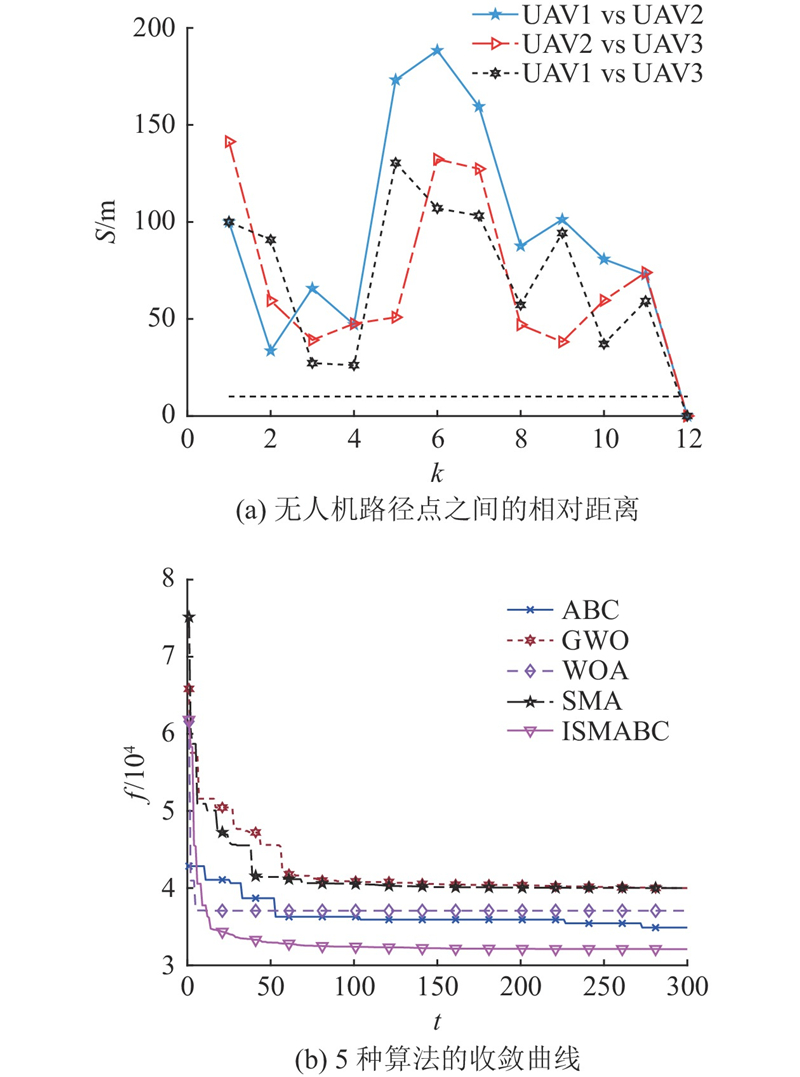
3.2.3. 场景3
图 9
图 10
表 9 场景3的路径长度和到达时间
Tab.9
| 场景3 | l/m | T/s |
| UAV1 | 1 453.8 | [72.69, 145.38] |
| UAV2 | 1 228.1 | [61.405, 122.81] |
| UAV3 | 1 228.3 | [61.415, 122.83] |
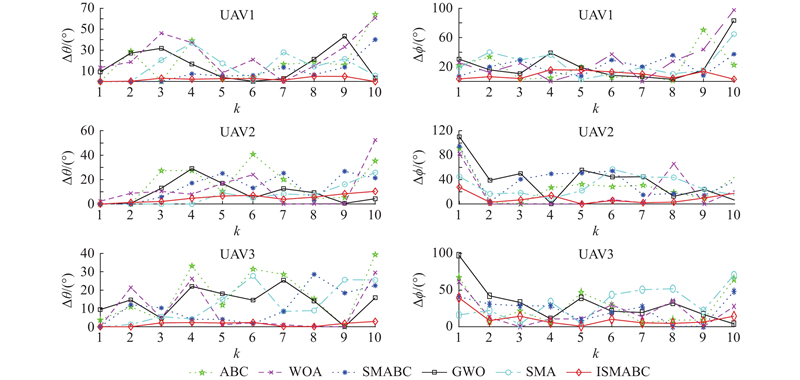
为了验证精英反向学习策略对UAV飞行质量的影响,分析场景3中3架UAV的路径平滑度. 将未加入精英反向学习策略的算法命名为SMABC,将SMABC算法与ISMABC以及其他对比算法规划出的路径俯仰角及航向角变化幅度进行对比,结果如图11所示. 可以看出,利用ISMABC算法规划出来的3条路径俯仰角和航向角的变化幅度较小,相对于ABC、GWO、WOA、SMA和SMABC算法更具有优势,证明采用精英反向学习策略可以降低无人机的状态波动,改善 UAV的飞行质量.
图 11
图 11 场景3中3架UAV俯仰角与航向角的变化幅度
Fig.11 Variation of pitch angle and heading angle of three UAVs in scenario 3
4. 结 语
本文针对战场环境下多架UAV协同路径规划的问题,提出混合黏菌蜂群算法ISMABC. 在算法设计上,引入多种优化策略,以增强寻优能力. 采用佳点集策略初始化种群位置,引入非线性收敛因子,提高算法的搜索效率和收敛速度. 通过计算并比较个体的适应度,选取全局适应度最优的个体,针对全局最优个体采用精英反向学习策略,构造反向种群,增加种群的多样性. 为了增强算法摆脱局部最优值的能力,在人工蜂群算法搜索能力的基础上引入全局最优引导,提高算法的开发能力. 通过4种策略的相互作用,提高了黏菌算法的整体性能,但优化时间略有增加. 下一步考虑将该算法应用在动态路径规划中,检验算法的实用性.
参考文献
Adaptive leader–follower formation control for swarms of unmanned aerial vehicles with motion constraints and unknown disturbances
[J].DOI:10.1016/j.cja.2020.03.020 [本文引用: 1]
Classifications, applications, and design challenges of drones: a review
[J].DOI:10.1016/j.paerosci.2017.04.003 [本文引用: 1]
Three-dimensional path planning using grey wolf optimizer for UAVs
[J].DOI:10.1007/s10489-018-1384-y [本文引用: 1]
The discrete time-cost tradeoff problem revisited
[J].DOI:10.1016/0377-2217(94)00187-H [本文引用: 1]
A novel phase angle-encoded fruit fly optimization algorithm with mutation adaptation mechanism applied to UAV path planning
[J].DOI:10.1016/j.asoc.2018.05.030 [本文引用: 1]
A novel hybrid grey wolf optimizer algorithm for unmanned aerial vehicle (UAV) path planning
[J].DOI:10.1016/j.knosys.2020.105530 [本文引用: 1]
Three-dimension path planning for UCAV using hybrid meta-heuristic ACO-DE algorithm
[J].DOI:10.1016/j.simpat.2009.10.006 [本文引用: 1]
Hybrid slime mould algorithm with adaptive guided differential evolution algorithm for combinatorial and global optimization problems
[J].DOI:10.1016/j.eswa.2021.114689 [本文引用: 1]
Slime mould algorithm: a new method for stochastic optimization
[J].DOI:10.1016/j.future.2020.03.055 [本文引用: 4]
A modified artificial bee colony algorithm
[J].DOI:10.1016/j.cor.2011.06.007 [本文引用: 2]
Enhanced grasshopper optimization algorithm using elite opposition-based learning for solving real-world engineering problems
[J].DOI:10.1007/s00366-021-01368-w [本文引用: 1]
Harris hawks optimization: algorithm and applications
[J].DOI:10.1016/j.future.2019.02.028 [本文引用: 1]
Grey wolf optimizer
[J].DOI:10.1016/j.advengsoft.2013.12.007 [本文引用: 2]
The whale optimization algorithm
[J].DOI:10.1016/j.advengsoft.2016.01.008 [本文引用: 1]
A novel swarm intelligence optimization approach: sparrow search algorithm
[J].DOI:10.1080/21642583.2019.1708830 [本文引用: 1]