排队长度是评价道路交叉口服务水平和效率的关键指标之一，对信号优化和交通状态评估均有重要作用^[1]. 传统排队长度估计研究多利用固定检测器采集交通信息，数据容易缺失，因而误差较大^[2-3]. 随着智能网联车（intelligent connected vehicles，ICVs）渗透率提升，ICVs随机分布于混合交通流中，利用ICVs的轨迹数据对新型混合交通流状态分析成为可能，这也为混合交通流排队长度估计模型提供了新的切入点.

目前，排队长度估计方法主要分为2类. 第1类基于交通波理论，Ramezani等^[4]基于交通波理论描述排队形成和消散过程，以粗略估计混合交通流的排队长度；王钰等^[5]引入“消散延误”的概念来实时估计交叉口排队长度，但假设车流到达率为常数；Mohajerpoor等^[6]依据车辆延误提出基于交通波理论的排队长度估计方法；李爱杰等^[7]使用单截面低频定点检测器估计每周期最大排队长度，但估计误差较大；Yao等^[8]结合概率模型和交通波理论，通过估计停止车辆的体积估计排队长度，该方法要求车流到达分布已知；唐进等^[9]运用密度聚类方法识别车辆运动状态，推算出信号交叉口的排队长度，但该方法仅适用于渗透率已知的情况；刘旭星等^[10]根据网联车轨迹数据提出周期初始队列长度和最大排队长度的估计方法，但该方法仅适用于渗透率较高的情况. 第2类是基于概率论的方法，Li等^[11]在低渗透率条件下利用车辆轨迹和交通信号数据估计队列长度；Comert^[12-13]使用停止线检测器与车辆轨迹估计排队长度，模型要求车流到达分布已知；随后针对低渗透率条件提出实时队列长度估计模型但估计精度较差；Zhao等^[14]根据停车位置分布估计ICVs渗透率，进而估计排队长度，但该方法严重依赖历史数据；Mei等^[15]基于贝叶斯方法估计队列的最大队列长度，该方法在渗透率较低时误差较大；Wong等^[16]提出无偏的单源数据渗透率（single-source data penetration rate，SSDPR）估计方法，在渗透率较低时估计方差和误差较大；Tan等^[17]提出基于车道的队列长度估计方法来估计饱和与非饱和状态下的排队长度；Talukder等^[18]使用最小二乘法和小波变换实现排队长度估计，但小波变换的参数标定未给出；Zhao等^[19]基于最大似然估计方法估计排队长度，但无法估计周期内的某一车道的排队长度；Zhao等^[20]根据交叉口停车位置分布估计ICVs渗透率，但无法实时估计排队长度.

综上，已有排队长度估计模型均基于一定的假设，如渗透率(高渗透率)固定、车辆到达分布固定、排队车辆绝对静止或单一交通流等. 随着ICVs的普及，其渗透率会随时间发生变化，ICVs随机分布在各车道中. 并且，由于智能控制算法的存在，低速前进和停车2种运动状态交替出现，排队车辆并非处于绝对静止状态. 已有排队长度估计模型无法适应新的ICVs和人驾车辆(human-driven vehicles, HDVs)混行交通场景. 为了解决上述问题，提出ICVs和HDVs混合交通流排队长度估计模型，所提模型考虑排队车辆的特殊运动状态，旨在实现信号交叉口排队长度的实时估计；此外，为了解决渗透率估计严重依赖历史数据和难以动态估计的问题，引入滚动迭代估计渗透率的方法.

ICVs的加入有助于获取更加详细的交通流数据. 本研究对象为ICVs和HDVs在停车线前的排队行为，ICVs和HDVs的主要差异在于是否能够向数据中心传输数据^[21]，但该主要差异并不会影响车辆的具体行为，为了更符合实际，假设ICVs和HDVs随机混合在城市道路交通流中.

ICVs在队列中的分布影响排队长度的估计，如图1所示为车辆排队过程观察示意图. 图中，$ {Q_k} $表示编号为$k$的队列实际排队长度，其中$ k \in \{ 1,2,3,\cdots\} $；${q_k}$表示编号为$k$的队列观测长度，$ {N_k} \leqslant {q_k} \leqslant {Q_k} $，${N_k}$表示编号为$k$的队列中ICVs的长度. 排队长度为${Q_1}$、${Q_2}$、${Q_4}$、${Q_5}$、${Q_7}$和${Q_9}$的队列中，不同数量的ICVs随机分布在排队队列中；排队长度为${Q_3}$、${Q_6}$和${Q_8}$的队列中不存在ICVs. 不存在ICVs的队列分为2类：队列本身没有车辆和队列不存在ICVs. 存在ICVs的队列称为可观测队列，不存在ICVs的队列称为不可观测队列，设$ {Q^{{\text{obs}}}} $和${Q^{{\text{hid}}}}$分别表示可观测队列和不可观测队列的排队长度.

所提出的ICVs和HDVs混行交叉口排队长度估计模型，包括可观测队列的排队长度估计模型和不可观测队列的排队长度估计模型. 模型构建和验证的详细流程如图2所示.

可观测队列的排队长度${Q^{{\text{obs}}}}$估计模型由2部分组成，包括队列排队长度的估计模型和基于概率统计的队尾长度修正模型.

定位到某车道队列中距停车线最远的ICV，获取该车的位置和速度信息. 为了研究方便，将其转化为相应的排队长度(排队车辆数)进行计算，队列排队长度粗略估计结果如下：

(1)$ {D_{mni}} = \max \;({d_{mni}});\;i \in N_{mn}^{\text{C}}. $

(2)$ {L_{mn}^{{\mathrm{obs}}}} = {{{D_{mni}}}}/{{L_{mn}^{\text{V}}}}. $

式中：${d_{mni}}$为第$m$周期第$n$车道队列第$ i $辆ICV到停车线的距离；$ {D_{mni}} $为第$m$周期第$n$车道队列中处于排队状态并距离停车线最远的ICV到停车线的距离，第$ i $辆ICV速度满足$ {v_{mni}} \leqslant {v_{\min }} $可判定处于排队状态，${v_{mni}}$为第$m$周期第$n$车道队列中的第$ i $辆ICV的速度，${v_{\min }}$为速度阈值；$N_{mn}^{\text{C}}$表示第$m$周期第$n$车道队列中的ICVs的数量；$ {L_{mn}^{{\mathrm{obs}}}} $表示第$m$周期第$n$车道队列的粗略排队长度；$ L_{mn}^{\text{V}} $为第$m$周期第$n$车道队列中车辆的平均车头间距.

式(2)决定排队长度估计的初始值，其中包含2个参数$ {D_{mni}} $和$ L_{mn}^{\text{V}} $，现有研究多仅利用$ {D_{mni}} $对队列排队长度进行片面估计，而忽视了ICVs带来的另外一个优势：混合交通流中的ICVs速度也能够实时获取. 因此，对于$ L_{mn}^{\text{V}} $，不再仅依靠传统经验分析法获取历史平均车头间距，而是可以利用混合交通流中ICVs的速度数据进行动态分析调整. 在实际交通环境中，队列中的车辆并非处于绝对静止状态，大部分车辆处于低速和停车反复切换的运动状态，队列中游车辆处于低速运动状态^[22]，此时的$ L_{mn}^{\text{V}} $和停车状态下的$ L_{mn}^{\text{V}} $存在明显差异，继续采用式(2)求解车辆排队长度具有较大的误差. 因此，本研究考虑对式(2)进行修正，利用ICVs速度来修正$ L_{mn}^{\text{V}} $，构建适用于车头间距动态变化的交通环境的车辆排队长度估计，修正后的公式如下：

(3)$ {L_{mn}^{{\mathrm{obs}}}} = f({D_{mni}},\;V,\;\zeta ). $

式中：$ V $为队列中所有车辆的平均速度，$\zeta $为调整系数.

根据交通流的基本关系图，在排队过程中，车头间距和速度存在线性关系^[23]：

(4)$ V = - A+BL_{mn}^{\text{V}}. $

式中：$A$和$B$表示调整系数.

所有车辆的平均速度无法获取，因为HDVs速度无法获取. ICVs的平均速度$ {V_{\mathrm{c}}} $、渗透率$ p $、HDVs平均速度$ {V_{\mathrm{h}}} $和$ V $的关系如下：

(5)$ V = p{V_{\mathrm{c}}}+(1 - p){V_{\mathrm{h}}}. $

联合式(2)、(4)和(5)可以得到

(6)$ {L_{mn}^{{\mathrm{obs}}}} = \frac{{B{D_{mni}}}}{{p{V_{\mathrm{c}}}+(1 - p){V_{\mathrm{h}}}+A}}. $

式(6)涉及2个未知参数A和B，因为本研究假设ICVs随机混合在混合队列中，ICVs和HDVs的平均速度相近，即$ {V_{\mathrm{c}}} \approx {V_{\mathrm{h}}} $，式(6)可以简化为

(7)$ {L_{mn}^{{\mathrm{obs}}}} = \frac{{B{D_{mni}}}}{{{V_{\mathrm{c}}}+A}}. $

对于参数A和B，采集信号交叉口的车辆排队数据并构建数据集${D}:{\{ \hat L_{mn}^{{\text{obs}}},{\hat V_{\text{c}}},{\hat D_{mni}}\} _k} $，采用最小二乘法求解参数$A $和$B $，表达式如下：

(8)$\widehat \zeta = {{{\mathrm{argmin}}} _\zeta }\;\sum\limits_{k = 1}^K {{{\left[ {\hat L_{mn}^{{\text{obs}}} - f({{\hat D}_{mni}},{{\hat V}_{\text{c}}},\zeta )} \right]}^2}} . $

式中：$\hat L_{mn}^{{\text{obs}}}、{\hat V_{\text{c}}}、{\hat D_{mni}} $表示统计值，$\zeta = \{ A,B\} $，$K $表示数据集${D} $大小.

当渗透率$p$较高时，使用式(7)估计排队长度误差不会很大，因为ICVs的位置位于或者接近排队队列队尾的可能性较大. 但目前ICVs的渗透率将会长期保持在较低水平，故使用式(7)估算排队长度将会产生较大的误差. 事实上，只要$p$达不到100%，就无法准确估计排队长度，因此须引入队尾排队长度修正模型，如图3所示. 排队车辆在交叉口进口道处，每个车道的队列(不包含第0列)中至少有一辆ICV的概率如下：

(9)$ \left.\begin{array}{l}P_j=1-\beta^\lambda, j =1,2,\cdots, r\;;\\\beta=1-p.\end{array}\right\}$

式中：${P_j}$表示图3中第$j$列排队车辆中至少有一辆ICV的概率，其中$j$为交叉口进口道排队车辆距离信号灯的列数；$\lambda $表示车道数；$\beta $表示HDV的比例；$r$表示距离停车线最远的HDV至距离停车线最近的ICV之间的列数.

观察第0列，可以发现排队车辆可能占不满车道，那么式(9)无法估计第0列至少有一辆ICV的概率. Shahrbabaki等^[23]利用概率统计和排列组合的方式得到了第0列ICV的概率，其假设第0列的车辆数为$\gamma $，$1 \leqslant \gamma \leqslant \lambda $，该列中全部是HDV的概率为${\beta ^\lambda }$，则至少有一辆ICV的概率为$1 - {\beta ^\gamma }$，由于$1 \leqslant \gamma \leqslant \lambda $，所有可能的车道组合总数为${2^\lambda } - 1 $，在没有更好的估计结果的情况下，假设选择组合中的每一种情况发生的概率相同，则第0列至少有一辆ICV的概率为

(10)$ {P_0} = {{\displaystyle\sum\limits_{\gamma = 1}^\lambda {C_\lambda ^\gamma (1 - {\beta ^\gamma })} }}/{{{(2^\lambda } - 1)}}. $

基于概率统计定理，可以得到：

1）如果在第0列中至少有一辆ICV，排队长度估计没有误差，概率为${P_0}$；

2）如果在第0列中没有ICV，但在第１列中至少有一辆，则估计存在1辆车的误差，概率为$ (1 - {P_0}){P_1} $；

3）以此类推，如果在第$0,1,2,\cdots,r - 1$列中没有ICV，但在第$r$列中至少有一辆，则估计存在$r$辆车的误差，概率为$ (1 - {P_0})\prod\limits_{j = 1}^{r - 1} {(1 - {P_j}){P_r}} $.

为了验证队尾位置误差修正函数的可信性，分别以车道数$ \lambda =3、4 $，渗透率$p $=10%、20%、30%、40%、50%为例，计算队尾排队长度修正模型的估计误差概率，如表1所示.表中，${P_{\text{e}}} $表示修正误差概率，G表示距离停车线最远的ICV之后的HDV数量.

表1列出了根据概率误差函数计算出的$ \lambda =3、4 $的估计误差概率. 可以推断出，渗透率或车道数越高，误差越小，说明了利用队尾误差函数修正排队长度的合理性.

以此得到队尾位置误差修正函数，如下：

(11)$ {o_{{{\mathrm{e}}}}}(p,\lambda ,r) = \sum\limits_{j = 1}^r {j (1 - {P_0})\prod\limits_{j = 1}^{r - 1} {(1 - {P_j}){P_r}} } . $

利用式(8)~ (10)进行简化，最终得到队尾位置误差修正函数：

(12)$ {o_{{\text{{e}}}}}(p,\lambda ,r) = \frac{{{{(1+\beta )}^\lambda } - 1}}{{({2^\lambda } - 1)(1 - {\beta ^\lambda })}}. $

利用${o_{{\text{{e}}}}} $来修正式(2)，结果如下：

(13)$ {\hat {Q}_{mn}^{{\text{obs}}}} = {L_{mn}^{{\mathrm{obs}}}}+{{{o_{{\text{e}}}}}}/{\lambda }. $

式中：${\hat {Q}_{mn}^{{\text{obs}}}} $为第$m $周期第$n $车道可观测队列的预测排队长度.

利用式(13)估计排队长度，并不依赖实时排队信息和先验信息，也不需要检测器就可以实现排队长度估计.

不可观测队列的排队长度${Q^{{\text{hid}}}}$估计主要采用贝叶斯定理，原理是利用事件发生的先验概率和类条件概率估计事件发生的后验概率. 由于在信号交叉口周期性排队的队列中没有网联车，估计不可观测队列的排队长度较为困难.不过，尽管排队的队列中没有ICV，也包含排队信息. Zhao等^[20]提出基于贝叶斯定理求排队长度期望的方法，本研究根据其模型的思想，对不可观测队列的排队车辆数${Q^{{\text{hid}}}}$进行估计，${Q^{{\text{hid}}}}$的期望值如下：

(14)$ E({Q_{mn}}\left| {{q_{mn}}} \right.) = \sum\limits_{l = 0}^{{l_{\max }}} {P({Q_{mn}}\left| {{q_{mn}}} \right.)l} . $

式中：${Q_{mn}} $表示第$m $周期第$n $车道的队列长度，${q_{mn}} $表示第$m $周期第$n $车道的队列观测长度，${l_{\max }} $为部分可观测队列的最大排队长度，$l $表示部分可观测队列的排队长度.

基于贝叶斯定理，公式的推导过程如下：

(15)$ P({Q_{mn}}\left| {{q_{mn}}} \right.) = \frac{{P({q_{mn}}\left| {{Q_{mn}}} \right. = l)P({Q_{mn}} = l)}}{{\sum\limits_{j = 0}^{{l_{\max }}} {P({q_{mn}}\left| {{Q_{mn}}} \right. = j)P({Q_{mn}} = j)} }},$

(16)$ P({Q_{mn}} = l) = \frac{{N({Q_{mn}} = l)}}{{\sum\limits_{j = 0}^{{l_{\max }}} {N({Q_{mn}} = j)} }} ,$

(17)$ P({q_{mn}}\left| {{Q_{mn}}} \right. = l) = {p^{N_{mn}^{\text{C}}}}{(1 - p)^{l - N_{mn}^{\text{C}}}}, $

(18)$ P({q_{mn}}\left| {{Q_{mn}}} \right. = j) = {p^{N_{mn}^{\text{C}}}}{(1 - p)^{j - N_{mn}^{\text{C}}}}.$

式中：${N({Q_{mn}} = l)} $表示排队长度为$l $的队列数目.

根据式(15)~(18)可以得到，不可观测队列的排队长度关于$p $的单变量方程表达式如下：

(19)$ \hat {Q}_{mn}^{{\text{hid}}} = E({Q_{mn}}\left| {{q_{mn}}} \right.) = \sum\limits_{l = 0}^{{l_{\max }}} {\frac{{N({q_{mn}} = l)}}{{\sum\limits_{j = 0}^{{l_{\max }}} {N({q_{mn}} = j){{(1 - p)}^{j - l}}} }}l} .$

式中：$\hat Q_{mn}^{{\text{hid}}} $表示第$m $周期第$n $车道不可观测队列的预测排队长度，$N({q_{mn}} = l) $表示部分观测队列排队长度为$l $的队列数目.

在交叉口各进口道的混合队列中，每一辆车为ICV的概率是相同的，为渗透率$p$，即

(20)$ p = {{\displaystyle\sum\limits_{n = 1}^\lambda {N_{mn}^{\text{C}}} }}/{{Q_m^{{\text{Total}}}}}, $

(21)$ p = {{\displaystyle\sum\limits_{n = 1}^\lambda {N_{mn}^{\text{C}}} }}{ {/}}{{\displaystyle\sum\limits_{n = 1}^\lambda {(\hat Q_{mn}^{{\text{hid}}}+\hat Q_{mn}^{{\text{obs}}})} }}. $

式中：$Q_m^{{\text{Total}}}$表示第$m$周期的车辆数总和.

式(21)的左右两侧都是关于$p$的表达式，在估计开始时，渗透率未知，利用式(21)，所有车道ICVs数量$\displaystyle\sum\nolimits_{n = 1}^\lambda {N_{mn}^{\text{C}}} $已知，在初次迭代时，利用每个周期最后一辆ICV的位置统计队列长度，此队列长度作为式(21)的分母代入，得到初始估计渗透率$p$. 由于实际队列长度必然大于等于该估计值，初始$p$为估计值的上限，上限可以取为${{\sum\nolimits_{n = 1}^\lambda {N_{mn}^{\text{C}}} }}/{{\sum\nolimits_{n = 1}^\lambda {{q_{mn}}} }}$. 一旦得到$p$，根据式(7)、(13)和(19)就可以得到${Q^{{\text{obs}}}} $和${Q^{{\text{hid}}}}$. 设置一个较小的步长，以此过程进行反复迭代，从0迭代到$p$的上限，直至式(21)两边的误差处在一个可接受的范围，进而停止迭代计算，得到渗透率$p$的估计值.

数据采集地点为西安市未央路-凤城七路交叉口，如图4所示，黄色方框内是本研究的排队队列. 对数据进行处理与分析，获得排队队列的车辆数.

为了更加真实地模拟ICVs和HDVs混合交通流的特征，在不同的渗透率条件下，设置多个随机种子来随机模拟队列中ICVs的空间分布情况，以获取不同条件下的排队数据，该过程的详细编码流程如图5所示，排队数据统计结果如表2所示. 表中，$C$为周期时长，${N^{\text{C}}}$为统计周期数，${T_{\text{g}}}$为绿灯时长，${\text{Lane1\text{、}Lane2\text{、}Lane3}}$分别表示车道1、2、3的平均排队车辆数.

根据式(21)可以看出，渗透率与ICVs的数量、${Q^{{\text{obs}}}}$和${Q^{{\text{hid}}}}$有关，式(21)两边都是渗透率的表达式，因此本研究采取迭代计算的方式估计渗透率，使用此方法避免了渗透率难以获取的问题，且可以在每个周期对实时渗透率进行估计. 如表3所示为渗透率估计结果. 表中，${N^{{\text{All}}}}$表示总车辆数，${N^{{\text{ICV}}}}$表示ICVs的数量，${N^{{\text{HDV}}}}$表示HDVs的数量，$\widehat p$表示估计渗透率. 非高峰渗透率的实时估计结果表明：渗透率的取值下限为0，上限为42.05%，误差小于0.1%的渗透率的取值为19.03%. 此次随机过程中ICVs的数量为156，总车辆数为777辆，求得实际的渗透率为20.07%，使用迭代计算方式得到的求解结果与实际渗透率基本一致. 在本研究的不同渗透率条件下的排队长度估计过程中，均采用该渗透率估计模型实时估计队列中ICVs的渗透率，以满足实时队列估计的需求.

将车辆队列分为${Q^{{\text{obs}}}}$和${Q^{{\text{hid}}}}$估计，根据式(13)、(19)估计排队长度，选取平均绝对误差(mean absolute error, MAE)和平均绝对误差百分比(mean absolute percentage error, MAPE)指标作为排队长度的估计指标：

(22)$ {\text{MAE}} = \frac{1}{{{N^{\text{C}}}\lambda }}\sum\limits_{m = 1}^{{N^{\text{C}}}} {\sum\limits_{n = 1}^\lambda {\left| { {{\hat Q_{mn}}} - {Q_{mn}}} \right|} } ,$

(23)$ {\text{MAPE}} = \frac{1}{{{N^{\text{C}}}\lambda }}\sum\limits_{m = 1}^{{N^{\text{C}}}} {\sum\limits_{n = 1}^\lambda {\left| {\frac{{{{\hat Q_{mn}}} - {Q_{mn}}}}{{{Q_{mn}}}}} \right|} } . $

式中：$ {{\hat Q_{mn}}}$为第$m $周期第$n $车道队列的预测排队长度.

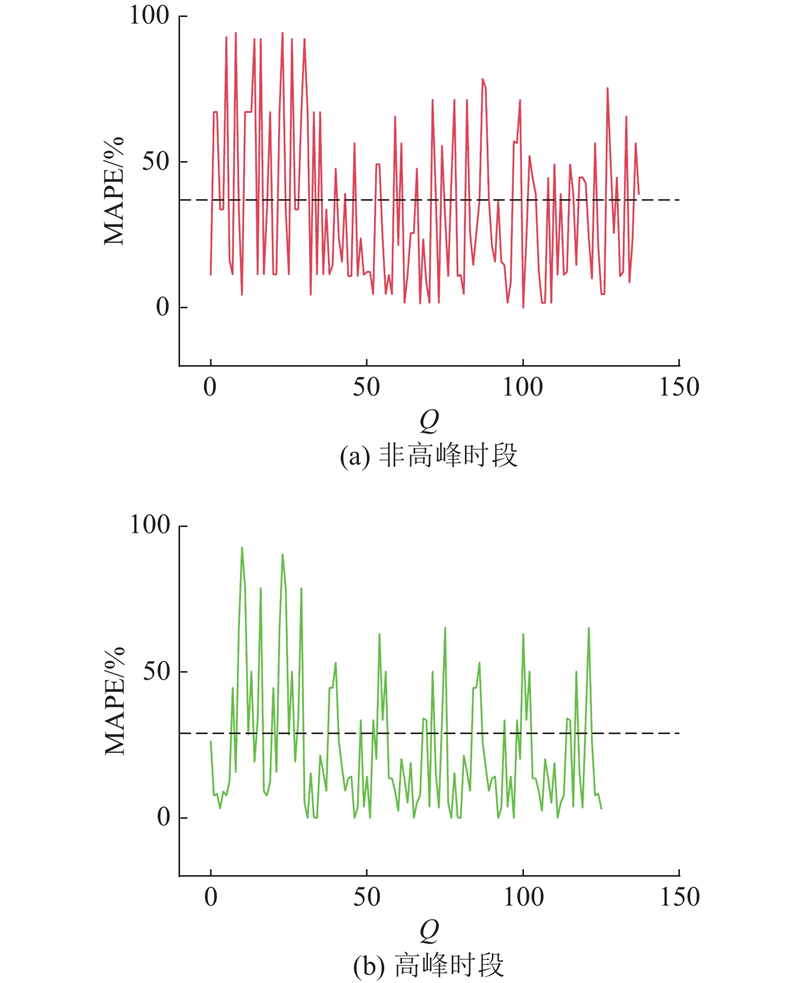
为了更准确地描述结果，在每个时段设置3个随机种子(seed8、seed10和seed12)来随机表示路网的ICVs分布情况，以验证模型的准确性和鲁棒性. 本研究中提到的MAE和MAPE数据均为统计周期内排队队列MAE和MAPE的平均值. 以seed8为例，如图6(a)、(b)表示在统计周期内非高峰时段和高峰时段每个队列的估计误差，Q为统计周期内的队列数. 如表4所示为基于本研究模型的估计排队长度. 表中，${Q_{{\text{a}}}} $表示真实的统计排队长度，${Q_{{\text{p}}}} $表示本研究模型的估计长度，${\text{A - MAE}} $表示不同随机种子场景下计算出的MAE的均值，${\text{A - MAPE}} $表示不同随机种子场景下计算出的MAPE的均值. 可以看出，在非高峰时段，队列排队长度均值为5.63，预测值的均值为4.46，${\text{A - MAE}} $约为1.17，偏差不大，但由于实际统计的排队长度较短，导致${\text{A - MAPE}} $较大，均值为20.86%，从评价指标来看，预测精度较差. 在高峰时段，队列排队长度均值为10.03，预测值的均值为8.59，${\text{A - MAE}} $约为1.44，${\text{A - MAPE}} $较非高峰时段的均值较小，均值为14.33%，预测精度较好. 对比发现，在高峰时段，排队长度的估计误差小于非高峰时段的误差，这是因为在非高峰时段排队车辆少，缺乏充足排队、ICVs位置和速度数据.

为了进一步验证渗透率$p$对排队长度估计结果的影响，针对非高峰时段14:30—16:30和高峰时段18:20—20:20，选择设置渗透率分别为10%、20%、30%、50%、80%、90%，计算不同时段的队列排队长度估计值，并与真实值进行对比分析.

以$p = 20\text{%} $为例，如图7(a)所示为统计周期内非高峰时段每个队列的估计误差. 如表5所示为不同渗透率下基于本研究模型的非高峰时段估计排队长度. 可知，当$p $为10%、50%、90%时，队列排队长度的MAPE均值分别为29.35%、12.48%、6.90% . 总体来说，MAPE均值随着渗透率的增加而降低，这是因为在渗透率高的条件下，队列最后一辆车为ICVs的概率较高，能够获取更加准确的队尾位置信息和混合队列平均速度，因此能获得更加准确的排队长度估计值.

以$p = 20\text{%}$为例，如图7(b)所示为统计周期内高峰时段每个队列的估计误差. 如表6所示为不同渗透率下基于本研究模型的高峰时段估计排队长度. 可知，当$p $为10%、50%、90%时，队列排队长度的MAPE均值分别为26.50%、7.16%、1.45%. 随着渗透率的升高，MAPE均值不断下降. 在高峰时段，由于获取的数据比非高峰时段丰富，高峰时段的估计精度要高于非高峰时段的.

文献[21]提出了基于贝叶斯定理的估计方法来估计信号交叉口的排队长度，与本研究提出的排队估计模型不同的是该方法估计${Q^{{\text{obs}}}} $和${Q^{{\text{hid}}}} $均采用贝叶斯定理，排队长度估计结果如下.

以$p = 20 \text{%} $为例，在非高峰时段，如图8(a)所示表示统计周期内每个队列的估计误差. 如表7所示为不同渗透率下基于贝叶斯定理的非高峰时段估计排队长度. 可以看出，当$p $=10%时，$\widehat p $=9.90%，队列排队长度的MAE=3.36，估计误差较大，队列排队长度的MAPE=59.68%；当$p $=50%时，$\widehat p $=54.24%，队列排队长度的MAE=1.24，估计误差适中，队列排队长度的MAPE=22.06%；当$p $=90%时，$\widehat p $=92.02%，队列排队长度的MAE=1.00，估计误差较小，队列排队长度的MAPE=17.85%.

在高峰时段，如图8(b)所示表示统计周期内每个队列的估计误差. 如表8所示为不同渗透率下基于贝叶斯定理的高峰时段估计排队长度. 可知，当$p $=10%时，$\widehat p $=10.12%，队列排队长度的MAE=3.48，估计误差较大，队列排队长度的MAPE=34.66%；当$p $=50%时，$\widehat p $=50.95%，队列排队长度的MAE=0.64，估计误差适中，队列排队长度MAPE=6.42%；当$p $=90%时，$\widehat p $=90.51%，队列排队长度的MAE=0.11，估计误差较小，队列排队长度MAPE=1.05%.

总体来说，基于贝叶斯定理的估计方法所得到的估计排队长度的变化趋势和本研究模型的保持一致，即，估计精度随着渗透率的增加而降低，且在高峰时段的估计精度较高.

为了更加清晰直观地展示和对比不同渗透率、不同估计方法以及不同时段对排队长度估计的MAPE的影响情况，如图9所示展示了不同条件下本研究模型和基于贝叶斯定理的模型估计排队长度的MAPE变化情况. 可以看出：1）随着渗透率的升高，MAPE下降，预测的准确性提高；2）同种预测方法下的不同数据样本的对比表明，高峰时段的MAPE较非高峰时段的较小，预测精度较高；3）不同预测方法下的相同数据样本的对比表明，与基于贝叶斯定理的模型相比，所提模型估计的MAPE较小，预测精度较高；4）所提模型无论是在非高峰和高峰时段，还是低渗透率和高渗透率条件下，均优于贝叶斯估计模型，估计结果较准确.

（1）提出基于概率统计和贝叶斯定理的ICVs和HDVs混合交通流排队长度估计模型，将车辆排队队列分为可观测队列和不可观测队列进行估计，推导出排队长度与网联车位置和速度、排队队列的频率和渗透率的关系式，并采用迭代计算的方式估计渗透率.

（2）所提模型解决了现有模型依赖先验信息(利用历史车辆信息来确定车辆的到达分布以及渗透率)的不足，在没有先验信息的条件下就可以实现对排队长度的估计，并且在求解渗透率时采用迭代计算的方式来精确地估计渗透率，进而解决现有模型中渗透率估计困难的问题.

（3）通过设置随机种子来随机模拟车辆排队的分布状态，实现了对不同渗透率和不同数据集的条件下模型估计精度的分析，并与基于贝叶斯定理的排队长度估计模型对比，分析结果表明本研究模型有效提高了交叉口车辆队列的排队长度估计精度.

本研究所提模型仍存在不足，后续将继续从以下几个方面进行进一步研究：整合不同因素对排队长度估计结果的影响，考虑信号控制交叉口绿灯时间不同对排队长度的影响；本研究对象为直行车道排队长度估计，后续将扩展至直行和左转混合车道的排队长度估计；本研究场景为单点交叉口，后续将研究多个交叉口联动对排队长度估计的影响.