本文链接:
作为磁吸附式爬壁机器人的关键部件,磁吸附模块的结构对机器人的整体质量及运动性能有重要影响。因此,基于轻量化思想对磁吸附模块的结构参数进行优化设计具有很大的意义。近几十年来,许多学者分别从单一充磁方向磁铁阵列和Halbach阵列出发,研发了不同类型的磁吸附模块产品。其中,充磁方向单一的磁吸附模块可由单个或多个永磁体组成,且所有永磁体的充磁方向均指向同一个方向。Lu等[7]针对爬壁机器人作业管道直径不同的问题,设计了一种变磁力吸附机构并利用有限元法进行了优化分析,得到了满足稳定工况的最优磁体宽度。张栋等[8]设计了一种悬摆式磁吸附模块,并利用Maxwell软件中自带的连续非线性规划(sequential non-linear programming, SNLP)算法对其参数进行了优化。Sahbel等[9]利用响应面方法建立了磁体间距、气隙和磁轭厚度与吸附力之间的数学模型,并使用方差分析法对预测模型进行了统计分析。随着磁吸附模块不断向小型化、便携化发展,单一充磁方向磁铁阵列逐渐被Halbach阵列替代。Halbach阵列是一种新型的永磁体排列方式,通过将充磁方向不同的永磁体按照一定规律排列,以实现在永磁体的一侧汇聚磁力线,在另一侧削弱磁力线,从而获得比较理想的单边磁场[10]。通过采用不同的组合形式,Halbach阵列的应用范围十分广泛。近年来,越来越多的研发人员将Halbach阵列应用于爬壁机器人的磁吸附模块。现阶段,基于Halbach阵列的磁吸附模块的优化设计通常采用有限元仿真方法。钟道方等[11]利用Maxwell软件对块状磁吸附模块进行了仿真分析,并运用控制变量法得到了其结构参数的最优值。潘柏松等[12]基于Halbach阵列提出了一种轮式磁吸附模块的拓扑结构,通过有限元仿真分析了轭铁厚度、极对数等结构参数对吸附力的影响,并采用多岛遗传算法对结构参数进行了全局优化。有限元仿真方法虽具有计算速度快、求解结果精度高的优点,但无法得到磁吸附模块所产生磁力与结构参数之间有效的函数关系,需要多次仿真才能得到结构参数相对理想的磁吸附模块。为解决上述问题,部分学者结合仿真技术和数学模型对磁吸附模块优化方法进行了研究。陈勇[13]运用Fourier级数法建立了Halbach阵列磁感应强度与磁场强度的数学模型,并采用多目标免疫遗传算法对磁吸附模块的结构参数进行了优化设计。Jiao等[14]提出了一种基于等效磁通密度的Halbach阵列磁力计算方法,得到了改变结构参数后Halbach阵列磁力的变化趋势,并利用ANSYS软件对几种能产生较大磁力的磁吸附模块结构进行对比,确定了可产生最大磁力的磁吸附模块结构。但上述方法涉及Fourier级数,导致计算过程十分复杂。为此,赵智浩等[15-16]针对双磁路磁吸附模块提出了一种新的优化思路,即采用正交设计法和二阶响应面模型(second-order response surface model, 2-RSM)建立了磁吸附模块结构参数与磁力之间的数学模型,并利用遗传算法对结构参数进行了优化求解,从而得到了吸附效率较高的磁吸附模块。使用代理模型可提高磁吸附模块结构参数优化设计的效率,但所建立的2-RSM仅适用于双磁路磁吸附模块。随着磁路的增加,磁吸附模块结构优化的设计变量增多,且设计变量之间的解析关系也变得更为复杂,2-RSM已无法满足预测精度的要求。因此,基于所设计爬壁机器人的吸附稳定性及轻量化要求,如何得到吸附效率高的磁吸附模块尚需进一步探索。
为此,本文结合虚拟仿真技术、四阶响应面模型(fourth-order RSM, 4-RSM)和蜣螂优化(dung beetle optimization, DBO)算法,提出了一种磁吸附模块结构优化方法。首先,介绍爬壁机器人及其磁吸附模块的结构设计方案。然后,构建磁吸附模块磁力与结构参数之间的4-RSM,并验证该代理模型的可靠性。最后,以机器人的吸附稳定性和结构参数为约束条件,以磁吸附模块轻量化为目标,建立磁吸附模块结构参数优化模型,并采用DBO算法进行优化求解,以获得吸附效率高、轻量化的磁吸附模块。
1 磁吸附模块结构设计
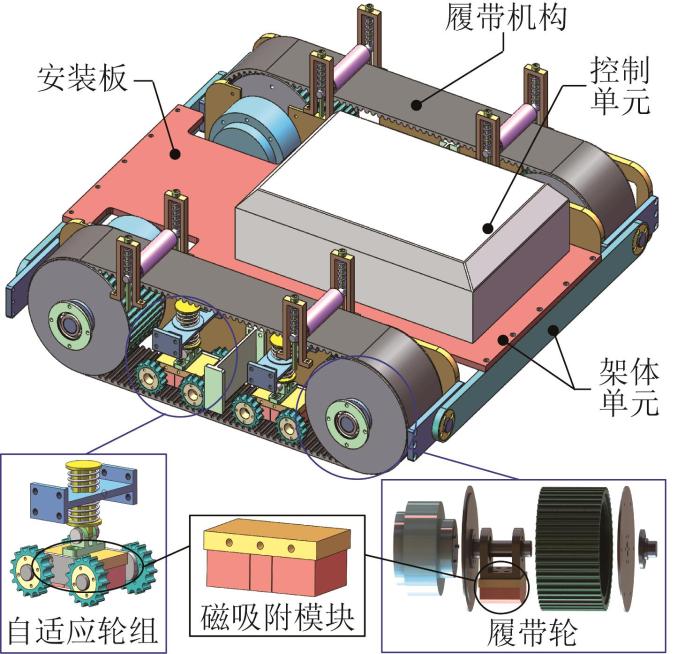
本文所设计的爬壁机器人的结构方案如图1所示。机器人两侧对称布置2个履带机构,与架体单元相连接。履带机构依靠履带轮—同步带的传动方式进行运动。机器人内部设置多组磁吸附模块,且自适应轮组可起分散载荷的作用,能够保证履带始终与壁面贴合,使得机器人稳定地吸附在壁面上。磁吸附模块分别布置于履带轮内部与自适应轮组中。在履带轮中,磁吸附模块通过支架和轴承安装在磁铁旋转轴上。由于转动副的存在,磁吸附模块能够保持相对静止,磁力方向始终与壁面垂直。磁铁旋转轴为固定式连接,故所有履带轮内部的磁吸附模块与壁面之间的距离均是固定不变的。在自适应轮组中,磁吸附模块由自适应轮支撑,随着壁面曲率的变化,自适应轮组中的弹簧伸缩及铰链转动,使得磁吸附模块与壁面之间的距离也保持固定不变。
图1
图2
图3
图3
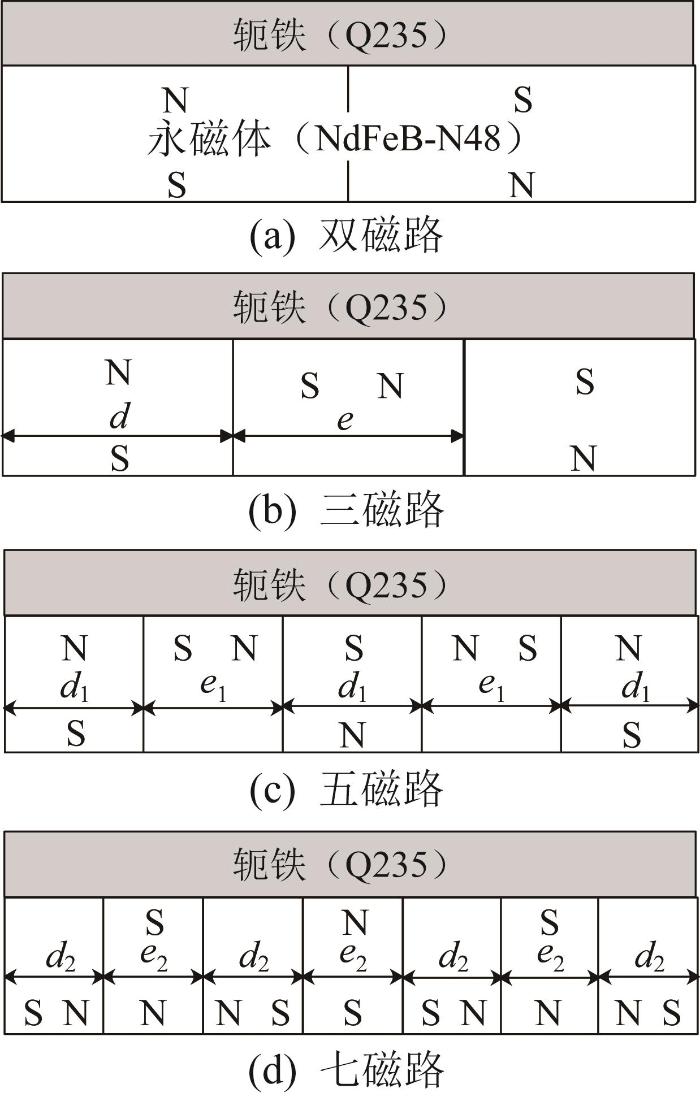
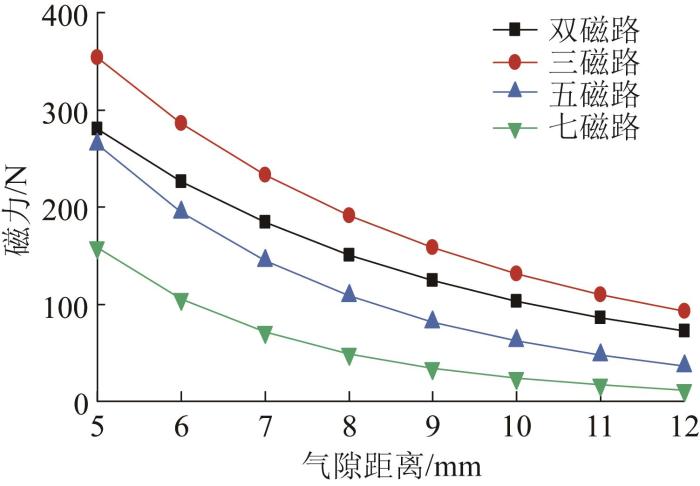
不同磁路模式下磁力随气隙距离的变化情况
Fig.3
Variation of magnetic force with air gap distance under different magnetic circuit modes
图4
图4
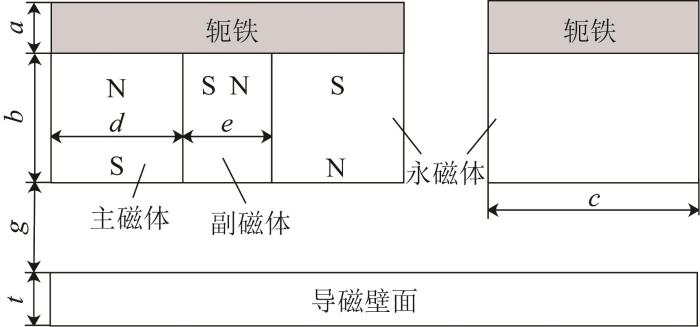
三磁路磁吸附模块结构示意
Fig.4
Structure schematic of magnetic adsorption module with three-magnetic circuit
2 磁吸附模块结构参数优化策略
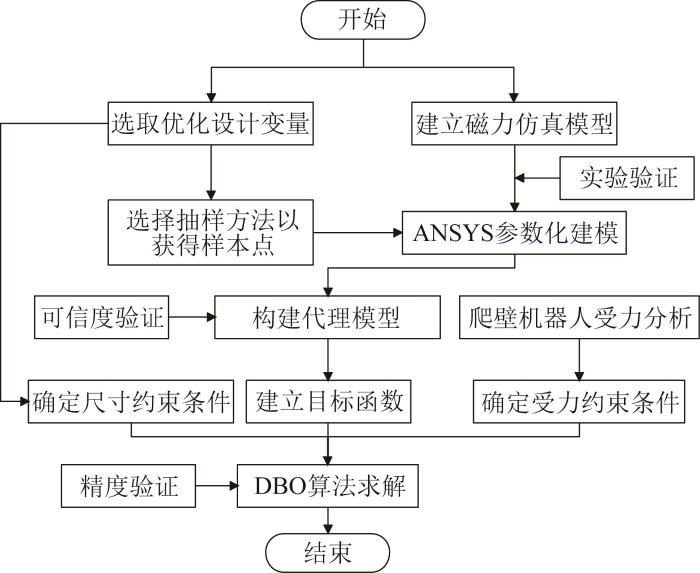
爬壁机器人稳定地吸附在壁面上需要较大的磁力。所需磁力增大会导致磁吸附模块的尺寸增大,造成磁吸附模块的质量增大,从而导致整个机器人的质量增大。因此,有必要对磁吸附模块的结构参数进行优化,以保证在满足磁力要求的同时实现质量最小化。磁吸附模块结构参数的优化策略如图5所示。
图5
图5
磁吸附模块结构参数优化策略
Fig.5
Optimization strategy for structural parameters of magnetic adsorption module
2.1 优化设计变量
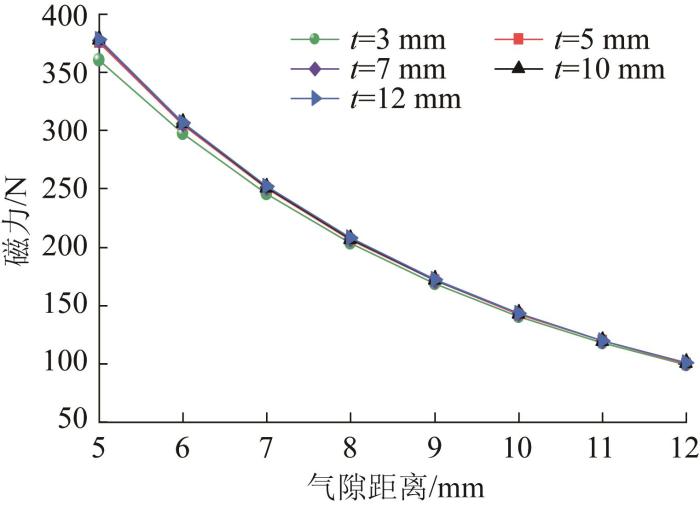
图6
图6
不同壁面厚度下磁力的变化情况
Fig.6
Variation of magnetic force under different wall thicknesses
表1 磁吸附模块各设计参数的取值范围 (mm)
Table 1
| 设计参数 | 初始值 | 取值范围 | |
|---|---|---|---|
| 最小值 | 最大值 | ||
| a | 8 | 5 | 12 |
| b | 16 | 5 | 29 |
| c | 35 | 26 | 37 |
| d | 22 | 12 | 30 |
| e | 11 | 4.5 | 21.5 |
| t | 10 | 10 | 10 |
| g | 10 | 10 | 10 |
2.2 优化设计约束条件
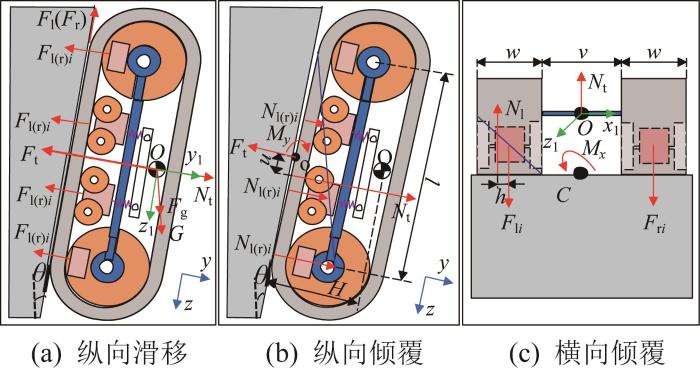
图7
根据图7所示的受力分析,可得机器人在抵抗纵向滑移、纵向倾覆、横向倾覆时所需的最小磁力应满足以下条件:
式中:F1、F2、F3分别为抵抗纵向滑移、纵向倾覆、横向倾覆时所需的最小磁力,G为机器人整体重力,Fg为负载重力,w为履带宽度,v为两侧履带的距离,l为履带接地长度,H为机器人重心与壁面的距离,μ为摩擦系数,k为安全系数,θ为壁面倾角,n为磁吸附模块的数量。
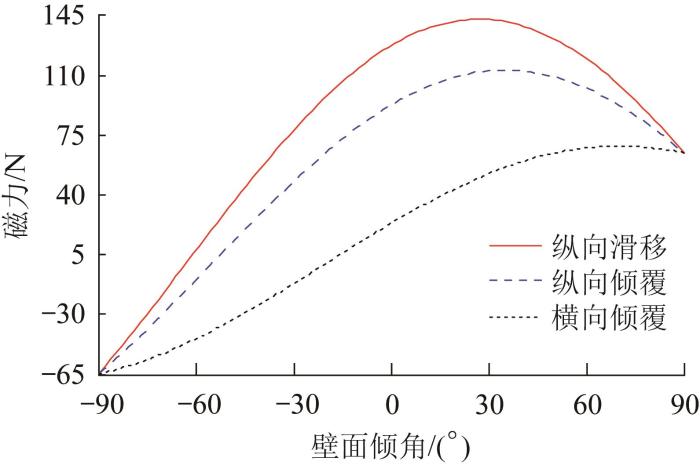
图8
图8
抵抗3种失稳情况时所需的最小磁力
Fig.8
Minimum magnetic force required to resist three types of instability situations
由图8可得,爬壁机器人在抵抗纵向滑移时所需的磁力最大。此时,壁面倾角为27°,则每个磁吸附模块所产生的磁力应满足Fi ≥142.56 N。
2.3 优化目标
为了实现爬壁机器人的轻量化设计,确定优化目标为磁吸附模块整体质量最小化,则目标函数可表示为:
其中:
式中:
2.4 优化模型
在保证爬壁机器人实现应有功能的前提下,根据安装空间对磁吸附模块的结构参数进行进一步调整。为更好地对比优化前后的结果,将2.1节中磁吸附模块的结构参数作为初始参数,即X=(a, b, c, d, e)=(8, 16, 35, 22, 11) mm,该结构参数下对应的磁力仿真值为142.92 N,取整为143 N,满足2.2节中的约束条件。最终得到的优化数学模型可表示为:
3 基于虚拟仿真的磁力代理模型构建
3.1 磁力仿真模型实验验证
为了验证磁吸附模块磁力仿真模型的可靠性,为后续代理模型的建立提供基础,根据1节中的三磁路结构和设定的初始尺寸,制造了一块磁吸附模块样品,并使用拉力传感器对其磁力进行测试。设定模拟壁面的钢板厚度为10 mm,将其固定在实验平台的底部。拉力传感器的一端与磁吸附模块连接,另一端与固定座连接,通过叠加垫片的方式来改变磁吸附模块与壁面之间的气隙距离,使其在5~12 mm范围内变化。磁吸附模块磁力测试实验平台如图9所示。
图9
图9
磁吸附模块磁力测试实验平台
Fig.9
Experimental platform of magnetic force test for magnetic adsorption module
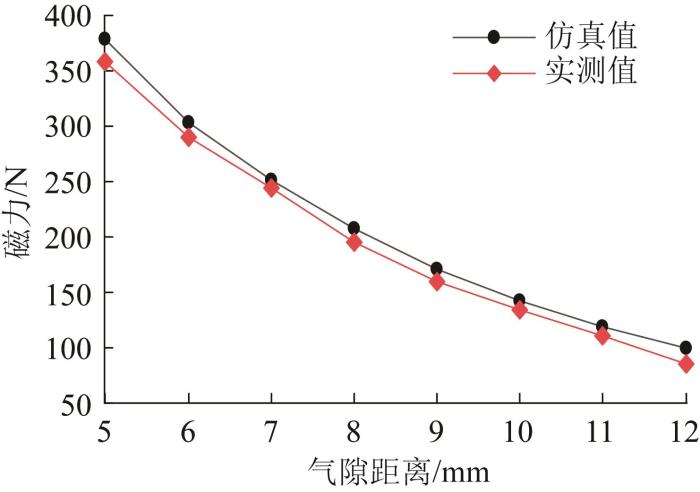
图10
图10
磁吸附模块磁力的仿真值与实测值对比
Fig.10
Comparison of simulated and measured magnetic force values of magnetic adsorption module
3.2 磁力代理模型的建立
代理模型的建立主要由两部分构成:一是选择代理模型的初始样本点,二是选择合适的代理模型。
3.2.1 初始样本采样
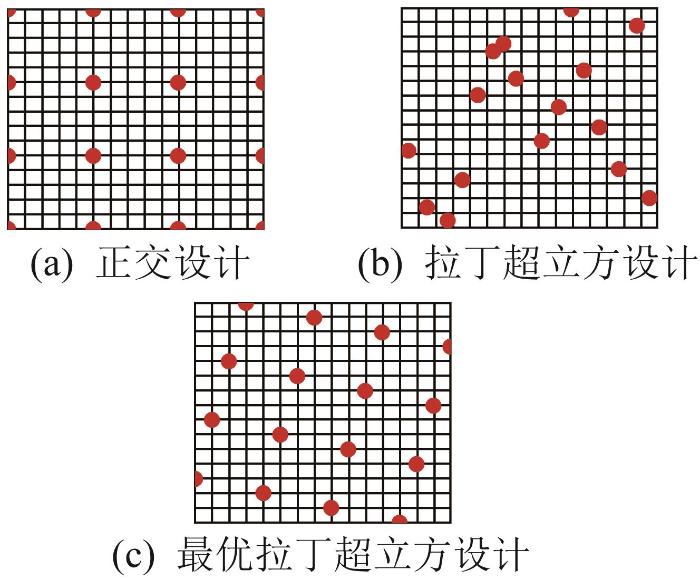
图11
图11
不同试验设计方法的采样效果
Fig.11
Sampling effect of different experimental design methods
基于上述分析,本文采用最优拉丁超立方设计方法在磁吸附模块结构参数取值范围内进行抽样,得到100组样本数据,并运用ANSYS参数化建模得到对应的磁力仿真值,部分数据如表2所示。
表2 构建磁力代理模型的部分样本点及对应的磁力仿真值
Table 2
| 样本点 | a/mm | b/mm | c/mm | d/mm | e/mm | F(X)/N |
|---|---|---|---|---|---|---|
| 1 | 5.354 | 21.48 | 29.89 | 21.45 | 13.26 | 128.570 |
| 2 | 5.990 | 22.94 | 28.44 | 12.91 | 14.46 | 69.073 |
| 3 | 8.889 | 7.42 | 36.22 | 21.64 | 18.24 | 87.366 |
| 4 | 8.040 | 15.18 | 36.11 | 14.55 | 7.93 | 65.284 |
| 5 | 10.727 | 22.70 | 35.89 | 28.55 | 13.43 | 272.450 |
| 6 | 6.838 | 27.55 | 33.33 | 26.73 | 11.71 | 213.010 |
| 7 | 7.192 | 16.64 | 35.78 | 17.27 | 20.81 | 142.230 |
| 8 | 9.030 | 5.73 | 34.67 | 16.55 | 11.37 | 37.808 |
| 9 | 8.747 | 24.39 | 28.67 | 12.73 | 8.96 | 49.399 |
| 10 | 8.323 | 20.52 | 31.22 | 21.09 | 7.59 | 109.780 |
| 11 | 11.222 | 20.27 | 36.78 | 16.73 | 9.65 | 107.380 |
| 12 | 6.273 | 21.97 | 34.22 | 26.36 | 4.50 | 137.260 |
| 13 | 11.364 | 20.03 | 26.56 | 15.09 | 12.57 | 66.402 |
| 14 | 5.424 | 25.12 | 33.11 | 15.64 | 18.58 | 135.950 |
| 15 | 11.010 | 8.15 | 27.44 | 24.73 | 7.76 | 66.603 |
| 16 | 8.182 | 13.48 | 26.78 | 13.09 | 12.23 | 42.979 |
| 17 | 6.131 | 13.97 | 36.56 | 19.82 | 13.09 | 126.730 |
| 18 | 6.768 | 5.97 | 29.56 | 14.36 | 16.35 | 28.872 |
| 19 | 10.020 | 5.24 | 31.56 | 23.45 | 12.91 | 50.487 |
| 20 | 11.646 | 19.79 | 32.67 | 14.18 | 17.38 | 99.943 |
| … | … | … | … | … | … | … |
| 79 | 11.717 | 21.73 | 27.00 | 24.55 | 12.74 | 141.920 |
| 80 | 5.636 | 24.88 | 35.44 | 19.09 | 8.96 | 124.080 |
| 81 | 6.414 | 12.27 | 26.11 | 20.00 | 15.49 | 77.611 |
| 82 | 11.434 | 10.58 | 30.00 | 22.55 | 19.27 | 104.780 |
| 83 | 11.505 | 22.45 | 31.67 | 14.73 | 8.45 | 67.949 |
| 84 | 5.707 | 6.70 | 33.89 | 16.36 | 8.28 | 39.014 |
| 85 | 10.444 | 8.88 | 36.67 | 23.64 | 9.82 | 105.650 |
| 86 | 5.283 | 13.24 | 27.56 | 25.45 | 9.31 | 88.687 |
| 87 | 8.465 | 17.85 | 26.00 | 25.27 | 10.17 | 113.340 |
| 88 | 9.242 | 17.12 | 34.44 | 21.27 | 13.94 | 153.140 |
| 89 | 11.788 | 17.85 | 34.11 | 24.18 | 7.42 | 147.230 |
| 90 | 11.929 | 9.36 | 34.56 | 18.73 | 15.83 | 84.310 |
| 91 | 11.152 | 11.30 | 34.89 | 27.64 | 17.21 | 172.770 |
| 92 | 9.455 | 9.85 | 32.44 | 15.82 | 20.30 | 69.653 |
| 93 | 5.212 | 17.36 | 32.89 | 14.00 | 11.54 | 71.916 |
| 94 | 10.798 | 19.06 | 28.89 | 26.18 | 5.02 | 119.520 |
| 95 | 11.293 | 11.79 | 33.78 | 12.00 | 9.99 | 42.234 |
| 96 | 9.525 | 5.48 | 29.44 | 15.45 | 8.79 | 24.149 |
| 97 | 7.051 | 5.00 | 35.22 | 24.91 | 11.88 | 58.269 |
| 98 | 10.869 | 14.45 | 30.56 | 28.91 | 12.06 | 167.910 |
| 99 | 11.081 | 10.09 | 29.33 | 12.36 | 15.32 | 40.109 |
| 100 | 6.980 | 24.64 | 26.67 | 18.91 | 19.61 | 126.210 |
3.2.2 4-RSM的构建
对具有复杂耦合关系的数据进行拟合时,多项式代理模型是一个不错的选择。多项式拟合不仅具有较高的预测精度,还可以得到显性的函数关系。本文利用MATLAB统计工具箱中的函数拟合了磁吸附模块磁力与结构参数的4-RSM,具体函数表达式如下:
F
表3 代理模型的精度评价指标
Table 3
| 代理模型 | R2 | ERMS |
|---|---|---|
| 2-RSM | 0.987 3 | 0.025 46 |
| 4-RSM | 0.994 4 | 0.016 96 |
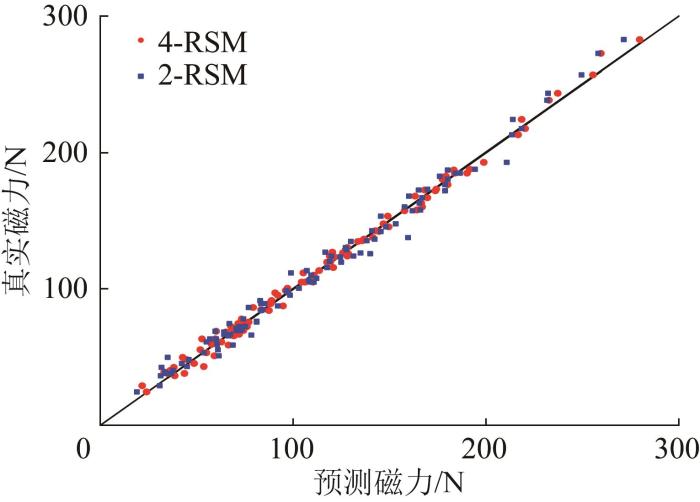
图12
图12
不同代理模型的预测效果对比
Fig.12
Comparison of prediction effect of different surrogate models
表4 不同结构参数组合下磁力的相对误差对比
Table 4
| 组别 | 结构参数/mm | 磁力仿真值/N | 磁力预测值/N | 相对误差/% | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| a | b | c | d | e | 2-RSM | 4-RSM | 2-RSM | 4-RSM | ||
| 初始 | 8 | 16 | 35 | 22 | 11 | 142.92 | 134.53 | 138.44 | 5.87 | 3.13 |
| 测试1 | 7 | 13 | 29 | 18 | 13 | 76.93 | 74.02 | 78.82 | 3.78 | 2.46 |
| 测试2 | 9 | 17 | 32 | 21 | 14 | 135.27 | 129.75 | 133.10 | 4.08 | 1.60 |
| 测试3 | 10.5 | 23 | 35 | 25.5 | 18 | 256.96 | 245.66 | 248.84 | 4.40 | 3.16 |
| 测试4 | 12 | 29 | 37 | 30 | 21 | 398.49 | 380.92 | 393.51 | 4.41 | 1.25 |
4 磁吸附模块结构参数优化求解
长期以来,优化求解问题一直是研究热点,其存在于各种实际系统中,如故障诊断系统、能源管理系统等。大量复杂的优化问题难以使用传统的数学规划技术来求解。因此,学者们开发了大量的群体智能优化算法,这些算法均具有易实现、自主学习能力强等优点。其中,DBO算法是一种基于种群的智能算法,其灵感来自蜣螂的滚球、跳舞、觅食、偷窃和繁殖行为。DBO算法兼顾全局探索和局部开发,具有收敛速度快和求解精度高的特点,可有效地处理实际优化问题[22]。
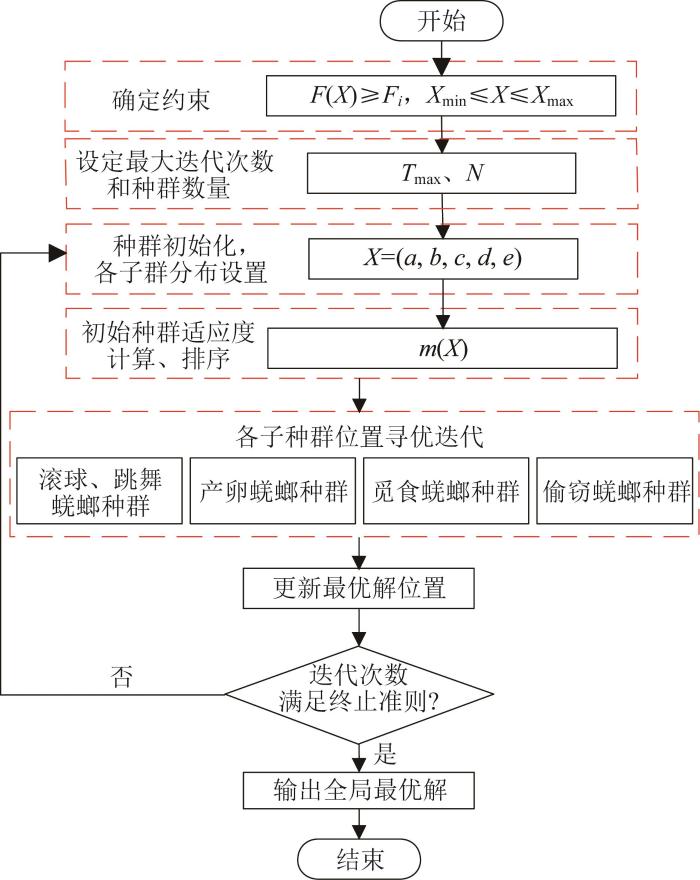
图13
图13
基于DBO算法的磁吸附模块结构参数优化求解流程
Fig.13
Optimization solution process of structural parameters of magnetic adsorption module based on DBO algorithm
表5 DBO算法的主要参数
Table 5
| 参数 | 数值 |
|---|---|
| 种群数量/个 | 90 |
| 迭代数/次 | 1 000 |
| 各子种群数量(滚球∶产卵∶觅食∶偷窃) | 6∶6∶7∶11 |
| 滚球蜣螂缺陷系数 | 0.1 |
| 滚球蜣螂常值 | 0.3 |
| 滚球、跳舞行为概率 | 0.5 |
| 觅食蜣螂常值 | 0.5 |
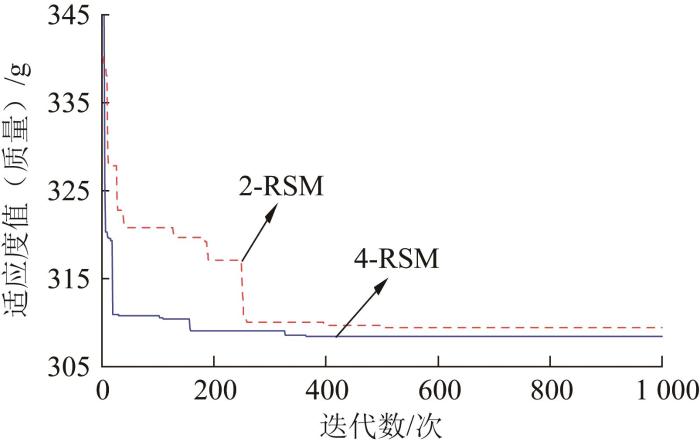
利用DBO算法对文献[15]中的2-RSM和本文的4-RSM进行求解,迭代过程如图14所示,最终得到的磁吸附模块结构参数的最优解如表6所示。由图14可以看出,DBO算法在很少的迭代次数内即可使目标函数逼近全局最优点,且迭代过程中适应度值的波动很小,说明将该算法应用于本文是十分有效的。由表6可以看出,基于2-RSM优化得到的结构参数a、c、d、e均趋于设定的临界点,该结构参数组合下磁吸附模块磁力的预测值与仿真值(118.03 N)之间的相对误差高达21.2%,不满足优化设计的约束条件,故整个优化过程无效。基于4-RSM得到的最优结构参数下磁力预测值与仿真值(138.11 N)之间的相对误差为3.5%,误差很小,说明所建立的4-RSM具有很高的可信度,且所预测的磁力值与约束条件相差较小。优化后磁吸附模块的质量减小了12.7%,整个优化过程简单有效。
图14
图14
基于2-RSM和4-RSM的优化求解迭代过程
Fig.14
Optimization solution iterative process based on 2-RSM and 4-RSM
表6 磁吸附模块结构参数优化结果
Table 6
| 结构参数与性能参数 | 初始值 | 优化值 | |
|---|---|---|---|
| 2-RSM | 4-RSM(取整①) | ||
| a/mm | 8 | 5 | 5(5) |
| b/mm | 16 | 11.85 | 11.803 9(11.8) |
| c/mm | 35 | 37 | 37(37) |
| d/mm | 22 | 30.00 | 25.568(25.6) |
| e/mm | 11 | 4.98 | 13.8145(13.8) |
| m(X)/g | 353.43 | 309.41 | 308.49(308.66) |
| F(X)/N | — | 143.00 | 143.00(143.12) |
①取整表示对结构参数取整,将取整后参数代入对应公式后重新计算质量m(X)与磁力F(X)。
5 爬壁机器人负载实验
根据优化得到的结构参数,研制了磁吸附模块,并将其安装在爬壁机器人样机中,通过开展负载实验来测试机器人的负载能力。通过静力学分析可以得出,爬壁机器人在抵抗纵向滑移时所需的磁力最大。因此,仅针对机器人的纵向运动进行负载能力测试。如图15所示,在实验过程中,机器人吸附在壁面上,通过加载不同的哑铃片(负载),直到机器人发生纵向滑移。实验结果表明,机器人的最大负载可达18 kg,满足机器人的初始载荷设计要求(15 kg),进而验证了磁吸附模块优化的有效性以及优化结果的正确性。
图15
6 结 论
本文基于轻量化目标提出了一种结合虚拟仿真技术、4-RSM和DBO算法的磁吸附模块结构优化方法。所做工作及相关结论如下:
1)比较了4种典型的Halbach阵列磁路模式的吸附效率。结果表明,与双磁路、五磁路和七磁路模式相比,三磁路模式所产生的磁力相对更高。
2)结合最优拉丁超立方设计、ANSYS参数化建模和MATLAB统计工具箱,建立了磁吸附模块磁力与结构参数之间的4-RSM。同时,通过相关系数R2和均方根误差ERMS以及5组结构参数下磁吸附模块磁力仿真值与预测值的比较,验证了所构建的4-RSM具有较高的可信度。
3)建立了以磁吸附模块轻量化为目标、以机器人吸附稳定性和结构参数为约束条件的优化模型,并采用DBO算法进行优化求解。结果表明,建立的4-RSM能够有效地表达磁吸附模块磁力与结构参数之间的耦合关系,且其预测误差较小。优化后磁吸附模块的质量减小了12.7%。
4)基于优化结果制作了磁吸附模块和爬壁机器人样机,并通过实验测试了机器人的负载能力。实验结果满足机器人的设计要求,进一步验证了优化过程的有效性。
值得注意的是,本文采用代理模型的思路来构建磁力模型,该方法对其他类似磁吸附式爬壁机器人的磁力分析同样有效,可为其磁吸附模块的设计与优化提供指导。
参考文献
爬壁机器人焊缝高效修形技术研究
[J].
Research on high efficiency weld modification technology for wall-climbing robot
[J].DOI:10.3901/jme.2023.09.012 [本文引用: 1]
一种滚动密封爬壁机器人失效分析
[J].
Failure analysis of a rolling sealed wall climbing robots
[J].
可自适应变曲率立面的分体柔性爬壁机器人设计与分析
[J].
Design and analysis of split-flexible wall-climbing robot with adaptive variable curvature facade
[J].DOI:10.3901/jme.2021.03.049 [本文引用: 1]
爬壁机器人发展现状与关键技术研究综述
[J].
Review on development status and key technologies of wall-climbing robots
[J].
爬壁机器人研究现状及发展趋势
[J].
Research status and development trend of wall climbing robot
[J].DOI:10.3901/jme.2023.05.011 [本文引用: 1]
永磁吸附履带式爬壁机器人转向动力特性分析
[J].
Steering dynamic characteristics analysis of permanent magnetic tracked wall-climbing robot
[J].
Design and optimization of the magnetic adsorption mechanism of a pipeline-climbing robot
[J].
爬壁机器人悬摆式磁吸附机构的设计与优化
[J].
Design and optimization of pendulous magnetic adsorption mechanism for wall-climbing robots
[J].
Experimental and numerical optimization of magnetic adhesion force for wall climbing robot applications
[J].
Strong rare earth cobalt quadrupoles
[J].
轮腿式爬壁机器人的永磁吸附装置设计与优化
[J].
Design and optimization of permanent magnet adsorption device for wheel-legged wall-climbing robot
[J].
基于Halbach阵列爬壁机器人永磁轮吸附单元的设计与优化
[J].
The optimization of a novel permanent-magnetic wheel adsorption unit for wall-climbing robot based on Halbach array
[J].DOI:10.3969/j.issn.1006-4303.2015.04.009 [本文引用: 1]
Halbach阵列机器人磁吸附单元理论分析与实验研究
[D].
Theoretical and experiment research on magnetic adhesion device for wall-climbing robot based on Halbach array
[D].
Magnetic circuit analysis of Halbach array and improvement of permanent magnetic adsorption device for wall-climbing robot
[J].
履带式爬壁机器人磁吸附单元的参数分析与优化
[J].
Parameter analysis and optimization of magnetic adsorption unit for crawler wall-climbing robot
[J].
The multi-objective optimization design for the magnetic adsorption unit of wall-climbing robot
[J].
除锈爬壁机器人壁面行走控制技术研究
[D].
Research on wall travelling control for ship rust removal wall climbing robot
[D].
石化储罐壁面检测爬壁机器人设计及其特性研究
[D].
Wall-climbing robot design and property study based on surface testing of petrochemical tank
[D].
On efficient global optimization via universal Kriging surrogate models
[J].
Robust design optimization using surrogate models
[J].
多参数非线性系统全局敏感性分析与动态代理模型研究
[D].
The study on global sensitivity analysis and dynamic metamodel of multiple-parameters nonlinear system
[D].
Dung beetle optimizer: a new meta-heuristic algorithm for global optimization
[J].