助力行走型下肢外骨骼机器人是一种可穿戴式助力装备,其结合了先进的控制技术、通信技术以及轻便的结构,主要用于辅助下肢生理功能退化的穿戴者行走,以提升其运动机能,这大大促进了智能化机器与人类的力量结合。近20年来,越来越多的老人和残障人士遭遇了下肢生理功能退化问题。由2019年联合国经济和社会事务部调查结果可知,日本的老年人口占比居世界之最,其次是意大利、德国、法国、英国、加拿大和中国等,这些国家的老年人口占比均超过了10%。可想而知,随着年老、体弱人群的日益增多,失能或半失能人群的照料与护理已成为重要的社会问题[1 ] 。在下肢外骨骼助力机器人的辅助下,老年人或有运动功能障碍的人群可实现正常行走。关节驱动力矩作为运动或保持某种姿态的重要参数,其已成为下肢外骨骼助力机器人稳定性判定和控制方面的研究重点和热点[2 -3 ] 。
经查阅大量文献与资料可知,在实际应用中,下肢外骨骼助力机器人主要分为以下4种。第1种为最常见的医疗康复型外骨骼机器人,用于辅助偏瘫患者或运动机能受损人群进行康复训练,为其提供重新站立的可能和希望,典型代表产品有可穿戴式机器人HAL(hybrid assistive limb, 混合辅助假肢)、ReWalk下肢康复外骨骼[4 -5 ] 等;第2种是助老助残型下肢外骨骼机器人,主要用于协助老年人行走及上下楼梯,典型代表产品有哈佛大学研制的柔性下肢外骨骼和中国科学院深圳先进技术研究院自主研发的下肢外骨骼机器人[6 -7 ] 等;第3种是军事负重型外骨骼机器人,用于提升军人的负载能力及行走速度,可有效增强军人的越野耐力,典型代表产品有伯克利仿生科技公司开发的通用型负重外骨骼(human universal load carrier, HULC)和西安交通大学研制的负重型下肢外骨骼机器人[8 -9 ] 等;第4种是无动力聚力型下肢外骨骼机器人,其不需要外加动力源,能够协助穿戴者减小体力消耗以达到增强体力的目的,典型代表产品有德黑兰大学研制的人用无动力外骨骼(unpowered exoskeleton for human, UEFH)和中国科学院深圳先进技术研究院自主研制的无动力型下肢外骨骼机器人[10 -11 ] 等。
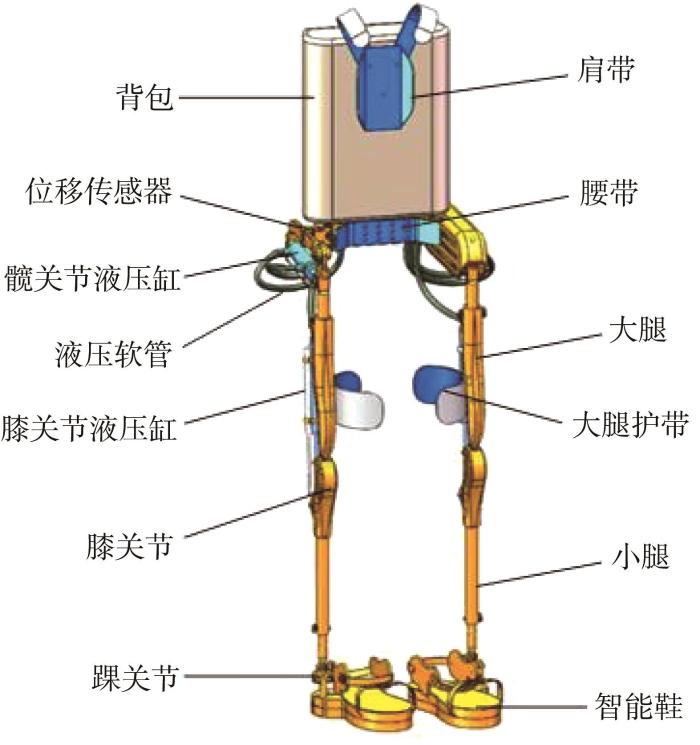
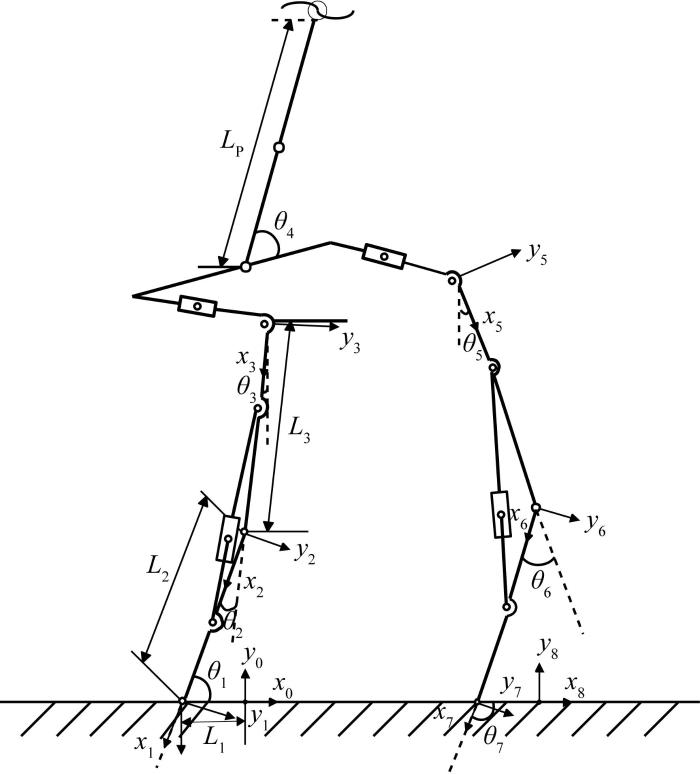
为实现下肢外骨骼助力机器人穿戴柔顺性和控制精准性的提升,基于安徽工程大学机器人产业技术研究院设计开发的电液伺服驱动下肢外骨骼助力机器人APWR-A01(其结构如图1 所示)[12 -14 ] ,利用合适的动力学分析方法来求解其助行过程中的动力学参数变化情况。
图1
图1
电液伺服驱动下肢外骨骼助力机器人的结构示意
Fig.1
Structure diagram of electro-hydraulic servo driven lower limb exoskeleton assisted robot
1 下肢外骨骼助力机器人动力学分析
1.1 动力学分析方法选择
在研究外骨骼机器人动力学问题时,首先要构建其动力学模型。针对外骨骼机器人的动力学特性,国内和国外的很多学者都进行了深入研究,提出了牛顿‒欧拉法[15 ] 、拉格朗日法[16 ] 、凯恩法[17 ] 、虚功原理法[18 ] 、微分几何原理法[19 ] 、高斯法[20 ] 以及旋量对偶数法[21 ] 等动力学分析方法。其中,部分方法的优缺点如表1 所示。
鉴于本文是通过简化下肢外骨骼助力机器人机械结构并建立其动力学模型来求解其各关节的驱动力矩的,以及相关的运动学参数可利用三维运动捕捉系统快速测得,笔者结合不同动力学分析方法的优缺点,选用牛顿‒欧拉法来对机器人关节的驱动力和驱动力矩进行迭代计算。
1.2 步态特征分析
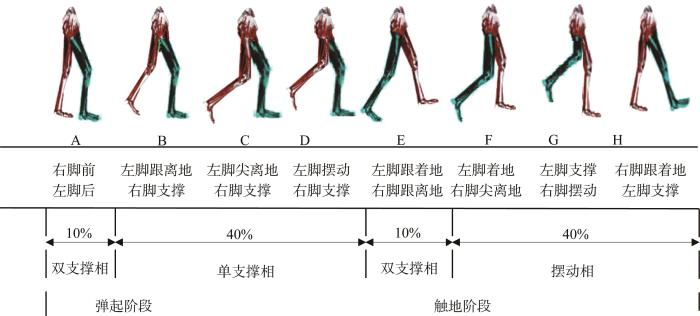
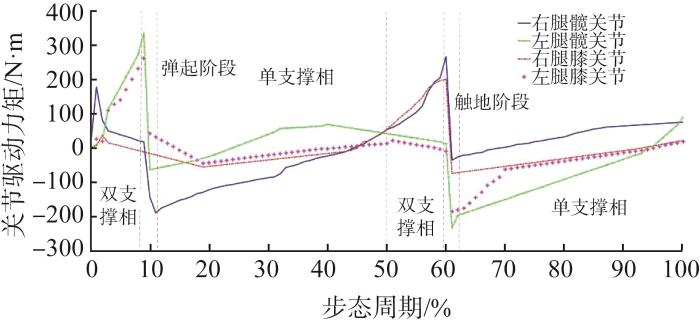
通过对人体行走步态周期进行分析可知,其可划分为支撑相(包括单支撑相和双支撑相)与摆动相。双支撑相是指双脚与地面接触,人体重心由后迈步大腿向前腿转移的阶段;单支撑相(支撑脚全部着地,对侧脚处于摆动相)有3个阶段,分别为弹起阶段、触地阶段和摆动阶段,具体表现为人体单腿支撑,摆动腿从脚尖离地到脚跟着地的变化过程,该阶段人体下肢支撑全身质量,人体重心转移到单腿上,单腿支撑及单腿向前摆动。人体行走步态周期如图2 所示(以右腿为例,下文同)。
图2
图2
人体行走步态周期示意
Fig. 2
Schematic diagram of gait cycle of human walking
1.3 动力学建模与分析
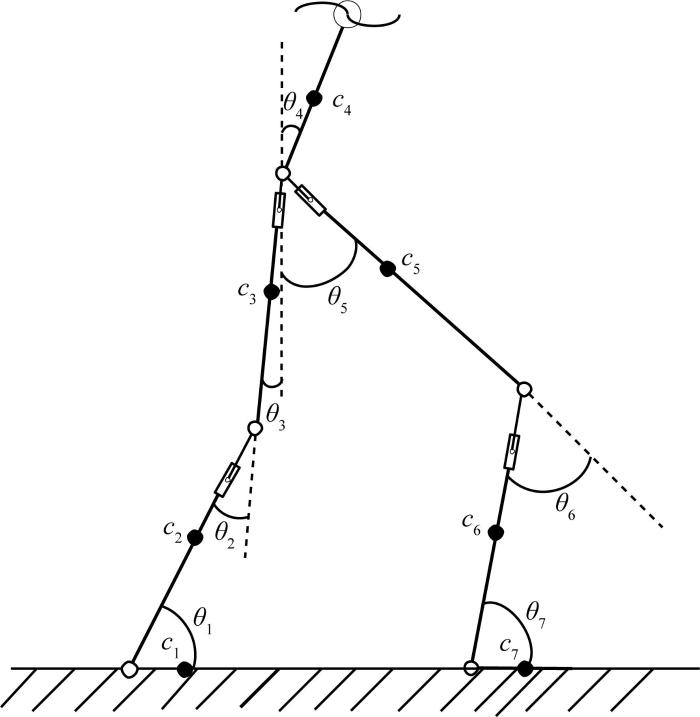
将下肢外骨骼助力机器人简化为七连杆结构,构建其在不同步态相位下的动力学模型。
1.3.1 摆动相阶段动力学建模与分析
基于简化的七连杆结构,构建下肢外骨骼助力机器人摆动相动力学模型,如图3 所示。图中各变量的含义如表2 所示,其中θ i ( x h , y h ) O -XY 下的绝对坐标。
图3
图3
下肢外骨骼助力机器人摆动相动力学模型
Fig.3
Dynamic model of swing phase for lower limb exoskeleton assisted robot
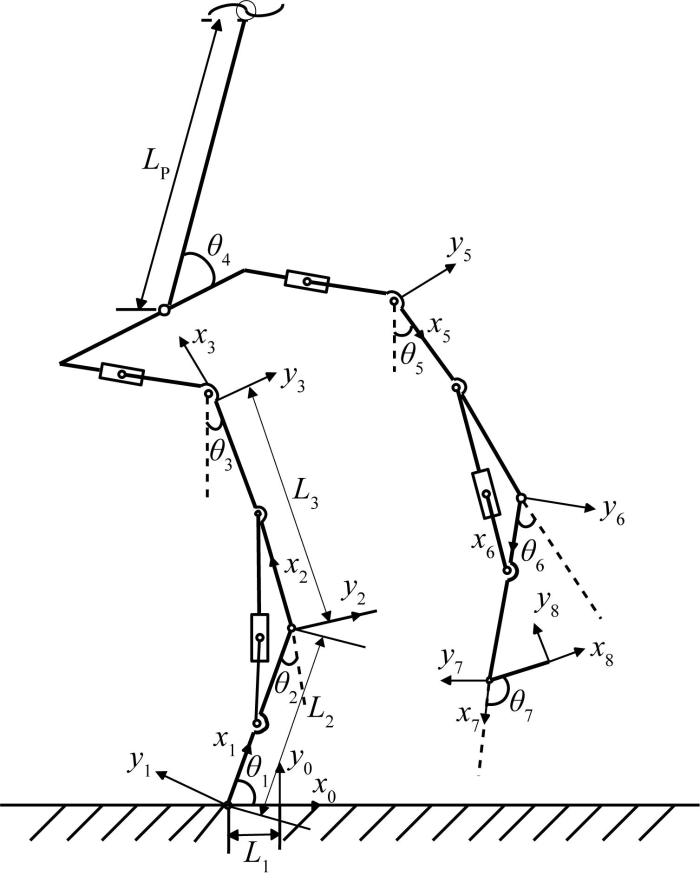
由于在行走过程中,下肢外骨骼助力机器人在冠状面与横断面上的运动范围不明显,因此将上述结构简化为矢状面简图,如图4 所示。
图4
图4
下肢外骨骼助力机器人矢状面摆动相简图
Fig.4
Sagittal swing phase diagram of lower limb exoskeleton assisted robot
由图4 可知,下肢外骨骼助力机器人各连杆结构的参数之间具有相关性,通过牛顿‒欧拉法可逐步推导得到相邻连杆的参数传递方程。
在下肢外骨骼助力机器人的步态相位转换过程中,各连杆角速度之间的关系为:
i + 1 ω i + 1 = R i i + 1 i ω i + θ ˙ i + 1 Z ̂ i + 1 Z ̂ i + 1 (1)
式中:i + 1 ω i + 1 i ω i i +1}({i })中连杆i +1(i )的角速度; i i + 1 R i }到坐标系{i +1}的转换矩阵;i + 1 Z ̂ i + 1 i +1}中Z 方向的单位向量。
i + 1 ω ˙ i + 1 = R i i + 1 R i ω ˙ i + R i i + 1 R i ω i × θ ˙ i + 1 Z ̂ i + 1 Z ̂ i + 1 + θ ¨ i + 1 Z ̂ i + 1 Z ̂ i + 1 (2)
式中:i + 1 ω ˙ i + 1 i ω ˙ i i +1}({i })中连杆i +1(i )的角加速度。
i + 1 v i + 1 = R i i + 1 i ω ˙ i × P i P i + 1 + i ω i × ( i ω i × i P i + 1 ) + v i v i (3)
式中:i + 1 v i + 1 i v i i +1}({i })中连杆i +1(i )的速度;i P i + 1 i }中连杆i +1的位置矢量。
i + 1 v ˙ c i + 1 = i + 1 ω ˙ i + 1 × P i + 1 P c i + 1 + i + 1 ω i + 1 × ( i + 1 ω i + 1 × P i + 1 P c i + 1 ) + v ˙ i + 1 v ˙ i + 1 (4)
式中:i + 1 v ˙ c i + 1 、 P i + 1 P c i + 1 i +1}中连杆i +1质心的加速度和位置矢量。
i + 1 F c i + 1 = m i v ˙ i + 1 v ˙ c i + 1 (5)
式中:i + 1 F c i + 1 i +1}中连杆i +1质心处的惯性力。
利用牛顿‒欧拉法求解下肢外骨骼助力机器人各连杆所受的力和力矩,由此可以求得其各关节的驱动力和驱动力矩。各连杆所受的力 f i n i
f i = R i + 1 i f i + 1 + F i (6)
n i = N i + R i + 1 i n i + 1 + P c i F i + R i + 1 i f i + 1 (7)
式中: F i N i i 的驱动力和驱动力矩。
ω 1 = 0 0 θ ˙ 1 ω ˙ 1 = 0 0 θ ¨ 1 ν 1 = g s θ 1 g c θ 1 0 ν ˙ c 1 = - 1 2 L 2 θ ˙ 1 2 + g s θ 1 1 2 L 2 θ ˙ 1 2 + g c θ 1 0
F 1 = - 1 2 m 2 L 2 θ ˙ 1 2 + m 2 g s θ 1 1 2 m 2 L 2 θ ˙ 1 2 + m 2 g c θ 1 0 N 1 = 0 0 I 1 Z Z θ ¨ 1
式中:s表示sin,c表示cos;g 为重力加速度;I 1 ZZ
ω 2 = 0 0 θ ˙ 1 + θ ˙ 2 ω ˙ 2 = 0 0 θ ¨ 1 + θ ¨ 2 v ˙ 2 = L 2 θ ¨ 1 s θ 2 - θ ˙ 1 2 c θ 2 + g s θ 12 L 2 θ ¨ 1 c θ 2 - θ ˙ 1 2 s θ 2 + g c θ 12 0
v ˙ c 2 = L 2 θ ¨ 1 s θ 2 - θ ˙ 1 2 c θ 2 + g s θ 12 - 1 2 L 3 θ ˙ 1 + θ ˙ 2 2 L 2 θ ¨ 1 c θ 2 + θ ˙ 1 2 s θ 2 + g c θ 12 + 1 2 L 3 θ ˙ 1 + θ ˙ 2 2 0
F 2 = m 3 L 2 θ ¨ 1 s θ 2 - θ ˙ 1 2 c θ 2 + g s θ 12 - 1 2 L 3 θ ˙ 1 + θ ˙ 2 2 m 3 L 2 θ ¨ 1 c θ 2 + θ ˙ 1 2 s θ 2 + g c θ 12 + 1 2 L 3 θ ˙ 1 + θ ˙ 2 2 0
N 2 = 0 0 I 2 Z Z ( θ ¨ 1 + θ ¨ 2 )
式中:c θ i j = c o s ( θ i + θ j ) , s θ i j = s i n ( θ i + θ j )
ω 3 = 0 0 θ ˙ 1 + θ ˙ 2 + θ ˙ 3 + θ ˙ 4 ω ˙ 3 = 0 0 θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + θ ¨ 4
v ˙ 3 = L 2 θ ¨ 1 s θ 234 - θ ˙ 1 2 c θ 234 + g s θ 1234 + L 3 s θ 34 θ ¨ 1 + θ ¨ 2 - c θ 34 θ ˙ 1 + θ ˙ 2 2 L 2 θ ¨ 1 c θ 234 + θ ˙ 1 2 s θ 234 + g c θ 1234 + L 3 s θ 34 θ ˙ 1 + θ ˙ 2 2 + c θ 34 θ ¨ 1 + θ ¨ 2 0
v ˙ c 3 = L 2 θ ¨ 1 s θ 234 - θ ˙ 1 2 c θ 234 + g s θ 1234 + L 3 s θ 34 θ ¨ 1 + θ ¨ 2 + θ ¨ 3 - c θ 34 θ ˙ 1 + θ ˙ 2 + θ ˙ 3 2 - L 4 θ ˙ 1 + θ ˙ 2 + θ ˙ 3 + θ ˙ 4 2 L 2 θ ¨ 1 c θ 234 + θ ˙ 1 2 s θ 234 + g c θ 1234 + L 3 s θ 34 θ ˙ 1 + θ ˙ 2 + θ ˙ 3 2 + c θ 34 θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + L 4 θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + θ ¨ 4 0
F 3 = m 3 + m 4 L 2 θ ¨ 1 s θ 234 - θ ˙ 1 2 c θ 234 + g s θ 1234 + L 3 s θ 34 θ ¨ 1 + θ ¨ 2 + θ ¨ 3 - c θ 34 θ ˙ 1 + θ ˙ 2 + θ ˙ 3 2 - L 4 θ ˙ 1 + θ ˙ 2 + θ ˙ 3 + θ ˙ 4 2 m 3 + m 4 L 2 θ ¨ 1 c θ 234 + θ ˙ 1 2 s θ 234 + g c θ 1234 + L 3 s θ 34 θ ˙ 1 + θ ˙ 2 + θ ˙ 3 2 + c θ 34 θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + L 4 θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + θ ¨ 4 0
N 3 = 0 0 I 3 Z Z + I 4 Z Z θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + θ ¨ 4
根据牛顿‒欧拉迭代法,取 n 3 中作用在右腿各连杆上力矩沿垂直于该杆方向(Z ̂ τ 3
τ 3 = n 3 Z ̂ 3 = I 3 Z Z + I 4 Z Z θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + θ ¨ 4 + 1 2 m 3 + m 4 L P L 2 θ ¨ 1 c θ 234 + θ ˙ 1 2 s θ 234 + g c θ 1234 + L 3 s θ 34 θ ˙ 1 + θ ˙ 2 + θ ˙ 3 2 + c θ 34 θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + L P θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + θ ¨ 4 (8)
τ 2 = n 2 Z ̂ 2 = I 2 Z Z θ ¨ 1 + θ ¨ 2 + τ 3 + L 3 m 4 L 2 θ ¨ 1 c θ 2 + θ ˙ 1 2 s θ 2 + L 3 θ ¨ 1 + θ ¨ 2 + A 4 + B 4 + m 1 + m 2 + 3 2 m 3 + m 4 g c θ 12 + C 4 + m 1 + m 2 + 1 2 m 3 D 1 + m 1 + 1 2 m 2 E 1 + 1 2 m 1 F 1 (9)
A 4 = L P - s θ 34 θ ˙ 1 + θ ˙ 2 + θ ˙ 3 + θ ˙ 4 2 + c θ 34 θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + θ ¨ 4
B 4 = m 1 + m 2 + 3 2 m 3 L 2 θ ¨ 1 c θ 2 + θ ˙ 1 2 s θ 2
C 4 = m 1 + m 2 + m 3 + 1 4 m 4 L 3 θ ¨ 1 + θ ¨ 2
D 1 = L 3 - s θ 4 θ ˙ 1 + θ ˙ 2 + θ ˙ 3 + θ ˙ 4 2 + c θ 4 θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + θ ¨ 4
E 1 = L 2 c θ 45 θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + θ ¨ 4 + θ ¨ 5 - s θ 45 θ ˙ 1 + θ ˙ 2 + θ ˙ 3 + θ ˙ 4 + θ ˙ 5 2
F 1 = L 1 s θ 456 θ ˙ 1 + θ ˙ 2 + θ ˙ 3 + θ ˙ 4 + θ ˙ 5 + θ ˙ 6 2 - c θ 456 θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + θ ¨ 4 + θ ¨ 5 + θ ¨ 6
τ 1 = n 1 Z ̂ 1 = I 1 Z Z θ ¨ 1 + τ 2 + L 2 m 4 A 5 + m 1 + 5 4 m 2 + 2 m 3 + m 4 L 2 θ ¨ 1 + m 1 + m 2 + 3 2 m 3 + m 4 B 5 + m 1 + m 2 + 1 2 m 3 C 5 + m 1 + 1 2 m 2 D 2 - 1 2 m 1 E 2 (10)
A 5 = L P - s θ 234 θ ˙ 1 + θ ˙ 2 + θ ˙ 3 + θ ˙ 4 2 + c θ 234 θ ¨ 1 +
θ ¨ 2 + θ ¨ 3 + θ ¨ 4
B 5 = L 3 - s θ 2 θ ˙ 1 + θ ˙ 2 2 + c θ 2 θ ¨ 1 + θ ¨ 2
C 5 = L 3 - s θ 235 θ ˙ 1 + θ ˙ 2 + θ ˙ 3 + θ ˙ 5 2 + c θ 235 θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + θ ¨ 5
D 2 = L 2 - s θ 2356 θ ˙ 1 + θ ˙ 2 + θ ˙ 3 + θ ˙ 5 + θ ˙ 6 2 + c θ 2356 θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + θ ¨ 5 + θ ¨ 6
E 2 = L 1 - s θ 23567 θ ˙ 1 + θ ˙ 2 + θ ˙ 3 + θ ˙ 5 + θ ˙ 6 + θ ˙ 7 2 +
c θ 23567 θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + θ ¨ 5 + θ ¨ 6 + θ ¨ 7
τ 7 = n 7 Z ̂ 7 = I 7 Z Z θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + θ ¨ 5 + θ ¨ 6 + θ ¨ 7 + 1 2 m 1 L 1 L 2 θ ¨ 1 c θ 23567 + θ ˙ 1 2 s θ 23567 + g c θ 123567 + A 1 + B 1 + C 1 + 1 2 L 1 θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + θ ¨ 5 + θ ¨ 6 + θ ¨ 7 (11)
A 1 = L 3 s θ 567 ( θ ˙ 1 + θ ˙ 2 + θ ˙ 3 2 + c θ 567 θ ¨ 1 + θ ¨ 2 + θ ¨ 3
B 1 = L 3 s θ 67 θ ˙ 1 + θ ˙ 2 + θ ˙ 3 + θ ˙ 5 2 + c θ 67 θ ¨ 1 +
θ ¨ 2 + θ ¨ 3 + θ ¨ 5
C 1 = L 2 s θ 7 θ ˙ 1 + θ ˙ 2 + θ ˙ 3 + θ ˙ 5 + θ ˙ 6 2 + c θ 7 θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + θ ¨ 5 + θ ¨ 6
τ 6 = n 6 Z ̂ 6 = I 6 Z Z θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + θ ¨ 5 + θ ¨ 6 + τ 7 + L 2 m 1 + 1 2 m 2 L 2 θ ¨ 1 c θ 2356 + θ ˙ 1 2 s θ 2356 + g c θ 12356 + A 2 + B 2 + m 1 + 1 4 m 2 L 2 θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + θ ¨ 5 + θ ¨ 6 + 1 2 m 1 C 2 (12)
A 2 = L 3 s θ 56 θ ˙ 1 + θ ˙ 2 + θ ˙ 3 2 + c θ 56 θ ¨ 1 + θ ¨ 2 + θ ¨ 3
B 2 = L 3 s θ 6 θ ˙ 1 + θ ˙ 2 + θ ˙ 3 + θ ˙ 5 2 + c θ 6 θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + θ ¨ 5
C 2 = L 1 c θ 7 θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + θ ¨ 5 + θ ¨ 6 + θ ¨ 7 - s θ 7 θ ˙ 1 + θ ˙ 2 + θ ˙ 3 + θ ˙ 5 + θ ˙ 6 + θ ˙ 7 2
τ 5 = n 5 Z ̂ 5 = I 5 Z Z θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + θ ¨ 5 + τ 6 + L 3 m 1 + m 2 + 1 2 m 3 L 2 θ ¨ 1 c θ 235 + θ ˙ 1 2 s θ 235 + g c θ 1235 + A 3 + m 1 + m 2 + 1 4 m 3 L 3 θ ¨ 2 + θ ¨ 3 + θ ¨ 5 + m 1 + 1 2 m 2 B 3 + 1 2 m 1 C 3 (13)
A 3 = L 3 s θ 5 θ ˙ 1 + θ ˙ 2 + θ ˙ 3 2 + c θ 5 θ ¨ 1 + θ ¨ 2 + θ ¨ 3
B 3 = L 2 - s θ 6 θ ˙ 2 + θ ˙ 3 + θ ˙ 5 + θ ˙ 6 2 + c θ 6 θ ¨ 2 + θ ¨ 3 + θ ¨ 5 + θ ¨ 6
C 3 = L 1 c θ 67 θ ¨ 2 + θ ¨ 3 + θ ¨ 5 + θ ¨ 6 + θ ¨ 7 + s θ 67 θ ˙ 2 + θ ˙ 3 + θ ˙ 5 + θ ˙ 6 + θ ˙ 7 2
1.3.2 双支撑相阶段动力学建模与分析
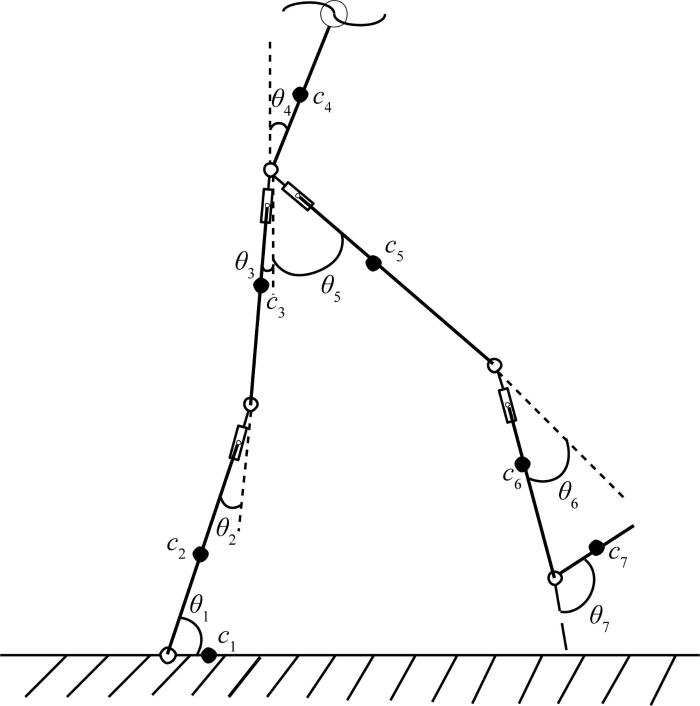
对于单支撑相,其与摆动相的区别在于支撑脚和摆动脚相反,故本文不再赘述。类似地,构建下肢外骨骼助力机器人双支撑相动力学模型,如图5 所示,简化的矢状面简图如图6 所示。
图5
图5
下肢外骨骼助力机器人双支撑相动力学模型
Fig.5
Dynamic model of dual-support phase for lower limb exoskeleton assisted robot
图6
图6
下肢外骨骼助力机器人矢状面双支撑相简图
Fig.6
Sagittal dual-support phase diagram of lower limb exoskeleton assistied robot
根据图6 ,利用牛顿‒欧拉法推导得到双支撑相阶段右腿髋关节的驱动力矩τ 3
τ 3 = n 3 Z ̂ 3 = I 3 Z Z + I 4 Z Z θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + θ ¨ 4 + 1 2 m 3 + m 4 L P L 1 θ ¨ 1 c θ 234 + θ ˙ 1 2 s θ 234 + g c θ 1234 + L 2 s θ 34 θ ˙ 1 + θ ˙ 2 2 + c θ 34 θ ¨ 1 + θ ¨ 2 + L 3 s θ 4 θ ˙ 1 + θ ˙ 2 + θ ˙ 3 2 + c θ 4 θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + L P θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + θ ¨ 4 (14)
τ 5 = n 5 Z ̂ 5 = I 3 Z Z + I 4 Z Z θ ¨ 7 + θ ¨ 6 + θ ¨ 5 + θ ¨ 4 + 1 2 m 3 + m 4 L P L 1 θ ¨ 7 c θ 456 + θ ˙ 7 2 s θ 456 + g c θ 4567 + L 2 s θ 45 θ ˙ 7 + θ ˙ 6 2 + c θ 45 θ ¨ 7 + θ ¨ 6 + L 3 s θ 4 θ ˙ 7 + θ ˙ 6 + θ ˙ 5 2 + c θ 4 θ ¨ 7 + θ ¨ 6 + θ ¨ 5 + L P θ ¨ 7 + θ ¨ 6 + θ ¨ 5 + θ ¨ 4 (15)
双支撑相阶段右腿膝关节的驱动力矩τ 2 τ 2 = n 2 Z ̂ 2 = I 2 Z Z θ ¨ 1 + θ ¨ 2 + τ 3 + L 3 m 4 L 2 θ ¨ 1 c θ 2 + θ ˙ 1 2 s θ 2 + L 3 θ ¨ 1 + θ ¨ 2 + A 6 + m 1 + m 2 + 5 4 m 3 B 6 + m 1 + m 2 + 3 2 m 3 + m 4 g c θ 12 + m 1 + m 2 + 3 2 m 3 C 6 + m 1 + m 2 + 1 2 m 3 D 3 + m 1 + 1 2 m 2 E 3 - 1 2 m 1 F 3 (16)
A 6 = L P - s θ 34 θ ˙ 7 + θ ˙ 6 + θ ˙ 7 + θ ˙ 4 2 + c θ 34 θ ¨ 7 + θ ¨ 6 + θ ¨ 5 + θ ¨ 4
B 6 = L 3 θ ¨ 1 + θ ¨ 2
C 6 = L 2 θ ¨ 1 c θ 2 + θ ˙ 1 2 s θ 2
D 3 = L 3 - s θ 3 θ ˙ 1 + θ ˙ 2 + θ ˙ 3 + θ ˙ 5 2 + c θ 3 θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + θ ¨ 5
E 3 = L 2 - s θ 56 θ ˙ 1 + θ ˙ 2 + θ ˙ 3 + θ ˙ 5 + θ ˙ 6 2 + c θ 56 θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + θ ¨ 5 + θ ¨ 6
F 3 = L 1 - s θ 567 θ ˙ 1 + θ ˙ 2 + θ ˙ 3 + θ ˙ 5 + θ ˙ 6 + θ ˙ 7 2 + c θ 567 θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + θ ¨ 5 + θ ¨ 6 + θ ¨ 7
τ 6 = n 6 Z ̂ 6 = I 6 Z Z θ ¨ 7 + θ ¨ 6 + τ 5 + m 4 A 7 + B 7 + m 1 + m 2 + 3 2 m 3 L 2 θ ¨ 7 c θ 6 + θ ˙ 7 2 s θ 6 + m 1 + m 2 + m 3 + m 4 + 1 2 m 3 g c θ 67 + m 1 + m 2 + m 3 + 1 4 m 3 L 3 θ ¨ 7 + θ ¨ 6 + m 1 + m 2 + 1 2 m 3 C 7 + m 1 + 1 2 m 2 D 4 - 1 2 m 1 E 4 (17)
A 7 = L 2 θ ¨ 7 c θ 6 + θ ˙ 7 2 s θ 6 + L 3 θ ¨ 7 + θ ¨ 6
B 7 = L P - s θ 45 θ ˙ 7 + θ ˙ 6 + θ ˙ 5 + θ ˙ 4 2 + c θ 45 θ ¨ 7 + θ ¨ 6 + θ ¨ 5 + θ ¨ 4
C 7 = L 3 - s θ 5 θ ˙ 7 + θ ˙ 6 + θ ˙ 5 + θ ˙ 3 2 + c θ 5 θ ¨ 7 + θ ¨ 6 + θ ¨ 5 + θ ¨ 3
D 4 = L 2 - s θ 32 θ ˙ 6 + θ ˙ 5 + θ ˙ 3 + θ ˙ 2 2 + c θ 32 θ ¨ 7 + θ ¨ 6 + θ ¨ 5 + θ ¨ 3 + θ ¨ 2
E 4 = L 1 - s θ 321 θ ˙ 7 + θ ˙ 6 + θ ˙ 5 + θ ˙ 3 + θ ˙ 2 + θ ˙ 1 2 + c θ 321 θ ¨ 7 + θ ¨ 6 + θ ¨ 5 + θ ¨ 3 + θ ¨ 2 + θ ¨ 1
τ 1 = n 1 Z ̂ 1 = I 1 Z Z θ ¨ 1 + τ 2 + L 2 m 4 A 8 + m 1 + 5 4 m 2 + 2 m 3 + m 4 L 2 θ ¨ 1 + m 1 + m 2 + 3 2 m 3 + m 4 L 3 - s θ 2 θ ˙ 1 + θ ˙ 2 2 + c θ 2 θ ¨ 1 + θ ¨ 2 + m 1 + m 2 + 1 2 m 3 B 8 + m 1 + 1 2 m 2 C 8 - 1 2 m 1 D 5 (18)
A 8 = L P - s θ 234 θ ˙ 1 + θ ˙ 2 + θ ˙ 3 + θ ˙ 4 2 + c θ 234 θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + θ ¨ 4
B 8 = L 3 - s θ 235 θ ˙ 1 + θ ˙ 2 + θ ˙ 3 + θ ˙ 5 2 + c θ 235 θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + θ ¨ 5
C 8 = L 2 - s θ 2356 θ ˙ 1 + θ ˙ 2 + θ ˙ 3 + θ ˙ 5 + θ ˙ 6 2 + c θ 2356 θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + θ ¨ 5 + θ ¨ 6
D 5 = L 1 - s θ 23567 θ ˙ 1 + θ ˙ 2 + θ ˙ 3 + θ ˙ 5 + θ ˙ 6 + θ ˙ 7 2 + c θ 23567 θ ¨ 1 + θ ¨ 2 + θ ¨ 3 + θ ¨ 5 + θ ¨ 6 + θ ¨ 7
τ 7 = n 7 Z ̂ 7 = I 7 Z Z θ ¨ 7 + τ 6 + m 4 A 9 + m 1 + 5 4 m 2 + 2 m 3 + m 4 L 2 θ ¨ 7 + m 1 + m 2 + 3 2 m 3 + m 4 L 3 - s θ 6 θ ˙ 7 + θ ˙ 6 2 + c θ 6 θ ¨ 7 + θ ¨ 6 + m 1 + m 2 + 1 2 m 3 B 9 + m 1 + 1 2 m 2 C 9 - 1 2 m 1 D 6 ( 19 )
A 9 = L P - s θ 456 θ ˙ 7 + θ ˙ 6 + θ ˙ 5 + θ ˙ 4 2 + c θ 456 θ ¨ 7 + θ ¨ 6 + θ ¨ 5 + θ ¨ 4
B 9 = L 3 - s θ 356 θ ˙ 7 + θ ˙ 6 + θ ˙ 5 + θ ˙ 3 2 + c θ 356 θ ¨ 7 + θ ¨ 6 + θ ¨ 5 + θ ¨ 3
C 9 = L 2 - s θ 2356 θ ˙ 7 + θ ˙ 6 + θ ˙ 5 + θ ˙ 3 + θ ˙ 2 2 + c θ 2356 θ ¨ 7 + θ ¨ 6 + θ ¨ 5 + θ ¨ 3 + θ ¨ 2
D 6 = L 1 - s θ 12356 θ ˙ 7 + θ ˙ 6 + θ ˙ 5 + θ ˙ 3 + θ ˙ 2 + θ ˙ 1 2 + c θ 12356 θ ¨ 7 + θ ¨ 6 + θ ¨ 5 + θ ¨ 3 + θ ¨ 2 + θ ¨ 1
为求解下肢外骨骼助力机器人各关节的驱动力矩,将其结构参数(见表3 )代入上述各式,可获得驱动力矩理论值。
2 下肢外骨骼助力机器人动力学参数理论计算
选取不同步态周期相位,将人体运动的角度数据、速度数据及下肢外骨骼助力机器人的结构参数代入牛顿‒欧拉动力学迭代方程,并运用MATLAB软件对上述公式进行计算,求得不同步态相位下机器人各关节的驱动力矩理论值并进行分析。
1)选取支撑相中期(步态周期的11%处),此时下肢外骨骼助力机器人左脚跟离地,右脚支撑,该阶段机器人各关节的动力学参数值如表4 所示。2)选取支撑相末期(步态周期的32%处),此时下肢外骨骼助力机器人左脚摆动,右脚支撑,该阶段机器人各关节的动力学参数值如表5 所示。3)选取摆动相中期(步态周期的80%处),此时下肢外骨骼助力机器人左脚支撑,右脚摆动,该阶段机器人各关节的动力学参数值如表6 所示。
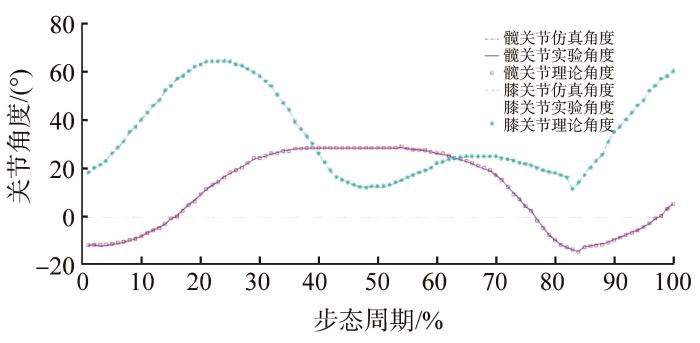
通过计算得到单个步态周期内下肢外骨骼助力机器人各关节的理论驱动力矩及其峰值,分别如图7 和表7 所示。
图7
图7
单个步态周期内下肢外骨骼助力机器人各关节驱动力矩的理论值
Fig.7
Theoretical values of driving torque of each joint of lower limb exoskeleton assisted robot in a single gait cycle
由图7 以及表4 至表7 可以看出,在理论计算过程中,当下肢外骨骼助力机器人运动至左脚弹起阶段(左脚离地,右脚支撑)时,左腿髋关节与膝关节的驱动力矩急速增大,并在达到该阶段的最大值后逐步减小;在左脚触地阶段时,左腿对地面有比较大的冲击,此时左腿关节的驱动力矩比较大,方向与弹起阶段相反,但在达到最大值后随着运动继续而减小,而右腿即将摆动,因此右腿关节的驱动力矩呈快速增大的趋势。该变化趋势符合人体运动实际,但只通过理论计算不能验证下肢外骨骼助力机器人动力学模型的正确行与可行性。
3 实验验证
3.1 ADAMS 仿真实验
3.1.1 ADAMS动力学仿真模型构建
在SolidWorks软件中建立下肢外骨骼助力机器人的三维模型并设置各项结构参数,如长度、质量等。然后将该三维模型导入ADAMS(automatic dynamic analysis of mechanical systems,机械系统动力学自动分析)仿真软件中,构建其动力学仿真模型,如图8 所示,并采用CUBSPL样条函数进行仿真计算。
图8
图8
下肢外骨骼助力机器人的ADAMS动力学仿真模型
Fig.8
ADAMS dynamic simulation model of lower limb exoskeleton assisted robot
3.1.2 ADAMS仿真实验结果分析
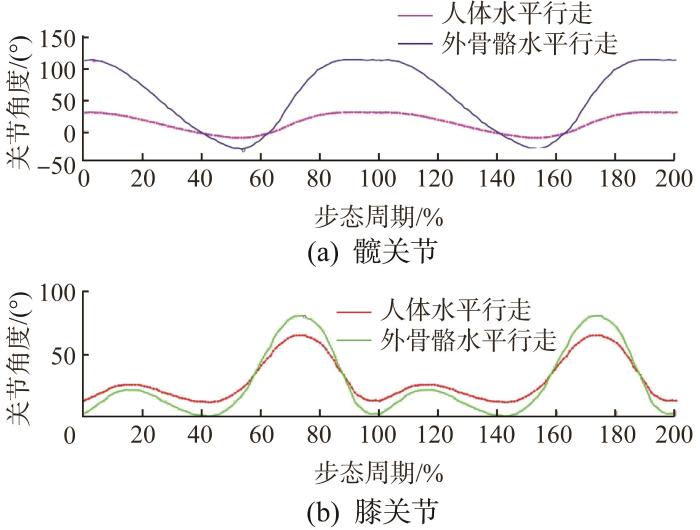
从图9 所示的下肢外骨骼助力机器人各关节角度的仿真结果(与人体水平行走时的关节角度对比)可以看出,其髋关节的屈曲角度和伸展角度可达到最大值,分别为117°与37°;膝关节的最大屈曲角度可以达到80.5°,最大伸展角度趋于0°;对应的髋关节液压缸位移范围为-30~70 mm,膝关节液压缸位移范围为0~124 mm。对比结果验证了该下肢外骨骼助力机器人各关节的运动范围与人体下肢关节相匹配,符合人体解剖学要求。
图9
图9
下肢外骨骼助力机器人水平行走时的关节角度仿真结果
Fig.9
Simulation results of joint angles of lower limb exoskeleton assisted robot during horizontal walking
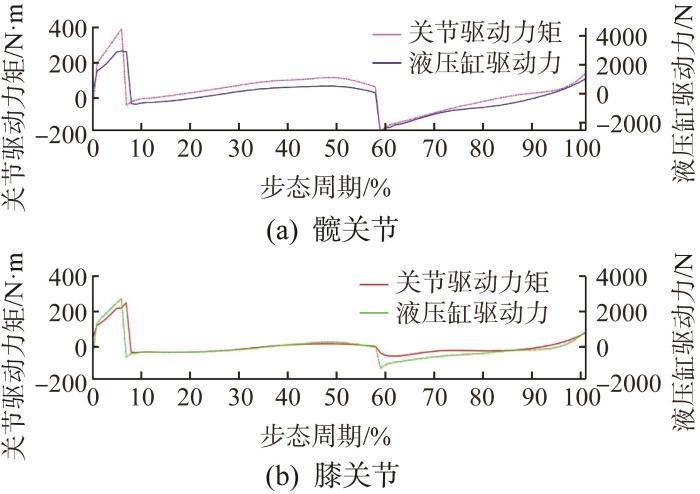
从图10 所示的下肢外骨骼助力机器人水平行走时的关节驱动力矩仿真结果可以看出,在左脚弹起阶段,各关节的驱动力矩达到最大值,其中髋关节的驱动力矩峰值为342.4 N·m,膝关节的驱动力矩峰值为282 N·m;在左脚触地阶段,髋关节的驱动力矩峰值达到-383.1 N·m,膝关节的驱动力矩峰值为-238.6
图10
图10
下肢外骨骼助力机器人水平行走时的关节驱动力矩和液压缸驱动力仿真结果
Fig.10
Simulation results of joint driving torque and hydraulic cylinder driving force of lower limb exoskeleton assisted robot during horizontal walking
3.2 人机协同助行实验
3.2.1 人机协同助行实验方案设计
为了验证下肢外骨骼助力机器人结构与动力学分析方法的可行性与有效性,开展人机协同助行实验,并采用瑞典Qualisys公司生产的三维运动捕捉系统(见图11 )进行数据采集。首先进行实验场地布置,确定实验范围,通过无线红外高速摄像头捕获反光标记点,以采集下肢外骨骼助力机器人各关节运动的空间轨迹及动力学参数。
图11
图11
人机交互实验室
Fig. 11
Human-machine interaction laboratory
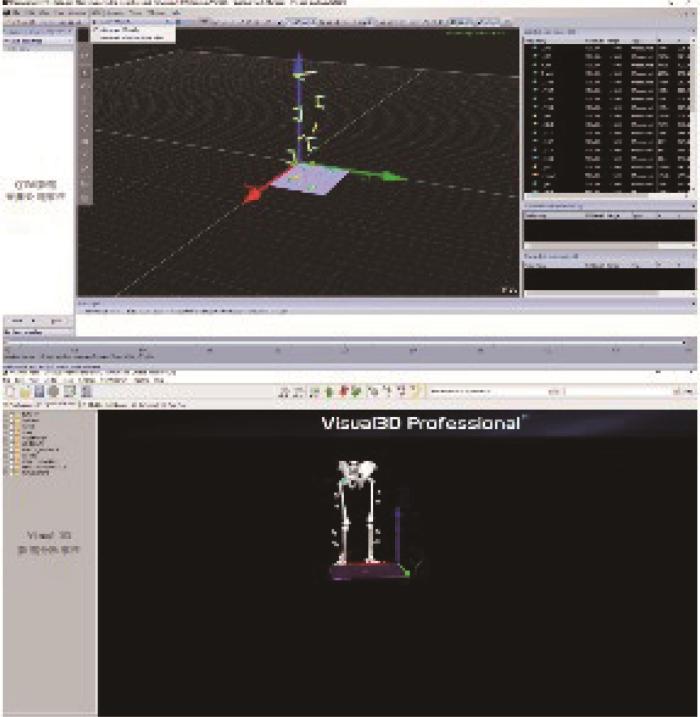
采用Visual 3D步态分析软件(见图12 )对测得的三维运动数据进行分析,得到下肢外骨骼助力机器人各关节的动力学参数及运动分析图。
图12
图12
Visual 3D步态分析软件
Fig.12
Visual 3D gait analysis software
1)接通采集摄像头和个人计算机的电源;打开QTM(Qualisys track manager, Qualisys 跟踪管理器)软件,选择新建项目功能,给相机编组,添加Kistler压力板并标定位置;穿戴下肢外骨骼助力机器人,并在规定位置贴标记点,如图13 所示。
图13
图13
人机协同助行实验现场
Fig.13
Human-machine cooperative walking aid experiment site
2)在QTM软件中新建页面并打开高精度相机界面,点击“开始”,选择运动时间(本文设置为6 s)。穿戴者先静止站立,观察摄像头是否能识别所有标记点,然后开始测试,测试完成后将采集的数据保存为QTM文件并命名。静态实验完成后,开始进行人机协同助行实验,在开始前须保证所有标记点都在摄像头捕捉范围内,助行实验完成后将采集的数据保存为QTM文件并命名。
3)完成数据采集后,在QTM软件中进行标记点关系连接,先建立静态关节连接图并导出对应的V3D文件,再自动生成动态关节连接图并导出对应的V3D文件。
4)利用Visual 3D步态分析软件建立静态与动态的人体骨骼模型:导入静、动态关节连接图的V3D文件(C3D格式),先对静态关节与动态关节进行配对,然后构建骨骼模型。
5)打开导入的动态关节连接图的V3D文件,点击“开始运动”,实验过程中在Visual 3D步态分析软件中显示人体运动步态,实验完成后选择Pipeline导出测得的关节角度、速度等数据,并在MATLAB软件中绘制相应曲线并进行分析。
3.2.2 人机协同助行实验结果分析
基于上述实验方案完成人机协同助行实验,获得下肢外骨骼助力机器人的质心加速度、关节角度、关节驱动力矩与液压缸位移等数据,并在MATLAB软件中绘制得到对应的曲线,结果如图14 和图15 所示。
图14
图14
下肢外骨骼助力机器人髋、膝关节角度对比
Fig.14
Comparison of angle of hip joint and knee joint of lower limb exoskeleton assisted robot
图15
图15
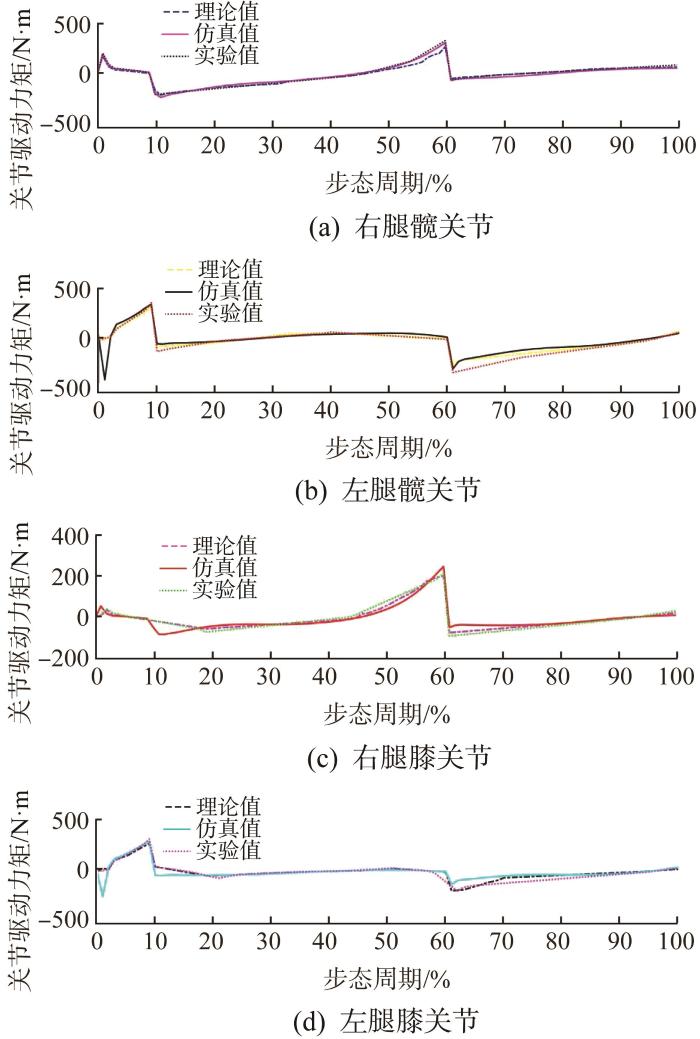
下肢外骨骼助力机器人髋、膝关节驱动力矩对比
Fig.15
Comparison of driving torque of hip joint and knee joint of lower limb exoskeleton assisted robot
从图14 所示的下肢外骨骼助力机器人髋、膝关节角度对比结果可以看出,在整个步态周期内,摆动相阶段髋关节角度的误差范围为-0.5°~1°,膝关节角度的误差在-1.4°~1.9°;而在支撑相阶段髋关节角度的误差为-0.2°~0.2°,膝关节角度的误差在-0.1°~0.5°;仿真结果及实验结果与理论分析结果基本一致。由此说明,下肢外骨骼助力机器人能很好地跟随人体关节运动,且髋、膝关节角度的误差在允许范围之内,对动力学分析的影响基本可以忽略,这为髋、膝关节驱动力矩对比提供了数据支撑。
从图15 所示的下肢外骨骼助力机器人髋、膝关节驱动力矩对比结果可以看出,在左脚弹起阶段与触地阶段,关节驱动力矩的仿真结果和实验结果存在误差,髋关节驱动力矩的最大误差约为3%,膝关节驱动力矩的最大误差约为4.8%,这是因为本文在动力学建模理论时未考虑人机交互力,即没有引入动态精准的人机交互力激励,但产生的误差在允许范围之内。结果表明,该下肢外骨骼助力机器人可以很好地匹配人体运动,基于理论分析、ADAMS仿真和实验研究得到的髋关节与膝关节驱动力矩的变化趋势基本一致。鉴于穿戴者的运动姿势及其与机器人的交互力等因素的影响,关节驱动力矩在变化过程中存在的差异在允许范围之内。上述结果验证了本文动力学建模及分析方法的正确性与优越性。
4 结 论
基于所研制的下肢外骨骼助力机器人,将其简化为七连杆结构,并利用牛顿‒欧拉法推导了其关节驱动力矩方程,通过代入相关参数计算得到了各关节驱动力矩的变化曲线。通过ADAMS仿真实验和人机协同助行实验验证了动力学理论建模与分析的正确性。结果表明,该下肢外骨骼助力机器人能够很好地匹配人体关节运动,完成正常的下肢助行运动。
通过动力学分析可以看出,所研制的下肢外骨骼助力机器人具有一定发展前景,可很好地满足下肢生理功能退化人群的需求。在后续研究中,可在人机系统相位转换过程中考虑人机交互力的影响;此外,目前只分析了穿戴者行走过程中独立步态相位的动力学变化规律,后续可对下肢外骨骼助力机器人相位转换的连续性做进一步探讨。
参考文献
View Option
[1]
MA Y WU X Y YANG S X et al Online gait planning of lower-limb exoskeleton robot for paraplegic rehabilitation considering weight transfer process
[J]. IEEE Transactions on Automation Science and Engineering , 2021 , 18 (2 ): 414 -425 . doi:10.1109/tase.2020.2964807
[本文引用: 1]
[3]
[本文引用: 1]
ZHANG Yan LI Fan-ru LI Wei et al Dynamic analysis and simulation of the lower extremity exoskeleton based on human-machine interaction
[J]. Applied Mathematics and Mechanics , 2019 , 40 (7 ): 780 -790 .
DOI:10.21656/1000-0887.390212
[本文引用: 1]
[4]
WATANABE H TANAKA N INUTA T et al Locomotion improvement using a hybrid assistive limb in recovery phase stroke patients: a randomized controlled pilot study
[J]. Archives of Physical Medicine and Rehabilitation , 2014 , 95 (11 ): 2006 -2012 . doi:10.1016/j.apmr.2014.07.002
[本文引用: 1]
[5]
ESQUENAZI A TALATY M PACKEL A et al The ReWalk powered exoskeleton to restore ambulatory function to individuals with thoracic-level motor-complete spinal cord injury
[J]. American Journal of Physical Medicine and Rehabilitation , 2012 , 91 (11 ): 911 -921 . doi:10.1097/phm.0b013e318269d9a3
[本文引用: 1]
[6]
PANIZZOLO F A GALIANA I ASBECK A T et al A biologically-inspired multi-joint soft exosuit that can reduce the energy cost of loaded walking
[J]. Journal of NeuroEngineering and Rehabilitation , 2016 , 13 (1 ): 43 . doi:10.1186/s12984-016-0150-9
[本文引用: 1]
[8]
KAZEROONI H Human augmentation and exoskeleton systems in Berkeley
[J]. International Journal of Humanoid Robotics , 2007 , 4 (3 ): 575 -605 . doi:10.1142/S0219843607001187
[本文引用: 1]
[9]
何健 ,王海波 ,李雪峰 ,等 负重型下肢外骨骼液压动力单元的研究
[J].液压与气动 ,2017 (11 ):6 -11 .
[本文引用: 1]
HE Jian WANG Hai-bo LI Xue-feng et al Hydraulic power unit of lower limb power assisted exoskeleton
[J]. Chinese Hydraulics & Pneumatics , 2017 (11 ): 6 -11 .
[本文引用: 1]
[10]
NASIRI R AHMADI A AHMADABADI M N Reducing the energy cost of human running using an unpowered exoskeleton
[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering , 2018 , 26 (10 ): 2026 -2032 . doi:10.1109/tnsre.2018.2872889
[本文引用: 1]
[11]
[本文引用: 1]
WANG Yong-feng ZHAO Guo-ru KONG Xiang-zhan et al Design and analysis of unpowered lower-limb exoskeleton with muscle strength synergistic compensation
[J]. Chinese Journal of Engineering Design , 2021 , 28 (6 ): 764 -775 .
DOI:10.3785/j.issn.1006-754X.2021.00.080
[本文引用: 1]
[12]
[本文引用: 1]
WANG Bu-yun WANG Zhi-hong XU De-zhang Mechanical design and kinematics analysis on a wearable power-assisted robot for lower extremity exoskeleton
[J]. Mechanical Science and Technology for Aerospace Engineering , 2018 , 37 (4 ): 553 -559 .
DOI:10.13433/j.cnki.1003-8728.2018.0410
[本文引用: 1]
[13]
WANG Bu-yun WANG Yue-peng LIANG Yi et al Design on articular motion and servo driving with experimental analysis for lower limb exoskeleton robot
[J]. Journal of Mechanical Engineering , 2019 , 55 (23 ): 55 -66 .
DOI:10.3901/JME.2019.23.055
[14]
王月朋 下肢外骨骼助力机器人稳定性判别研究
[D].芜湖 :安徽工程大学 ,2021 :68 -70 .
[本文引用: 1]
WANG Yue-peng Research on stability criterion of power-assisted robot for lower limb exoskeleton
[D]. Wuhu : Anhui Polytechnic University , 2021 : 68 -70 .
[本文引用: 1]
[16]
[本文引用: 1]
ZHANG Ming-kui CHENG Wen-ming LIU Fang Coupling effect between load characteristics and joint driving characteristics of powered exoskeleton
[J]. Journal of Zhejiang University (Engineering Science) , 2017 , 51 (4 ): 807 -816 .
DOI:10.3785/j.issn.1008-973X.2017.04.023
[本文引用: 1]
[19]
[本文引用: 1]
XIE Zheng WANG Ming-jiang HUANG Wu-long et al Exoskeleton robot system based on real-time gait analysis for walking assist
[J]. Journal of Biomedical Engineering , 2017 , 34 (2 ): 265 -270 .
DOI:10.7507/1001-5515.201607075
[本文引用: 1]
[20]
李石磊 下肢外骨骼机器人步态规划与控制方法研究
[D].哈尔滨 :哈尔滨工业大学 ,2017 :46 -53 .
[本文引用: 2]
LI Shi-lei Gait planning and control method of lower extremity exoskeletal robot
[D]. Harbin : Harbin Institute of Technology , 2017 : 46 -53 .
[本文引用: 2]
[21]
[本文引用: 1]
GUO Bing-jing HAN Jian-hai LI Xiang-pan et al Personalized gait planning method for the lower-limb rehabilitation training robot with the physiotherapist interaction
[J]. Robot , 2018 , 40 (4 ): 479 -490 , 499 .
DOI:10.13973/j.cnki.robot.180139
[本文引用: 1]
Online gait planning of lower-limb exoskeleton robot for paraplegic rehabilitation considering weight transfer process
1
2021
... 助力行走型下肢外骨骼机器人是一种可穿戴式助力装备,其结合了先进的控制技术、通信技术以及轻便的结构,主要用于辅助下肢生理功能退化的穿戴者行走,以提升其运动机能,这大大促进了智能化机器与人类的力量结合.近20年来,越来越多的老人和残障人士遭遇了下肢生理功能退化问题.由2019年联合国经济和社会事务部调查结果可知,日本的老年人口占比居世界之最,其次是意大利、德国、法国、英国、加拿大和中国等,这些国家的老年人口占比均超过了10%.可想而知,随着年老、体弱人群的日益增多,失能或半失能人群的照料与护理已成为重要的社会问题[1 ] .在下肢外骨骼助力机器人的辅助下,老年人或有运动功能障碍的人群可实现正常行走.关节驱动力矩作为运动或保持某种姿态的重要参数,其已成为下肢外骨骼助力机器人稳定性判定和控制方面的研究重点和热点[2 -3 ] . ...
下肢助力外骨骼的动力学分析及仿真
1
2013
... 助力行走型下肢外骨骼机器人是一种可穿戴式助力装备,其结合了先进的控制技术、通信技术以及轻便的结构,主要用于辅助下肢生理功能退化的穿戴者行走,以提升其运动机能,这大大促进了智能化机器与人类的力量结合.近20年来,越来越多的老人和残障人士遭遇了下肢生理功能退化问题.由2019年联合国经济和社会事务部调查结果可知,日本的老年人口占比居世界之最,其次是意大利、德国、法国、英国、加拿大和中国等,这些国家的老年人口占比均超过了10%.可想而知,随着年老、体弱人群的日益增多,失能或半失能人群的照料与护理已成为重要的社会问题[1 ] .在下肢外骨骼助力机器人的辅助下,老年人或有运动功能障碍的人群可实现正常行走.关节驱动力矩作为运动或保持某种姿态的重要参数,其已成为下肢外骨骼助力机器人稳定性判定和控制方面的研究重点和热点[2 -3 ] . ...
下肢助力外骨骼的动力学分析及仿真
1
2013
... 助力行走型下肢外骨骼机器人是一种可穿戴式助力装备,其结合了先进的控制技术、通信技术以及轻便的结构,主要用于辅助下肢生理功能退化的穿戴者行走,以提升其运动机能,这大大促进了智能化机器与人类的力量结合.近20年来,越来越多的老人和残障人士遭遇了下肢生理功能退化问题.由2019年联合国经济和社会事务部调查结果可知,日本的老年人口占比居世界之最,其次是意大利、德国、法国、英国、加拿大和中国等,这些国家的老年人口占比均超过了10%.可想而知,随着年老、体弱人群的日益增多,失能或半失能人群的照料与护理已成为重要的社会问题[1 ] .在下肢外骨骼助力机器人的辅助下,老年人或有运动功能障碍的人群可实现正常行走.关节驱动力矩作为运动或保持某种姿态的重要参数,其已成为下肢外骨骼助力机器人稳定性判定和控制方面的研究重点和热点[2 -3 ] . ...
基于人机耦合的下肢外骨骼动力学分析及仿真
1
2019
... 助力行走型下肢外骨骼机器人是一种可穿戴式助力装备,其结合了先进的控制技术、通信技术以及轻便的结构,主要用于辅助下肢生理功能退化的穿戴者行走,以提升其运动机能,这大大促进了智能化机器与人类的力量结合.近20年来,越来越多的老人和残障人士遭遇了下肢生理功能退化问题.由2019年联合国经济和社会事务部调查结果可知,日本的老年人口占比居世界之最,其次是意大利、德国、法国、英国、加拿大和中国等,这些国家的老年人口占比均超过了10%.可想而知,随着年老、体弱人群的日益增多,失能或半失能人群的照料与护理已成为重要的社会问题[1 ] .在下肢外骨骼助力机器人的辅助下,老年人或有运动功能障碍的人群可实现正常行走.关节驱动力矩作为运动或保持某种姿态的重要参数,其已成为下肢外骨骼助力机器人稳定性判定和控制方面的研究重点和热点[2 -3 ] . ...
基于人机耦合的下肢外骨骼动力学分析及仿真
1
2019
... 助力行走型下肢外骨骼机器人是一种可穿戴式助力装备,其结合了先进的控制技术、通信技术以及轻便的结构,主要用于辅助下肢生理功能退化的穿戴者行走,以提升其运动机能,这大大促进了智能化机器与人类的力量结合.近20年来,越来越多的老人和残障人士遭遇了下肢生理功能退化问题.由2019年联合国经济和社会事务部调查结果可知,日本的老年人口占比居世界之最,其次是意大利、德国、法国、英国、加拿大和中国等,这些国家的老年人口占比均超过了10%.可想而知,随着年老、体弱人群的日益增多,失能或半失能人群的照料与护理已成为重要的社会问题[1 ] .在下肢外骨骼助力机器人的辅助下,老年人或有运动功能障碍的人群可实现正常行走.关节驱动力矩作为运动或保持某种姿态的重要参数,其已成为下肢外骨骼助力机器人稳定性判定和控制方面的研究重点和热点[2 -3 ] . ...
Locomotion improvement using a hybrid assistive limb in recovery phase stroke patients: a randomized controlled pilot study
1
2014
... 经查阅大量文献与资料可知,在实际应用中,下肢外骨骼助力机器人主要分为以下4种.第1种为最常见的医疗康复型外骨骼机器人,用于辅助偏瘫患者或运动机能受损人群进行康复训练,为其提供重新站立的可能和希望,典型代表产品有可穿戴式机器人HAL(hybrid assistive limb, 混合辅助假肢)、ReWalk下肢康复外骨骼[4 -5 ] 等;第2种是助老助残型下肢外骨骼机器人,主要用于协助老年人行走及上下楼梯,典型代表产品有哈佛大学研制的柔性下肢外骨骼和中国科学院深圳先进技术研究院自主研发的下肢外骨骼机器人[6 -7 ] 等;第3种是军事负重型外骨骼机器人,用于提升军人的负载能力及行走速度,可有效增强军人的越野耐力,典型代表产品有伯克利仿生科技公司开发的通用型负重外骨骼(human universal load carrier, HULC)和西安交通大学研制的负重型下肢外骨骼机器人[8 -9 ] 等;第4种是无动力聚力型下肢外骨骼机器人,其不需要外加动力源,能够协助穿戴者减小体力消耗以达到增强体力的目的,典型代表产品有德黑兰大学研制的人用无动力外骨骼(unpowered exoskeleton for human, UEFH)和中国科学院深圳先进技术研究院自主研制的无动力型下肢外骨骼机器人[10 -11 ] 等. ...
The ReWalk powered exoskeleton to restore ambulatory function to individuals with thoracic-level motor-complete spinal cord injury
1
2012
... 经查阅大量文献与资料可知,在实际应用中,下肢外骨骼助力机器人主要分为以下4种.第1种为最常见的医疗康复型外骨骼机器人,用于辅助偏瘫患者或运动机能受损人群进行康复训练,为其提供重新站立的可能和希望,典型代表产品有可穿戴式机器人HAL(hybrid assistive limb, 混合辅助假肢)、ReWalk下肢康复外骨骼[4 -5 ] 等;第2种是助老助残型下肢外骨骼机器人,主要用于协助老年人行走及上下楼梯,典型代表产品有哈佛大学研制的柔性下肢外骨骼和中国科学院深圳先进技术研究院自主研发的下肢外骨骼机器人[6 -7 ] 等;第3种是军事负重型外骨骼机器人,用于提升军人的负载能力及行走速度,可有效增强军人的越野耐力,典型代表产品有伯克利仿生科技公司开发的通用型负重外骨骼(human universal load carrier, HULC)和西安交通大学研制的负重型下肢外骨骼机器人[8 -9 ] 等;第4种是无动力聚力型下肢外骨骼机器人,其不需要外加动力源,能够协助穿戴者减小体力消耗以达到增强体力的目的,典型代表产品有德黑兰大学研制的人用无动力外骨骼(unpowered exoskeleton for human, UEFH)和中国科学院深圳先进技术研究院自主研制的无动力型下肢外骨骼机器人[10 -11 ] 等. ...
A biologically-inspired multi-joint soft exosuit that can reduce the energy cost of loaded walking
1
2016
... 经查阅大量文献与资料可知,在实际应用中,下肢外骨骼助力机器人主要分为以下4种.第1种为最常见的医疗康复型外骨骼机器人,用于辅助偏瘫患者或运动机能受损人群进行康复训练,为其提供重新站立的可能和希望,典型代表产品有可穿戴式机器人HAL(hybrid assistive limb, 混合辅助假肢)、ReWalk下肢康复外骨骼[4 -5 ] 等;第2种是助老助残型下肢外骨骼机器人,主要用于协助老年人行走及上下楼梯,典型代表产品有哈佛大学研制的柔性下肢外骨骼和中国科学院深圳先进技术研究院自主研发的下肢外骨骼机器人[6 -7 ] 等;第3种是军事负重型外骨骼机器人,用于提升军人的负载能力及行走速度,可有效增强军人的越野耐力,典型代表产品有伯克利仿生科技公司开发的通用型负重外骨骼(human universal load carrier, HULC)和西安交通大学研制的负重型下肢外骨骼机器人[8 -9 ] 等;第4种是无动力聚力型下肢外骨骼机器人,其不需要外加动力源,能够协助穿戴者减小体力消耗以达到增强体力的目的,典型代表产品有德黑兰大学研制的人用无动力外骨骼(unpowered exoskeleton for human, UEFH)和中国科学院深圳先进技术研究院自主研制的无动力型下肢外骨骼机器人[10 -11 ] 等. ...
基于稳定阈度分析的外骨骼动态步长规划方法
1
2017
... 经查阅大量文献与资料可知,在实际应用中,下肢外骨骼助力机器人主要分为以下4种.第1种为最常见的医疗康复型外骨骼机器人,用于辅助偏瘫患者或运动机能受损人群进行康复训练,为其提供重新站立的可能和希望,典型代表产品有可穿戴式机器人HAL(hybrid assistive limb, 混合辅助假肢)、ReWalk下肢康复外骨骼[4 -5 ] 等;第2种是助老助残型下肢外骨骼机器人,主要用于协助老年人行走及上下楼梯,典型代表产品有哈佛大学研制的柔性下肢外骨骼和中国科学院深圳先进技术研究院自主研发的下肢外骨骼机器人[6 -7 ] 等;第3种是军事负重型外骨骼机器人,用于提升军人的负载能力及行走速度,可有效增强军人的越野耐力,典型代表产品有伯克利仿生科技公司开发的通用型负重外骨骼(human universal load carrier, HULC)和西安交通大学研制的负重型下肢外骨骼机器人[8 -9 ] 等;第4种是无动力聚力型下肢外骨骼机器人,其不需要外加动力源,能够协助穿戴者减小体力消耗以达到增强体力的目的,典型代表产品有德黑兰大学研制的人用无动力外骨骼(unpowered exoskeleton for human, UEFH)和中国科学院深圳先进技术研究院自主研制的无动力型下肢外骨骼机器人[10 -11 ] 等. ...
基于稳定阈度分析的外骨骼动态步长规划方法
1
2017
... 经查阅大量文献与资料可知,在实际应用中,下肢外骨骼助力机器人主要分为以下4种.第1种为最常见的医疗康复型外骨骼机器人,用于辅助偏瘫患者或运动机能受损人群进行康复训练,为其提供重新站立的可能和希望,典型代表产品有可穿戴式机器人HAL(hybrid assistive limb, 混合辅助假肢)、ReWalk下肢康复外骨骼[4 -5 ] 等;第2种是助老助残型下肢外骨骼机器人,主要用于协助老年人行走及上下楼梯,典型代表产品有哈佛大学研制的柔性下肢外骨骼和中国科学院深圳先进技术研究院自主研发的下肢外骨骼机器人[6 -7 ] 等;第3种是军事负重型外骨骼机器人,用于提升军人的负载能力及行走速度,可有效增强军人的越野耐力,典型代表产品有伯克利仿生科技公司开发的通用型负重外骨骼(human universal load carrier, HULC)和西安交通大学研制的负重型下肢外骨骼机器人[8 -9 ] 等;第4种是无动力聚力型下肢外骨骼机器人,其不需要外加动力源,能够协助穿戴者减小体力消耗以达到增强体力的目的,典型代表产品有德黑兰大学研制的人用无动力外骨骼(unpowered exoskeleton for human, UEFH)和中国科学院深圳先进技术研究院自主研制的无动力型下肢外骨骼机器人[10 -11 ] 等. ...
Human augmentation and exoskeleton systems in Berkeley
1
2007
... 经查阅大量文献与资料可知,在实际应用中,下肢外骨骼助力机器人主要分为以下4种.第1种为最常见的医疗康复型外骨骼机器人,用于辅助偏瘫患者或运动机能受损人群进行康复训练,为其提供重新站立的可能和希望,典型代表产品有可穿戴式机器人HAL(hybrid assistive limb, 混合辅助假肢)、ReWalk下肢康复外骨骼[4 -5 ] 等;第2种是助老助残型下肢外骨骼机器人,主要用于协助老年人行走及上下楼梯,典型代表产品有哈佛大学研制的柔性下肢外骨骼和中国科学院深圳先进技术研究院自主研发的下肢外骨骼机器人[6 -7 ] 等;第3种是军事负重型外骨骼机器人,用于提升军人的负载能力及行走速度,可有效增强军人的越野耐力,典型代表产品有伯克利仿生科技公司开发的通用型负重外骨骼(human universal load carrier, HULC)和西安交通大学研制的负重型下肢外骨骼机器人[8 -9 ] 等;第4种是无动力聚力型下肢外骨骼机器人,其不需要外加动力源,能够协助穿戴者减小体力消耗以达到增强体力的目的,典型代表产品有德黑兰大学研制的人用无动力外骨骼(unpowered exoskeleton for human, UEFH)和中国科学院深圳先进技术研究院自主研制的无动力型下肢外骨骼机器人[10 -11 ] 等. ...
负重型下肢外骨骼液压动力单元的研究
1
2017
... 经查阅大量文献与资料可知,在实际应用中,下肢外骨骼助力机器人主要分为以下4种.第1种为最常见的医疗康复型外骨骼机器人,用于辅助偏瘫患者或运动机能受损人群进行康复训练,为其提供重新站立的可能和希望,典型代表产品有可穿戴式机器人HAL(hybrid assistive limb, 混合辅助假肢)、ReWalk下肢康复外骨骼[4 -5 ] 等;第2种是助老助残型下肢外骨骼机器人,主要用于协助老年人行走及上下楼梯,典型代表产品有哈佛大学研制的柔性下肢外骨骼和中国科学院深圳先进技术研究院自主研发的下肢外骨骼机器人[6 -7 ] 等;第3种是军事负重型外骨骼机器人,用于提升军人的负载能力及行走速度,可有效增强军人的越野耐力,典型代表产品有伯克利仿生科技公司开发的通用型负重外骨骼(human universal load carrier, HULC)和西安交通大学研制的负重型下肢外骨骼机器人[8 -9 ] 等;第4种是无动力聚力型下肢外骨骼机器人,其不需要外加动力源,能够协助穿戴者减小体力消耗以达到增强体力的目的,典型代表产品有德黑兰大学研制的人用无动力外骨骼(unpowered exoskeleton for human, UEFH)和中国科学院深圳先进技术研究院自主研制的无动力型下肢外骨骼机器人[10 -11 ] 等. ...
负重型下肢外骨骼液压动力单元的研究
1
2017
... 经查阅大量文献与资料可知,在实际应用中,下肢外骨骼助力机器人主要分为以下4种.第1种为最常见的医疗康复型外骨骼机器人,用于辅助偏瘫患者或运动机能受损人群进行康复训练,为其提供重新站立的可能和希望,典型代表产品有可穿戴式机器人HAL(hybrid assistive limb, 混合辅助假肢)、ReWalk下肢康复外骨骼[4 -5 ] 等;第2种是助老助残型下肢外骨骼机器人,主要用于协助老年人行走及上下楼梯,典型代表产品有哈佛大学研制的柔性下肢外骨骼和中国科学院深圳先进技术研究院自主研发的下肢外骨骼机器人[6 -7 ] 等;第3种是军事负重型外骨骼机器人,用于提升军人的负载能力及行走速度,可有效增强军人的越野耐力,典型代表产品有伯克利仿生科技公司开发的通用型负重外骨骼(human universal load carrier, HULC)和西安交通大学研制的负重型下肢外骨骼机器人[8 -9 ] 等;第4种是无动力聚力型下肢外骨骼机器人,其不需要外加动力源,能够协助穿戴者减小体力消耗以达到增强体力的目的,典型代表产品有德黑兰大学研制的人用无动力外骨骼(unpowered exoskeleton for human, UEFH)和中国科学院深圳先进技术研究院自主研制的无动力型下肢外骨骼机器人[10 -11 ] 等. ...
Reducing the energy cost of human running using an unpowered exoskeleton
1
2018
... 经查阅大量文献与资料可知,在实际应用中,下肢外骨骼助力机器人主要分为以下4种.第1种为最常见的医疗康复型外骨骼机器人,用于辅助偏瘫患者或运动机能受损人群进行康复训练,为其提供重新站立的可能和希望,典型代表产品有可穿戴式机器人HAL(hybrid assistive limb, 混合辅助假肢)、ReWalk下肢康复外骨骼[4 -5 ] 等;第2种是助老助残型下肢外骨骼机器人,主要用于协助老年人行走及上下楼梯,典型代表产品有哈佛大学研制的柔性下肢外骨骼和中国科学院深圳先进技术研究院自主研发的下肢外骨骼机器人[6 -7 ] 等;第3种是军事负重型外骨骼机器人,用于提升军人的负载能力及行走速度,可有效增强军人的越野耐力,典型代表产品有伯克利仿生科技公司开发的通用型负重外骨骼(human universal load carrier, HULC)和西安交通大学研制的负重型下肢外骨骼机器人[8 -9 ] 等;第4种是无动力聚力型下肢外骨骼机器人,其不需要外加动力源,能够协助穿戴者减小体力消耗以达到增强体力的目的,典型代表产品有德黑兰大学研制的人用无动力外骨骼(unpowered exoskeleton for human, UEFH)和中国科学院深圳先进技术研究院自主研制的无动力型下肢外骨骼机器人[10 -11 ] 等. ...
肌力协同补偿的无动力下肢外骨骼设计与分析
1
2021
... 经查阅大量文献与资料可知,在实际应用中,下肢外骨骼助力机器人主要分为以下4种.第1种为最常见的医疗康复型外骨骼机器人,用于辅助偏瘫患者或运动机能受损人群进行康复训练,为其提供重新站立的可能和希望,典型代表产品有可穿戴式机器人HAL(hybrid assistive limb, 混合辅助假肢)、ReWalk下肢康复外骨骼[4 -5 ] 等;第2种是助老助残型下肢外骨骼机器人,主要用于协助老年人行走及上下楼梯,典型代表产品有哈佛大学研制的柔性下肢外骨骼和中国科学院深圳先进技术研究院自主研发的下肢外骨骼机器人[6 -7 ] 等;第3种是军事负重型外骨骼机器人,用于提升军人的负载能力及行走速度,可有效增强军人的越野耐力,典型代表产品有伯克利仿生科技公司开发的通用型负重外骨骼(human universal load carrier, HULC)和西安交通大学研制的负重型下肢外骨骼机器人[8 -9 ] 等;第4种是无动力聚力型下肢外骨骼机器人,其不需要外加动力源,能够协助穿戴者减小体力消耗以达到增强体力的目的,典型代表产品有德黑兰大学研制的人用无动力外骨骼(unpowered exoskeleton for human, UEFH)和中国科学院深圳先进技术研究院自主研制的无动力型下肢外骨骼机器人[10 -11 ] 等. ...
肌力协同补偿的无动力下肢外骨骼设计与分析
1
2021
... 经查阅大量文献与资料可知,在实际应用中,下肢外骨骼助力机器人主要分为以下4种.第1种为最常见的医疗康复型外骨骼机器人,用于辅助偏瘫患者或运动机能受损人群进行康复训练,为其提供重新站立的可能和希望,典型代表产品有可穿戴式机器人HAL(hybrid assistive limb, 混合辅助假肢)、ReWalk下肢康复外骨骼[4 -5 ] 等;第2种是助老助残型下肢外骨骼机器人,主要用于协助老年人行走及上下楼梯,典型代表产品有哈佛大学研制的柔性下肢外骨骼和中国科学院深圳先进技术研究院自主研发的下肢外骨骼机器人[6 -7 ] 等;第3种是军事负重型外骨骼机器人,用于提升军人的负载能力及行走速度,可有效增强军人的越野耐力,典型代表产品有伯克利仿生科技公司开发的通用型负重外骨骼(human universal load carrier, HULC)和西安交通大学研制的负重型下肢外骨骼机器人[8 -9 ] 等;第4种是无动力聚力型下肢外骨骼机器人,其不需要外加动力源,能够协助穿戴者减小体力消耗以达到增强体力的目的,典型代表产品有德黑兰大学研制的人用无动力外骨骼(unpowered exoskeleton for human, UEFH)和中国科学院深圳先进技术研究院自主研制的无动力型下肢外骨骼机器人[10 -11 ] 等. ...
下肢外骨骼助力机器人本体结构设计与运动学分析
1
2018
... 为实现下肢外骨骼助力机器人穿戴柔顺性和控制精准性的提升,基于安徽工程大学机器人产业技术研究院设计开发的电液伺服驱动下肢外骨骼助力机器人APWR-A01(其结构如图1 所示)[12 -14 ] ,利用合适的动力学分析方法来求解其助行过程中的动力学参数变化情况. ...
下肢外骨骼助力机器人本体结构设计与运动学分析
1
2018
... 为实现下肢外骨骼助力机器人穿戴柔顺性和控制精准性的提升,基于安徽工程大学机器人产业技术研究院设计开发的电液伺服驱动下肢外骨骼助力机器人APWR-A01(其结构如图1 所示)[12 -14 ] ,利用合适的动力学分析方法来求解其助行过程中的动力学参数变化情况. ...
下肢外骨骼助力机器人关节驱动设计及试验分析
0
2019
下肢外骨骼助力机器人关节驱动设计及试验分析
0
2019
下肢外骨骼助力机器人稳定性判别研究
1
2021
... 为实现下肢外骨骼助力机器人穿戴柔顺性和控制精准性的提升,基于安徽工程大学机器人产业技术研究院设计开发的电液伺服驱动下肢外骨骼助力机器人APWR-A01(其结构如图1 所示)[12 -14 ] ,利用合适的动力学分析方法来求解其助行过程中的动力学参数变化情况. ...
下肢外骨骼助力机器人稳定性判别研究
1
2021
... 为实现下肢外骨骼助力机器人穿戴柔顺性和控制精准性的提升,基于安徽工程大学机器人产业技术研究院设计开发的电液伺服驱动下肢外骨骼助力机器人APWR-A01(其结构如图1 所示)[12 -14 ] ,利用合适的动力学分析方法来求解其助行过程中的动力学参数变化情况. ...
下肢外骨骼机器人动力学分析与设计
1
2013
... 在研究外骨骼机器人动力学问题时,首先要构建其动力学模型.针对外骨骼机器人的动力学特性,国内和国外的很多学者都进行了深入研究,提出了牛顿‒欧拉法[15 ] 、拉格朗日法[16 ] 、凯恩法[17 ] 、虚功原理法[18 ] 、微分几何原理法[19 ] 、高斯法[20 ] 以及旋量对偶数法[21 ] 等动力学分析方法.其中,部分方法的优缺点如表1 所示. ...
下肢外骨骼机器人动力学分析与设计
1
2013
... 在研究外骨骼机器人动力学问题时,首先要构建其动力学模型.针对外骨骼机器人的动力学特性,国内和国外的很多学者都进行了深入研究,提出了牛顿‒欧拉法[15 ] 、拉格朗日法[16 ] 、凯恩法[17 ] 、虚功原理法[18 ] 、微分几何原理法[19 ] 、高斯法[20 ] 以及旋量对偶数法[21 ] 等动力学分析方法.其中,部分方法的优缺点如表1 所示. ...
助力外骨骼负载特征与驱动特征耦合效应
1
2017
... 在研究外骨骼机器人动力学问题时,首先要构建其动力学模型.针对外骨骼机器人的动力学特性,国内和国外的很多学者都进行了深入研究,提出了牛顿‒欧拉法[15 ] 、拉格朗日法[16 ] 、凯恩法[17 ] 、虚功原理法[18 ] 、微分几何原理法[19 ] 、高斯法[20 ] 以及旋量对偶数法[21 ] 等动力学分析方法.其中,部分方法的优缺点如表1 所示. ...
助力外骨骼负载特征与驱动特征耦合效应
1
2017
... 在研究外骨骼机器人动力学问题时,首先要构建其动力学模型.针对外骨骼机器人的动力学特性,国内和国外的很多学者都进行了深入研究,提出了牛顿‒欧拉法[15 ] 、拉格朗日法[16 ] 、凯恩法[17 ] 、虚功原理法[18 ] 、微分几何原理法[19 ] 、高斯法[20 ] 以及旋量对偶数法[21 ] 等动力学分析方法.其中,部分方法的优缺点如表1 所示. ...
新型下肢外骨骼机器人动力学仿真
1
2021
... 在研究外骨骼机器人动力学问题时,首先要构建其动力学模型.针对外骨骼机器人的动力学特性,国内和国外的很多学者都进行了深入研究,提出了牛顿‒欧拉法[15 ] 、拉格朗日法[16 ] 、凯恩法[17 ] 、虚功原理法[18 ] 、微分几何原理法[19 ] 、高斯法[20 ] 以及旋量对偶数法[21 ] 等动力学分析方法.其中,部分方法的优缺点如表1 所示. ...
新型下肢外骨骼机器人动力学仿真
1
2021
... 在研究外骨骼机器人动力学问题时,首先要构建其动力学模型.针对外骨骼机器人的动力学特性,国内和国外的很多学者都进行了深入研究,提出了牛顿‒欧拉法[15 ] 、拉格朗日法[16 ] 、凯恩法[17 ] 、虚功原理法[18 ] 、微分几何原理法[19 ] 、高斯法[20 ] 以及旋量对偶数法[21 ] 等动力学分析方法.其中,部分方法的优缺点如表1 所示. ...
基于助力式外骨骼系统的动力学分析与研究
1
2017
... 在研究外骨骼机器人动力学问题时,首先要构建其动力学模型.针对外骨骼机器人的动力学特性,国内和国外的很多学者都进行了深入研究,提出了牛顿‒欧拉法[15 ] 、拉格朗日法[16 ] 、凯恩法[17 ] 、虚功原理法[18 ] 、微分几何原理法[19 ] 、高斯法[20 ] 以及旋量对偶数法[21 ] 等动力学分析方法.其中,部分方法的优缺点如表1 所示. ...
基于助力式外骨骼系统的动力学分析与研究
1
2017
... 在研究外骨骼机器人动力学问题时,首先要构建其动力学模型.针对外骨骼机器人的动力学特性,国内和国外的很多学者都进行了深入研究,提出了牛顿‒欧拉法[15 ] 、拉格朗日法[16 ] 、凯恩法[17 ] 、虚功原理法[18 ] 、微分几何原理法[19 ] 、高斯法[20 ] 以及旋量对偶数法[21 ] 等动力学分析方法.其中,部分方法的优缺点如表1 所示. ...
基于实时步态分析的行走辅助外骨骼机器人系统
1
2017
... 在研究外骨骼机器人动力学问题时,首先要构建其动力学模型.针对外骨骼机器人的动力学特性,国内和国外的很多学者都进行了深入研究,提出了牛顿‒欧拉法[15 ] 、拉格朗日法[16 ] 、凯恩法[17 ] 、虚功原理法[18 ] 、微分几何原理法[19 ] 、高斯法[20 ] 以及旋量对偶数法[21 ] 等动力学分析方法.其中,部分方法的优缺点如表1 所示. ...
基于实时步态分析的行走辅助外骨骼机器人系统
1
2017
... 在研究外骨骼机器人动力学问题时,首先要构建其动力学模型.针对外骨骼机器人的动力学特性,国内和国外的很多学者都进行了深入研究,提出了牛顿‒欧拉法[15 ] 、拉格朗日法[16 ] 、凯恩法[17 ] 、虚功原理法[18 ] 、微分几何原理法[19 ] 、高斯法[20 ] 以及旋量对偶数法[21 ] 等动力学分析方法.其中,部分方法的优缺点如表1 所示. ...
下肢外骨骼机器人步态规划与控制方法研究
2
2017
... 在研究外骨骼机器人动力学问题时,首先要构建其动力学模型.针对外骨骼机器人的动力学特性,国内和国外的很多学者都进行了深入研究,提出了牛顿‒欧拉法[15 ] 、拉格朗日法[16 ] 、凯恩法[17 ] 、虚功原理法[18 ] 、微分几何原理法[19 ] 、高斯法[20 ] 以及旋量对偶数法[21 ] 等动力学分析方法.其中,部分方法的优缺点如表1 所示. ...
... 人机协同助行实验的具体方案设计如下[20 ] : ...
下肢外骨骼机器人步态规划与控制方法研究
2
2017
... 在研究外骨骼机器人动力学问题时,首先要构建其动力学模型.针对外骨骼机器人的动力学特性,国内和国外的很多学者都进行了深入研究,提出了牛顿‒欧拉法[15 ] 、拉格朗日法[16 ] 、凯恩法[17 ] 、虚功原理法[18 ] 、微分几何原理法[19 ] 、高斯法[20 ] 以及旋量对偶数法[21 ] 等动力学分析方法.其中,部分方法的优缺点如表1 所示. ...
... 人机协同助行实验的具体方案设计如下[20 ] : ...
理疗师交互下的下肢康复训练机器人个性化步态规划方法
1
2018
... 在研究外骨骼机器人动力学问题时,首先要构建其动力学模型.针对外骨骼机器人的动力学特性,国内和国外的很多学者都进行了深入研究,提出了牛顿‒欧拉法[15 ] 、拉格朗日法[16 ] 、凯恩法[17 ] 、虚功原理法[18 ] 、微分几何原理法[19 ] 、高斯法[20 ] 以及旋量对偶数法[21 ] 等动力学分析方法.其中,部分方法的优缺点如表1 所示. ...
理疗师交互下的下肢康复训练机器人个性化步态规划方法
1
2018
... 在研究外骨骼机器人动力学问题时,首先要构建其动力学模型.针对外骨骼机器人的动力学特性,国内和国外的很多学者都进行了深入研究,提出了牛顿‒欧拉法[15 ] 、拉格朗日法[16 ] 、凯恩法[17 ] 、虚功原理法[18 ] 、微分几何原理法[19 ] 、高斯法[20 ] 以及旋量对偶数法[21 ] 等动力学分析方法.其中,部分方法的优缺点如表1 所示. ...