随着电动汽车技术的飞速发展,涌现出了大量的主动安全系统来提高车辆的操纵稳定性[1]. 分布式驱动电动汽车搭载了先进的线控转向和线控驱动系统,具有驱动车轮转角/转矩独立控制的优势[2-3],为主动安全系统提供了硬件基础和控制平台,便于开发主动四轮转向(active four-wheel steering, AFWS)[4]、直接横摆力矩控制(direct yaw moment control, DYC)[5]和路径跟踪[6-7]等先进控制策略. 然而,随着底盘控制系统数量的增加,不同执行器智能体之间的控制目标冲突、功能叠加等问题日渐突出. 如何协调多个主动安全子系统之间的工作,以提高分布式驱动电动汽车的操纵稳定性,已成为亟待解决的关键问题.
为了协调线控转向和驱动系统,Wu等[8]建立基于主动前轮转向(active front steering, AFS)和DYC的分层协调控制策略. 为了实时获得车辆运动状态,Sun等[9]建立非线性模糊观测器,在此基础上提出主动后轮转向(active rear steering, ARS)和DYC的协调控制方法,改善了车辆在极端条件下的操纵稳定性. 上述研究有效提高了车辆在危险工况下的操纵稳定性,但主要采用集成或分层控制策略来协调多个控制系统[10-11],并根据轮胎侧偏特性或相平面来划分不同控制器的工作区域,以解决不同稳定性控制系统之间存在的功能叠加问题. 然而,工作区域的划分不能充分地反映不同稳定性系统之间的相互作用. 动态博弈理论主要用于多智能体之间的冗余控制[12-13]. Liang等[14-15]建立基于Pareto合作博弈的AFS/DYC协调控制策略,将AFS和DYC分别定义为2个独立的博弈对象,共同提高车辆的侧向稳定性. Ji等[16]应用Stackelberg主从博弈理论建立AFWS控制器. 针对驾驶人和AFS系统,Na等[17]在人机共享转向控制系统中采用动态博弈控制理论,搭建基于非合作博弈的驾驶人/AFS转向交互模型. 然而,上述博弈模型通常只包括2个博弈对象,没有综合考虑AFS、ARS和DYC这3个系统之间的博弈关系. 因此,建立更为完善的混合博弈框架对于提高车辆操纵稳定性具有重要意义.
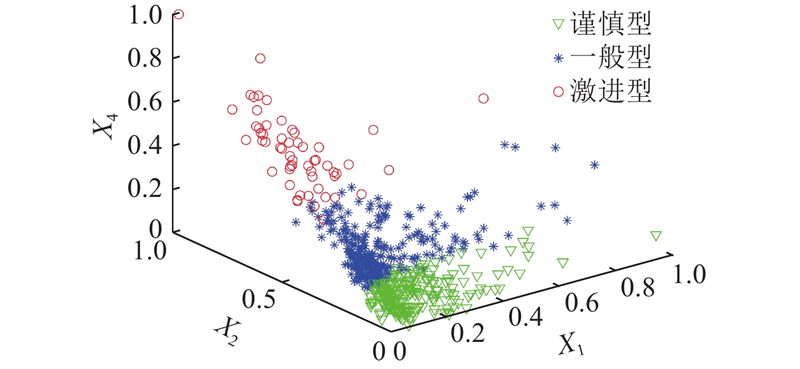
根据以上分析,驾驶特性的差异使得驾驶人对车辆的行驶状态、车辆动力性控制系统的性能的预期产生差异,进一步地影响驾驶人对转向系统的操作. 因此,车辆横向稳定性控制研究需要综合考虑驾驶人的驾驶特性和各控制子系统的控制性能. 本研究将驾驶风格分为谨慎型、一般型和激进型,并根据驾驶人在环试验获得不同驾驶风格的驾驶人在不同车速、道路曲率和路面附着系数下的车辆稳定性因数;建立基于Stackelberg主从博弈和Pareto合作博弈的AFWS和DYC混合博弈控制模型,提高分布式驱动电动汽车的操纵稳定性.
1. AFWS和DYC协调控制策略
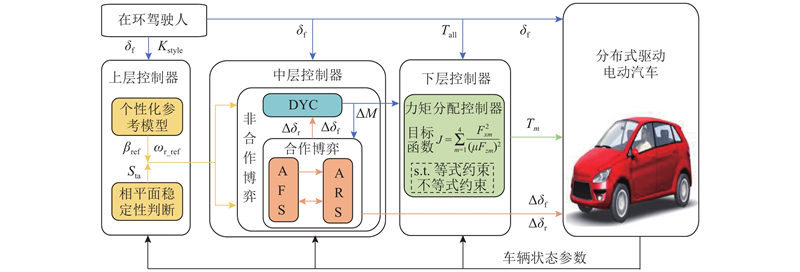
针对分布式驱动电动汽车搭载的AFS、ARS和DYC系统,设计考虑驾驶风格的AFWS/DYC稳定性协调控制策略,整体结构如图1所示,包括上层、中层和下层控制器. 上层控制器由个性化参考模型和稳定性判断模块组成,用于计算理想横摆角速度
图 1
图 1 考虑驾驶风格的AFWS/DYC稳定性协调控制整体结构图
Fig.1 Overall structure diagram of AFWS/DYC stability coordination control considering driving styles
2. 上层控制器
2.1. 考虑驾驶风格的个性化稳定性控制参考模型
传统的稳定性控制参考模型根据驾驶人操纵信息以及车辆状态信息,采用拥有线性二自由度的车辆动力学模型计算理想的横摆角速度和质心侧偏角. 考虑到不同风格的驾驶人对稳定性控制的介入时机和对车辆响应的需求具有差异性,通过邀请不同驾驶风格的驾驶人进行在环试验,获取其所需的稳定性控制介入时机,以及在不同车速和路面附着系数下对车辆响应特性的需求. 建立考虑驾驶风格的个性化稳定性控制参考模型:
式中:
由于横摆角速度受轮胎与路面间附着力的限制,参考横摆角速度还需要满足
式中:
综上,修正后的横摆角速度为
式中:
2.1.1. 驾驶风格分析
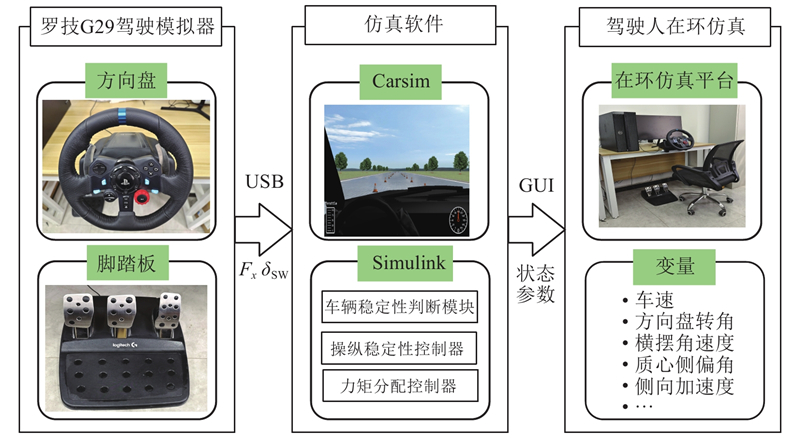
通过PreScan、MATLAB/Simulink仿真软件和罗技G29驾驶模拟器搭建驾驶风格数据采集平台,如图2所示. 罗技G29驾驶模拟器的驾驶人操作输入主要包括方向盘和加速、制动踏板的操作. 方向盘配备双马达力反馈系统,旋转角度范围为0~900°;制动踏板采用非线性刹车踏板仿效压敏制动系统,能够满足基本的驾驶人操控力输入特性和角输入特性.
图 2
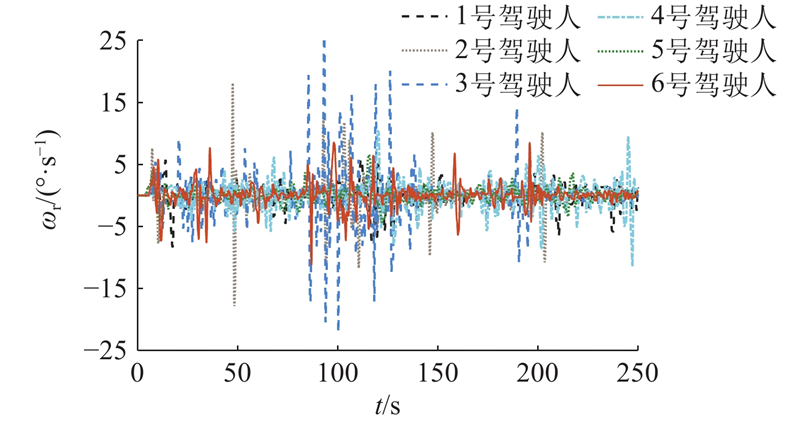
为了采集驾驶人在换道过程中的数据,招募拥有驾驶执照并且具有城市道路驾驶经验的驾驶人进行驾驶风格数据采集试验. 试验召集27名受试驾驶人,包括23名男性驾驶人和4名女性驾驶人. 总计进行19.6 h试验,共采集到7 058 171条数据,其中6位驾驶人的部分横摆角速度
图 3
图 3 不同驾驶人的横摆角速度试验数据
Fig.3 Lateral angular velocity test data of different drivers
表 1 驾驶风格聚类中心
Tab.1
| 标签 | X1 | X2 | X3 | X4 | X5 |
| 1 | 0.104 9 | 0.083 5 | 0.008 1 | 0.093 2 | 0.047 3 |
| 2 | 0.104 9 | 0.083 5 | 0.008 1 | 0.093 2 | 0.047 3 |
| 3 | 0.050 2 | 0.523 1 | 0.043 3 | 0.532 2 | 0.531 2 |
图 4
2.1.2. 考虑驾驶风格的个性化参考模型车辆稳定性因数确定
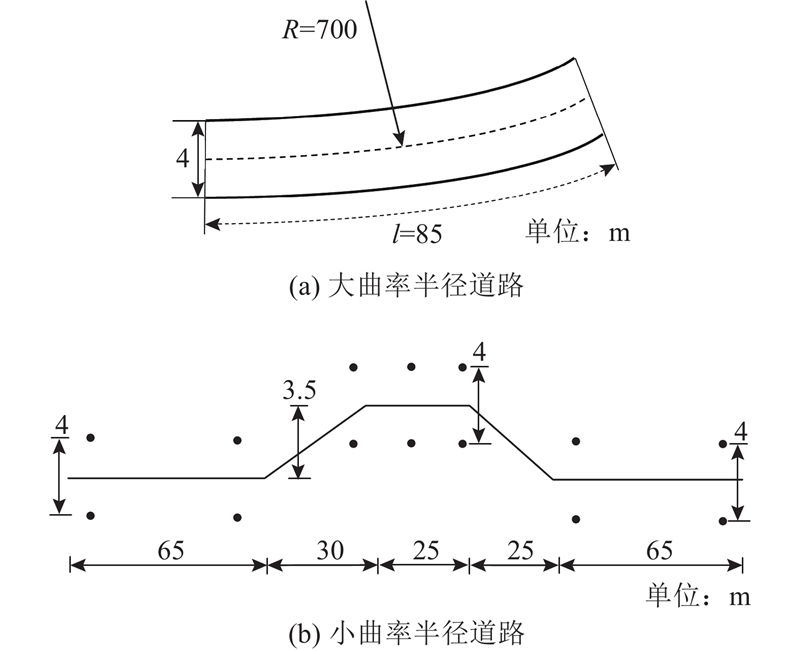
同一名驾驶人在不同车速、道路曲率和路面附着系数下,对车辆的响应需求不同. 通过驾驶人在环试验获得不同驾驶风格的驾驶人在不同车速、道路曲率和路面附着系数下的车辆稳定性因数. 在驾驶人在环试验平台,设计小曲率半径与大曲率半径2种道路,如图5所示. 其中,大曲率半径道路是长度为85 m、半径为700 m的弯道,小曲率半径道路为双移线道路. 为了建立不同车速、不同路面附着系数等多种工况,将设置的路面附着系数和车速参数对
图 5
图 6
根据驾驶风格分类结果邀请具有明显驾驶风格的驾驶人进行驾驶人在环试验,包括9名谨慎型驾驶人、6名一般型驾驶人和2名激进型驾驶人. 为了快速确定符合驾驶人期望的理想参考模型的车辆稳定性因数,在线性二自由度车辆动力学模型的基础上考虑驾驶风格,设定驾驶风格增益系数
式中:
驾驶人在试验过程中通过直接修改驾驶风格增益系数来达到理想的车辆响应效果. 根据式(1)和(4),得到考虑驾驶风格的稳定性因数:
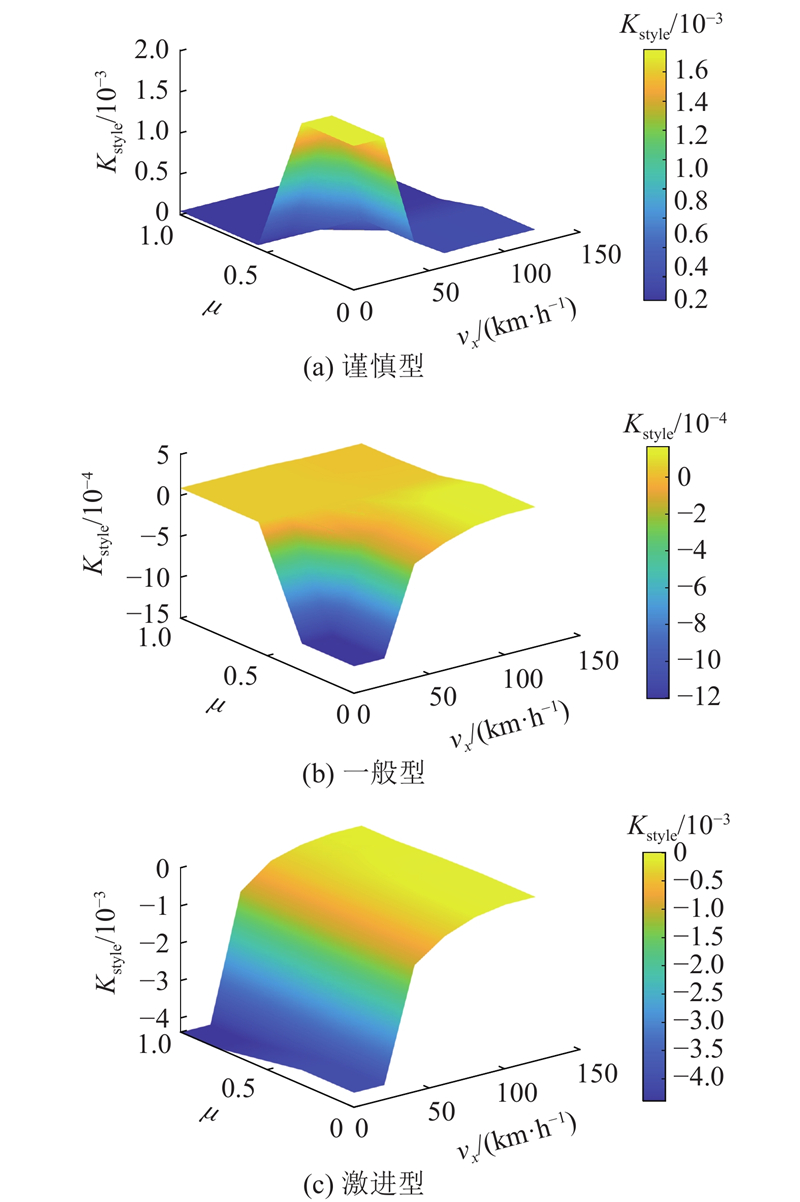
每位驾驶人在每种工况下进行9次模拟驾驶试验(驾驶风格增益系数G从0.8至1.2每间隔0.05取值),在18种不同车速、路面附着系数及道路曲率的工况下总共完成162次试验. 驾驶人根据自身感受对不同增益系数进行评价,确定转向风格增益系数偏好,再根据该增益系数计算出对应的车辆稳定性系数. 由于激进型驾驶人较少,激进型驾驶人每人分别进行3轮试验,每次试验间隔1周进行,其他风格的驾驶人只进行1轮试验. 对试验结果进行处理,得到不同车速、路面附着系数及驾驶风格下的Kstyle数据,如图7所示.
图 7
图 7 不同驾驶风格的车辆稳定性因数
Fig.7 Vehicle stability factors for different driving styles
2.2. 基于$\beta {\text{ - }}\omega $
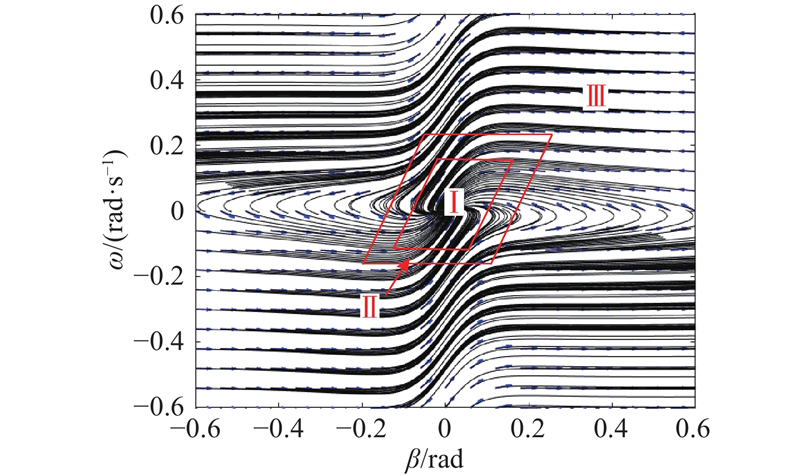
为了准确判断当前车辆是否处于失稳状态,采用基于
式中:
双直线法只能根据质心侧偏角进行稳定性划分,但是路面能够提供的附着力是有限的. 结合双直线法和最大横摆角速度限制可以得到稳定域边界,不同车速和路面附着系数下的边界系数如表2所示.
表 2 不同车速与路面附着系数下的稳定域边界系数
Tab.2
| 20 | 0.2 | 1.7 | 0.27 |
| 20 | 0.4 | 2.3 | 0.40 |
| 20 | 0.8 | 3.2 | 0.66 |
| 40 | 0.4 | 2.3 | 0.35 |
| 60 | 0.4 | 2.3 | 0.30 |
| 80 | 0.4 | 2.3 | 0.27 |
| 100 | 0.4 | 2.3 | 0.27 |
由表2可知,
根据稳定性判断结果在AFWS与DYC之间进行切换. 为了使AFWS与DYC的控制权重实现线性变化,将稳定域边界内缩35%得到过渡域边界,最终将相平面划分为3部分,如图8所示,其中I区为稳定域,II区为过渡域,III区为失稳域.
图 8
图 8
Fig.8
Stability region partitioning in
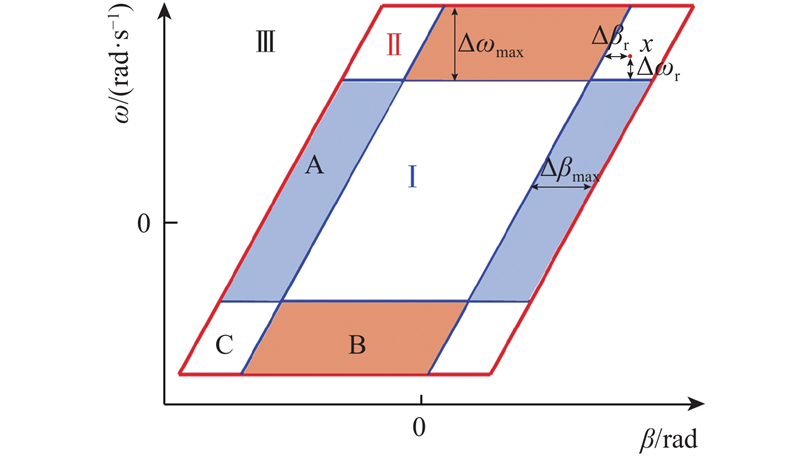
采用基于相平面位置的车辆失稳程度指标
图 9
图 9
Fig.9
Transition region partitioning in
当车辆状态处于Ⅰ区时,失稳程度指标为0,处于稳定状态;当车辆状态处于Ⅲ区时,失稳程度指标为1,车辆处于失稳状态. A区内
3. 中层控制器
3.1. 基于混合博弈理论的AFWS/DYC稳定性控制策略
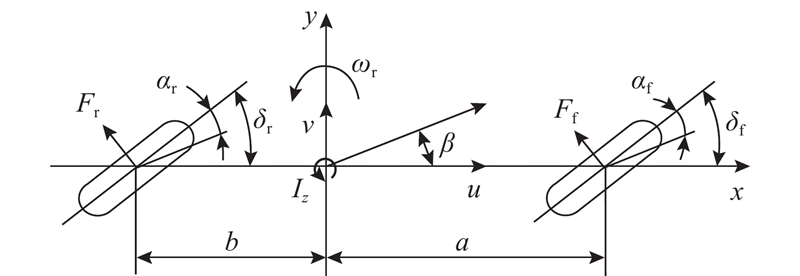
在小转角和轮胎线性区域内,线性二自由度(2 degrees of freedom, 2DOF)车辆动力学模型可以良好地反映车辆的转向响应特性,因此只考虑车辆的侧向和横摆运动对行驶稳定性的影响. 二自由度车辆动力学模型如图10所示.
图 10
线性2DOF车辆动力学状态方程为
式中:系统状态变量
其中,
采用前向欧拉法,忽略高阶项可得离散化的车辆模型:
式中:k表示第k个采样时刻;
本研究设计的基于混合博弈理论的控制器框架如图1所示. DYC在轮胎处于非线性区域时仍能较好地控制车辆稳定性,且工作区域更大,因此,构建AFWS与DYC的非合作的Stackelberg主从博弈模型. 将DYC作为领导者,追随稳定性控制目标
在基于分布式模型预测控制的博弈方法中,预测方程不仅用于预测系统未来的输出状态,而且为博弈参与者之间的信息交流提供基础. 假设车辆的状态矩阵在模型预测控制的滚动域中保持不变,在预测时域
式中:
其中
由于AFS与ARS追求相同的横向稳定性控制目标,且有相同的工作区域,采用基于分布式模型预测控制的合作博弈框架来表示2个系统的交互. 参与者的个体利益目标被定义为追求自身状态与目标之间的误差最小化,同时追求自身输出的最小化,因此采用二次型成本函数表示参与者的个体利益:
式中:
在合作博弈中,采用权重相加的方法实现各参与者的目标全局共享. 各参与者效益指标的成本函数为
式中:
同时,参与者的成本函数受到式(11)的约束. 求解如下所示的优化问题即可得到合作博弈的Pareto解:
通过终端等式约束方法证明系统稳定性,同时根据系统预测方程式(11),定义:
优化式(14),可以将其转化为最小二乘问题:
式中:
可以得到上述问题的最优解为
式中:
将式(15)代入式(17)可以得到AFS与ARS的解为
式中:
由式(18)可知,第
式中:
随着
将
式中:
结果是收敛的,最优解中的
DYC作为领导者,考虑跟随者的策略,将式(21)代入式(11),整理后可得其预测方程:
式中:
构建领导者DYC的成本函数,并写为线性二次型形式:
式中:
参考跟随者,根据预测方程(22)定义:
领导者优化问题转化为最小二乘问题,得到
将式(25)代入跟随者的最优解式(21),可得到跟随者的解:
3.2. 基于失稳程度的协调控制策略
根据车辆失稳程度指标
根据Sigmoid函数,建立参数
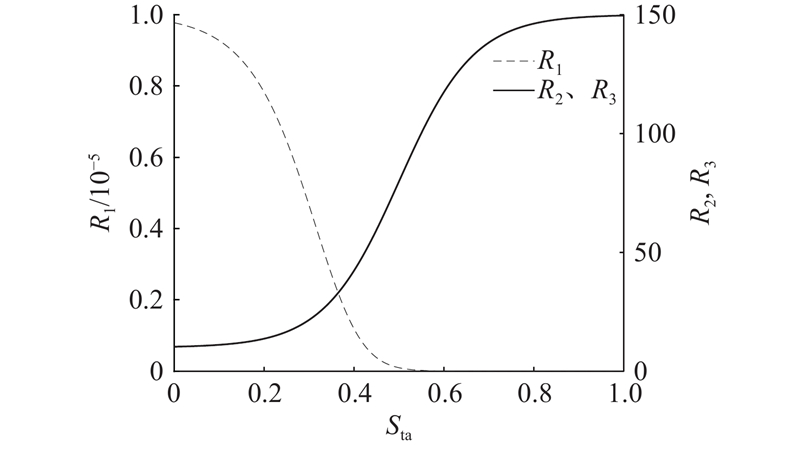
领导者与跟随者的控制输出权重R1、R2、R3为
控制输出权重R1、R2、R3随失稳程度指标的变化曲线如图11所示,随着车辆在Ⅱ区内逐渐从稳定状态向失稳边界靠近,
图 11
4. 下层控制器
下层控制器将附加转角作用于转向车轮,同时考虑路面附着情况、附加纵向合力以及电机的最大转矩,以轮胎负荷率最小为目标,基于最优化方式将附加横摆力矩转化为轮胎纵向力分配到各车轮.
4.1. 目标函数
维持车辆稳定的附加横摆力矩需要转化为驱动车轮的纵向力. 为了更合理地利用车轮的纵向附着力,以车辆各轮胎负荷率平方之和最小作为优化目标,定义目标函数:
式中:
4.2. 约束条件
4.2.1. 等式约束
附加横摆力矩的分配策略应保证目标车速的维持,同时产生维持车辆稳定性的附加横摆力矩,即
式中:
4.2.2. 不等式约束
(a)附着条件约束.
由于路面能提供的附着力是有限的,轮胎纵向力受路面附着的约束,即
(b)电机最大转矩约束.
电机存在最大转矩限制,因此在计算车轮纵向力时也需要将该因素考虑在内,即:
式中:
附加横摆力矩分配转化为优化问题:
式中:
5. 仿真分析
5.1. 驾驶人开环试验
表 3 整车参数
Tab.3
| 参数 | 取值 | 参数 | 取值 | |
| m/kg | 1 230 | 1 343.1 | ||
| b/m | 1.56 | 1.04 | ||
| 30 797 | 30 797 |
图 12
在CarSim/Simulink平台输入车辆参数和工况参数后,得到开环试验仿真结果,如图13所示. 由图13(a)可知,稳定性控制器介入后车辆的横向位移
图 13
表 4 不同参考模型中状态量的最大值与标准差
Tab.4
| 模型 | ||||
| 无控制 | 13.04 | 2.06 | 9.09 | 1.15 |
| 二自由度模型 | 10.51 | 1.12 | 8.74 | 0.70 |
| 谨慎型 | 10.52 | 1.13 | 8.69 | 0.69 |
| 一般型 | 10.52 | 1.14 | 8.76 | 0.71 |
| 激进型 | 10.54 | 1.18 | 8.94 | 0.77 |
5.2. 驾驶人在环试验
基于CarSim、Simulink和罗技G29搭建如图14所示的驾驶人在环试验平台,进行驾驶人在环试验. 采用双移线工况进行试验,分为中速、低附着和高速、高附着2种工况.
图 14
在中速、低附着工况下,
图 15
图 15 中速、低附着工况下不同驾驶人在环试验结果
Fig.15 In-loop testing results for different drivers under medium speed and low adhesion conditions
表 5 中速、低附着工况下不同驾驶人驾驶车辆在施加稳定性控制前、后的状态量最大值
Tab.5
| 模型 | |||
| 谨慎型无控制 | 10.37 | 2.25 | 56.43 |
| 谨慎型 | 6.76 | 0.60 | 66.24 |
| 一般型无控制 | 11.15 | 2.31 | 54.59 |
| 一般型 | 6.21 | 0.61 | 66.78 |
| 激进型无控制 | 20.64 | 4.73 | 72.85 |
| 激进型 | 9.83 | 1.22 | 65.03 |
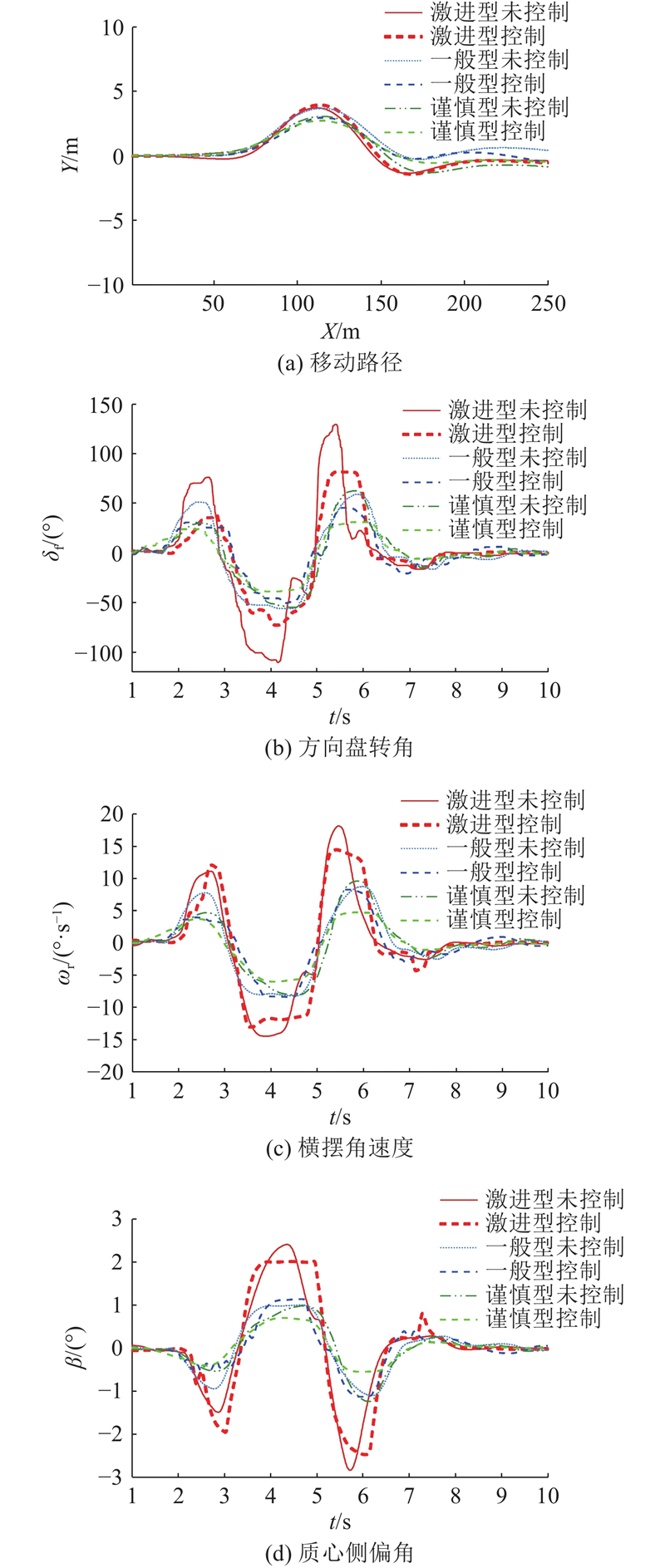
在高速、高附着工况下,
图 16
图 16 高速、高附着工况下不同驾驶人的在环试验结果
Fig.16 In-loop testing results for different drivers under high-speed and high adhesion conditions
表 6 高速、高附着工况下不同驾驶人驾驶的车辆在施加稳定性控制前、后的状态量最大值
Tab.6
| 模型 | |||
| 谨慎型无控制 | 5.97 | 1.24 | 62.96 |
| 谨慎型 | 9.62 | 0.69 | 38.93 |
| 一般型无控制 | 8.79 | 1.11 | 59.13 |
| 一般型 | 8.28 | 1.14 | 43.14 |
| 激进型无控制 | 18.14 | 2.83 | 129.38 |
| 激进型 | 14.47 | 2.48 | 81.90 |
6. 结 论
为了改善分布式驱动电动汽车的操纵稳定性,并考虑不同驾驶人的驾驶风格,开展了考虑驾驶风格的AFWS/DYC稳定性协调控制策略研究,主要特点如下.
(1)通过邀请不同驾驶风格的驾驶人进行在环试验,分析不同驾驶风格驾驶人在不同车速以及路面附着系数下对车辆响应的差异化需求,从而建立了考虑驾驶风格的个性化稳定性控制参考模型.
(2)在驾驶风格在线辨识和考虑驾驶风格的个性化稳定性控制参考模型研究的基础上,设计了基于博弈理论的个性化AFWS/DYC横向稳定性控制器. 采用分层控制策略,其中上层控制器由考虑驾驶风格的个性化稳定性控制参考模型和基于
参考文献
Active safety control of automated electric vehicles at driving limits: a tube-based MPC approach
[J].DOI:10.1109/TTE.2021.3100843 [本文引用: 1]
A post impact stability control for four hub-motor independent-drive electric vehicles
[J].DOI:10.1109/TVT.2021.3136186 [本文引用: 1]
分布式驱动电动汽车底盘集成控制技术综述
[J].DOI:10.3969/j.issn.1001-7372.2023.04.018 [本文引用: 1]
Review of chassis integrated control technology for distributed drive electric vehicles
[J].DOI:10.3969/j.issn.1001-7372.2023.04.018 [本文引用: 1]
Rear-steering based decentralized control of four-wheel steering vehicle
[J].DOI:10.1109/TVT.2020.3020154 [本文引用: 1]
Handling and stability integrated control of AFS and DYC for distributed drive electric vehicles based on risk assessment and prediction
[J].DOI:10.1109/TITS.2022.3193891 [本文引用: 1]
Path planning and following control of autonomous bus under time-varying parameters against parametric uncertainties and external disturbances
[J].DOI:10.1109/TVT.2022.3170440 [本文引用: 1]
Path following control of autonomous four-wheel-independent-drive electric vehicles via second-order sliding mode and nonlinear disturbance observer techniques
[J].DOI:10.1109/TIE.2020.2973879 [本文引用: 1]
Research on intervention criterion and stability coordinated control of AFS and DYC
[J].
Integration sliding mode control for vehicle yaw and rollover stability based on nonlinear observation
[J].DOI:10.1177/01423312221099414 [本文引用: 1]
分布式驱动无人车路径跟踪与稳定性协调控制
[J].
Integrated control of unmanned distributed driven vehicles path tracking and stability
[J].
面向极限工况的分布式驱动电动汽车动力学集成控制方法
[J].
Integrated dynamic control strategy for extreme maneuvers of 4WIDEVs
[J].
A game theory approach to energy management of an engine–generator/battery/ultracapacitor hybrid energy system
[J].DOI:10.1109/TIE.2016.2539245 [本文引用: 1]
Game-theoretic modeling of the steering interaction between a human driver and a vehicle collision avoidance controller
[J].DOI:10.1109/THMS.2014.2363124 [本文引用: 1]
A distributed integrated control architecture of AFS and DYC based on MAS for distributed drive electric vehicles
[J].
A decentralized cooperative control framework for active steering and active suspension: multi-agent approach
[J].
Interactive control paradigm-based robust lateral stability controller design for autonomous automobile path tracking with uncertain disturbance: a dynamic game approach
[J].
Linear quadratic game and non-cooperative predictive methods for potential application to modelling driver-AFS interactive steering control
[J].
Personalized controller design for electric power steering system based on driver behavior
[J].
“车适应人”线控汽车理想特性参考模型神经网络建模
[J].
Neural network modeling of ideal characteristics reference model for “car adaption for driver” x-by-wire vehicle
[J].
基于驾驶人转向意图的双电机驱动电动汽车稳定性控制策略
[J].DOI:10.3969/j.issn.1001-7372.2022.01.028 [本文引用: 1]
Vehicle stability control strategy for a dual-motor drive electric vehicle considering driver steering intention
[J].DOI:10.3969/j.issn.1001-7372.2022.01.028 [本文引用: 1]
Optimal coordinated control of ARS and DYC for four-wheel steer and in-wheel motor driven electric vehicle with unknown tire model
[J].
Extension coordinated control of distributed-driven electric vehicles based on evolutionary game theory
[J].