一直以来,国内外学者对齿侧间隙与传动误差的研究没有中断过. 张磊磊等[3]定量分析圆柱齿轮机构的圆周侧隙与圆柱齿轮机构各个环节影响因素之间的关系. 陈文华等[4]采用蒙特卡洛模拟方法,分析圆柱齿轮机构的传动误差. 孙涛等[5]利用CETOL三维公差软件,对圆柱齿轮机构的齿侧间隙进行三维公差仿真. 王光建等[6]通过实验对一级圆柱齿轮的齿侧间隙变化曲线进行拟合,实现了对齿轮副整个大周期齿侧间隙的快速预测. Yang等[7]提出基于电流信号来预测一级圆柱齿轮齿侧间隙的方法. Giovannitti等[8]提出利用电机编码器信号对工业机器人的齿轮侧隙进行估计的方法. 安凯[9]分析齿侧间隙对空间机械臂末端定位误差的影响. Guida等[10]分析不同程度的齿侧间隙和不同关节的齿侧间隙对UR5协作机器人性能的影响.
目前研究都集中在圆柱齿轮机构的齿侧间隙的理论建模和公差仿真分析上,对圆锥齿轮机构的齿侧间隙理论建模、齿侧间隙公差仿真未见报道;针对全齿轮耦合机器人齿侧间隙对末端精度影响的研究未见报道. 本文对圆柱齿轮机构的齿侧间隙进行理论建模,开展三维公差仿真分析. 将圆柱齿轮机构的齿侧间隙理论建模和三维公差仿真方法应用到圆锥齿轮机构中,分析机器人关键传动链的末端误差,提出机器人侧隙补偿方法,开展实验验证.
1. 机器人齿侧间隙的建模与仿真方法
1.1. 全齿轮耦合机器人及传动原理
全齿轮机器人外壳均采用不锈钢材料,伺服电机均放置于屏蔽室外,且各个关节均实现全密封设计,保证机器人在核环境下正常运行.
图 1
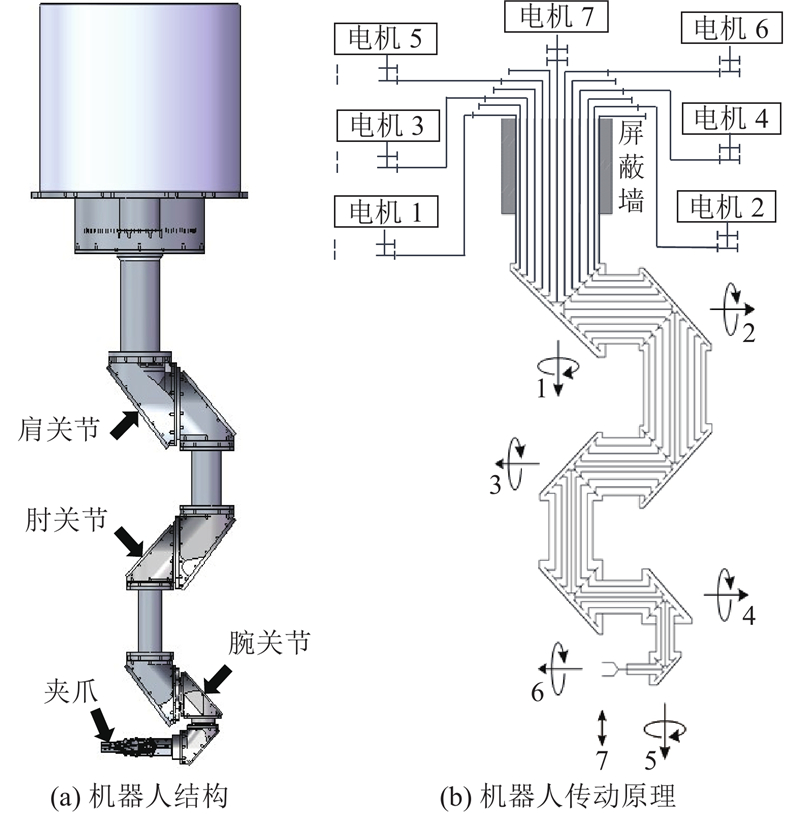
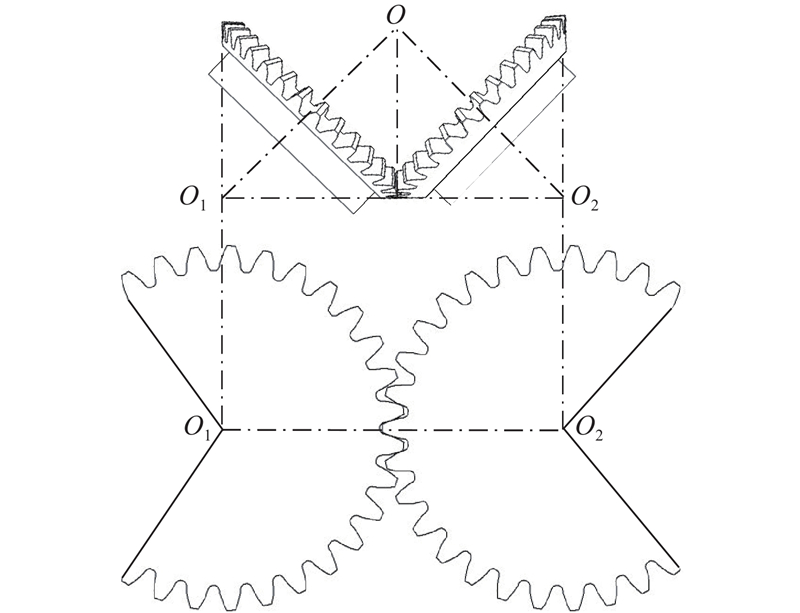
图 1 全齿轮机器人的结构与传动原理
Fig.1 Structure and transmission principle of fully gear-coupled robot
图 2
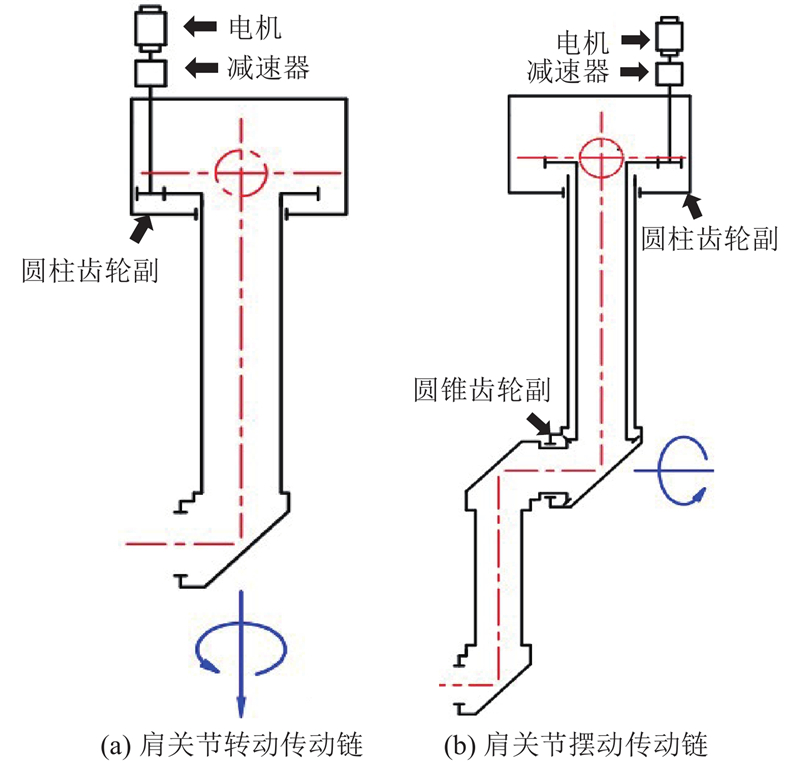
在分别控制机器人7个自由度的7条传动链中,其中肩关节偏摆传动链控制肩关节的偏摆,肩关节偏摆轴心线与夹爪中心的距离最大,微小的齿轮传动误差会导致机器人末端产生较大的偏差,因此要优先保证肩关节偏摆传动链的传动精度.
图 3
1.2. 齿侧间隙的影响因素和理论建模方法
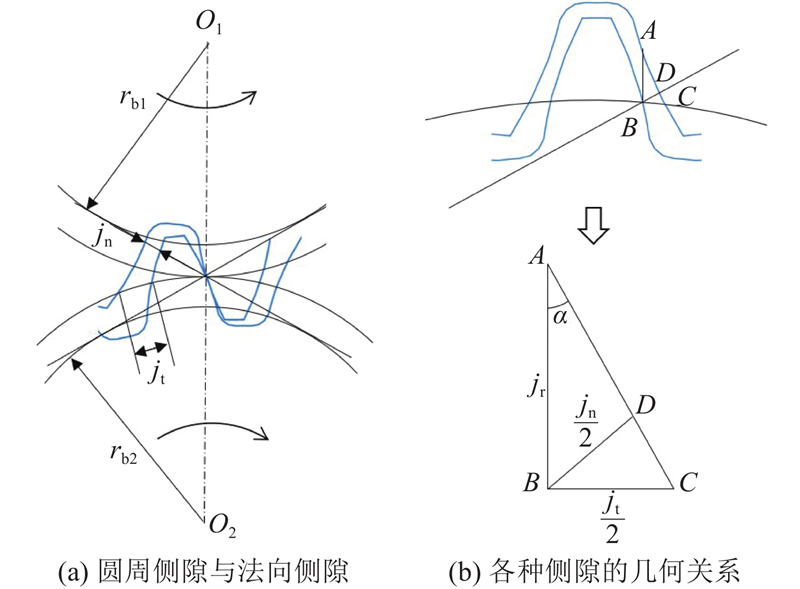
齿轮副中经常采用的侧隙有圆周侧隙
如图4所示,圆周侧隙是指齿轮副中,当其中一个齿轮固定时另一个齿轮分度圆处能够自由转动的圆弧长. 法向侧隙是指主、从动轮工作齿面接触时,非工作齿面的最短法向距离. 径向侧隙是指主、从动工作状态下的中心距与无侧隙啮合状态下的中心距之差. 三者关系如下:
图 4
式中:
以法向侧隙为分析目标开展公差建模与公差仿真分析. 影响齿轮机构法向侧隙的影响因素有很多,大致可以分为齿轮固有误差、装置误差和其他误差3大类. 齿轮固有误差是指齿轮在制造时产生的制造误差,如齿厚偏差、齿轮几何偏心、齿形误差、周节误差、齿向误差等. 装置误差是指当齿轮与轴、轴承、箱体等零部件装配成齿轮机构时,轴、轴承、箱体等的固有误差和装配误差等,如中心距偏差、配合偏心误差、轴承游隙. 其他误差是指由温度、振动、负载等带来的误差,本文研究的核工业机器人所处的环境温度为25°,负载小于10 kg,无较大振动,温度变化、振动、负载等带来的其他误差可以忽略不计.
针对驱动侧的圆柱齿轮机构,结合已有的圆柱齿轮机构侧隙建模理论[19],对圆柱齿轮机构法向侧隙进行理论建模.
针对关节处的圆锥齿轮机构,由于圆锥齿轮结构相对复杂,齿侧间隙与各类误差之间的关系较圆柱齿轮复杂,提出将圆锥齿轮副假想成如图5所示的一组假想圆柱齿轮副的方法. 两者的齿轮法向侧隙相同,将圆锥齿轮机构的公差折算到圆柱齿轮机构中,利用圆柱齿轮机构法向侧隙的建模理论,对圆锥齿轮机构的法向侧隙进行建模.
图 5
图 5 圆锥齿轮副与假想圆柱齿轮副的示意图
Fig.5 Schematic diagram of bevel gear pairs and imaginary cylindrical gear pairs
1.3. 齿侧间隙公差仿真的方法
为了验证圆柱或圆锥齿轮机构法向侧隙建模计算的正确性,利用三维公差软件Three Dimensional Control Systems进行验证,以下简称3DCS. 3DCS软件是尺寸偏差分析工具,模拟机构的设计制造与装配过程,可以根据实际情况添加如尺寸公差及形位公差的相关公差参数,定义零件间的装配方式,添加齿轮法向侧隙为测量目标. 运用蒙特卡洛法模拟分析方法分析2000次,得到超差率和贡献度结果,为后续分析与优化提供一定的理论与方法.
蒙特卡洛模拟方法具体是指按照齿轮机构各项误差的概率分布函数产生2 000组随机数,模拟不同的齿轮机构装配情况,得到在一定置信度下的齿轮法向侧隙的范围.
2. 驱动端圆柱齿侧间隙的建模与仿真
2.1. 圆柱齿轮机构法向侧隙的建模
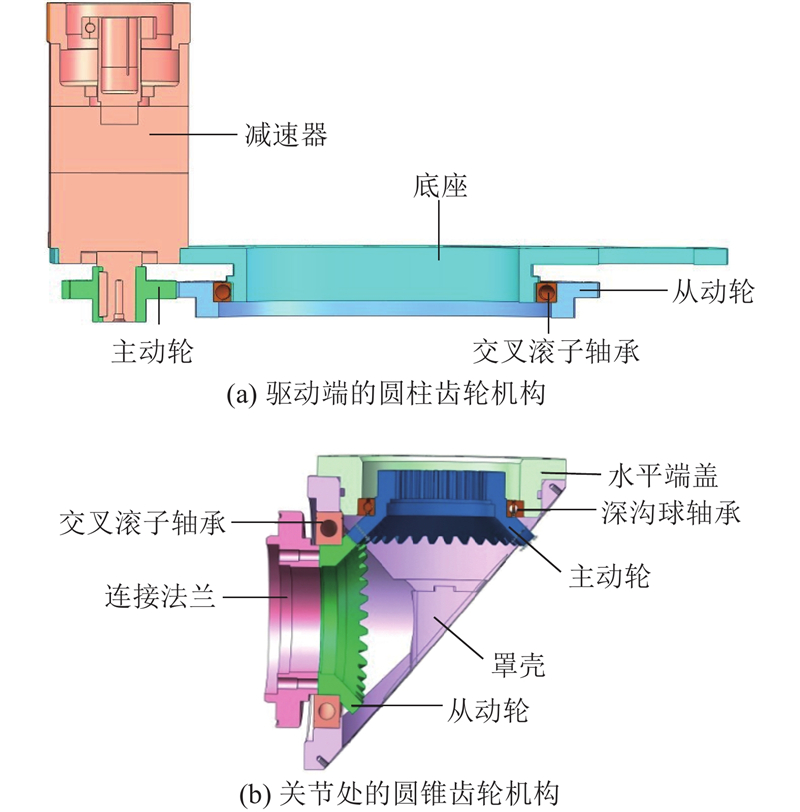
以图3 (a)所示的圆柱齿轮机构为分析目标,该齿轮传动装置共有5个部分,分别为行星减速器、主动轮、从动轮、底座和交叉滚子轴承. 圆柱齿轮机构法向侧隙的影响要素有5个:齿轮的齿厚偏差、底座的中心距偏差、齿轮几何偏心、轴承径向游隙、减速器输出轴的圆跳动误差.
1) 齿轮齿厚偏差对侧隙的影响.
圆柱齿轮齿厚偏差
式中:
2) 齿轮副中心距偏差对侧隙的影响.
圆柱齿轮副中心距偏差
式中:
3) 齿轮几何偏心对侧隙的影响.
圆柱齿轮的几何偏心e使得中心距会产生
4) 轴承径向游隙对侧隙的影响.
轴承径向游隙
式中:
5) 减速器输出轴圆跳动误差对侧隙的影响.
行星减速器输出轴与齿轮配合偏心误差主要来源于减速器输出轴的圆跳动误差
综合以上分析,依据各个误差之间相互独立的假设,可以推出圆柱齿轮机构总的法向侧隙的均值
式中:
圆柱齿轮机构的主要数据如表1、2所示. 表中,z为齿数,m为模数,d为分度圆直径. 将相关数据代入式(12)、(13),可以求得
表 1 圆柱齿轮机构的参数与公差
Tab.1
| 项目 | 主动轮 | 从齿轮 |
| 28 | 110 | |
| m/mm | 2.5 | 2.5 |
| 20 | 20 | |
| d/mm | 70 | 275 |
| −19 | −21 | |
| −30 | −32 | |
| 27 | 31 | |
| S/μm | 8 | — |
| — | 2 | |
| — | 30 |
表 2 圆柱齿轮传动参数
Tab.2
| 参数 | 数值 |
| 减速比 | 3.929 |
| 中心距 | 172.5 |
| 齿轮精度等级 | 5-f |
| 中心距极限偏差/μm | ±20 |
| 最小极限法向侧隙/μm | 15 |
2.2. 圆柱齿轮机构法向侧隙的仿真分析
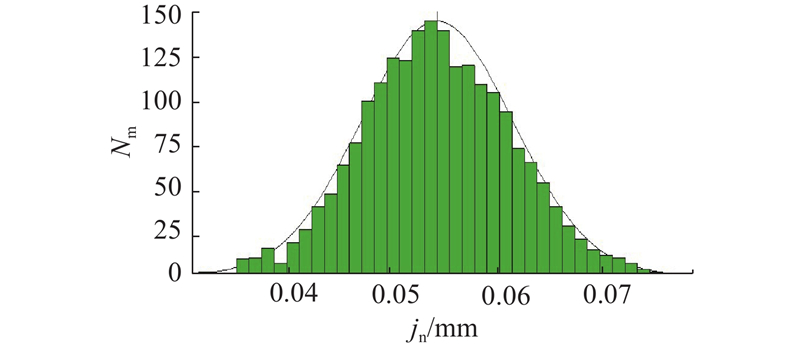
在3DCS中,设置主动轮的运动参数,并设置工作齿面间最短距离为0,保证工作齿面保持相互接触,以模拟齿轮相互配合的状态. 设置非工作齿面间的最短法向距离,即齿轮副法向侧隙,作为测量目标,可得圆柱齿轮副法向侧隙的仿真结果,如图6所示. 图中,Nm为仿真次数.
图 6
通过3DCS仿真可知,齿轮装置的各个公差的贡献度如表3所示. 各个公差的贡献度反映了对法向侧隙的影响程度,贡献度越大,对法向侧隙的影响程度越高.
表 3 圆柱齿轮公差的贡献度
Tab.3
| 序号 | 尺寸名称 | 公差/mm | 贡献度/% |
| 1 | 主动轮齿厚偏差 | 0.005 | 22.0 |
| 2 | 从动轮齿厚偏差 | 0.005 | 22.0 |
| 3 | 齿轮副中心距偏差 | 0.040 | 21.7 |
| 4 | 从动轮几何偏心 | 0.016 | 13.0 |
| 5 | 轴承径向游隙 | 0.014 | 10.6 |
| 6 | 主动轮几何偏心 | 0.014 | 9.9 |
| 7 | 减速器输出轴圆跳动 | 0.008 | 0.8 |
在结果中,齿厚偏差和齿轮中心距对齿轮副法向侧隙的影响较大,减速器输出轴圆跳动对结果有微小影响,公差贡献度为公差优化提供了依据,便于公差的重新分配.
2.3. 圆柱齿轮机构回程误差的分析
圆柱齿轮机构法向侧隙的理论建模结果与三维仿真结果对比如表4所示. 理论建模结果与公差仿真结果很接近,验证了圆柱齿轮机构建模理论的正确性.
表 4 圆柱齿轮机构法向侧隙的对比
Tab.4
| 项目 | jnmin/μm | jnmax/μm | |
| 理论建模 | 32 | 53 | 74 |
| 三维仿真 | 34 | 54 | 75 |
圆柱齿轮机构回程误差与法向侧隙的关系如下:
式中:
根据式(14),代入仿真数据,可得平均回程误差
3. 关节处圆锥齿侧间隙的建模与仿真
3.1. 圆锥齿轮机构法向侧隙的建模
以如图3 (b)所示的圆锥齿轮传动机构为分析目标,该齿轮传动装置共有7个部件,分别为主动轮、从动轮、罩壳、肩关节水平端盖、肩关节连接法兰、深沟球轴承和交叉滚子轴承. 影响圆锥齿轮机构法向侧隙的影响要素如下:齿轮的齿厚偏差、轴间距偏差、轴交角偏差、齿轮几何偏心、关键配合面的面轮廓度误差、深沟球轴承和交叉滚子轴承的径向游隙,圆锥齿轮公差的基本假设与圆柱齿轮的基本假设相同.
圆锥齿轮副法向侧隙可以等价成在背锥面上的一组圆柱齿轮啮合时的法向侧隙,即将圆锥齿轮机构的公差等价折算到圆柱齿轮机构中,得到圆锥齿轮机构回程误差的建模方法.
1) 齿轮齿厚偏差对侧隙的影响.
圆锥齿轮齿厚偏差
2) 齿轮副轴间距偏差对侧隙的影响.
圆锥齿轮副轴间距偏差
图 7
图 7 圆锥齿轮副与假想圆柱齿轮副的侧隙关系图
Fig.7 Side backlash relationship between bevel gear pairs and imaginary cylindrical gear pairs
3) 齿轮副轴交角偏差对侧隙的影响.
圆锥齿轮副轴交角偏差
式中:
4) 齿轮几何偏心对侧隙的影响.
齿轮几何偏心e等价于假想圆柱齿轮副的中心距产生
5) 轮廓度误差对侧隙的影响.
齿面、罩壳断面、水平端盖轮廓度误差
式中:
6) 轴承径向游隙对侧隙的影响.
轴承径向游隙
综合以上分析,依据各个误差之间相互独立的假设,可以推出圆锥齿轮机构总的法向侧隙的均值
式中:
表 5 圆锥齿轮机构的参数与公差
Tab.5
| 参数 | 数值 |
| z | 31 |
| m/mm | 3.5 |
| 20 | |
| d/mm | 108.5 |
| B/mm | 9 |
| 102.1 | |
| −32 | |
| −53 | |
| 10 | |
| 30 |
表 6 圆锥齿轮传动参数
Tab.6
| 参数 | 数值 |
| 减速比 | 1 |
| 9 | |
| 10 | |
| 20 | |
| 齿轮精度等级 | 5-f |
| 19 | |
| P/μm | 12 |
与圆柱齿轮机构的计算方法相同,根据表5、6的数据,求得圆锥齿轮机构均值
3.2. 圆锥齿轮机构法向侧隙的仿真分析
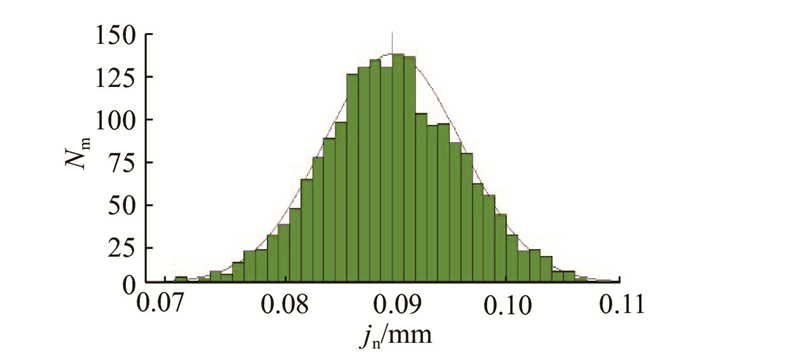
在3DCS中,与圆柱齿轮机构的公差仿真设置相同,设置非工作齿面间的最短法向距离,即齿轮副法向侧隙,作为测量目标,可得圆锥齿轮副法向侧隙的仿真结果,如图8所示.
图 8
公差贡献度如表7所示. 齿轮齿厚偏差和齿轮几何偏心对齿轮副法向侧隙的影响较大,轴交角偏差和轴承径向游隙对结果有微小影响,公差贡献度为后续的公差优化提供了依据.
表 7 圆锥齿轮的公差贡献度
Tab.7
| 序号 | 尺寸名称 | 公差/mm | 贡献度/% |
| 1 | 主动轮齿厚偏差 | 0.011 | 30.0 |
| 2 | 从动轮齿厚偏差 | 0.011 | 30.0 |
| 3 | 主动轮几何偏心 | 0.028 | 15.1 |
| 4 | 从动轮几何偏心 | 0.028 | 10.2 |
| 5 | 面轮廓度误差 | 0.012 | 9.1 |
| 6 | 轴交角偏差 | 0.020 | 3.6 |
| 7 | 轴承径向游隙 | 0.010 | 2.0 |
3.3. 圆锥齿轮机构回程误差的分析
圆锥齿轮机构法向侧隙的理论建模结果与三维仿真结果如表8所示. 理论建模结果与公差仿真结果很接近,验证了圆锥齿轮机构建模理论的正确性.
表 8 圆锥齿轮机构法向侧隙的对比
Tab.8
| 项目 | jnmin/μm | jnmax/μm | |
| 理论建模 | 70 | 90 | 110 |
| 三维仿真 | 72 | 90 | 108 |
圆锥齿轮机构回程误差与法向侧隙的关系如下:
式中:
根据式(29),代入仿真数据,可得平均回程误差
4. 机器人末端误差的分析与实验
4.1. 机器人末端误差的影响因素分析
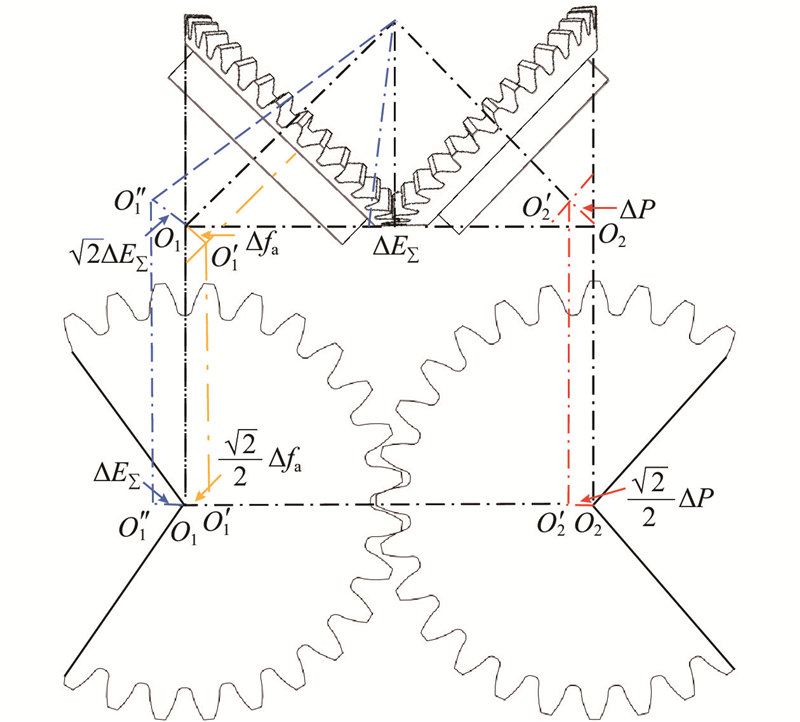
机器人内部有7条传动链,分别控制机器人的7个自由度的运动,均对机器人末端误差产生影响. 如图9所示,肩关节偏摆传动链控制肩关节的偏摆,且轴心线与夹爪中心的距离最大,肩关节偏摆传动链微小的传动误差会导致机器人末端产生较大的偏差,相比其他传动链引起的末端偏差更大.
图 9
4.2. 机器人末端误差的计算
齿轮传动链回程误差
式中:
机械臂末端位移的误差公式如下:
式中:
参考行星减速器厂家的数据可知,
4.3. 齿轮传动消隙与侧隙补偿方法
为了减小齿侧间隙及导致的机器人末端误差,从以下2个方面着手. 1)通过在圆锥齿轮机构中增加垫片,减小圆锥齿轮机构齿侧间隙. 2)当肩关节摆动越过竖直状态时,对电机转角进行补偿,减小回程误差.
1) 圆锥齿轮加垫消隙法.
关节处圆锥齿轮法向侧隙为0.070~0.110 mm,远大于最小极限法向侧隙0.019 mm,较大的侧隙会造成较大的回程误差. 通过在圆锥齿轮机构的主、从动轮和轴承之间分别添加厚度为
由式(32)计算得到,所需的垫片厚度为0.048 mm. 经过公差仿真验证可知,加垫片后圆锥齿轮机构的齿侧间隙调整为0.025~0.061 mm,大于齿轮副最小极限法向侧隙0.019 mm,与理论分析基本一致.
式中:
加垫片后,通过理论计算可得
2) 齿轮回程侧隙补偿法.
由于齿侧间隙的存在,当机械臂绕关节轴线进行摆动时,如机器人肩关节从右侧经由竖直状态摆动到左侧时,由于机器臂自重对齿轮产生的扭矩方向发生了改变,齿轮副啮合面发生改变,从而产生回程误差. 为了尽量消除重力作用下回程误差的影响,当机械臂越过竖直状态时,电机旋转
式中:
理论上齿轮回程侧隙补偿后
4.4. 实验分析
图 10
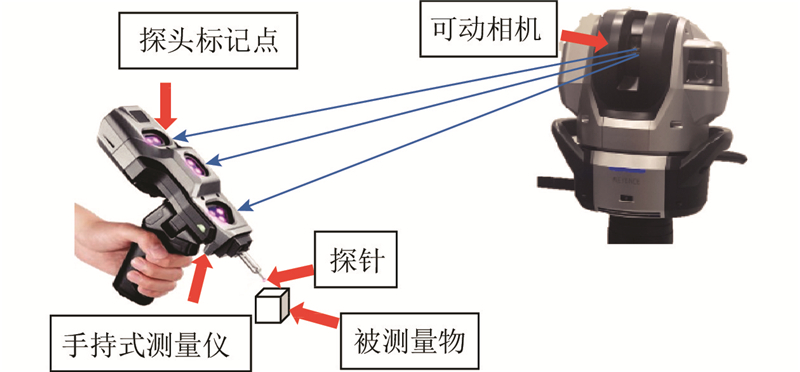
采用手持式探针三坐标测量仪,对机器人末端测点进行测量. 如图11所示,安装于地面上的可动相机通过对手持式测量仪上的多组探头标记点进行识别,计算得到手持式测量仪的位姿,从而测量得到探针处的坐标值.
图 11
为了消除机械臂末端刚度对测量点位置精度的影响,从竖直状态开始,如图10所示,电机驱动肩关节绕关节轴线逆时针摆动
5. 结 论
(1) 分析全齿轮耦合机器人的7个传动链可知,肩关节偏摆传动链对机器人末端精度的影响最大. 在机器臂自重作用下,当肩关节从机器人右侧区域摆动到左侧区域时,齿轮副啮合面发生更换,从而产生回程误差,反之亦然.
(2) 利用3DCS三维仿真软件对驱动侧圆柱齿轮机构齿侧间隙的理论公式进行验证,证明了圆柱齿轮机构齿侧间隙建模的有效性,得到圆柱齿轮机构回程误差的均值和最值.
(3) 考虑将圆锥齿轮机构齿轮副投影到锥齿轮背锥面上,生成一对假想圆柱齿轮,对圆锥齿轮机构齿侧间隙进行建模,并与3DCS公差仿真验证,得到圆锥齿轮机构回程误差的均值和最值.
(4) 为了减小齿侧间隙导致的机器人末端误差,采用以下2个方案. 1)在圆锥齿轮机构中增加2块厚度为0.048 mm的垫片,减小圆锥齿轮机构齿侧间隙. 2)当肩关节摆动越过竖直状态时,对电机转角进行补偿以降低回程误差,通过实验验证机器人末端位移误差减小了0.98 mm,降低了64%.
参考文献
后处理全齿轮传动机械臂的设计
[J].
Design of gearing chain-based manipulator for post-processing
[J].
A study on the stiffness of the end of the suspended master-slave remote control manipulator
[J].DOI:10.1007/s40430-022-03774-7 [本文引用: 1]
齿轮侧隙对齿轮传动精度的影响分析
[J].
Analysis on influence of gear backlash on gear transmission accuracy
[J].
齿轮系统传动误差的蒙特卡洛模拟分析
[J].DOI:10.3321/j.issn:0254-3087.2004.04.005 [本文引用: 1]
Monte-carlo simulation analysis of transmission error for gear drive systems
[J].DOI:10.3321/j.issn:0254-3087.2004.04.005 [本文引用: 1]
基于CETOL的含齿侧间隙的齿轮系统尺寸链及动力学分析
[J].
Dimensional chain and dynamics analysis of the gear system with backlash based on CETOL
[J].
基于双齿面传动误差的侧隙连续测量与预测
[J].
Measurement and prediction of backlash based on two-sided transmission error
[J].
Gear backlash detection and evaluation based on current characteristic extraction and selection
[J].DOI:10.1109/ACCESS.2020.2999478 [本文引用: 1]
A virtual sensor for backlash in robotic manipulators
[J].DOI:10.1007/s10845-022-01934-z [本文引用: 1]
关节齿隙对空间机械臂末端定位精度的影响
[J].DOI:10.3969/j.issn.1000-1093.2014.08.025 [本文引用: 1]
Effect of gear backlash on positioning precision of manipulator end-effectors
[J].DOI:10.3969/j.issn.1000-1093.2014.08.025 [本文引用: 1]
扭簧加载双片齿轮消隙机构综合啮合刚度
[J].DOI:10.3901/JME.2013.01.023 [本文引用: 1]
Research on synthesis meshing stiffness of torsional spring-loaded double-gear anti-backlash mechanism
[J].DOI:10.3901/JME.2013.01.023 [本文引用: 1]
弹簧消隙齿轮传动链回差分析估算
[J].
Return difference analysis and estimation of spring anti backlash gear transmission chain
[J].
双电机驱动机床进给系统消隙控制
[J].DOI:10.3969/j.issn.1007-449X.2014.03.010 [本文引用: 1]
Anti-backlash control of machine tool feed system driven by dual-motors
[J].DOI:10.3969/j.issn.1007-449X.2014.03.010 [本文引用: 1]
Design optimization analysis of an anti-backlash geared servo system using a mechanical resonance simulation and experiment
[J].DOI:10.5194/ms-12-305-2021 [本文引用: 1]
Optimal gearshift control for a novel hybrid electric drivetrain
[J].DOI:10.1016/j.mechmachtheory.2016.06.016
The experimental research on gear eccentricity error of backlash-compensation gear device based on transmission error
[J].
双电机消隙技术在串联机械臂中的仿真与应用
[J].
Simulation and application of anti-backlash technical with dual-motor in tandem manipulators
[J].
齿轮传动精度的分析与计算
[J].DOI:10.3969/j.issn.1003-0794.2006.07.008 [本文引用: 1]
Analysis and calculation of precision of gear transmission
[J].DOI:10.3969/j.issn.1003-0794.2006.07.008 [本文引用: 1]