Molinos等[3]提出动态窗口树、运动曲线环境自适应以及多算法融合等方法,以改进动态窗口法(dynamic window approach, DWA)缺乏全局指导、局部最优的缺陷;代婉玉等[4]提出沿边转弯、速度与转向角消息转换机制以及区域分级策略等方法,改进时间弹性带法(time elastic band, TEB)控制不稳定的缺陷. 相较于DWA和TEB,人工势场法[5-6]的数学模型更简单、计算复杂度更小,在实际动态环境中的实时性更优,但存在目标不可达、局部极小值陷阱问题. 解决传统人工势场法的局部极小值陷阱问题主要采用如下3种思路. 1)改变势场受力情况[7-8]:通过打破受力平衡状态使机器人脱离陷阱. 2)多算法融合[9]:切换其他路径规划算法引导机器人脱离陷阱. 3)提前预测陷阱[10]:边移动边对外部环境进行预测,或者在机器人移动前提前堵住易陷入局部极小值陷阱的路径. Yao等[11]基于思路1)、3),提出黑洞势场强化Q学习的方法,在原有势场中叠加黑洞势场,通过黑洞力打破部分局部极小值陷阱处的受力平衡,同时通过强化学习使机器人自动学习跳出陷阱. 该方法在不同环境下具有极强的适应能力,但额外添加的黑洞势场会使力多重叠加,并且需要预先进行大量训练. Min等[12]基于思路3),提出经验混合人工势场法,将基础案例推理与人工势场法结合,创新性地将障碍物与线型、角度型2种内置障碍物模型进行配准,并将过去躲避障碍物的经验存储在经验库中. 该方法适用于未知与非结构化环境中实时避障,但无论是进行障碍物的检索与匹配,还是进行避障经验的查找都要耗费大量时间.
为了有效解决局部极小值陷阱,避免使用高性能GPU进行训练,实现动态环境下快速自主避障,本研究结合3种思路对传统人工势场法进行改进,提出以静态避障为主、动态避障为辅的双机制切向避障. 同时,为了获取在亟需避障时及时避障、无须避障时快速返回最优路径的效果,将基于状态决策进行全局规划模块与局部规划模块的高效结合.
1. 改进人工势场法
1.1. 传统人工势场法
1986年Khatib[13]提出人工势场法,该方法实现简单,表达式为
式中:
图 1
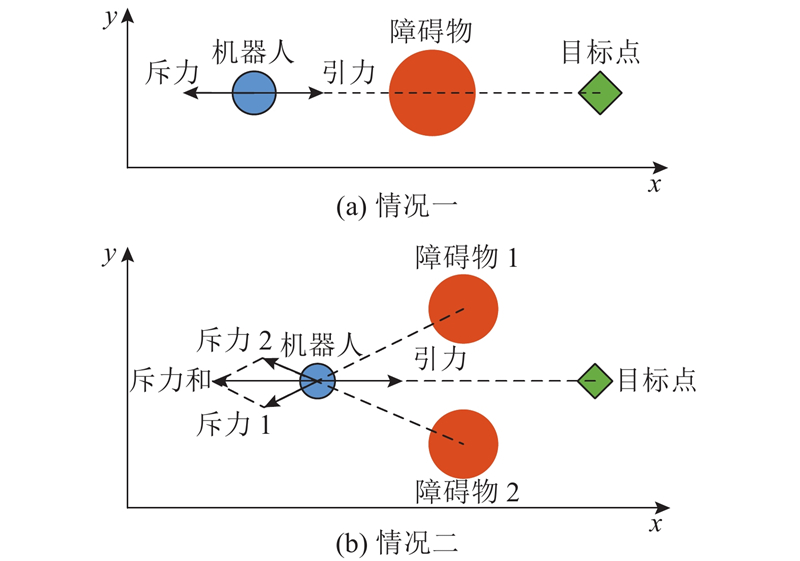
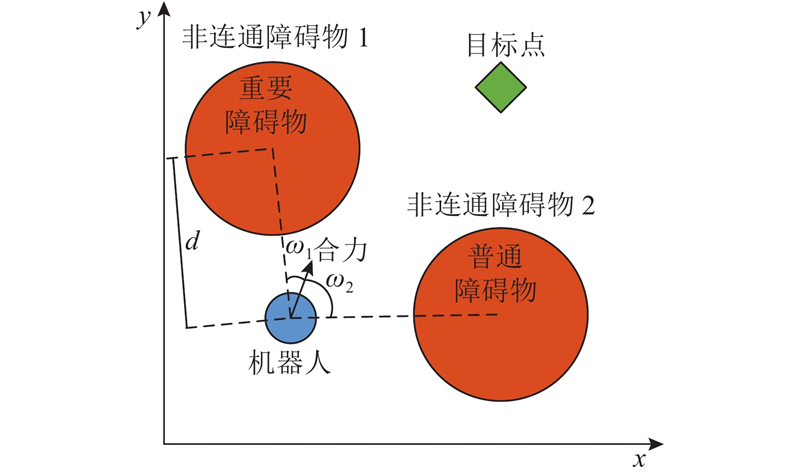
图 1 传统人工势场法的局部极小值陷阱
Fig.1 Local minimum trap of traditional artificial potential field method
1.2. 人工势场法下双机制切向避障机制
1.2.1. 陷阱预测
机器人在势场中沿梯度下降方向移动,出现局部极小值陷阱的原因:引力与斥力共线反向,导致合力为0,运动陷入停滞. Hessian矩阵是对二阶导数的矩阵描述,可以用来检查梯度下降方向上的点是不是局部极小值点. 本研究将通过Hessian矩阵在全局地图中预测局部极小值陷阱.
当函数定义在实数域且二阶偏导数连续时,矩阵
式中:
在二元函数的临界点处,二阶方向导数的正负仅与特征值的正负相关. 当特征值均为正时,Hessian矩阵正定,该点为局部极小值点;当特征值均为负时,Hessian矩阵负定,该点为局部极大值点. 假设选取的位置坐标与目标点的距离为
对式(4)求偏导数组成二阶Hessian矩阵:
将选取的位置坐标代入式(5)进行特征分解后,依据特征值正负判断当前采样点是不是局部极小值点.
1.2.2. 栅格地图预处理
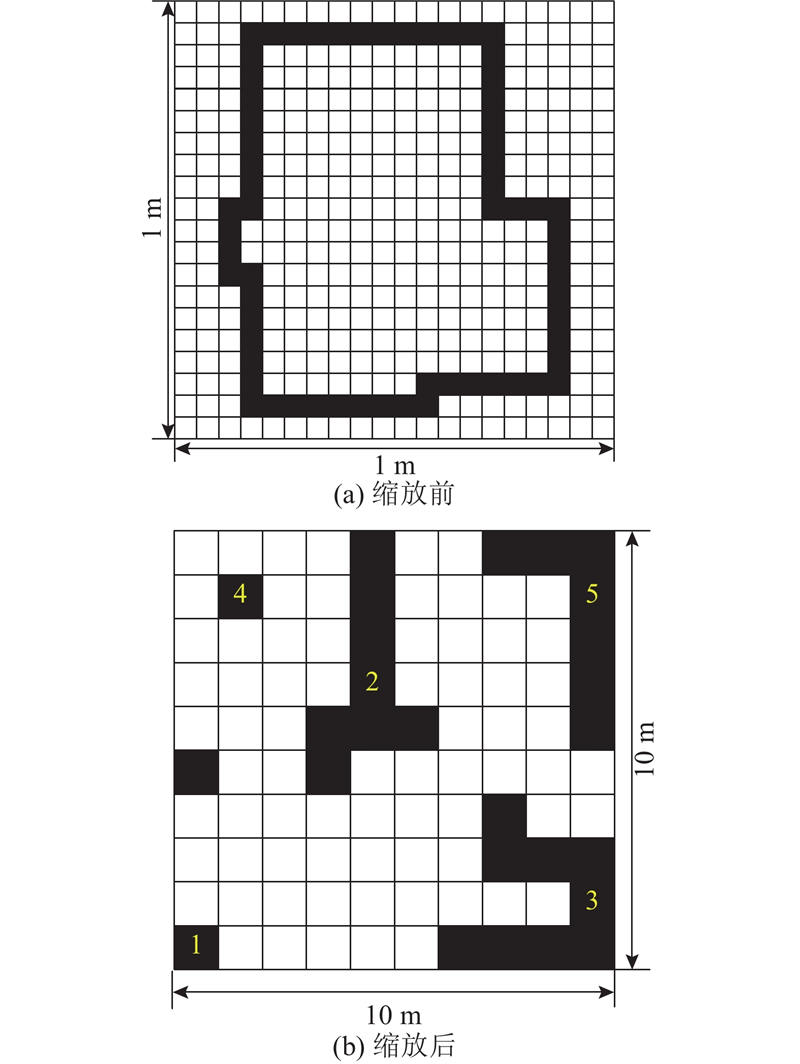
栅格地图的分辨率大小影响地图的精细度. 当栅格分辨率设置较大,建图时将丢失部分细节;当分辨率设置较小,需要更多的存储空间和计算资源,但表示的地图信息更加详细. 为了减轻当全局地图相对较大时陷阱预测的计算压力,在不影响地图精细度的情况下,在对栅格地图进行缩放处理后再进行陷阱预测,如图2所示. 建图时按图2(a)(分辨率为0.05 m)进行栅格映射. 地图预处理时,当20×20栅格内存在占据栅格时,缩放至10×10栅格后标注为占据栅格,否则为空闲栅格,从而将20×20栅格内的不规则障碍物缩放为图2(b)侧1号占据栅格(分辨率为1 m). 经过缩放后的栅格地图资源占用减少0.75,需要遍历的空闲栅格坐标大大减少.
图 2
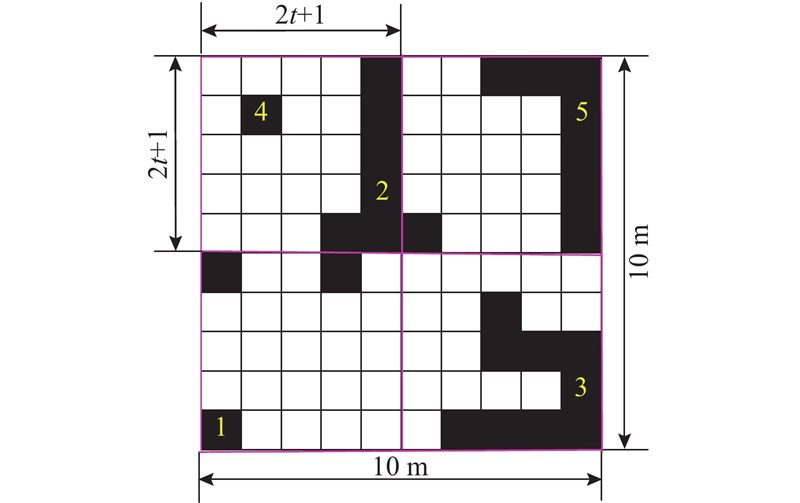
缩放后,栅格地图的右半部分占据栅格密度较大,相较于空闲栅格密度较大的左半部分更易陷入局部极小值陷阱. 为了进一步减少陷阱预测的计算量,通过区域搜索,选取存在局部极小值陷阱概率更高的障碍物密集区域,遍历该区域中梯度下降方向上的空闲坐标点,计算Hessian矩阵特征值检测是否存在局部极小值陷阱,如图3所示. 以缩放后全局地图原点为起始点构建长度为
图 3
式中:
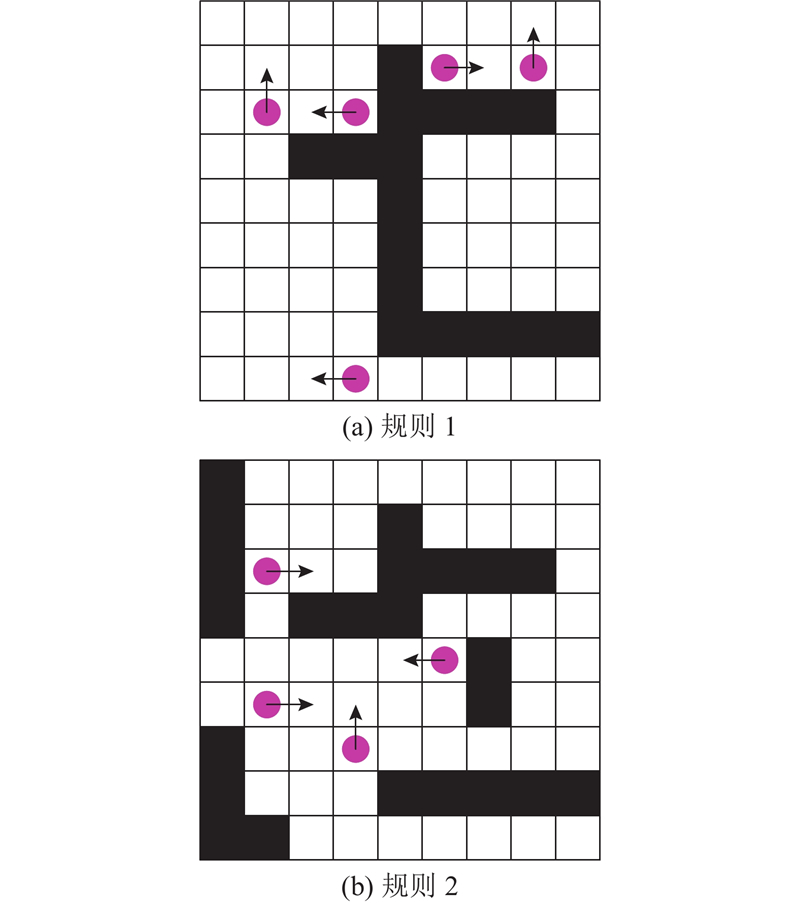
如图4所示,机器人在不同位置仅受到来自一个方向的斥力作用,具体判定规则如下.
图 4
图 4 连通障碍物斥力方向判定
Fig.4 Direction determination of repulsive force for connected obstacles
规则1(条件3与条件4与条件5):机器人所受单个连通障碍物的斥力,方向垂直于优先级最高的占据栅格. 条件3:机器人周围仅一个连通障碍物. 条件4:机器人位于该连通障碍物的斥力影响范围内. 条件5:机器人左侧占据栅格优先级>右侧占据栅格优先级>上侧占据栅格优先级>下侧占据栅格优先级.
规则2(条件6与条件7与条件8):机器人所受多个连通障碍物的斥力,方向来自距离最近的连通障碍物,斥力方向选择遵循规则1. 条件6:机器人周围存在多个连通障碍物. 条件7:机器人位于多个连通障碍物的斥力影响范围内. 条件8:机器人与多个连通障碍物的距离差较大且存在最小值.
规则3(条件6与条件7与条件9与条件10):机器人所受多个连通物的斥力,方向来自优先级最高的连通障碍物,斥力方向选择遵循规则1. 条件9:机器人与多个连通障碍物的距离差较小. 条件10:左侧连通障碍物优先级>右侧连通障碍物优先级>上侧连通障碍物优先级>下侧连通障碍物优先级.
1.2.3. 静态切向避障机制
对于连通障碍物,通过势场法结合斥力方向判定规则,机器人在不同位置仅受到来自一个方向的斥力,减少了因在C形、U形连通障碍物区域受到来自不同方向斥力的叠加而陷入局部极小值陷阱的问题.
针对非连通障碍物,提出切向避障的机制,避免机器人面对非连通障碍物时陷入局部极小值陷阱. 机器人只需在障碍物影响移动路径时进行避障,为此进行非连通障碍物的重要性评估,将非连通障碍物分成重要障碍物与普通障碍物. 当机器人与障碍物的距离小于2倍
图 5
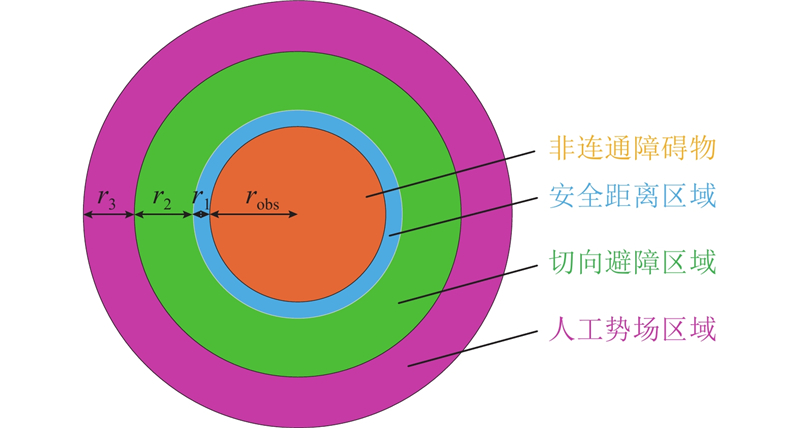
针对重要障碍物,将其斥力影响范围划分为人工势场区域(宽度
图 6
图 6 非连通障碍物斥力影响范围划分
Fig.6 Influence range division of repulsive force for non-connected obstacles
式中:
若陷阱预测后未检测到局部极小值点,3个区域的划分宽度为
式中:
图 7
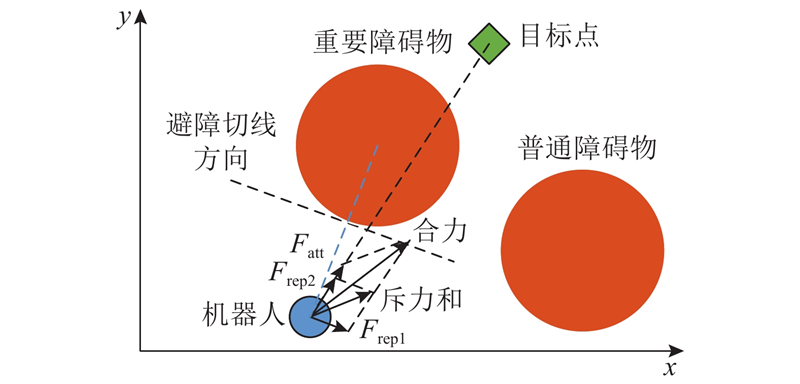
图 7 非连通障碍物静态切向避障
Fig.7 Static tangential obstacle avoidance for non-connected obstacles
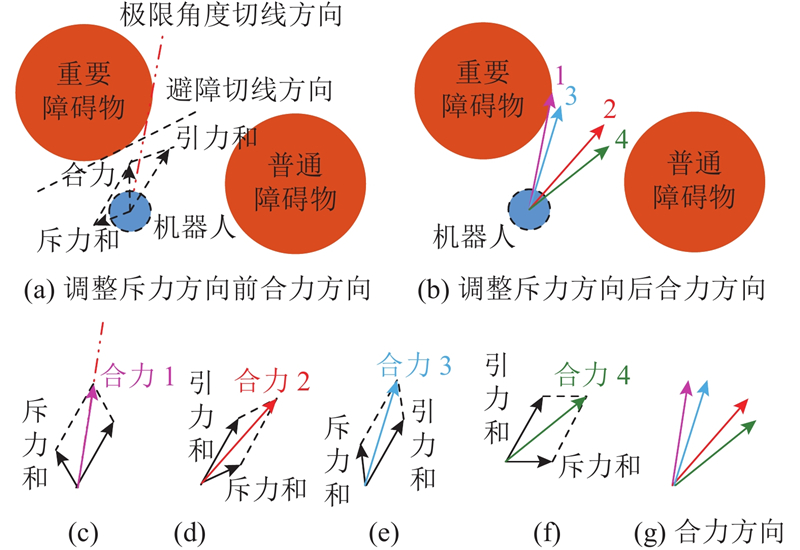
将斥力分力调整为避障切线方向原因如下:假设机器人为1个质点,那么完成避障的极限角度为机器人当前所在位置与重要障碍物的切线方向,如图8(c)合力1;当斥力和向逆时针方向旋转,合力与障碍物存在交集或向偏离引力和方向移动,导致与障碍物碰撞或绕行;斥力和方向顺时针旋转,合力贴近引力和方向,实现对重要障碍物的最优避障. 当旋转角度小于避障切线方向、大于极限角度,合力方向如图8(e)合力3,机器人与重要障碍物的距离较小;旋转角度大于避障切线方向时,合力方向如图8(f)合力4,与普通障碍物存在碰撞风险. 结合上述分析并开展多组仿真实验,斥力分力调整为避障切线方向,如图8(d)合力2,避障效果较优,静态切向避障的过程如图9所示.
图 8
图 8 斥力调整方向后的合力方向分析
Fig.8 Analysis of resultant force direction after repulsive force adjustment
图 9
1.2.4. 动态切向避障机制
传统人工势场法的势场函数仅考虑机器人与障碍物的相对距离,未考虑机器人与动态障碍物间相对速度. 由于不同的动态障碍物具有不同的速度,有时动态障碍物的出现与机器人无碰撞风险,有时机器人周围会出现多个动态障碍物. 在障碍物斥力影响范围内,将式(1)中斥力势场函数改进为
式中:
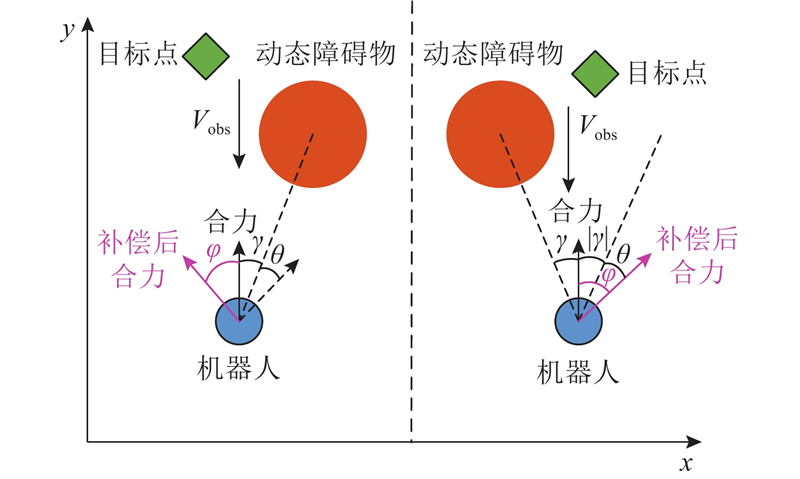
静态切向避障机制是在障碍物静止不动的前提下进行切向避障,对于动态障碍物,该机制须改进,如图10所示. 图中,速度为
图 10
图 10 动态切向避障补偿角的补偿原理
Fig.10 Compensation principle of compensation angle for dynamic tangential obstacle avoidance
式中:
式中:
2. 基于双机制切向避障的混合路径规划系统设计
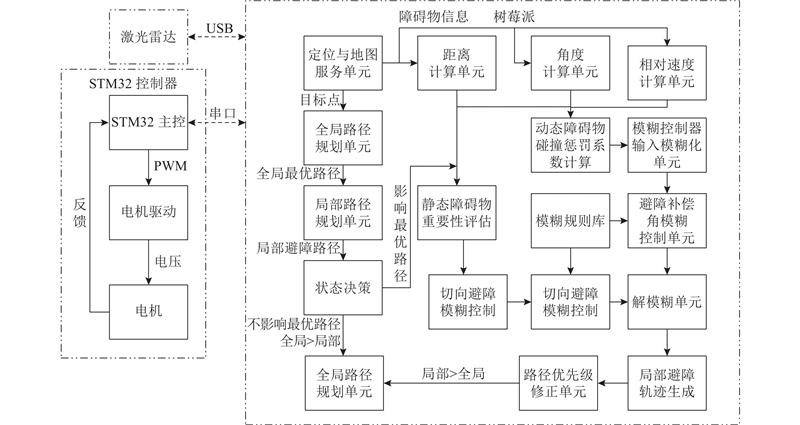
2.1. 系统设计
图 11
图 12
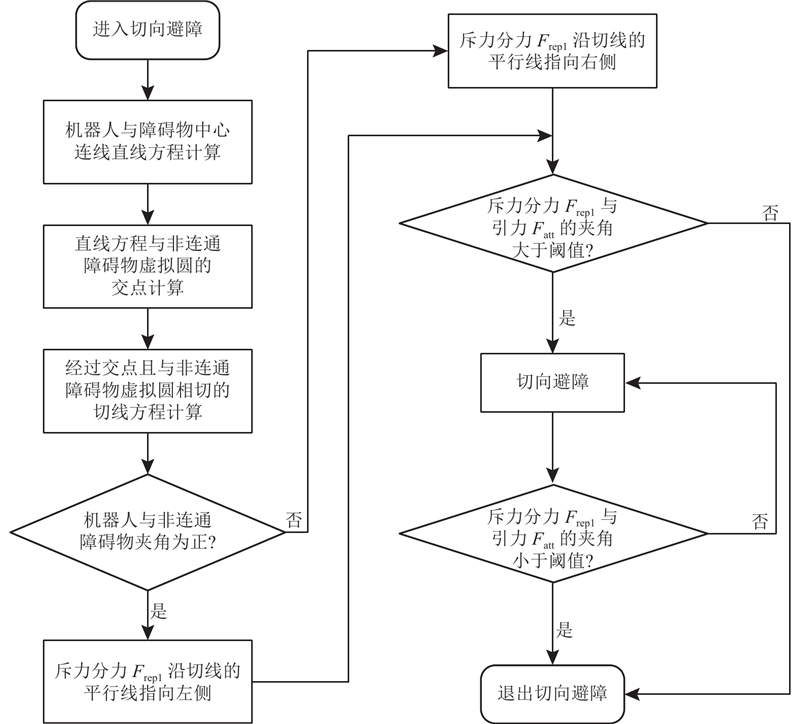
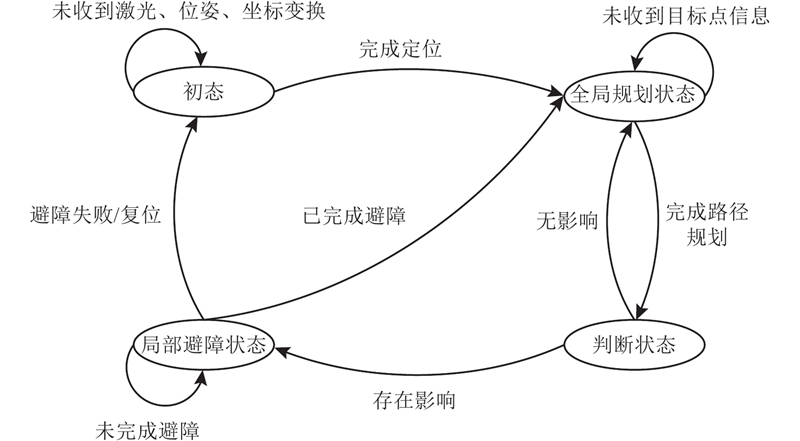
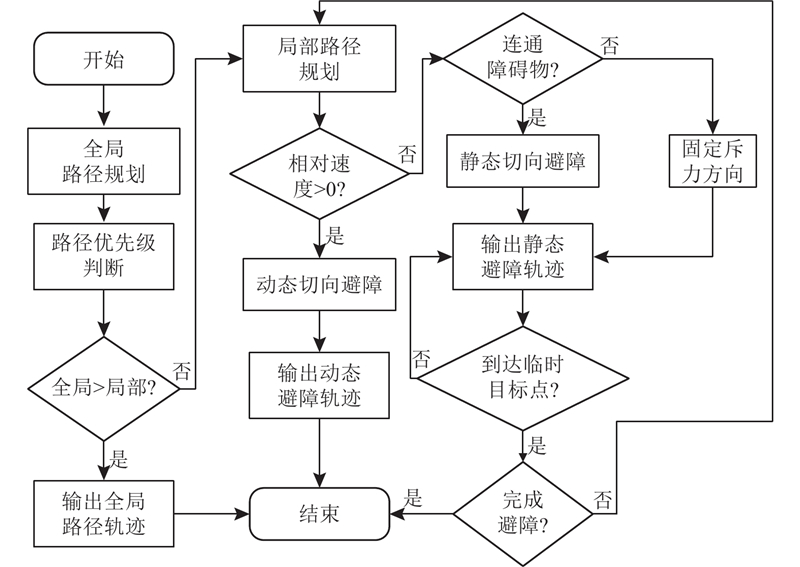
基于上述状态决策思想统筹全局路径规划与双机制切向避障,实现混合路径规划,流程如图13所示. 1)初始化势场法参数:输入起点、终点坐标、小车线速度、角速度等,转至步骤2). 2)全局路径规划:进行一次全局路径与局部路径规划,在该状态下全局路径优先级高于局部路径,机器人沿全局路径移动,移动一段距离后进行优先级判断,转至步骤3). 3)路径优先级判断:计算机器人与全局路径前进方向上障碍物的距离,检测是否存在距离全局路径较近的障碍物或临时出现的静态、动态障碍物,影响机器人移动安全性. 若存在这样的障碍物,进入局部路径规划,转至步骤4);若不存在,则输出全局路径轨迹,转至步骤5). 4)局部路径规划:根据机器人与障碍物的相对速度决定进行静态或动态避障,动态障碍物在势场下进行动态切向避障,非连通静态障碍物在势场下进行静态切向避障,连通静态障碍物在势场下固定斥力方向,优先级调整为局部路径高于全局路径,并以当前位置为起点重新进行一次全局规划;选取全局路径前进方向上一点作为临时目标点,机器人沿局部避障路径向该点移动;输出局部避障轨迹,转至步骤5). 5)判断是否到达临时目标点:若已到达,转至步骤6);否则转至步骤4). 6)判断机器人是否完成避障:若完成避障,转至步骤7),否则保持局部路径规划状态直至到达临时目标点;如果选取的临时目标点附近存在突发障碍物时,则重新进行一次全局路径规划并选取一点作为新临时目标点. 若避障失败,机器人陷入停滞,则复位至步骤1)开始一轮全新的规划. 7)结束:完成本轮路径规划.
图 13
2.2. 局部规划模糊控制器设计
本研究设计的双机制切向避障通过判断机器人与障碍物的距离、夹角后确定是否避障,这与模糊控制不需要过程的精确模型的特点较为贴合,因此将模糊控制与双机制切向避障相结合来实现局部规划模糊控制器设计. Mamdani法是机器人控制中常用的模糊方法,中心去模糊法是重心法与最大隶属度法去模糊的折中,因此本研究采用这2种方法进行模糊化与解模糊.
将切向避障模糊控制器设计成三输入一输出,模糊变量语义对照如表1所示. 将机器人与障碍物的距离
表 1 切向避障语义对照表
Tab.1
| 输入参数 | 语义 | 输入参数 | 语义 | 输出参数 | 语义 | ||
| DN(近) | ZJ(零) | ZE(紧急制动) | |||||
| DM(适中) | PS(正小) | APF(人工势场法) | |||||
| DF(远) | PB(正大) | LQM(向左切向避障) | |||||
| NB(负大) | QB(大) | RQM(向右切向避障) | |||||
| NS(负小) | QS(小) | — | — |
表 2 避障角补偿语义对照表
Tab.2
| 输入参数 | 语义 | 输入参数 | 语义 | 输出参数 | 语义 | ||
| HJ(很近) | JD(较大) | ZE(零) | |||||
| JJ(较近) | HD(很大) | PS(小) | |||||
| SZ(适中) | HX(很小) | MD(中) | |||||
| JY(较远) | JX(较小) | PB(大) | |||||
| HY(很远) | SZ(适中) | — | — | ||||
| HX(较小) | JD(较大) | — | — | ||||
| JX(较小) | HD(很大) | — | — | ||||
| SZ(适中) | — | — | — | — |
3. 仿真验证与实物平台测试
3.1. 仿真环境下算法有效性验证
为了验证所提算法的性能,开展机器人使用不同算法在易陷入局部极小值陷阱、狭窄可行区域避障的对比实验,参与对比的算法包括本研究算法、沿边走法、虚拟目标点法和虚拟障碍法. 如图14所示,搭建60 m×60 m的二维实验环境,起点与目标点分别在(0,0)和(50,50),引力增益系数与斥力增益系数设置为20、30,机器人的移动步长为0.7 m,非连通障碍物的斥力影响范围设置为障碍物的半径加5 m. 在如图14(a)的实验环境中,4种算法都到达目标点,但本研究方法路径更短、更平滑. 如图14(b)的实验环境为易陷入局部极小值陷阱与产生路径震荡现象的狭长U形区域. 虚拟目标点法[14]规划失败,在U形陷阱内陷入循环状态;沿边走法[15]进入U陷阱后,沿着连通障碍物的边界移动,逃脱了局部较小值陷阱,路径明显较长;虚拟障碍物法[16]未陷入局部极小值陷阱,但在连通障碍物间狭窄通道存在路径震荡现象;本研究方法未产生其他参与对比算法的缺陷. 在不同复杂度的实验环境中统计4种算法的规划结果,如表3所示,表中,C为规划成功次数,T为完成规划运行时间,L为规划路径的总长,S为规划路径中的拐点数. 可以看出,在不同环境复杂度下,本研究方法完成规划的稳定性较高,平均运行时间相较于沿边走法、虚拟目标点法、虚拟障碍物法分别提高21%、20%、19%;在复杂环境下的提升效果尤佳,平均运行时间分别提高33%、23%、20%.
图 14
图 14 不同仿真环境下改进人工势场法性能对比
Fig.14 Performance comparison of improved artificial potential field method under different simulation environments
表 3 不同环境复杂度时不同算法的规划结果统计
Tab.3
| 算法 | 环境复杂度 | C | T/s | L/m | S |
| 沿边走 | 简单 | 20 | 12.7 | 48.2 | 6 |
| 较复杂 | 20 | 21.5 | 80.6 | 8 | |
| 复杂 | 19 | 52.7 | 197.4 | 17 | |
| 虚拟目标点 | 简单 | 20 | 14.0 | 51.8 | 5 |
| 较复杂 | 14 | 26.0 | 96.4 | 7 | |
| 复杂 | 9 | 45.7 | 169.7 | 7 | |
| 虚拟障碍物 | 简单 | 20 | 14.7 | 53.2 | 4 |
| 较复杂 | 18 | 25.1 | 95.5 | 6 | |
| 复杂 | 13 | 44.5 | 166.1 | 7 | |
| 本研究 | 简单 | 20 | 12.2 | 42.2 | 2 |
| 较复杂 | 20 | 20.9 | 78.8 | 5 | |
| 复杂 | 18 | 35.4 | 130.1 | 9 |
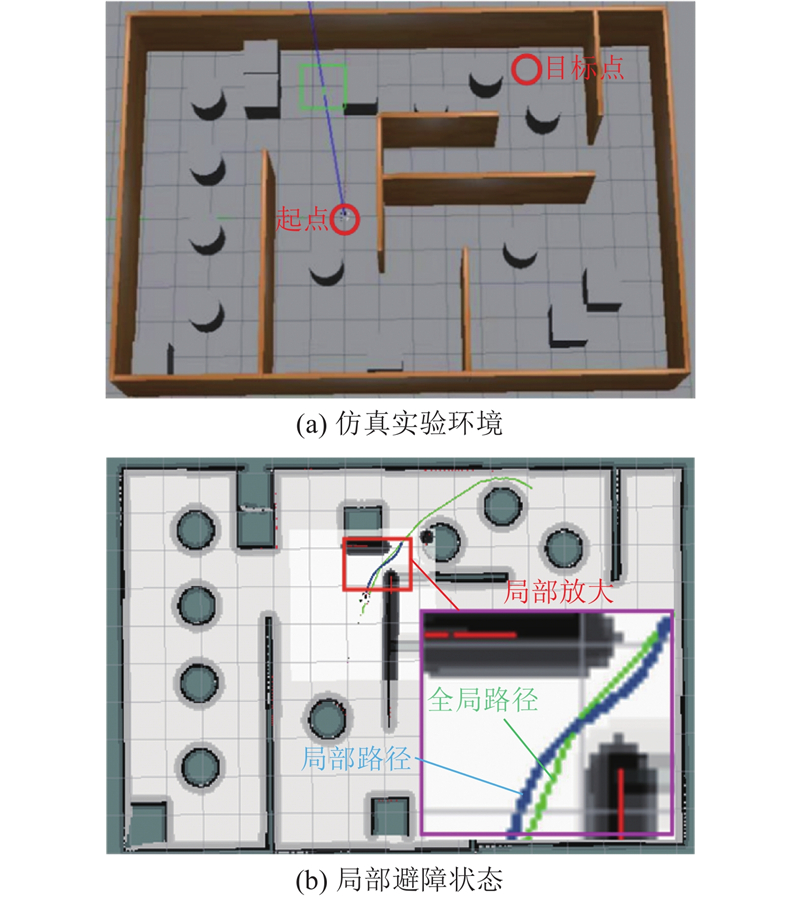
图 15
图 15 Gazebo仿真环境的避障验证
Fig.15 Obstacle avoidance verification of Gazebo simulation environment
表 4 仿真环境下混合路径规划模块实验参数
Tab.4
| 参数 | 数值 | 参数 | 数值 | |
| 最大线速度 | 0.4 | 全局代价地图可视化 话题发布频率 | 1.0 | |
| 最大角速度 | 1.5 | 局部代价地图可视化 话题发布频率 | 3.0 | |
| 全局代价地图 刷新频率 | 1.5 | 速度控制指令话题 发布频率 | 10.0 | |
| 局部代价地图 刷新频率 | 5.0 | — | — |
3.2. 实物平台测试
为了进一步验证所提算法在真实环境中的性能,搭建全向移动平台. 机器人的激光雷达数据由镭神N10P提供;机器人操作系统主要平台为树莓派4B系统核心板;采用底盘控制器主控(型号为STM32F407ZET6)接收并解析上位机发布的速度指令驱动电机转动.
3.2.1. 室内环境下静态障碍物避障测试
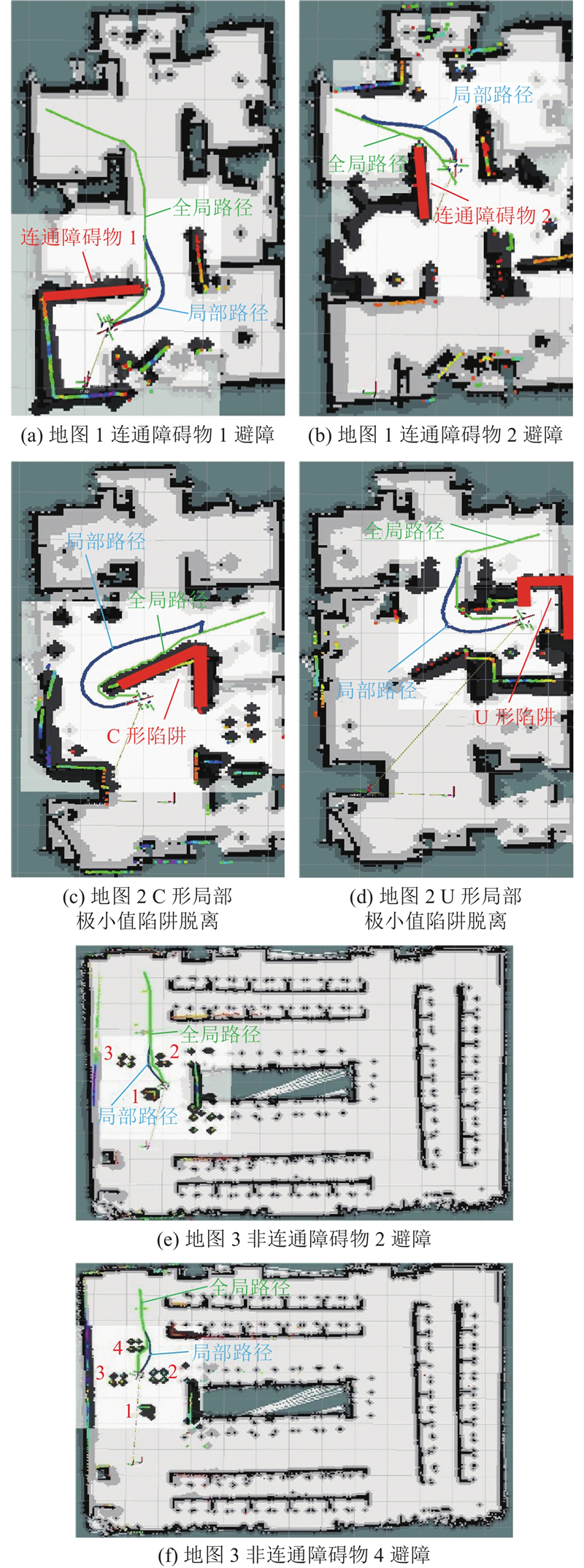
在不同的实验环境中对全向移动平台开展避障测试. 图16(a)、(b)中,机器人在地图1中由于固定斥力方向,受到优先级最高的上侧连通障碍物1与左侧连通障碍物2的斥力作用,固定斥力方向垂直向下与垂直向右,不再叠加其他连通障碍物斥力,深色避障路径相较于浅色全局路径,明显与障碍物保持充裕的安全距离,避免发生碰撞. 图16(c)、(d)中,在地图2中以易产生受力平衡的C形、U形区域为起点进行规划,机器人未陷入停滞状态并成功到达目标点. 图16(e)、(f)中机器人对存在影响的非连通障碍物2与4进行静态切向避障,对不存在影响的非连通障碍物3不进行避障,并且未在多个非连通障碍物间陷入停滞. 测试结果表明,本研究的静态避障机制在不同环境中实现了自主避障,在几种典型的易陷入局部极小值陷阱的连通或非连通障碍物环境中,也有效避免了机器人陷入停滞状态.
图 16
图 16 室内环境下静态避障结果
Fig.16 Static obstacle avoidance results in indoor environment
将局部规划器采用DWA、TEB在图16的3幅地图中进行25次多点导航测试,并逐步向地图中添加障碍物改变环境复杂度,结果如图17(a)所示,
图 17
图 17 全向移动平台测试结果比对
Fig.17 Test results comparison of omnidirectional mobile platforms
3.2.2. 室内环境下动态障碍物避障测试
如图18所示,进行本研究方法躲避行人的有效性验证实验. 实验结果表明,机器人进行避障角补偿后能够躲避行人. 可以看出,1号人员与机器人的相对距离较近、夹角较小,风险系数为次高避障优先级,2号人员与机器人的夹角较大,风险系数为次低避障优先级,对1号人员进行避障角补偿符合规则.
图 18
图 18 室内环境下动态避障结果
Fig.18 Dynamic obstacle avoidance results in indoor environment
4. 结 语
本研究提出基于人工势场法的双机制切向避障算法. 所提算法将障碍物分成连通与非连通障碍物,并针对阻碍实现自主避障的局部极小值陷阱采取不同解决策略. 采用人工势场法并固定连通障碍物斥力方向,减少了不同方向力的叠加,避免机器人陷入停滞;通过陷阱预测得到的局部极小值点,对非连通障碍物的斥力影响范围进行划分,将局部极小值陷阱限制在切向避障区域内,机器人进入该区域后进行切向避障避免陷入停滞. 在此基础上,针对室内环境中可能出现的动态障碍物,通过避障补偿角实现动态切向避障. 实验结果表明,在不同的地图中,相比主流算法,所提算法能够在不同环境复杂度下有效避免陷入局部极小值陷阱,在避障耗时与整体导航耗时上有较大提升,在复杂环境中提升效果尤佳. 同时,实物测试平台的避障自主性较优,减少了人为干预. 本研究须在规划前对已完成建模的地图环境进行陷阱预测,而在实际应用中地图往往是未知的,未来计划在本研究的基础上进行未知环境下的实时陷阱预测研究.
参考文献
Path planning of mobile robot by mixing experience with modified artificial potential field method
[J].
Real time obstacle avoidance for manipulators and mobile robots
[J].DOI:10.1177/027836498600500106 [本文引用: 1]
UAV path planning based on improved artificial potential field method
[J].
改进人工势场法的路径规划研究
[J].
Research on path planning of improved artificial potential field
[J].
Improvements on the virtual obstacle method
[J].
A comprehensive review of coverage path planning in robotics using classical and heuristic algorithms
[J].DOI:10.1109/ACCESS.2021.3108177 [本文引用: 1]
Path planning for autonomous mobile robots: a review
[J].DOI:10.3390/s21237898 [本文引用: 1]
Dynamic window based approaches for avoiding obstacles in moving
[J].DOI:10.1016/j.robot.2019.05.003 [本文引用: 1]
改进TEB算法的局部路径规划算法研究
[J].
Research on local path planning algorithm based on improved TEB algorithm
[J].
Safe artificial potential field: novel local path planning algorithm maintaining safe distance from obstacles
[J].DOI:10.1109/LRA.2023.3290819 [本文引用: 1]
Research on path planning algorithm for driverless vehicles
[J].
An advanced potential field method proposed for mobile robot path planning
[J].DOI:10.1177/0142331218824393 [本文引用: 1]
Improved artificial potential field and dynamic window method for amphibious robot fish path planning
[J].DOI:10.3390/app11052114 [本文引用: 1]
A hybrid formation path planning based on A* and multi-target improved artificial potential field algorithm in the 2D random
[J].DOI:10.1016/j.aei.2022.101755 [本文引用: 1]
Reliable path planning algorithm based on improved artificial potential field method
[J].DOI:10.1109/ACCESS.2022.3212741 [本文引用: 1]
Path planning method with improved artificial potential field: a reinforcement learning perspective
[J].DOI:10.1109/ACCESS.2020.3011211 [本文引用: 1]