汽车线控转向(steering by wire, SBW)系统[1]以电信号取代机械连接,通过电子控制单元驱动转向执行机构,可以提升车辆的操控性. 为了优化该系统的控制性能,国内外学者在控制器设计领域开展大量的研究. Huang等[2]设计2种基于比例积分微分(proportional-integral-derivative, PID)控制器的控制回路. Meng等[3]采用模糊PID提升平均精度,但难以自适应优化参数. 为了提高参数的整定效率,Jin等[4]应用群智能算法优化PID参数,降低了调试成本,但受限于算法早熟收敛. Li等[5]提出基于自抗扰控制(active disturbance rejection control, ADRC)的转向角跟踪方法,抗扰性优于PID,但参数过多. Zhao等[6]改进ADRC结构以减少参数,但依赖经验调试. 线性自抗扰控制[7](linear active disturbance rejection control, LADRC)通过线性扩张状态观测器(linear extended state observer, LESO)实现扰动估计与补偿,在保证精度的同时更易整定,更适合SBW工程应用的需求. 针对LADRC参数优化问题,Han等[8]使用模糊控制增强系统的鲁棒性,但依赖人工规则库且优化能力有限. Xu等[9]使用粒子群算法优化LADRC,提升参数的自适应性,但该算法易早熟收敛. Lian等[10]提出的鹦鹉优化算法(parrot optimizer, PO)通过模拟鹦鹉觅食、社交、停留等行为特征,展现出优异的全局搜索能力,但存在收敛速度慢、局部搜索弱的问题.
本文提出融合佳点集初始化、反向学习策略、黄金正弦算法及樽海鞘算法[11](salp swarm algorithm,SSA)的鹦鹉优化算法(parrot swarm intelligence search algorithm integrating good lattice points opposition-based learning strategy golden sine strategy and salp swarm algorithm,GOGS-PO),以增强种群多样性与收敛特性,避免早熟收敛. 将GOGS-PO应用于LADRC参数优化中,实现了SBW的高性能控制.
1. 汽车线控转向系统
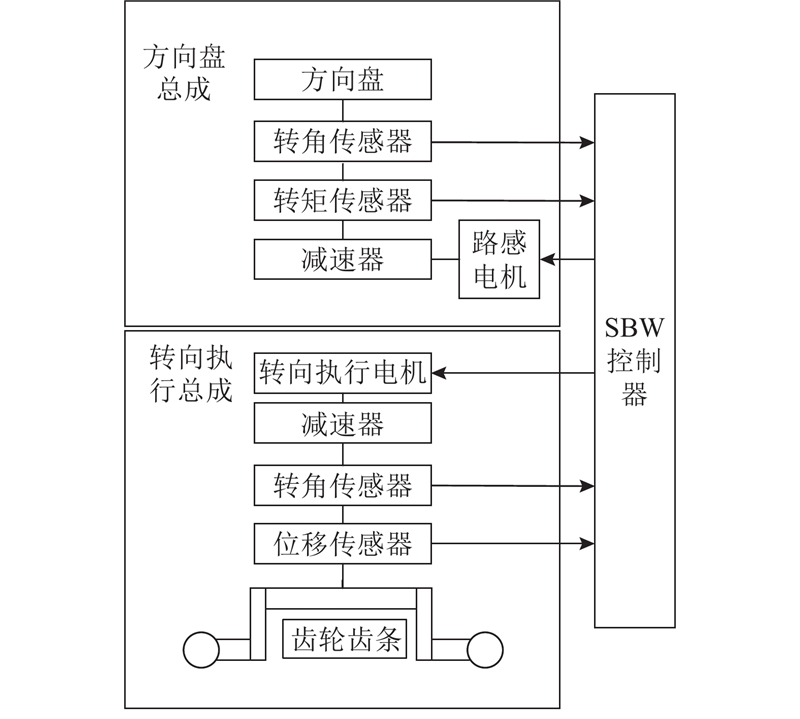
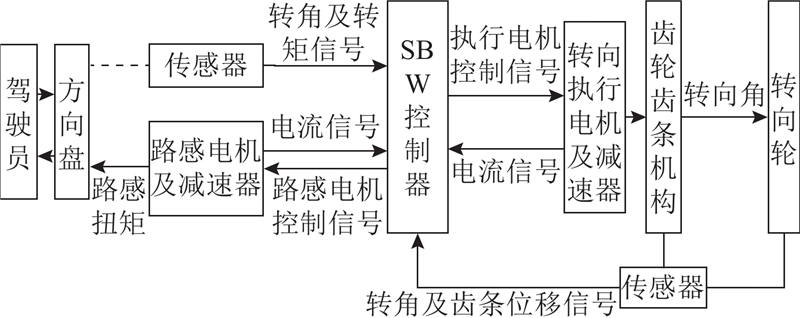
1.1. 结构及工作原理
图 1
图 2
1.2. 微分方程及动力学建模
方向盘总成[14]包括方向盘、转角传感器、转矩传感器等部件. 根据牛顿定律,建立动力学模型如下:
式中:Ts、Js、
式中:Tm为转向电机转矩,Jm为转向电机轴的转动惯量,Bm为转向电机轴的阻尼系数,Km为转向电机轴的扭转刚度,
式中:um为转向执行电机的电枢电压,im为转向执行电机的电枢电流,Rm为转向执行电机的电枢绕组电阻,Lm为转向执行电机的电枢绕组电感,Kb为转向执行电机的反电动势比例系数,Cm为转向执行电机的电磁转矩系数.
齿轮齿条转向器动力学模型可以表示为
式中:m r、Br分别为齿条质量和阻尼系数,Kkt为主销扭转刚度系数,Gw1和Gw2分别为齿条到左、右前轮的传动比,θw1和θw2分别为左、右转向轮转角,Fs为转向器的摩擦力. 转向轮动力学模型可以表示为
式中:Jw、Bw分别为前轮绕主销的转动惯量和阻尼系数,Tw1和Tw2分别为左、右前轮的回正力矩.
2. LADRC-SBW控制器模型
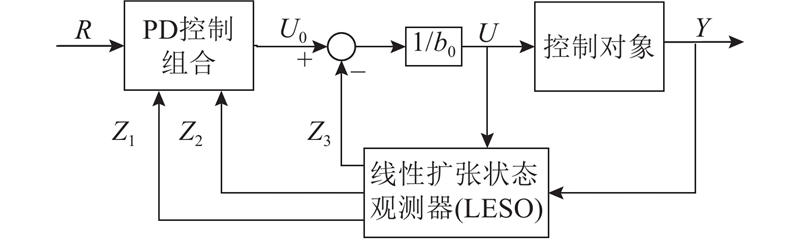
2.1. LADRC控制器
图 3
采用无对象模型的线性扩张状态观测器,被控对象为
式中:Y为系统输出,U为系统控制信号,w为系统外部扰动,t为时间,b为系统增益. A1、A0和w都为未知量,取常量b0作为b的估计值,则式(9)可以转化为
式中:F为包含内部扰动及外部扰动的总扰动. 取状态变量X1、X2、X3,令
式中:X3为扩张状态变量. 将式(11)写为状态空间表达式的形式:
式中:
对应的LESO表达式为
式中:Z为观测器的状态向量. 为了求解状态误差反馈增益矩阵W,将式(13)转化为
式中:Yc为观测器的输出;Uc为观测器的组合输入,Uc = [U, Y]T. 设W=[w1,w2,w3]T,则将特征方程的极点配置在−w0,可以解得
式中:w0为观测器带宽.
观测器对总扰动F进行观测之后,可以引入控制律对控制器进行扰动补偿. 线性误差反馈控制律为
式中:U0为扰动补偿前的控制量. 对于二阶系统,使用PD控制器设计U0,公式为
式中:R为给定的目标值,Z1和Z2为LESO输出的状态,Kp和Kd分别为控制器的比例系数和微分系数. 在控制器设计中,采用−KdZ2替代−Kd(Ṙ−Z2),有效消除了对参考输入量的微分运算,从而抑制了因目标值快速变化引发的系统振荡问题. 此外,通过将系统极点配置于−wc处,可以推导得到控制参数Kp = wc 2,Kd = 2wc,其中wc为控制器带宽.
2.2. Simulink与Carsim的联合仿真建模
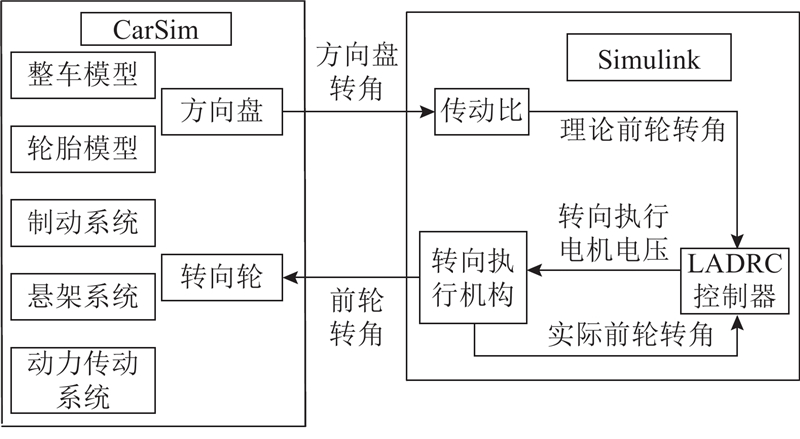
利用Carsim软件的兼容特性,通过Simulink平台的S-function接口实现两者协同仿真. 在Simulink中构建线控转向系统模型,用以替换Carsim内置DEMO车体模型中的机械式转向机构. 模型结构如图4所示.
图 4
3. 鹦鹉优化策略
3.1. 算法原理
利用鹦鹉算法,模拟在训练鹦鹉过程中观察到的关键行为. 4种行为分别为觅食行为、停留行为、交流行为以及对陌生人恐惧的行为.
1)觅食行为中,鹦鹉主要通过观察食物的位置或考虑主人的位置来估计食物的大致位置,然后向各自的位置飞去. 觅食行为的数学模型如下:
式中:Xi(t)为鹦鹉的当前位置;Xi(t+1)为更新后的位置;XM(t)为当前种群的平均位置;D为解向量的维度;Levy(D)为莱维飞行,用来描述鹦鹉的飞行;Xbest为从初始化到当前搜索的最佳位置;t为当前迭代次数;rand (0,1)为(0,1.0)内服从均匀分布的随机数;Tmax为最大迭代次数.
2)停留行为是指鹦鹉突然飞向主人,并在身体某一部位停留一段时间,数学模型如下:
式中:1D为维度为D的全1向量;Xbest·Levy(D)表示沿最优解方向随机探索;rand (0,1)×1D表示随机停留在主人的某一身体部位,即进行小范围随机搜索.
3)交流行为包括飞向鸟群和不飞向鸟群的交流,数学模型如下:
式中:0.2rand (0,1)·(1−t/Tmax)(Xi(t)−XM(t)) 表示鹦鹉个体加入群体进行交流的过程;0.2rand (0,1)·exp [−t/(rand (0,1)·Tmax)]表示鹦鹉交流后立即飞走的过程;P为[0,1.0]内的随机数,决定发生其中某种行为.
4)鹦鹉会对陌生人产生恐惧心理,并与主人共同寻找安全的地方,数学模型如下:
式中:rand (0,1)·cos (0.5πt/Tmax)·(Xbest − Xi(t))表示重新定向飞向主人的过程,cos (rand (0,1)·π)·(t/Tmax)2/Tmax
3.2. 多策略改进鹦鹉算法
3.2.1. 佳偶双栖初始化策略
在初始化阶段,PO通常随机生成一组候选解作为初始种群,这可能导致种群多样性不足,特别是在高维复杂解空间中,易使种群集中于局部区域,进而削弱算法的全局探索能力. 为了进一步提高全局能力,设计佳偶双栖初始化策略. 结合鹦鹉常常成对行动的习性,2个个体之间相互学习,交流信息,促使初始种群的位置更分散,使得种群均匀分布,提高种群质量. 具体公式如下.
式中:
3.2.2. 设计停留因子优化停留行为
针对鹦鹉优化算法易陷入局部最优、出现早熟收敛的问题,设计停留因子. 该因子通过动态调节个体在局部区域的停留时间,增强算法跳出局部最优解的能力. 具体公式如下:
式中:μmin和μmax分别为停留因子的最小值和最大值. 更新后的停留行为对应的数学模型为
3.2.3. 黄金正弦算法优化恐惧陌生人行为
黄金正弦算法[16](golden sine algorithm,GSA)基于黄金分割原理在解空间内高效缩小搜索范围,具有参数少、收敛快、结构简单的优势. 结合快速收敛特性与鹦鹉恐惧陌生人行为,在平衡探索与开发的同时,有效地提升收敛精度. 改进后的行为模型如下:
式中:b1、b2为黄金分割系数,r1为(0,2π)内服从均匀分布的随机数,r2为(0,π)内服从均匀分布的随机数.
3.2.4. 融合SSA的交流行为
标准PO的交流行为易因过度模仿而损失种群多样性,信息传播效率过低将限制全局搜索能力. 引入SSA的领导者角色,通过提供可模仿的优质解来增强信息引导,有助于提升收敛速度与优化性能. 更新后的公式如下:
式中:umax、lmin分别为最大上边界值和最小下边界值;k1为收敛因子,
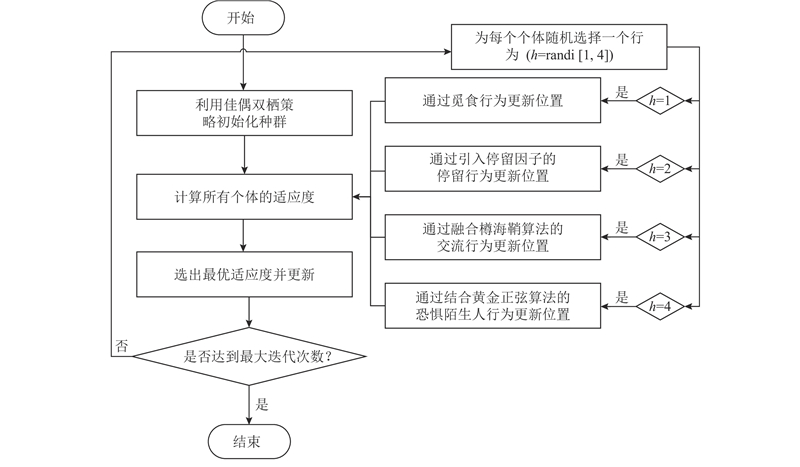
GOGS-PO优化策略的流程如图5所示.
图 5
3.3. 优化策略的测试
表 1 算法性能测试的基准函数
Tab.1
| 函数 | 表达式 | 取值范围 |
| Sphere | [−100,100]n | |
| Schwefel 2.22 | [−10,10]n | |
| Schwefel 1.2 | [−100,100]n | |
| Schwefel 2.21 | [−100,100]n | |
| Schwefel | [−500,500]n | |
| Ackley | [−32,32]n |
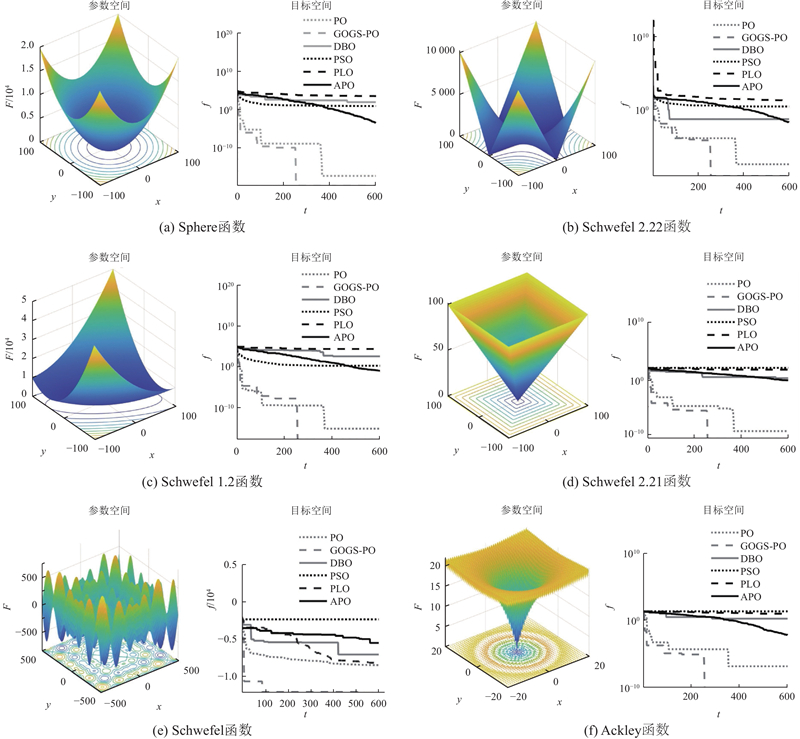
图 6
从图6可知,GOGS-PO在以上6种测试函数中都表现出较好的收敛性能. 其中,Sphere、Schwefel 2.22、Schwefel 1.2和Schwefel 2.21为单峰测试函数,用于评估算法的收敛速度,对应线控转向系统在常规工况下的快速响应能力. Schwefel和Ackley为高维多模态测试函数,用于衡量算法在全局搜索和局部搜索之间的平衡能力,反映了系统在湿滑及冰雪路面工况下的鲁棒性. 图6(a)~(d)中,GOGS-PO凭借引入的领导者机制,有效地缩小搜索范围,从而更快收敛至最优解,有助于提升转向控制的响应速度. 图6(e)、(f)中,停留因子增强了算法的全局探索能力,使其在复杂空间中有效避免局部最优,保障车辆在各种工况下的转向稳定性. 由此可见,GOGS-PO的收敛速度和收敛精度均优于其他对比算法.
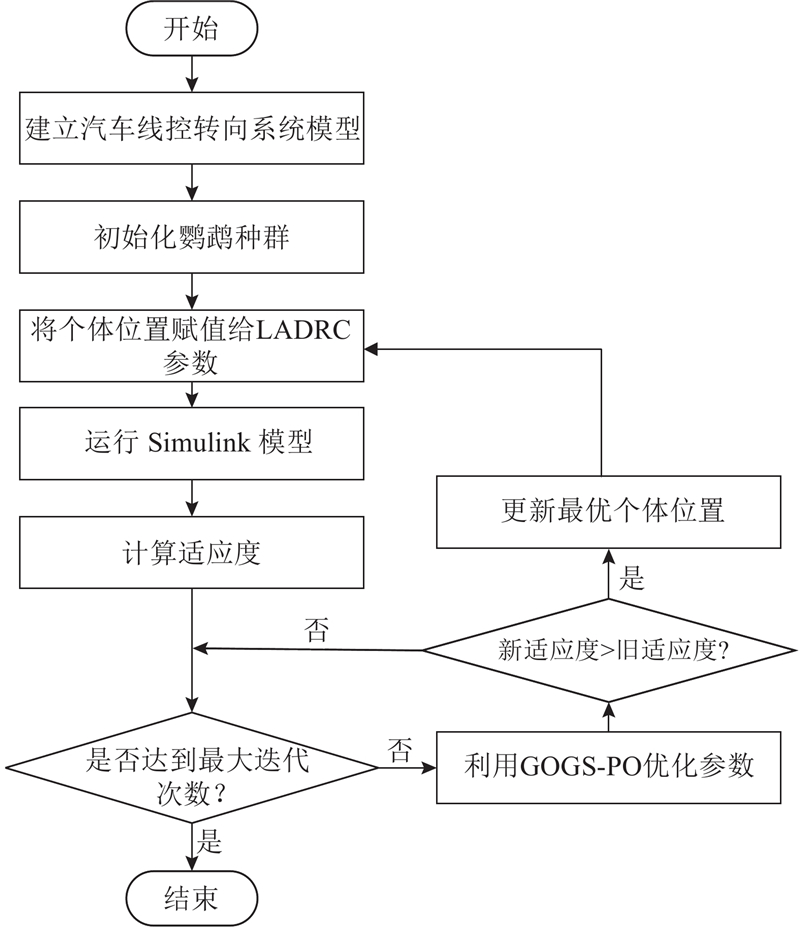
4. GOGS-PO优化的LADRC控制器设计
图 7
5. 仿真结果分析
实验硬件平台为Intel Core i7-14700HX 2.10 GHz CPU、RTX4060Ti GPU、16 GB内存的计算机,仿真软件为MatlabR2023b. Carsim中的车辆参数设置如表2所示.
表 2 车辆的主要参数
Tab.2
| 参数 | 数值 |
| 整车总质量m/kg | |
| 前轴到质心距离a/m | 1.05 |
| 后轴到质心距离b/m | 1.61 |
| 质心高度h/m | 0.65 |
| 转向电机轴转动惯量Jm/(kg∙m2) | |
| 转向电机轴阻尼系数Bm/(N∙m∙(rad∙s −1 ) −1) | |
| 转向电机轴扭转刚度Km/(N∙m∙rad−1) | 176 |
| 齿条质量mr/kg | 2.25 |
| 齿条的阻尼系数Br/(N∙m∙(rad∙s −1 ) −1) | 635 |
5.1. 线控转向系统整车模型的仿真验证
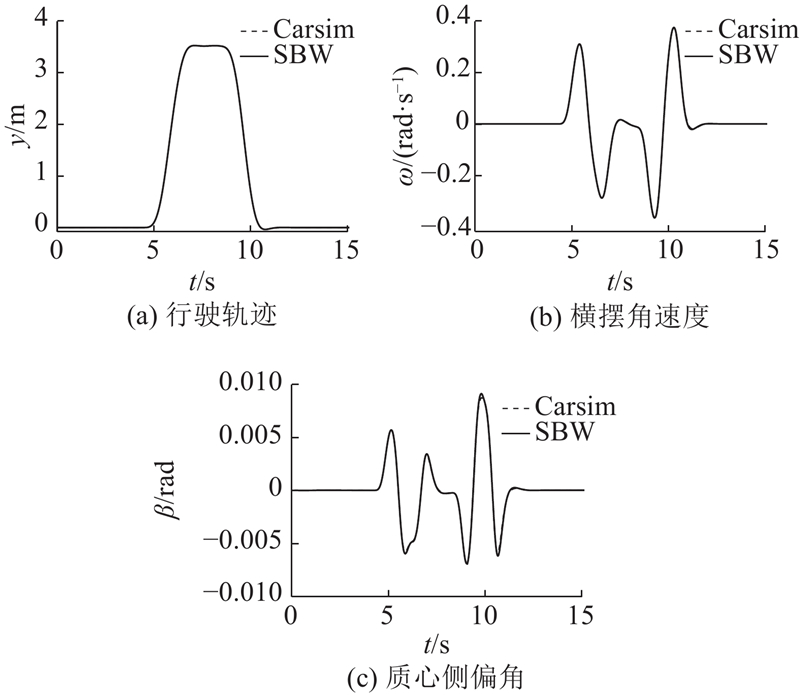
双移线试验是评估车辆操纵稳定性的重要闭环测试方法. 在附着系数为0.85、车速为50 km/h的工况下,对比所建线控转向模型与Carsim传统转向模型的仿真性能. 如图8所示,两者的行驶轨迹、横摆角速度ω及质心侧偏角β曲线基本拟合,即汽车响应特性十分接近. 仿真结果表明,本文构建的线控转向模型可以与Carsim软件进行联合仿真,验证了模型的可行性.
图 8
5.2. 低路面附着系数仿真实验
图 9
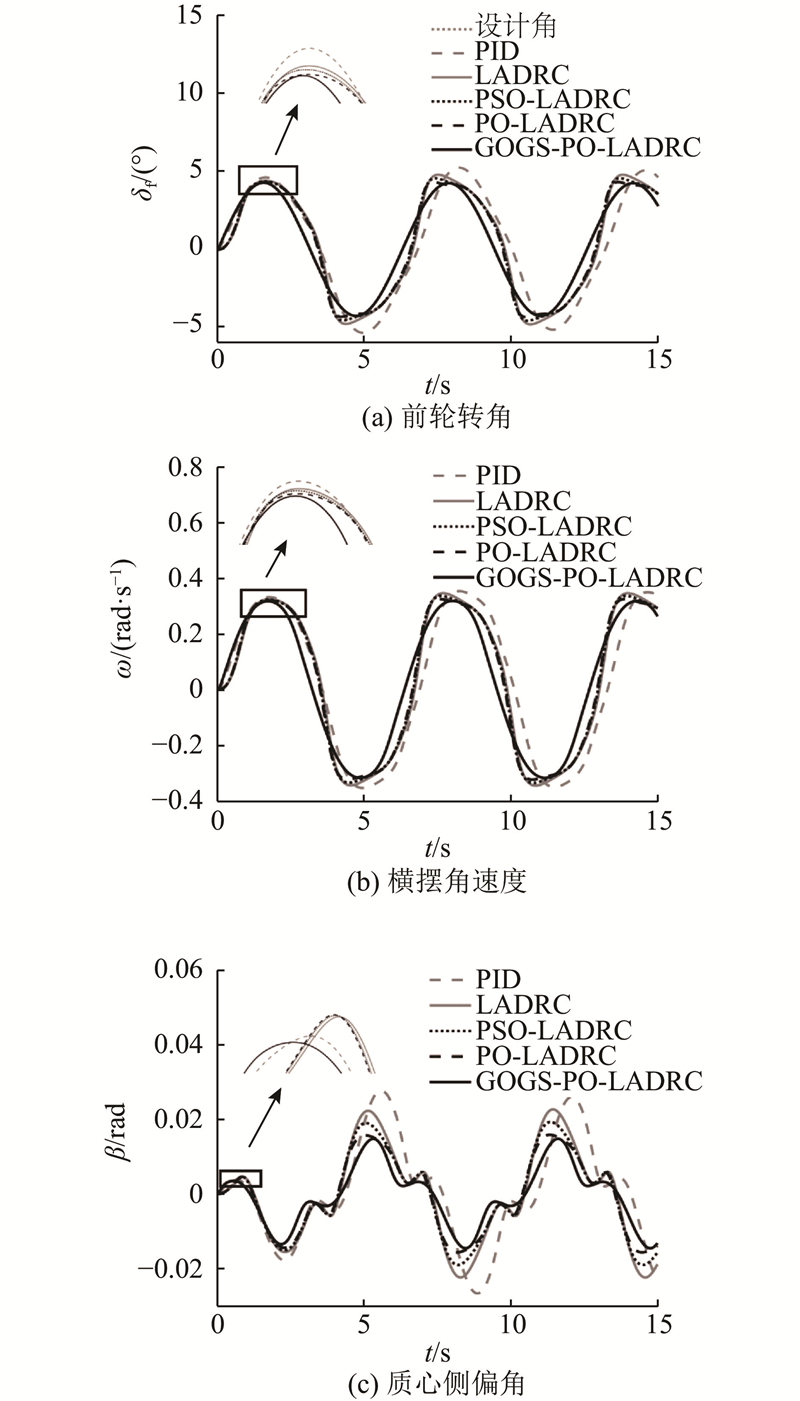
图 9 湿滑路面条件下不同控制策略的仿真
Fig.9 Simulation of different control strategy for slippery pavement
图 10
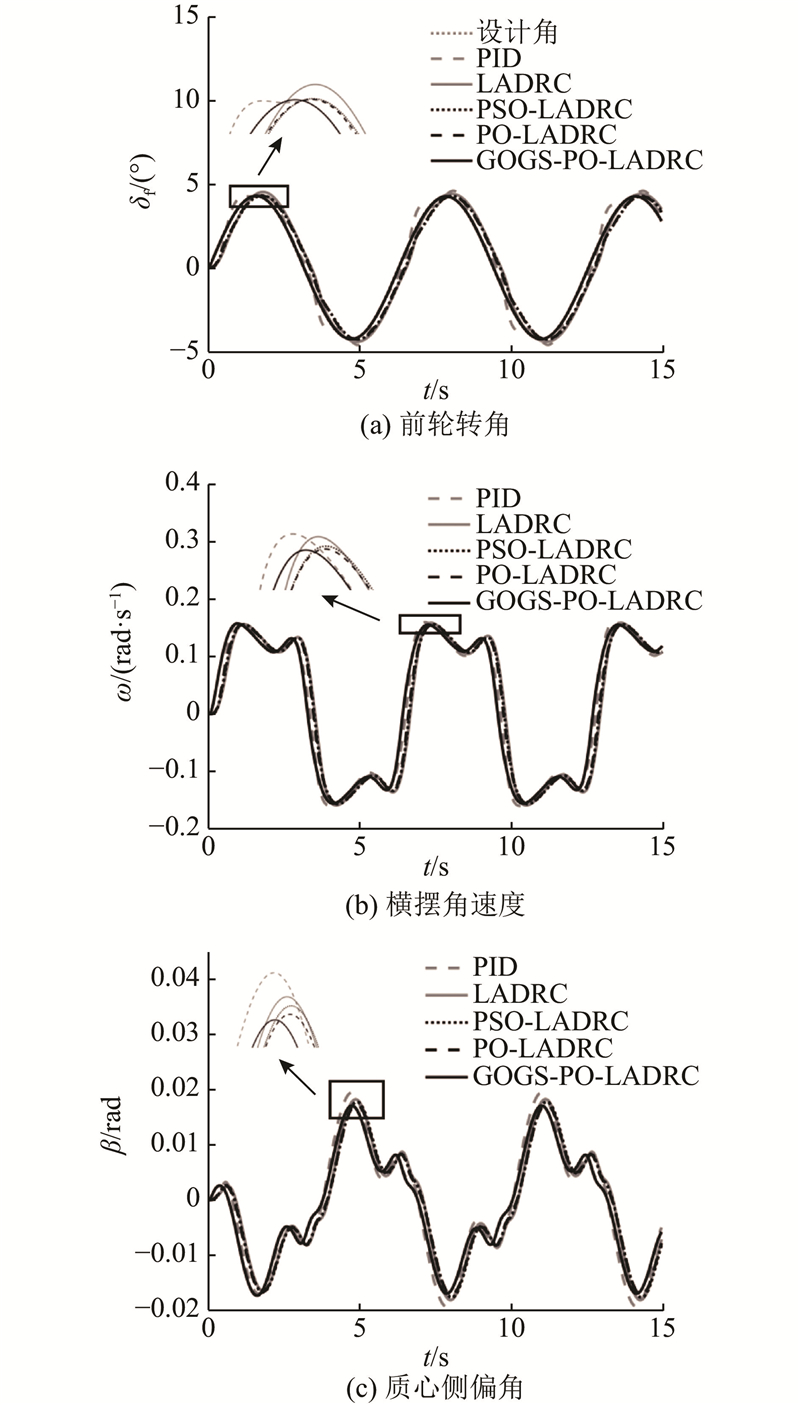
图 10 冰路面条件下不同控制策略的仿真
Fig.10 Simulation of different control strategy for ice pavement
表 3 湿滑路面上不同控制策略的仿真参数
Tab.3
| 控制策略 | ωmax/(rad·s−1) | e/(°) | |
| PID | |||
| LADRC | |||
| PSO-LADRC | |||
| PO-LADRC | |||
| GOGS-PO-LADRC |
表 4 冰路面上不同控制策略的仿真参数
Tab.4
| 控制策略 | ωmax/(rad·s−1) | e/(°) | |
| PID | |||
| LADRC | |||
| PSO-LADRC | |||
| PO-LADRC | |||
| GOGS-PO-LADRC |
在湿滑与冰路面工况下,GOGS-PO-LADRC控制器的横摆角速度、质心侧偏角及前轮转角误差均为5种策略中的最小值,表明该控制器有最优的综合控制性能. 虽然在冰路面上参数差距较小,但仍表现出更优的控制效果,验证了该控制器的有效性与操纵稳定性.
5.3. 湿滑路面上坡的仿真实验
在湿滑上坡工况下,车辆面临路面附着力下降与坡道重力分量的挑战,对转向稳定性有更高的要求. 开展双移线工况仿真实验,设置坡道坡度为10°,路面附着系数为0.45,车速为50 km/h. 仿真结果如图11所示.
图 11
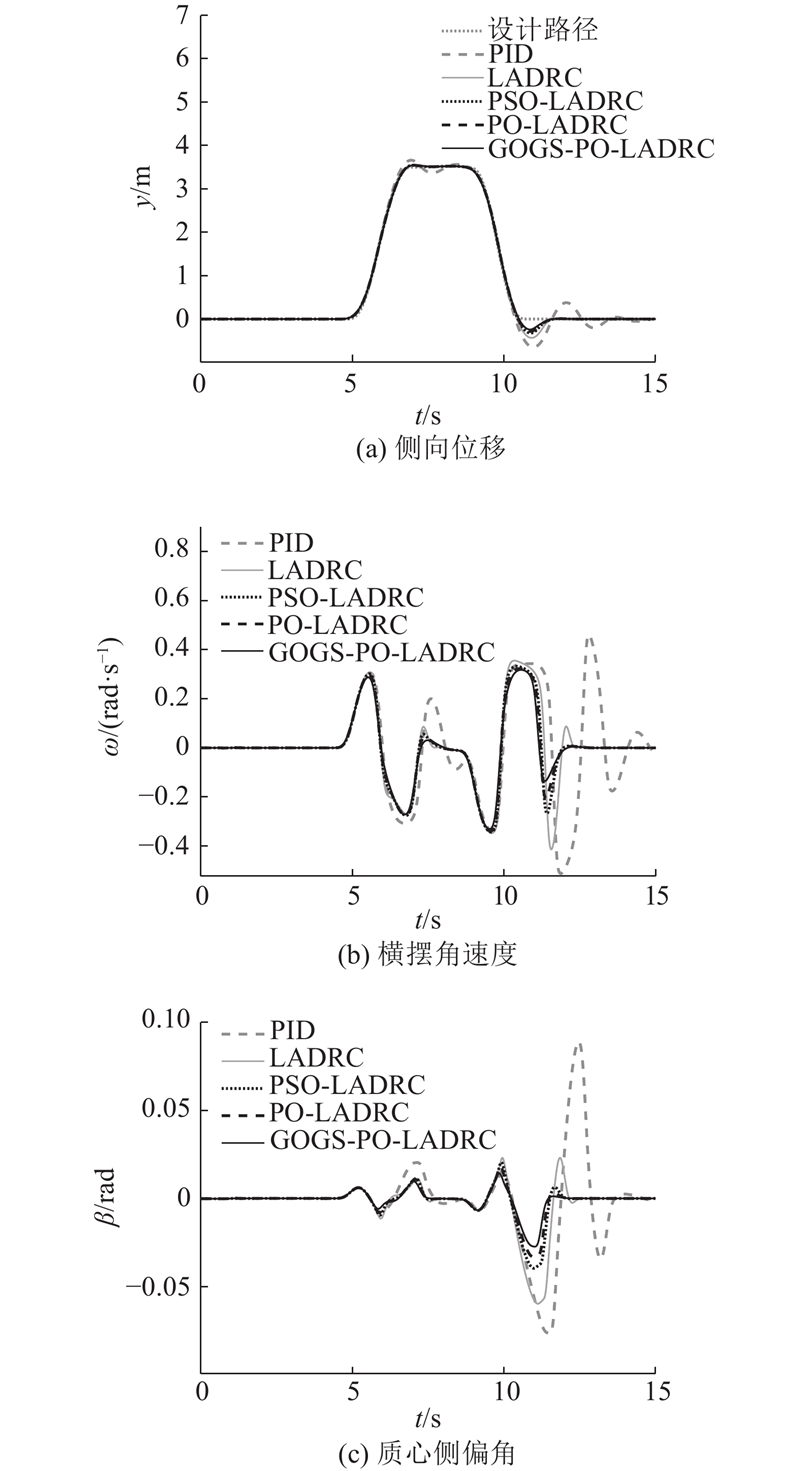
图 11 湿滑路面上坡工况下的不同控制策略仿真
Fig.11 Simulation of different control strategies on slippery uphill road
结果表明,在湿滑路面上坡工况中,GOGS-PO-LADRC的侧向位移更接近理想值,且横摆角速度和质心侧偏角的变化更平滑,峰值相较于其他控制方法更小. 不同控制策略下横摆角速度和质心侧偏角的峰值如表5所示.
表 5 湿滑路面上坡工况下不同控制策略的仿真参数
Tab.5
| 控制策略 | ωmax /(rad·s−1) | |
| PID | ||
| LADRC | ||
| PSO-LADRC | ||
| PO-LADRC | ||
| GOGS-PO-LADRC |
5.4. 统计显著性的测试
表 6 以横摆角速度峰值为评价指标的检验结果
Tab.6
| 控制策略 | 平均排名 | Nemenyi 分组 | 显著性结论 |
| GOGS-PO-LADRC | 1.00 | A | 显著最优 |
| PO-LADRC | 2.13 | A B | 与最优无显著差异 |
| PSO-LADRC | 3.07 | B C | 中等性能 |
| LADRC | 3.93 | C D | 显著次于前两名 |
| PID | 4.87 | D | 显著最差 |
表 7 以质心侧偏角峰值为评价指标的检验结果
Tab.7
| 控制策略 | 平均排名 | Nemenyi 分组 | 显著性结论 |
| GOGS-PO-LADRC | 1.2 | A | 显著最优 |
| PO-LADRC | 2.1 | A B | 与最优无显著差异 |
| PSO-LADRC | 3.0 | B C | 中等性能 |
| LADRC | 4.0 | C D | 显著次于前两名 |
| PID | 4.7 | D | 显著最差 |
表 8 以前轮转角误差为评价指标的检验结果
Tab.8
| 控制策略 | 平均排名 | Nemenyi 分组 | 显著性结论 |
| GOGS-PO-LADRC | 1.2 | A | 显著最优 |
| PO-LADRC | 2.5 | A B | 与最优无显著差异 |
| PSO-LADRC | 2.8 | B C | 中等性能 |
| LADRC | 4.0 | C D | 显著次于前两名 |
| PID | 4.5 | D | 显著最差 |
6. 结 语
提出基于GOGS-PO优化的线控转向系统LADRC控制器. 通过引入佳偶双栖初始化策略、动态停留因子、黄金正弦算法及樽海鞘算法领导者机制,有效提升了算法的种群多样性与收敛效率. 仿真结果表明,该控制器在不同工况下均能提高系统的跟踪精度与稳定性. 针对极端工况下因轮胎力饱和导致的估计误差,后续研究将引入强化学习机制,实现参数在线自适应整定,以进一步提升系统在极限条件下的鲁棒性.
参考文献
Research on variable transmission ratio control method to improve vehicle handling comfort based on steer-by-wire system
[J].DOI:10.3390/act13020048 [本文引用: 1]
Comparative study of two types of control loops aiming at trajectory tracking of a steer-by-wire system with Coulomb friction
[J].DOI:10.1177/0954407020946972 [本文引用: 1]
Automatic control method of automobile steering-by-wire based on fuzzy PID
[J].DOI:10.1504/IJVICS.2023.131596 [本文引用: 1]
Research on steering-by-wire system motor control based on an improved sparrow search proportional–integral–derivative algorithm
[J].DOI:10.3390/electronics13224553 [本文引用: 1]
Stability control of steer by wire system based on improved ADRC
[J].
基于线性自抗扰控制技术的伺服控制系统研究
[J].DOI:10.11985/2023.04.005 [本文引用: 1]
Research on servo control system based on linear active disturbance rejection control technology
[J].DOI:10.11985/2023.04.005 [本文引用: 1]
Attitude autopilot design based on fuzzy linear active disturbance rejection control
[J].DOI:10.3390/aerospace9080429 [本文引用: 1]
Development and experiment of semi-physical simulation platform for space manipulator
[J].DOI:10.3390/s24134354 [本文引用: 1]
Parrot optimizer: algorithm and applications to medical problems
[J].DOI:10.1016/j.compbiomed.2024.108064 [本文引用: 1]
Salp swarm algorithm: a bio-inspired optimizer for engineering design problems
[J].DOI:10.1016/j.advengsoft.2017.07.002 [本文引用: 1]
基于转速参考模型的线控转向主动回正控制
[J].DOI:10.3969/j.issn.2095-1469.2025.01.11 [本文引用: 1]
Active return-to-center control for steer-by-wire systems based on a steering wheel angular speed reference model
[J].DOI:10.3969/j.issn.2095-1469.2025.01.11 [本文引用: 1]
汽车线控转向系统稳定性控制策略研究
[J].
Research on the stability control strategy of vehicle steer-by-wire system
[J].
Methods for modeling the steering wheel torque of a steer-by-wire vehicle
[J].
Research on a hierarchical control strategy for anti-lock braking systems based on active disturbance rejection control (ADRC)
[J].DOI:10.3390/app15031294 [本文引用: 1]
An adaptive dung beetle optimization algorithm with golden sine for optimizing numerical unconstrained problems
[J].DOI:10.9734/cjast/2024/v43i44365 [本文引用: 1]
Dung beetle optimizer: a new meta-heuristic algorithm for global optimization
[J].DOI:10.1007/s11227-022-04959-6 [本文引用: 1]
Polar lights optimizer: algorithm and applications in image segmentation and feature selection
[J].DOI:10.1016/j.neucom.2024.128427 [本文引用: 1]
Arctic puffin optimization: a bio-inspired metaheuristic algorithm for solving engineering design optimization
[J].DOI:10.1016/j.advengsoft.2024.103694 [本文引用: 1]