1. 相关工作
识别和了解人体关节角度与姿态有助于评估关节康复情况,为运动能力改善提供基准,并在治疗方案制定中发挥关键作用. Lalwala等[3]研究动态负荷的下肢运动学,Vianello等[4]根据姿势和末端执行器速度预测关节运动,Mousse等[5]提出提高跌倒检测准确性的姿态识别算法,Takano等[6]利用2D相机图像估计人体姿态. 明确人体在运动过程中的运动模式和骨骼关节活动机制,能够为外骨骼设计提供必要的数据支持. Simon等[7]进行肩-髋-膝关节角度分析,设计出增强背部支撑的外骨骼;Lerner等[8]制造出关节完全伸展的外骨骼;Barrutia等[9]使用机械关节模拟器分析行走中的矢状面运动学特征;陈栋等[10]基于步态重建和关节运动信息设计柔性踝关节外骨骼机器人,通过优化模态参数实现人机一体化. Missiroli等[11]设计出提供关节屈曲伸展重力支撑的外骨骼,使肌肉活动减少了32%;De Groof等[12]设计出具有伸展扭矩功能的外骨骼,旨在防止关节伸展不足和过度屈曲;Perry等[13]在可变加载的条件下研究外骨骼装置对关节屈曲性能的影响.
获取准确的关节运动信息对推动康复设备发展至关重要. 常见的关节运动学检测方法包括皮肤标记和运动捕捉. Hachaj等[14]通过关节运动捕捉计算加速度,Dobos等[15]比较了单摄像头无标记和3D光学标记技术在运动学数据采集中的准确度,Ziegler等[16]利用3D标记位置识别下肢几何和步态轨迹. 摄像机和惯性传感器可捕捉实时数据,但成本高且操作复杂[17]. 关节运动学与配准技术密切相关,配准技术能将不同数据源的信息对齐,为运动学分析提供准确输入. Saadat等[18]提出在X光透视图像中插值预测3D位置并微调的方法,通过从粗到精的配准在提高配准速度的同时保持了位置预测的准确性;Matsuki等[19]利用图像配准研究胫骨相对于股骨的平移和旋转. 配准须消耗大量计算资源,且数据质量对精度影响较大. 分析关节运动过程中的生物力学特性有助于疾病预防[20]. Thienkarochanakul等[21]发现膝关节软骨层和半月板内侧区域承受较高应力,易受损;Sidhu等[22]在模拟器上测量运动过程中关节肌肉和组织松弛度;Ng等[23]采用有限元方法分析了胫骨近端骨移植物的生物力学;Park等[24]发现行走过程中膝关节的内侧软骨接触压力高于外侧.
2. 运动关节姿态重建
2.1. 基于锥规划的关节姿态重建
基于锥规划的运动关节姿态重建方法利用半正定约束降低计算复杂度,提高重建的计算效率,并通过形貌特征描述符进行匹配计算,提升姿态重建的精度. 锥规划的目标是在某些锥约束下最小化线性目标函数,典型特点是变量必须落在某个锥形区域内. 锥规划的数学公式为
式中:
式中:
式中:
式中:
式中:
1)在
2)在局部参考坐标系中,根据给定的体素尺寸沿X、Y、Z向划分体素. 如果体素内包含特征,则该体素标记为1,否则标记为0.
3)连接所有体素标记,形成局部体素网格描述符.
4)在
5)在
计算
式中:
式中:
式中:
对
其中
令
式中:
式中:N为P上的特征数量,
2.2. 基于载荷传递的拓扑优化
基于载荷传递和力线的拓扑优化能够准确地反映复杂载荷条件下的力学行为,为结构设计提供更有效的解决方案. 在三维流形模型中,表面上任意点的坐标可由张量积函数表示:
式中:
式中:
式中:
式中:
式中:
对于三维流形模型,主应力通过求解应力的特征方程得到,
式中:
式中:
式中:
3. 膝关节数值试验和结果分析
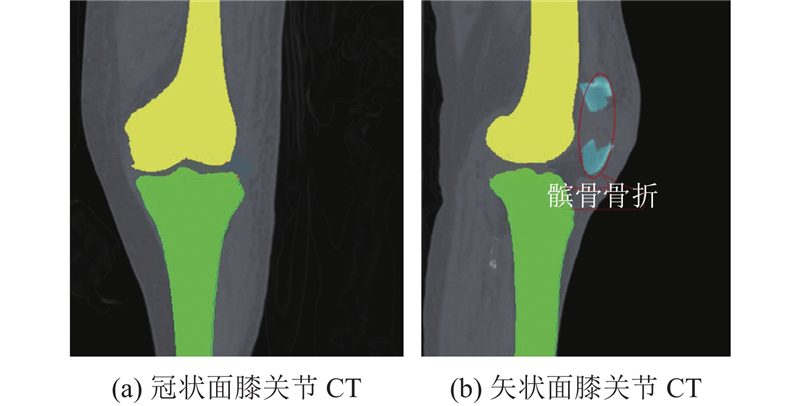
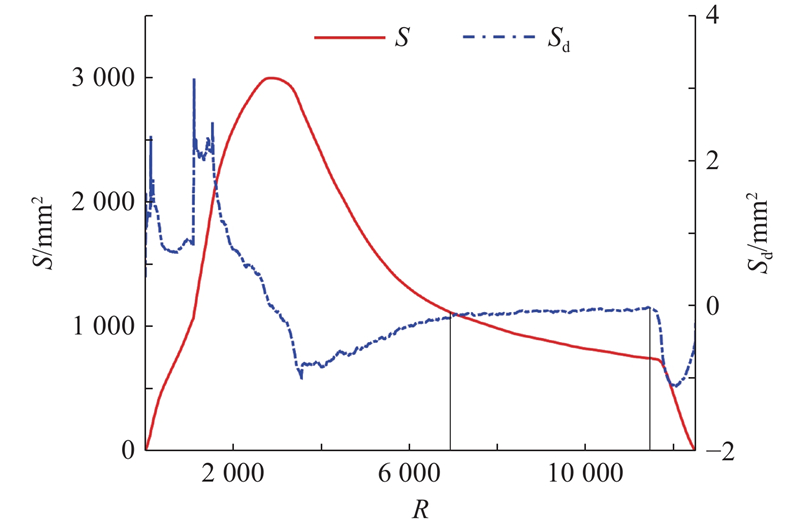
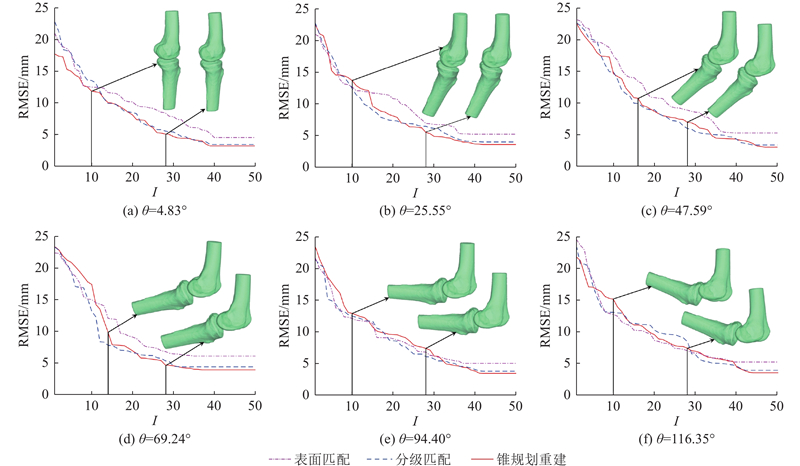
膝关节是人体最大、最复杂的关节之一,在支撑和运动中作用关键. 以左膝关节为例,进行屈曲运动姿态的重建. 如图1所示,根据CT图像进行三维重建,重建的股骨体积为115 935.90 mm3,重建的胫骨体积为73 515.11 mm3. 股骨截面面积S和截面面积差分Sd随分层层数R的变化曲线如图2所示. S最大值为3 001.01 mm2(第2 840层),最小值为0.07 mm2(第12 500层),平均值为1 377.81 mm2,标准差为803.51 mm2. Sd最大值为3.14 mm2(第1 109层),最小值为−1.11 mm2(第12 066层),平均值为−8.80×10−6 mm2,标准差为0.69 mm2. 第6 923~11 471层相邻截面的面积差分变化平缓,为股骨骨干区域;第1~6 923层相邻截面的面积差分变化剧烈,为股骨髁区域. 计算胫骨截面面积和截面面积差分,识别胫骨平台和胫骨骨干区域. 根据运动关节的形貌和咬合特征,通过锥规划迭代计算,对运动关节的屈曲姿态进行精确重建. 定义膝关节的屈曲角度为矢状面上股骨与胫骨解剖轴线之间的角度. 不同方法(表面匹配[29]、分级匹配[30]、锥规划重建)重建的左膝关节运动姿态均方根误差迭代曲线如图3所示. 图中,I为迭代次数,
图 1
图 2
图 2 股骨远端层截面面积和层截面面积差分
Fig.2 Layer area and layer area difference of distal femur
图 3
图 3 不同方法重建的左膝关节运动姿态均方根误差迭代曲线
Fig.3 Iterative curves of root mean square error for left knee joint motion posture reconstruction using different methods
表 1 不同方法重建的左膝关节运动姿态迭代过程均方根误差对比
Tab.1
| 表面匹配 | 分层匹配 | 锥规划重建 | |||||||||
| RMSEMAX | RMSEMIN | RMSEMAX | RMSEMIN | RMSEMAX | RMSEMIN | ||||||
| 4.83 | 23.37 | 5.01 | 8.82 | 21.34 | 3.77 | 8.38 | 21.61 | 3.42 | 8.88 | ||
| 25.55 | 20.96 | 5.24 | 9.53 | 22.80 | 4.02 | 8.30 | 22.59 | 3.62 | 8.29 | ||
| 47.59 | 20.64 | 5.29 | 11.02 | 22.48 | 3.40 | 8.96 | 21.44 | 3.03 | 8.52 | ||
| 69.24 | 22.40 | 6.10 | 10.02 | 23.31 | 4.38 | 8.25 | 23.39 | 3.90 | 8.65 | ||
| 94.40 | 23.37 | 5.01 | 8.82 | 21.34 | 3.77 | 8.38 | 21.61 | 3.42 | 8.88 | ||
| 116.35 | 24.46 | 5.20 | 9.33 | 23.52 | 3.09 | 9.24 | 21.68 | 3.50 | 9.16 | ||
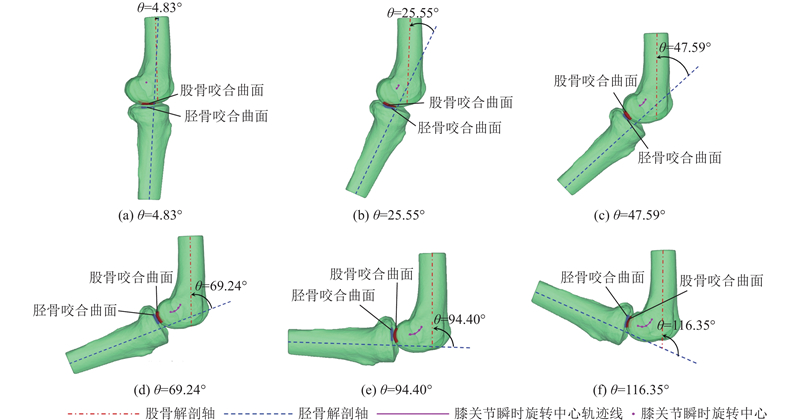
根据屈曲运动特征,对股骨和胫骨的咬合曲面进行分割. 如图4所示为矢状面上左胫股关节的锥规划重建运动姿态. 膝关节运动是旋转副与移动副的耦合运动,当关节进行屈曲运动时,其旋转中心的变化轨迹为J形曲线,不同屈曲角度下的瞬时旋转中心参数如表2所示,其中
图 4
图 4 矢状面上左胫股关节的锥规划重建运动姿态
Fig.4 Cone programming reconstruction for motion posture of left tibiofemoral joint in sagittal plane
最大误差用于检测极端重建失误,计算式为
如表3所示为不同方法的运动左膝关节姿态重建精度对比. 可以看出,相比表面匹配方法,锥规划重建方法的均方根误差降低了42.76%,平均绝对误差降低了44.85%,最大误差降低了28.26%;相比分层匹配方法,锥规划重建方法的均方根误差降低了10.95%,平均绝对误差降低了12.29%,最大误差降低了6.05%.
表 2 不同屈曲角度下的瞬时旋转中心参数
Tab.2
| dc/mm | cc/m−1 | |
| 4.83 | 11.25 | 3.36×10−3 |
| 25.55 | 13.28 | 1.21×10−2 |
| 47.59 | 17.15 | 2.17×10−2 |
| 69.24 | 21.29 | 1.82×10−2 |
| 94.40 | 21.78 | 1.80×10−2 |
| 116.35 | 25.94 | 3.29×10−3 |
表 3 不同方法的左膝关节运动姿态重建精度对比
Tab.3
| 表面匹配 | 分层匹配 | 锥规划重建 | |||||||||
| RMSE | MAE | ME | RMSE | MAE | ME | RMSE | MAE | ME | |||
| 4.83 | 4.55 | 0.02 | 20.34 | 3.47 | 0.01 | 15.42 | 3.21 | 0.01 | 14.59 | ||
| 25.55 | 5.24 | 0.03 | 20.16 | 4.02 | 0.02 | 17.01 | 3.62 | 0.02 | 16.12 | ||
| 47.59 | 5.29 | 0.03 | 20.34 | 3.40 | 0.02 | 15.42 | 3.03 | 0.01 | 14.59 | ||
| 69.24 | 6.10 | 0.03 | 20.89 | 4.38 | 0.03 | 19.46 | 3.90 | 0.02 | 18.29 | ||
| 94.40 | 5.01 | 0.03 | 22.12 | 3.77 | 0.02 | 18.91 | 3.42 | 0.02 | 17.43 | ||
| 116.35 | 5.20 | 0.04 | 24.66 | 3.87 | 0.02 | 19.35 | 3.50 | 0.02 | 18.44 | ||
4. 康复外骨骼个性化定制设计
4.1. 外骨骼膝关节结构变瞬心设计
图 5
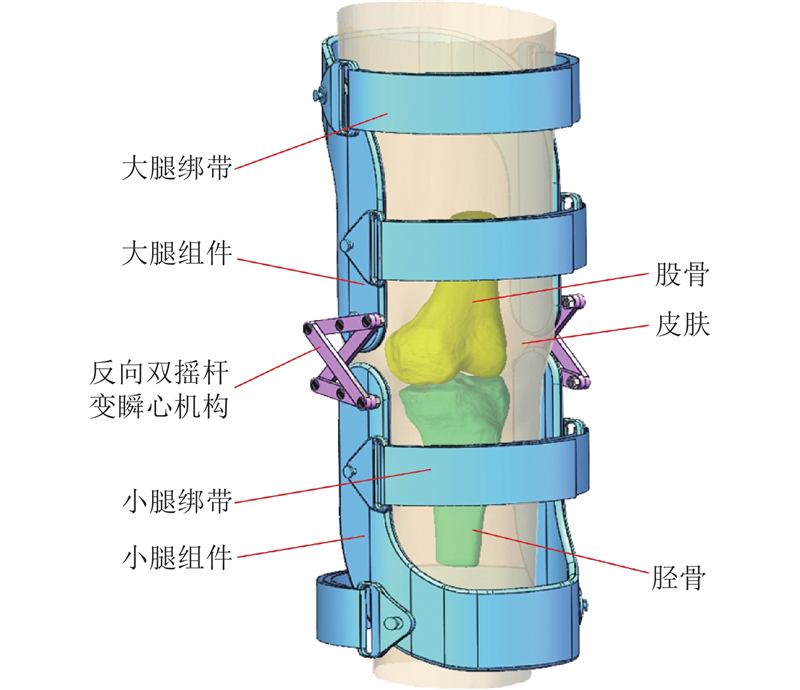
图 5 左膝关节的人体工学康复外骨骼概念设计
Fig.5 Conceptual design of ergonomic rehabilitation exoskeleton for left knee joint
图 6
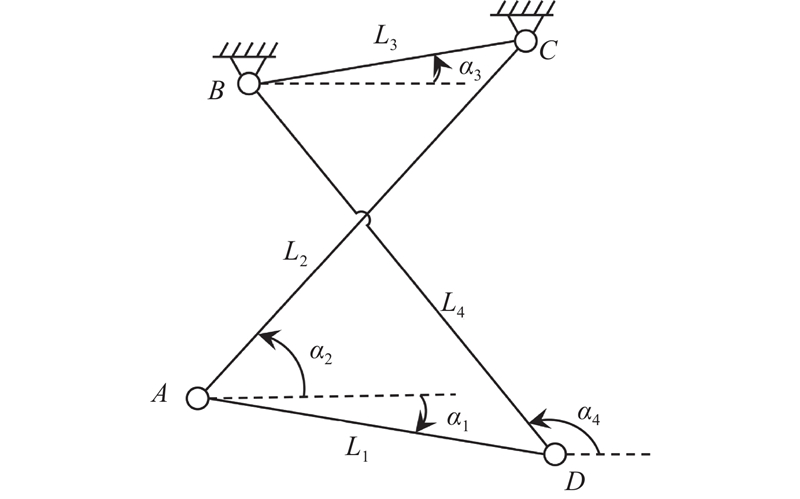
图 6 左膝关节外骨骼变瞬心机构运动学模型
Fig.6 Kinematic model of variable instantaneous center mechanism of left knee joint exoskeleton
根据三心定理,机构瞬时旋转中心P表示为
式中:
式中:
表 4 不同方案的变瞬心机构设计参数
Tab.4
| 参数 | 数值 | ||
| 方案一 | 方案二 | 方案三 | |
| 41.31 | 42.25 | 40.84 | |
| 58.16 | 56.48 | 55.25 | |
| 43.30 | 41.54 | 40.43 | |
| 55.18 | 55.64 | 53.72 | |
| 4.76~25.15 | 4.42~26.60 | 3.99~24.36 | |
| 36.46~43.97 | 33.19~41.95 | 38.08~45.93 | |
| 9.75 | 10.17 | 10.02 | |
| 131.44~144.73 | 130.42~145.93 | 131.94~145.30 | |
图 7
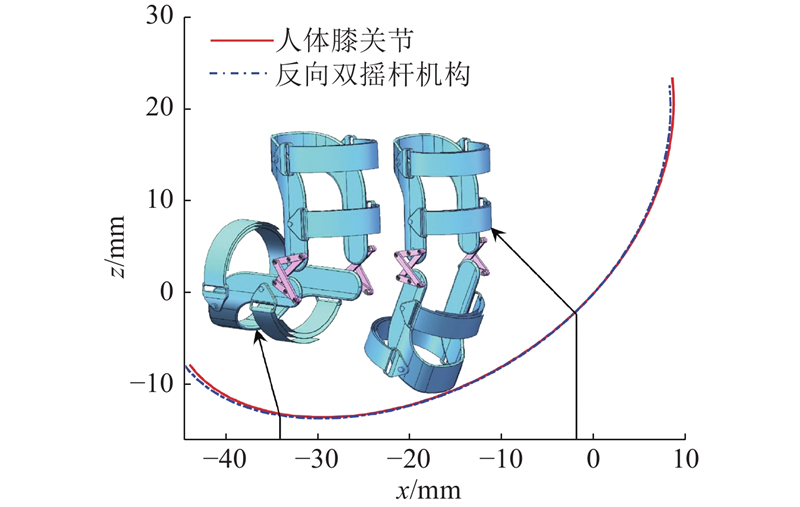
图 7 矢状面上2种瞬时旋转中心的轨迹对比
Fig.7 Trajectory comparison for two types of instantaneous rotation centers in sagittal plane
4.2. 基于载荷传递的外骨骼结构轻质性设计
膝关节在负重活动中承受的力和接触力随屈曲角度的增大而增大[31-32],以
图 8
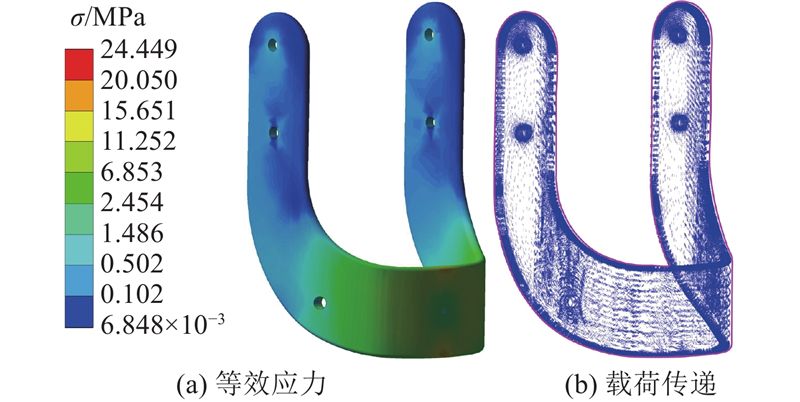
图 8 康复外骨骼左小腿组件等效应力及载荷传递分布
Fig.8 Distribution of equivalent stress and load transfer for rehabilitation exoskeleton of left shank component
图 9
图 9 康复外骨骼左小腿组件应变能迭代曲线
Fig.9 Strain energy iteration curve of rehabilitation exoskeleton of left shank component
表 5 不同体积约束下拓扑优化结构的应变能
Tab.5
| JMAX/(105 J) | JMIN/(105 J) | |
| 45 | 7.33 | 5.42 |
| 40 | 7.93 | 5.44 |
图 10
图 10 数字光处理打印的康复外骨骼左小腿组件
Fig.10 Rehabilitation exoskeleton of left shank component printed by digital light processing
5. 结 论
(1)提出基于锥规划重建的运动关节康复外骨骼定制设计方法. 针对个性化的运动关节康复需求,基于锥规划重建对人体工学的康复外骨骼进行定制设计,有效避免了局部最优解的产生,提高了运动姿态重建的精度. 相比分层匹配方法,锥规划重建方法的均方根误差降低了10.95%,平均绝对误差降低了12.29%,最大误差降低了6.05%. 通过锥规划重建关节的运动姿态定制化设计康复外骨骼,能够提高康复外骨骼运动舒适性.
(2)设计考虑下肢关节变瞬心运动特性的定制康复外骨骼结构. 通过锥规划精确重建个体膝关节的运动姿态变化,获得瞬时旋转中心的精确运动轨迹,定制化设计康复外骨骼,有效匹配人体关节的变瞬心J形曲线运动. 设计的外骨骼反向双摇杆变瞬心机构与人体运动关节的瞬时旋转中心均方根误差为0.90 mm,平均绝对误差为0.82 mm,最大误差为1.61 mm. 在运动域中,定制的康复外骨骼可精确拟合人体膝关节瞬时旋转中心轨迹,提高与个体关节运动轨迹的匹配性.
(3)提出基于载荷传递的结构拓扑优化方法. 通过重建关节运动姿态,利用有限元精确分析应力分布、力线和载荷传递情况,以应变能最小为目标进行拓扑优化,在体积和应力约束下优化结构的材料分布. 提出的优化方法可以适应个性化需求的结构定制设计,实现不同条件下的轻质性设计.
今后,将在研究中进一步探讨不同材料和结构设计对外骨骼承载性的影响. 未来将在结构域、性能域进行综合分析,结合多域性能需求,进一步优化康复外骨骼的设计.
参考文献
Osteoarthritis in 2020 and beyond: a lancet commission
[J].DOI:10.1016/S0140-6736(20)32230-3 [本文引用: 1]
Global estimates of the need for rehabilitation based on the Global Burden of Disease study 2019: a systematic analysis for the Global Burden of Disease Study 2019
[J].DOI:10.1016/S0140-6736(20)32340-0 [本文引用: 1]
Development and validation of an active muscle simplified finite element human body model in a standing posture
[J].DOI:10.1007/s10439-022-03077-x [本文引用: 1]
Human posture prediction during physical human-robot interaction
[J].DOI:10.1109/LRA.2021.3086666 [本文引用: 1]
Action description from 2D human postures in care facilities
[J].DOI:10.1109/LRA.2020.2965394 [本文引用: 1]
Kinematic effects of a passive lift assistive exoskeleton
[J].DOI:10.1016/j.jbiomech.2021.110317 [本文引用: 1]
Computational modeling of neuromuscular response to swing-phase robotic knee extension assistance in cerebral palsy
[J].DOI:10.1016/j.jbiomech.2019.02.025 [本文引用: 1]
A human lower limb mechanical phantom for the testing of knee exoskeletons
[J].DOI:10.1109/TNSRE.2023.3276424 [本文引用: 1]
基于力反馈导纳控制的踝关节柔性外骨骼
[J].
Ankle flexible exoskeleton based on force feedback admittance control
[J].
Rigid, soft, passive, and active: a hybrid occupational exoskeleton for bimanual multijoint assistance
[J].DOI:10.1109/LRA.2022.3142447 [本文引用: 1]
Design and control of an individualized hip exoskeleton capable of gait phase synchronized flexion and extension torque assistance
[J].DOI:10.1109/ACCESS.2023.3311352 [本文引用: 1]
Providing unloading by exoskeleton improves shoulder flexion performance after stroke
[J].DOI:10.1007/s00221-021-06070-3 [本文引用: 1]
RMoCap: an R language package for processing and kinematic analyzing motion capture data
[J].DOI:10.1007/s00530-019-00633-9 [本文引用: 1]
Validation of pitchAITM markerless motion capture using marker-based 3D motion capture
[J].DOI:10.1080/14763141.2022.2137425 [本文引用: 1]
Simultaneous identification of human body model parameters and gait trajectory from 3D motion capture data
[J].DOI:10.1016/j.medengphy.2020.08.009 [本文引用: 1]
Evaluation of a multi-sensor Leap Motion setup for biomechanical motion capture of the hand
[J].DOI:10.1016/j.jbiomech.2021.110713 [本文引用: 1]
A fast and robust framework for 3D/2D model to multi-frame fluoroscopy registration
[J].DOI:10.1109/ACCESS.2021.3114366 [本文引用: 1]
In vivo kinematics of early-stage osteoarthritic knees during pivot and squat activities
[J].DOI:10.1016/j.gaitpost.2017.07.116 [本文引用: 1]
Three-dimensional musculoskeletal model of the lower extremity: integration of gait analysis data with finite element analysis
[J].DOI:10.1007/s40846-022-00734-3 [本文引用: 1]
Stress distribution of the tibiofemoral joint in a healthy versus osteoarthritis knee model using image-based three-dimensional finite element analysis
[J].DOI:10.1007/s40846-020-00523-w [本文引用: 1]
Lateral subvastus lateralis versus medial parapatellar approach for total knee arthroplasty: a cadaveric biomechanical study
[J].DOI:10.1016/j.knee.2020.09.022 [本文引用: 1]
Biomechanical analysis of proximal tibia bone grafting and the effect of the size of osteotomy using a validated finite element model
[J].DOI:10.1007/s11517-019-01988-x [本文引用: 1]
Finite element analysis of knee and ankle joint during gait based on motion analysis
[J].DOI:10.1016/j.medengphy.2018.11.003 [本文引用: 1]
Biomechanical strengthening design for limb articulation based on reconstructed skeleton kinesthetics
[J].
Customized design for ergonomic products via additive manufacturing considering joint biomechanics
[J].DOI:10.1016/j.cjmeam.2023.100085
Load-bearing optimization for customized exoskeleton design based on kinematic gait reconstruction
[J].
Biomechanical evaluation for bone arthrosis morphology based on reconstructed dynamic kinesiology
[J].DOI:10.1016/j.medengphy.2024.104278 [本文引用: 1]
A surface registration technique for estimation of 3-D kinematics of joints
[J].
Fusion of multimodality image and point cloud for spatial surface registration for knee arthroplasty
[J].
Mechanical loads at the knee joint during deep flexion
[J].DOI:10.1016/S0736-0266(01)00178-4 [本文引用: 1]
Biomechanical analysis of tibial torque and knee flexion angle
[J].DOI:10.2165/00007256-200636080-00001 [本文引用: 1]
Design and analysis of lower limb exoskeleton with external payload
[J].DOI:10.1007/s12008-023-01272-1 [本文引用: 1]