传统的人工驾驶车辆(human-driven vehicles, HV)在停车区域完成停车后,驾驶员往往需要步行一段距离才能到达目的地,在进行停车选择时,空间选择存在一定的局限性. 停车场在不同地理区位(包括自然地理区位、经济地理区位和交通地理区位)下车位利用的不平衡性是许多城市面临的难题. 随着现代交通的发展,自动驾驶技术逐渐成熟,对于高级别的自动驾驶车辆(autonomous vehicles, AV),能够在目的地让出行者下车后,以空载状态选择继续巡航或者前往合适的停车地点,在出行者活动结束时返回指定位置接载出行者. AV具有自动泊车和巡航功能,为出行者提供了新的停车选择方案[1-3].
虽然AV能够从一定程度上解决热点区域由于停车资源匮乏造成的“停车难”问题[4-6],但由于在选择搜索并导航到价格低廉甚至免费的停车位的过程中,不可避免地产生空载行驶里程,这种额外交通量可能会对道路资源产生一定的压力,并有可能导致交通拥堵和延误增加,这对城市交通系统可能是考验[7-9]. Levin等[10]指出AVs可能会增加行驶里程,以避免市中心的高额停车费. Harper等[11]发现,随着AVs的普及,城市地区的停车需求预期减少,而停车需求会转移到郊区经济型停车场. 这种转移可能导致AVs在市中心与停车地点之间的空载里程增加. Zhang等[12]进一步揭示这种空载行驶会加剧因停车搜索产生的交通拥堵. Mondal等[13]的研究证实了AVs的空载行驶会增长车辆的总行驶里程,对城市交通造成了负面影响.
近年来,已经有部分关于AV停车行为的研究,但这一领域的研究仍然处于初级阶段. 这些研究最显著的特点是揭示了AV停车行为、行驶里程和成本之间的关系. 许多研究都发现,AV空载行驶可能会引发交通问题,但很少有研究提出相应的解决策略. Millard-Ball[8]提出针对AV停车实施拥堵定价的概念,认为由于AV的巡航能力模糊了停车和行驶之间的界限,收费系统应该包括时间收费和距离(能源)收费,考虑路权及额外的社会和环境成本,但没有具体的收费模型和实验分析. 鉴于现有研究的不足,本文设计AV停车空载收费模型并进行数值分析,研究不同的空载收费策略对AV停车选择、行驶模式及整个交通网络的影响. 本文的主要贡献有以下2点. 1)基于多智能体(Multi-agent)方法刻画AV停车选择行为逻辑,对实际路网、交通需求和停车收费等条件进行描述. 2)提出静态和动态2种空载行驶收费策略,在大规模路网上测试其对AV停车模式的反应和影响.
1. 方法简介
1.1. 多智体停车模拟框架
对于AV的特点,重新定义其在城市活动中的停车行为,将该过程分为以下3个阶段. 1)用户从住处出发,乘坐AV前往城市某地进行特定的活动. 针对不同的活动目的,假设用户的活动时间t在[0,T]连续分布. 2)在到达目的地后,每个AV用户将面临停车决策:他们可以选择在公共停车场停车,将他们的AV送回家,或者选择在该区域内巡航. 在作出停车选择后,AV将自动执行所选的停车方案. 3)在用户活动结束后,AV将执行返程行驶. AV的停车过程是动态变化的,根据路网状态的变化动态调整停车模式和行驶路径. 本文模型基于Multi-agent框架运作,模拟城市内所有私家车的行程,使用动态用户分配(dynamic user assignment, DUA)将它们分配到道路网络中. 考虑当前的模拟时间步和用户的活动持续时间,该模型将评估各种停车的可能性. 特别关注AV空载收费机制对停车选择行为的影响,将道路通行费纳入车辆的总出行成本,这种收费制度会促使用户在权衡不同的停车选项时,考虑远距离空载行驶所产生的额外成本. 每个AV用户会综合考虑各方面因素,根据概率选择具有最低瞬时成本的停车选项,计算相应的行驶路径. 若选择在公共停车场停车或返回住所停车,AV会遵循到达所选停车地点的最有效路径. 若选择继续空载巡航,AV则会执行随机游走模式,无序地在区域内移动,直至接到新的指令或活动结束. 空载巡航路径分配是具有挑战性的任务,本文的研究重点并非在于优化巡航路径的决策过程,选择随机游走模型是为了在保持运动经济效率和减少对周围交通影响之间折中,评估巡航路径在实际交通情境中的平均影响.
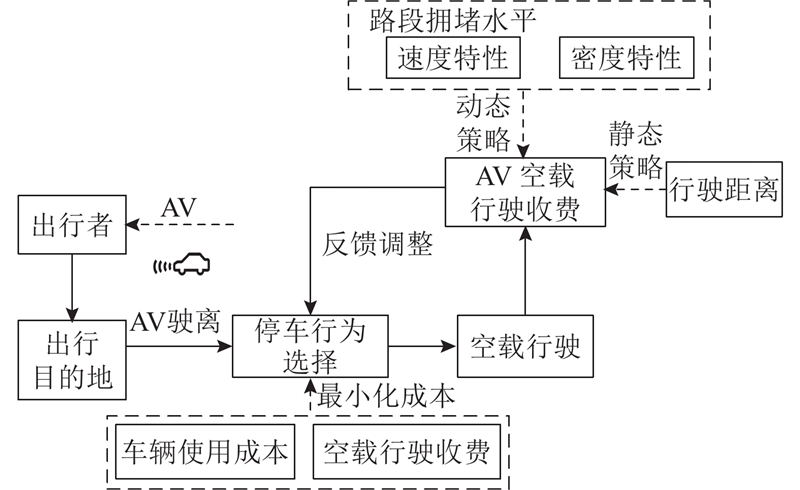
如图1所示为使用的仿真系统逻辑框架. 该系统涉及4种主要的智能体:AV-出行者、停车系统、路侧单元(roadside unit, RSU)、交通控制中心(traffic control management, TCM). 各个智能体之间可以实现实时通讯、信息交互,使得各智能体作出不同反应. 各类智能体的功能和属性如表1所示. AV-出行者智能体可以模拟车辆在路网上的驾驶行为,执行停车决策过程. 停车系统智能体负责动态更新停车资源信息、管理车位分配及处理停车位预订的相关信息. 路侧单元智能体的主要任务是实时获取并更新管辖区域内各路段的交通状态,将路况信息与交通控制中心的智能体完成传递. 此外,它能够响应AV-出行者智能体的巡航需求,控制车辆的巡航行为. 将交通控制中心作为整个系统的核心,不断地追踪和记录所有的路段及停车资源实时状况,动态调整和更新路段权重,实现AV-出行者智能体的空载收费和停车诱导.
图 1
表 1 AV停车仿真模型不同类型智能体的特性
Tab.1
| 智能体种类 | 功能 | 属性 |
| AV-出行者 | 实现车辆微观行驶、停车模式选择、路径选择 | 速度、加速度、车辆类型、活动时间、路径选择规则、停车模式决策规则 |
| 停车系统 | 动态更新停车资源,完成停车位预订和分配 | 停车场容量、车位预定信息、停车位价格、空闲停车位数量、停车位位置 |
| RSU | 实现道路状态识别,控制车辆巡航 | 静态信息(限速、车道数、长度)、动态信息(车辆数、车速、行程时间) |
| TMC | 更新和整合道路资源、停车资源,完成空载收费发布, 实现停车诱导 | 车辆信息、道路状态信息、停车场信息、空载收费策略 |
1.2. 停车选择行为的建模
模拟AV在空载收费策略下3种不同停车模式(前往公共停车场、返回住所和持续空载巡航)的选择行为. 为了实现这一模拟,使用多项式Logit(multinomial logit, MNL)模型. 在模型中,每个停车模式的效用被分解为确定性部分和随机误差. 对于每种模式i,效用函数定义为
式中:
基于效用函数,可以计算选择每个模式的概率. 对于模式i,选择概率如下:
在该框架下,出行者选择特定停车模式的决策基于各种模式的选择概率. 若出行者选择前往公共停车场的概率
下面分别定义每种停车模式的成本. 其中,选择前往公共停车场停车的成本被量化为4个部分,包括车辆往返目的地与停车场的行驶成本、公共停车场的停车费、出行者等待AV返程接载的等待成本、由空载收费策略产生的空载行驶惩罚费用. 该模式的成本函数表示成如下形式:
式中:
式中:
式中:
其中
式中:
式中:
选择返回住所停车的成本被量化为3个部分,包括从目的地往返住所的行驶成本、用户等待AV返回接载所产生的等待成本以及空载行驶的惩罚费用. 该模式的成本函数表示成如下形式:
式中:
选择持续空载巡航的成本被量化为3个部分,包含AV在目的地所属RSU辖区内持续空载巡航所产生的行驶成本、用户等待AV返回接载所产生的等待成本以及空载行驶的惩罚费用. 该模式的成本函数表示成如下形式:
式中:
1.3. 空载收费策略
设计2种不同的空载行驶收费策略:基于行程距离的静态收费和考虑拥堵差异的动态收费. 下面详细介绍这2种方法及其关键特点.
静态收费策略以车辆行驶距离描述空载惩罚费用,简单且容易执行. 考虑到路网中各区域的交通压力和资源占用差异,将路网G划分为有限个子区域,并为每个子区域设置不同的收费费率. 空载行驶收费由AV在各子区域的行驶长度与对应收费费率的乘积求和得出,计算公式如下:
式中:
静态定价模型存在局限性. AV倾向于选择最短的路线以降低通行费,不考虑所选路线的实际拥挤程度. 这可能导致车辆未选择其他通畅的路线,增加了某些路段的交通压力. 为了更精确地引导AV规避拥堵的行为,缓解交通压力,引入动态收费策略.
该策略与交通拥堵程度相关. 提出有效的方法来量化和识别交通拥堵情况,该方法同时考虑路网速度及密度. 其中路段
式中:
低速行驶不意味着道路拥堵. 除了速度指标外,还采用密度指标作为衡量路网状况的另一个关键参数. 路段
式中:
其中
根据式(14)、(15),建立路段拥堵系数(road congestion factor, RCF). RCF定义为路段速度指标和密度指标的算术平均值,
每个RSU管域(通讯范围)内均包含若干路段,根据式(5)定义了区域拥堵系数(zone congestion factor, ZCF),为RSU内RCF基于各自路段长度进行加权后的平均值. 这意味着每个RCF都会根据其长度在整个RSU内的占比进行调整,计算公式如下:
当考虑路段的拥堵情况时,除了关注路段自身的状态,还考虑了所在区域的状态,提出综合路段拥堵系数(comprehensive road congestion factor, CRCF). 在CRCF的计算中,加入RSU的拥堵情况作为考虑因素,定义为RCF与ZCF的算术平均值,
参考文献[16]的标准,基于CRCF取值定义交通拥堵等级:CRCF = 0表示交通状态为自由流,CRCF = 0.5表示交通状态为中度拥堵,CRCF = 1表示交通状态为重度拥堵.
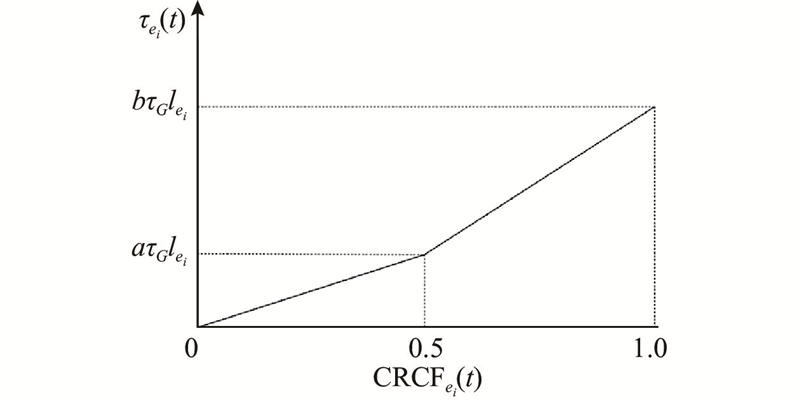
动态策略引入与CRCF相关的2阶分段增长函数来描述路段的收费水平变化,取中度拥堵值(
图 2
图 2 动态空载收费策略的分段增长函数
Fig.2 Segmental growth function of dynamic empty-load charging strategy
式中:
考虑历史费用的影响,引入记忆因子
式中:
综上所述,AV在路径k行驶产生的动态空载收费费用可以按照如下公式计算:
此外,对于持续空载巡航模式收费
式中:
当采用动态空载行驶收费策略时,
式中:
2. 算例分析
2.1. 仿真设置
选取南宁市主城区为研究区域(见图3),探讨空载收费策略在大规模城市路网中的应用效果. 根据交通流量的差异,将研究区域细分为子区域
图 3
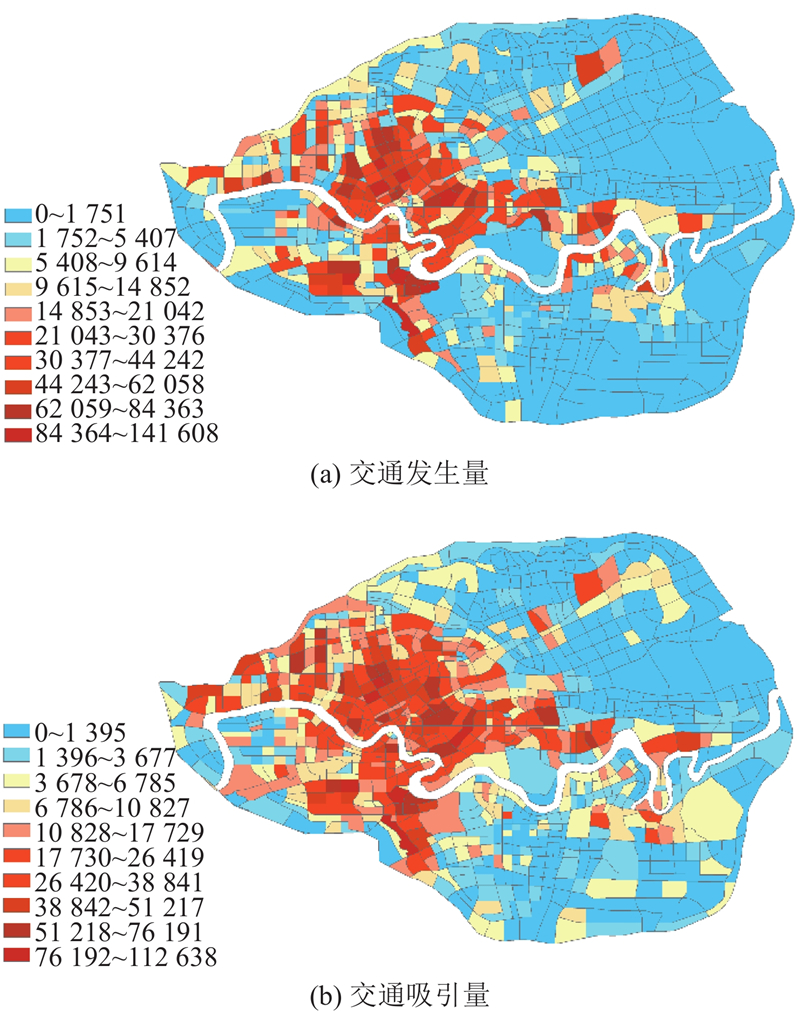
解析2021年南宁市民的出行调查数据(1.14%抽样、3.68万户)以获取日出行需求和停车需求,该数据详细记录了市民一整天的活动链条. 剔除起讫点在研究区域外的出行样本,针对小汽车样本进行扩样处理,扩样后的出行需求如图4所示. 停车需求根据出行者每次活动的到达时间、活动地点及活动时长信息生成. 路网交通量配准通过高德地图API获取的交通态势数据实现.
图 4
图 4 研究区域交通小区的需求生成分布(小汽车)
Fig.4 Traffic demand generation in traffic subareas of study area (cars)
表 2 AV停车行为仿真模型的仿真场景
Tab.2
| 场景编号 | 收费策略 | 收费区域 | |
| 1 | 无收费(基础场景) | — | — |
| 2 | 静态收费策略 | 区域 | |
| 区域 | |||
| 3 | 动态收费策略 | 区域 | 最小值:0 最高值 |
| 区域 | 最小值:0 最高值 |
表 3 跟驰和换道模型的参数
Tab.3
| 参数 | 数值 | |
| HV | AV | |
| 加速度 | 2.6 | 3.8 |
| 减速度 | 3.5 | 4.5 |
| 紧急情况下减速度 | 9.0 | 9 |
| 驾驶容差 | 0.5 | 0 |
| 最小跟车间隙 | 2.5 | 1.5 |
| 期望车头时距 | 1.0 | 0.6 |
表 4 停车场费率
Tab.4
| 区域类别 | 分段费率/(元·h−1) | 每日最高限价/元 |
| 一类区域 | 前3小时:4 3小时后:6 | 50 |
| 二类区域 | 3 | 30 |
| 三类区域 | 2 | 15 |
表 5 预约接载比例
Tab.5
| 活动目的 | ρres | |
| 通勤 | 30% | 70% |
| 商务 | 50% | 50% |
| 生活 | 50% | 50% |
| 通学 | 100% | 0 |
| 其他 | 100% | 0 |
2.2. 仿真结果与分析
2.2.1. 停车模式的选择
如表6所示为3种不同场景下AV的停车模式行为特征,包括选择比例
表 6 不同场景下AV停车模式特征
Tab.6
| 场景 | 停车模式 | |||||
| 场景1 | 停车场停车 | 45.69 | 22.22 | 5.92 | 3.75 | 15.99 |
| 住宅停车 | 54.01 | 17.03 | 9.19 | 1.85 | 8.62 | |
| 巡航替代停车 | 0.30 | 10.91 | 0.40 | 27.28 | 10.20 | |
| 均值 | — | 19.38 | 7.67 | 2.53 | 11.99 | |
| 场景2 | 停车场停车 | 62.00 | 25.61 | 6.70 | 3.82 | 14.69 |
| 住宅停车 | 37.80 | 19.72 | 9.30 | 2.12 | 7.54 | |
| 巡航代替停车 | 0.20 | 10.60 | 0.37 | 28.65 | 17.32 | |
| 均值 | — | 23.35 | 7.67 | 3.04 | 11.99 | |
| 场景3 | 停车场停车 | 59.27 | 24.29 | 6.61 | 3.68 | 15.01 |
| 住宅停车 | 40.55 | 18.97 | 9.26 | 2.05 | 7.55 | |
| 巡航代替停车 | 0.18 | 10.63 | 0.38 | 27.97 | 17.43 | |
| 均值 | — | 22.11 | 7.67 | 2.88 | 11.99 |
2.2.2. 交通网络状态
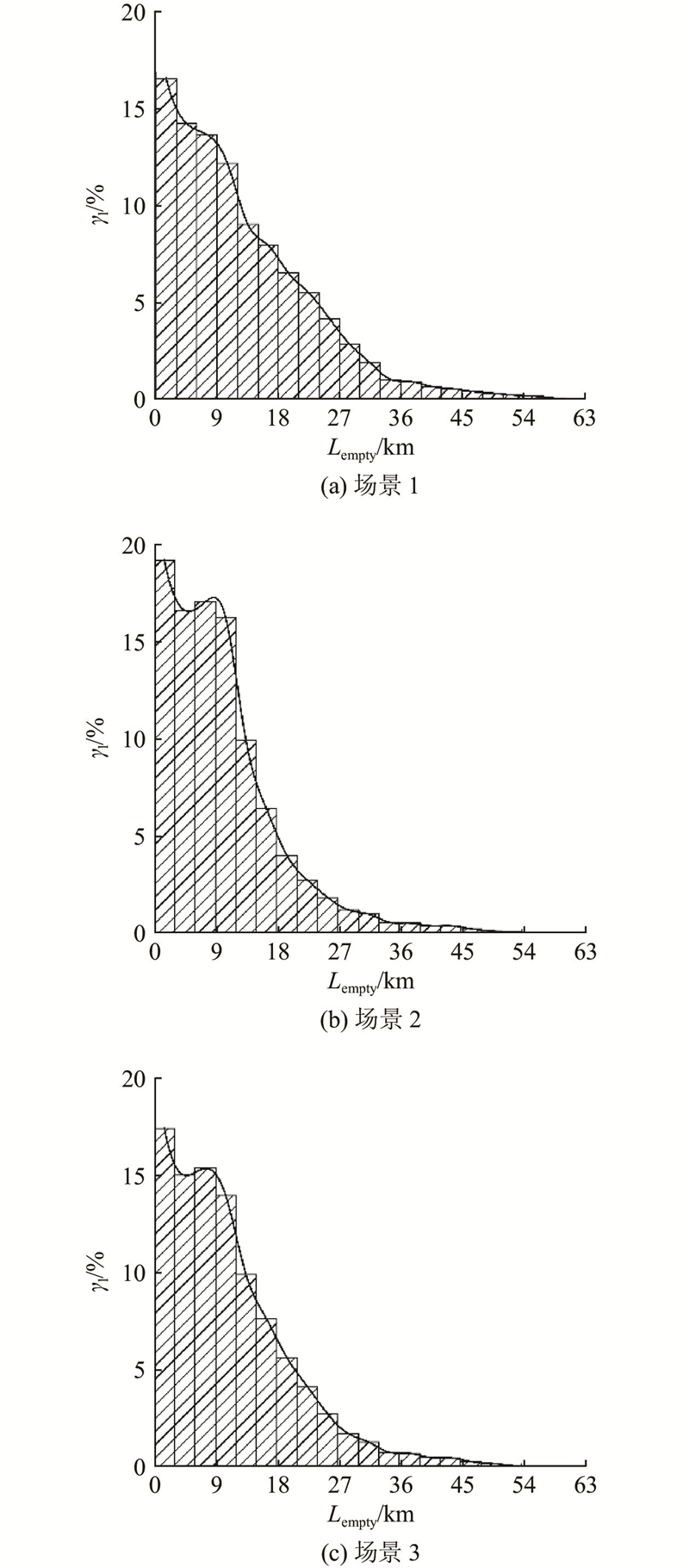
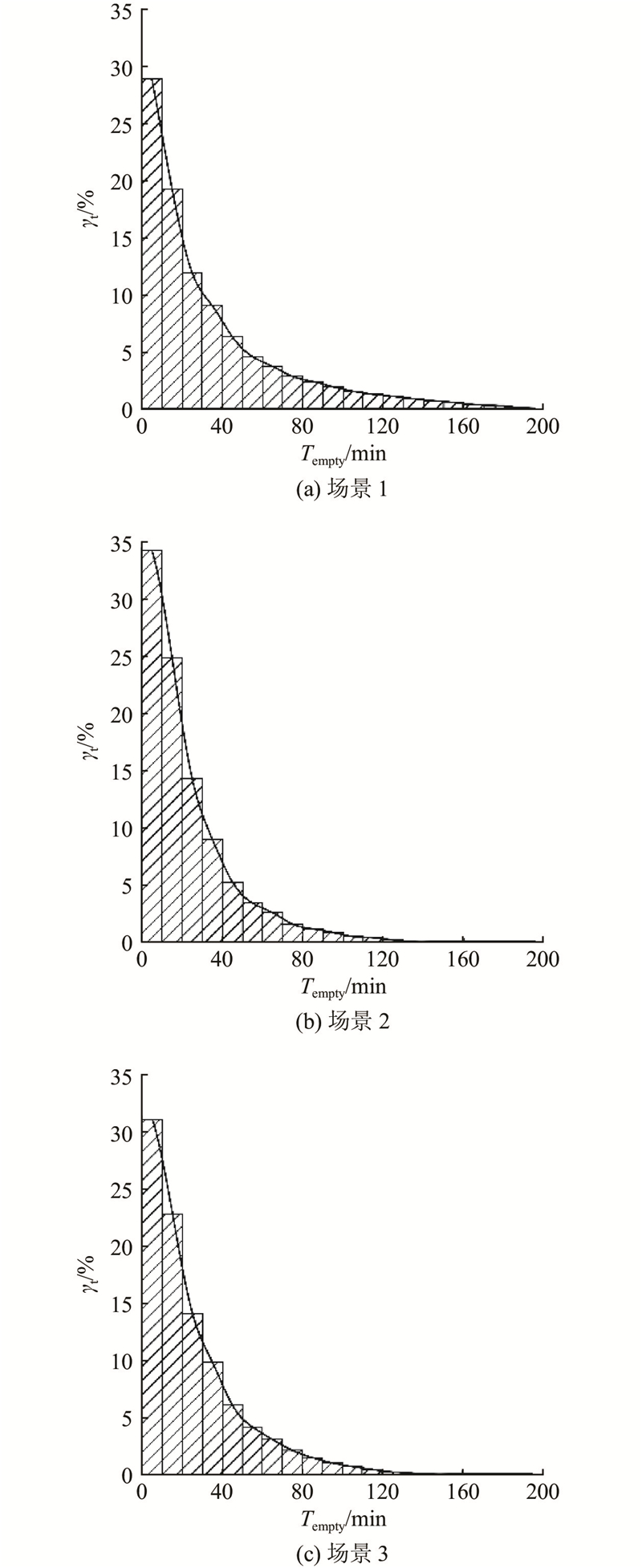
为了探索空载收费策略对交通网络性能的影响,以行驶里程、行程时间、交通量、速度和延误为评价指标,分析3种不同场景下的交通网络性能表现. 如图5、6所示分别为AV在不同场景下的空载行驶距离
图 5
图 5 不同场景下AV空载行驶里程的变化
Fig.5 Variation of AV empty-load driving mileage for different scenario
图 6
图 6 不同场景下AV空载行程时间的变化
Fig.6 Variation of AV empty-load travel time for different scenario
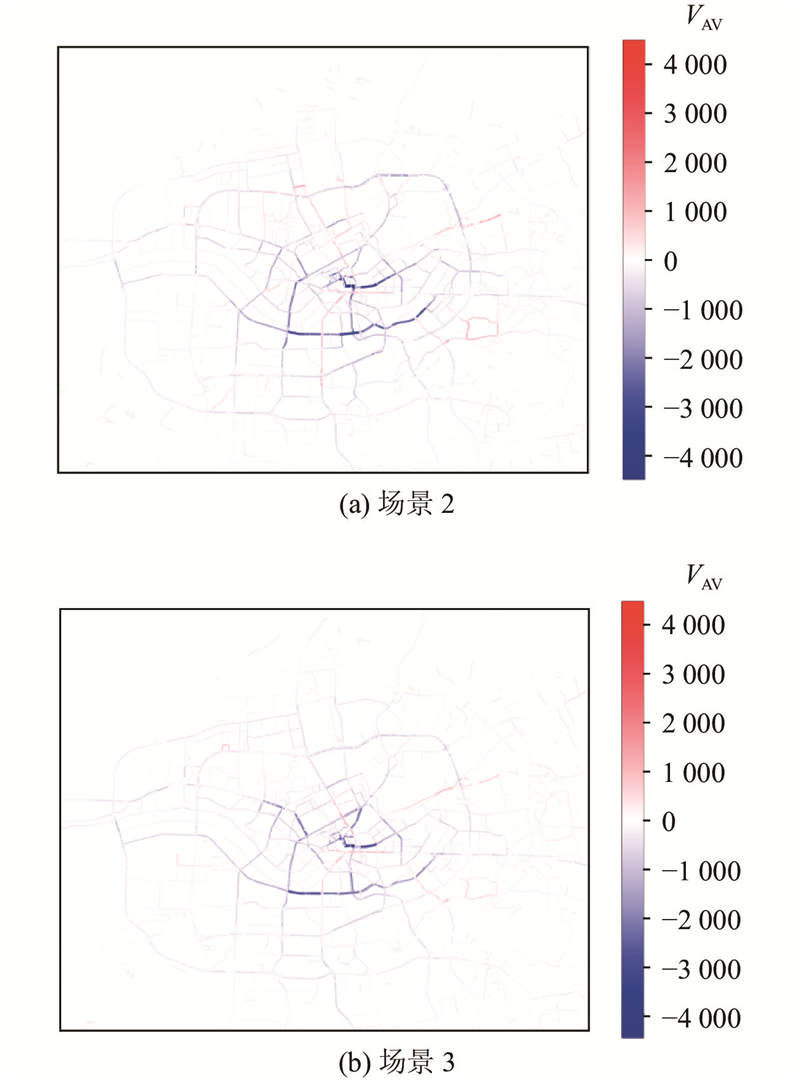
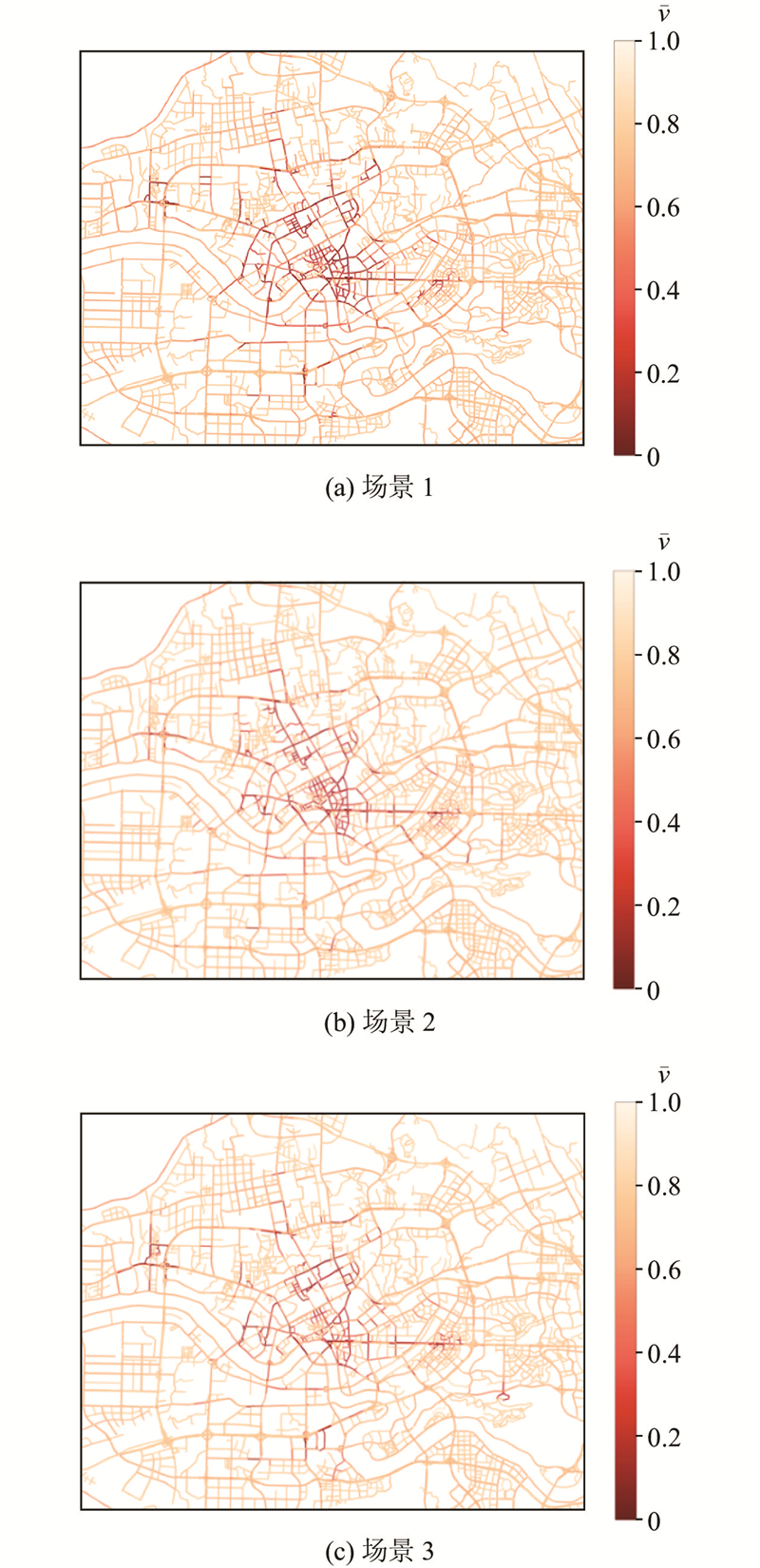
如图7所示为空载收费策略对路网交通量的影响. 图中,VAV为以场景1为基准的交通量变化,正值表示该路段交通量相对于场景1上升,负值表示相对于场景1交通量下降. 从图7可知,2种收费策略都在一定程度上降低了交通流量. 场景2对市中心拥堵的作用更强,因为在区域内实施了相同费率,但场景3的路网流量分布更均衡. 如图8所示为3种场景下的路网相对速度${\bar v}$(路段平均速度与限速的比值). 可知,2种收费策略对路网的运行速度均产生了积极的影响. 尽管场景2的空载距离和时间都较场景3少,但场景3的平均速度(27.38 km/h)实际上超过了场景2的25.96 km/h. 如表7所示为收费场景相对于非收费场景各道路类型的行驶里程、速度及延误变化. 表中,γm、γv、γd分别为以场景1为基准的行驶里程、速度及延误的变化比例. 从表7可知,场景3相对于场景2在降低路网延误上表现更加显著,降幅为43.52%,场景2为39.80%,这说明场景3中的车辆更可能选择拥堵程度较低的道路,从整体效果上优于场景2. 尽管收费策略在一些路段产生了影响,但部分路段受到出行计划(如出发时间、起终点和路径选择)的干扰较大,导致某些路段未显著受益于收费策略,存在交通拥堵的现象. 此外,收费策略在快速路和主干道上的效果尤为显著. 考虑到基本场景下这些路段已饱和,减少该路段的空载行驶行为,可以显著提高平均速度并减少延误.
图 7
图 7 交通量变化vs.无收费场景(场景1)
Fig.7 Variation in traffic volume compared to no-charge scenario (scenario 1)
图 8
图 8 不同场景早高峰相对速度的比较
Fig.8 Comparison of relative speeds during morning peak across different scenario
表 7 不同道路类型的行驶里程、速度及延误变化vs.无收费场景(场景1)
Tab.7
| 道路类型 | 场景2 | 场景3 | |||||
| γm | γv | γd | γm | γv | γd | ||
| 高速公路 | −2.69 | 0.02 | −0.41 | −1.76 | 0.01 | −0.39 | |
| 快速路 | −13.67 | 3.38 | −56.53 | −11.78 | 3.87 | −53.99 | |
| 主干道 | −7.34 | 3.48 | −43.52 | −6.55 | 4.25 | −44.22 | |
| 次干道 | −9.05 | 3.59 | −36.64 | −6.07 | 3.71 | −43.21 | |
| 三级道路 | −5.13 | 2.41 | −27.62 | −4.39 | 3.06 | −32.81 | |
| 居住区道路 | −6.46 | 2.44 | −31.44 | −6.27 | 1.45 | −43.15 | |
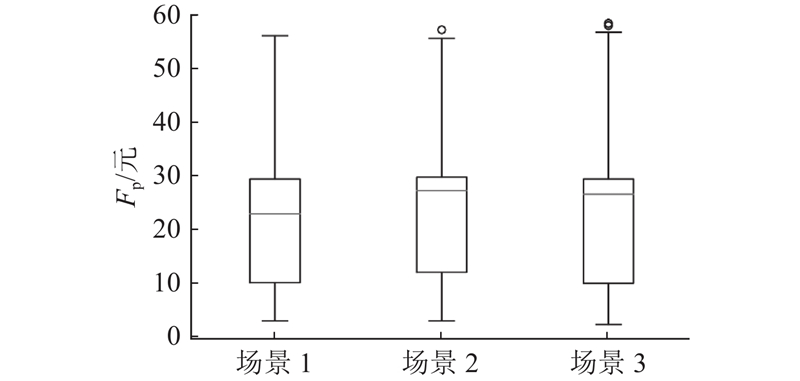
2.2.3. 停车场与空载收费收益
探讨不同场景停车场收费
图 9
图 10
3. 结 论
(1)在无收费场景下,AV更倾向于追求个体的最大利益,产生频繁的空载巡航,即为寻找最佳的停车位置而长时间、长距离地行驶. 这种行为不仅增加了车辆的无效行驶距离,也浪费了道路资源,特别是在高需求的地区.
(2)空载收费策略主要影响AV在空载距离和停车场收费之间的权衡,使得出行者需要重新评估停车行为决策. 空载收费策略在一定程度上提高了出行者的停车成本,鼓励AV选择成本较低的路线或直接选择在停车场停车,降低空载巡航里程.
(3)2种空载收费策略均对路网运行状态产生积极影响,静态策略和动态策略下的车辆空载行驶里程分别降低了20.16%和10.85%,路网延误分别降低了39.80%和43.52%. 尽管静态策略相较于动态策略使空载距离和时间下降得更多,但动态策略能够更好地改善交通状态.
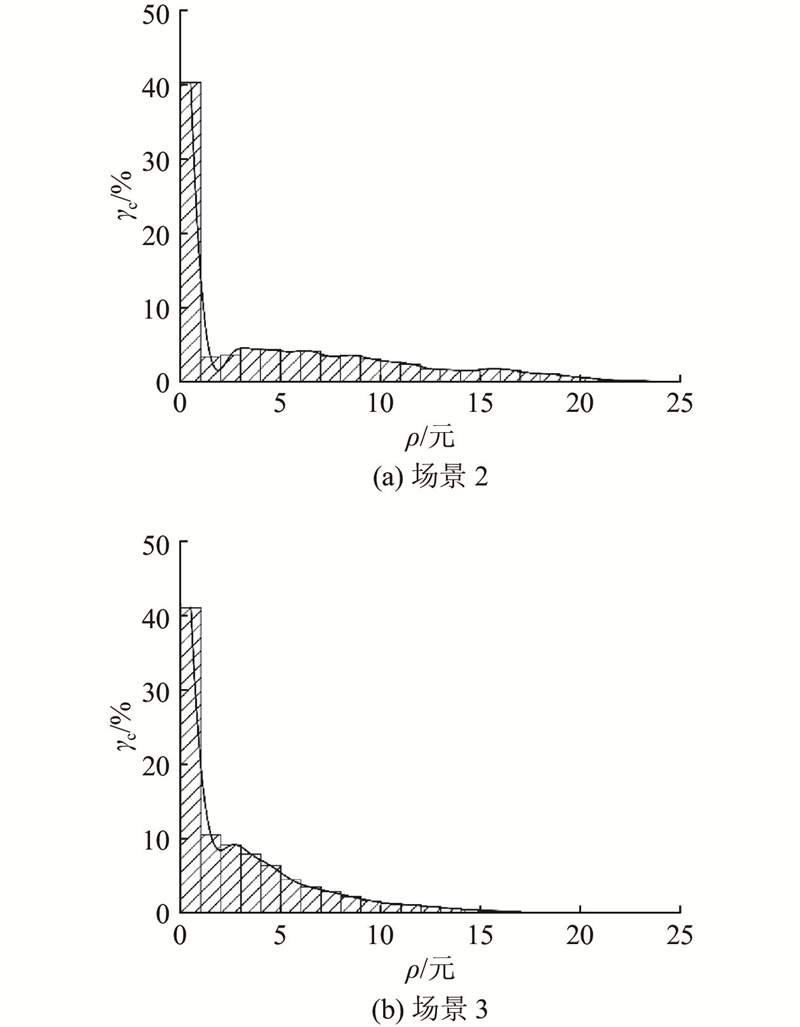
(4)静态策略费用惩罚高于动态策略,差异在于动态策略的灵活性. 动态策略允许车辆选择非拥堵路段来减少费用,导致在高额费用区间的占比相对较低. 静态策略主要基于行驶的距离来确定收费,这使得收费模式更易受到空载行驶距离分布的影响.
(5)动态策略能够有效地将交通流量从拥堵区域转移至交通负荷较低的路段,既分散了繁忙地段的压力,又确保了周边道路资源的充分利用. 此外,从收费标准与公平性考虑,动态收费相较于静态收费更易获得公众的认同和接受.
参考文献
自动代客泊车背景下的共享停车供需匹配模型及对应禁忌搜索算法
[J].
Shared parking supply-demand matching model and designed tabu search algorithm based on autonomous valet parking
[J].
Perpendicular parking path generation and optimal path tracking algorithm for auto-parking of trailers
[J].
Curbing cruising-as-substitution-for-parking in automated mobility
[J].
The impacts of automated vehicles on center city parking
[J].
Autonomous driving cars in smart cities: recent advances, requirements, and challenges
[J].
Impact of automated vehicles on traffic assignment, mode split, and parking behavior
[J].
The autonomous vehicle parking problem
[J].
Using an activity-based model to explore the potential impacts of automated vehicles
[J].
Effects of autonomous vehicle ownership on trip, mode, and route choice
[J].
Exploring the economic, environmental, and travel implications of changes in parking choices due to driverless vehicles: an agent-based simulation approach
[J].
A network traffic assignment model for autonomous vehicles with parking choices
[J].
Accounting for ride-hailing and connected and autonomous vehicle empty trips in a four-step travel demand model
[J].
Estimating energy consumption on the basis of microscopic driving parameters for electric vehicles
[J].
Refocus+: multi-layers real-time intelligent route guidance system with congestion detection and avoidance
[J].