许多专家学者将折纸结构应用于机器人设计中,开发出了许多性能优异、结构新奇的折纸机器人,其中行走类折纸机器人是以折纸机构作为外部骨架或整体骨架的移动机器人[10-13]. Felton等[10]以复合材料制成的集成机电层压板(PCB)作为机器人主体,通过电路板层的加热元件通电使聚苯乙烯层(PSPS)加热收缩,使机器人沿设计折痕处折叠为四足爬行机器人,由电机驱动机器人爬行. Faal等[14]使用薄板折叠构成机器人骨架,关节铰链由薄板弯曲构成,机器人整体骨架实现了可一体化设计、加工和制造,通过折纸产生平面连杆机构,实现行走功能. 江新阳等[15]通过将三浦折纸折痕转角理论与腿部等效运动学模型相结合,设计新型的折纸行走机器人,该机器人有2种不同的腿部构型,在运动过程中分别起到摆动与支撑功能,通过控制输入角来控制机器人腿部的动作,从而实现行走.
目前许多行走类折纸机器人仅使用四折痕折纸单元或其他单一类型的折纸机构设计机器人构型,设计出的机器人多为单自由度驱动,其足端运动轨迹较固定,无法根据实际要求灵活改变足端抬起高度和摆动幅度. 本文基于四折痕三浦折纸和六折痕折纸2种不同的折纸机构,设计多自由度的腿部构型,通过改变折面夹角可以灵活控制抬腿高度及摆动幅度,以适应不同的路面情况. 机器人腿部分布参考螃蟹对称分布,得到形似螃蟹、可像螃蟹一样横向移动的新型仿螃蟹六足折纸机器人.
本文将折痕等效为关节,折面等效为连杆,建立机器人的等效球面机构运动学模型,计算得到对称假设下机器人的运动自由度. 将能体现机器人运动状态的顶点等效为关节,轴线折痕等效为连杆,建立机器人的简化连杆模型. 以折面夹角为运动变量,连杆夹角为中间变量,对该折纸机器人进行足端轨迹设计及横向三角步态规划. 利用楔形面板技术对折面增厚,建立折纸机器人的三维模型. 通过三维模型的运动仿真及试验样机的运动控制试验,对该机器人的运动步态和移动性能进行验证.
1. 可折展步行足的设计及分析
1.1. 折纸单元构型的简介
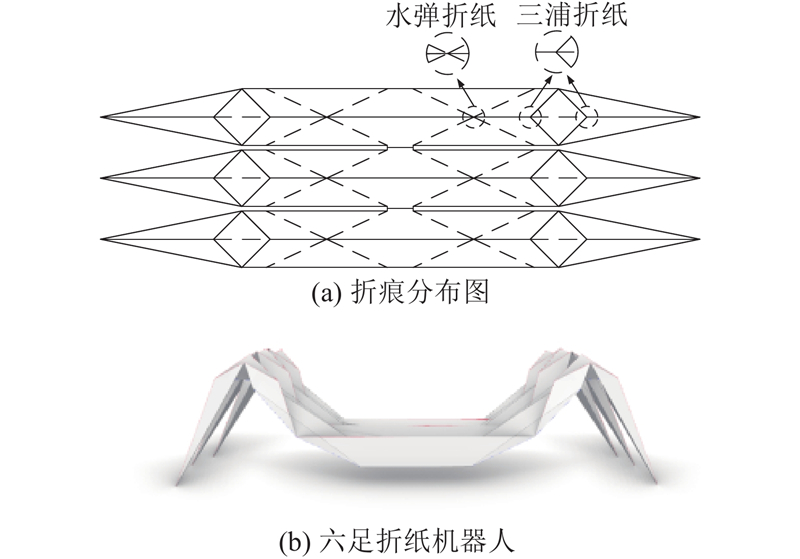
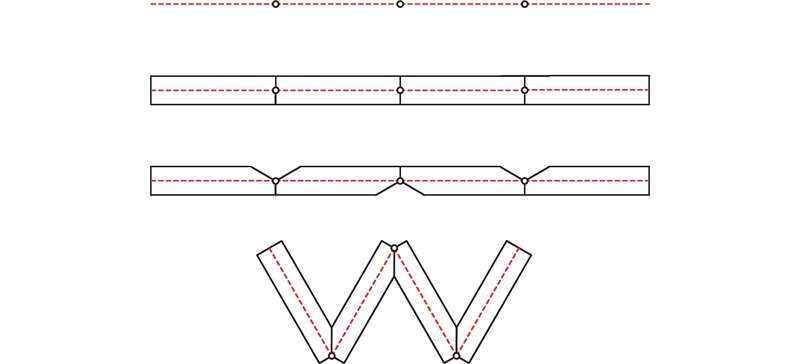
耦合2种不同的折纸机构(三浦折纸和六折痕折纸),设计仿螃蟹六足折纸机器人. 通过沿折痕折叠,该机器人可以由平面状态折叠为仿螃蟹构型,折痕分布图及立体构型如图1所示. 折纸机构中的折痕交点称为顶点,该折纸机器人单腿由1个六折痕折纸和2个三浦折纸构成,是多顶点复合折纸机构.
图 1
图 1 六足折纸机器人的折痕图与折叠构型
Fig.1 Crease pattern and folding configuration of hexapod origami robot
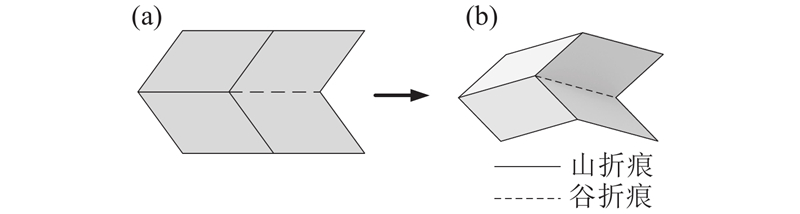
三浦折纸有4块折面,通过3条山折痕和1条谷折痕连接(山折痕即凸折痕,谷折痕即凹折痕),且谷折痕和其中一条山折痕共线,其余2条山折痕关于这2条共线折痕对称分布,如图2所示. 通过改变折面之间的夹角,可以实现三浦折纸的折展运动. 由于所采用的三浦折纸机构折痕是对称的,且为单自由度机构,折展过程中三浦折纸的各折面运动具有对称性,对称面为共线折痕所在的平面.
图 2
图 3
由于该机器人的腿部是多顶点复合折纸机构,由多个不同的折纸单元组合而成,需要对其整体进行自由度分析,得到机器人运动所需的变量个数.
1.2. 可折展步行足自由度的分析
该折纸机器人腿部仿照螃蟹的腿部构型进行设计,保证在运动过程中有较强的稳定性. 机器人左右分布有6条步行足,以保证机器人运动的平稳性. 如图4所示为该机器人的一对步行足由展平状态到折叠状态的过程.
图 4
以折痕为关节,根据D-H法在顶点
图 5
因为每个折纸单元的折痕相交于一点,折痕之间的距离为0,每个顶点相邻折面之间的变换矩阵为
式中:
六折痕折纸单元等效于球面六杆机构
从图5(a)可知,球面六杆机构
从式(3)、(4)可知,该球面六杆机构的运动关于平面对称时,折面运动可由运动变量
三浦折纸单元等效于球面四杆机构,对于顶点
从图5(b)可知,球面四杆机构
将球面四杆机构
式(6)、(7)中分别有1个运动变量
图 6
式中:
其中
2. 机器人腿部运动模型的分析
仿螃蟹折纸机器人腿部由1个六折痕折纸单元和2个三浦折纸单元依次组合而成,每条腿由10块折面组成. 为了分析机器人单条腿的自由度,将折痕等效为关节,折面等效为连杆,此时机器人腿部等效为3个球面机构构成的空间连杆机构. 通过在每一折面上建立坐标系,得到机器人单腿运动学模型. 通过该运动学模型,可以得到每块折面的空间位置和姿态. 当计算机器人足端的运动轨迹时,重点在于得出机器人轴线折痕的位移,需要对该折纸机器人的运动模型进行简化.
在对称假设下,该机器人腿部运动时4条处于对称轴上的折痕始终位于对称面内作平面运动,因此可以将机器人顶点等效为关节,轴线折痕等效为连杆,将机器人腿部等效为平面连杆,由此得到的运动学模型仅包含4条轴线折痕,极大地简化了机器人腿部模型. 下面分别对机器人腿部各个组成单元的轴线折痕夹角与折面夹角进行分析,得到各折纸单元的折面运动与轴线折痕运动之间的关系.
2.1. 三浦折纸单元的理论模型
如图7(a)所示为三浦折纸折痕图. 由于三浦折纸为单自由度机构,且折痕分布对称,折面运动关于面
图 7
折痕
式中:
将各边长代入式(11),可得
从式(14)可知,
图 8
图 8
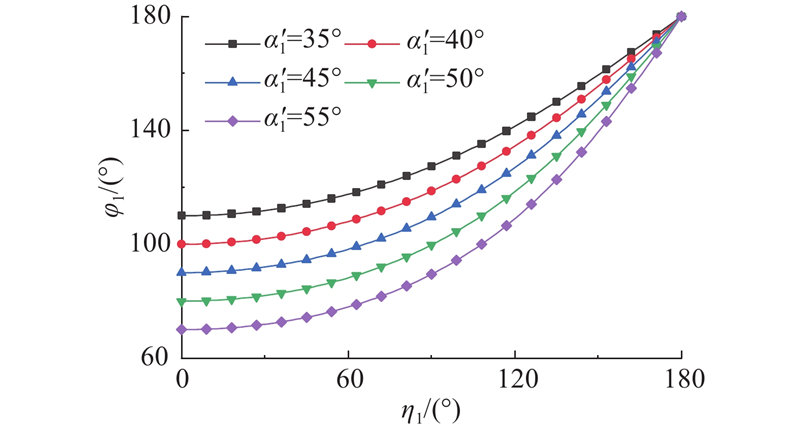
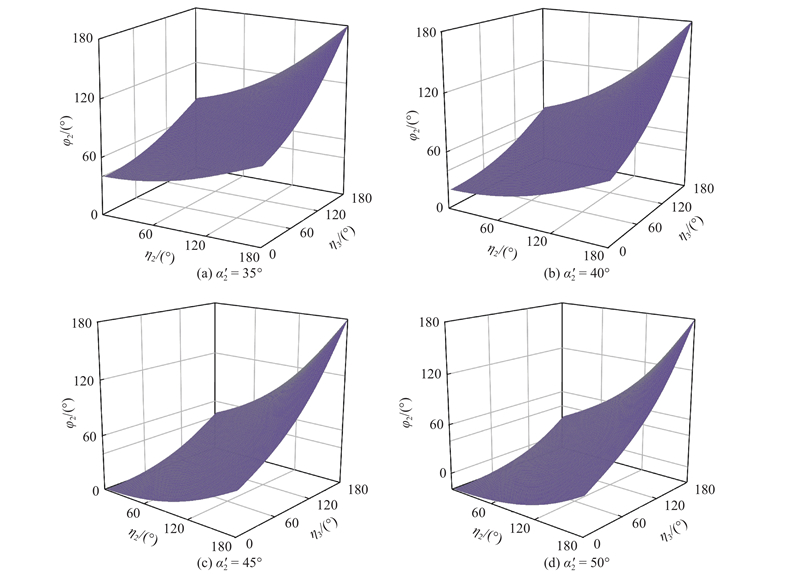
不同三浦折纸的折痕设计夹角下,折痕
Fig.8
Variation of angles between creases
2.2. 六折痕折纸单元的理论模型
如图9(a)所示为机器人使用的六折痕折纸单元,其整体为6个三角形折面组成的矩形,矩形的边长分别为
图 9
式中:
其中,
将式(19)~(24)代入式(16)~(18),可得
将
从式(28)可知,
图 10
图 10
不同六折痕折纸折痕设计夹角下,折痕
Fig.10
Variation of angles between creases
2.3. 折纸步行足的等效运动模型
在面对称假设下,组成折纸机器人的三浦折纸和六折痕折纸单元的轴线处折痕都可以等效为平面连杆,且连杆之间的夹角与折面夹角相关(见式(14)、(28)). 在机器人折面运动对称这一假设约束条件下,单足运动自由度为2. 如图11(a)所示为机器人一对折纸腿的折叠构型,以二面角
图 11
图 11 一对折纸腿的空间构型及单腿折痕等效连杆
Fig.11 Spatial configuration of pair of origami legs and equivalent connecting rod with single leg crease
以
三浦折纸和六折痕折纸的轴线折痕夹角仅与折痕设计夹角及折面夹角相关,与折面形状无关,故连杆夹角
2.4. 足端运动范围的分析
由式(29)~(33)可知,折纸机器人右腿足端位移与
图 12
3. 折纸机器人的三维模型及样机
3.1. 折纸机器人厚板模型
楔形面板(tapered panel)是基于球面机构的零厚度折纸机构增厚方法. 如图13所示,通过在零厚度折纸机构两侧均匀地添加厚度,去除面板中影响折叠运动的部分,可得相应的厚板模型. 利用该方法得到的厚板折纸的运动学模型与零厚度折纸为球面机构,且由于其关节位于折板中间,仅一侧有楔形缺口,使折板仅能向一侧转动,避免了折面反折引起的折纸机构多解的问题. 经楔形技术处理的带厚度折面保留了一部分实体使相邻折面不能完全折叠,利用该方法得到的厚板折纸模型最大折叠角小于180°.
图 13
根据楔形面板方法,增加该机器人各折面的厚度,去除物理干涉部分后,可以得到该机器人一对足的厚板模型,如图14所示. 该厚板模型中折板的最大转动范围为
图 14
3.2. 折纸机器人模型
为了避免折板之间的物理干涉,对每块折板均使用楔形面板技术进行处理,随后在各折板之间以铰链结构实现连接,由减速电机和齿轮驱动折板转动,得到如图15所示的机器人三维模型. 该机器人主体由30块多边形折板及1块不规则的机身组成,各折板之间由铰链结构进行连接,3对足通过铰链结构与机身上的6个支座连接.
图 15
当该机器人完全展平时,机身宽度为620 mm,厚度仅为20 mm. 当机器人折叠时,由于楔形面板技术的局限性,使其不能完全折叠,折板实际的转动范围为
该机器人以编码电机为驱动原件,如图16所示,编码电机经传动齿轮使得驱动折板发生转动,相邻折板之间由铰链进行约束,由此带动机器人腿部各折板运动. 通过添加折面运动对称约束条件,得出该折纸机器单腿可以通过2个自由变量控制运动. 实际上通过2个对称分布,转动同步的电机实现这一约束条件,实际驱动单元为如图16所示的3个呈Y状分布的电机. 由于对称分布的2个电机转动角度相同,此时只需要2组控制信号控制一条腿部运动,大大减少了控制信号的数量. 此时,机器人腿部折面运动对称,可以将机器人腿部运动等效为平面连杆,降低足端运动的求解难度. 当处于两侧的驱动电机转角相等时,两侧驱动折板运动对称,该机器人的足端位置可由式(29)、(30)得出.
图 16
考虑到机器人最大驱动力矩的限制,取折板的转动范围为
图 17
4. 机器人运动控制
4.1. 足端轨迹规划
在机器人行走过程中,步行足由抬起、摆动、落下到再次抬起为一个运动周期,其中机器人足端着地开始到再次抬腿离地期间,腿的相位变化过程称为支撑相. 机器人足端离地到再次落地期间,腿的相位变化过程称为摆动相. 支撑相决定机器人运动的平稳性,摆动相决定机器人的步幅和跨越障碍物时的抬腿高度. 为了保证机身的平稳运动,机器人支撑相的足端轨迹一般为直线,摆动相为连接该线段两端的曲线. 设计的仿螃蟹折纸机器人通过控制机器人的折面转动来实现足端运动的控制,由于两侧步行足运动之间存在耦合关系,传统的足端轨迹曲线设计难以适用,须结合实际运动模型对足端运动轨迹进行设计.
利用楔形面板技术得到的厚板机器人可以等效为平面连杆,结合3.2节的分析可知,此时的折面夹角
取
图 18
图 18
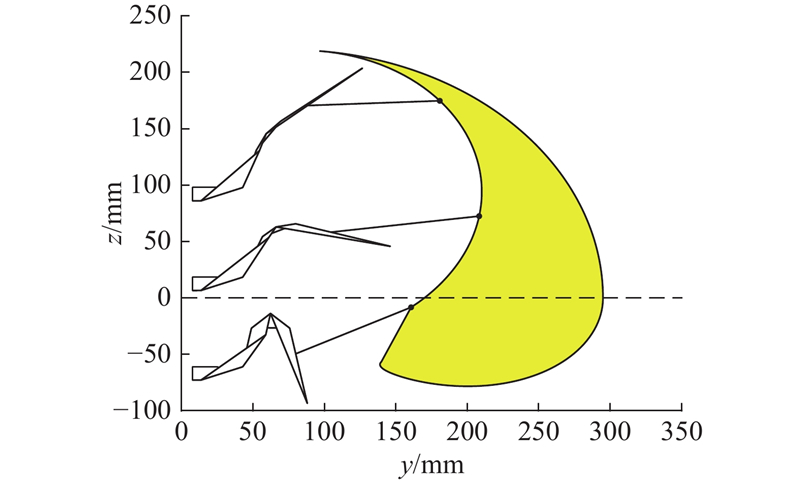
二面角
Fig.18
Corresponding foot trajectory as dihedral angle
由于机器人一对步行足之间由2块刚性折面相连,
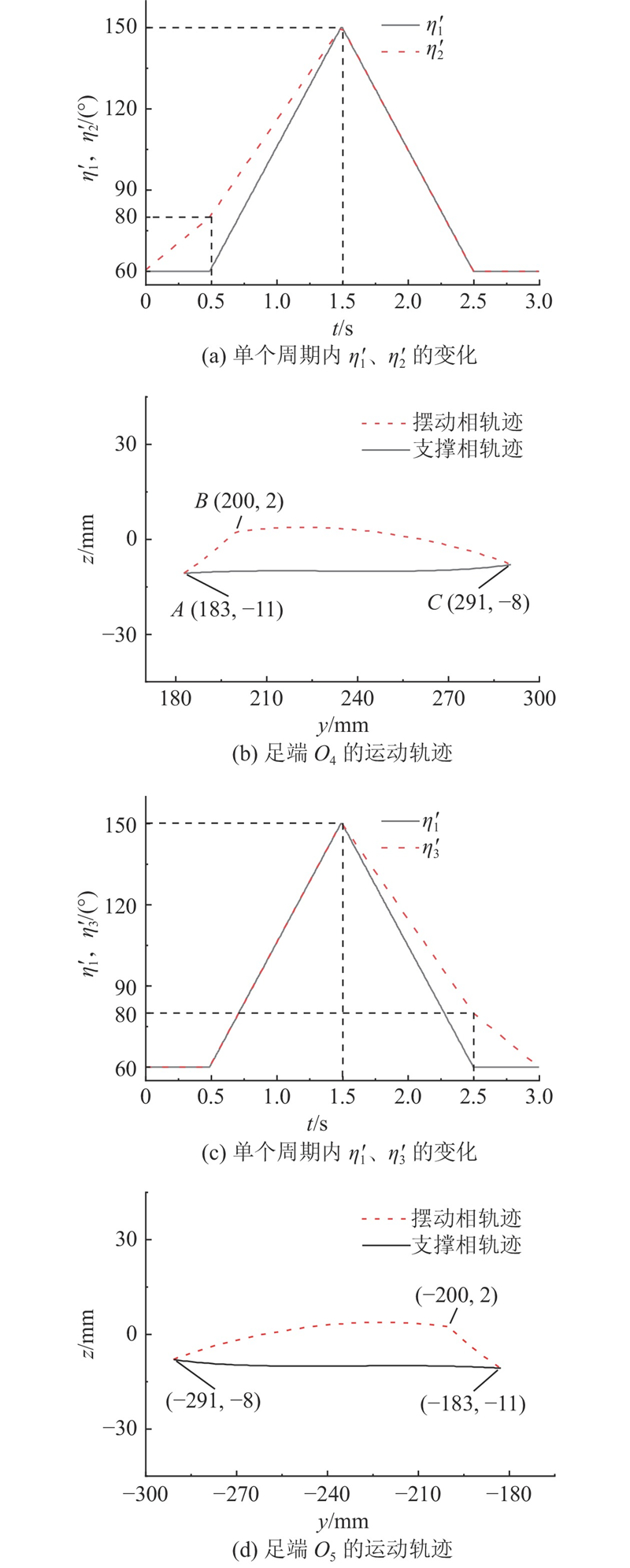
如图19(a)所示,在初始时刻,
图 19
图 19 单个周期内折纸腿折面夹角变化与足端轨迹
Fig.19 Change of angle of folding surface of origami leg and trajectory of foot end in single period
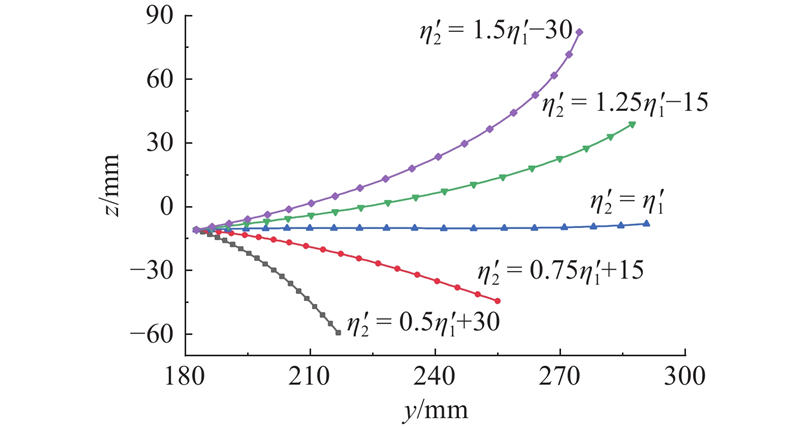
机器人一对步行足的运动可由
图 20
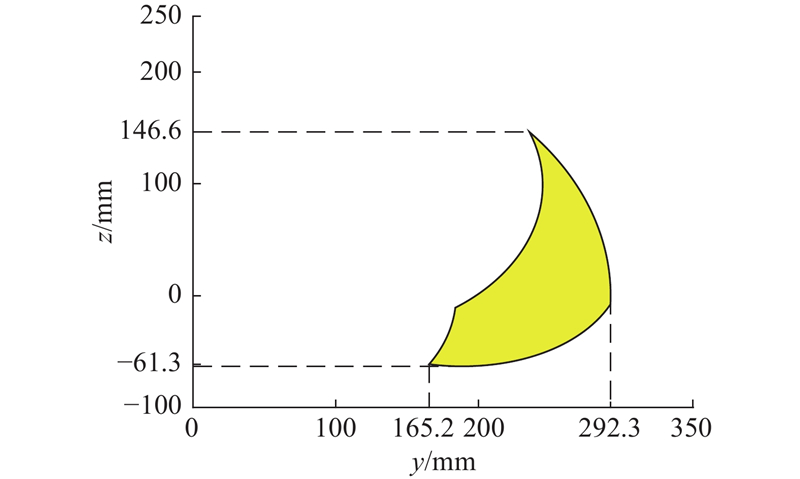
图 20 减小机器人步距后的足端轨迹
Fig.20 Trajectory of foot after reducing robot’s step length
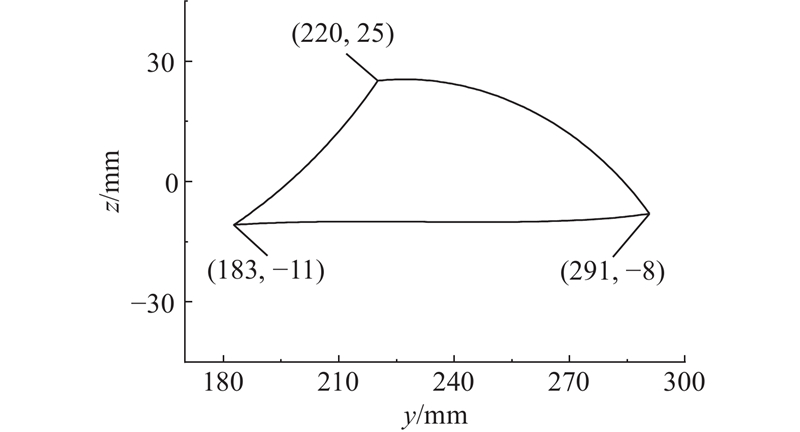
图 21
图 21 增大机器人抬腿高度后的足端轨迹
Fig.21 Trajectory of foot after increasing robot’s leg lifting height
该机器人共有6条腿,为了实现机器人的平稳移动,需要这6条腿的运动相互协调,因此还需要对机器人的运动步态进行分析.
4.2. 横向三角步态
机器人的3对腿与身体通过铰链连接在一起,假设每对腿的运动对称面都与机身垂直,此时该六足机器人的简化运动模型如图22所示,按顺序对6条腿进行编号.
图 22
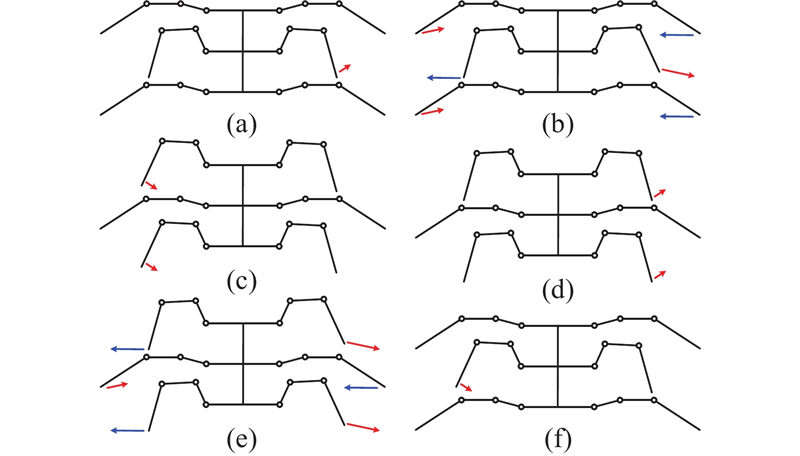
如图23(a)~(f)所示为机器人横向行走示意图. 在初始状态下,6条腿均处于支撑状态. 当机器人向右横向移动时,⑤号腿预先抬起(见图23(a));随后①、③号腿抬起与⑤号腿一同在空中向右摆动(见图23(b)),②、④、⑥号腿足端与地面接触并向左运动,推动机身右移. 由于该机器人的足端运动特性,⑤号腿率先落地,此时①、③号腿仍处于摆动相,其余各腿静止并等待①、③号腿下落(见图23(c)). 待①、③号腿落下后,此时6条腿又一次处于支撑状态. 以①、③、⑤号腿为一组,②、④、⑥号腿为一组,图23(d)~(f)中,2组腿实现了支撑相和摆动相的交替. 图23(f)中,待⑤腿落下后,机器人六足重回到23(a)所示的运动姿态. 按上述步骤循环往复,可以实现该六足折纸机器人的横向三角步态运动. 该折纸机器人一对步行足的运动存在耦合关系,为了协调机器人三对足的运动,在运动步态中添加了等待相邻步行足预先抬起与下落的步态,如图23(a)、(c)、(d)、(f)所示,因此该机器人整体的完整的步态周期为4 s.
图 23
图 24
图 24 六足机器人的横向三角步态仿真
Fig.24 Simulation of lateral triangular gait of hexapod robot
图 25
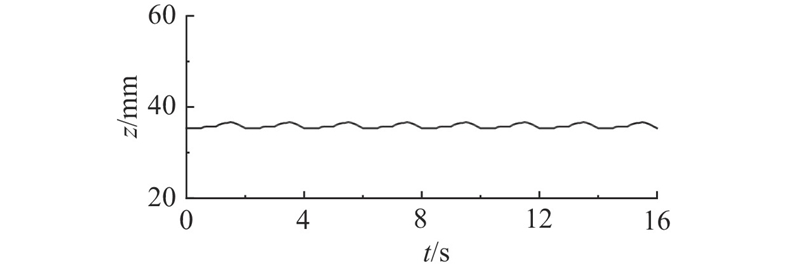
图 25 行走过程中机身垂直地面方向位移
Fig.25 Body moves vertically relative to ground during walking
4.3. 折纸机器人的试验样机与行走试验
图 26
表 1 六足折纸机器人的设计参数
Tab.1
| 参数 | 数值 | 参数 | 数值 | |
| 75 | α1/ (°) | 30 | ||
| 55 | α2/ (°) | 45 | ||
| 70 | α3/ (°) | 45 | ||
| 110 | — | — |
机器人的驱动折板上有3D打印的齿轮结构,通过电机带动齿轮旋转来实现折板的转动,进而控制整条腿的运动. 该机器人的电路系统由电源模块、STM32主控板、电机驱动板、减速编码电机组成. 电源模块为微控制器及电机驱动板供电,微控制器经过电机驱动板控制电机转动. 当电机转动时,轴端的霍尔编码器向微控制器发送脉冲信号,通过脉冲计数确定电机转动角度,由此实现对折板转动角度的精确控制.
相较于一般折纸机器人,该折纸机器人的运动更加灵活,可以通过改变机器人控制信号,改变机器人足端的抬腿高度和跨度. 如图27(a)、(b)所示分别为低抬腿小步幅和高抬腿大步幅运动时的足端轨迹.
图 27
各折纸腿在STM32主控板的控制下,以三角步态实现整体的左右移动,如图28所示. 试验结果表明,各足可以按照设计的运动方式横向移动,平均移动速度约为0.03 m/s. 由于足端与地面的接触面积较小,运动时足端与地面会发生相对滑动;由于加工及安装过程中存在误差,机器人折板的实际转动角度与理想转角之间存在一定的误差,导致机器人的实际运动路线略有偏移. 在实际制作过程中,机器人的机械结构误差难以完全避免,后续研究过程中将为机器人加装视觉传感器,若机器人运动发生偏离,则改变运动步态以调整运动方向. 在该机器人的运动过程中,电机转动加速度存在突变,这对机器人运动的平稳性及精确性都有很大影响,我们将进一步优化机器人的运动控制算法,以避免电机加速度突变,使机器人运动更加精确和平稳.
图 28
5. 结 论
(1) 耦合三浦折纸和六折痕折纸2种不同的折纸机构,设计复合折纸腿. 利用D-H闭环方程计算该折纸腿的自由度,得出对称假设下机器人单腿运动自由度为2.
(2) 将多顶点折纸腿的轴线折痕等效为连杆,顶点等效为关节,机器人腿部运动等效为平面连杆运动,简化了机器人足端位置的求解,并基于该模型得到机器人足端的理论运动范围.
(3) 利用楔形面板方法设计机器人的实体厚板模型,结合机器人厚板模型设计机器人的足端运动轨迹. 通过步态规划使机器人实现了横向三角步态运动,机器人样机运动的试验结果与三维模型运动的仿真结果基本吻合.
运动试验结果表明,该机器人运动过程中会发生路线偏移的情况,且缺乏相应的反馈调节手段,在控制算法方面存在较大的改进空间.
参考文献
Symmetric waterbomb origami
[J].
折纸及其折痕设计研究综述
[J].
A review of origami and its crease design
[J].
折纸结构和折纸超材料动力学研究进展
[J].
Advances in the dynamics of origami structures and origami metamaterials
[J].
折纸运动学综述
[J].
Review on origami kinematics
[J].
Mobility in metamorphic mechanisms of foldable/erectable kinds
[J].DOI:10.1115/1.2829470 [本文引用: 2]
Kinematics and mobility analysis of carton folds in packing manipulation based on the mechanism equivalent
[J].DOI:10.1243/095440602760400931
Matrix representation of topological changes in metamorphic mechanisms
[J].DOI:10.1115/1.1866159 [本文引用: 2]
广义Waterbomb折纸管的刚性折叠运动特性
[J].DOI:10.3901/JME.2020.19.143 [本文引用: 1]
Rigid folding of generalized Waterbomb origami tubes
[J].DOI:10.3901/JME.2020.19.143 [本文引用: 1]
Research on programmable spatial capture mechanism and its motion characteristics based on origami principle
[J].DOI:10.1016/j.mechmachtheory.2022.105179 [本文引用: 2]
A method for building self-folding machines
[J].DOI:10.1126/science.1252610 [本文引用: 2]
Programmable origami strings
[J].
Spotlight on origami robots
[J].DOI:10.1126/scirobotics.aat0938
折纸机器人
[J].DOI:10.1360/N092018-00213 [本文引用: 1]
Origami robots
[J].DOI:10.1360/N092018-00213 [本文引用: 1]
Hierarchical kinematic design of foldable hexapedal locomotion platforms
[J].DOI:10.1115/1.4030468 [本文引用: 1]
基于折纸机构设计的新型行走机器人
[J].
Novel walking robot based on the design of origami mechanism
[J].
Thick-panel origami cube
[J].DOI:10.1016/j.mechmachtheory.2021.104411 [本文引用: 1]
A methodology for thick-panel origami pattern design
[J].DOI:10.1016/j.mechmachtheory.2023.105423
Thick rigidly foldable structures realized by an offset panel technique
[J].
Origami of thick panels
[J].DOI:10.1126/science.aab2870 [本文引用: 1]
微型六足仿生机器人及其三角步态的研究
[J].
Research on miniature hexapod bio-robot and its tri pod gait
[J].