目前常用的全局路径规划算法包括基于采样的快速扩展随机树方法(RRT)[5]、概率路线图(PRM)[6]、基于搜索的Dijkstra[7]、A*算法[8]、D*算法[9]以及基于智能仿生的蚁群算法[10]、遗传算法[11]和粒子群算法[12]等,局部路径规划算法包括动态窗口法(dynamic window approach, DWA)[13]、模糊逻辑法[14]和人工势场法[15]等. A*算法是被广泛应用于移动机器人路径规划的经典算法. 在实际应用中,传统的A*算法存在遍历节点多、拐点多及路径不平滑等问题,这些问题降低了机器人的运动效率. 近年来,DWA成为了较流行的局部路径规划算法,具有模型简单、路径平滑、实时避障等诸多优点. 由于缺乏引导性,DWA在大尺度复杂环境中容易受局部最优解的影响,甚至可能无法到达目标点[16].
为了弥补传统A*和DWA算法在路径规划问题中的不足,许多学者进行了各种不同层面的改进. 陈娇等[17]提出关键折点提取算法,剔除全局路径上的冗余节点,结合DWA对每段局部路径进行优化,提升了路径的安全性和平滑性,但该算法的遍历节点数和运行时间没有得到优化. 迟旭等[18]提出改进的A*算法,该算法采用提取关键点的策略,提升了平滑性和安全性,然而该算法存在路径不够平滑、遍历节点多的问题. 劳彩莲等[19]提出扩展搜索邻域并优化搜索角度,使得路径更加平滑,融合改进后的A*算法与DWA算法,以保证全局最优,然而由于没有区分已知障碍物和未知动态障碍物,在动态路径规划中容易相互影响,导致动态避障的灵敏度降低. 张志文等[20]提出用Floyd算法优化A*算法的优化方法,融合改进后的A*算法与DWA算法,解决了A*算法遍历节点多、拐点多、不平滑等问题,但未在动态环境下验证方法的有效性. Li等[21]利用移动机器人的尺寸与障碍物的自由空间关系改进DWA算法,但在复杂环境中,该方法可能会导致机器人频繁启停或停止运动. 程传奇等[22]采用关键点选取策略优化改进A*算法的启发函数,融合DWA算法,但该方案未在动态环境下进行验证.
上述已有方法取得了有益效果,但存在遍历节点多、存在冗余点、拐角大和路径不平滑、适应性差、避障灵敏度低等问题. 针对上述问题,本文将环境信息引入A*算法的评价函数中,对启发式函数的权重进行自适应调整. 引入冗余点删除策略和Floyd算法,消除冗余节点并减少遍历节点和拐点,使得路径更加平滑. 提取改进A*算法规划路径的关键点,作为DWA算法的中间引导点,对障碍物进行分类处理,自适应调整速度,实现改进A*算法和DWA算法的融合,使得搜索路径能够自适应复杂环境的变化,提高了算法的搜索效率和灵活性.
1. 改进A*算法
1.1. 传统A*算法
A*算法基于启发式函数进行搜索引导,通过选取最小代价估值的方式规划(搜索)合理路径. 该算法由评价函数
式中:
通常,传统A*算法会采用Manhattan距离、Euclidean距离和Chebyshev距离作为定义启发函数的方式,3种启发函数距离的示意图如图1所示.
图 1
设当前节点
1.2. 改进A*算法
针对传统A*算法存在的遍历节点多、存在冗余点、拐角大和路径不平滑等问题,对传统A*算法进行以下2个方面的改进. 1)引入环境信息,根据环境信息调整启发函数的权重,设计更贴近真实代价的启发函数,以提高搜索效率. 2)结合Floyd算法,采用冗余点删除策略,减少拐点数量,提高路径平滑度.
1.2.1. 自适应评价函数
传统算法的
考虑潜在后继节点到目标点的估计代价,计算当前节点和目标点之间的路径上出现障碍物的数量
式中:
将环境障碍物的概率引入评价函数
当前点与目标点之间的障碍物较少时,应加大
1.2.2. 路径平滑优化策略
为了避免A*算法规划出的路径中包含冗余点和不必要的转折点,影响机器人控制的效果,引入冗余点删除策略和Floyd算法对路径进行二次优化. 该策略的实施步骤如下.
1)从规划路径的第2个节点开始对当前节点进行判断,判断依据是当前节点是否和前一个节点以及前一个节点的父节点在同一直线上且未经过障碍物. 若是,中间所有节点均是冗余点,则将其删除;否则,前一节点为必经节点,将其列为关键转折点,并更新路径.
2)反复执行此操作,遍历所有路径节点,直至不存在冗余转折点,最终得到只包含起点、转折点和终点的路径,完成第一次优化.
3)利用Floyd算法对路径进行二次优化,进一步消除冗余节点,使得规划路径更加平滑,提高机器人的运动效率.
路径平滑优化策略的过程如图2所示. 实验结果表明,路径平滑优化策略的算法只包括起点、目标点和转折点,能够有效地减少路径长度和冗余点,与传统的A*算法相比,效果显著.
图 2
2. 随机避障动态窗口法(ROA-DWA)
针对传统动态窗口法缺乏全局引导,易陷入局部最优,动态障碍物和静态障碍物的冲突距离同等对待、避障灵敏度低等问题,对传统DWA算法的评价函数进行改进,使其结合全局路径信息,根据环境的复杂程度自适应地调整速度. 对障碍物进行分类处理,使已知障碍物对路径的影响最小化,从而使机器人平稳、快速地到达目标点,避免与障碍物发生碰撞,能够以较大速度快速避障的同时,提高机器人的安全性.
2.1. 机器人运动学模型和机器人速度采样
在DWA算法中,需要采样机器人在一个区域内的速度空间. 通过机器人的运动学模型,在采样周期内模拟机器人的运动轨迹. 假设机器人作匀速直线运动,那么速度空间中的线速度和角速度变化可以反映机器人的运动状态. 机器人的运动模型如下所示:
在利用DWA算法实现机器人路径规划和运动控制的过程中,采样速度空间中的多组速度被用于模拟机器人在一定时间间隔内的轨迹. 为了考虑实际的约束条件,对采样速度范围进行限制. 机器人的速度受多方面因素的影响,包括最大最小速度、电机性能及制动距离等.
1)移动机器人最大、最小速度约束.
机器人的采样速度应该控制在移动机器人最佳角速度和线速度区间内,则约束如下:
式中:
2)机器人电机加减速约束.
机器人的采样速度应考虑电机性能,应保证当前速度在最大减速度和最大加速度的可变范围内,则约束如下:
式中:
3)机器人安全距离约束.
为了保证机器人无碰撞到达目标点,在进行局部路径规划时,在机器人最大减速度的条件下,使得移动机器人在到达障碍物之前线速度和角速度均减速至0,则约束如下:
式中:
综上所述,动态窗口速度为
2.2. 改进的随机避障评价函数
在速度空间中,可以采集到多组运动轨迹,不同的运动轨迹可以规划出不同的路径. 设计评价函数,对多组轨迹进行评估,使得机器人选择最短且安全的路径. 设计的评价函数为
式中:
3. 改进A*与ROA-DWA融合算法
结合改进A*算法与ROA-DWA,以兼顾全局路径最优和局部避障能力,流程如图3所示. 使用改进的A*算法,规划出全局最优的节点序列. 利用路径平滑优化策略对路径进行优化,提取路径关键点作为ROA-DWA的中间引导点,进行局部路径规划. 融合算法根据环境复杂程度自适应地调整速度,对障碍物进行分类处理,使得已知障碍物对路径的影响最小化.这种方法综合了ROA-DWA的随机避障能力和改进A*算法的全局路径规划能力,实现了动态路径规划的全局最优性和局部避障能力,被应用在移动机器人的实时运动中.
图 3
4. 仿真实验验证
4.1. 改进A*算法的仿真实验
图 4
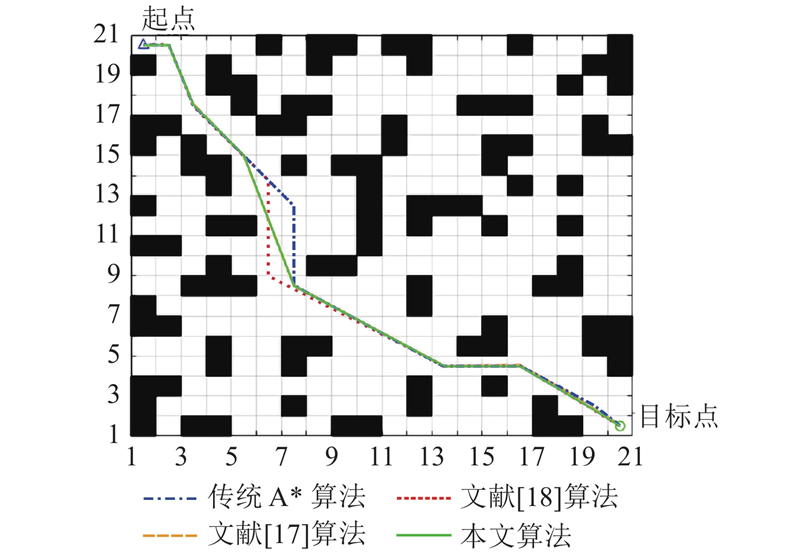
图 4 20×20栅格地图的仿真结果对比图
Fig.4 Comparison of simulation results for 20×20 raster map
图 5
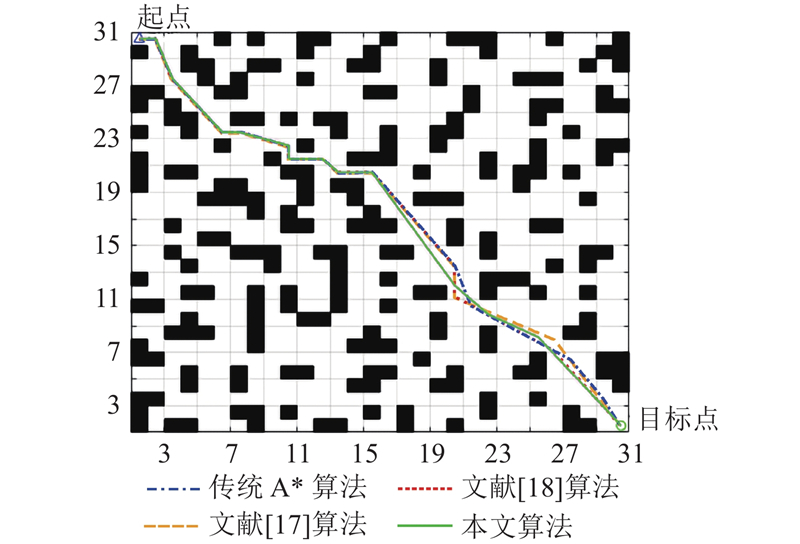
图 5 30×30栅格地图的仿真结果对比图
Fig.5 Comparison of simulation results for 30×30 raster map
图 6
图 6 50×50栅格地图的仿真结果对比图
Fig.6 Comparison of simulation results for 50×50 raster map
表 1 全局路径规划的仿真数据
Tab.1
| 地图尺寸 | 算法 | L/m | T/s | N | P | |
| 20×20 | 传统A*算法 | 29.796 | 0.528 | 149 | 7 | 265.45 |
| 文献[17]算法 | 29.376 | 0.325 | 149 | 7 | 254.85 | |
| 文献[18]算法 | 29.583 | 0.281 | 121 | 8 | 265.45 | |
| 本文改进算法 | 29.376 | 0.146 | 113 | 7 | 254.85 | |
| 30×30 | 传统A*算法 | 44.556 | 0.966 | 301 | 13 | 627.67 |
| 文献[17]算法 | 44.368 | 0.743 | 301 | 12 | 652.81 | |
| 文献[18]算法 | 44.274 | 0.677 | 215 | 12 | 559.44 | |
| 本文改进算法 | 44.266 | 0.183 | 195 | 11 | 544.32 | |
| 50×50 | 传统A*算法 | 80.636 | 3.099 | 1087 | 25 | 1543.96 |
| 文献[17]算法 | 79.868 | 2.853 | 1087 | 25 | 1524.61 | |
| 文献[18]算法 | 79.374 | 1.573 | 544 | 28 | 1478.82 | |
| 本文改进算法 | 77.784 | 1.379 | 499 | 25 | 1406.98 |
从表1可知,通过改进A*算法的评价函数,引入环境信息,在不同地图尺寸下提高了搜索效率,与传统A*算法、文献[17]算法和文献[18]算法相比,都表现出了明显的性能优势. 在路径长度方面,本文算法相较于传统A*算法、文献[17]算法和文献[18]算法分别平均减少了69.64%、60.70%、44.45%. 在遍历节点数方面,该算法相较于传统A*算法、文献[17]算法和文献[18]算法分别平均减少了37.82%、37.82%、8.06%;在转折点数方面,该算法相较于传统A*算法、文献[17]算法和文献[18]算法分别平均减少了9.73%、2.78%、10.52%. 在累计转角方面,该算法相较于传统A*算法、文献[17]算法和文献[18]算法分别平均减少了8.29%、7.70%、3.38%,且随着地图的扩大,传统A*算法的性能受到的影响更大,本文算法由于根据环境信息改变启发函数的权重,效率更高且更平滑,在大型地图中具有更好的优势. 利用本文所提出的改进A*算法,有效地提高了路径规划准确性和效率,验证了本文算法评价函数的可行性和有效性.
4.2. 改进A*算法与ROA-DWA融合仿真实验
为了验证本文融合算法既能够适应静态环境,又能够很好地适应动态环境,在30×30的栅格地图中进行如下实验. 在A*算法规划路径时,随机添加了4个未知静态障碍物;在仿真环境中添加了1个动态未知障碍物. 融合算法仿真实验的评价函数的各项参数为
表 2 机器人运动学参数
Tab.2
| 参数 | 数值 | 参数 | 数值 | |
| vmax/(m·s−1) | 2.0 | ωmax/( | 40.0 | |
| amax/( | 0.4 | βmax/( | 100.0 | |
| vres/( | 0.01 | ωres/( | 1.0 | |
| Tres/s | 0.1 | Tpred/s | 3.0 |
4.2.1. 静态环境下的仿真
在静态已知和静态未知的环境下,为了验证提出的融合算法的可行性和有效性,在20×20的地图中进行仿真实验. 静态环境下的仿真结果如图7所示. 图中,虚线为全局路径,并加入静态未知障碍物;实线为利用融合算法生成的路径.
图 7
本文的融合算法提取了改进A*算法路径上的关键点作为ROA-DWA算法的中间引导点,对已知和未知障碍物进行分类,避免已知障碍物对路径的影响,尽量靠近已知静态障碍物,远离未知静态障碍物,使得所规划的路径平滑度、安全性更高,更符合机器人运动特性.
4.2.2. 动态环境下仿真
图 8
表 3 融合算法仿真数据
Tab.3
从表3可知,文献[17]的融合算法和文献[18]的融合算法未对障碍物进行分类处理,尽管可以避开静态未知障碍物并到达终点,但遇到动态未知障碍物时,机器人无法处理,容易与动态未知障碍物发生碰撞,避障灵敏度低. 改进A*-ROA-DWA融合算法的路径长度相较于文献[17]融合算法和文献[18]融合算法分别增加了0.39%、0.7%,是由于改进A*-ROA-DWA融合算法对动态障碍物有着较大的冲突预判距离,当遇到动态未知障碍物时,可以避开动态障碍物. 由于改进A*-ROA-DWA融合算法提取改进A*算法规划路径的关键点作为ROA-DWA算法的中间引导点,对障碍物进行分类处理,可以根据路径弯曲程度自适应地调节速度,运行时间分别减少了36.24%、29.96%,平均曲率分别减少了23.81%、15.79%. 本文融合算法解决了传统融合算法缺乏全局引导、将机器人与动态障碍物和静态障碍物的冲突距离同等对待、安全性低等问题,使得机器人能够平稳到达目标点的同时提升了安全性.
采用汉明距离[23]来量化环境复杂度,环境复杂度越高,环境越复杂. 环境复杂度越高,则机器人运行姿态角度变化越大. 汉明距离的表达式为
式中:
图9给出改进A*-ROA-DWA融合算法在动态环境下设置不同数量的未知静态障碍物的机器人状态变化. 图中,v为线速度,
图 9
从图9可知,当机器人检测到未知静态障碍物(控制节点个数为100~200和200~300)时,机器人有明显的降速过程. 改进A*ROA-DWA融合算法可以根据环境复杂程度自适应地调节速度,转弯时提前减速,平直路径且无障碍物时速度接近2
综上所述,该算法解决了A*算法和动态窗口法所规划的路径平滑度低、不符合机器人运动特性、易陷入局部最优、避障灵敏度低等问题,使得所规划的路径更平滑,安全性更高,更符合机器人的运动特性.
5. 实验验证
为了验证本文算法在实际应用中的有效性,选取Dashgo B1移动机器人平台进行实验验证. 为了方便调试和机器人的自主导航,采用64位ubuntu16.04操作系统和ROS系统,在局域网内完成主机与PC端的网络通讯,采用Gmapping算法对实验室环境进行地图构建. 移动机器人的实验参数如下:最大线速度为0.6
图 10
图 10 融合算法的路径规划实验设备与实验场地
Fig.10 Experimental equipment and laboratory space of path planning for fusion algorithm
图 11
表 4 传统融合算法和本文融合算法性能的对比
Tab.4
| 算法 | L/m | T/s | K/m−1 |
| 传统融合算法 | 7.269 | 28.469 | 0.23 |
| 本文融合算法 | 7.176 | 25.724 | 0.21 |
6. 结 论
(3)本文融合算法相较于传统融合算法,所规划路径的路径长度减小了1.28%,运行时间减少了9.64%,平均曲率减小了8.70%. 这表明本文融合算法所规划的路径更加平滑,在确保全局最优的前提下,能够及时避开出现在环境中的动态和静态障碍物,提高了机器人在复杂环境中的适应能力. 通过仿真和实验验证,验证了本文算法的可行性和有效性.
参考文献
高温混合障碍空间中的移动机器人路径规划
[J].
Path planning for mobile robots in high-temperature hybrid obstacle space
[J].
Multiobjective approach for robot motion planning in search tasks
[J].
基于改进蚁群算法的移动机器人路径规划研究
[J].
Research on path planning of mobile robots based on improved ant colony algorithm
[J].
无碰撞检测RRT~*的移动机器人运动规划方法
[J].
A motion planning method for mobile robots with collision-free detection RRT~*
[J].
Probabilistic roadmaps for path planning in high-dimensional configuration spaces
[J].DOI:10.1109/70.508439 [本文引用: 1]
Fuzzy Dijkstra algorithm for shortest path problem under uncertain environment
[J].DOI:10.1016/j.asoc.2011.11.011 [本文引用: 1]
基于改进A~*算法的室内移动机器人路径规划
[J].
Path planning for indoor mobile robots based on improved A~* algorithm
[J].
移动机器人路径动态规划有向D~*算法
[J].
Path dynamic planning for mobile robot based on directed D~* algorithm
[J].
改进变步长蚁群算法的移动机器人路径规划
[J].
Improved variable-step ant colony algorithm for mobile robot path planning
[J].
Matrix-binary codes based genetic algorithm for path planning of mobile robot
[J].
Multi-objective path planning for unmanned surface vehicle with currents effects
[J].
基于改进的A~*算法与动态窗口法的移动机器人路径规划
[J].
Path planning for mobile robots based on improved A~* algorithm and dynamic window method
[J].
Analysis and use of fuzzy intelligent technique for navigation of humanoid robot in obstacle prone zone
[J].DOI:10.1016/j.dt.2018.03.008 [本文引用: 1]
Mobile robot path planning using membrane evolutionary artificial potential field
[J].
基于改进动态窗口法的户外清扫机器人局部路径规划
[J].
Local path planning for outdoor sweeping robots based on improved dynamic window method
[J].
改进A~*和动态窗口法的移动机器人路径规划
[J].
Improved A~* and dynamic window method for mobile robot path planning
[J].
基于改进A~*算法与动态窗口法融合的机器人随机避障方法研究
[J].
Research on randomized obstacle avoidance method for robots based on the fusion of improved A~* algorithm and dynamic window method
[J].
基于改进A~*与DWA算法融合的温室机器人路径规划
[J].DOI:10.6041/j.issn.1000-1298.2021.01.002 [本文引用: 1]
Greenhouse robot path planning based on improved A~* and DWA algorithm fusion
[J].DOI:10.6041/j.issn.1000-1298.2021.01.002 [本文引用: 1]
改进A*算法的机器人路径规划研究
[J].
Improved A* algorithm for robot path planning
[J].
Obstacle avoidance for mobile robot based on improved dynamic window approach
[J].
融合改进A~*算法和动态窗口法的全局动态路径规划
[J].
Fusion of improved A~* algorithm and dynamic window method for global dynamic path planning
[J].
基于环境复杂度的移动机器人变步长RRT路径规划算法与仿真研究
[J].
Research on variable step size RRT path planning algorithm and simulation of mobile robot based on environment complexity
[J].