3-PUU并联机构的运动学分析与验证

doi:10.3785/j.issn.1006-754X.2024.03.157

3-PUU并联机构的运动学分析与验证

陈明方^,^,, 黄良恩, 张永霞, 姚国一

昆明理工大学机电工程学院，云南昆明 650500

Kinematics analysis and validation of 3-PUU parallel mechanism

CHEN Mingfang^,^,, HUANG Liangen, ZHANG Yongxia, YAO Guoyi

Faculty of Mechanical and Electrical Engineering, Kunming University of Science and Technology, Kunming 650500, China

收稿日期: 2023-04-25 修回日期: 2023-06-25

基金资助:

国家自然科学基金资助项目. 51965029
国家重点研发计划项目. 2018YFB1306103

Received: 2023-04-25 Revised: 2023-06-25

作者简介 About authors

陈明方（1975—），男，湖北黄冈人，教授，博士生导师，博士，从事机器人控制算法研究，E-mail:mfchen_robot@126.com，https://orcid.org/0000-0002-3323-8168 , E-mail：mfchen_robot@126.com

摘要

为提升少自由度并联机构设计的效率和准确性，针对自主设计的3-PUU并联机构进行了理论分析和实验研究。首先，利用螺旋理论和修正的Kutzbach-Grubler公式分析了并联机构的自由度；同时，解算了并联机构的运动学正反解和雅可比矩阵，并基于雅可比矩阵分析了其约束奇异和运动奇异。然后，利用极限边界搜索法分析了并联机构的工作空间，并以雅可比矩阵条件数的倒数作为局部灵巧度来构造全局灵巧度，分析了并联机构的运动性能。接着，搭建了并联机构的ADAMS/Simulink联合仿真模型，基于给定的动平台运动方程，通过仿真得到了动平台位置的仿真曲线及误差曲线。最后，利用并联机构样机、PC（personal computer，个人计算机）、STM32单片机、伺服电机及激光跟踪仪搭建了实验平台，并测定了并联机构动平台的位置曲线。结果表明，该并联机构具有较大的可达工作空间且其运动性能较好；通过对比理论结果与仿真结果可知，所构建的并联机构运动学模型正确；动平台位置的实测值与理论值之间存在一定误差，主要原因是并联机构存在机械误差以及控制系统精度不足，但实测曲线与理论曲线的变化趋势基本一致，进一步验证了并联机构运动学模型的正确性。研究结果可为少自由度并联机构的设计提供参考。

关键词： 3-PUU并联机构 ; 运动学分析 ; 奇异性 ; 工作空间 ; 灵巧度 ; ADAMS/Simulink仿真

Abstract

In order to improve the efficiency and accuracy of the design of parallel mechanisms with few degrees of freedom, the theoretical analysis and experimental research were conducted on a self-designed 3-PUU parallel mechanism. Firstly, the degree of freedom of the parallel mechanism was analyzed by using the screw theory and the modified Kutzbach-Grubler formula. At the same time, the forward and inverse kinematics solutions and Jacobian matrix of the parallel mechanism were solved, and its constraint singularity and kinematic singularity were analyzed based on the Jacobian matrix. Then, the workspace of the parallel mechanism was analyzed by using the limit boundary search method, and the global dexterity was constructed by taking the reciprocal of Jacobian matrix condition number as the local dexterity, so as to analyze the kinematic performance of the parallel mechanism. Next, an ADAMS/Simulink co-simulation model of the parallel mechanism was built. Based on the given motion equation of the moving platform, the simulation curves and error curves of the moving platform position were obtained through simulation. Finally, the experimental platform was built by using the parallel mechanism prototype, PC (personal computer), STM32 microcontroller, servo motor and laser tracker, and the position curves of the moving platform were measured. The results showed that the parallel mechanism had a large reachable workspace and good kinematic performance. By comparing theoretical results with simulation results, it could be concluded that the constructed kinematics model of the parallel mechanism was correct. There were some errors between the measured and theoretical values of the moving platform position, mainly due to the mechanical errors of the parallel mechanism and the insufficient precision of the control system. However, the variation trends of the measured curve and the theoretical curve were basically consistent, which further verified the correctness of the kinematics model of the parallel mechanism. The research results can provide reference for the design of parallel mechanisms with few degrees of freedom.

Keywords： 3-PUU parallel mechanism ; kinematics analysis ; singularity ; workspace ; dexterity ; ADAMS/Simulink simulation

PDF (8065KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

陈明方, 黄良恩, 张永霞, 姚国一. 3-PUU并联机构的运动学分析与验证. 工程设计学报[J], 2023, 30(6): 763-778 doi:10.3785/j.issn.1006-754X.2024.03.157

CHEN Mingfang, HUANG Liangen, ZHANG Yongxia, YAO Guoyi. Kinematics analysis and validation of 3-PUU parallel mechanism. Chinese Journal of Engineering Design[J], 2023, 30(6): 763-778 doi:10.3785/j.issn.1006-754X.2024.03.157

与串联机构相比，并联机构具有刚度大、稳定性好、精度高和运动负荷小等优点。近年来，并联机构已被广泛应用于车间生产线、分拣系统和食品包装设备等^[1]。

目前，国内外学者针对并联机构做了大量研究，主要包括自由度、运动学、工作空间、奇异性、动静力学分析以及运动误差补偿等^[2-6]。周毅钧等^[7]基于螺旋理论分析了3-SPS/PPS并联机构的构型和自由度。Fernandes等^[8]设计了一种医用3PUU并联机构，并解算了其运动学正反解和工作空间。Laski等^[9]对3UPU并联机构的运动学和工作空间进行了分析。孟庆梅等^[10]为了提高半对称三平移Delta-CU并联机构动平台的运动精度，提出了基于模糊神经网络的误差参数识别模型和误差补偿方法。李菊等^[11]基于虚功原理建立了2P4R并联机构的动力学模型，并完成了动力学分析。

并联机构运动学正反解的求解方法包括数值法和解析法^[12-13]。由于数值法的计算速度较慢且无法获得机构的封闭解，因此大多数学者采用解析法来进行求解分析^[14-15]。1990年，Innocenti等^[16]首次采用解析法获得了Stewart机构的运动学正解。张树梅等^[17]根据6-PTRT并联机构的几何约束关系，计算了其运动学反解，并通过坐标变换得到了运动学正解。刘秀莹等^[18]基于闭环矢量对球面并联机构的运动学正反解进行了分析，并利用遗传算法优化了其运动学参数。Zenebe等^[19]利用牛顿法解算了Stewart机构的运动学正解。

并联机构的奇异性主要包括2类：一类是由机构设计不合理导致的约束奇异，另一类是因机构存在不可达位置点而导致的运动奇异。奇异性的分析方法主要有数值法、几何法、解析法和雅可比矩阵法^[20-21]。黄胜军等^[22]利用Gosselin奇异性分析法，得到了冗余驱动并联机构的奇异位形，并基于数值法分析了2种奇异位形。为了分析3-RSR并联机构的运动奇异性，宛宇等^[23]提出了一种基于螺旋理论、几何代数和空间线性几何理论的新方法。

并联机构的工作空间主要是指可达工作空间，其求解方法主要有几何法、离散点法和数值法^[1]。刘秀莹等^[18]利用球面并联机构具有双球心的特点，分析了其动球心和动平台的可达工作空间。田海波等^[24]采用蒙特卡罗法解算了三构态变胞并联机构的工作空间，并基于工作空间的点云图计算了工作空间的体积。程颖等^[25]通过极限边界搜索法分析了六自由度微动并联机构的工作空间，并采用激光跟踪仪测定了其样机的实际工作空间，结果验证了该机构具有较大的工作空间。

少自由度并联机构类型多样，不同类型并联机构的动力传递形式不同，其适用场景也不同。为提升少自由度并联机构设计的效率和准确性，笔者以自主设计的3-PUU并联机构为研究对象，利用解析法分析其运动学正反解，并通过解算雅可比矩阵来分析其约束奇异和运动奇异。然后，在分析工作空间的基础上，以雅可比矩阵条件数的倒数作为灵巧度指标，分析并联机构的运动性能。接着，通过ADAMS/Simulink联合仿真来分析并联机构动平台位置、速度和加速度的变化情况^[26-29]，以验证所构建的运动学模型的正确性。最后，通过搭建实验平台来测定并联机构动平台的位置，以进一步验证其运动学模型的正确性。

1 3-PUU并联机构运动学理论分析

1.1　结构分析及建模

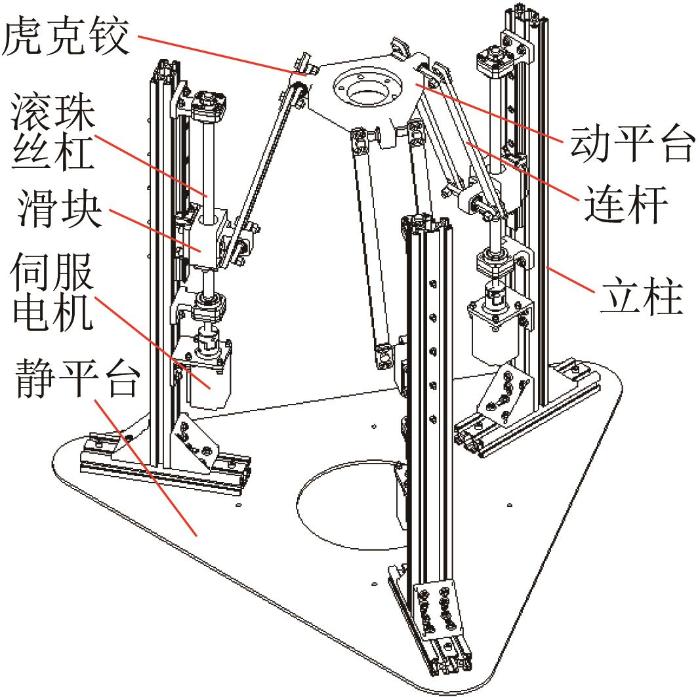
3-PUU并联机构的三维模型如图1所示。其中，静平台为并联机构的基体，与立柱、滚珠丝杠、连杆和动平台等构成并联机构的本体；连杆为平行四边形铰链，3根连杆对称布置，其在静平台上投影的夹角为120°；连杆两端通过虎克铰（U）分别与滑块、动平台连接，共形成3条相同的支链；滑块由滚珠丝杠驱动，形成移动副（P）；伺服电机的动力通过滚珠丝杠转动传递给滑块，滑块通过虎克铰将动力传递给连杆，最终连杆通过虎克铰将动力传递至动平台。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 3-PUU并联机构三维模型

Fig.1 Three-dimensional model of 3-PUU parallel mechanism

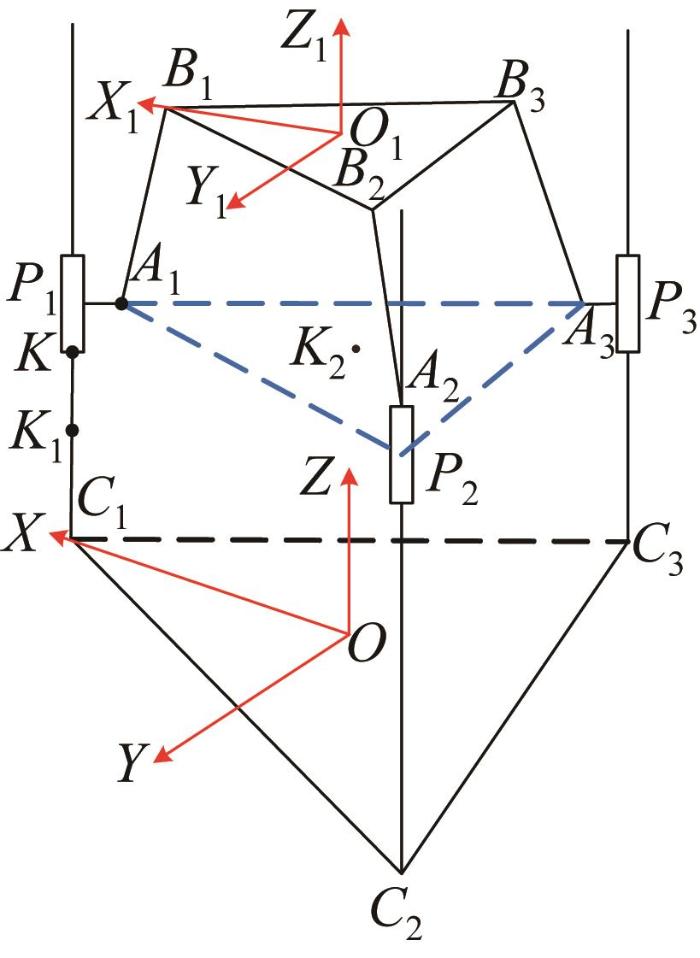
图2所示为3-PUU并联机构的运动学模型。为方便描述，将各滚珠丝杠的下端点均记为K₁，各滑块下端点均记为K，与滑块连接的虎克铰中心记为A_i (i=1, 2, 3)；B_i (i=1, 2, 3)为动平台顶点，且△B₁B₂B₃为正三角形，动平台外接圆的半径r=100 mm；C_i (i=1, 2, 3)为静平台顶点，P_i (i=1, 2, 3)为各滑块的中心。连杆长度l=350 mm，虎克铰转动范围为±60°，滑块的有效行程为200 mm，静平台与滚珠丝杠下端距离 $l_{C_{1} K_{1}}$ =335 mm；△A₁A₂A₃也为正三角形，其几何中心为K₂，其外接圆半径R=200 mm。在动、静平台的中心处分别建立动、静坐标系O₁-X₁Y₁Z₁、O-XYZ，其中：线段P₁A₁位于静坐标系中X轴的上方，且与X轴平行。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 3-PUU并联机构运动学模型

Fig.2 Kinematics model of 3-PUU parallel mechanism

1.2　自由度分析

为了确定3-PUU并联机构的自由度，先基于螺旋理论对其各支链进行分析，再利用修正的Kutzbach-Grubler公式求解自由度：

\{\begin{array}{l} F = d (n - j - 1) + \sum_{h = 1}^{j} f_{h} + v - ξ \\ d = 6 - λ \end{array}

(1)

式中：F为机构自由度，n为机构总构件数，d为机构运动空间自由度数，λ为公共约束，j为机构运动副数，f_h 为第h个运动副的自由度数，ξ为局部自由度数， $v$ 为去除公共约束后的冗余约束数。

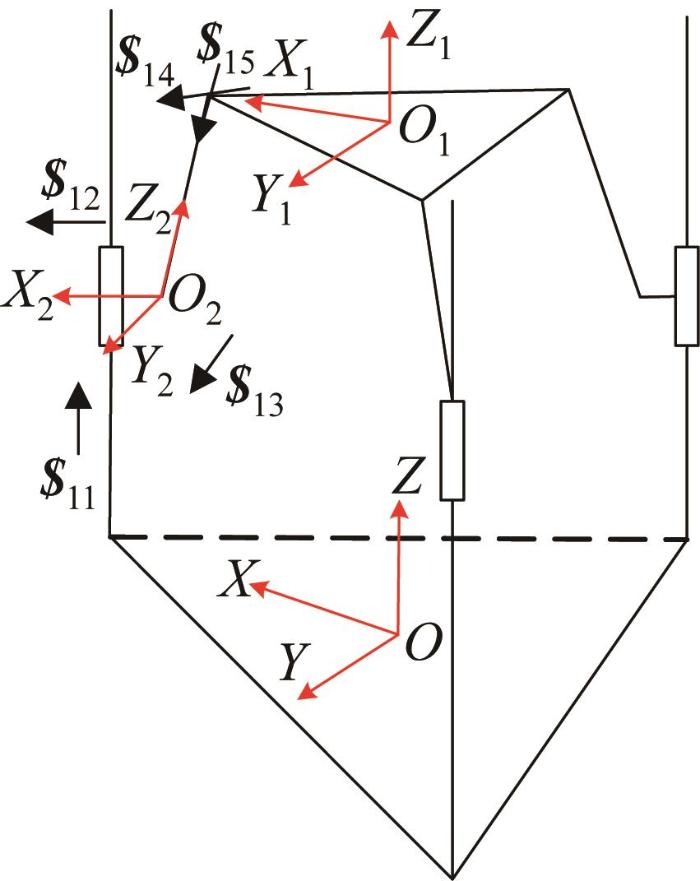
由于3-PUU并联机构的3条支链完全相同，因此选择其中一条支链（记作支链1）进行分析。在支链1上靠近移动副的虎克铰中心建立坐标系O₂-X₂Y₂Z₂，并设第m条支链上第q个运动副处的运动螺旋为 $_mq。鉴于虎克铰相当于2个转动副，故一条支链共有5个运动螺旋。图3所示为3-PUU并联机构支链1的运动螺旋。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 3-PUU并联机构支链1的运动螺旋

Fig.3 Motion spiral of branch chain 1 of 3-PUU parallel mechanism

根据图3，支链1的运动螺旋可表示为：

\{\begin{array}{l} $_{11} = (\begin{matrix} 0, & 0, & 0; & \begin{matrix} a_{1} & \begin{matrix} a_{2} & a_{3} \end{matrix} \end{matrix} \end{matrix}) \\ $_{12} = (\begin{matrix} 1, & 0, & 0; & \begin{matrix} 0, & \begin{matrix} 0, & 0 \end{matrix} \end{matrix} \end{matrix}) \\ $_{13} = (\begin{matrix} 0, & 1, & 0; & \begin{matrix} 0, & 0, & 0 \end{matrix} \end{matrix}) \\ \begin{matrix} $_{14} = (\begin{matrix} 1, & 0, & 0; & \begin{matrix} 0, & b_{1}, & b_{2} \end{matrix} \end{matrix}) \\ $_{15} = (\begin{matrix} 0, & 1, & 0; & \begin{matrix} c_{1}, & \begin{matrix} 0, & c_{2} \end{matrix} \end{matrix} \end{matrix}) \end{matrix} \end{array}

(2)

式中：a₁、a₂、a₃、b₁、b₂、c₁、c₂为与机构的结构特性和运动特性相关的参数，其值取决于机构运动副的空间位置。

由式(2)可知，支链1的5个运动螺旋线性无关，则可得到1个反螺旋。根据螺旋理论互易积乘法，可得3条支链的反螺旋：

\{\begin{matrix} $_{1}^{r} = (\begin{matrix} 0, & 0, & 0; & \begin{matrix} 0, & \begin{matrix} 0, & 1 \end{matrix} \end{matrix} \end{matrix}) \\ $_{2}^{r} = (\begin{matrix} 0, & 0, & 0; & \begin{matrix} 0, & \begin{matrix} 0, & 1 \end{matrix} \end{matrix} \end{matrix}) \\ $_{3}^{r} = (\begin{matrix} 0, & 0, & 0; & \begin{matrix} \begin{matrix} 0, & 0, \end{matrix} & 1 \end{matrix} \end{matrix}) \end{matrix}

(3)

式中： $$_{1}^{r}$ 、 $$_{2}^{r}$ 、 $$_{3}^{r}$ 分别为支链1，2，3的反螺旋。

根据式(3)，3-PUU并联机构的每条支链恰好存在一个约束螺旋，则整个机构的冗余约束 $v$ =0。由于与动平台相连的虎克铰上的3个约束力偶垂直于虎克铰所在平面并作用于动平台，且各约束力偶不共面，即约束力偶线性无关，因此该并联机构的基础螺旋系可表示为：

\{\begin{matrix} $_{B 1}^{r} = (\begin{matrix} 0, & 0, & 0; & \begin{matrix} 1, & 0, & 0 \end{matrix} \end{matrix}) \\ $_{B 2}^{r} = (\begin{matrix} 0, & 0, & 0; & \begin{matrix} 0, & 1, & 0 \end{matrix} \end{matrix}) \\ $_{B 3}^{r} = (\begin{matrix} 0, & 0, & 0; & \begin{matrix} 0, & 0, & 1 \end{matrix} \end{matrix}) \end{matrix}

(4)

式中： $$_{B 1}^{r}$ 、 $$_{B 2}^{r}$ 、 $$_{B 3}^{r}$ 分别为支链1，2，3的基础螺旋。

由上述基础螺旋系可知，约束力偶限制了动平台的3个转动自由度。因此，3-PUU并联机构仅存在平动自由度。

3-PUU并联机构的总构件数为8、移动副数为3、虎克铰数为6，运动副数为9，局部自由度为0，公共约束为0。由此可得，该并联机构所有运动副的自由度为：

\sum_{h = 1}^{j} f_{h} = 3 \times 1 + 6 \times 2 \times 1 = 15

(5)

将各参数和式(5)代入式(1)，可得3-PUU并联机构的自由度：

F = (6 - 0) (8 - 9 - 1) + 15 = 3

综上，3-PUU并联机构的动平台仅有沿X、Y、Z方向的3个平动自由度，无转动自由度。

1.3　运动学正反解分析

1.3.1　运动学反解

已知3-PUU并联机构动平台中心O₁的位置坐标，求解滑块相对于静平台顶点C_i (i=1, 2, 3)的位置，即可得到机构的运动学反解。由于该并联机构的滑块仅沿Z方向运动，将各滑块在静坐标系中的竖坐标（即Z坐标）记作z_i (i=1, 2, 3)。根据图2，将顶点A_i (i=1, 2, 3)和动平台中心O₁在静坐标系O-XYZ中的坐标以及顶点B_i (i=1, 2, 3)在动坐标系O₁-X₁Y₁Z₁中的坐标表示为：

\{\begin{array}{l} A_{1 O} = (\begin{matrix} R, & 0, & z_{1} \end{matrix}) \\ A_{2 O} = (\begin{matrix} - \frac{1}{2} R, & \frac{\sqrt[]{3}}{2} R, & z_{2} \end{matrix}) \\ A_{3 O} = (\begin{matrix} - \frac{1}{2} R, & - \frac{\sqrt[]{3}}{2} R, & z_{3} \end{matrix}) \end{array}

(6)

o_{1 O} = (\begin{matrix} x_{O}, & y_{O}, & z_{O} \end{matrix})

(7)

\{\begin{array}{l} B_{1 O_{1}} = (\begin{matrix} r, & 0, & 0 \end{matrix}) \\ B_{2 O_{1}} = (\begin{matrix} - \frac{1}{2} r, & \frac{\sqrt[]{3}}{2} r, & 0 \end{matrix}) \\ B_{3 O_{1}} = (\begin{matrix} - \frac{1}{2} r, & - \frac{\sqrt[]{3}}{2} r, & 0 \end{matrix}) \end{array}

(8)

根据杆长条件 $l ² = {|l_{A_{i} B_{i}}|}^{2}$ (i=1, 2, 3)和安装条件z_O >z_i (i=1, 2, 3)，建立3-PUU并联机构的运动学反解方程：

\{\begin{array}{l} z_{1} = z_{O} - \sqrt[]{l^{2} - (x_{O} {+ r - R)}^{2} - y_{O}^{2}} \\ z_{2} = z_{O} - \sqrt[]{l^{2} - {[x_{O} + \frac{1}{2} (R - r)]}^{2} - {[y_{O} - \frac{\sqrt[]{3}}{2} (R - r)]}^{2}} \\ z_{3} = z_{O} - \sqrt[]{l^{2} - {[x_{O} + \frac{1}{2} (R - r)]}^{2} - {[y_{O} + \frac{\sqrt[]{3}}{2} (R - r)]}^{2}} \end{array}

(9)

1.3.2　运动学正解

通过式(9)反求得到3-PUU并联机构动平台中心O₁在静坐标系O-XYZ中的坐标，即可得到其运动学正解，具体可表示为：

\{\begin{array}{l} x_{O} = \frac{2 z_{1}^{2} - (z_{3}^{2} + z_{2}^{2}) - 2 z_{O} (2 z_{1} - z_{2} - z_{3})}{6 (R - r)} \\ y_{O} = \frac{z_{2}^{2} - z_{3}^{2} - 2 z_{O} (z_{2} - z_{3})}{2 \sqrt[]{3} (R - r)} \\ z_{O} = \frac{- e_{2} + \sqrt[]{e_{2}^{2} - 4 e_{1} e_{3}}}{2 e_{1}} \end{array}

(10)

其中：

\{\begin{array}{l} e_{1} = \frac{(2 z_{1} - z_{3} - z_{2})^{2} + 3 (z_{2} - z_{3})^{2} + 9 {(R - r)}^{2}}{9 {(R - r)}^{2}} \\ \begin{array}{l} e_{2} = - \{\frac{[2 z_{1}^{2} - (z_{2}^{2} + z_{3}^{2}) - 12 {(R - r)}^{2}] (2 z_{1} - z_{3} - z_{2})}{9 {(R - r)}^{2}} + \\ \frac{3 (z_{2} - z_{3}) (z_{2}^{2} - z_{3}^{3}) + 18 z_{1} {(R - r)}^{2}}{9 {(R - r)}^{2}}\} \end{array} \\ \begin{array}{l} e_{3} = \frac{{[z_{1}^{2} - \frac{1}{2} (z_{2}^{2} + z_{3}^{2})]}^{2}}{9 {(R - r)}^{2}} + \frac{(z_{2}^{2} - z_{3}^{2})^{2}}{12 {(R - r)}^{2}} - \\ \frac{2 z_{1}^{2} - (z_{2}^{2} + z_{3}^{2})}{3} + {(r - R)}^{2} - l^{2} + z_{1}^{2} \end{array} \end{array}

(11)

2 3-PUU并联机构的雅可比矩阵和奇异性分析

2.1　速度雅可比矩阵分析

并联机构的速度雅可比矩阵可以表征滑块速度与动平台速度之间的关系。求解式(9)关于时间的一阶全微分，可得3-PUU并联机构各滑块的速度：

\{\begin{array}{l} \frac{d z_{1}}{d t} = \frac{d z_{O}}{d t} - \frac{- (x_{O} + r - R) \frac{d x_{O}}{d t} - y_{O} \frac{d y_{O}}{d t}}{\sqrt[]{l^{2} - (x_{O} {+ r - R)}^{2} - y_{O}^{2}}} \\ \frac{d z_{2}}{d t} = \frac{d z_{O}}{d t} - \frac{- [x_{O} + \frac{1}{2} (R - r)] \frac{d x_{O}}{d t} - [y_{O} - \frac{\sqrt[]{3}}{2} (R - r)] \frac{d y_{O}}{d t}}{\sqrt[]{l^{2} - {[x_{O} + \frac{1}{2} (R - r)]}^{2} - {[y_{O} - \frac{\sqrt[]{3}}{2} (R - r)]}^{2}}} \\ \frac{d z_{3}}{d t} = \frac{d z_{O}}{d t} - \frac{- [x_{O} + \frac{1}{2} (R - r)] \frac{d x_{O}}{d t} - [y_{O} + \frac{\sqrt[]{3}}{2} (R - r)] \frac{d y_{O}}{d t}}{\sqrt[]{l^{2} - {[x_{O} + \frac{1}{2} (R - r)]}^{2} - {[y_{O} + \frac{\sqrt[]{3}}{2} (R - r)]}^{2}}} \end{array}

(12)

整理可得，各滑块与动平台速度之间的关系如下：

[\begin{matrix} {\dot{z}}_{1} \\ {\dot{z}}_{2} \\ {\dot{z}}_{3} \end{matrix}] = J [\begin{matrix} {\dot{x}}_{O} \\ {\dot{y}}_{O} \\ {\dot{z}}_{O} \end{matrix}]

(13)

其中：

J = [\begin{matrix} \frac{(x_{O} + r - R)}{z_{O} - z_{1}} & \frac{y_{O}}{z_{O} - z_{1}} & 1 \\ \frac{x_{O} + \frac{1}{2} (R - r)}{z_{O} - z_{2}} & \frac{y_{O} - \frac{\sqrt[]{3}}{2} (R - r)}{z_{O} - z_{2}} & 1 \\ \frac{x_{O} + \frac{1}{2} (R - r)}{z_{O} - z_{3}} & \frac{y_{O} + \frac{\sqrt[]{3}}{2} (R - r)}{z_{O} - z_{3}} & 1 \end{matrix}]

式中： J 为速度雅可比矩阵。

2.2　奇异性分析

本文采用几何法和解析法对3-PUU并联机构的奇异性进行分析。速度雅可比矩阵 J 的行列式可表示为：

d e t (J) = \frac{\sqrt[]{3} (R - r) (j_{1} + j_{2})}{(z_{O} - z_{1}) (z_{O} - z_{2}) (z_{O} - z_{3})}

(14)

其中：

j_{1} = \frac{(R - r - x_{O} - \sqrt[]{3} y_{O}) (2 z_{O} - z_{2} - z_{3})}{2}

j_{2} = (x_{O} + \frac{R - r}{4}) (z_{O} - z_{1})

2.2.1　约束奇异

当R=r时，在3-PUU并联机构的工作空间内存在约束奇异，但由于本文设计时即已令r<R，因此该约束奇异不存在。当z_O =z_i (i=1, 2, 3)时，从极限角度考虑，det $(J)$ 的分母为三阶无穷小，分子为一阶无穷小，其值趋于无穷大，此时动平台与滑块的Z坐标相同，将出现运动干涉，但设计时又已令R<l+r，因此该约束奇异也不存在。综上可知，本文所研究的3-PUU并联机构不存在约束奇异。

2.2.2　运动奇异

当z_O ≠z_i (i=1, 2, 3)，R≠r，而det $(J)$ 的分子为0（即j₁+j₂=0）时，存在如下关系：

\begin{array}{l} \frac{(R - r - x_{O} - \sqrt[]{3} y_{O}) (2 z_{O} - z_{2} - z_{3})}{2} + \\ (x_{O} + \frac{R - r}{4}) (z_{O} - z_{1}) = 0 \end{array}

(15)

整理式(15)可得：

\begin{array}{l} \frac{z_{2} + z_{3} - 2 z_{1}}{2} x_{O} - \frac{\sqrt[]{3} (2 z_{O} - z_{2} - z_{3})}{2} y_{O} + \\ \frac{(R - r) [5 z_{O} - z_{1} - 2 (z_{2} + z_{3})]}{4} = 0 \end{array}

(16)

当z_O ≠z_i (i=1, 2, 3)、R≠r，而j₁=j₂=0时，存在如下关系：

\{\begin{array}{l} x_{O} + \frac{R - r}{4} = 0 \\ R - r - x_{O} - \sqrt[]{3} y_{O} = 0 \end{array}

(17)

整理式(17)可得：

5 x_{O} + \sqrt[]{3} y_{O} = 0

(18)

综上可知，当3-PUU并联机构动平台的运动满足式(16)或式(18)时，该机构存在运动奇异；当运动不满足式(16)和式(18)时，该机构不存在运动奇异。

3 3-PUU并联机构的工作空间与运动性能分析

3.1　工作空间分析

并联机构的工作空间分为可达工作空间和灵活工作空间。其中：可达工作空间是指机构末端能到达的位置点集合，灵活工作空间是指机构末端能从任意方向到达的位置点集合^[1]。本文采用数值法中的极限边界搜索法来求解3-PUU并联机构的可达工作空间，具体求解思路如下。

1）给定动平台能到达的极限空间范围。

2）采用平行于XOY平面的平面簇，将动平台能到达的空间区域等分成高度为ΔZ的圆柱体子空间。

3）在子空间内建立极坐标系，使极径 $ρ$ 从0增至最大极径，转角α从0增大至2π，以搜索子空间内的坐标点；同时，将搜索点的坐标分别代入运动学反解方程和虎克铰转角的约束方程，求解得到滑块的位置和虎克铰的转角。

4）判断步骤3）中所求结果是否满足滑块位置和虎克铰转角的约束条件，保留并画出满足约束条件的搜索点。

5）令Z坐标增加ΔZ后继续搜索下一个子空间内的坐标点，直至完成所有子空间内坐标点的搜索，即可获得并联机构的可达工作空间。

对于3-PUU并联机构，其滑块位置和虎克铰转角的约束条件为：

\{\begin{array}{l} 335 \leq z_{i} \leq 535 m m \\ - 60 ° \leq θ_{i} \leq 60 ° \end{array} (i = 1, 2, 3)

(19)

式中：θ_i 为虎克铰转角。

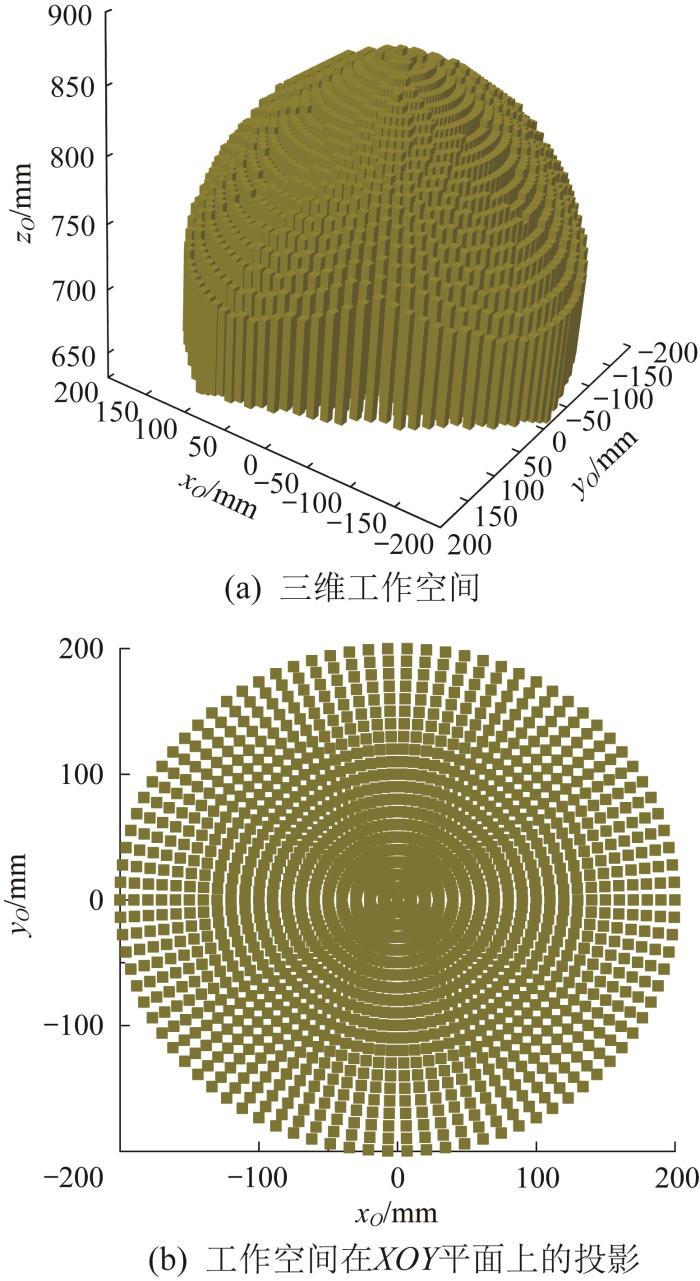
利用MATLAB软件编程求得3-PUU并联机构的可达工作空间，结果如图4所示。由图4(a)可知，该并联机构具有较大的可达工作空间，当动平台高度为700 mm时，动平台的平面运动范围最大。由图4(b)可知，在XOY平面上，动平台的运动范围为半径等于200 mm的圆形区域。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 3-PUU并联机构的可达工作空间

Fig.4 Reachable workspace of 3-PUU parallel mechanism

3.2　运动性能分析

3.2.1　灵巧度评价

机构的灵巧度对机构设计来说极其重要^[30-31]，其可用于评价机构输入与输出之间的传递性能，即衡量机构运动性能的优劣。并联机构灵巧度的评价指标不唯一，鉴于并联机构的速度雅可比矩阵表征了输入端速度与输出端速度的映射关系，则可利用速度雅可比矩阵的条件数来定量分析并联机构的运动性能。

根据式(13)，3-PUU并联机构中滑块与动平台速度之间的关系可表示为：

D = J E

(20)

即：

E = J^{- 1} D

(21)

其中：

\{\begin{array}{l} D = {[\begin{matrix} {\dot{z}}_{1} & {\dot{z}}_{2} & {\dot{z}}_{3} \end{matrix}]}^{T} \\ E = {[\begin{matrix} {\dot{x}}_{O} & {\dot{y}}_{O} & {\dot{z}}_{O} \end{matrix}]}^{T} \end{array}

式中： D 为滑块速度矢量， E 为动平台速度矢量。

设滑块速度的误差为Δ D 、动平台速度的误差为Δ E，则有：

Δ D = J Δ E

(22)

对式(21)和式(22)取二范数，并将式(21)、式(22)的两端同时相乘，可得：

‖E ‖\times‖ Δ D‖ = ‖J^{- 1} D‖ \times ‖J Δ E‖

(23)

根据三角不等式原理，可得滑块速度与动平台速度的相对误差之间的关系^[25]：

\frac{‖Δ D‖}{‖D‖} \leq ‖J‖ \times ‖J^{- 1}‖ \times \frac{‖Δ E‖}{‖E‖}

(24)

根据式(24)，速度雅可比矩阵的条件数M可表示为：

M = ‖J‖ \times ‖J^{- 1}‖

(25)

当并联机构的位形改变时，速度雅可比矩阵的条件数随之改变，其取值范围一般为1 $\leq$ M $\leq$ +∞，存在无穷大的情况。因此，可取条件数的倒数作为灵巧度的衡量指标，记作M₁，其取值范围为0 $\leq$ M₁ $\leq$ 1。当灵巧度M₁=0时，表示机构处于奇异状态；当灵巧度M₁=1时，表示机构具有最佳灵巧度，即运动性能最好。综上可知，灵巧度M₁越大，并联机构的运动性能越好。

由于速度雅可比矩阵会随着并联机构动平台位置的变化而变化，M₁仅能描述并联机构工作空间内某个位置点的灵巧度，属于局部性评价指标。因此，采用灵巧度在整个工作空间内的分布情况，即全局灵巧度 $\bar{M_{1}}$ ，对3-PUU并联机构的运动性能进行评价。全局灵巧度 $\bar{M_{1}}$ 越大，表示并联机构的运动性能越好。全局灵巧度 $\bar{M_{1}}$ 可表示为：

\bar{M_{1}} = \frac{\int_{W} M_{1} d W}{\int_{W} d W}

(26)

式中：W为机构的工作空间。

由于积分部分计算较困难，以求和代替积分，则式(26)可简化为：

\bar{M_{1}} = \frac{\sum_{s = 1}^{N} M_{1, s}}{N}

(27)

式中：N为工作空间内的取样点数，M_1,_s 为第s个取样点的灵巧度。

3.2.2　算例分析

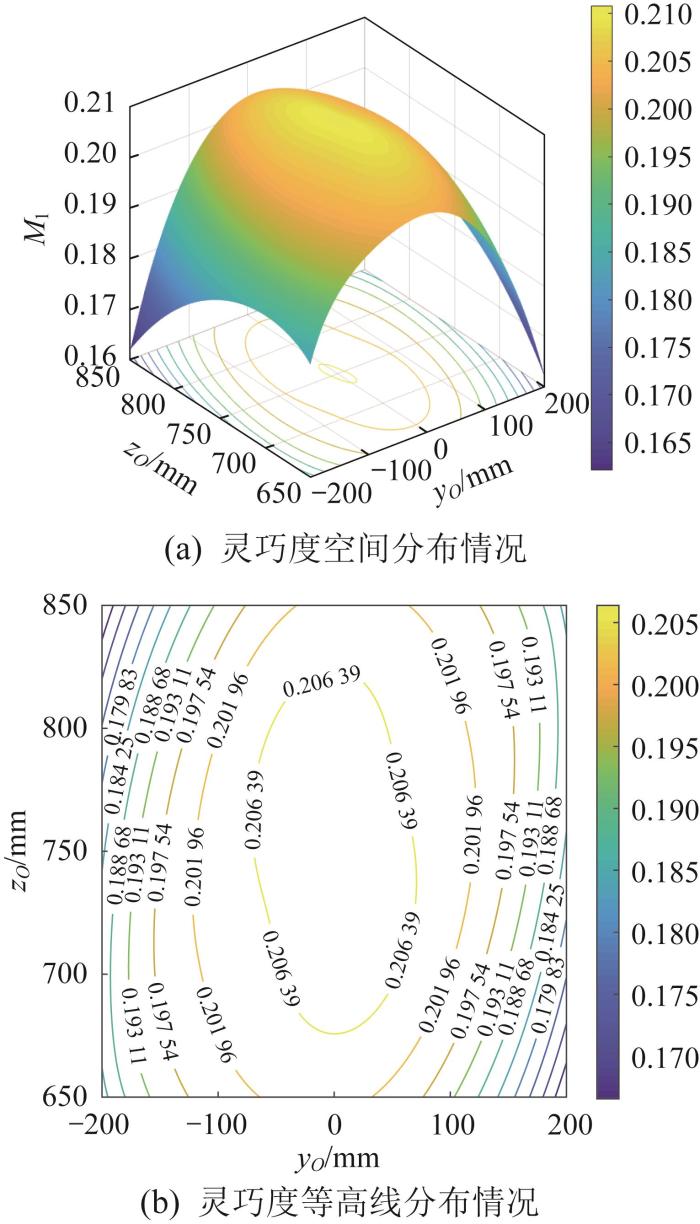
本文3-PUU并联机构的设计参数如下：R=200 mm、r=100 mm、连杆长度l=350 mm。根据该并联机构的可达工作空间，可确定其动平台中心O₁的运动范围为：-200 $\leq$ x_O $\leq$ 200 mm，-200 $\leq$ y_O $\leq$ 200 mm，650 $\leq$ z_O $\leq$ 850 mm。利用上文构建的运动学反解方程和速度雅可比矩阵，在MATLAB软件中编写程序，求解得到3-PUU并联机构的灵巧度的分布情况。

图5所示为x_O =0 mm时3-PUU并联机构的灵巧度随y_O 、z_O 变化的分布情况。由图5(a)可知，灵巧度的分布近似关于直线y_O =0 mm对称，越靠近直线y_O =0 mm，机构的灵巧度越好；当y_O =0 mm、z_O =750 mm时，机构的灵巧度最佳。由图5(b)可知，在直线y_O =0 mm的两侧，离直线y_O =0 mm越远，机构的灵巧度越差；当-200 $\leq$ y_O $\leq$ -100 mm或100 $\leq$ y_O $\leq$ 200 mm时，灵巧度的变化速度均较快；当-100 $\leq$ y_O $\leq$ 0 mm或0 $\leq$ y_O $\leq$ 100 mm时，灵巧度的变化速度均较慢。由此可知，当x_O =0 mm时，动平台沿Y轴的运动应尽可能满足-100 $\leq$ y_O $\leq$ 0 mm或0 $\leq$ y_O $\leq$ 100 mm。另外，由图5(b)还可知，在-100 $\leq$ y_O $\leq$ 0 mm和0 $\leq$ y_O $\leq$ 100 mm区域内，灵巧度的分布关于直线z_O =750 mm对称，且分布均匀。因此，当x_O =0 mm时，动平台沿Z轴的运动范围应尽可能满足650 $\leq$ z_O $\leq$ 850 mm。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 x_O =0 mm时3-PUU并联机构的灵巧度分布

Fig.5 Dexterity distribution of 3-PUU parallel mechanism under x_O =0 mm

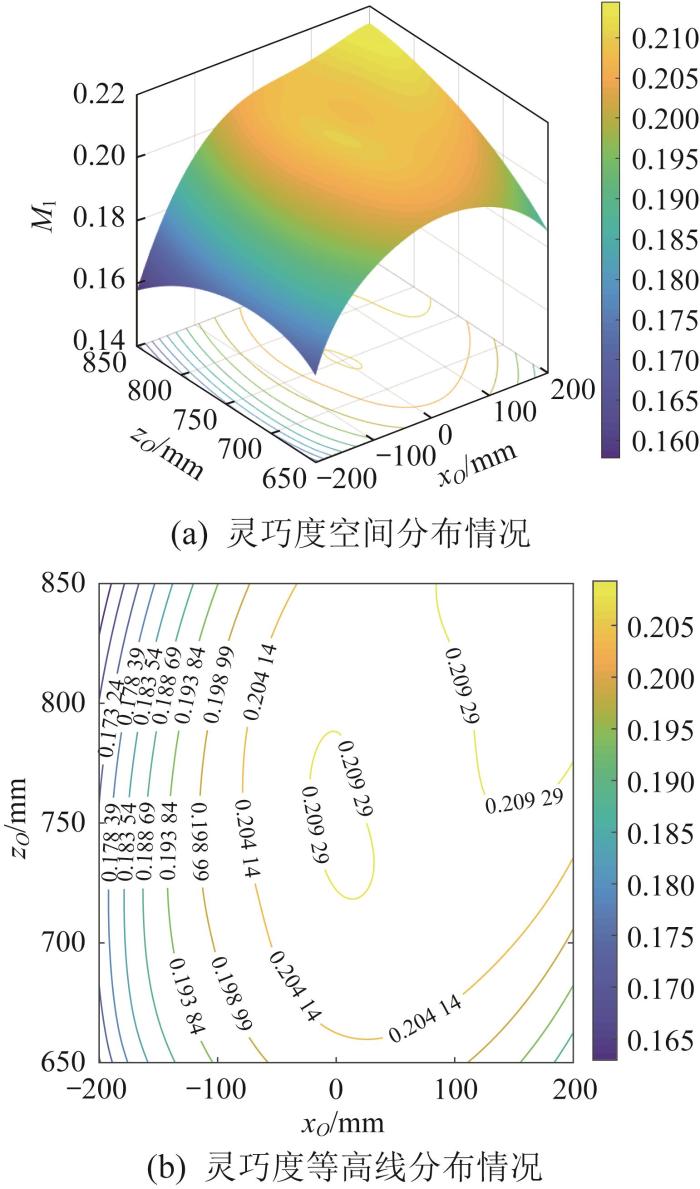
图6所示为y_O =0 mm时3-PUU并联机构的灵巧度随x_O 、z_O 变化的分布情况。由图6(a)可知，当x_O =0 mm、z_O =750 mm时，机构的灵巧度达到最优，且x_O >0 mm时的灵巧度优于x_O <0 mm时的灵巧度；当x_O <0 mm时，灵巧度随x_O 的减小而减小，即机构的灵巧度变差。由图6(b)可知，当-200 $\leq$ x_O $\leq$ -100 mm时，灵巧度的变化速度较快；当-100 $\leq$ x_O $\leq$ 200 mm时，灵巧度的变化速度较慢。由此可知，当y_O =0 mm时，动平台沿X轴的运动尽可能满足-100 $\leq$ x_O $\leq$ 200 mm。另外，由图6(b)还可知，在-100 $\leq$ x_O $\leq$ 200 mm且700 $\leq$ z_O $\leq$ 850 mm时，灵巧度的变化速度较慢。由此可知，当y_O =0 mm时，动平台沿Z轴的运动范围应尽可能满足700 $\leq$ z_O $\leq$ 850 mm。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 y_O =0 mm时3-PUU并联机构的灵巧度分布

Fig.6 Dexterity distribution of 3-PUU parallel mechanism under y_O =0 mm

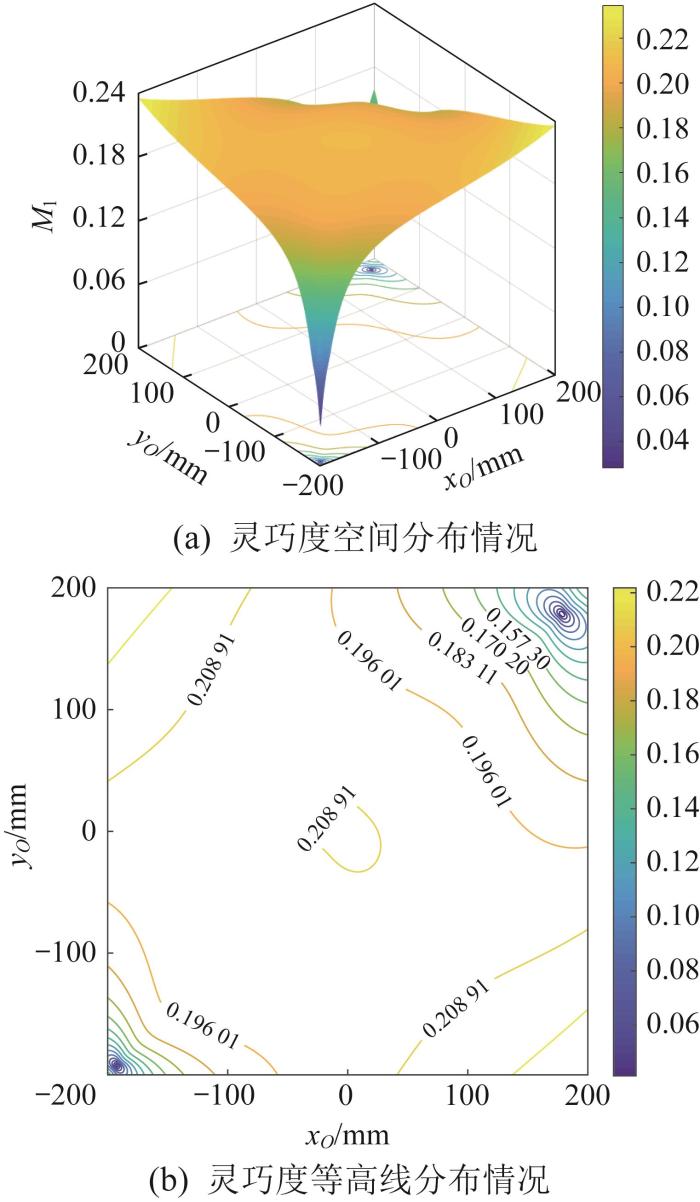
图7所示为z_O =750 mm时3-PUU并联机构的灵巧度随x_O 、y_O 变化的分布情况。由图7(a)可知，当x_O =0 mm、y_O =0 mm时，机构的灵巧度达到最优。由图7(b)可知，当-400 $\leq$ x_O +y_O $\leq$ -300 mm或300 $\leq$ x_O +y_O $\leq$ 400 mm时，灵巧度的变化速度均较快，而-300 $\leq$ x_O +y_O $\leq$ 300 mm时，灵巧度的变化速度较慢。由此可知，当z_O =750 mm时，动平台的运动应满足-300 $\leq$ x_O+y_O $\leq$ 300 mm。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 z_O =750 mm时3-PUU并联机构的灵巧度分布

Fig.7 Dexterity distribution of 3-PUU parallel mechanism under z_O =750 mm

令3-PUU并联机构工作空间内的取样点数为401，根据图5至图7，可得每个取样点对应的灵巧度。将各取样点对应的灵巧度代入式(27)，可得机构的全局灵巧度。当x_O =0 mm时，全局灵巧度 $\bar{M_{1}}$ =0.201；当y_O =0 mm时， $\bar{M_{1}}$ =0.203；当z_O =750 mm时， $\bar{M_{1}}$ =0.184。

根据上述分析，3-PUU并联机构的全局灵巧度均逼近最大灵巧度，且由各灵巧度分布图可知，3-PUU并联机构的灵巧度在较大范围内未发生突变，即运动性能良好。

4 3-PUU并联机构运动学仿真分析

4.1　仿真模型构建

为了验证所构建的3-PUU并联机构的运动学模型的正确性，利用ADAMS与MATLAB/Simulink软件进行联合仿真。鉴于本文直接根据并联机构的运动学反解来解算运动学正解，故只需验证正运动学模型。

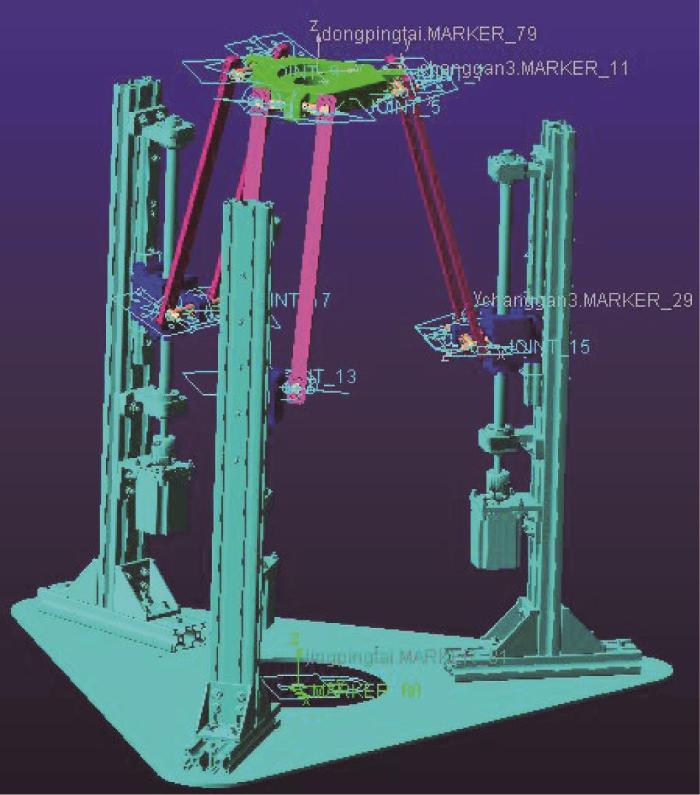
首先，在SolidWorks软件中将3-PUU并联机构中不产生相对运动的部分组合成整体，并将整个机构的三维模型导入ADAMS软件。在ADAMS软件中，对导入的模型添加运动副、约束和驱动，搭建3-PUU并联机构虚拟样机模型，如图8所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 3-PUU并联机构虚拟样机模型

Fig.8 Virtual prototype model of 3-PUU parallel mechanism

然后，导出3-PUU并联机构虚拟样机模型的机械系统文件并导入MATLAB/Simulink软件，得到如图9所示的Simulink仿真模型。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 3-PUU并联机构正运动学的Simulink仿真模型

Fig.9 Simulink simulation model for forward kinematics of 3-PUU parallel mechanism

4.2　正运动学模型仿真验证

为验证3-PUU并联机构的正运动学模型，本文给定动平台中心O₁的2种运动轨迹，分别记作S₁和S₂。其中运动轨迹S₁可表示为：

\{\begin{array}{l} x_{O} = 25 c o s 30 π t \\ y_{O} = 25 s i n 30 π t \\ z_{O} = 750 \end{array}

(28)

运动轨迹S₂可表示为：

\{\begin{array}{l} x_{O} = 25 t c o s 30 π t \\ y_{O} = 25 t s i n 30 π t \\ z_{O} = 750 \end{array}

(29)

式中：t为时间。

根据给定的运动轨迹，完善3-PUU并联机构正运动学的仿真模型，其输入如图10所示。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 3-PUU并联机构正运动学仿真模型的输入

Fig.10 Input of forward kinematics simulation model of 3-PUU parallel mechanism

设Simulink仿真时间为2 s，为清晰反映仿真结果，下文均取0.2 s内的仿真结果与理论结果进行对比分析。

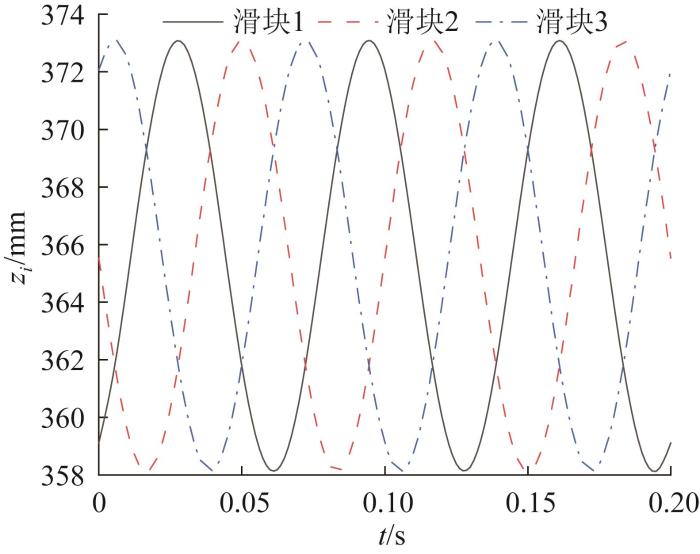
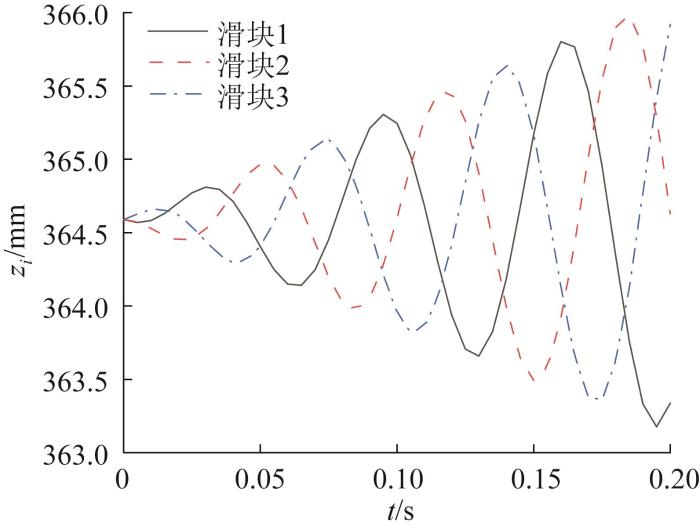
根据式(28)和式(29)以及3-PUU并联机构的运动学反解方程，可得其各滑块在静坐标系O-XYZ下的位置曲线。给定运动轨迹S₁和S₂下各滑块的位置曲线分别如图11和图12所示。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 给定运动轨迹S₁下各滑块的位置曲线

Fig.11 Position curve of each slider under given motion trajectory S₁

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 给定运动轨迹S₂下各滑块的位置曲线

Fig.12 Position curve of each slider under given motion trajectory S₂

以滑块的位置曲线作为3-PUU并联机构仿真模型的输入，得到动平台中心O₁在静坐标系O-XYZ下的位置、速度和加速度曲线，并与理论计算结果进行对比，同时分析两者的误差，以验证运动学模型的正确性。

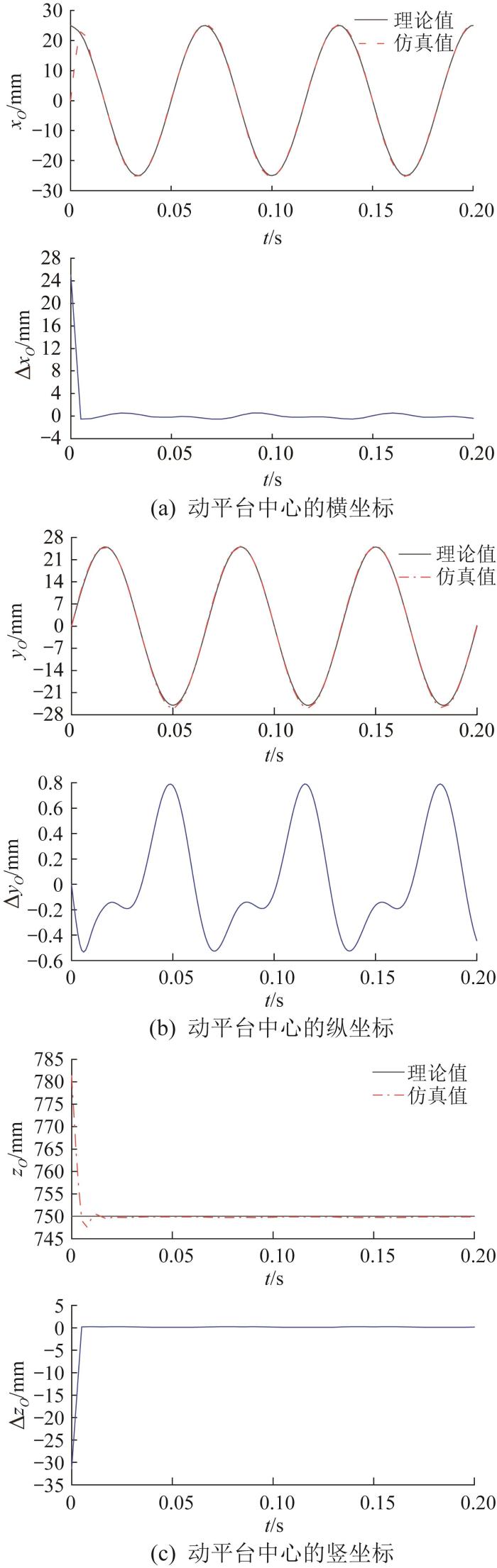
图13所示为运动轨迹S₁对应的3-PUU并联机构动平台位置的仿真验证结果。由于运动轨迹S₁为圆弧轨迹，在仿真开始时，并联机构的动平台需先运动至圆弧轨迹的起点处。从图13中可以看出，在初始仿真阶段，动平台沿X、Z方向运动的仿真结果与理论结果之间的误差（分别记作Δx_O 、Δy_O 和Δz_O ）较大。当动平台运动至圆弧轨迹的起点后，即仿真时间大于0.01 s后，仿真曲线与理论曲线基本重合，两者的误差小于1 mm。由于本文采用Simulink与ADAMS联合仿真，两者属于交互式仿真，因此仿真输入与输出间会存在一定滞缓，但误差在合理范围内。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 运动轨迹S₁对应的动平台位置的仿真验证结果

Fig.13 Simulation verification results of position of moving platform corresponding to motion trajectory S₁

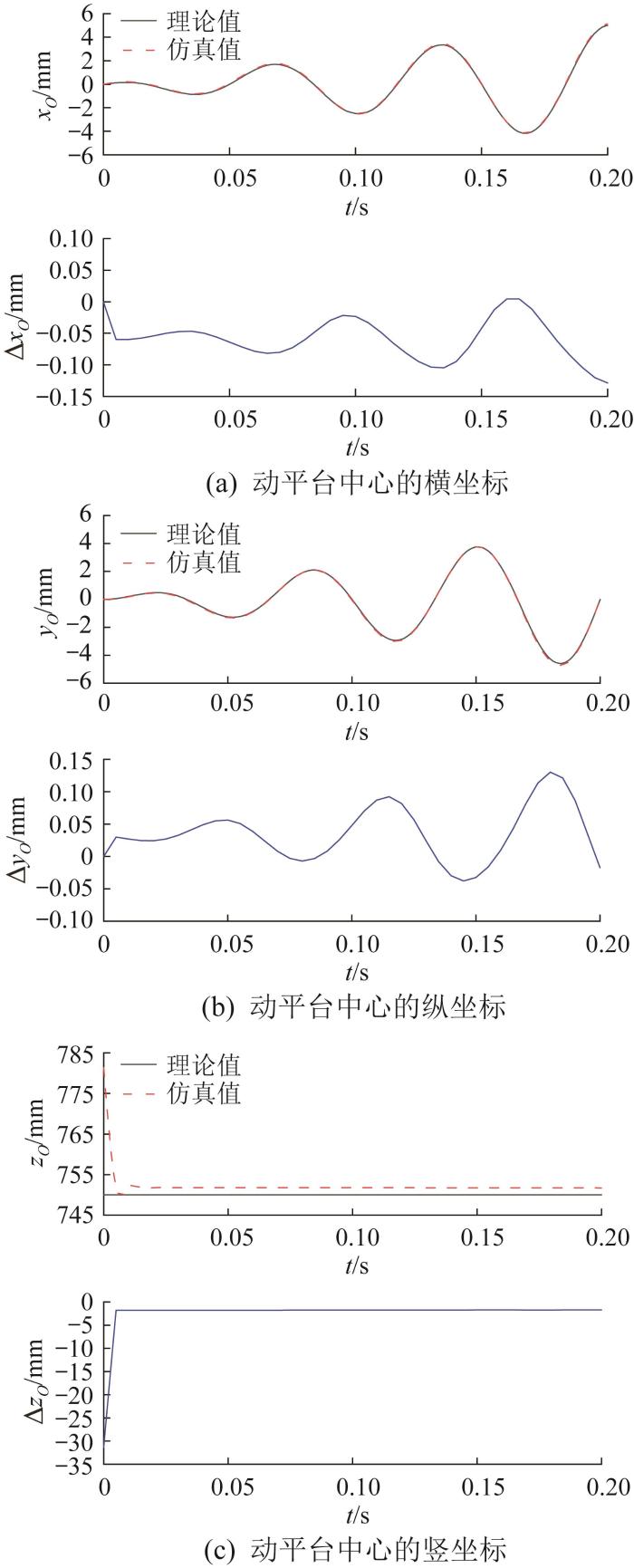
图14所示为运动轨迹S₂对应的3-PUU并联机构动平台位置的仿真验证结果。运动轨迹S₂为螺旋轨迹，在仿真开始时，并联机构动平台在Z方向上需从初始位置运动至给定位置。因此，初始仿真阶段动平台沿Z轴运动的仿真结果与理论结果之间的误差较大。当动平台运动至给定高度后，其位置的仿真曲线与理论曲线基本重合。同样由于是交互式仿真，仿真结果存在误差，但误差在合理范围内。

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 运动轨迹S₂对应的动平台位置的仿真验证结果

Fig.14 Simulation verification results of position of moving platform corresponding to motion trajectory S₂

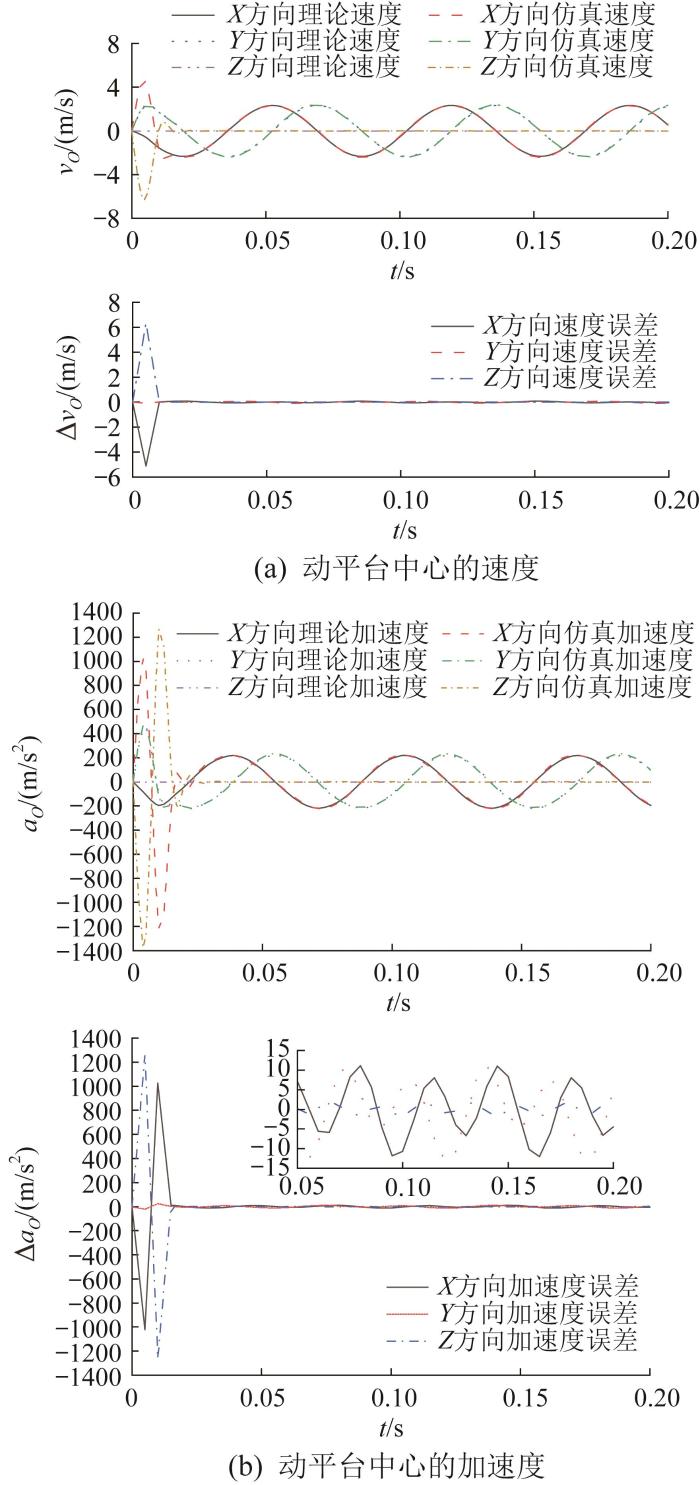
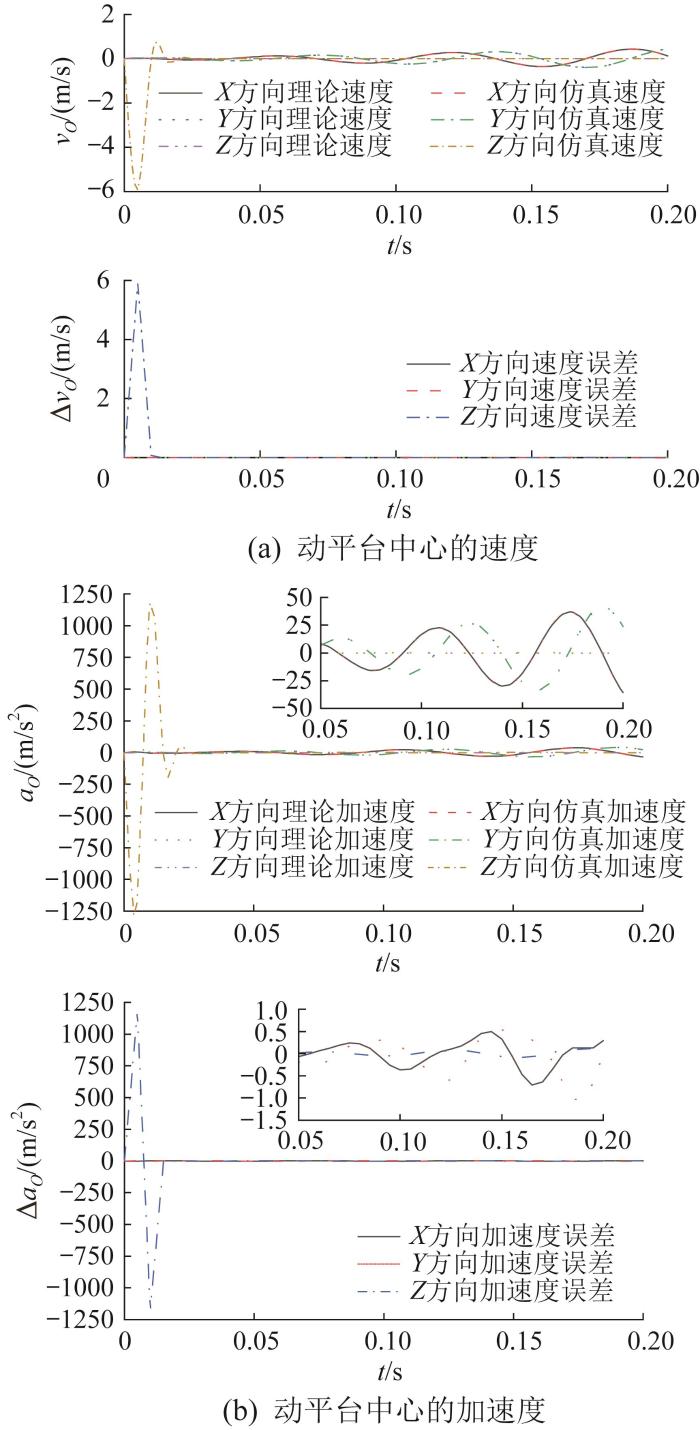
对图13和图14所示的位置曲线进行微分处理，即可得到动平台中心O₁的速度v_O 、加速度a_O。图15和图16所示分别为运动轨迹S₁和S₂对应的动平台中心的速度、加速度曲线（对应误差记作Δv_O 、Δa_O ）。由于在初始仿真阶段，动平台需由初始高度运动至给定位置，此时理论位置曲线与仿真位置曲线存在一定误差，则理论速度、加速度曲线与仿真速度、加速度曲线也存在一定误差。

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 运动轨迹S₁对应的动平台速度、加速度的仿真验证结果

Fig.15 Simulation verification results of velocity and acceleration of moving platform corresponding to motion trajectory S₁

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 运动轨迹S₂对应的动平台速度、加速度的仿真验证结果

Fig.16 Simulation verification results of velocity and acceleration of moving platform corresponding to motion trajectory S₂

由图15(b)和图16(b)中的局部放大图可知，在0.02 s后，尽管2种运动轨迹对应的理论速度、加速度曲线均与对应的仿真曲线基本重合，但仍存在一定误差。由式(28)和式(29)可知，仿真时动平台的运动速度较大，在较短时间内所产生的位置误差会导致速度和加速度存在一定误差。

根据上述分析，在不考虑动平台运动的初始误差时，3-PUU并联机构动平台的位置、速度、加速度仿真曲线与对应的理论曲线均基本重合，验证了所构建的运动学模型的正确性。

5 3-PUU并联机构运动学实验验证

5.1　实验平台搭建

为进一步验证所构建的运动学模型的正确性以及并联机构设计的合理性，笔者团队试制了如图17所示的3-PUU并联机构样机并开展实验验证。

图17

新窗口打开| 下载原图ZIP| 生成PPT

图17 3-PUU并联机构样机

Fig.17 3-PUU parallel mechanism prototype

以PC（personal computer，个人计算机）、STM32单片机、伺服驱动器和伺服电机为硬件，Keli5为软件，搭建3-PUU并联机构动平台的控制系统。在实验中，选取滑块的下端点作为滑块运动的参考点。另外，由于3-PUU并联机构样机各构件实际尺寸的影响，动平台沿Z方向的运动将存在一定误差，在实际应用时应消除该误差的影响。

本文搭建的3-PUU并联机构实验平台如图18所示，将高精度的R-20 Radian型激光跟踪仪安装在合适位置处，将靶球置于动平台的中心处。利用Keil5软件编写控制程序并将其下载至STM32单片机中，随后单片机的控制信号输出至伺服驱动器，进而由滚珠丝杠将伺服电机的动力传递给滑块，滑块再将动力传递至动平台，最终实现动平台运动。在实验过程中，激光跟踪仪实时跟踪动平台中心的位置，并将位置坐标传递至PC中的数据采集软件TrackerClib。

图18

新窗口打开| 下载原图ZIP| 生成PPT

图18 3-PUU并联机构实验平台

Fig.18 Experimental platform of 3-PUU parallel mechanism

5.2　实验验证

在实验中，给定3-PUU并联机构样机动平台中心的运动轨迹为圆形轨迹（分成180等份，每一等份采集一个轨迹点的位置），其可表示为：

\{\begin{array}{l} x_{O} = 25 c o s (\frac{π}{90} T) \\ y_{O} = 25 s i n (\frac{π}{90} T) \\ z_{O} = 700 \end{array}

(30)

式中：T为动平台中心的运动轨迹点。

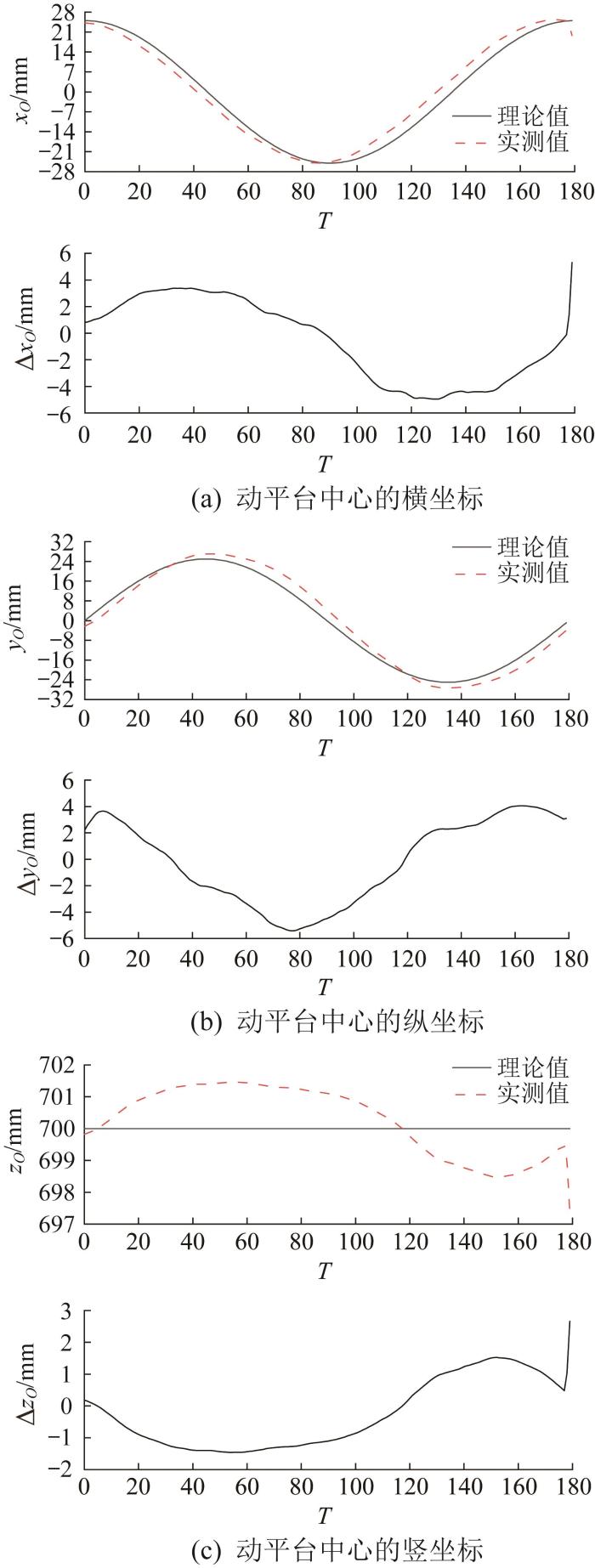
本文以离散方式均匀采集动平台运动轨迹上的180个点，为降低偶然误差的影响，取多次测量的均值作为动平台中心的位置坐标。根据测量数据，可得动平台的运动误差。表1所示为部分轨迹点坐标的理论值、实测值和误差。进一步可得到动平台中心位置的实测曲线、理论曲线及误差曲线，结果如图19所示。

表1 动平台中心位置的部分采样结果 (mm)

Table 1 Partial sampling results of moving platform center position

轨迹点T	位置理论值			位置实测值			误差
轨迹点T	x_O	y_O	z_O	x_O	y_O	z_O	Δx_O	Δy_O	Δz_O
10	23.776	7.725	700.000	22.253	4.217	700.248	1.523	3.508	-0.248
60	-11.737	22.074		-14.327	25.285	701.449	2.590	-3.211	-1.449
110	-19.700	-15.392		-15.546	-13.462	700.467	-4.154	-1.930	-0.467
160	18.579	-16.728		21.658	-20.727	698.571	-3.079	3.999	1.429

新窗口打开| 下载CSV

图19

新窗口打开| 下载原图ZIP| 生成PPT

图19 动平台中心位置的实验验证结果

Fig.19 Experimental verification results of position of moving platform center

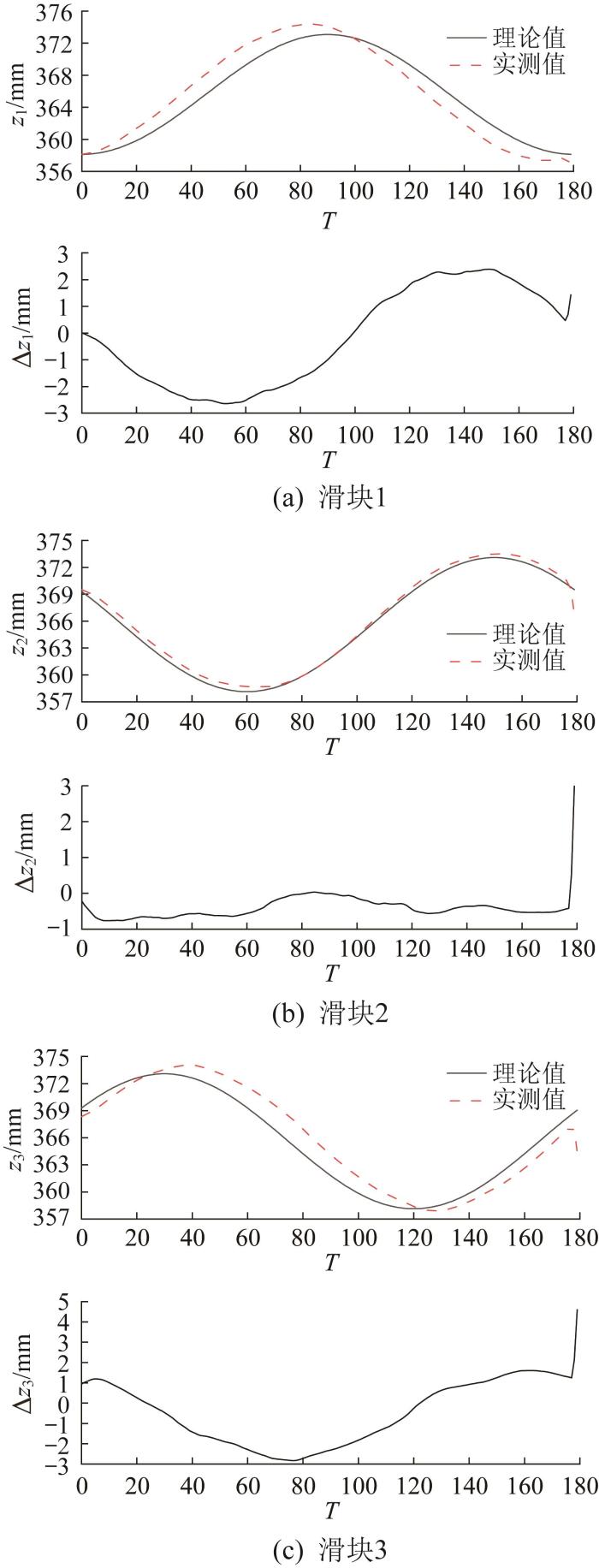
根据图19所示的动平台中心位置的实测值，通过运动学反解方程求解得到各滑块的实际位置。部分轨迹点对应的滑块位置的理论值、实测值及误差（分别记作Δz₁、Δz₂和Δz₃）如表2所示。图20所示为各滑块位置的实测曲线、理论曲线及误差曲线。

表2 部分滑块位置的采样结果 (mm)

Table 2 Partial sampling results of slider position

轨迹点T	位置理论值			位置实测值			误差
轨迹点T	z₁	z₂	z₃	z₁	z₂	z₃	Δz₁	Δz₂	Δz₃
10	358.488	367.080	371.124	359.018	367.844	370.049	-0.530	-0.764	1.075
60	369.050	358.135	369.507	371.616	358.713	371.739	-2.566	-0.578	-2.232
110	371.465	366.565	358.663	370.364	366.850	359.933	1.101	-0.285	-1.270
160	360.014	372.709	363.972	358.082	373.232	362.378	1.932	-0.523	1.594

新窗口打开| 下载CSV

图20

新窗口打开| 下载原图ZIP| 生成PPT

图20 滑块位置的实验验证结果

Fig.20 Experimental verification results of slider position

5.3　实验结果分析

由图19可知，3-PUU并联机构动平台中心位置的实测曲线与理论曲线的变化趋势基本一致。由图20可知，该并联机构各滑块位置的实测曲线与理论曲线的变化趋势也基本一致。结果表明，3-PUU并联机构设计合理，且所构建的运动学模型正确。

由图19和图20所示的误差曲线可知，3-PUU并联机构动平台及滑块的实际位置与理论位置之间存在一定误差，这主要是由并联机构存在机械误差以及控制系统精度不足造成的。3-PUU并联机构的机械误差主要包括制造误差、安装误差和运动副误差。其中，制造误差主要为动平台尺寸、静平台尺寸及连杆尺寸的误差。安装误差主要是运动副的安装误差，包括移动副、虎克副误差，可借用辅助工装进行机构装配，以降低安装误差。制造误差与机床的制造精度有关，其补偿方式主要包括硬件补偿和软件补偿。硬件补偿可通过在并联机构上安装传感器实时反馈动平台的运动情况来完成，虽然补偿精度高，但价格昂贵，且安装传感器会对机构的运动产生一定影响。软件补偿是通过辨识机构的结构参数并修改控制器中运动学模型来实现的，其原理简单，但不适用于无法修改程序的情况。

下一步将针对3-PUU并联机构的误差补偿进行研究。通过设计位置、速度、力闭环控制系统并结合并联机构的运动学标定方法，来提高其动平台的运动精度。

6 结论

为提升少自由度并联机构设计的效率和准确性，本文针对自主设计的3-PUU并联机构进行了运动学分析和实验验证，主要结论如下。

1）通过对3-PUU并联机构进行螺旋分析和自由度计算，得到该机构仅存在3个平动自由度。

2）完成了对3-PUU并联机构运动学正反解的分析，并结合速度雅可比矩阵分析了该机构的约束奇异和运动奇异。通过分析可知，该机构无约束奇异，且当动平台的运动不满足式(16)或式(18)时，机构无运动奇异。

3）解算了3-PUU并联机构的可达工作空间，并根据局部灵巧度和全局灵巧度，分析了其运动性能。结果表明，该并联机构的运动性能良好。

4）利用ADAMS和MATLAB/Simulink软件搭建了3-PUU并联机构的联合仿真模型，仿真结果验证了所构建的运动学模型的正确性。

5）搭建了3-PUU并联机构实验平台，并开展了实验研究。结果表明，其动平台、滑块的实测位置曲线与理论位置曲线的变化趋势基本一致，进一步验证了所构建的运动学模型的正确性。由于存在机械误差，实测值与理论值之间存在一定误差，需进一步分析机械误差，建立误差模型以完成机构的误差补偿。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

陈聪

新型3-PUU并联机器人工作空间优化与运动学标定

［D］.重庆：重庆大学，2018：1-3.

[本文引用: 3]

CHEN

Workspace optimization and kinematic calibr-ation of a new 3-PUU parallel robot

［D］. Chongqing： Chongqing University， 2018： 1-3.

[本文引用: 3]

[2]

朱伟，顾开荣，王传伟，等.

一种3T1R并联机构设计及运动学性能分析

［J］.中国机械工程，2018，29（1）：14-21. doi：10.3969/j.issn.1004-132X.2018.01.003