以煤为主是我国长期不变的基本国情,煤炭在我国能源结构和国民经济中扮演着重要的压舱石角色[1-3]. 随着我国煤矿开采技术快速发展,煤矿开采深度逐渐增加,以岩爆、冲击地压为代表的深部开采诱发的煤矿顶板事故的发生频率和强度日渐增长,造成了严重的生命财产损失,其防护问题已经成为研究热点. 我国煤矿顶板事故防护问题的研究以冲击地压巷道支护技术和静态、动态及动静态信息融合预测与预警方法为主要方向[4]. 以冲击地压巷道支护技术为例,该技术从巷道支护强度和刚度提升阶段逐步转入强力吸能支护阶段,因此,须在完善冲击地压巷道支护理论的同时研制强吸能支护装备. 王国法等[5]提出液压支架双伸缩抗冲击立柱来解决支架的抗冲击问题,将传统立柱活塞部分的空腔与中缸连通,增加发生冲击时参与缓冲的油液量,从而延长冲击作用时间,减小整体的液压弹性系数. 唐治等[6-7]提出并设计了与液压立柱结合使用的内外翻转式吸能构件与矿用六边形折痕吸能防冲构件. 构件防冲能力体现在:其在压溃过程中吸收冲击能;压溃空间给煤岩提供了一定的能量释放空间;在构件恒力变形阶段发挥作用. 研究结果表明,将这2种吸能防冲构件与现有常规立柱结合使用,可以改善立柱受冲击载荷时的受力情况,从而增强立柱的防冲性能. 此外,潘一山团队[8-12]针对自移式防冲巷道支架与吸能防冲立柱的设计、诱导式吸能装置的特性、恒阻让位装置的特性等进行研究. 王成龙等[13]结合磁流变缓冲技术提出新型液压支架抗冲击技术,利用AMESim与Simulink联合仿真对比分析缓冲技术的有效性,同时针对液压支架在冲击地压工况下的特点,设计用于磁流变缓冲元件的多种工况控制系统和模糊PI控制系统,对多种工况控制系统的控制策略和模糊PI控制的模糊规则进行研究.
如何提高支护装备的抗冲击性能和实现冲击工况下吸能状态的实时调整是实现智能化抗冲击的关键. 以压溃吸能方式为主导的防冲吸能构件在压溃变形后不具备复用性,且无法根据冲击状态调整吸能状态,缺乏对多种工况的适应性. 受制于空间尺寸、磁流变阻尼器结构尺寸与磁流变液剪切饱和因素,磁流变阻尼器无法更高效地发挥其吸能状态调节能力.
自然界中的动物经过长期的自然选择,已经进化出各种比传统工程防护结构更为高效、可靠且适应性强的机体防护机制,以抵抗来自周围复杂环境的碰撞和冲击载荷. 这些天然的生物防御系统具有可恢复特性、实时调节适应性、优异的抗冲击特性以及高能量耗散率. 以袋鼠为例,其腿部的优异抗冲击机制能够保证其在长时间、高速、远距离跳跃和落地过程中机体的机能不受损伤. 刑运等[14]针对动物进化出的抗冲击策略及其仿生机理进行研究,归纳分析生物抗冲击结构的力学性能,讨论动物抗冲击策略与防护机制及其仿生应用研究的未来发展方向,为仿生抗冲击装置的研究提供有益的仿生依据.
本研究选择袋鼠为生物样本,以袋鼠腿部抗冲击机理、仿生机构运动学和动力学以及磁流变控制技术为基础,以ZQ4000/16/31型巷道超前液压支架为应用对象,结合响应曲面法[19]研发基于仿生袋鼠腿的应用于巷道超前液压支架的磁流变智能抗冲击机构. 该仿生机构能够根据冲击状态调整整体吸能状态,降低了巷道超前液压支架立柱在冲击载荷作用下的吸能量,为提高支架抗冲击能力提供了新的解决方案.
1. 仿生机构的运动学和动力学模型
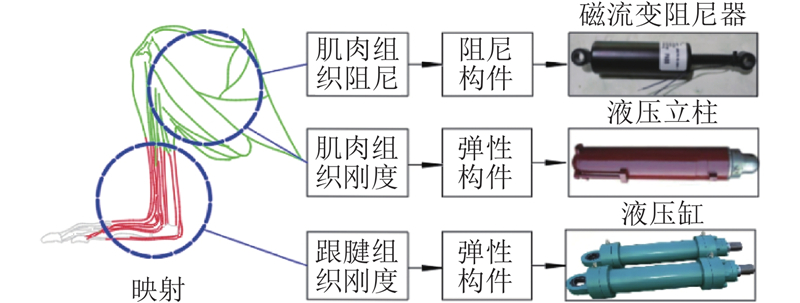
袋鼠腿部高效的抗冲击原理得益于它们独特的骨骼结构和肌肉结构. 与落地抗冲击特性相关的袋鼠腿部生物结构包括骨骼、关节、肌肉以及跟腱等. 肌肉结构的刚度为袋鼠站立状态提供稳定的支撑力;肌肉的阻尼产生可调节的阻尼力,同时存储部分冲击能量;跟腱的刚度能够存储部分冲击能量. 结合上述分析,将巷道超前液压支架与袋鼠腿进行类比:液压支架立柱工作时必须提供稳定的支护力,仿生机构在承受冲击载荷时要可调节地吸收、消耗部分冲击能量. 将袋鼠腿部肌肉组织作等效映射,如图1所示.
图 1
图 1 肌肉功能-等效元件功能映射
Fig.1 Muscle function to equivalent component function mapping
将肌肉组织阻尼映射为阻尼构件,即磁流变阻尼器,其在变化的电流下能够输出实时变化的阻尼力. 将肌肉组织刚度映射为液压立柱,在支护状态下提供稳定的支护力. 将跟腱组织刚度映射为弹性构件,即液压缸,其在仿生机构受到冲击时能够表现出一定的弹性吸能行为.
1.1. 运动学模型
图 2
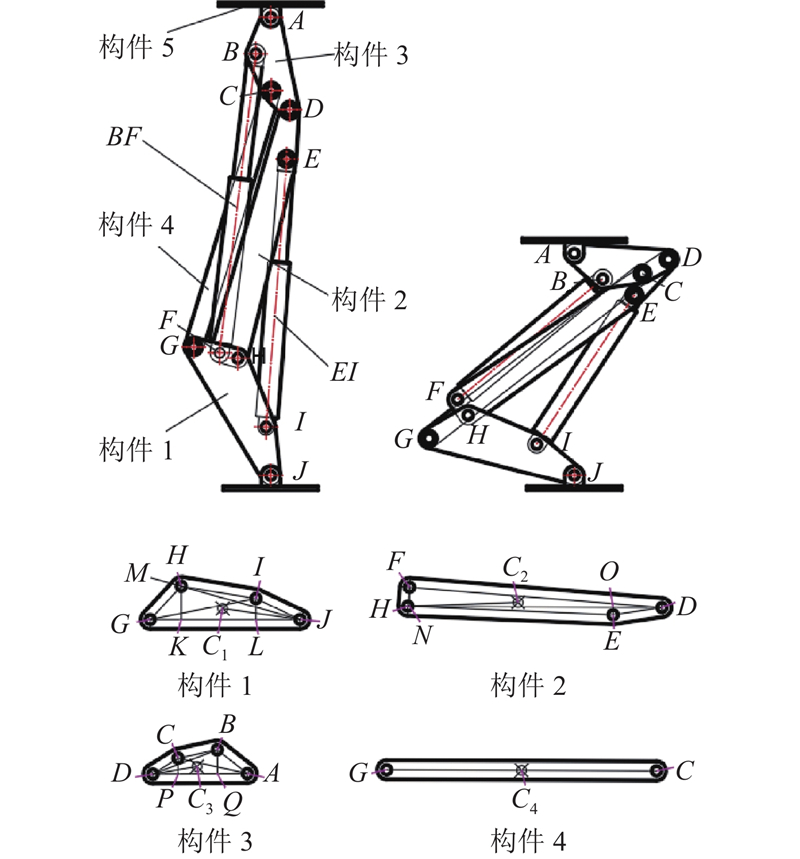
图 2 仿生机构的机构简图与构件铰链点示意图
Fig.2 Schematic diagram of bionic mechanism and illustration of component hinge points
表 1 ZQ4000/16/31型巷道超前液压支架立柱主要参数
Tab.1
| 参数 | 数值 |
| 初撑力 | 3 092 kN |
| 工作阻力 | 4 000 kN |
| 支架立柱一级/二级缸径 | 250/180 mm |
| 支架立柱一级/二级柱径 | 230/160 mm |
| 额定工作压力 | 40.74 MPa |
| 行程 | 1.6~3.1 m |
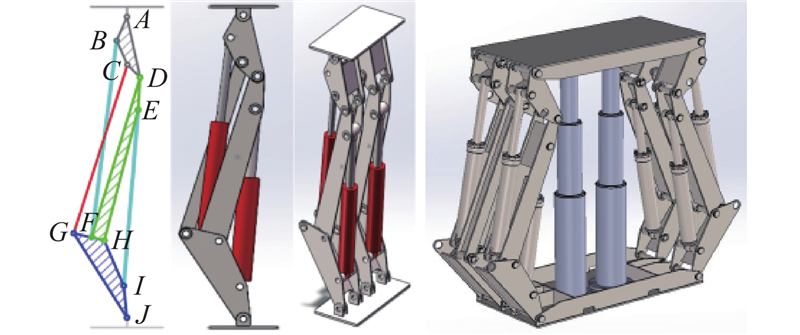
如图3所示,2个仿生机构并联安装于ZQ4000/16/31型巷道超前液压支架的两侧. 无仿生机构时,作用于支架顶梁的冲击力产生的冲击能量全部由支架的立柱吸收;安装仿生机构后,系统根据立柱下腔压力变化控制磁流变阻尼器的励磁线圈电流,进而改变磁流变液内磁场,使磁流变液的剪切极限增大或减小,最终使仿生机构输出随冲击变化的阻尼力,以消耗冲击能量,减少立柱吸能.
图 3
图 3 仿生机构在液压支架中的安装位置
Fig.3 Installation position of bionic mechanism in hydraulic support
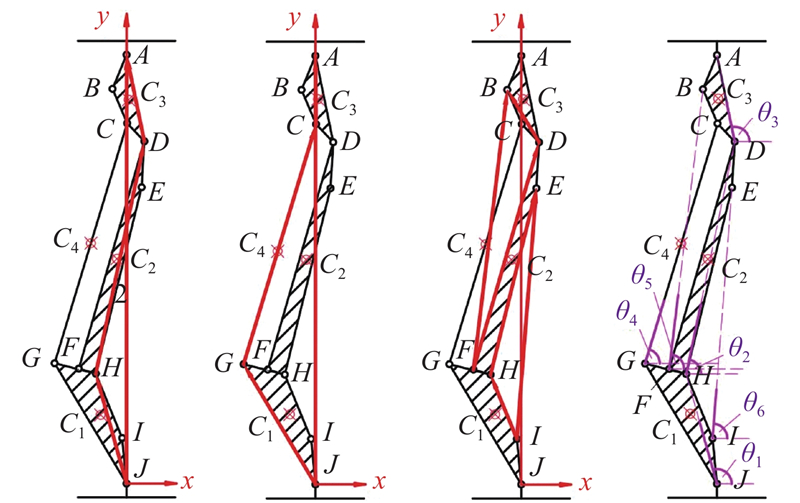
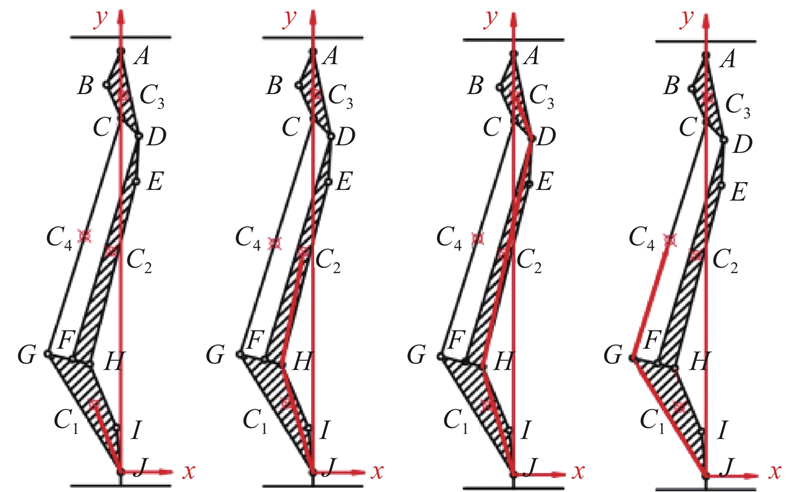
建立仿生机构的运动几何模型. 首先,利用封闭矢量法对仿生机构进行运动分析. 建立机构的封闭矢量图,如图4所示. 建立封闭矢量方程组,将其改写为投影式,得到机构位置方程组:
图 4
式中:Lmn为点m到点n的线段长度,其中m、n取铰链点A、B、C、D、E、F、G、H、I、J以及质心点C1、C2、C3、C4;θ1~θ6为构件1~4、磁流变阻尼器和液压缸的角位移;SJA为构件5的高度,即支护高度;SIE为液压缸伸出长度与缸长之和;SBF为磁流变阻尼器伸出长度与缸长之和. 对机构位置方程取一阶、二阶导数,可以求解构件1~5的速度、角速度、角加速度等运动量.
为了求解质心的相关运动量,根据图5列写构件1~4的质心C1、C2、C3、C4的4个非封闭矢量方程.将非封闭矢量方程投影于直角坐标系,列写其质心位移投影方程:
图 5
图 5 关于质心运动量的非封闭矢量图
Fig.5 Non-closed vector diagrams of centroid motion quantities
对上述质心位移投影方程求一阶、二级导数可得质心速度、角速度、角加速度等运动量.
利用仿生机构运动学几何模型可以求解机构在1.6~3.1 m高度下任意位姿对应的铰链点位置与构件运动状态,为仿生机构动力学分析中的动态静力学分析部分的铰链位置、等效量和动力学微分方程等效量的求解奠定基础.
1.2. 动力学模型
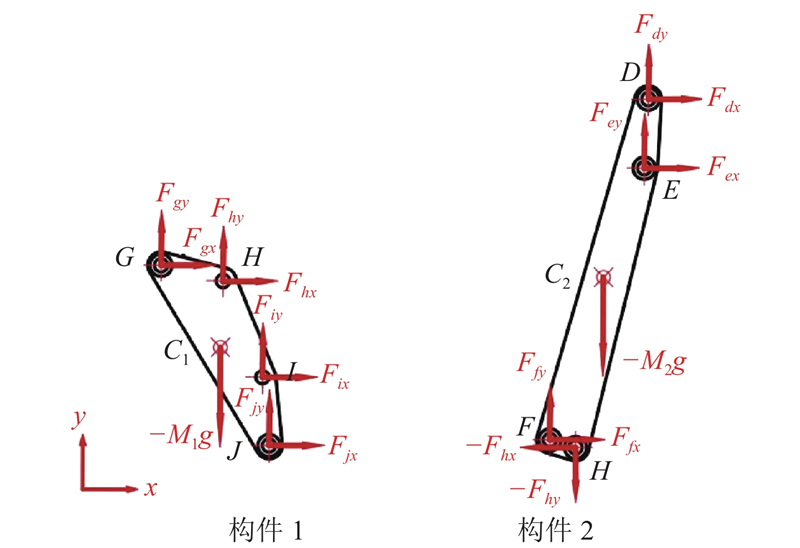
图 6
图 6 仿生机构的构件1与构件2受力分析
Fig.6 Force analysis of component 1 and component 2 in bionic mechanism
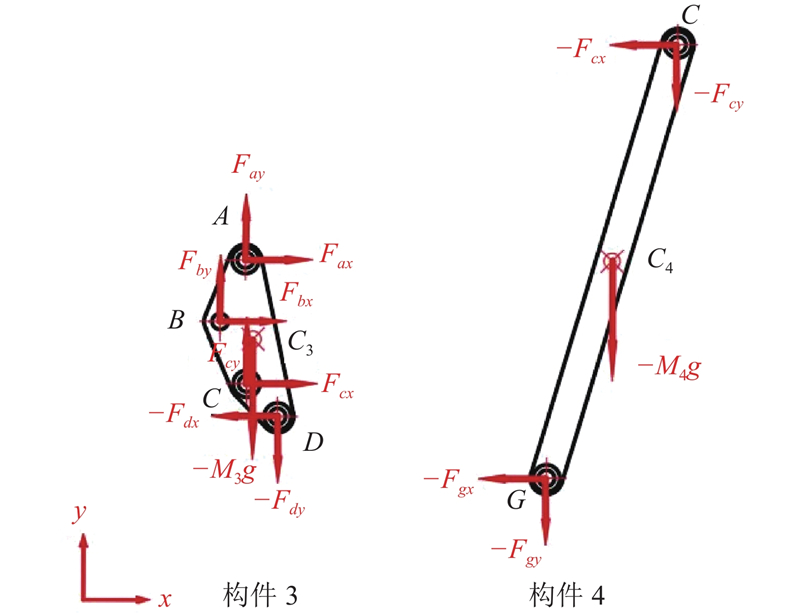
图 7
图 7 仿生机构的构件3与构件4受力分析
Fig.7 Force analysis of component 3 and component 4 in bionic mechanism
表 2 不同电流对应的磁流变阻尼器等效阻尼系数
Tab.2
| I/A | Ceq/ (N·s·mm−1) | I/A | Ceq/ (N·s·mm−1) | |
| 0.0 | 152.25 | 1.0 | 354.32 | |
| 0.5 | 252.03 | 1.5 | 452.12 |
式中:
xm和ym分别为点m在直角坐标系x轴和y轴上的位置,其中m取铰链点A、B、C、D、E、F、G、H、I、J以及质心点C1、C2、C3、C4.
利用式(6)所示的动态静力学分析结果求解等效阻抗力Fres(s,v,t),将Fex、Fey、Fix、Fiy、Fbx、Fby、Ffx、Ffy等效于A点后,等效阻抗力表示为
式中:s为等效构件位移,v为等效构件速度,t为迭代时间.
取构件5作为等效构件,可以得到等效构件上的等效力:
式中:Fimp(t)为任意冲击力输入.
根据式(7)、(8)与所取等效构件,构造仿生机构的动力学微分方程:
式中:Me(s)为等效质量,
根据式(9)构造三变量四阶Runge-Kutta法迭代格式:
推导仿生机构的动力学模型与三变量四阶Runge-Kutta法迭代求解格式,可以得到在任意冲击载荷输入下,不同构件运动学尺寸对应的仿生机构冲击位移与冲击速度响应,为后续对仿生机构的抗冲击特性进行响应面优化奠定基础.
2. 基于响应曲面法的优化设计
仿生机构尺寸参数是由袋鼠腿部结构的平均crural系数[24]以及ZQ4000/16/31型巷道超前液压支架部分的技术参数确定的. 磁流变阻尼器、液压缸的装配位置参数仅满足装配条件,并未考虑其对抗冲击特性的影响. 因此需要对机构进行优化.
2.1. 优化变量可行域的确定
首先,选取股骨长度LJG和腓骨长度与股骨长度的比值α(LHD/LJG)为1组优化变量(LJG, α),股骨长度LJG和跖骨长度与股骨长度的比值β(LDA/LJG)为1组优化变量(LJG, β).
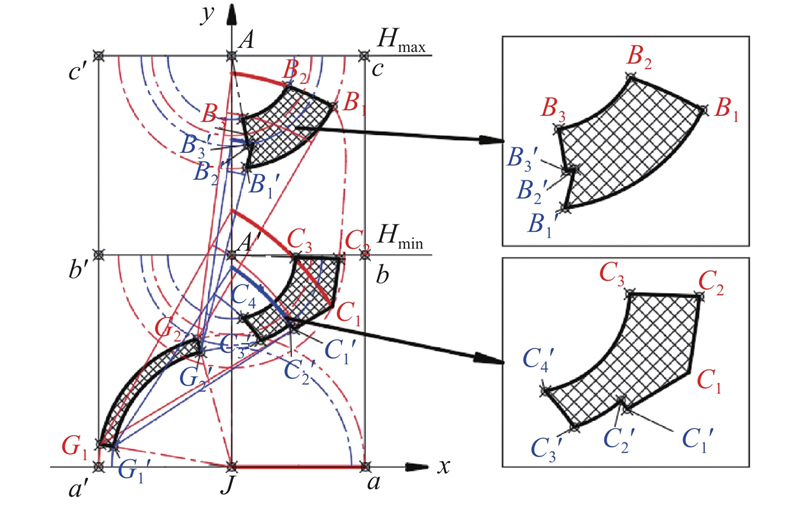
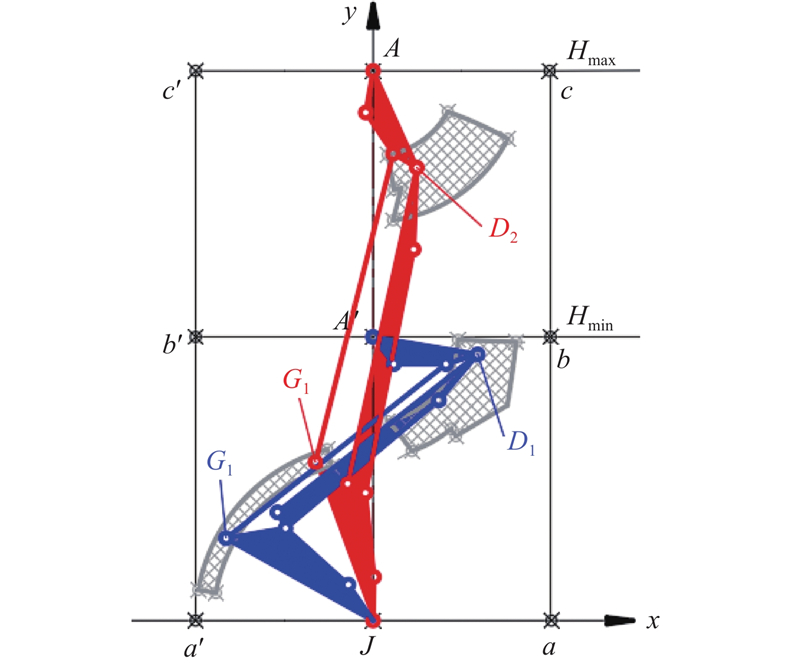
最后,利用MATLAB编写程序,细化优化变量的可行域. 根据机构位置方程,在支架的顶梁高度极限位置SJA=3.1 m与SJA=1.6 m处判断是否有解,从而细化初步的可行域. 此外,在仿生机构支护状态下,应避免处于死点姿态[25]. 细化后,铰链点D、G的可行域如图8所示.图中,a'a为仿生机构最大宽度,a'a=2 000 mm; b'b为支架支护高度下限;c'c为支架支护高度上限. b'b到a'a的距离Hmin=1 600 mm,即ZQ/
图 8
图 9
图 9 数据点(α, β, LJG)对应的仿生机构位姿
Fig.9 Poses of bionic mechanism corresponding to data point (α, β, LJG)
细化可行域后,结合仿生机构中每个构件的几何结构,确定铰接点位置(LLI, LJL)、(LEO, LDO)、(LFN, LHN)、(LBQ, LAQ)的可行域. (LJG, α)、(LJG, β)、(LLI, LJL)、(LEO, LDO)、(LFN, LHN)、(LBQ, LAQ)的初值、可行域以及步长如表3所示.
表 3 仿生机构的不同优化变量的可行域
Tab.3
| α | β | LJG/mm | LLI/mm | LJL/mm | LFN/mm | LHN/mm | LEO/mm | LDO/mm | LBQ/mm | LAQ/mm | |
| 初值 | 1.83 | 0.64 | 960 | 150 | 300 | 95 | 50 | 50 | 350 | 150 | 240 |
| 可行域 | 1.80~1.85 | 0.62~0.68 | 940~980 | 120~180 | 280~325 | 80~120 | 10~70 | 35~65 | 310~390 | 100~150 | 190~290 |
| 步长 | 0.01 | 0.01 | 10 | 7.5 | 10 | 5 | 10 | 5 | 10 | 5 | 10 |
2.2. 基于响应曲面法的仿生袋鼠腿抗冲击机构优化
图 10
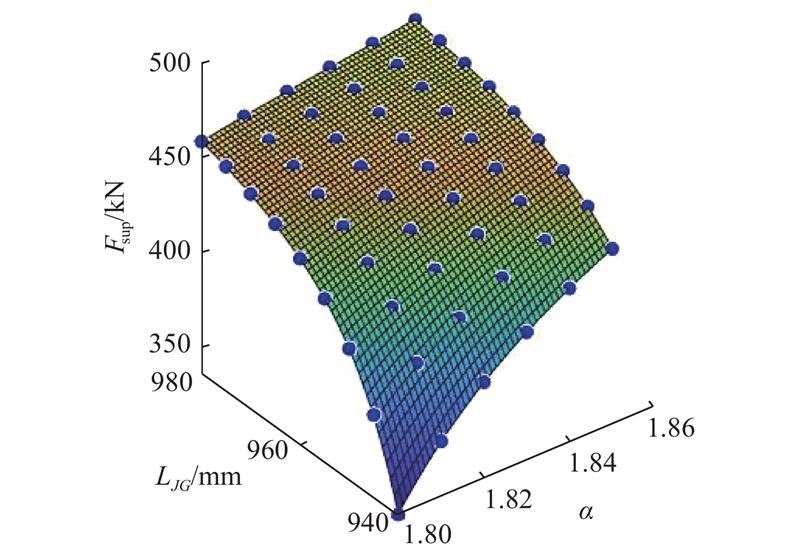
图 10 机构支护力Fsup关于参数LJG与α的响应面
Fig.10 Response surface of mechanical support force Fsup to parameters LJG and α
图 11
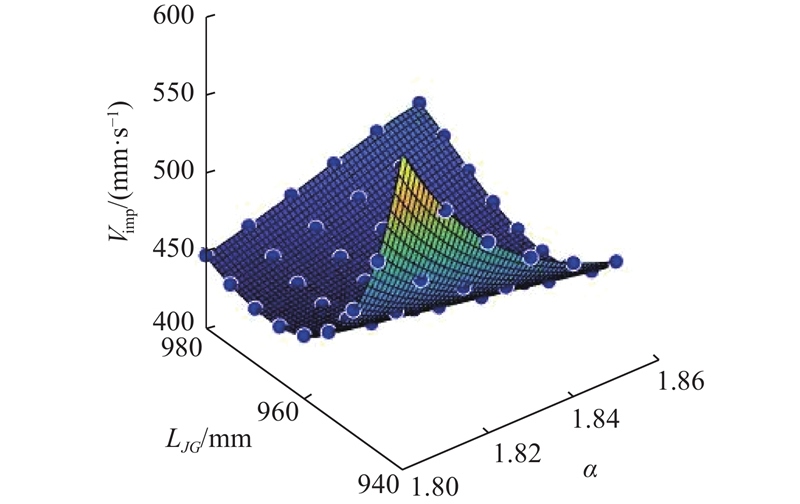
图 11 冲击速度Vimp关于参数LJG与α的响应面
Fig.11 Response surface of impact velocity Vimp to parameters LJG and α
式中:Lg为导向长度,Lp为活塞长度,活塞直径D=170 mm.
液压缸的活塞长度Lp取值为250 mm. 对于磁流变阻尼器,为了留出电磁线圈等组件的装配空间,Lp取值为300 mm. 利用上述装配体条件作为约束条件构造α与LJG的优化问题:
式中:Vimp(α, LJG)为机构等效构件最大冲击速度的响应面方程;Fsup(α, LJG)为机构支护力的响应面方程;LEI_max为支护状态下的液压缸长度;LBF_max为支护状态下的阻尼器长度;LEI_min为非支护状态下液压缸的长度;LBF_min为非支护状态下阻尼器的长度;LEP1为液压缸/阻尼器活塞杆耳板长度;LEP2为液压缸/阻尼器缸体板长度.
图 12
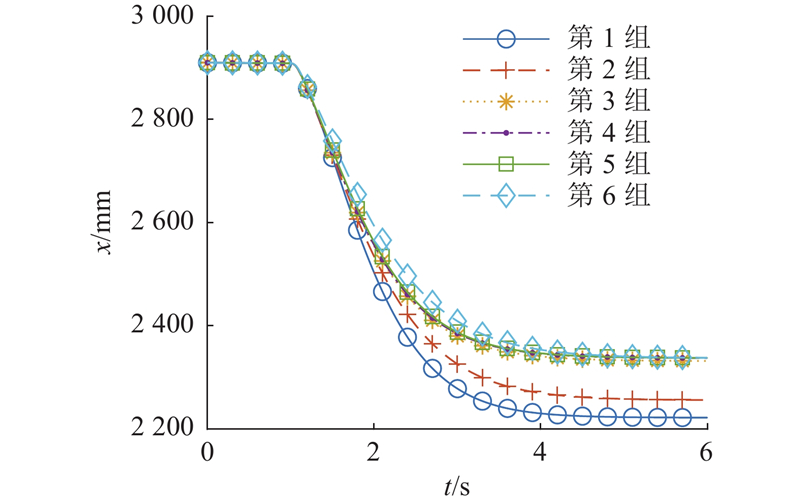
图 12 响应面优化过程中的冲击位移响应
Fig.12 Impact displacement response during process of response surface optimization
图 13
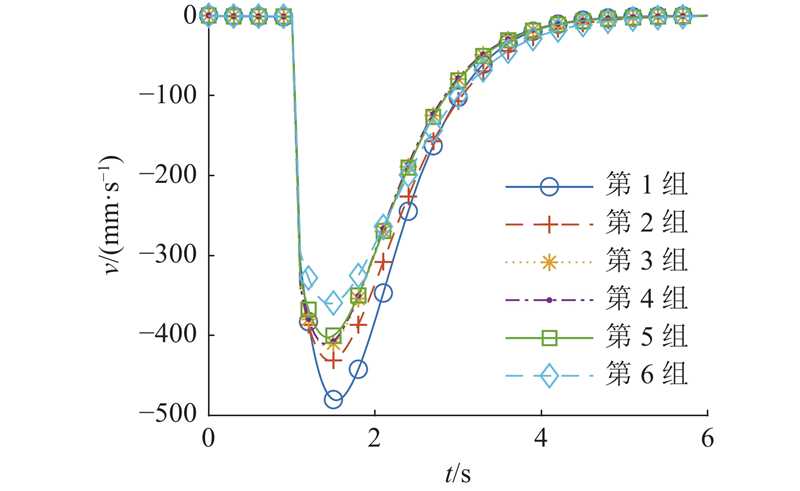
图 13 响应面优化过程中的冲击速度响应
Fig.13 Impact velocity response during response surface optimization process
LBQ=150 mm, LAQ=204 mm, LEO=44 mm, LDO=310 mm, LFN=120 mm, LHN=10 mm, LLI=126 mm, LJL=280 mm.
3. 仿真分析
围绕冲击位移、 冲击压力和吸能特性,对应用仿生机构的支架与传统支架进行对比分析.
通过ADAMS、AMESim与Simulink联合仿真进行仿真分析,建立联合仿真模型. 首先,根据优化后的运动学尺寸与表1中的主要几何参数,在ADAMS软件中建立应用仿生机构的ZQ4000/16/31型巷道超前液压支架的动力学模型. 建立冲击重物模型,模拟重物下落至支架顶梁所产生的冲击力,冲击力为支架工作阻力的1.1~1.4倍[26],如图14中左图所示. 将其以fmu文件形式导入AMESim软件中,作为机械场部分的仿真模型. 其次,在Simulink软件中建立磁流变阻尼器力学模型,如图14中右图所示;该模型建立了冲击速度v、励磁线圈电流I与输出阻尼力F之间的关系,包含MR-7850型磁流变液的磁感应强度、磁场强度与剪切极限的关系. 将其导入AMESim中的SL2Amecosim模块,作为磁场部分的仿真. 最后,根据表1所示的ZQ4000/16/31型巷道超前液压支架立柱支护性能参数,在AMESim中建立应用仿生袋鼠腿抗冲击机构的ZQ4000/16/31型巷道超前液压支架的液压系统模型,并搭建液压回路与控制回路,分别用于液压场与信号场部分的仿真. 液压管路与信号线路如图15所示.
图 14
图 14 支架动力学模型和磁流变阻尼器力学模型
Fig.14 Dynamic model of support and mechanical model of magnetorheological damper
图 15
图 15 应用仿生机构的ZQ4000/16/31型巷道超前液压支架联合仿真模型
Fig.15 Co-simulation model of ZQ4000/16/31 roadway advance support with bionic mechanism
3.1. 冲击位移对比
调节磁流变阻尼器等效阻尼系数Ceq,根据表2数据,使等效阻尼系数Ceq=150 N·s/mm,250 N·s/mm,350 N·s/mm,450 N·s/mm. 将其与普通ZQ4000/16/31型巷道超前液压支架(Ceq=0 N·s/mm)进行对比分析,分析指标包括冲击后的顶梁位置x、立柱下腔最大压力Pcol、立柱吸能量Ecol和磁流变阻尼器吸能量Emag.
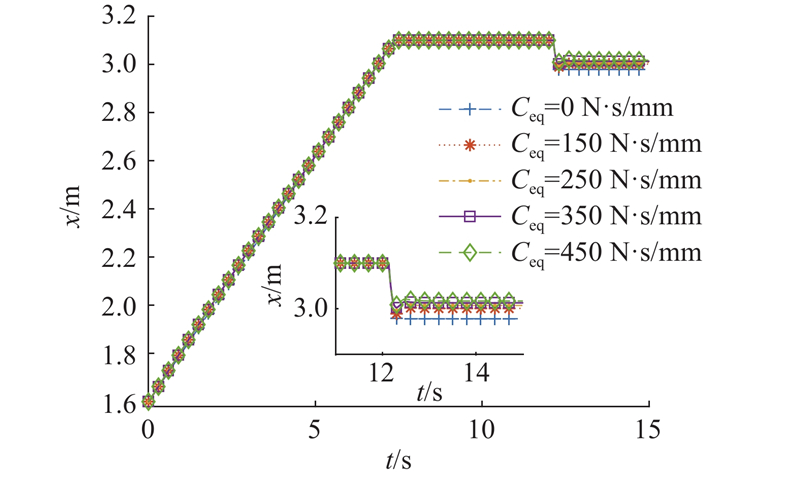
如图16所示,普通ZQ4000/16/31型巷道超前液压支架在冲击后的顶梁位移为122 mm;当等效阻尼系数为150 N·s/mm时,顶梁位移为99 mm,与普通支架相比,位移下降18.85%;当等效阻尼系数为250 N·s/mm时,顶梁位移为92 mm,下降24.59%;当等效阻尼系数为350 N·s/mm时,顶梁位移为87 mm,下降28.69%;当等效阻尼系数为450 N·s/mm时,顶梁位移为83 mm,下降31.97%. 因此,普通的ZQ4000/16/31型巷道超前液压支架在冲击后的顶梁位移明显大于应用仿生袋鼠腿抗冲击机构的ZQ4000/16/31型巷道超前液压支架的顶梁位移,且随着磁流变阻尼器等效阻尼系数的增大,冲击后的顶梁位移有显著下降.
图 16
图 16 不同等效阻尼系数下的冲击位移对比
Fig.16 Comparison of impact displacements under different equivalent damping equivalent coefficients
3.2. 冲击压力对比
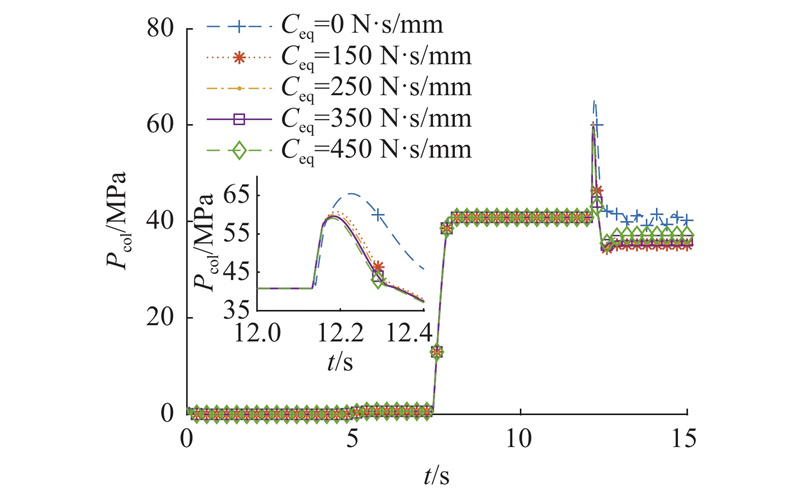
如图17所示,普通ZQ4000/16/31型巷道超前液压支架在冲击后的立柱下腔最大压力Pcol=65.55 MPa;当等效阻尼系数为150 N·s/mm时,立柱下腔最大压力为60.87 MPa,与普通支架相比,降低了7.14%;当等效阻尼系数为250 N·s/mm时,立柱下腔最大压力为60.24 MPa,降低了8.10%;当等效阻尼系数为350 N·s/mm时,立柱下腔最大压力为59.67 MPa,降低了8.97%;当等效阻尼系数为450 N·s/mm时,立柱下腔最大压力为59.13 MPa,降低了9.79%. 因此,普通ZQ4000/16/31型巷道超前液压支架在冲击后的立柱下腔最大压力明显高于应用仿生袋鼠腿抗冲击机构的ZQ4000/16/31型巷道超前液压支架的立柱下腔最大压力,并且随着磁流变阻尼器等效阻尼系数的增大,冲击后的立柱下腔最大压力有显著下降.
图 17
图 17 不同等效阻尼系数下冲击后立柱下腔最大压力对比
Fig.17 Comparison of maximum pressures in lower chamber of column after impact under different equivalent damping coefficients
3.3. 吸能特性对比
巷道顶板的冲击能量EIMP有以下转化途径:1)转化为磁流变阻尼器的阻尼消耗Ed;2)转化为液压油压缩变形的能量与安全阀溢流时液体的动能Eh;3)转化为顶梁与仿生机构构件的动能Ek;4)转化为仿生机构构件弹性变形的弹性势能Ep. 因此,冲击能量的转化可以描述为
上述冲击能量的转化途径以Ed、Eh与Ek为主. 针对Eh中的立柱吸能Ecol和冲击能量中的磁流变阻尼器耗能Ed (即吸能量Emag),对普通ZQ4000/16/31型巷道超前液压支架和磁流变阻尼器等效阻尼系数分别为150、250、350、450 N·s/mm的支架的受冲性能进行对比分析.
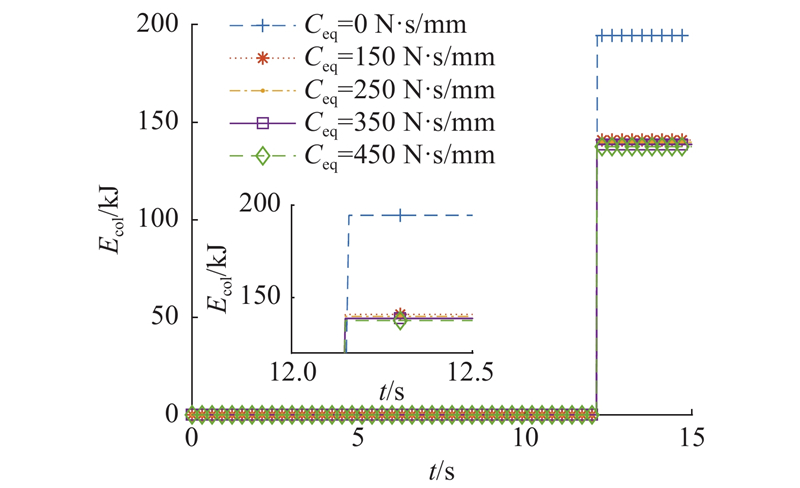
由图18可知,普通ZQ4000/16/31型巷道超前液压支架在冲击过程开始(第12 s)至冲击过程结束这一阶段的立柱吸能为194.5 kJ;当磁流变阻尼器等效阻尼系数为150 N·s/mm时,立柱吸能为140.9 kJ,与普通支架相比,降低了27.56%;当等效阻尼系数为250 N·s/mm时,立柱吸能为139.8 kJ,降低了28.12%;当等效阻尼系数为350 N·s/mm时,立柱吸能为138.7 kJ,降低了28.69%;当等效阻尼系数为450 N·s/mm时,立柱吸能为137.5 kJ,降低了29.31%.
图 18
图 18 不同等效阻尼系数下液压支架立柱吸能量
Fig.18 Energy absorption of hydraulic support column under different equivalent damping coefficients
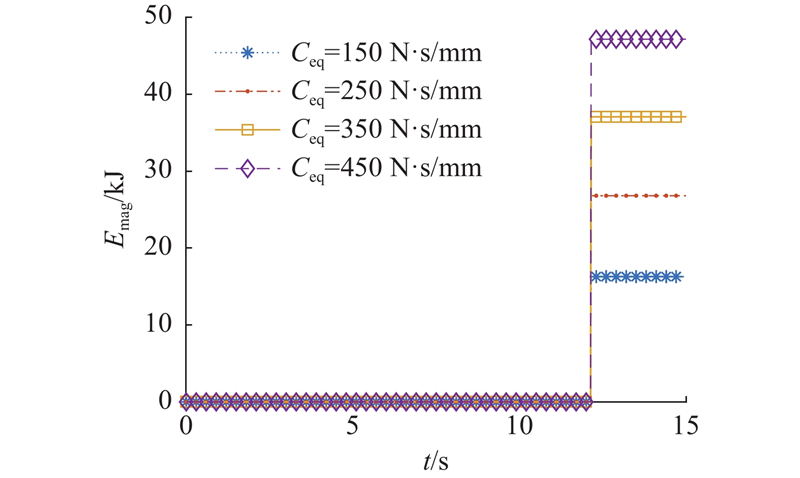
如图19所示,随着磁流变阻尼器等效阻尼系数的增加,磁流变阻尼器吸能量Emag增加. 当等效阻尼系数为150 N·s/mm时,磁流变阻尼器吸能量为16.29 kJ;当等效阻尼系数为250 N·s/mm时,吸能量为26.81 kJ;当等效阻尼系数为350 N·s/mm时,吸能量为37.07 kJ;当等效阻尼系数为450 N·s/mm时,吸能量为47.16 kJ.
图 19
图 19 不同等效阻尼系数下磁流变阻尼器的吸能量
Fig.19 Energy absorption of magnetorheological damper under different equivalent damping coefficients
由上述对比分析可知,应用仿生袋鼠腿抗冲击机构的ZQ4000/16/31型巷道超前液压支架的立柱吸能显著小于普通ZQ4000/16/31巷道超前液压支架,其抗冲击性能得到了显著的提升.
4. 结 语
基于袋鼠腿的生物结构特性,结合磁流变控制技术,研究应用于巷道液压支架的仿生袋鼠腿智能抗冲击机构. 首先建立仿生袋鼠腿机构的运动学和动力学模型,确定优化参数的可行域、响应面以及响应面方程. 其次结合优化变量可行域与响应面方程,以冲击位移与冲击速度最小化为优化目标,实现基于响应曲面法的仿生机构各构件关键参数和液压缸、磁流变阻尼器的铰接点位置的优化. 最后根据优化后的运动学几何参数建立仿生机构模型,并将优化后的仿生机构并联安装于ZQ4000/16/31型巷道超前液压支架立柱两端. 以磁流变阻尼器的等效阻尼系数Ceq为变量,将Ceq由150 N·s/mm递增至450 N·s/mm,以顶梁冲击位移、立柱下腔压力、立柱吸能量以及磁流变阻尼器吸能量为研究指标进行联合仿真分析.
研究结果表明,基于仿生袋鼠腿的的巷道超前液压支架磁流变智能抗冲击机构具备对多种工况的适应性. 通过改变磁流变阻尼器的等效阻尼系数Ceq,可以实时调整仿生机构的整体吸能状态. 当Ceq从150 N·s/mm递增至450 N·s/mm时,ZQ4000/16/31型巷道超前液压支架因安装仿生机构而产生的冲击后顶梁位移降低量由18.55%增至31.97%,立柱下腔压力降由7.14%增至9.79%,立柱吸能降低量由27.56%增至29.31%,磁流变阻尼器吸能量由16.29 kJ增至47.16 kJ.
该仿生机构的应用能够有效降低巷道超前液压支架立柱在冲击载荷作用下的吸能量,提高了巷道超前液压支架的抗冲击能力. 未来的工作将开展物理样机的性能测试,并在此基础上进行该类型机构的优化和现场应用.
参考文献
我国煤炭需求、探查潜力与高效利用分析
[J].DOI:10.6038/cjg20161224 [本文引用: 1]
Analysis of exploration, potential reserves and high efficient utilization of coal in China
[J].DOI:10.6038/cjg20161224 [本文引用: 1]
2025年中国能源消费及煤炭需求预测
[J].
Prediction on the energy consumption and coal demand of China in 2025
[J].
煤矿智能化(初级阶段)研究与实践
[J].
Research and practice on intelligent coal mine construction (primary stage)
[J].
我国煤矿冲击地压防治现状与难题
[J].
Present situation and problems of coal mine rock burst prevention and control in China
[J].
液压支架双伸缩抗冲击立柱动态分析
[J].DOI:10.3969/j.issn.1006-6225.2010.02.021 [本文引用: 1]
Dynamic analysis of double-telescopic prop against shocking in powered support
[J].DOI:10.3969/j.issn.1006-6225.2010.02.021 [本文引用: 1]
液压立柱内外翻转式吸能防冲构件特性数值分析
[J].DOI:10.11731/j.issn.1673-193x.2015.07.012 [本文引用: 1]
Numerical analysis on properties of inside-outside overturning energy absorption and anti-impact components of hydraulic column
[J].DOI:10.11731/j.issn.1673-193x.2015.07.012 [本文引用: 1]
矿用六边形折痕构件吸能防冲特性数值分析
[J].
Numerical analysis of the mining hexagonal crease components and their energy absorption and anti-impact features
[J].
矿用扩径式吸能构件吸能防冲特性研究
[J].
Energy absorption and anti-impact properties of mine diameter-expanding energy absorption components
[J].
自移式吸能防冲巷道超前支架设计与研究
[J].
Design and study of self-moving energy absorption and anti-impact roadway advanced support
[J].
诱导式防冲支护装置的屈曲吸能特性研究
[J].DOI:10.11731/j.issn.1673-193x.2016.06.008
Study on buckling energy-absorption properties of induced supporting device for rock burst prevention
[J].DOI:10.11731/j.issn.1673-193x.2016.06.008
矿用扩径式吸能防冲构件特性数值分析
[J].
Numerical analysis on energy absorption and anti-impact properties of mine diameter expanding energy absorption components
[J].
吸能型防冲立柱液体冲击问题研究
[J].
A study on liquid shock of energy-absorbing anti-impact hydraulic column
[J].
基于磁流变缓冲的液压支架抗冲击技术研究
[J].DOI:10.11832/j.issn.1000-4858.2021.06.006 [本文引用: 1]
Anti shock support based on MR damper
[J].DOI:10.11832/j.issn.1000-4858.2021.06.006 [本文引用: 1]
动物进化的抗冲击策略及其仿生机理研究
[J].DOI:10.6052/1000-0992-20-027 [本文引用: 1]
Research progress of impact-resistance strategies and biomimetic mechanism in animal evolution
[J].DOI:10.6052/1000-0992-20-027 [本文引用: 1]
PAM仿袋鼠腿悬架仿真建模及垂向参数特性研究
[J].DOI:10.3969/j.issn.1673-2057.2019.05.013 [本文引用: 1]
Modeling and vertical parameter characteristics study of PAM bionic kangaroo leg suspension
[J].DOI:10.3969/j.issn.1673-2057.2019.05.013 [本文引用: 1]
基于Hill肌肉模型的仿袋鼠腿悬架控制特性研究
[J].
Control characteristics study of bionic kangaroo leg suspension based on Hill muscle model
[J].
带有仿袋鼠腿结构的双横臂悬架建模及特性分析
[J].
Modeling and characteristic analysis of a double-wishbone suspension with a bionic kangaroo leg structure
[J].
含圆弧形缓冲结构的仿袋鼠腿悬架建模与行为特性研究
[J].DOI:10.7652/xjtuxb202109004 [本文引用: 1]
Research on modeling and behavioral characteristics of bionic kangaroo leg suspension with circular arc-buffer structures
[J].DOI:10.7652/xjtuxb202109004 [本文引用: 1]
自动锁付机构夹头多响应优化设计
[J].
Multi-response optimization design of automatic locking mechanism chuck
[J].
一种新型引磁式磁流变阻尼器研究
[J].
New magneto-inducible magnetorheological damper
[J].
磁流变阻尼器Bingham力学模型改进及参数辨识
[J].DOI:10.3969/j.issn.1001-3997.2024.01.003 [本文引用: 1]
Improvement of Bingham mechanical model of MRD and parameter identification
[J].DOI:10.3969/j.issn.1001-3997.2024.01.003 [本文引用: 1]
磁流变阻尼器性能及振动控制
[J].DOI:10.3969/j.issn.1000-8055.2004.03.004 [本文引用: 1]
Performance of magnetorheological damper with its application to vibration control
[J].DOI:10.3969/j.issn.1000-8055.2004.03.004 [本文引用: 1]
磁流变阻尼器等效线性阻尼系数计算
[J].DOI:10.3969/j.issn.1004-132X.2014.13.004 [本文引用: 1]
Calculation of equivalent linear damping coefficient of a magnetorheological damper
[J].DOI:10.3969/j.issn.1004-132X.2014.13.004 [本文引用: 1]
Walking on five legs: investigating tail use during slow gait in kangaroos and wallabies
[J].