多旋翼无人机(UAV)被用于工业和农业中的诸多领域[1],如物流运输[2]、地理测量[3]、林业作业[4]等. 合理的路径规划是无人机安全作业的基础,无人机在满足如效率、能耗或避障等关键约束下,生成位移、速度及加速度等参数的时间序列值,实现稳定飞行控制的目标[5]. Rao等[6]提出基于人工势场的改进A*算法,解决了多机协同运输的路径规划问题. 杨森等[7]将能量消耗作为优化目标并利用遗传算法(genetic algorithm, GA)规划物流无人机路线. Phung等[8]为了实现大型建筑群的高效检测,提出基于旅行商模型的离散粒子群算法,该算法结合了视觉感知规划,因此系统对GPU的要求较高. Aslan等[9]专注于在有障碍物的三维环境中寻找最佳路径,提出基于目标距离的GDRRT*(goal distance rapid random tree)方法,该策略具有较好的鲁棒性,但搜寻效率不足. 上述研究主要聚焦于单一优化目标,适用于结构较为简单的场景. 多目标优化策略是有效实现复杂环境或复杂任务中路径规划的技术手段. Peng等[10]提出基于链接与预测的动态多目标进化算法,利用预测模型控制策略,实时更新环境信息进而实现避障的目标. Guerrero等[11] 将微型无人机的能耗与飞行距离作为优化目标,构建Zermelo旅行商模型,基于兴趣点网格划分算法实现路径规划,但兴趣点的数量及分布设计主要基于人工经验,难以适用于复杂场景. Phung等[12]提出基于球面矢量的粒子群优化算法,通过建立粒子位置与无人机速度、转角和爬升/俯冲角的对应关系,实现障碍规避和能耗最优的优化目标.
相较于蚁群算法、粒子群算法及其他传统启发式优化方法,第二代非支配排序遗传算法(non-dominated sorting genetic algorithm II, NSGA-II)利用分层及拥挤度排序策略,能够改善种群多样性及加速收敛[13],在复杂场景中的多目标优化领域有广泛应用. Yu等[14]提出基于NSGA-II的节点优化策略,以解决无人机飞行距离和数据传输能耗同步最小化问题. Bashir等[15]重新设计交叉和变异算子,并引入梯度准则,以提升算法的收敛效率,实现避障和能耗同步优化,但算法的最终收敛精度受初始值影响较大. 当搜索过程在高维空间(优化目标大于3个)时,NSGA-II的迭代成本会急剧增加,算法通过估算拥挤度来增强个体多样性的能力会被削弱,甚至无法实现[16]. 第三代非支配排序遗传算法(NSGA-III)用参考点代替拥挤度排序,在高维空间优化过程中的鲁棒性比二代强. 基于NSGA-III,Ghambari等[17]构造包括飞行距离、稳定性和无人机数量规模的优化目标,用果蝇算法代替部分遗传过程,NSGA-III收敛精度提高但算法效率不足. Tavana等[18]设计新型NSGA-III以改善人机协作过程中的设备反应灵敏性. 在农业采摘领域,Goel等[19]运用glow-worm群体启发式算法实现机器人在三维空间中的动态避障路径规划,Zhang等[20]实现移动小车在最小化导航成本约束下的路径规划目标. NSGA-III在如机械臂、移动小车的机器人领域的多目标优化方面有广泛应用,然而针对无人机路径规划的研究鲜少.
在复杂场景中,无人机全局路径规划研究存在如下问题:1)研究大多集中在构建1个[6, 20]或2个[17, 21]优化目标;2)在高维空间(目标函数大于3)优化时,基于启发式[22]、非凸优化[23]、机器学习[21]等算法难以在计算效率和精度之间取得良好的平衡;3)基于点到点模型获取的初始轨迹,往往存在几何特征不连续的尖锐区域,会引起无人机在飞行过程中位置、速度和加速度的频繁突变[5]. 为了解决复杂场景中无人机飞行全局最优路径高效规划问题,本研究提出联合NSGA-III和高阶光顺插值的轨迹优化算法,基于环境信息与飞行任务构建多目标函数,利用优化算法生成初始最优路径,通过判断潜在风险区域并采用五次B样条进行光顺拟合.
1. 基于多目标约束的路径优化问题描述
充分考虑机械性能、环境特性和应用要求等因素的隐含限制,是实现无人机安全作业的重要保障. 随着外在约束的增加以及约束之间的内在冲突,飞行路径的计算过程可能相当困难,为此将环境信息和作业目标进行抽象,转换成可执行目标函数并构成高维优化空间. 本研究综合考虑路径长度、安全避障和稳定性3个重要约束.
1.1. 路径长度
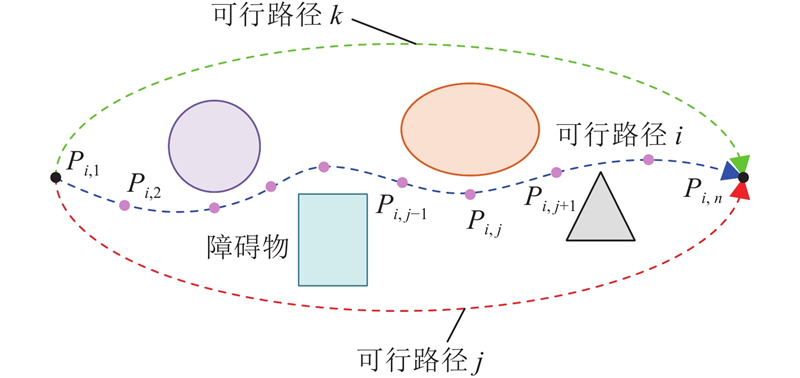
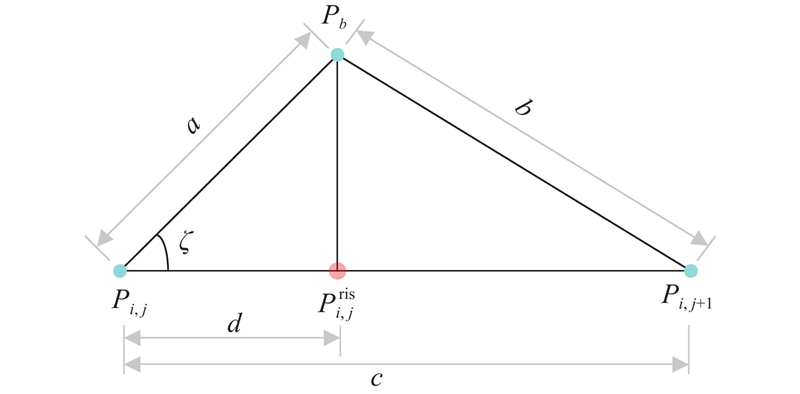
路径长度是影响无人机飞行效率及能耗指标的关键因素. 如图1所示,将第i条路径上的第j个航迹点记为
图 1
其中
1.2. 障碍威胁
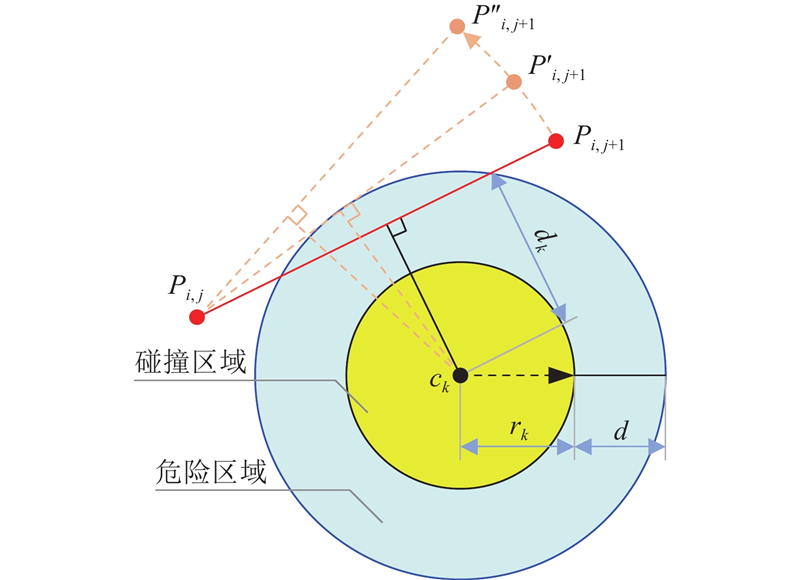
在复杂的环境中,随机分布的障碍物是影响无人机飞行轨迹的重要因素. 当无人机接近障碍物时,发生碰撞的概率随时间(或两者距离)而变化. 如图2所示,为了度量碰撞风险,基于包络法将障碍物进行圆形包络,圆心和半径分别为
图 2
式中:
式中:
1.3. 飞行稳定性
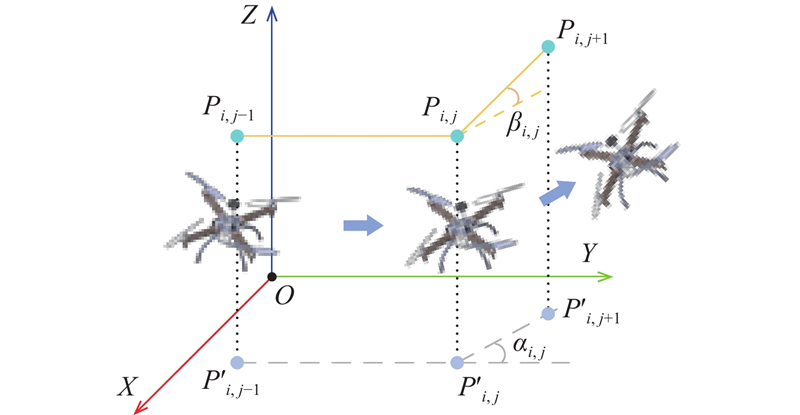
水平方向的转向夹角
图 3
同理,垂直爬升夹角计算式为
无人机沿期望路径飞行时,2个角度的变化曲线应尽可能平滑,从而增强飞行稳定性. 目标函数为
式中:
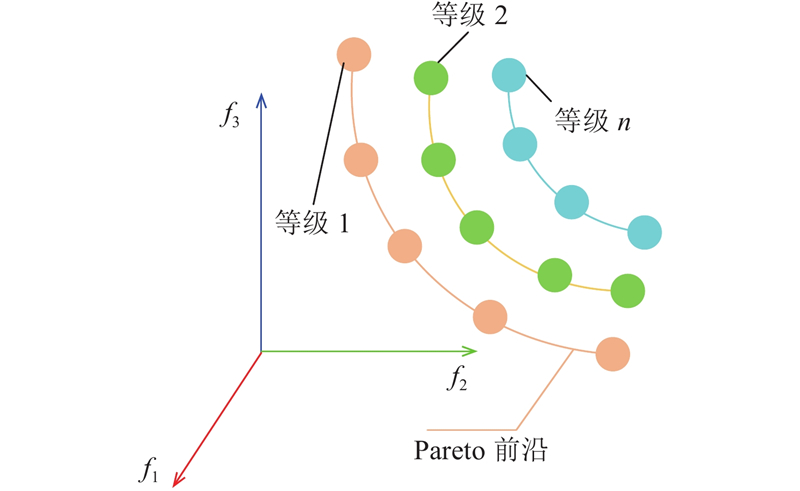
综合考虑包括飞行效率、障碍规避和稳定性约束,分布在Pareto前沿的优化目标函数为
式中:
2. 基于第三代非支配排序遗传算法的初始优化路径求解
启发式优化算法基于仿生和自然进化过程来搜索最优解,具有适应性广、鲁棒性强的优点,但在处理复杂系统时,易陷入局部最优、收敛效率不足. 本研究采用基于参考点规则的NSGA-III,以提升无人机轨迹规划的效率和精度.
2.1. 基于非支配关系的种群分层策略
不同于NSGA-II,NSGA-III通过设计参考点取代传统基于拥挤度排序的原则,能够进一步提升样本个体的多样性和进化效率[11]. 总样本
图 4
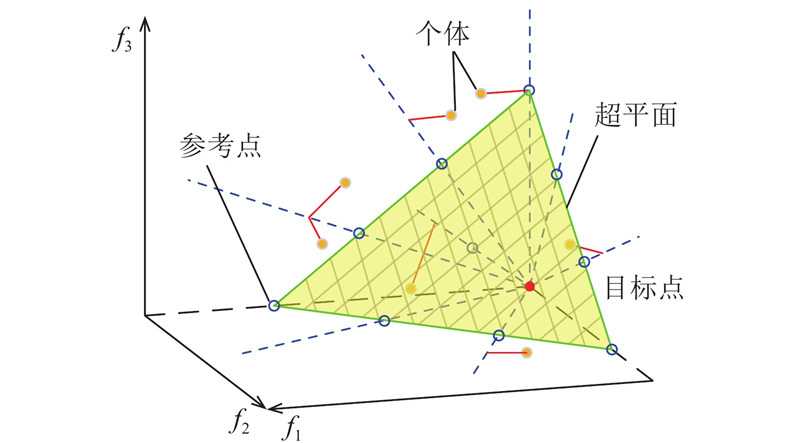
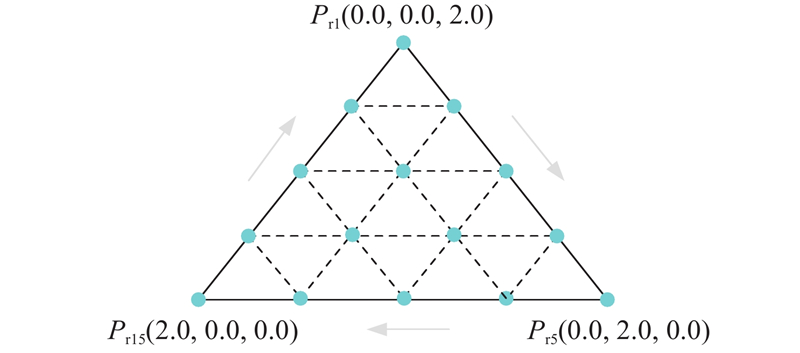
2.2. 优化空间的超平面与参考点设计
NSGA-III采用参考点准则,基于Dennis[10]法构造归一化超平面,参考点
其中
图 5
其中
基于式(10)、(11),参考线
式中:
2.3. 高维空间的最优解集计算
(1)初始化. 初始化规模为
式中:
(2)选择、交叉和变异. 选择方式:根据种群内个体的适应度函数值进行选择排序,在多目标优化函数中,多个适应度函数值须相加. 本研究开发领域是飞行路径规划领域,因此提出算术交叉方式以及限制范围的个体变异方式,当生成的1个随机数小于交叉概率
式中:α为交叉比率,
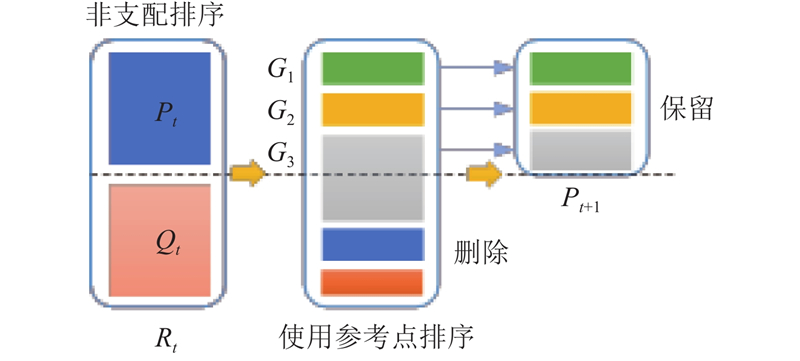
(3)分层与排序. 基于支配关系对群体
(4)获得新种群. 由于群体规模从2m减少到m,须淘汰50%的个体. 对于不能完全保留的层级,采用基于参考点的方法进行排序. 根据优劣关系,按降序保存,形成下一代种群
(5)迭代. 重复步骤(2)至(4),直到完成所有迭代计数或达到收敛精度. 基于参考点的种群进化过程如图6所示.
图 6
(6)计算最优解集. 多目标优化通常存在多组最优解,进而构成Pareto前沿.
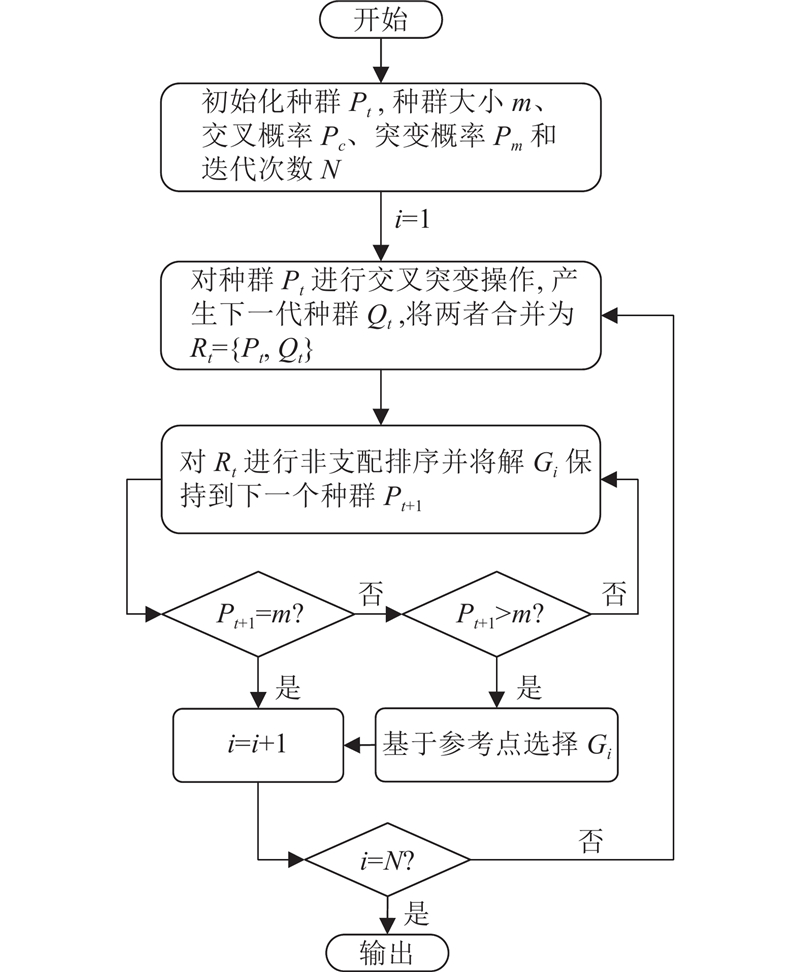
算法通过保留优先层级个体确保收敛性,同时基于参考点提升样本的多样性,进而增强全局优化解搜索的能力,算法流程如图7所示.
图 7
图 7 第三代非支配排序遗传算法的优化流程图
Fig.7 Optimisation flowchart of non-dominated sorting genetic algorithm III
3. 具有高阶光顺性约束的运动空间插值
优化算法求解的初始路径通常由大量的线段组成,其几何特征难以保证二阶及以上的微分连续性. 为了改善无人机飞行轨迹的光顺性,考虑障碍物约束并利用样条插值进行轨迹的二次优化.
3.1. 基于潜在风险点的线性插值
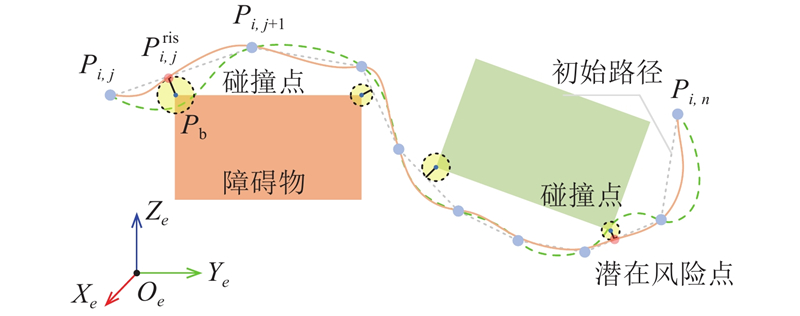
基于多目标优化的初始路径自动满足避障约束,但轨迹的光顺性不足. 路径通常由一系列离散点
图 8
图 8 以潜在风险点为过渡路径的插值方法
Fig.8 Interpolation method using potential risk points as transition paths
基于常规路径点
图 9
式中:c为
线性插值后,潜在风险点被规避,新路径为
3.2. 基于五次B样条的非线性插值
B样条具有自由度高、局部可修改性好的优点,被广泛用于机器人路径规划. 采用五次B样条对初始轨迹
式中:
其中
同理推导B样条轨迹的加速度
4. 仿真分析与实验
4.1. 基于多目标优化的初始轨迹生成
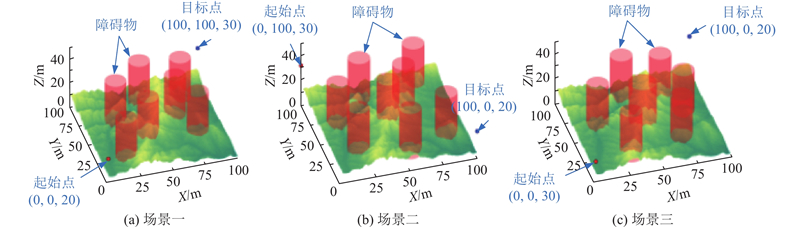
无人机在复杂环境中飞行,综合考虑效率、避障及运动稳定性,以期望它沿最佳轨迹从起始点到目标位置运动. 为了验证NSGA-III的收敛效率和精度,与广泛使用的改进A*[6],改进RRT*[9]及NSGA-II[14]进行综合比较. 仿真实验基于Matlab R2020b,并在Intel i5-12490F上运行,处理器为3.00 GHzCPU,内存为16.0 GB. 算法迭代次数N=500,初始种群规模m=201,其他关键初始值设置如下. 改进A*:实际成本
表 1 超平面的参考点坐标
Tab.1
| 编号 | 坐标 | 编号 | 坐标 | 编号 | 坐标 | ||
| Pr1 | (0.0,0.0,2.0) | Pr6 | (0.5,0.0,1.5) | Pr11 | (1.0,0.5,0.5) | ||
| Pr2 | (0.0,0.5,1.5) | Pr7 | (0.5,0.5,1.0) | Pr12 | (1.0,1.0,0.0) | ||
| Pr3 | (0.0,1.0,1.0) | Pr8 | (0.5,1.0,0.5) | Pr13 | (1.5,0.0,0.5) | ||
| Pr4 | (0.0,1.5,0.5) | Pr9 | (0.5,1.5,0.0) | Pr14 | (1.5,0.5,0.0) | ||
| Pr5 | (0.0,2.0,0.0) | Pr10 | (1.0,1.0,0.0) | Pr15 | (2.0,0.0,0.0) |
图 10
图 11
为了评价各类算法在计算效率及精度方面的性能,分别计算优化后的路径长度、迭代时间及飞行稳定性优化百分比,计算式为
式中:
表 2 不同算法在3种场景中的优化性能对比
Tab.2
| 场景 | 算法 | ||||||
| 场景一 | 改进RRT* | 164.9 | — | 37.83 | 48.43 | 259.08 | 71.68 |
| 改进A* | 156.2 | 5.28 | 73.36 | — | 914.93 | — | |
| NSGA-Ⅱ | 154.6 | 6.25 | 35.76 | 51.25 | 108.25 | 88.17 | |
| NSGA-Ⅲ | 149.7 | 9.22 | 37.03 | 49.52 | 101.85 | 88.87 | |
| 场景二 | 改进RRT* | 158.9 | — | 36.43 | 33.08 | 178.89 | 43.96 |
| 改进A* | 157.5 | 0.88 | 54.44 | — | 319.23 | — | |
| NSGA-Ⅱ | 144.8 | 8.87 | 24.08 | 55.76 | 29.04 | 90.90 | |
| NSGA-Ⅲ | 144.0 | 9.37 | 18.16 | 66.64 | 25.19 | 92.11 | |
| 场景三 | 改进RRT* | 166.42 | — | 37.36 | 50.07 | 262.96 | 55.55 |
| 改进A* | 162.42 | 2.40 | 74.83 | — | 591.59 | — | |
| NSGA-Ⅱ | 153.91 | 7.52 | 27.59 | 63.13 | 74.97 | 87.33 | |
| NSGA-Ⅲ | 152.80 | 8.18 | 24.24 | 67.61 | 70.20 | 88.13 |
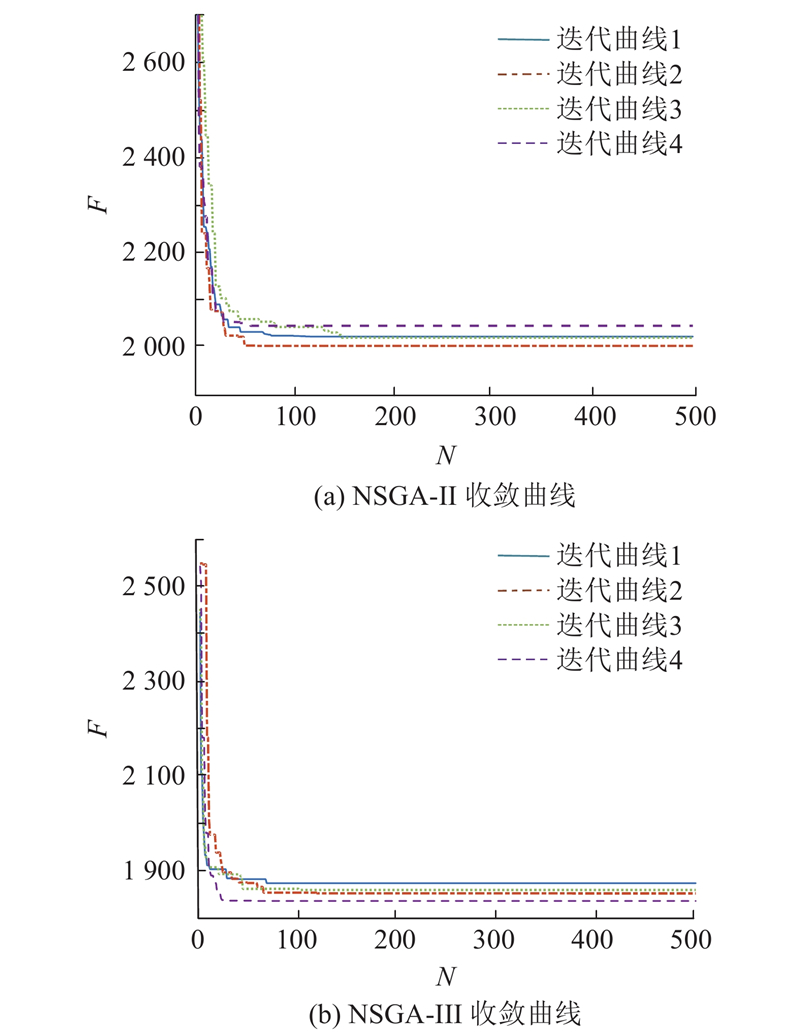
图 12
图 12 非支配排序遗传算法的优化迭代过程
Fig.12 Optimization iteration process of non-dominated sorting genetic algorithm
图 13
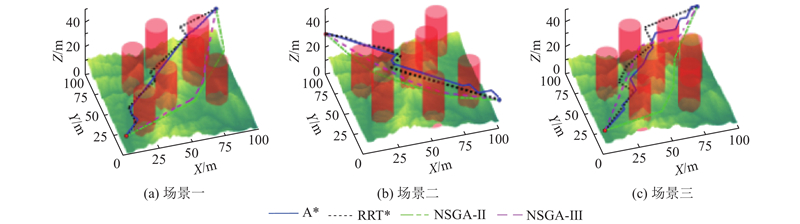
图 13 不同算法在3种场景中的无人机飞行路径三维视图
Fig.13 3D views of UAV flight paths in three scenarios with different algorithms
图 14
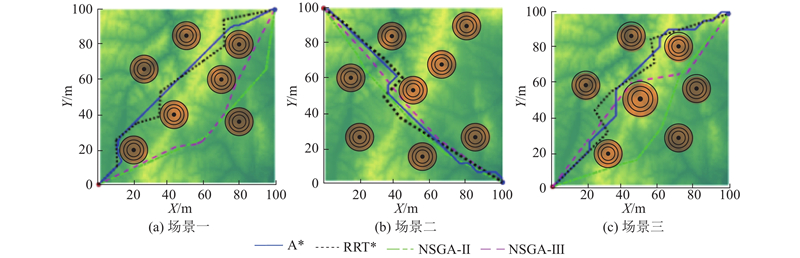
图 14 不同算法在3种场景中的无人机飞行路径俯视图
Fig.14 Top view of UAV flight paths in three scenarios with different algorithms
表 3 不同算法特点的定性描述
Tab.3
| 算法 | 计算复杂度 | 求解效率 | 最优解搜寻能力 |
| 改进RRT* | + | ++ | + |
| 改进A* | ++ | + | ++ |
| NSGA-II | +++ | +++ | +++ |
| NSGA-III | ++++ | ++++ | ++++ |
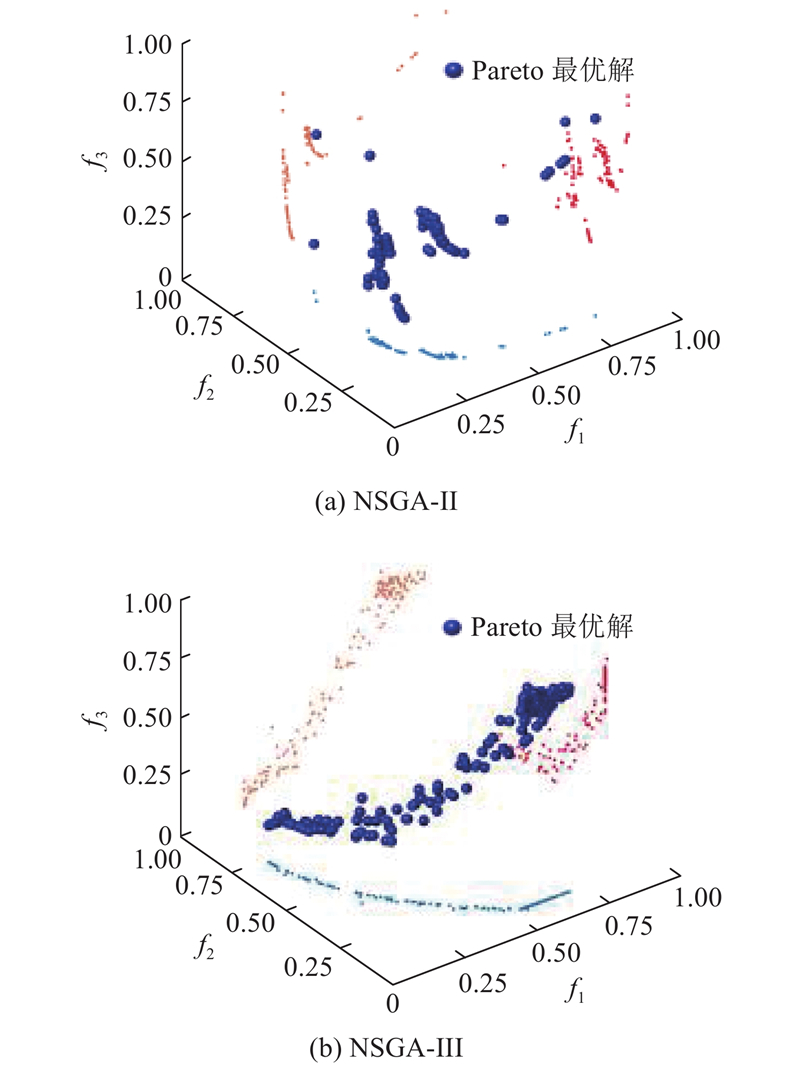
由于多目标优化往往不存在唯一的最优解,基于非支配关系的任意目标函数权重组合均能得到1组最优解,由此可形成Pareto前沿. NSGA-II和NSGA-III形成的Pareto前沿分别如图15所示,3种颜色的点分别指代Pareto前沿在3个平面的投影. 可以看到,NSGA-III的Pareto前沿分布较为均匀,在各个投影面上都能形成分布均匀的Pareto前沿,NSGA-II的结果疏密相间,随机性较大,体现出NSGA-III在高维空间优化过程中具有更好的全局性和稳定性.
图 15
图 15 不同非支配排序遗传算法的最优结果分布
Fig.15 Distribution of optimal results for different non-dominated sorting genetic algorithms
4.2. 初始路径的二次光顺性优化
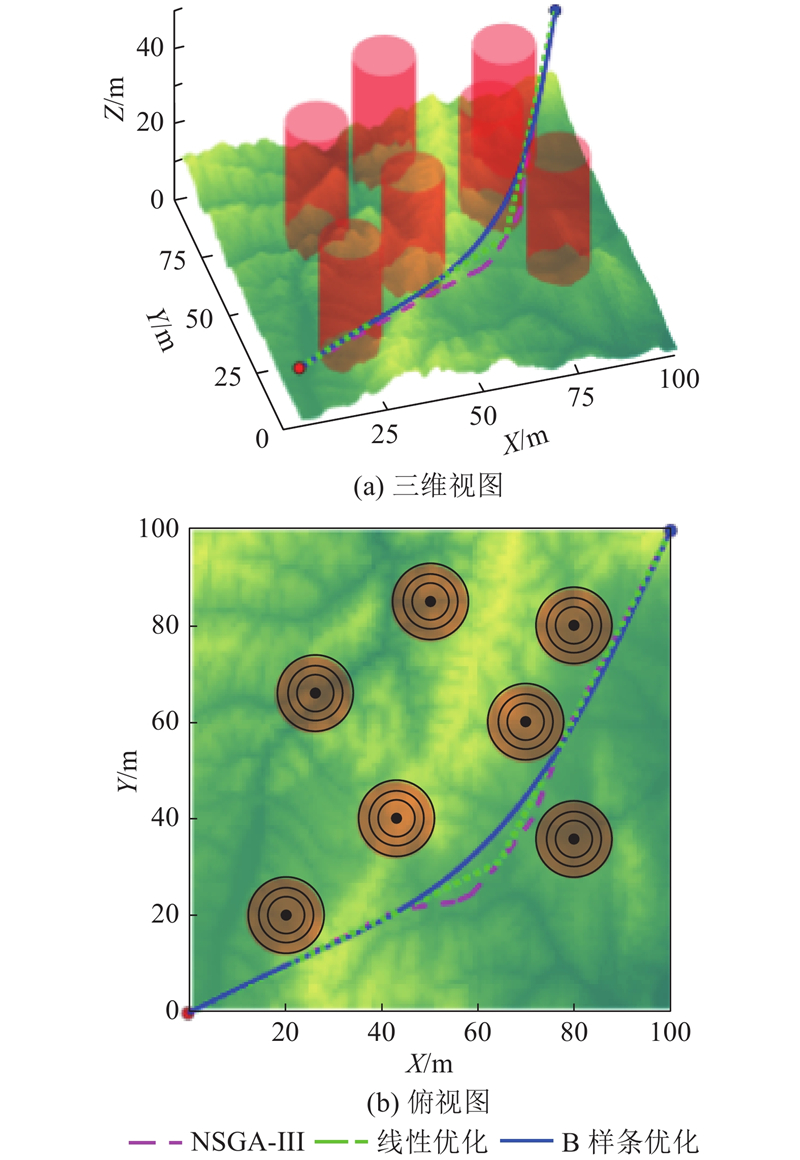
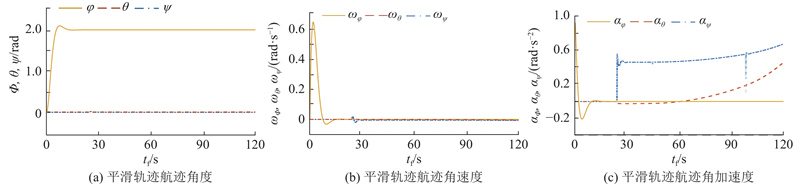
满足约束条件下生成的初始最优路径几何特性差,轨迹常存在尖点难以满足C3连续. 无人机的飞行速度和加速度的变化可能是不连续的,进而造成运动过程中的频繁启停、冲击和震荡. 为了提高飞行轨迹的平滑性,基于NSGA-III的初代优化路径采用五次B样条进行非线性拟合. 为了防止插值过程中发生路径碰撞,先进行线性插值,将潜在风险点增加为路径点,通过二次优化后的飞行轨迹如图16所示. 通过控制无人机3个方向的姿态角度(俯仰角
图 16
图 16 二次优化后的无人机飞行轨迹(场景一)
Fig.16 UAV flight trajectory after secondary optimization (scenario 1)
图 17
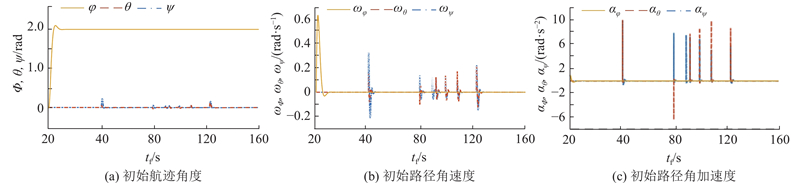
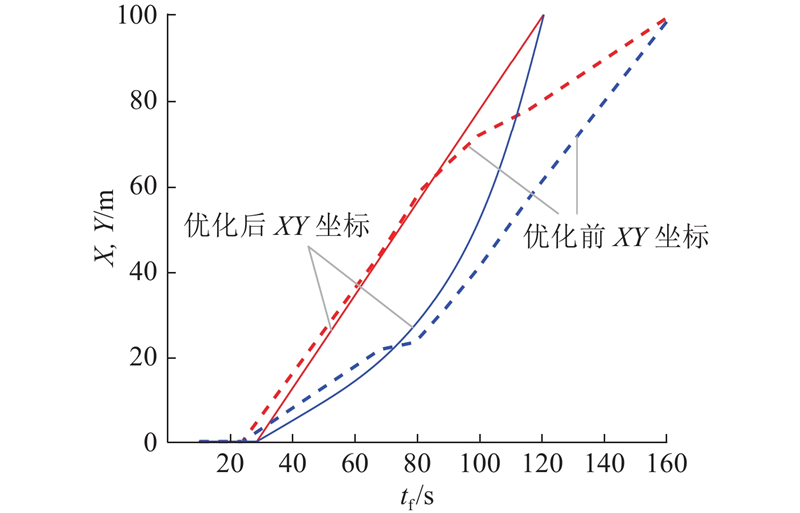
图 17 初始最优路径的飞行时间变化曲线
Fig.17 Flight-time variation curve for initial optimal path
图 18
图 19
4.3. 飞行实验
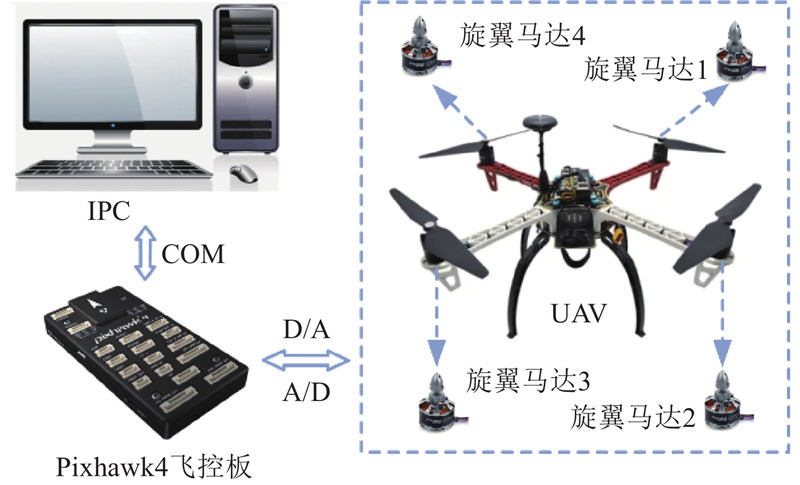
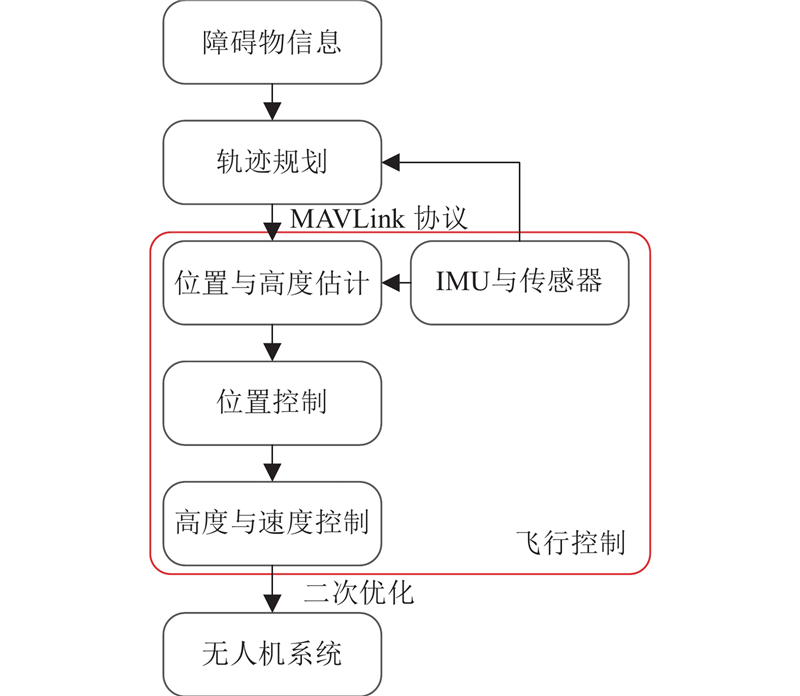
通过建立四旋翼无人机的实验平台,利用PIX4飞控系统对无人机进行控制,上位机与无人机之间通过COM通信端口进行数据传输与交换,实验平台的系统架构如图20所示. 无人机在复杂环境下飞行时的控制系统和计算过程如图21所示. 基于仿真中的虚拟场景,利用7个障碍物构建真实的实验环境,要求无人机在满足避障、效率和稳定性约束下,从起始点飞行到目标位置. 利用NSGA-III生成初始航迹,采用线性和非线性插值方法提高轨迹的光顺性,实验过程及通过地面站实时监控无人机的实际飞行轨迹如图22所示. 通过建立多目标优化模型,利用NSGA-III生成Pareto前沿,生成包括避障在内的多目标优化路径,采用平滑插值方法,增强轨迹的光顺性,提升飞行过程中的稳定性、效率及轨迹跟踪精度. 由图22可以看出优化后的期望轨迹与无人机实际飞行轨迹重合度更高,证明优化后路径能够满足无人机的运动约束.
图 20
图 21
图 22
图 22 第三代非支配排序遗传算法优化前后的无人机飞行实验结果
Fig.22 UAV flight experimental results before and after optimization by non-dominated sorting genetic algorithm III
5. 结 语
1)高维空间中NSGA-III具有较强的全局优化解搜寻能力. 相比基于随机搜索策略的改进RRT*、基于贪婪法则的改进A*算法与基于拥挤度排序的NSGA-II,基于参考点机制的NSGA-III能够在保证全局收敛的基础上获得更好的优化解. 2)在多目标优化过程中,相比NSGA-II,NSGA-III的Pareto前沿分布均匀,算法在全局搜寻过程中具有更强的鲁棒性与更稳定的收敛一致性. 3)利用基于风险点的线性插值与B样条拟合实现二次优化,能够显著改善初始轨迹的几何光顺性,降低无人机速度及加速度波动,相比优化前的初始轨迹,飞行的稳定性提升66.7%,效率提升25%. 由于NSGA-III的初始种群是通过随机采样来生成的,在一定程度上存在较大的计算开销,后续计划在初始种群生成策略方面继续改进NSGA-III,提高算法的计算效率.
参考文献
面向灾难搜索救援场景的空地协同无人群体任务规划研究
[J].DOI:10.3901/JME.2019.11.001 [本文引用: 1]
Swarm robot task planning based on air and ground coordination for disaster search and rescue
[J].DOI:10.3901/JME.2019.11.001 [本文引用: 1]
Efficiency of UAV-based last-mile delivery under congestion in low-altitude air
[J].DOI:10.1016/j.trc.2020.102878 [本文引用: 1]
集中式光伏电站巡检无人机视觉定位与导航
[J].
Vision-based localization and navigation for UAV inspection in photovoltaic farms
[J].
水平棚架式梨树多旋翼无人机液体授粉试验
[J].
Experiment on liquid pollination of pear tree with horizontal scaffolding based on multi-rotor UAV
[J].
Implementation of optimized dynamic trajectory modification algorithm to avoid obstacles for secure navigation of UAV
[J].DOI:10.1016/j.asoc.2020.106168 [本文引用: 2]
Path planning for dual UAVs cooperative suspension transport based on artificial potential field-A* algorithm
[J].DOI:10.1016/j.knosys.2023.110797 [本文引用: 3]
基于能量优化的无人机机动轨迹生成方法
[J].
Energy optimized maneuver trajectory generation for unmanned aerial vehicles
[J].
Enhanced discrete particle swarm optimization path planning for UAV vision-based surface inspection
[J].DOI:10.1016/j.autcon.2017.04.013 [本文引用: 1]
Goal distance-based UAV path planning approach, path optimization and learning-based path estimation: GDRRT*, PSO-GDRRT* and BiLSTM-PSO-GDRRT
[J].DOI:10.1016/j.asoc.2023.110156 [本文引用: 2]
UAV path planning for structure inspection in windy environments
[J].
Safety-enhanced UAV path planning with spherical vector-based particle swarm optimization
[J].DOI:10.1016/j.asoc.2021.107376 [本文引用: 1]
An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: solving problems with box constraints
[J].DOI:10.1109/TEVC.2013.2281535 [本文引用: 1]
A hybrid algorithm based on grey wolf optimizer and differential evolution for UAV path planning
[J].DOI:10.1016/j.eswa.2022.119327 [本文引用: 2]
An obstacle avoidance approach for UAV path planning
[J].DOI:10.1016/j.simpat.2023.102815 [本文引用: 1]
Real-time path planning of controllable UAV by subgoals using goal-conditioned reinforcement learning
[J].DOI:10.1016/j.asoc.2023.110660 [本文引用: 1]
Multi-objective control chart design optimization using NSGA-III and MOPSO enhanced with DEA and TOPSIS
[J].DOI:10.1016/j.eswa.2015.11.007 [本文引用: 1]
Three dimensional path planning for UAVs in dynamic environment using glow-worm swarm optimization
[J].DOI:10.1016/j.procs.2018.07.028 [本文引用: 1]
Many-objective evolutionary algorithm based agricultural mobile robot route planning
[J].DOI:10.1016/j.compag.2022.107274 [本文引用: 2]
面向飞机外表面检测任务的无人机覆盖路径规划方法
[J].DOI:10.3901/JME.2023.16.243 [本文引用: 2]
Coverage path planning method of unmanned aerial vehicle for aircraft surface detection task
[J].DOI:10.3901/JME.2023.16.243 [本文引用: 2]
Completion time minimization with path planning for fixed-wing UAV communications
[J].DOI:10.1109/TWC.2019.2914203 [本文引用: 1]