ABS常用的控制方法包括逻辑门限控制、PID控制、模糊PID控制、最优控制、神经网络控制等. 市场上成熟的ABS系统产品主要采用逻辑门限控制方法[4],它不直接以滑移率为控制目标,控制性能不足[5]. 为了改进ABS的控制策略,许多学者进行了深入研究. 王骏骋等[6]设计最优滑移率滑模控制方法,验证滑模控制器在防抱死制动系统中的有效性. Zhang等[7]利用遗传优化PID控制方法对汽车稳定控制系统进行仿真研究,验证了该方法的有效性. 马忠武等[8]设计神经网络模糊PID控制策略,寻找最佳PID非线性组合控制率,此方法涵盖神经网络、模糊PID的优点,制动性能更好,有效缩短了制动距离. 李志清等[9]将遗传算法和模糊PID控制算法相结合,解决模糊PID参数难以选取及存在局限性问题. 控制器在汽车制动过程中要达到最优控制效果,模糊控制器隶属度函数和模糊规则必须通过理论分析或在实践中总结得到. 将群智能算法应用于确定控制器参数中是目前的研究热点. 陈鑫等[10]利用粒子群算法优化PID控制器,整定PID控制参数,满足ABS实时性要求. 天鹰优化算法(Aquila optimizer,AO) [11]是新型群体智能算法,通过模仿天鹰在捕猎过程中的自然习性进行寻优,具有寻优能力强、快速收敛的特点,适于优化模糊控制器的比例因子. 本研究改进AO,提出融合差分进化、非线性收敛因子和自由捕猎策略的天鹰搜索算法(differential evolution combining nonlinear convergence factor and free foraging strategy for Aqulia optimizer,DEFFAO),采用离线方式对比例因子全局寻优,提高ABS控制性能,确保车辆在制动时的安全性和稳定性.
1. 汽车防抱死制动系统
1.1. 整车制动车轮受力分析
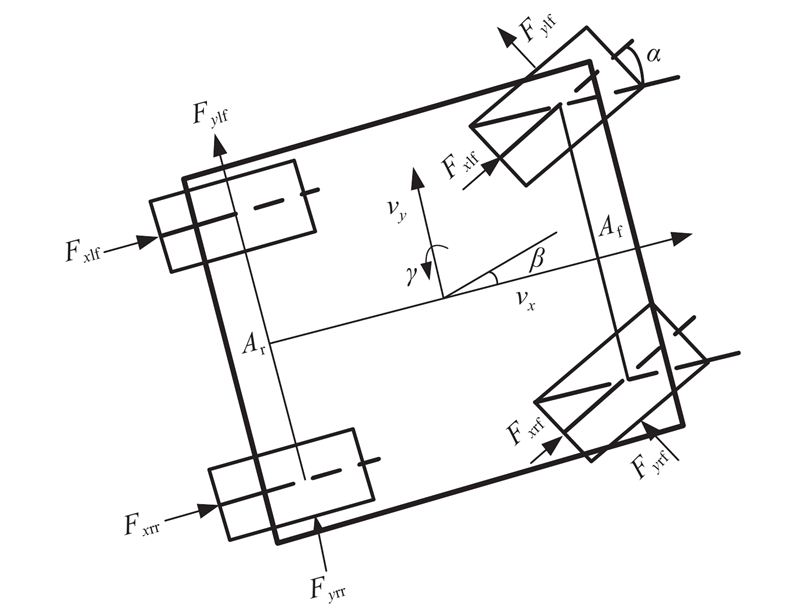
在车辆制动过程中,车轮既受到制动器制动力矩作用,又受到地面给车轮提供的摩擦力矩作用. 假设车辆质量均匀分布,忽略空气阻力、路面倾斜度及车轮滚动阻力等非关键性因素的影响,建立七自由度整车模型,进行制动受力分析,如图1所示. 车辆沿x轴和y轴的运动方程如下:
图 1
式中:m为整车质量,vx为车辆纵向速度,vy为车辆横向速度,Fx为车辆横向力,Fy为车辆纵向力,Fxlf、Fxrf、Fxlr、Fxrr分别为左前轮、右前轮、左后轮、右后轮的纵向力,Fylf、Fyrf、Fylr、Fyrr分别为左前轮、右前轮、左后轮、右后轮的横向力,Iz为整车转动惯量,Af为前轮轮距,Ar为后轮轮距,lf和lr分别为前轴轴心和后轴轴心到质心间的距离,γ为车辆横摆角速度,β为车辆质心侧偏角. 各轮胎的垂直载荷为
式中:Fzlf、Fzrf、Fzlr和Fzrr分别为左前轮、右前轮、左后轮及右后轮的垂直载荷,g为重力加速度,h为车辆质心与地面之间距离. 车轮运动的动力学方程为
车轮滑移率公式为
式中:i∈{lf,lr,rf,rr},元素分别代表左前轮,左后轮,右前轮和右后轮;I为车轮转动惯量;S为车轮滑移率;ωi为各车轮的转动角速度;R为车轮半径;Mbi为车轮滚动阻力偶矩,当Tdi>0,为驱动力矩,当Tdi<0时,为制动力矩.
1.2. 车辆轮胎模型
轮胎是车辆与地面连接的纽带,在建立车轮滑移率与地面附着系数之间的关系时,必须对轮胎进行建模[12]. 建模方法一般有2种:基于物理原理和经验公式建立模型. 在ABS研究中,Burckhardt、魔术公式以及双线性模型应用较广泛,其中双线性简化轮胎模型是应用最广的,适应汽车行驶的多种工况. 本研究采用这种模型,根据路面附着系数与滑移率间的关系推导双线性轮胎数学表达式:
式中:ST为最佳滑移率,ug为S=1时的车轮附着系数,uh为峰值附着系数,u为纵向附着系数. 典型路况参数如表1所示.
表 1 典型路况的实验参数
Tab.1
| 典型路面 | ST | uh | ug |
| 干燥混凝土 | 0.2 | 0.75 | |
| 光滑冰路面 | 0.1 | 0.07 |
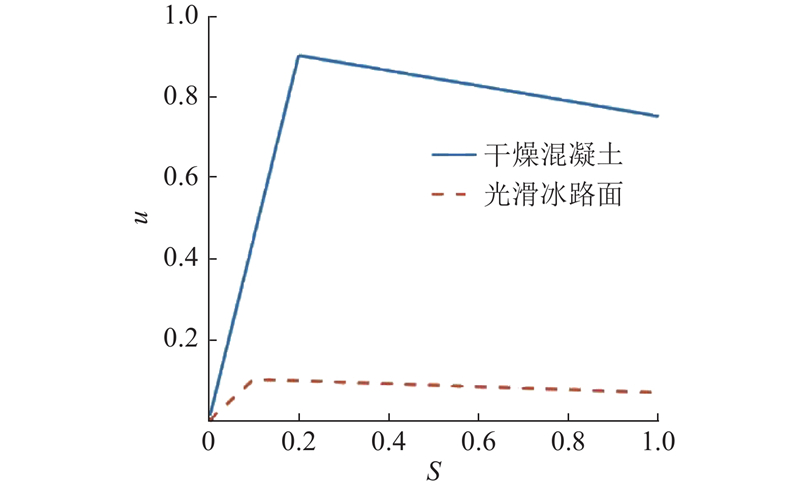
不同路面的滑移率与附着系数关系不同,由式(15)可以得到不同路面条件下滑移率的关系模型,式(16)、(17)分别为干燥混凝土路面和光滑冰路面上的关系模型. 不同路面附着系数与滑移率关系如图2所示.
图 2
图 2 双线性轮胎模型滑移率与路面附着关系曲线
Fig.2 Relationship curve between slip ratio and road adhesion of bilinear tire model
1.3. 汽车制动系统模型
式中:tr为电磁阀的响应时间,K为比例系数. 一般电磁阀反应时间不超过10 ms,因此取tr=0.01 s,K=100. 制动器模型描述液压传动系统液压力和制动力矩之间的关系. 忽略环境及热衰退因素,将制动器假设为理想元件,输出理论制动力矩大小,数学方程为
其中Md>0为驱动力矩,Md<0为制动力矩;q为制动压力;Kq为制动器的制动因子.
1.4. 整车模型
整车具有多自由度,各部分之间互相影响,仅依靠微分方程进行建模和手动求解,效率较低且准确性难以保证. 利用Carsim建立整车仿真模型,在Simulink中建立汽车ABS控制算法模型,采用B级车型,主要参数如表2所示. 其中m1为前非簧载质量,m2为后非簧载质量,R为车轮半径,I为车轮转动惯量,v0为初始速度.
表 2 整车模型主要参数
Tab.2
| 参数 | 数值 | 参数 | 数值 | |
| m/kg | Iz/(kg·m2) | 1.44 | ||
| m1/kg | 60 | lf/m | 1.04 | |
| m2/kg | 60 | lr/m | 1.56 | |
| R/m | 0.4 | v0/(km·h−1) | 120 | |
| I/(kg·m2) | 0.6 | g/(m·s−2) | 9.8 |
2. 模糊PID控制器建模
PID控制规律为
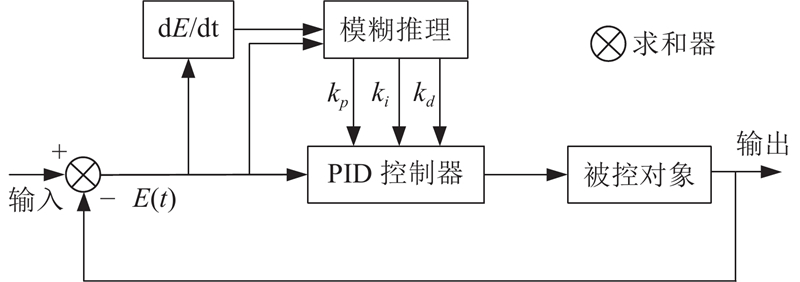
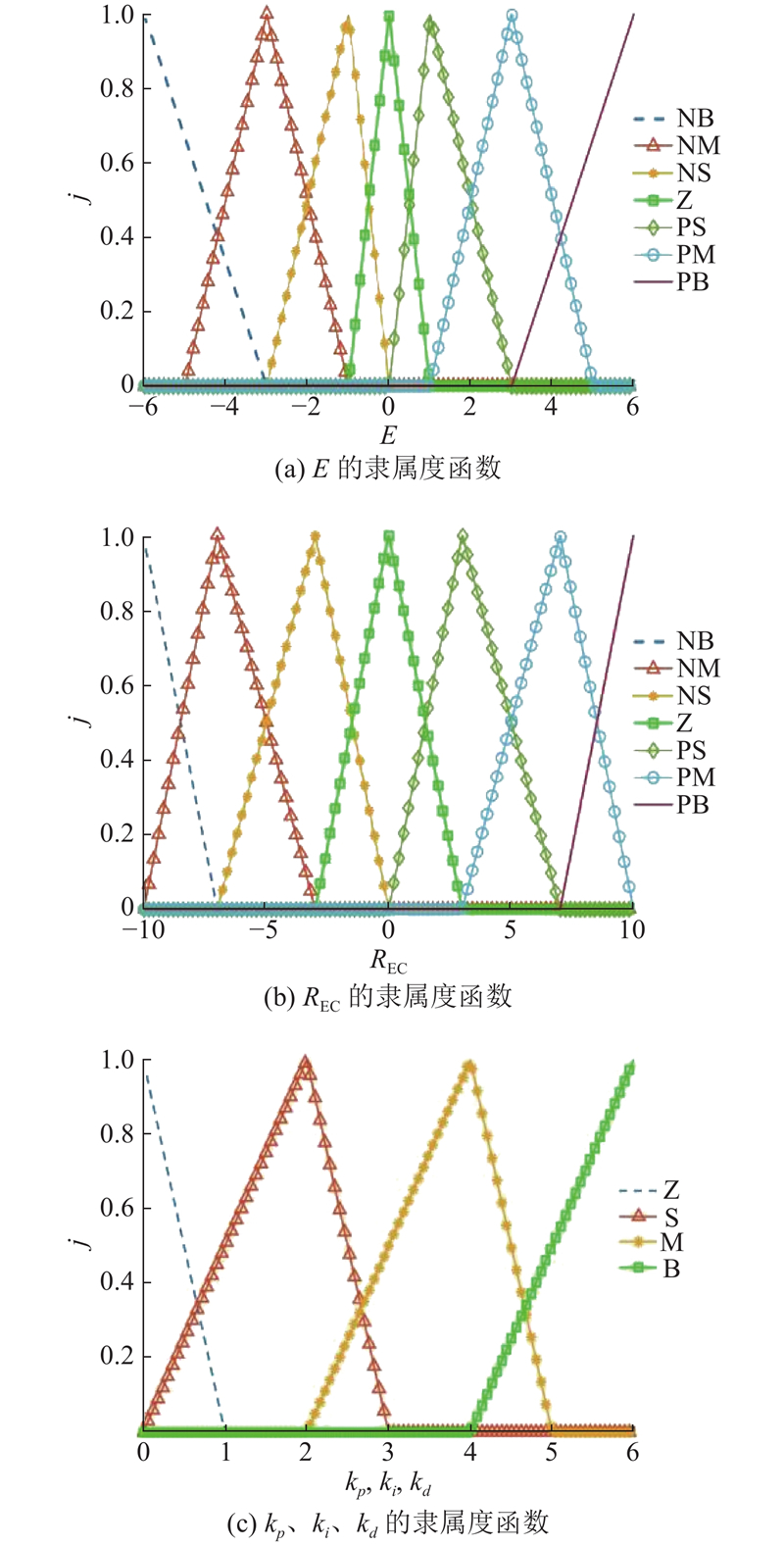
模糊PID控制器模型如图3所示,利用求和器对输入输出进行运算,进而将固定控制参数kp、ki、kd改为可变参数,在运行过程中根据误差E和误差变化率REC实时调整kp、ki、kd,以适应外部环境的变化并保持较高的控制精度. 选取S和ST的差值E为优化目标,作为模糊PID控制器输入信号,通过实时调整控制器参数,调节制动压力信号,保证制动过程中车轮滑移率保持在期望值附近. 输入输出的隶属度函数如图4所示,其中j为隶属度函数,NB为负大,NM为负中,NS为负小,Z为零,PS为正小,PM为正中,PB为正大,S为小,M为中,B为大. 误差和误差变化率均由7个模糊子集组成,量化等级分别为{−6,−3,−1,0,1,3,6}、{−10,−7,−3,0,3,7,10};输出由4个模糊子集组成,量化等级为{0,2,4,6}. 建立kp、ki、kd模糊控制规则表,如表3所示. 当E=NB,REC=NB时,kp=B、ki=Z、kd=S. 采用重心法对模糊控制的输出进行反模糊化,公式为
图 3
图 4
表 3 模糊控制规则
Tab.3
| E | kp, ki, kd | ||||||
| REC= NB | REC= NM | REC= NS | REC= Z | REC= PS | REC= PM | REC= PB | |
| NB | B,Z,S | B,Z,M | B,Z,B | B,Z,B | Z,Z,M | Z,Z,M | Z,Z,S |
| NM | B,S,M | M,S,M | M,Z,B | S,Z,B | Z,S,M | Z,S,M | Z,S,M |
| NS | M,M,Z | M,B,S | S,M,S | Z,B,S | S,M,S | S,M,S | S,M,Z |
| Z | M,B,Z | S,B,Z | Z,B,S | Z,B,Z | S,B,Z | S,B,Z | M,B,Z |
| PS | S,M,Z | S,B,S | S,M,S | Z,B,S | M,M,S | M,M,S | M,M,Z |
| PM | S,S,M | Z,S,M | S,Z,B | S,Z,B | M,S,M | M,S,M | B,S,M |
| PB | Z,Z,S | Z,Z,M | B,Z,B | B,Z,B | B,Z,M | B,Z,M | B,Z,S |
式中:Zpj和Zp均为论域元素.
3. 天鹰优化策略
3.1. 天鹰优化算法
AO模拟天鹰利用速度捕捉地面猎物,狩猎时经历4个过程:利用垂直弯腰高空翱翔探索,短滑翔攻击的轮廓飞行,低空飞行缓慢下降攻击,通过俯冲抓取在地上行走的猎物. 过程1的数学模型:
式中:X1(t+1)为t的下一次迭代解;Xbs(t)为第t次迭代得到的最优解,表示当时猎物的大概位置;T为最大迭代次数;(1−t/T)用于控制天鹰搜索;XM(t)为第t次迭代时当前解的平均位置;rand∈(0, 1.0)的随机数. 过程2的数学模型:
式中:X2(t+1)为天鹰在过程二中第t+1次迭代的解, D为搜索区域的维度,Levy (D)为莱维飞行函数,XR(t)为第t次迭代时[1,N]上的随机解,常数β=1.5、s=0.01,u∈(0,1.0)的随机数. y和x为搜索区域形状:
式中:o1∈(1,20)的随机数,用来确定搜索周期数;D1为1到D之间随机的整数. 过程3的数学模型:
式中:X3(t+1)为天鹰在过程三中第t+1次迭代的解,α和δ为(0,1.0)的开采调节参数,UB和LB为给出的上、下界. 过程4的数学模型:
式中:X4(t+1)为天鹰在过程4中第t+1次迭代的解;QF为平衡搜索策略的质量函数,QF (t)为第t次迭代时的质量函数值;G1为天鹰在捕食时采取的不同方法;G2为天鹰的飞行斜率,数值从2到0递减.
3.2. 改进的天鹰优化算法
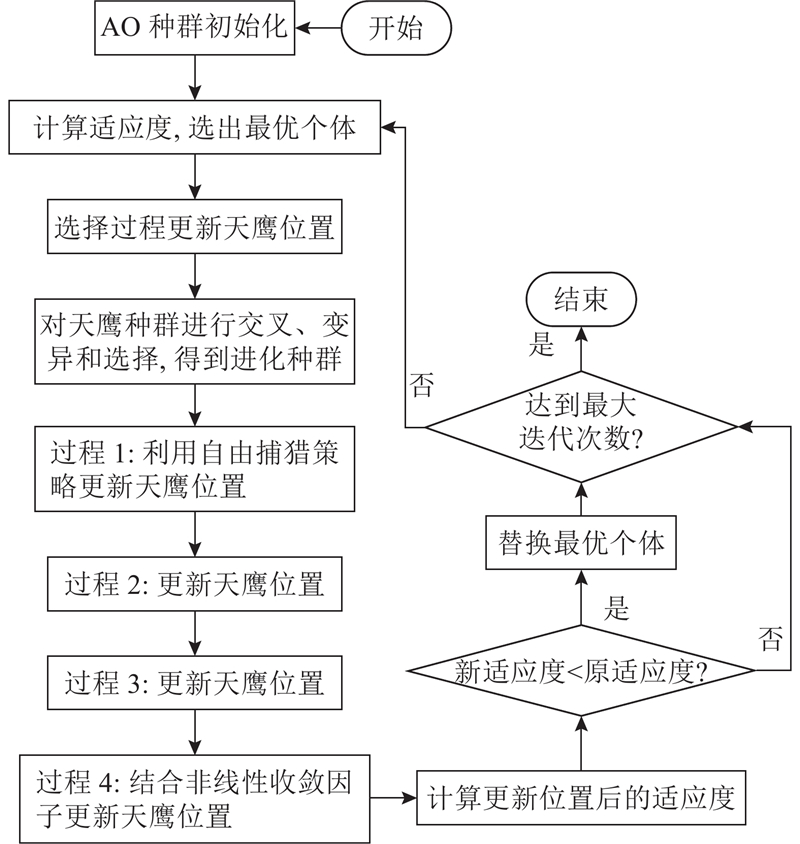
AO虽具有较强的搜索能力和收敛速度,但容易陷入局部最优,本研究所提算法的优化策略流程图如图5所示,分为如下3个步骤.
图 5
(1)天鹰自由捕猎策略. 在扩大开发过程中,利用全局最优位置与平均位置得到天鹰新的坐标位置,若在迭代后期种群陷入局部最优解范围,采用此种位置更新方式种群无法逃离局部束缚. 受蝠鲼算法的启发,引入天鹰自由捕猎策略:在天鹰优化算法中,当前个体不仅跟随前个体,且通过螺旋路径向最优位置移动,可有效遍历搜索空间,跳出局部最优值. 加强天鹰自身学习能力,在保证可以搜索最优解的同时,提高对搜索空间覆盖率. 将位置更新式(32)修订为
式中:c1和c2为0到1.0的随机数,Xr(t)为当前迭代中随机个体位置,n为螺旋系数.
(2)非线性收敛因子. G2为递减参数,表示天鹰追踪猎物从起始位置到最终位置的飞行斜率. 线性递减因子不能准确反映实际迭代过程,为了平衡局部和全局搜索能力,将其改为非线性收敛因子:
修改后,算法在迭代中期的G2数值较大,天鹰种群更依赖Levy飞行,可彻底搜索解空间,在迭代后期G2数值变小,受Levy飞行影响小,最优解及历史解对这一步搜索结果影响变大,提升迭代后期局部搜索能力.
(3)天鹰进化策略. 差分进化算法(differential evolution,DE)通过变异、交叉和选择的方法使种群进化,不断进行迭代使算法得到全局最优解. 具体步骤为1)变异:结合差分策略对个体进行遗传变异,从种群的父系中随机选取2个个体,求它们的向量差,再与待变异的个体进行矢量合成. 变异向量产生公式为
式中:r1,r2和r3均为随机整数,r1≠r2≠r3;缩放因子F∈[0,1.0],用于控制偏差的放大作用,对全局寻优影响较大. F越小,算法局部搜索性能越好;F越大,算法跳出局部最小值的可能性越大,但F过大会使收敛速度变慢. 2)交叉:随机选择个体,不断交叉产生交叉种群,具体为
式中:pc为交叉概率,反映交叉过程中通过概率方式来随机产生新个体,randi∈(1,D)的随机整数. pc越大,信息交换程度越高;pc越小,群体多样性越低,不利于全局优化. 3)选择:采用贪婪原则在原始种群和交叉种群中选择更优秀的个体作为下一代,
式中:fit (x)为x的适应度.
3.3. 优化策略的测试
为了验证算法性能,将DEFFAO与AO、飞蛾扑火算法(moth-flame optimization, MFO)[15]、鹈鹕优化算法(pelican optimization algorithm, POA)[16]及蜣螂优化算法(dung beetle optimizer, DBO)[17]在5种基准测试函数上进行对比,种群规模大小设置为50,迭代500次,测试函数的适应度如表4所示. 由表可知,DEFFAO的性能在大多数测试函数上优于对比算法. 根据没有免费午餐(no free lunch, NFL)定理[18]:不能期望一个算法能够在所有测试函数中都达到最佳性能. DEFFAO在这5个测试函数中的适应度最低,性能最好,验证了优化的有效性.
表 4 不同算法在5种测试函数中的适应度
Tab.4
| 测试函数 | fit | ||||
| MFO | POA | DBO | AO | DEFFAO | |
| Schwefel 2.22 | 60.087 | 6.212×10−47 | 3.846×10−52 | ||
| Schwefel 1.2 | 9.935×10−60 | 3.809×10−80 | 8.05×10−96 | ||
| Rosenbrock | 661.167 | 7.801×10−14 | |||
| Schwefel | − | − | − | − | − |
| shekel 5 | − | − | − | − | − |
4. 改进天鹰算法优化的模糊PID控制器设计
4.1. 控制方案
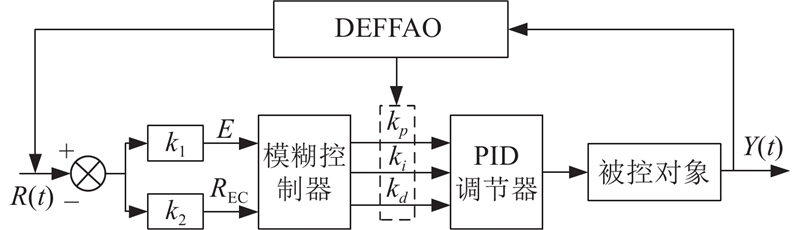
图 6
图 6 改进天鹰算法优化的模糊控制因子
Fig.6 Fuzzy control factor optimized by improved Aquila algorithm
4.2. 优化性能评价指标
DEFFAO优化后的结果须进行性能的标准评判,确定最佳解. 在迭代过程中,若后代更符合标准要求,则替换前一代天鹰的位置,以推进优化迭代. 该优化系统应用在ABS上,评价指标应侧重于ABS的控制性能. 在对稳定性、实时性要求很高的情况下,时间乘绝对误差积分[20] ITAE评价指标符合ABS要求,
式中:t为系统反应时间.
5. 仿真结果分析
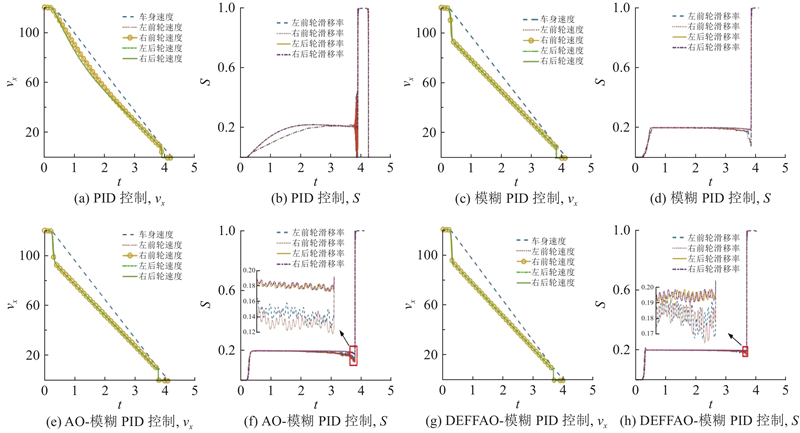
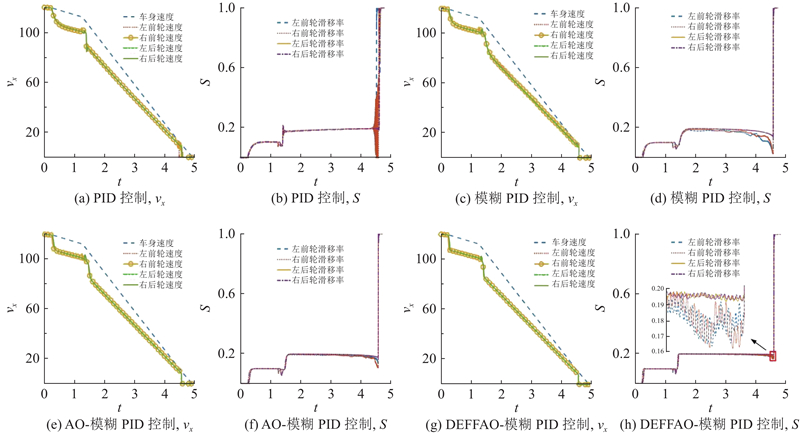
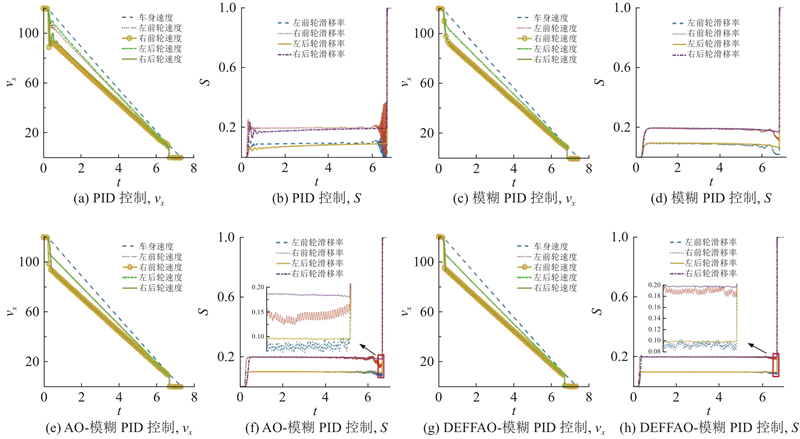
实验硬件平台为Intel Core i7-11800H 2.3 GHzCPU、RTX4060Ti GPU、16 GB 内存的计算机,仿真软件为MatlabR2022a. 汽车初始速度为120 km/h,分别在干燥混凝土路面、对接路面及对开路面利用PID、模糊PID、AO-模糊PID和DEFFAO-模糊PID控制器对汽车防抱死过程进行仿真,仿真结果如图7~9所示. 1)在干燥混凝土路面上,车速快速降低,4种控制器的制动时间分别为4.264、4.202、4.146和4.028 s. 由车速图可知,一侧车轮在制动时速度保持一致,这可以保证车辆直线行驶,防止在制动时车辆发生偏移. 由滑移率仿真曲线图可知,PID控制下滑移率收敛到理想值附近时间较长,其他3种控制器都可使滑移率快速到达理想值附近,而DEFFAO-模糊PID控制器下滑移率波动范围最小,可更稳定地保持在期望值附近. 相比传统的PID和模糊PID控制器,本研究提出的改进控制器在制动时间上降低了5.53%和4.14%. 2)对接路面前30 m为低附着系数路面,之后为高附着系数路面. 在对接路面上,4种控制器的制动时间分别为4.939、4.896、4.823和4.750 s,在低附着系数路面上期望滑移率为0.1,高附着系数路面上期望滑移率为0.2. 由车速图可知,开始车辆在低附着系数路面制动车速缓慢下降,直到进入高附着系数路面后车速迅速降低. 由滑移率曲线图可知,车轮滑移率都可达到理想值附近,PID控制器下滑移率波动范围最大,且到达理想值时间也比其他控制器长,DEFFAO-模糊PID控制器滑移率可快速收敛到理想值附近,波动范围小于0.05,使车轮与路面间附着系数最大,制动效果更好;相比传统PID和模糊PID控制器,制动时间降低了3.83%和2.98%. 3)对开路面为左侧车轮在低附着系数路面,右侧车轮在高附着系数路面. 在对开路面上,4种控制器的制动时间分别为7.481、7.435、7.332和7.278 s,左侧车轮期望滑移率为0.1,右侧车轮滑移率为0.2. 由车速图可知,车身左右两侧路面不同,左侧车轮速度减速比右侧车速慢,此种情况会导致车身偏移,须调节方向盘或者利用电子稳定系统(electronic stability program, ESP)使汽车稳定,本文只研究制动效果. 由滑移率曲线图可知,两侧车轮滑移率都可快速收敛到理想值0.1和0.2附近,PID控制器下滑移率逐渐逼近理想值,在车速较低时滑移率波动范围较大. DEFFAO-模糊PID控制器下滑移率可快速稳定保持在理想值附近,波动范围的绝对值不超过0.02;相比传统PID和模糊PID控制器,制动时间降低了2.71%和2.11%.
图 7
图 7 不同控制方法在干燥混凝土路面上的制动过程仿真曲线
Fig.7 Simulation curves of braking process on dry concrete pavement using different control methods
图 8
图 8 不同控制方法在对接路面上的制动过程仿真曲线
Fig.8 Simulation curves of braking process on docking road surface using different control methods
图 9
图 9 不同控制方法在对开路面上的制动过程仿真曲线
Fig.9 Simulation curves of braking process on split-coefficient surface using different control methods
在干燥混凝土路面、对接路面和对开路面,不同控制策略下的刹车距离x0和时间如表5所示. 由表可知,在3种路况中,PID控制的汽车制动效果最差,制动时间最长,距离最远;DEFFAO-模糊PID控制制动效果最好,制动时间和距离都有所减少,与AO-模糊PID相比,提升了制动性能. 该结果验证了所提算法整定模糊PID参数的有效性. 由仿真实验中的滑移率曲线可知,采用DEFFAO-模糊PID控制,可使ABS中实际滑移率保持在最佳滑移率处附近,在各个路况情况下反应迅速有效,适应性强.
表 5 不同控制方法在3种路况下的制动过程仿真参数
Tab.5
| 控制方法 | t/s | x0/m | |||||
| 干燥混凝土 | 对接路面 | 对开路面 | 干燥混凝土 | 对接路面 | 对开路面 | ||
| PID | 4.264 | 4.939 | 7.481 | ||||
| 模糊PID | 4.202 | 4.896 | 7.435 | ||||
| AO-模糊PID | 4.146 | 4.823 | 7.332 | ||||
| DEFFAO-模糊PID | 4.028 | 4.750 | 7.278 | ||||
6. 结 语
本研究提出优化ABS的模糊PID控制方法,设计天鹰自由捕猎策略和非线性收敛因子,结合差分进化策略优化AO,增强个体探索能力,避免陷入局部最优,提高鲁棒性和开发能力. 利用最优个体整定比例因子和量化因子参数,得到DEFFAO-模糊PID控制器,有效解决了设计模糊控制器时的人为因素影响. 在不同路况对汽车制动进行仿真测试,通过制动时间、制动距离及滑移率曲线证明了所提算法制动效果的优越性,有效提升了汽车制动性能. 本研究算法依赖仿真实验,未进行实车测试,且离线优化缺乏动态适应性,接下来工作会开展实车道路测试,设计在线学习机制提升鲁棒性.
参考文献
Electric-hydraulic compound control anti-lock braking system
[J].DOI:10.1007/s12239-022-0139-2 [本文引用: 1]
汽车ABS控制仿真分析
[J].
Simulation analysis of automobile ABS control
[J].
汽车防抱死制动系统的自抗扰控制研究
[J].DOI:10.3969/j.issn.1001-7372.2021.03.018 [本文引用: 1]
Active disturbance rejection control for automotive anti-lock braking system
[J].DOI:10.3969/j.issn.1001-7372.2021.03.018 [本文引用: 1]
基于线性自抗扰控制的汽车ABS滑移率控制研究
[J].
Research on ABS slip ratio control of vehicle based on linear active disturbance rejection control
[J].
Wheel slip ratio regulation for investigating the vehicle’s dynamic behavior during braking and steering input
[J].
分布驱动电动汽车电液复合制动最优滑模ABS控制
[J].
Optimal sliding mode ABS control for electro-hydraulic composite braking of distributed driven electric vehicle
[J].
Simulation research on PID control of automotive stability based on genetic algorithm optimization
[J].
基于神经模糊PID的ABS控制策略研究
[J].
Research on ABS control strategy based on neuro-fuzzy PID
[J].
遗传算法优化的空气悬架模糊PID控制
[J].
Fuzzy-PID control of air suspension based on genetic algorithm optimization
[J].
基于粒子群优化算法的PID控制液压防抱死系统
[J].
PID control anti-lock braking system based on particle swarm optimization algorithm
[J].
Aquila Optimizer: a novel meta-heuristic optimization algorithm
[J].
Automatic emergency braking/anti-lock braking system coordinated control with road adhesion coefficient estimation for heavy vehicle
[J].DOI:10.1049/itr2.12229 [本文引用: 1]
电动汽车复合制动控制研究现状综述
[J].DOI:10.3969/j.issn.1001-7372.2022.11.024 [本文引用: 1]
Review of electro-mechanical composite braking control for electric vehicles
[J].DOI:10.3969/j.issn.1001-7372.2022.11.024 [本文引用: 1]
Global and local moth-flame optimization algorithm for UAV formation path planning under multi-constraints
[J].DOI:10.1007/s12555-020-0979-3 [本文引用: 1]
Botnet detection in the Internet-of-Things networks using convolutional neural network with pelican optimization algorithm
[J].DOI:10.1080/00051144.2023.2288486 [本文引用: 1]
Dung beetle optimizer: a new meta-heuristic algorithm for global optimization
[J].DOI:10.1007/s11227-022-04959-6 [本文引用: 1]
An empirical demonstration of the no free lunch theorem
[J].DOI:10.13164/ma.2019.11 [本文引用: 1]
汽车电子机械制动系统的ABS自抗扰控制
[J].
ABS active disturbance rejection control for automotive electromechanical braking systems
[J].
Enhancing DC motor speed control performance using heuristic optimization and comparative analysis of control methods
[J].