随着新一代信息技术的快速发展,无人机在战争中的优势作用日益凸显[1],在实际军事行动中表现出优越的监视和打击能力. 单架无人机在面对多任务需求的复杂作战场景时,会由于自身条件不足导致任务执行失败. 美国空军科学顾问委员会指出,未来无人机应当以集群的方式协同工作[2]. 针对多无人机集群协同任务分配问题的传统研究多面向同构型无人机或单一任务类型展开[3-4],实际战场任务的复杂程度各异且通常有作战顺序,需要对不同功能和特性的无人机进行部署与组合来完成多样化的作战需求. 这使得异构无人机协同作战模式逐渐进入人们的视野[5]. 异构无人机协同任务分配须在考虑众多约束条件的同时优化多个指标,是复杂、多约束下的多目标优化问题,其方法研究主要集中于目标函数构建、约束条件设计以及算法选取3个方面.
1)目标函数构建须解决的问题有2类:选取构建方式和选取目标函数指标. 选取构建方式包括将评价任务分配方案优劣的多个目标函数通过赋予不同权重整合成单目标形式简化处理[6]和同步优化多个目标函数得到多个互不支配的可行解集[7],前者操作简单,但各个目标函数权重确定困难,后者能够解除上述问题的束缚,更适用于实际战场下的异构无人机协同任务分配问题. 在选取目标函数指标的问题上,多数研究将成本消耗(如无人机的飞行航程、任务完成时间)作为评价任务分配的依据[6-9],很少考虑作战任务执行效能,导致武器资源在任务执行过程中浪费严重或作战效果不佳. 为此,王峰等[10]设计任务费效比作为待优化的目标之一,应用于任务重分配环节. Xia等[11]研究察打一体机的任务执行效率问题. 2)在约束条件设计方面,除为了满足实战要求而设置的包括无人机自身性能、目标属性和一些特定任务需求等[12]约束条件外,针对异构无人机,出于任务优先顺序和无人机的异构性原因,死锁也是必须解决的问题. Lemaire等[13]通过交换2个违反时间顺序的任务来避免死锁,Chen等[14]提出基于图论和自由边翻转的死锁检测修复方法. 3)异构无人机任务分配的算法设计更为困难:一是此类问题的决策变量类型不止一种,二是该问题往往具有多约束和多个待优化的目标. 这使得现有的优化算法难以对该问题进行有效的求解,必须制定针对性的改进措施. 在针对混合变量的处理方法中,基于松弛方法和基于离散化方法的算法思路简单,但处理方式泛化能力不足且难以保证求解准确度[15],基于混合算子的方法能够同时采用不同类型变量的重组算子生成包含混合变量的解,无需额外的变量转化方法[7,9],应用更为灵活. 在优化算法选取上,新兴优化算法(如鲸鱼优化算法[16]、樽海鞘群算法[17])不断涌现,但是它们在解决此类包含混合变量且具有多约束限制的多目标优化问题上的应用还不够成熟,优化效果有待进一步验证. 相比而言,粒子群算法的发展较为成熟,在求解此类多目标优化问题上的有效性已经得到广泛的验证[18-20]. Wei等[21]采用帕累托前沿优化策略和基于概率的领导者选择策略引导粒子的方向,同时设置精英集来避免种群的退化;王万良等[22]通过设计不同的学习参数使各角色粒子获得不同的搜索策略来调整粒子的探索能力.
综上,现有多目标优化问题解决方案的评价指标不够全面;对死锁问题的研究存在局限性;大多数粒子群算法缺乏有效的调整机制,导致算法多样性和问题求解精度不足. 本研究针对异构无人机协同多任务分配模型和优化算法进行设计与改进,1)综合考虑执行任务的成本代价、任务打击效能和死锁等因素,构建包含无人机飞行总航程、任务完成总时间、弹药平均作用效能和多个约束条件的异构无人机协同多任务分配模型. 2)对传统粒子群算法进行多策略改进,提出基于混合策略的多目标粒子群优化算法(hybrid strategies based multi-objective particle swarm optimization algorithm, HS-MOPSO),在混合变量编码基础上提出基于约束的粒子动态优选初始化策略;提出基于支配关系的优势个体选择策略更新优势粒子;提出基于任务的小模块粒子更新及修正策略,实现在满足约束的前提下搜索到更多可行解. 3)针对所构建的无人机任务分配模型和所设计的优化算法设计多种实例场景,检验模型及算法的性能.
1. 异构无人机协同多任务分配模型
1.1. 问题描述
考虑异构无人机集群协同对地面多个目标依次执行侦察、打击和评估任务的分配问题,假设各无人机同时起飞且均以一定的速度匀速飞行. 无人机的总数为
表 1 任务分配模型参数
Tab.1
| 类别 | 参数 |
| 无人机 | 第 |
| 第 | |
| 第 | |
| 第 | |
| 第 | |
| 第 | |
| 第 | |
| 第 | |
| 第 | |
| 目标及任务 | 执行任务 |
| 第 | |
| 第 | |
| 目标 | |
| 执行目标 | |
| 完成任务 | |
| 完成任务 |
1.2. 三目标函数
为了更加全面地评估无人机的任务分配结果,从成本代价和任务执行效率角度出发,设计目标函数:
式中:
1.3. 约束条件
为了使模型贴合战场实际,从无人机属性、目标及任务属性考量,设置6个约束条件. 1)无人机类型约束:侦察或评估任务只能分配给侦察型无人机,打击任务只能分配给战斗型无人机,
2)无人机最多可携带弹药约束:无人机执行任务消耗的弹药数量不能超过其最多可携带弹药量,
3)无人机最大可飞行航程约束:无人机飞行的航程总和不能超过其最大可飞行航程,
4)任务执行时序约束:每个目标上的任务都要按照先侦察、再打击,最后评估的顺序进行,
5)任务完成所需时间资源约束:对目标的侦察与评估任务须累计达到规定的时间才被视作完成,
6)任务完成所需弹药资源约束:对目标的打击任务须累计达到规定弹药资源量才被视作完成,
异构无人机协同多任务分配模型为
考虑到
2. 基于混合策略的多目标粒子群优化算法
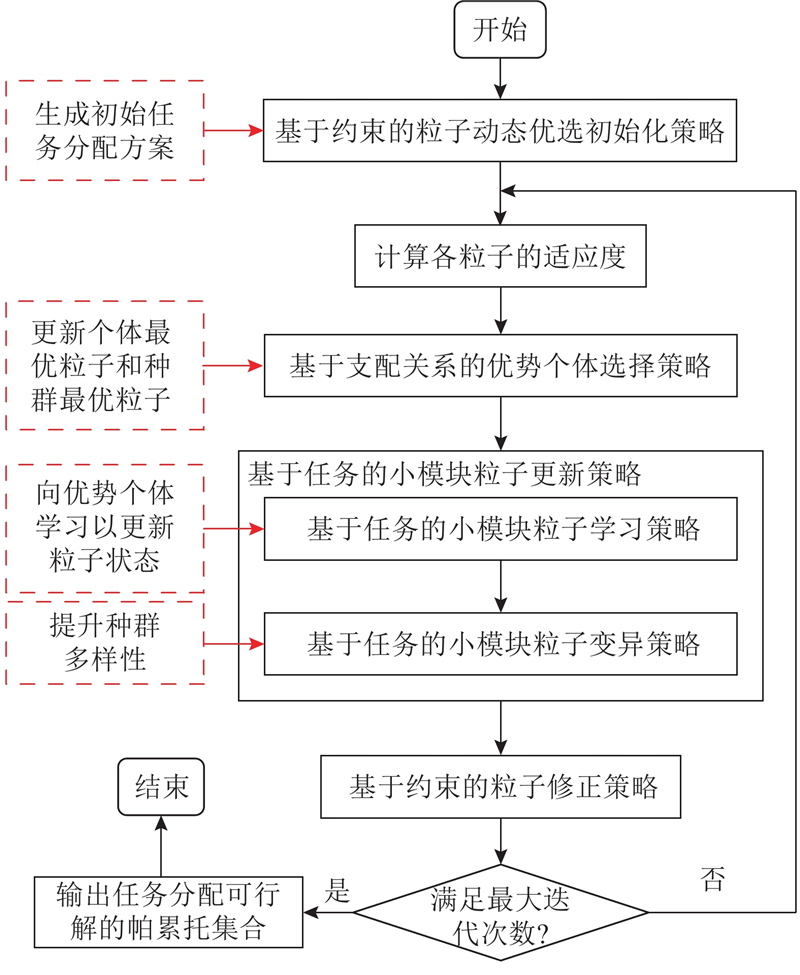
异构无人机协同多任务分配模型约束条件众多,优化变量复杂,既包含目标编号的离散变量又包含无人机编号的类别变量,传统粒子群优化算法难以有效求解,为此提出HS-MOPSO. 混合策略包含基于约束的粒子动态优选初始化策略、基于支配关系的优势个体选择策略和基于任务的小模块粒子更新及修正策略,算法总流程如图1所示.
图 1
图 1 基于混合策略多目标粒子群优化算法流程图
Fig.1 Flow chart of hybrid strategies based multi-objective particle swarm optimization algorithm
2.1. 基于约束的粒子动态优选初始化策略
2.1.1. 编码
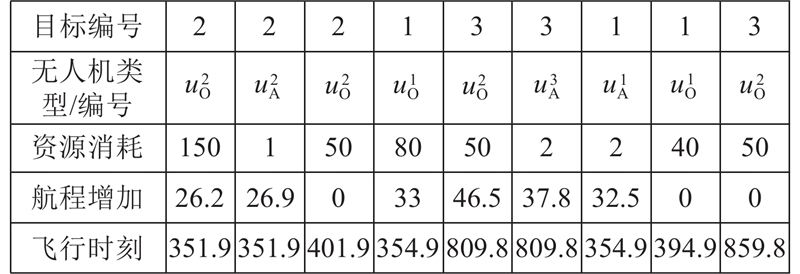
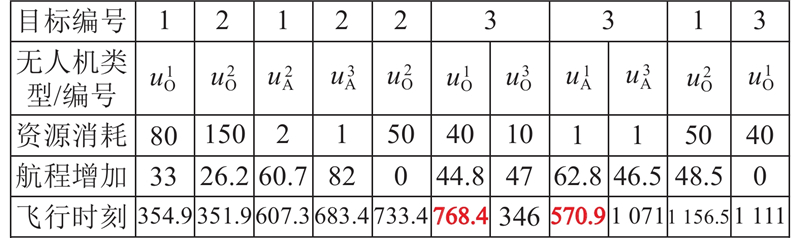
针对异构无人机协同多任务分配模型,设计混合变量编码的方式对粒子进行编码,实现目标、任务与无人机之间的良好匹配. 其中粒子前2行为编码信息,记录目标编号(同一目标编号先后出现依次代表侦察、打击和评估任务)和无人机类型/编号,在此基础上,为了有效解决死锁问题,也为了方便后续适应度计算与粒子操作,增设3行信息,分别记录资源消耗量、航程增加以及飞行时刻.
2.1.2. 基于约束的粒子动态优选初始化
基于上述粒子编码方式,提出基于约束的粒子动态优选初始化策略. 设计针对逐个任务依次进行可用无人机动态分配的方式,将约束条件嵌入对每个任务的分配过程中,确保初始生成的每个粒子均是符合约束条件的可行解,再依靠优选操作提高初始种群的质量,步骤如下. 1)设置初始化优选次数
图 2
2.2. 基于支配关系的优势个体选择策略
在标准粒子群优化算法中,粒子通过向个体最优粒子和种群最优粒子学习实现自我进化(下文将这2种最优粒子统称为优势个体),在现有研究中,个体最优粒子更新多重在种群最优粒子的更新且往往只依靠简单的随机选择操作[23],导致算法收敛精度不够,出现“早熟”的现象. 本研究提出基于支配关系的2种优势个体选择策略来保证优势个体的有效更新. 策略1为基于非劣解的优势个体选择策略:比较粒子之间的支配情况,若粒子
算法1 基于非劣解的优势个体选择策略
输入:当前个体
1. 判断
2.
3.
4. else:
5.
输出:新的优势个体
算法2 基于帕累托前沿的优势个体选择策略
输入:当前个体
1. 判断
2.
3.
4.
5.
6. else:
7. 将
8.
9.
10.
11.
输出:新的优势个体
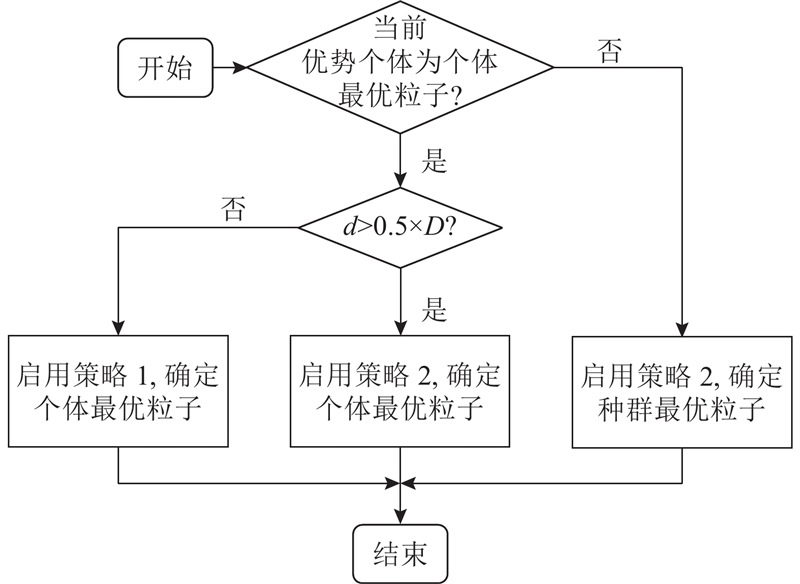
考虑到2种优势个体的差异性,为个体最优粒子和种群最优粒子设计不同的更新策略. 如图3所示,个体最优粒子综合2种策略分阶段进行选取. 在迭代前期,由于粒子收敛性较差,个体最优粒子首先通过策略1确定,使粒子快速收敛,快速提高搜索效率. 在迭代后期(以迭代次数d大于最大迭代次数
图 3
2.3. 基于任务的小模块粒子更新及修正策略
异构无人机协同多任务分配模型属于包含多约束的混合变量优化问题,标准粒子群优化算法的粒子更新方式难以生成满足约束限制的可行解,为此提出基于任务的小模块粒子更新策略. 该策略不再使用速度和位置的概念,而是将二者整合,即粒子在更新时主要以二进制交叉方法为基础,以单个任务模块为基本单位向优势个体进行学习或自身变异,这种精细化的学习与变异过程有利于搜索到更多高质量的可行解. 为了确保更新后的粒子表达满足约束条件,提出基于约束的粒子修正操作.
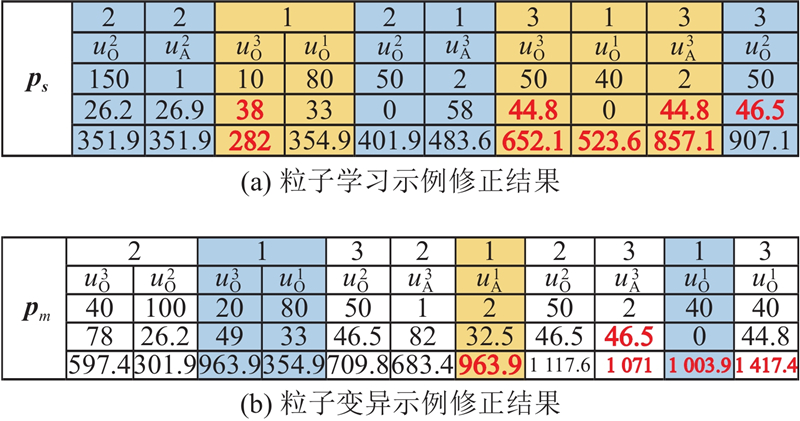
2.3.1. 基于任务的小模块粒子学习策略
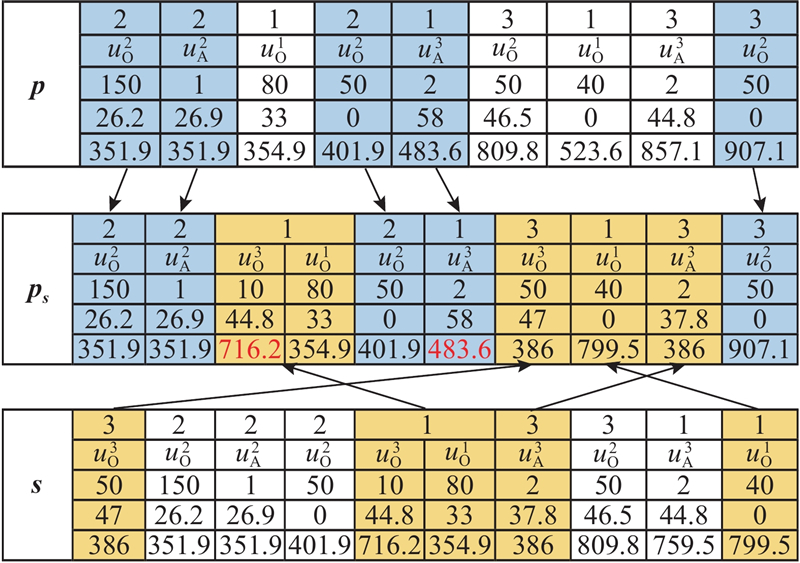
基于任务的小模块粒子学习过程描述为
即粒子
图 4
图 4 基于任务的小模块粒子学习示例
Fig.4 Example of task-based particle learning with small modules
2.3.2. 基于任务的小模块粒子变异策略
基于任务的小模块粒子变异过程描述为
即粒子
图 5
图 5 基于任务的小模块粒子变异示例
Fig.5 Example of task-based particle variation for small modules
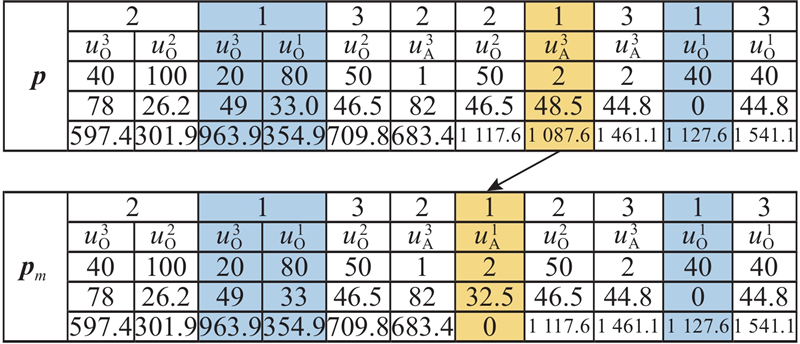
2.3.3. 基于约束的粒子修正策略
直接组合任务模块的粒子学习方式和随机模块变异操作会引起部分无人机分配的任务序列发生变化,导致飞行航程(粒子第四行)和飞行时刻信息(粒子第五行)出现错乱,发生违背问题约束的现象. 如在图4的
算法3 基于约束的粒子修正策略
输入:当前粒子
1. 清除
2. 求粒子
3.
4. 求分配的无人机编号
5. 求
6. 判断当前任务类型
7.
8.
9.
10. 计算该目标的前一个任务即侦察任务的完成时刻
11.
12.
13. 计算该目标的前一个任务即打击任务的完成时刻
14.
15. 将
输出:修正后的粒子
依据算法3,修正示例所得的结果,得到修正后的新粒子如图6所示,经过修正的数据加粗显示.
图 6
3. 仿真结果及分析
设置仿真实验,采用Windows 10 操作系统,仿真平台采用Matlab R2017b. 考虑不同作战规模共设计3种实例场景,分别为6架无人机(3架侦察型和3架战斗型)对3个目标、10架无人机(6架侦察型和4架战斗型)对6个目标和15架无人机(9架侦察型和6架战斗型)对10个目标. 以上3个场景简称为实例6×3、实例10×6和实例15×10. 假定无人机最大可飞行航程均为2 200 km. 无人机性能和目标属性信息详见附录表A1~A3. 附表A1中,
3.1. 算法有效性验证
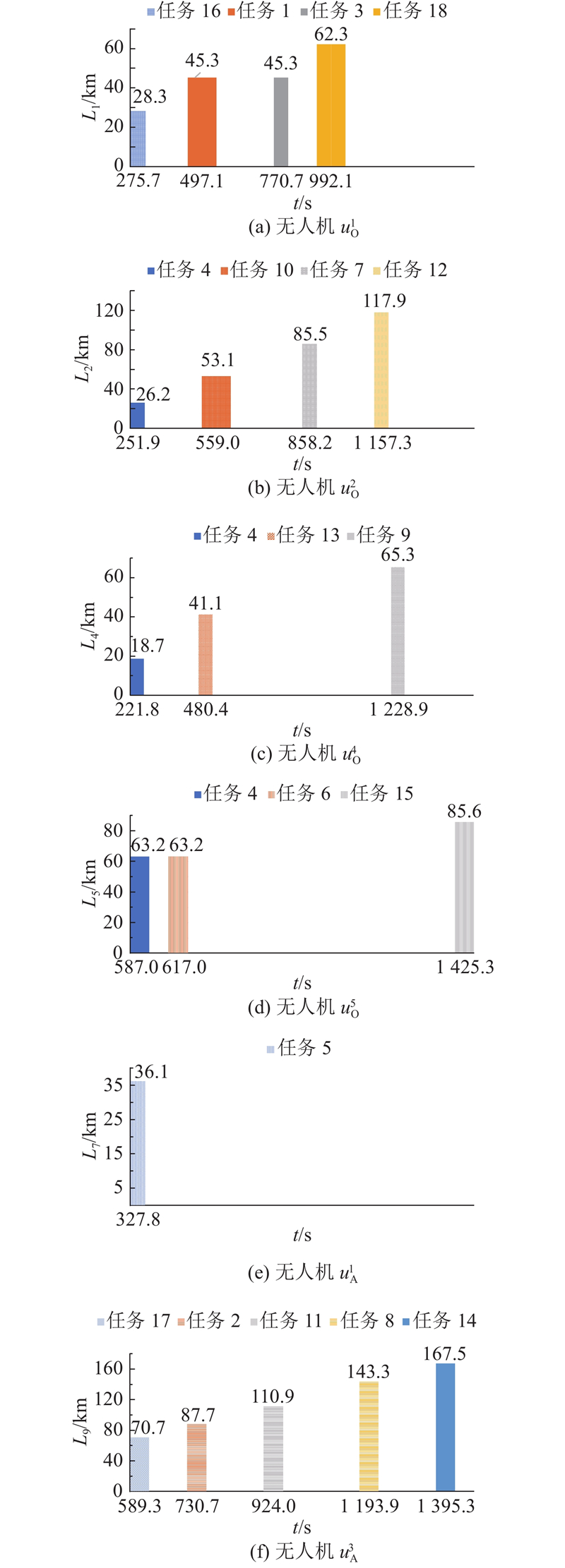
为了验证HS-MOPSO的有效性,将该算法分别应用于3个实例中进行仿真实验. 设置种群规模
表 2 无人机任务分配结果
Tab.2
| 实例 | 无人机 | 任务分配结果 |
| 6×3 | ||
| 10×6 | ||
| 15×10 | ||
图 7
3.2. 消融实验及结果
为了验证在模型中考虑等待时间对于解决死锁问题的有效性和HS-MOPSO每步策略的必要性,在实例6×3场景下进行消融实验.
3.2.1. 死锁检验消融实验
为了进一步验证等待时间对死锁的抑制作用,设计死锁检验实验,在目标函数的任务完成总时间计算公式中删除等待时间,结果如图8所示. 由图可知,
图 8
3.2.2. 混合策略消融实验
图 9
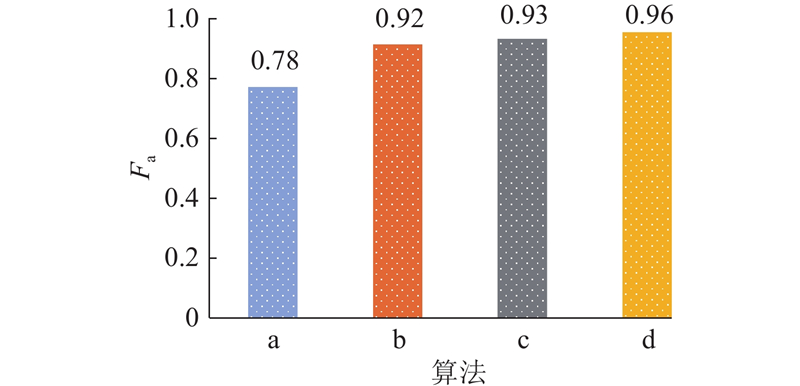
图 9 混合策略消融实验中不同算法的平均适应度
Fig.9 Average fitness of different algorithms in hybrid strategy ablation experiments
3.3. 算法性能对比
图 10
图 10 不同实例下5种粒子群优化算法的帕累托前沿
Fig.10 Pareto frontiers of five particle swarm optimization algorithms in different instances
图 11
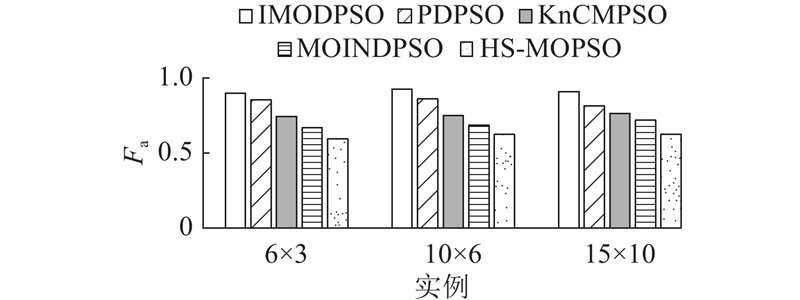
图 11 不同实例下5种粒子群优化算法的平均适应度
Fig.11 Average fitness of five particle swarm optimization algorithms in different instances
结果如表3所示. 可以看出,HS-MOPSO在3个实例场景中得到的Fa均最小,收敛效果显著. 对比算法的总体支配关系从优到劣依次为HS-MOPSO、MOINDPSO、KnCMPSO、PDPSO和IMODPSO.
表 3 所提算法相较对比算法在3个实例中的平均适应度下降幅度
Tab.3
| 对比算法 | A/% | ||
| 实例6×3 | 实例10×6 | 实例15×10 | |
| IMODPSO | 34 | 33 | 31 |
| PDPSO | 30 | 28 | 23 |
| KnCMPSO | 20 | 17 | 18 |
| MOINDPSO | 11 | 9 | 13 |
采用超体积HV和空间分布SP 2个指标分别评价5种算法在3个实验中的表现. HV数值越大,代表非支配解集的收敛性和多样性越好;SP数值越小,表明解集分布的越均匀. 综合2个指标的评价结果,可以对算法的性能做出更全面的综合评价. 将HV的指标参考点设置为(2 000,10 000,100),结果如表4所示,其中Mean为平均值,Var为方差,Worst为最差数据,Best为最优数据,下划线字体为最优值,加粗字体为次优值. 由表可知,HS-MOPSO在HV和SP评价中的综合表现均最优,在HV评价中共得到10组占优数据(包含9组最优数据和1组次优数据),说明该算法在收敛性和多样性上具有绝对优势. 表现其次的是MOINDPSO和KnCMPSO,均得到6组占优数据. 在SP评价中,HS-MOPSO在所有结果数据依然表现最优,共得到7组最优数据和2组次优数据,说明该算法解集分布最为均匀. 表现其次的是MOINDPSO,共得到3组最优数据和7组次优数据. 分析原因,IMODPSO和PDPSO选择优势个体的方式比较单一,算法收敛性不足;KnCMPSO采用向目标学习的粒子更新方式,每次学习须插入整个选中的目标模块,学习空间有限;MOINDPSO忽略对个体最优粒子的更新处理,收敛性不足. HS-MOPSO的3步改进策略可以有效提高算法的收敛性和多样性,综合表现最好.
表 4 不同粒子群优化算法在3个实例中的性能对比
Tab.4
| 实例 | 算法 | HV | SP | |||||||
| Mean | Var | Worst | Best | Mean | Var | Worst | Best | |||
| 6×3 | IMODPSO | 1.36×109 | 2.24×1015 | 1.26×109 | 1.44×109 | 8.54×10 | 2.20×103 | 2.09×102 | 2.28×10 | |
| PDPSO | 1.38×109 | 1.38×1015 | 1.31×109 | 1.46×109 | 1.43×102 | 1.05×104 | 3.66×102 | 1.63×10 | ||
| KnCMPSO | 1.56×109 | 2.11×1015 | 1.43×109 | 1.62×109 | 6.72×10 | 2.10×103 | 2.37×102 | 2.12×10 | ||
| MOINDPSO | 1.56×109 | 1.22×1015 | 1.49×109 | 1.63×109 | 5.76×10 | 2.74×103 | 2.26×102 | 1.59×10 | ||
| HS-MOPSO | 1.65×109 | 1.92×1015 | 1.54×109 | 1.68×109 | 4.88×10 | 3.11×102 | 1.09×102 | 1.88×10 | ||
| 10×6 | IMODPSO | 9.17×108 | 3.28×1015 | 7.96×108 | 1.02×109 | 7.92×10 | 5.88×103 | 3.61×102 | 2.35×10 | |
| PDPSO | 9.54×108 | 3.50×1015 | 8.08×108 | 1.03×109 | 3.13×102 | 7.29×104 | 1.05×103 | 5.70×10 | ||
| KnCMPSO | 1.23×109 | 8.66×1015 | 1.07×109 | 1.40×109 | 8.11×10 | 3.18×103 | 2.45×102 | 2.72×10 | ||
| MOINDPSO | 1.17×109 | 4.62×1015 | 1.08×109 | 1.34×109 | 4.84×10 | 1.08×103 | 1.68×102 | 1.46×10 | ||
| HS-MOPSO | 1.29×109 | 2.36×1015 | 1.17×109 | 1.38×109 | 4.76×10 | 6.97×102 | 1.10×102 | 2.11×10 | ||
| 15×10 | IMODPSO | 2.23×108 | 3.07×1015 | 1.54×108 | 3.38×108 | 7.23×10 | 5.15×102 | 1.28×102 | 4.04×10 | |
| PDPSO | 2.28×108 | 1.06×1016 | 5.96×107 | 4.39×108 | 7.19×102 | 2.09×106 | 6.85×103 | 2.10×10 | ||
| KnCMPSO | 5.99×108 | 7.30×1015 | 3.94×108 | 7.23×108 | 1.27×102 | 3.13×104 | 8.70×102 | 3.72×10 | ||
| MOINDPSO | 4.34×108 | 2.86×1015 | 3.52×108 | 5.58×108 | 6.44×10 | 7.51×102 | 1.28×102 | 3.00×10 | ||
| HS-MOPSO | 6.25×108 | 5.32×1015 | 5.12×108 | 7.66×108 | 5.74×10 | 9.90×102 | 1.38×102 | 3.07×10 | ||
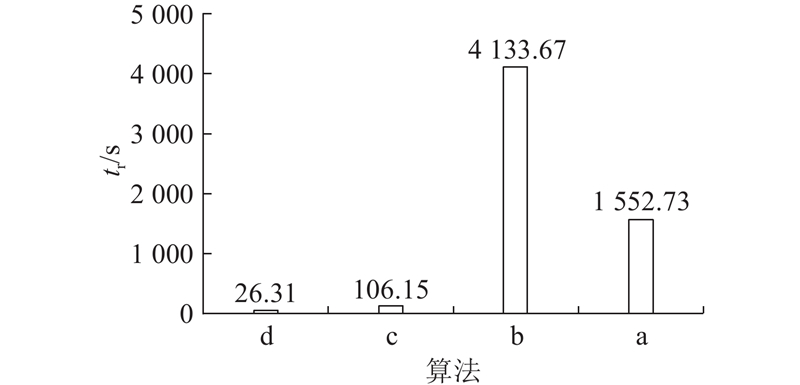
将每种对比算法在3个实例中的10次计算机运行时间平均值tr整理如表5所示. 由表可知,IMODPSO和PDPSO在运行时间方面表现较好,用时较短,MOINDPSO的表现次之,运行时间较长的是KnCMPSO和HS-MOPSO. 为了判断出HS-MOPSO每步策略对时间成本的影响,在实例6×3中绘制依次增加策略时的算法运行时间对比图,每种算法各运行10次取平均值结果如图12所示. 由图可知,基于约束的粒子动态优选初始化策略的加入并没有给算法c带来特别大的时间成本,但当基于支配关系的优势个体选择策略加入时,算法b的tr增至4 133.67 s,而在加入基于任务的小模块粒子更新策略后,算法a的tr迅速降至1552.73 s. HS-MOPSO的时间成本较大主要由基于支配关系的优势个体选择策略引起,原因是算法对优势粒子建立私有档案集的操作须实时比较更新以维护档案集的先进性. 由算法性能对比实验结果可知,HS-MOPSO在各方面的综合表现均为最优,进而说明该策略虽然增加了时间成本,但对于提高算法的收敛性起了至关重要的作用,对于最终优化效果的呈现必不可少. 其余几种算法虽然运行时间较短,但收敛精度均不够高. 考虑到所提算法的应用场景可归为离线的任务预分配阶段,收敛精度比运行时间成本更重要,且该算法能够解决困扰大部分算法的死锁难题,其价值得以体现.
表 5 不同粒子群优化算法在3个实例中的运行时间
Tab.5
| 实例 | tr/s | ||||
| IMODPSO | PDPSO | KnCMPSO | MOINDPSO | HS-MOPSO | |
| 6×3 | 22.70 | 23.44 | 388.81 | 67.50 | |
| 10×6 | 42.97 | 35.30 | 994.56 | 47.48 | |
| 15×10 | 48.54 | 34.90 | 959.29 | 46.14 | |
图 12
图 12 混合策略消融实验中不同算法的运行时间
Fig.12 Running time of different algorithms in hybrid strategy ablation experiments
4. 结 语
针对复杂约束条件下的异构无人机协同多任务分配问题,建立包含航程代价、时间代价和作战效能的三目标优化模型. 提出包含3种混合策略的多目标粒子群优化算法. 仿真结果表明,本研究构建模型能够有效抑制死锁难题,所提算法能够高效地求解复杂约束条件下的异构无人机协同多任务分配问题,且相较于对比算法在收敛性、多样性和解集分布等方面更具优势. 在后续的研究中,将考虑在更复杂多变的动态场景中实现任务的重分配,继续完善异构无人机协同任务分配模型和求解算法,还将考虑在满足精度要求的前提下增加一些提前收敛的措施,加快算法的优化进程,弥补现有的时间代价.
参考文献
Review of dynamic task allocation methods for UAV swarms oriented to ground targets
[J].DOI:10.23919/CSMS.2021.0022 [本文引用: 1]
The new killer drones: understanding the strategic implications of next-generation unmanned combat aerial vehicles
[J].DOI:10.1111/1468-2346.12342 [本文引用: 1]
基于改进多维粒子群的多无人机任务分配方法
[J].DOI:10.11809/bqzbgcxb2023.07.030 [本文引用: 1]
An improved multi-dimensional particle swarm-based approach to multi-UAV mission assignment
[J].DOI:10.11809/bqzbgcxb2023.07.030 [本文引用: 1]
Multi-UAV reconnaissance task allocation for heterogeneous targets using grouping ant colony optimization algorithm
[J].DOI:10.1007/s00500-021-05675-8 [本文引用: 1]
异构无人系统协同作战关键技术综述
[J].DOI:10.3873/j.issn.1000-1328.2020.06.006 [本文引用: 1]
Summary of key technologies for heterogeneous unmanned system cooperative operations
[J].DOI:10.3873/j.issn.1000-1328.2020.06.006 [本文引用: 1]
多无人机协同任务分配混合粒子群算法
[J].
Hybrid particle swarm algorithm for multi-UAV cooperative task allocation
[J].
基于协同进化的混合变量多目标粒子群优化算法求解无人机协同多任务分配问题
[J].DOI:10.11897/SP.J.1016.2021.01967 [本文引用: 2]
Co-evolution based mixed-variable multi-objective particle swarm optimization for UAV cooperative multi-task allocation problem
[J].DOI:10.11897/SP.J.1016.2021.01967 [本文引用: 2]
Digital-twin-assisted task assignment in multi-UAV systems: a deep reinforcement learning approach
[J].
基于KnCMPSO算法的异构无人机协同多任务分配
[J].
A knee point based coevolution multi-objective particle swarm optimization algorithm for heterogeneous UAV cooperative multi-task allocation
[J].
LeCMPSO算法求解异构无人机协同多任务重分配问题
[J].
Learning-guided coevolution multi-objective particle swarm optimization for heterogeneous UAV cooperative multi-task reallocation problem
[J].
Cooperative task assignment of a heterogeneous multi-UAV system using an adaptive genetic algorithm
[J].DOI:10.3390/electronics9040687 [本文引用: 1]
Multi-UAV task assignment with parameter and time-sensitive uncertainties using modified two-part wolf pack search algorithm
[J].DOI:10.1109/TAES.2018.2831138 [本文引用: 1]
Ant colony optimization for mixed-variable optimization problems
[J].DOI:10.1109/TEVC.2013.2281531 [本文引用: 1]
The whale optimization algorithm
[J].DOI:10.1016/j.advengsoft.2016.01.008 [本文引用: 1]
Salp swarm algorithm: a bio-inspired optimizer for engineering design problems
[J].DOI:10.1016/j.advengsoft.2017.07.002 [本文引用: 1]
基于多目标PSO混合优化的虚拟样本生成
[J].
Virtual sample generation method based on hybrid optimization with multi-objective PSO
[J].
Self-adjusting multitask particle swarm optimization
[J].
Particle swarm optimization for cooperative multi-robot task allocation: a multi-objective approach
[J].DOI:10.1109/LRA.2020.2972894 [本文引用: 1]
多角色多策略多目标粒子群优化算法
[J].
Multi-objective particle swarm optimization algorithm with multi-role and multi-strategy
[J].
离散粒子群优化算法求解多目标柔性作业车间调度问题
[J].
Adiscrete version of particle swarm optimization for multi-objective flexible job-shop scheduling problems
[J].
基于二进制混沌粒子群算法的认知决策引擎
[J].DOI:10.11918/hitxb20140302 [本文引用: 1]
Cognitive decision engine based on binary chaotic particle swarm optimization
[J].DOI:10.11918/hitxb20140302 [本文引用: 1]
An improved multiobjective discrete particle swarm optimization for hyperspectral endmember extraction
[J].DOI:10.1109/TGRS.2019.2917001 [本文引用: 1]
A multi-objective improved novel discrete particle swarm optimization for emergency resource center location problem
[J].DOI:10.1016/j.engappai.2022.104725 [本文引用: 1]