移动机器人在各种工业、服务和军事领域中发挥着越来越重要的作用. 许多国家都在积极推进国家战略，如Industry 4.0(德国)^[1]、the Advanced Manufacturing Partnership (美国)^[2]、Industry of the Future (法国)^[3]和中国制造2025(中国)^[4]，以抓住新一波工业革命带来的机遇. 其中数字孪生技术能够在多种场景下为机器人提供高质量、高效率和高精度的海量信息^[5]. 数字孪生技术最初由NASA提出^[6]，随后引起了学界的广泛关注. 例如，Cerrone等^[7]强调了须在数字孪生概念中考虑制造特征的核心方面. 为了保证数字孪生系统在当前人机环境集成过程中的鲁棒性和适应性，Huang等^[8]在数字孪生系统的建立过程中采用了人工智能、机器学习和深度学习等多种方法. 杨艳芳等^[9]制定了运动控制框架，重点关注环境和任务，并开发了相应的解决方案. 然而，这些方法并不适合腿足机器人运行时不断变化的动态环境. 此外，补偿机器人运动状态和数字孪生模型之间的误差也是这一技术推广应用的难点之一. Lumer-Klabbers等^[10]实现了数字孪生框架中机器人运动与实际操作的并行化. Liu等^[11]针对数字孪生车间建模复杂、开发周期长的问题，提出工业机器人虚实驱动系统的模块化构建方法. Hou等^[12]针对传统人工检测效率低、操作无监督、易出错等问题，提出基于数字孪生的飞机装配状态检测机器人系统. 这些研究结果表明，优化数字孪生系统框架有助于减少模型误差. 另外，在腿足机器人的实际应用中，往往会对网络通信提出更高的要求. Yamada等^[13]开发了机器人测试方法，以定量评估机器人远程操作的能力，并提出当机器人执行任务时，如果在复杂的环境中简单地通过局域网远程控制，不能评估机器人当前的环境和自身的状态，从而不能有效地控制和调整任务. Garg等^[14]提出数字孪生模型，该模型通过创建真实世界配置的3D数字环境来帮助机器人的在线/远程编程，将仿真分析的延迟控制在约40 ms.

腿足机器人作为近年来备受瞩目的移动机器人，能够较为从容地面对复杂场景. 虽然准确模拟腿足机器人的运动和行为有助于预测其在各种环境中的表现，但机器人和环境交互的不确定性容易导致数字孪生模型中产生较大的误差，从而影响机器人的效率和有效性. Swee等^[15]以蓝牙无线控制器为基础开发了六足机器人系统. Liang等^[16]提出新型腿足机器人的概念，通过软件仿真验证了其在地外行星探测计划中的性能. Lin等^[17]设计并开发了基于Java的3D机器人仿真系统，使用开源硬件和软件系统提供了一个灵活和可扩展的平台. 为了实时响应环境变化并执行相应的决策和行动，数字孪生系统须模拟腿足机器人的行动规划、动作轨迹和姿态控制. 因此，必须保证数字孪生模型的高保真度，并使其与物理机器人之间的差异最小化，以保证腿足机器人移动作业的精度.

此外，为了提高机器人定位系统的精度和鲁棒性，Wang等^[18]利用激光雷达辅助视觉惯性里程计提出mVIL-Fusion算法. Liu等^[19]提出基于频域优化的视觉辅助IMU校准方法FDO-Calibr，以抑制动态标定过程中的噪声. Gomez-Ojeda等^[20]提出PL-SLAM算法，在ORB-SLAM的基础上加入了线特征.

本研究的主要贡献如下：1）设计了针对腿足机器人的数字孪生系统体系框架，明确了架构、各模块结构、硬件框架和软件框架，可在移动场景下获得可靠准确的环境状态和机器人状态. 2）提出建立腿足机器人数字孪生模型的通用建模方法，并通过动力学加不确定性误差补偿的方法，保证孪生体的运动状态与实际机器人的运动状态高度一致. 3）通过点线特征匹配理论，优化了腿足机器人的自主定位精度和鲁棒性，结合环境建模数据实现高效里程计和实时移动建图.

结合腿足机器人在各种应用场景下的具体需求，将数字孪生系统分为体系结构和模块结构2个关键部分. 体系结构明确了体系框架中各部分的作用与相互联系；模块结构主要明确程序中依赖库、核心框架模块和插件模块之间的层级关系.

数字孪生的基本要素是物理空间和数字空间之间的相互作用^[21]. 其部署在腿足机器人上须满足例如可靠性、实时性和交互性等关键标准. 因此，本研究中系统的架构要求须满足：1）便于人机交互的图形用户界面(GUI)；2）腿足机器人虚实模型处理；3）系统内多种功能的集成；4)根据需要动态添加各种功能.

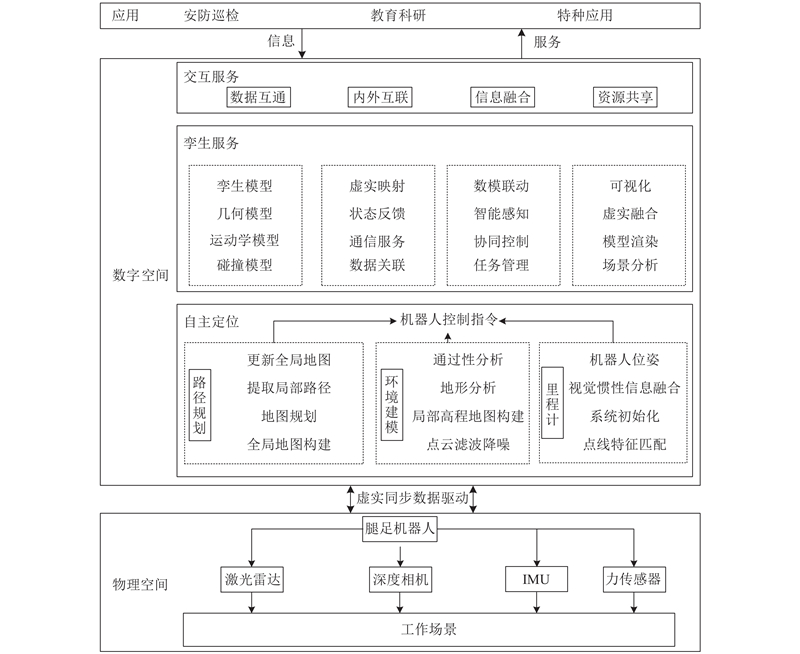
腿足机器人数字孪生系统将实际的腿足机器人与数字孪生模型相结合，对机器人物理实体在物理世界各种环境状态下的运动和行为进行模拟、分析和优化. 本研究中腿足机器人数字孪生系统的体系结构如图1所示，主要由数字空间和物理空间2部分组成. 物理空间包括腿足机器人、各种传感器和工作场景等. 数字空间包括交互服务、孪生服务和自主定位. 在物理空间中，一组传感器被用来捕获与腿足机器人及其工作环境有关的实时数据. 这些硬件组成将用于感知机器人周围环境、执行运动任务，并与数字空间进行虚实同步. 在数字空间内，3种功能(交互、孪生和定位)对获取的点云数据、图像数据、姿态数据和融合数据进行有针对性的分析、处理和整合. 通过实现数字空间和物理空间数据之间的相互交流、绘制分析图表，并优化和提升控制策略，从而以最小代价使物理实体具备新功能或者完成新实验. 借助数字孪生系统，可以实现复杂功能的执行，并生成包含各种物理数据的三维地图，这样可在不影响物理实体的情况下，通过新程序训练和学习数字孪生体的各种自主导航能力，从而节约实验资源和成本.

1) 交互服务：交互服务是系统架构的基础，须确保数字孪生数据的流畅通信. 为了有效地发挥人的决策能力，在信息缺失的情况下，需要一种积极的内外互联和互动机制. 此外，数字孪生系统应适应信息环境，将各种类型的信息与外部世界相结合. 这有利于资源共享，提高作业性能和效率.

2) 孪生服务：在保证数字孪生系统基本交互功能的基础上，核心孪生服务主要围绕4个关键技术展开. 首先，从几何、运动和碰撞模型中提取高保真的孪生模型. 其次，通过实时通信建立可靠的状态反馈，构建虚实模型之间的数据关联，实现准确全面的虚实映射关系. 再次，利用传感器的动态时空数据实现对孪生模型的智能感知. 通过对激光雷达、深度相机、惯性测量单元（inertial measurement unit, IMU）与力传感器等数据进行分析，捕捉到机器人在不同时间和不同位置的状态变化. 利用包括控制算法和人工输入在内的协同控制，建立与任务管理分配策略相一致的高效数模联动机制. 在特定场景下，孪生体可以为控制系统提供建议、预测未来的状态，帮助系统做出更明智的决策. 孪生模型不仅仅是一个被动更新的模型，其能够主动感知和理解所模拟物理实体的动态状态. 最后，通过深度虚实融合、动态模型绘制和专业场景分析，实现信息的实时可视化，提供一个直观的界面，使用户能够更好地理解孪生模型的输出、掌握系统状态. 通过实时可视化，操作者能够与孪生模型进行交互，例如调整关节控制、步态规划、反馈控制等，调整后的控制策略立即反馈到数字孪生系统中，更新模型的参数. 数字孪生系统再次模拟机器人的行为，生成新的实时可视化结果. 实现机器人在特定场景下的性能评估、行为分析，以及根据场景特征对控制策略的调整. 这一过程可以循环进行，用户通过不断调整和观察，逐步优化控制策略，当达到满意的性能水平时，用户可以决定采用当前的控制策略或者保存最佳参数.

3) 定位服务：为了满足多样化的应用需求，保证腿足机器人数字孪生系统的动态运行以及全面可靠的自主定位至关重要. 从机器人周围环境中提取点和线特征进行匹配，将视觉惯性信息与里程计初始化融合以确定机器人的位姿. 收集多个传感器的点云信息，通过滤波和降噪技术，生成具有鲜明特征的局部高程图. 使用本地地图，利用地形分析和通过性分析生成全局地图. 自主定位可以在动态环境中实现精确的里程定位和有效的环境建模. 其中，选取点和线特征进行匹配是在空间路标点的基础上重建空间路标线，以提高系统的精度.

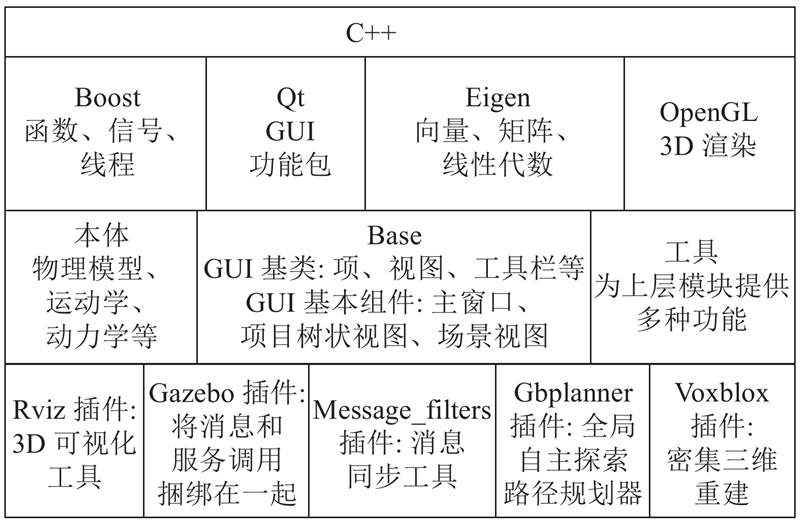
腿足机器人数字孪生系统通过用C++语言编写的动态链接插件模块来实现基本功能，将该模块分配给一个正在运行的进程. 然而，大多数机器人系统遵循分布式方法^[22]，将程序划分为用不同语言编写的后端和前端进程. 这些进程通过进程间通信或网络通信进行通信. 虽然这种体系结构利用了分布式计算的优势，但它可能会使系统更加复杂并带来额外开销.为了解决这个问题，本研究所提出的数字孪生系统采用简化的非分布式体系结构作为基础，只在需要时才加入分布式计算. 它利用机器人操作系统(robot operating system, ROS)节点系统，通过灵活的插件模块实现框架与分布式组件之间的无缝交互. 系统运行在Ubuntu 18.04和ROS Melodic上. 当前框架的模块结构如图2所示，其被设计为以C++语言为主的软件支撑库，由上至下具有依赖库、核心框架模块和插件模块3层结构. 这种设计使得系统在需要时可以有效地利用分布式计算资源，同时也保持了系统的简单性和可移植性.

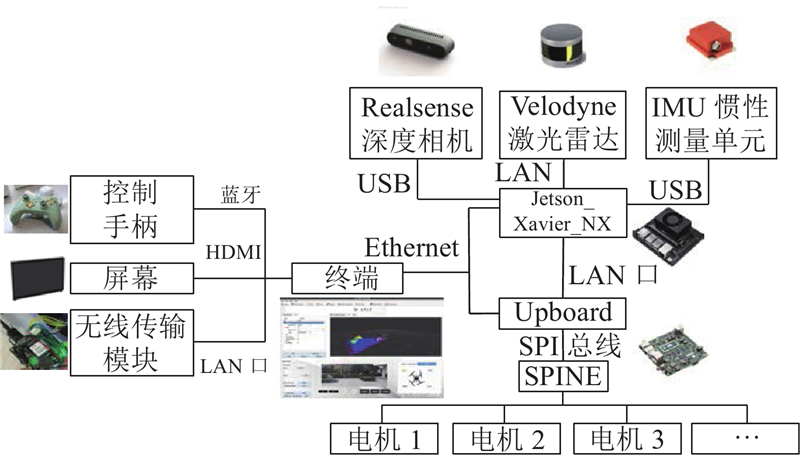
系统的硬件框架如图3所示，主要由终端、主控板和运动控制板3个部分与多种传感器组成. 这些组件一起工作，建立实时连接，实现多个硬件设备之间的信息共享，这是通过一个集成的通信网络来完成的. 该硬件框架基于终端控制器、多传感器融合与高度集成的执行器系统，为系统软件功能的实现提供了必要的支持和数据基础.

终端控制器主要涉及到对整个系统的控制、监控和用户交互. 终端上的GUI界面允许用户通过触摸屏与系统进行交互，可以启动、停止、调整机器人的运动、执行任务，它提供了选择机器人控制命令、访问配置文件和启动特定程序的选项. 无线传输模块通过有线LAN端口连接终端，实现终端到主控板和运动控制板的远程无线传输，设定任务执行的顺序和优先级，记录系统运行过程中的数据，包括传感器数据、控制指令、执行器输出等，增强系统的灵活性和便利性.

多传感器融合提高了数据的一致性和准确性，避免单一传感器可能引入的误差，增加了系统的容错性. 机器人搭载的深度相机、激光雷达和IMU是数字孪生系统中外部原始数据的主要来源. 这些数据被传输到主控板，负责实时定位算法的运行. 相机图像数据用于线特征提取和匹配，而IMU信息用于初始化里程表. 处理来自相机和激光雷达的点云数据以创建环境模型. 多传感器融合使得腿足机器人能够更灵活、智能地应对不同的任务和环境.

在多关节的腿足机器人中，须协调各个执行器的动作，高度集成的执行器系统可以确保整体运动的平衡和协调，提高能量的利用效率，实现机器人在复杂环境中的稳定运动和高效执行任务. 其中，控制指令通过通信网络和高速主控线传输到运动控制板，然后将这些指令转换为电机输出，从而实现对机器人运动的控制. 这种数据流和控制机制确保了数字孪生系统中传感器信息的集成、实时处理和精确的机器人控制.

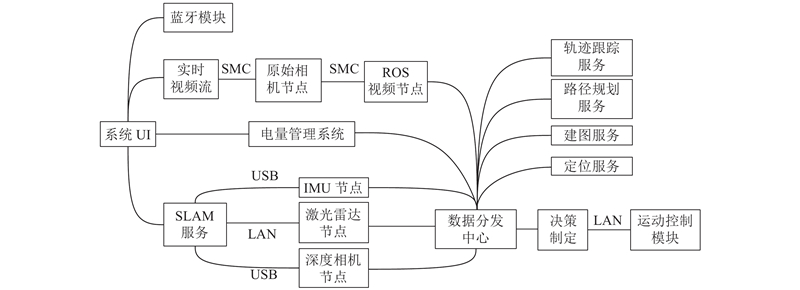
根据腿足机器人的软硬件特点及其交互界面，本系统的软件框架采用3级控制模式. 第1级由运动控制模块组成，该模块运行在运动控制板上. 第2级是数据分发中心，它在主控板上运行. 第3级是在终端上运行的系统UI. 这种3级控制模式保证了腿足机器人数字孪生系统内的有效控制和交互. 构建的数字孪生系统软件框架如图4所示，展示了不同层次控制之间的交互和协作.图中，SMC(shared memory communication)表示共享内存通信.

1) 运动控制模块. 在系统正常操作过程中，用户对腿足机器人具有最高级别的控制权限. 然而，在存在通信障碍干扰的情况下，运动控制模块接收决策程序的默认指令. 这些指令包括基本动作，如等待或返回腿足机器人到安全位置. 这种设计确保了腿足机器人即使在通信中断或其他干扰的情况下也能继续工作并做出适当的反应. 通过整合决策程序和预防策略，系统保持了一定程度的自主性和适应性，以处理意外情况. 这增强了腿足机器人的整体鲁棒性和可靠性，使其能够自主定位并应对挑战.

2) 数据分发中心. 数据分发中心是系统软件框架的关键组成部分. 它在促进数字孪生系统中的数据互操作性、信息融合和指令传输方面起着核心作用. 它对来自多个传感器的异构数据进行预处理，并根据需要将其分发到不同的应用程序服务. 实时视频流数据和电机反馈值也被存储并供用户访问，以便能够监控腿足机器人的当前状态. 通过实现组件之间的通信，数据分发中心可确保整个系统的高效数据交换和同步. 这样可以实现有效的信息融合，并为用户提供方便直观的实时数据访问，以监控腿足机器人的性能.

3) 系统UI. UI不仅负责视觉信息的传达和美观,更重要的是引导用户的交互和操作; 而GUI作为用户图形界面,只负责软件的视觉呈现. 使用Qt框架开发的系统UI，为腿足机器人数字孪生系统提供蓝牙模块、实时视频流、电源管理系统、SLAM服务和其他应用程序等组件. 通过Qt框架，系统UI确保了用户友好的交互体验，使用户能够访问和控制腿足机器人数字孪生系统的不同功能模块. 蓝牙模块支持可扩展的手柄，实时视频流的可视化清晰反映了系统当前状态和性能.

建立与物理实体相对应的虚拟模型对于数字孪生至关重要，为了适应不同腿足机器人的建模要求，建立了虚实模型之间的通用坐标系变换公式，可以表示任何腿足机器人模型. 然而，由于动力学模型上的差异以及物理实体与仿真机器人之间的差异，在控制运动方面，实现物理实体与仿真机器人之间的精准同步是一项挑战. 例如电机扭矩和地面摩擦力上的差异，这些差异会导致物理实体与仿真机器人运动的显著不同. 为了实现物理实体和数字孪生之间的同步控制，有必要对数字孪生模型与物理模型之间固有的不确定性进行补偿.

选取惯性坐标系{W}、质心坐标系{C}、机身坐标系{B}，计算三者之间变换关系的相关性. 质心坐标系{C}如图5所示，其中三轴方向与惯性坐标系相同，坐标原点定义为机器人的重心. 在机器人没有发生滚转和俯仰运动的前提下，由{C}绕着z_C正向(顺时针)旋转偏航角ψ后得到$ {{\boldsymbol{R}}}_B^W(\psi ) $，接着绕着y_C反向(逆时针)旋转俯仰角θ后而得到$ {{\boldsymbol{R}}}_B^W(\theta ) $，最后绕着x_C反向(逆时针)旋转滚转角ϕ后得到$ {{\boldsymbol{R}}}_B^W(\phi ) $. 由于$ {{\boldsymbol{R}}}_B^W \in {{\mathrm{SO}}}(3) $，其中，SO(3)表示特殊正交群，从而可以推导出{W}到{B}的旋转变换如下：

(1)$ {\begin{split} &{{\boldsymbol{R}}}_W^B(\phi ,\theta ,\psi ) = {({{\boldsymbol{R}}}_B^W(\phi ){{\boldsymbol{R}}}_B^W(\theta ){{\boldsymbol{R}}}_B^W(\psi ))^{\rm{T}}}= \\& \left[ {\begin{array}{*{20}{c}} {\cos\; \theta \cos\; \psi }&{\sin\; \phi \sin\; \theta \cos\; \psi - \cos\; \phi \sin\; \psi }&{\cos\; \phi \sin\; \theta \sin\; \psi +\sin\; \phi \sin\; \psi } \\ {\cos\; \theta \sin\; \psi }&{\sin\; \phi \sin\; \theta \sin\; \psi +\cos\; \phi \cos\; \psi }&{\cos\; \phi \sin\; \theta \sin\; \psi - \sin\; \phi \cos\; \psi } \\ { - \sin\; \theta }&{\sin\; \phi \cos\; \theta }&{\cos\; \phi \cos\; \theta } \end{array}} \right].\end{split}} $

利用ROS的Rviz插件创建腿足机器人及其周围环境的数字孪生模型. Rviz是ROS腿足机器人操作系统中的3D可视化工具，主要用于可视化各种数据，包括腿足机器人模型、坐标系统、路径规划、3D点云和图像. 在构建腿足机器人数字孪生系统的模型层时，使用了Rviz插件. 利用SolidWorks建立腿足机器人的URDF模型. 然后将模型导入到ROS中，并利用xacro格式生成紧凑的模型代码和可编程接口. 当须获取其他腿足机器人的数字孪生模型时，可以通过相似的代码编写以及插件编写实现. 程序开发使用C++语言进行，以实现对数字孪生模型的数据分析和处理.

机器人整体控制采用中枢模式发生器（central pattern generator, CPG）和模型预测控制（model predictive control, MPC）相结合的方式，控制框架如图6所示. 机器人的运动模式和步态转换由CPG的信号确定，MPC根据期望的状态参数，通过建立多点支撑力平衡模型并使用二次规划求解需要的驱动力矩.

CPG生成稳定且带有一定相位偏移周期的节律信号，这些节律信号直接与腿部运动轨迹相耦合. 采用一种解耦驱动强度和节律信号的控制方法，这种控制策略极大地简化了机器人系统的控制流程，提高了机器人的协调稳定性和反应速度. 采用笔者前期提出的σ-Hopf振荡器^[23]，其表达式如下：

(2)$\left[\begin{array}{c}\dot{x} \\\dot{y}\end{array}\right]=\left[ \begin{array}{c}-\alpha\left((x-a)^2+(y-b)^2-\mu\right) \;\;-\omega(t) \\\omega(t) \;\;-\alpha\left((x-a)^2+(y-b)^2-\mu\right)\end{array}\right]\left[\begin{array}{l}x-a \\y-b\end{array}\right], $

等同于

(3)$\dot{\boldsymbol{v}}=f(\boldsymbol{v}, \alpha, \mu, \omega(t)).$

式中：x和y为状态变量，(a, b)为极限环的中心，α为分岔参数；μ为振荡的幅度；$ \omega = \dfrac{{{\text{π}} }}{{\rho \varphi [{\exp\;(} - \lambda (y - {y_0}{)})+1]}} + \dfrac{{{\text{π}} }}{{(1 - \rho )\varphi [{}{\text{exp}}\;(\lambda (y - {y_0}{\text{)}}) + 1]}} $，λ为调节速度的可变强度，ρ表示占空比，φ为周期参数，y₀为信号中的一个点，调节将从那里开始，参数φ和ρ不相关，可以分别控制和调整信号的幅度、频率和波形. 可将式(2)重写为

(4)$ \left.\begin{split} & \dot{\boldsymbol{v}}=\left[\begin{array}{c}\dot{x} \\\dot{y}\end{array}\right]=\left[\begin{array}{cc}\sigma_1 & -\sigma \\\sigma & \sigma_1\end{array}\right]\left[\begin{array}{l}x-a \\y-b\end{array}\right]+{\boldsymbol{g}}(t)+{\boldsymbol{u}}(t), \\& \begin{array}{l}\sigma=\dfrac{{\text{π}}}{\varphi_{\mathrm{p}} \rho \left(\exp\; \left(-\lambda\left(y-y_0\right)\right)+1\right)}+ \\ \quad\;\;\; \dfrac{{\text{π}}}{\varphi_{\mathrm{p}}(1-\rho)\left(\exp\; \left(\lambda\left(y-y_0\right)\right)+1\right)}, \\\sigma_1=-\alpha\left((x-a)^2+(y-b)^2-\mu\right).\end{array}\end{split}\right\} $

式中：φ_p表示振荡器的周期时间；u(t)为传感器采集到的外部输入项，u(t)=−sign (y)u，u为外部输入通过外部传感信息控制振荡信号，t为振荡器的时间变量；g(t)为耦合输入，须通过振荡器网络控制信号相位差来完成协调. 由于全耦合双向环结构比单向环结构具有更好的过渡性能，构造全耦合的双向环结构. 对于本研究中的σ-Hopf振荡器，表达式如下：

(5)$\left.\begin{aligned} \dot{\boldsymbol{v}}_i=&f\left(\boldsymbol{v}_i, \mu_i, \sigma_i\left(\rho_i, \lambda, y_0, t\right)\right)-\\&\sum_{j \in R_i}^{n_i} k_{i j}(t)\left(\boldsymbol{v}_i-\frac{\mu_i}{\mu_j} \boldsymbol{R}\left(\Delta {\boldsymbol{\varPhi}}_{i j}\right) \boldsymbol{v}_j\right)+{\boldsymbol{u}}(t), \\ k_{i j}(t)=&\kappa_{j j} \mathrm{e}^{-\eta\left(t-t_0\right)}, \\ \boldsymbol{R}(\Delta {\boldsymbol{\varPhi}})=&\left[\begin{array}{cc}\cos \;(\Delta {\boldsymbol{\varPhi}}) & -\sin\; (\Delta {\boldsymbol{\varPhi}}) \\\sin\; (\Delta {\boldsymbol{\varPhi}}) & \cos\; (\Delta {\boldsymbol{\varPhi}})\end{array}\right].\end{aligned}\right\} $

式中：n_i表示与第i个神经元连接的其他神经元个数；R_i表示只包含第i个σ-Hopf振荡器的局部邻域的集合；k_ij(t)为正标量，表示耦合增益，并且对于不同形式的运动可以是时变的；η为下降因子，与时间相关；κ为初始系数；t₀为参数更改开始的时间；R(Δ${\boldsymbol{\varPhi}} $)为第i、j个振荡器之间的相位差ΔΦ_ij的二维旋转变换. 所需的相位偏移量ΔΦ_ij引导v_i与v_j同步. 当信号变得稳定时，较短的时间会导致较大的收敛强度，反之亦然，因此，收敛过程主要由k(t)的状态决定^[24]. 中枢神经网络如图7所示，其公式可以写为

(6)$\begin{split} &\left[\begin{array}{l}\dot{x}_i \\\dot{y}_i\end{array}\right]=\left[\begin{array}{cc}\sigma_{1 i} & -\sigma_i \\\sigma_i & \sigma_{1 i}\end{array}\right]\left[\begin{array}{l}x_i \\y_i\end{array}\right]-\\&\qquad\sum_{j \in R_i}^{n_i} k_{i j}(t)\left(\left[\begin{array}{l}x_i \\y_i\end{array}\right]-\boldsymbol{R}(\Delta {\boldsymbol{\varPhi}})\left[\begin{array}{l}x_j \\y_j\end{array}\right]\right).\end{split} $

该中枢神经网络由6个σ-Hopf模块和1个网络同步模块组成. 具体的调节过程详见文献[23].

MPC根据期望的状态参数，例如迈步步长、机身倾角，进行落足点规划和运动学计算得到期望的关节角度θ_d，通过单刚体模型求解机器人的最优控制向量. 状态估计主要根据传感器反馈数据估计质心位置和地形信息作为机器人的期望姿态角. 在节能模块中，根据膝关节角度的变化产生基本惯性补偿τ₁(τ₁=M_s)，M_s为膝关节的虚拟力矩.

摆动控制器计算并遵循腿的预期轨迹，跟踪轨迹的控制器使用反馈项来计算期望的关节力矩. 足端在惯性坐标系{W}中的位置表示如下：

(7)$ { }^W \boldsymbol{P}_{\mathrm{f}}={ }^W \boldsymbol{P}_{\mathrm{c}}+{ }_B^W {\boldsymbol{R}}\left({ }_R^B \boldsymbol{T}+{ }^R \boldsymbol{P}_{\mathrm{f}}\right). $

式中：^WP_c为惯性坐标系{W}中的躯干的描述，${}_R^B {\boldsymbol{T}}\ $为相对于机身坐标系{B}的平移矩阵，${ }_B^W {\boldsymbol{R}} $为相对于坐标系{W}的旋转矩阵，^RP_f为足端位置.

期望的落足点间接地控制躯干的姿势和速度. 在摆动阶段的初始时刻，根据腿的位置和速度以及目标落地点、腿落地速度和高度，在整个摆动持续时间中确定期望的足端位置P_f,d. 然后，通过逆运动学，获得期望的关节角度θ_d. 此外，关节的期望速度可以通过对轨迹的求导来获得. 根据弹簧阻尼模型计算加在摆动腿上的虚拟力：

(8)$ \boldsymbol{\tau}_2=K_{\mathrm{p}}\left(\boldsymbol{\theta}_{\mathrm{d}}-\boldsymbol{\theta_{\mathrm{c}}}\right)+K_{\mathrm{d}}\left(\dot{\boldsymbol{\theta}}_{\mathrm{d}}-\dot{\boldsymbol{\theta_{\mathrm{c}}}}\right). $

式中：K_p为摆动腿的刚度系数，K_d为摆动腿的阻尼系数，${\boldsymbol{\theta}}_{\mathrm{c}} $为机器人当前时刻的姿态角参数.

预测控制可以通过预测状态参数来稳定动态步态^[25]，将六足机器人的身体假设为单刚体模型，使得状态向量X=[$ {\boldsymbol{\varTheta}} $, P_c, ${\boldsymbol{\omega }} $, v_c]可以完整地描述六足机器人的运动状态^[26]. 根坐标系{R}位于根轴和髋轴的交点处. 在单刚体模型中，作为足端力的f_i直接施加到机器人上，定义为U=[f₁, f₂, f₃, f₄, f₅, f₆]，以控制机器人的位置和姿态，并且其可以描述为

(9)$\begin{split} \ddot{\boldsymbol{P}}_{\mathrm{c}}=&\frac{\displaystyle{\sum}_{i=1}^6 {\boldsymbol{f}}_i}{m_{\mathrm{r}}}-g \sum_{i=1}^6 \boldsymbol{P}_{{\rm{f}} i} \times {\boldsymbol{f}}_i=\frac{{\mathrm{d}}}{{\mathrm{d}} t}(\boldsymbol{I} {\boldsymbol{\omega}})=\\&\boldsymbol{I} \dot{{\boldsymbol{\omega}}}+{\boldsymbol{\omega}} \times(\boldsymbol{I} {\boldsymbol{\omega}}) \approx \boldsymbol{I} \dot{{\boldsymbol{\omega}}}.\end{split} $

式中：P_c为机器人在坐标系{W}中的位置，m_r为机器人的质量，g为重力加速度，P_fi为第i条腿在坐标系{C}中的腿位置，I为机器人的惯性矩阵，${\boldsymbol{\omega }} $为基座的角速度，R为{W}的旋转矩阵.

将刚体动力学模型离散化，用Δt表示采样时间，用前向欧拉方法离散连续状态空间表达式^[27]. 取机器人当前的实际状态为X_k，最优控制为U_k，可以得到下一时刻的状态参数，记为X_k+1，即

(10)$ \boldsymbol{X}_{k+1}=\boldsymbol{A}_k \boldsymbol{X}_k+\boldsymbol{B}_k \boldsymbol{U}_k. $

式中：A_k=I+∆tA_c，B_k=∆tB_c，k=0,1,2,···；A_c为状态矩阵，A_c∈R^13×13；B_c为控制矩阵，B_c∈R^13×12.

在本研究所提方法中，MPC需要一个参考轨迹、状态输入以及模型参数，即腿的位置和接触顺序. 参考生成器基于启发式方法，它将用户命令的速度v_c,d、角速度${\boldsymbol{\omega }}_{\mathrm{d}} $、机器人的当前姿态[${\boldsymbol{\varTheta}} $, P_c, $ {\boldsymbol{\omega }} $, v_c]作为输入，参考生成器输出MPC成本的参考，即状态X_ref. 根据用户输入的v_c,d和${\boldsymbol{\omega }}_{\mathrm{d}} $，可以将下一个循环中给定的有限预测域中的期望状态参数表示为

(11)$\left.\begin{split} & \boldsymbol{P}_{\mathrm{c}}^{\mathrm{ref}}=\boldsymbol{P}_{\mathrm{c}}+\Delta t \boldsymbol{R}_Z(\Delta \phi) \boldsymbol{v}_{\mathrm{c}, {\mathrm{d}}}, \\& \boldsymbol{v}_{\mathrm{c}}^{\mathrm{ref}}=\boldsymbol{v}_{\mathrm{c}}+\Delta t \dot{\boldsymbol{v}}_{\mathrm{c}}.\end{split}\right\} $

(12)$\left.\begin{split} & \boldsymbol{\theta}_{\text {ref }}=\boldsymbol{\theta}+\Delta t \boldsymbol{{\boldsymbol{\omega }}}_{\mathrm{d}}, \\&\boldsymbol{{\boldsymbol{\omega }}}_{\text {ref }}=\boldsymbol{{\boldsymbol{\omega }}}+\Delta t \dot{\boldsymbol{{\boldsymbol{\omega }}}}_{\mathrm{d}}.\end{split}\right\} $

式中：$ {\boldsymbol{P}}_{\mathrm{c}}^{\mathrm{r}\mathrm{e}\mathrm{f}} $、$ {\boldsymbol{v}}_{\mathrm{c}}^{\mathrm{r}\mathrm{e}\mathrm{f}} $、$ {\boldsymbol{\theta }}_{\mathrm{r}\mathrm{e}\mathrm{f}} $和$ {\boldsymbol{\omega }}_{\mathrm{r}\mathrm{e}\mathrm{f}} $为下一时刻的期望状态参数；P_c、v_c、${\boldsymbol{\varTheta}} $和${\boldsymbol{\omega }} $为机器人当前状态参数；R_z($ \Delta\phi $)为围绕Z轴的旋转矩阵，$\Delta\phi $=ϕ_ref−ϕ；$ {\dot{\boldsymbol{v}}}_{\mathrm{c}} $为线性加速度参数；$ {\dot{\boldsymbol{\omega }}}_{{\mathrm{d}}} $为预期角加速度参数. 关于具体计算，请参考笔者之前的论文^[28].

为了找到预期的足端的反作用力，使用离散化模型预测控制器，并将优化问题描述为求解预测域时域的最优控制量. 考虑模型预测控制问题，以解决k个循环的最优向量：

(13)$\left.\begin{split} & \min _{\boldsymbol{U}} \; \sum_{j=0}^{k-1}\left\|\boldsymbol{X}_{j+1}-\boldsymbol{X}_{j+1, \text { ref }}\right\| \boldsymbol{Q}_j+\left\|\boldsymbol{U}_j\right\| \boldsymbol{R}_j; \\&\quad {\mathrm{s}}.{\mathrm{t}}.\;\; \boldsymbol{X}_{j+1}=\boldsymbol{A}_j \boldsymbol{X}_j+\boldsymbol{B}_j \boldsymbol{U}_j, j=0, \cdots, k-1, \\&\quad \boldsymbol{c}_{\min } \leq \boldsymbol{U}_j \leq \boldsymbol{c}_{\max }, j=0, \cdots ,k-1 .\end{split} \right\}$

式中：X_{j+1, ref}为机器人下一时刻的期望状态；Q为优化权重系数，Q∈R⁶；R为能量消耗权重系数，R∈R⁶；c_min和c_max为足端力的上限和下限. 通过求解器qpOASES解决式(13)后，通过扭矩映射将矢量U应用于机器人，扭矩映射为τ₃=J^TU. 并且为了尽可能减小机器人腿部惯性的影响，加入腿部惯性补偿力矩，在站立阶段的关节力矩可以表示为

(14)$ {{\boldsymbol{\tau}}}_3=\boldsymbol{M}_{\mathrm{l}} \ddot{{\boldsymbol{q}}}+\boldsymbol{J}^{\mathrm{T}} \boldsymbol{U}. $

式中：M_l为腿的惯性矩阵，$ \ddot{{\boldsymbol{q}}} $为角加速度.

不确定性包括孪生模型与物理模型之间机器人的摩擦力和电机转矩误差. 设计消除摩擦力和电机转矩误差的函数公式. f=F_Nu，其中，F_N为正压力(不一定等于施加的重力)，u为动摩擦系数. 模拟地面与物理地面的动摩擦系数不同，设k₁为固定差值. F_N等于足部反馈力，仿真机器人与物理机器人的正压力为变量，设为x₁. 动摩擦误差的关系式如下：

(15)$ k_1=u_1-u_2, \quad x_1=F_{{\mathrm{N}} 1}-F_{{\mathrm{N}} 2}, \quad \varepsilon_1=k_1 x_1. $

式中：u₁为模拟表面摩擦系数，u₂为物理表面摩擦系数，F_N1为模拟机器人的正作用力，F_N2为物理机器人的正作用力，ε₁为动态摩擦误差. 电机转矩为转动惯量乘以角速度. 仿真与物理机器人的转动惯量之差为固定值设为k₂，角速度之差为变量值设为x₂. 则电机转矩误差为

(16)$ k_2=I_1-I_2, \quad x_2=\omega_1-\omega_2, \quad \varepsilon_2=k_2 x_2. $

式中：I₁为仿真机器人的转动惯量，I₂为物理机器人的转动惯量，ω₁为仿真机器人的角速度，ω₂为物理机器人的角速度，ε₂为电机的转矩误差. 因此，误差和为

(17)$ \varepsilon=\varepsilon_1+\varepsilon_2. $

将其加入到机器人控制程序中，当ε→0时，仿真结果与物理机器人拟合度最高.

在腿足机器人数字孪生模型中，自主定位精度决定机器人与环境交互的状态以及环境建模的精度，本研究采用基于滑动窗口的紧耦合单目视觉惯性里程法进行状态估计^[29]. 机器人在室内工作时，往往会处于弱纹理的环境中，在该环境中使用特征点法会出现无法提取到足够特征点的情况，这可能会导致系统跟踪失败. 在室内这种人工的结构化环境中通常会有比较丰富的线特征，其在光照变化下鲁棒性更强. 在视觉前端使用EDLines进行线特征的提取，相较于其他直线检测算法例如霍夫变换与LSD，EDLines^[30]在保证线段提取精度的同时又能保证较快的提取速度. 在提取完线特征后须对相邻帧的线特征进行线特征匹配，使用LBD描述子^[31]进行线特征的匹配，其具有旋转不变性的特点，在实际使用过程中，须将LBD描述符转换为二进制的描述子，通过计算汉明距离来比较线段之间的相似度，从而提高计算速度.

视觉惯性系统采用紧耦合的方法进行融合，将点特征视觉残差、线特征视觉残差和IMU的残差组合起来在滑动窗口内进行位姿优化，待优化的状态向量χ如下：

(18)$ {\left.\begin{aligned}& \boldsymbol{\chi} = \left[\boldsymbol{x}_0, \boldsymbol{x}_1, \cdots, \boldsymbol{x}_n, \boldsymbol{x}_{\mathrm{c}}^B, \lambda_0, \lambda_1, \cdots, \lambda_m, \boldsymbol{l}_1, \boldsymbol{l}_2, \cdots, \boldsymbol{l}_p\right], \\& \boldsymbol{x}_k = \left[\boldsymbol{p}_k^W, \boldsymbol{v}_k^W, \boldsymbol{q}_k^W, \boldsymbol{b}_{\mathrm{a}}, \boldsymbol{b}_{\mathrm{g}}\right], k \in[0, n], \\& \boldsymbol{x}_{\mathrm{c}}^B = \left[\boldsymbol{p}_{\mathrm{c}}^B, \boldsymbol{q}_{\mathrm{c}}^B\right].\end{aligned}\right\}} $

式中：$ {\boldsymbol{p}}_{k}^{W} $、$ {\boldsymbol{q}}_{k}^{W} $和$ {\boldsymbol{v}}_{k}^{W} $分别表示第k帧IMU在世界坐标系中的位置、方向和速度，b_a表示IMU的加速度偏差，b_g表示IMU的角速度偏差，$ {\boldsymbol{x}}_{{\mathrm{c}}}^{B} $为摄像机的外部参数，n为滑动窗口关键帧数，m为空间地标点个数，p为空间地标线个数，λ为空间地标点对应的反深度，$ \boldsymbol{l} $为空间地标线的参数正交表达式. 紧耦合优化的代价函数如下：

(19)$ \min _\chi\;\left({\boldsymbol{e}}_{\mathrm{m}}+{\boldsymbol{e}}_{\mathrm{I}}+{\boldsymbol{e}}_{\mathrm{p}}+{\boldsymbol{e}}_{\mathrm{l}}\right). $

式中：e_m为滑动窗口边缘化的先验信息，e_I为滑动窗口内相邻帧间IMU产生的IMU残差，e_p为滑动窗口下特征点的视觉重投影误差，e_l为滑动窗口下特征线的视觉重投影误差.

IMU的残差是由IMU的预积分值减去状态估计值得到的，考虑到连续两帧i和j之间的IMU测量，待优化的变量是两帧之间的位置、速度、旋转和IMU的偏置. 残差的表达式如下:

(20)$ {\boldsymbol{e}_{\mathrm{I}}=\left[\begin{array}{c}\boldsymbol{r}_{\boldsymbol{s}} \\\boldsymbol{r}_{\boldsymbol{v}} \\\boldsymbol{r}_{\boldsymbol{q}} \\\boldsymbol{r}\left(\boldsymbol{b}_{\mathrm{a}}\right) \\\boldsymbol{r}\left(\boldsymbol{b}_{\mathrm{g}}\right)\end{array}\right]=\left[\begin{array}{c}\boldsymbol{R}_{W i}\left(\boldsymbol{s}_j^W-\boldsymbol{s}_i^W-\boldsymbol{v}_i^W \Delta t_{i j}-\dfrac{1}{2} \boldsymbol{g}_W \Delta t_{i j}^2\right)-\hat{\boldsymbol{\alpha}}_{i j} \\\boldsymbol{R}_{W i}\left(\boldsymbol{v}_j^W-\boldsymbol{v}_i^W-\boldsymbol{g}_W \Delta t_{i j}\right)-\hat{\boldsymbol{\beta}}_{i j} \\2\left[\left(\hat{{\boldsymbol{\gamma}}}_{j i}\right)^{-1} \otimes\left(\boldsymbol{q}_i^W\right)^{-1} \otimes \boldsymbol{q}_j^W\right]_{x y z} \\\boldsymbol{b}_{{\mathrm{a}} j}-\boldsymbol{b}_{{\mathrm{a}} i} \\\boldsymbol{b}_{{\mathrm{g}} j}-\boldsymbol{b}_{{\mathrm{g}} i}\end{array}\right]}. $

式中：$\boldsymbol{R}_{W i} $为从世界坐标系到i帧的IMU坐标系下的旋转矩阵，$\boldsymbol{s}_i^W、\boldsymbol{v}_i^W、\boldsymbol{q}_i^W $表示第i个相机帧同步的IMU状态，$\boldsymbol{s}_j^W、 \boldsymbol{v}_j^W、 \boldsymbol{q}_j^W $表示第j个相机帧同步的IMU状态，分别为位置、速度和旋转；$ \Delta t_{i j} $表示第i帧和第j帧之间的时间间隔；${\boldsymbol{g}}_W $为世界坐标系下的重力加速度，$\hat{{\boldsymbol{\alpha}}}_{i j}、 \hat{{\boldsymbol{\beta}}}_{i j} $和$ \hat{{\boldsymbol{\gamma}}}_{i j} $分别为预积分得到的第i帧和第j帧之间的位移、速度和旋转变化量；b_ai和b_aj分别为第i帧和第j帧的加速度偏置；b_gi和b_gj分别为第i帧和第j帧的陀螺仪偏置.

噪声的影响会导致点特征的重投影误差的存在，假设相机I观测到的空间中的路标点P_m在像素坐标系中的齐次坐标为$ {\tilde {\boldsymbol{p}}}_{m}^{I}={\left[{u}_{m}^{I},{v}_{m}^{I},1\right]}^{\mathrm{T}} $，则P_m在相机坐标系{I}下的三维坐标$ {{\boldsymbol{P}}}_{m}^{I} $可以表示为

(21)$ {\boldsymbol{P}}_m^I = \left[ {\begin{array}{*{20}{c}} {X_m^I} \\ {Y_m^I} \\ {Z_m^I} \end{array}} \right] = \frac{1}{{{\lambda _m}}}\left[ {\begin{array}{*{20}{c}} {u_m^I} \\ {v_m^I} \\ 1 \end{array}} \right]. $

式中：λ_m为逆深度.

当相机运动到J位置时，P_m在相机J观测下的像素坐标系{J}中的坐标为$ {\boldsymbol{p}}_{m}^{J}={\left[{u}_{m}^{J},{v}_{m}^{J}\right]}^{\mathrm{T}} $，P_m在相机坐标系下的三维坐标$ {\boldsymbol{P}}_{m}^{J} $投影到图像平面上的像素坐标系坐标记为$ {\widehat{\boldsymbol{p}}}_{m}^{J}={\left[{\widehat{u}}_{m}^{J},{\widehat{v}}_{m}^{J}\right]}^{\mathrm{T}} $，由于噪声的影响$ {\boldsymbol{p}}_{m}^{J} $与$ {\widehat{\boldsymbol{p}}}_{m}^{J} $并不会处于同一位置. 将两点之间的距离称之为点特征的重投影误差，表达式如下：

(22)$ \boldsymbol{e}_p=\left[\begin{array}{l}\hat{u}_m^J-u_m^J \\\hat{v}_m^J-v_m^J\end{array}\right]. $

在世界坐标系有一个三维空间线L，在相机的图像平面上有2条线段，其中一条为通过EDlines算法提取出来的线段$ \boldsymbol{l} $，另一条为空间线投影到相机平面上的线特征$ {\boldsymbol{l}}' $，其由位姿变换得到. 将线特征上的重投影误差$ {\boldsymbol{e}}_{l} $建模为$ \boldsymbol{l} $上的2个端点到$ {\boldsymbol{l}}' $上的距离：

(23)$ \boldsymbol{e}_l=\left[\boldsymbol{d}_{\mathrm{s}}, \boldsymbol{d}_{\mathrm{e}}\right]^{\mathrm{T}}=\left[\frac{\boldsymbol{l}^{\rm{T}} \tilde{\boldsymbol{x}}_{\mathrm{s}}^I}{\sqrt{l_1^2+l_2^2}}, \frac{\boldsymbol{l}^{\rm{T}} \tilde{\boldsymbol{x}}_{\mathrm{e}}^I}{\sqrt{l_1^2+l_2^2}}\right]^{\mathrm{T}}. $

式中：d_s和d_e分别为$ \boldsymbol{l}' $上的2个端点到$ {\boldsymbol{l}}' $上的距离,$ \boldsymbol{l} $为空间线在图像平面上投影得到的直线方程，$ {\tilde {\boldsymbol{x}}}_{{\mathrm{s}}}^{I} $和$ {\tilde {\boldsymbol{x}}}_{{\mathrm{e}}}^{I} $分别为相机I观测到的图像上线段的2个端点的齐次坐标.

在腿足机器人平台上，系统由控制终端、Jetson Xavier NX开发板和Upboard运动控制板组成. 通过集成通信网络实现多硬件设备之间的实时连接和信息共享. 六足机器人利用双目摄像机和IMU作为传感器. 终端测试环境为Intel(R) Core(TM) i7-7700HQ四核处理器，8 Gb内存，NVIDIA GTX1060显卡，Ubuntu 18.04操作系统.

为了验证坐标系变换公式的通用性和模型误差补偿的有效性，在六足机器人和四足机器人2种不同的机器人平台上进行不确定性补偿实验，如图8所示. 目的是评估腿足机器人数字孪生系统在各种机器人配置和运动模式下的性能. 该系统通过应用坐标系变换公式和误差补偿技术，最大限度地减少了由实际机器人的摩擦力和电机转矩误差带来的不确定性，提高数字孪生模型的精度. 首先在三角步态中，机器人使用3条腿来支撑和移动. 将3对足分成2组，以三角形支架结构交替前行，这种方式可以保持机器人的稳定性. 其次，四足步态是指机器人使用4条腿来支撑和移动. 在四足步态中，机器人始终保持4条腿在地面上，提供稳定的支撑. 最后，波浪步态是六足机器人常用的一种步态，机器人的腿会像波浪一样依次移动，始终保持5条腿在地面上，这种步态使得机器人能够以较快的速度移动，同时保持较高的稳定性.

在四足机器人原地踏步虚实同步测试实验中，如图9所示，第1~3行分别对应机器人物理、仿真和数字孪生模型运动截图. 图9 (b)、(b1)、(b2)为机器人抬起右前和左后腿，左前和右后腿支撑；图9 (d)、(d1)、(d2)为机器人抬起左前和右后腿，右前和左后腿支撑；图9(a)、(a1)、(a2)、(c)、(c1)、(c2)为短暂四腿支撑阶段. 各平台机器人在控制下可以实现大致相同的动作，同步度较高.

在空载情况下，关节位置J_p随时间t的变化如图10所示，图10(a)、(c)进行了动力学补偿，图10(b)、(d)进行了动力学加不确定性补偿，后者的数字孪生模型表现出同步和准确的运动，与物理实体的动作非常相似，该模型有效地补偿了不确定性，从而提高了数字孪生系统在这些机器人平台上的性能和可靠性. 在触地情况下，增加动力学加不确定性补偿后，物理实体与数字孪生模型之间的误差如图11所示. 其中，关节误差E_j控制在约5%以内，足端位置误差E_p中z方向误差由于负载较大，波动较为明显，x方向误差控制在2 cm以内. 这些结果证实了腿足机器人数字孪生系统中坐标系变换公式和模型误差补偿技术的通用性和有效性，表明它适用于各种机器人配置和运动模式.

通过仿真实验和在六足机器人上的测试和应用，对腿足机器人数字孪生系统的可行性和准确性进行评估. 在仿真实验中，将数字孪生系统框架的性能与VINS-Fusion^[32]和ORB-SLAM3^[33]进行比较. 使用EuRoC数据集中的MH_05_difficult数据集，该数据集是在封闭的工厂环境中使用Asctec Firefly六边形旋翼直升机平台收集的^[34]. 该测试使用了来自单目相机和IMU的传感器数据，IMU运行在带有i9-10980HK处理器的工业计算机上. 所有测试方法均使用相同的运行过程.

当评价数字孪生系统中定位算法的表现时，从最重要的精度角度切入. 给出绝对位姿误差(absolute pose error, APE)、绝对位姿误差的均方根误差(root mean square error, RMSE)和相对位姿误差(relative pose error, RPE)3个评价指标，并定义公式中的符号表示，其中绝对位姿误差是计算相机位姿的真实值与定位算法估计值之间的差，可以反映算法精度和位姿全局一致性，而相对位姿误差是用于计算2个相同时间戳内位姿变化量的差，可以反映系统的漂移. 将估计位姿P₁,···,P_n∈SE(3)和真实位姿Q₁,···,Q_n∈SE(3)两者对齐，由此可以得出第i帧的绝对位姿误差APE：

(24)$ {F}_i=\boldsymbol{Q}_i^{-1} \boldsymbol{S} \boldsymbol{P}_i . $

式中：S为估计位姿到真实位姿的转换矩阵，S∈SE(3)，S是通过最小二乘法计算得到的. 在已知总帧数n与间隔$\varDelta $的情况下，可以得到$m = n - \varDelta \cdot F_i $，然后使用均方根误差RMSE统计得到

(25)$ \operatorname{RMSE}\left(F_{1: n}\right)=\left(\frac{1}{n} \sum_{\varDelta=1}^n\left\|\operatorname{trans}\;\left({F}_i\right)\right\|^2\right)^{{1}/{2}}. $

式中：trans (F_i)表示取相对位姿误差中的平移部分. 另外，相对位姿误差相当于直接测量里程计的误差，第i帧的相对位姿误差RPE定义如下：

(26)$\boldsymbol{E}_i=\left(\boldsymbol{Q}_i^{-1} \boldsymbol{Q}_{i+1}\right)^{-1}\left(\boldsymbol{P}_i^{-1} \boldsymbol{P}_{i+1}\right). $

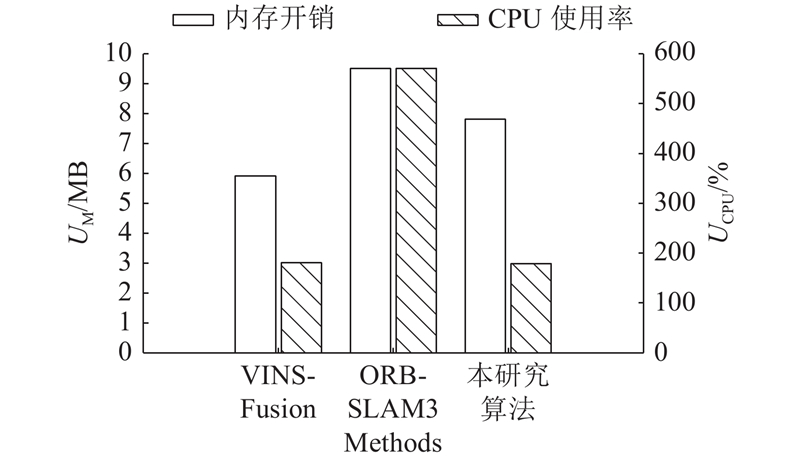
在MH_05_difficult数据集下，将腿足机器人数字孪生系统的定位算法、VINS-Fusion和ORB-SLAM3各运行10次. 在整个过程中计算和监控每个算法的平均CPU使用率和内存消耗. 如图12所示，显示了3种算法的平均CPU使用情况和内存消耗情况. 图中，U_M、U_CPU分别为平均内存消耗和CPU使用率. 结果表明，数字孪生系统的定位算法并不比VINS-Fusion算法占用更多的内存. 但是，由于须在系统内传输后台数据，需要较高的CPU使用率. 与ORB-SLAM3相比，本研究的定位算法中相应功能的内存开销降低了约68.7%，CPU使用率降低了约17.8%. 这是因为ORB-SLAM3须在内存中缓存映射特性和数据，从而导致更高的内存开销和更长的运行时间. 如表1所示给出了运行ORB-SLAM3算法后的绝对位姿误差APE和均方根误差RMSE，可以看出其相较于VINS-Fusion和本研究算法的低一个数量级. ORB-SLAM3在预选的关键帧上进行几何一致性检测，随后使用关键帧的3个常见视图执行局部一致性测试. 这种方法虽然提高了地图精度，但代价是增加了后台计算，使ORB-SLAM3算法在某些硬件限制下不稳定. 与VINS-Fusion相比，本研究所提出的定位算法具有更高的精度和鲁棒性，在APE方面提升了约37.7%，在RMSE方面提升了约36.9%. 这归功于在前端包含点线特征提取和匹配，它提供了基于结构化场景规则的额外约束条件，有助于减轻运动过程中的漂移，在保证实时性的前提下，提高了整体性能. 所提出的腿足机器人数字孪生系统在精度和鲁棒性方面表现出令人满意的性能. 与其他主流算法相比，该系统具有运行高效、能通过附加约束条件提高精度、鲁棒性较强等优点.

在实验中，将本研究腿足机器人数字孪生系统的定位算法部署在如图13所示的六足机器人上. 图中，左上角显示的是数字孪生系统返回的环境信息. 在终端上部署GUI界面，为用户提供选择腿足机器人控制命令、调用配置文件和启动特定程序的选项. 终端、Jetson Xavier NX导航板、运动控制板之间的通信是通过连接无线传输模块与有线LAN端口实现的. 安装在腿足机器人本体上的双目摄像头和IMU传感器是数字孪生系统外部数据的主要来源. 一旦收集到数据，它们就会被传输到导航板，该板执行定位算法的实时操作. 相机图像数据用于点和线特征的提取和匹配，IMU信息用于里程计初始化，处理相机点云数据用于环境建模和后续路径规划. 这种集成设置使数字孪生系统能够有效地感知环境和控制腿足机器人.

如图14所示展示了六足机器人的运行过程，在该实验中，测量的平均每米相对位姿误差为0.19030. 数字孪生模型在绕建筑一周完成后，能够回到原来的位置，APE小于1%，满足实际要求.

实验场景涉及到仿真检测领域，须重视控制软件系统在实际运行中的通信延迟问题，因此在实际硬件参数的基础上分析系统中无线模块的时延. 其中腿足机器人数字孪生系统中的通信延迟主要来自数据传输延迟，监测到六足机器人在终端上的地图刷新率约为6~9 Hz，对应于111~167 ms的延迟，这种延迟还受到导航板算法运行速度的影响.

因此，在通信模块中将机器人本体的状态信息数据通过独立的线程发送给主程序，这样使得监控机器人运行状态的延迟能够低于需要大量算力的定位算法延迟. 在实际测试中，后台程序对系统各节点之间的通信延迟进行监控和计算，如表2所示，硬件实验表明，通信延迟基本和网络延迟保持一致，大约为30 ms，能够满足数字孪生系统的实时性要求.

提出面向移动作业任务的腿足机器人数字孪生系统. 该系统优化了定位算法中点线特征的提取过程，实现了多种算法的高效融合，大大减少了在不同腿足机器人平台上部署的困难. 在此基础上，建立腿足机器人的数字孪生模型，引入不确定性补偿提高数字孪生模型的精度. 该系统不仅能够在各种腿足机器人平台上稳定高效运行，并且能得到低延时高精度的实时状态反馈. 下一步将结合路径规划方法和精细化环境建模，增强机器人在复杂场景下的通过性和自主性，提升整个系统的自适应性和状态精度.