DDPG算法是成熟的DRL算法,可以用于解决连续动作控制的问题. 该算法主要基于Actor-Critic框架组成,利用Actor-online网络 $ \;\mu $ $ {\boldsymbol{a}}_{t} = \mu \left( {{{\boldsymbol{s}}_t}\left| {{{\boldsymbol{\theta}\,} ^\mu }} \right.} \right) $ $ Q $ $ r_t = Q\left( {{{\boldsymbol{s}}_t},{{\boldsymbol{a}}_t}\left| {{{\boldsymbol{\theta}} ^Q}} \right.} \right) $ ${{\boldsymbol{\theta}\,} ^\mu }$ $ {{\boldsymbol{\theta}} ^Q} $ $\; \mu ' $ $ Q' $ [4 ] . 当更新Actor和Critic网络时,从经验重放缓冲区中取样 $ N $ $ \left[ {{{\boldsymbol{s}}_t},{{\boldsymbol{a}}_t},{r_t},{{\boldsymbol{s}}_{t + 1}}} \right] $
[1]
LUO W, SUN P, ZHONG F, et al. End-to-end active object tracking and its real-world deployment via reinforcement learning [EB/OL]. [2021-05-20]. https://ieeexplore.ieee.org/document/8642452/footnotes#footnotes.
[本文引用: 3]
[2]
李轶锟. 基于视觉的四旋翼飞行器地面目标跟踪技术[D]. 南京: 南京航空航天大学, 2019.
LI Yi-kun. Ground target tracking technology of quadrotor based on vision [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2019.
[3]
刘亮. 四旋翼飞行器移动目标跟踪控制研究[D]. 西安: 西安电子科技大学, 2020.
[本文引用: 2]
LIU Liang. Research on moving target tracking control of quadrotor aircraft [D]. Xi'an: Xi'an University of Electronic Science and Technology, 2020.
[本文引用: 2]
[4]
LI B, YANG Z, CHEN D, et al Maneuvering target tracking of UAV based on MN-DDPG and transfer learning
[J]. Defence Technology , 2021 , 17 (2 ): 457 - 466
[本文引用: 7]
[5]
罗伟, 徐雪松, 张煌军 多旋翼无人机目标跟踪系统设计
[J]. 华东交通大学学报 , 2019 , 36 (3 ): 72 - 79
[本文引用: 1]
LUO Wei, XU Xue-song, ZHANG Huang-jun Design of multi rotor UAV target tracking system
[J]. Journal of East China Jiaotong University , 2019 , 36 (3 ): 72 - 79
[本文引用: 1]
[6]
张兴旺, 刘小雄, 林传健, 等 基于Tiny-YOLOV3的无人机地面目标跟踪算法设计
[J]. 计算机测量与控制 , 2021 , 29 (2 ): 76 - 81
ZHANG Xing-wang, LIU Xiao-xiong, LIN Chuan-jian, et al Design of UAV ground target tracking algorithm based on Tiny-YOLOV3
[J]. Computer Measurement and Control , 2021 , 29 (2 ): 76 - 81
[7]
张昕, 李沛, 蔡俊伟 基于非线性导引的多无人机协同目标跟踪控制
[J]. 指挥信息系统与技术 , 2019 , 10 (4 ): 47 - 54
[本文引用: 1]
ZHANG Xin, LI Pei, CAI Jun-wei Multi UAV cooperative target tracking control based on nonlinear guidance
[J]. Command Information System and Technology , 2019 , 10 (4 ): 47 - 54
[本文引用: 1]
[8]
黄志清, 曲志伟, 张吉, 等 基于深度强化学习的端到端无人驾驶决策
[J]. 电子学报 , 2020 , 48 (9 ): 1711 - 1719
DOI:10.3969/j.issn.0372-2112.2020.09.007
[本文引用: 1]
HUANG Zhi-qing, QU Zhi-wei, ZHANG Ji, et al End-to-end autonomous driving decision based on deep reinforcement learning
[J]. Acta Electronica Sinica , 2020 , 48 (9 ): 1711 - 1719
DOI:10.3969/j.issn.0372-2112.2020.09.007
[本文引用: 1]
[9]
VOLODYMYR M, KORAY K, DAVID S, et al Human-level control through deep reinforcement learning
[J]. Nature , 2019 , 518 (7540 ): 529
[本文引用: 1]
[11]
MATTHEW B, SAM R, et al Reinforcement learning, fast and slow
[J]. Trends in Cognitive Sciences , 2019 , 23 (5 ): 408 - 422
[本文引用: 1]
[12]
LIU Q, SHI L, SUN L, et al Path planning for UAV-mounted mobile edge computing with deep reinforcement learning
[J]. IEEE Transactions on Vehicular Technology , 2020 , 69 (5 ): 5723 - 5728
DOI:10.1109/TVT.2020.2982508
[本文引用: 1]
[13]
KHAN A, FENG Jiang, LIU Shao-hui, et al Playing a FPS Doom video game with deep visual reinforcement learning
[J]. Automatic Control and Computer Sciences , 2019 , 53 (3 ): 214 - 222
DOI:10.3103/S0146411619030052
[14]
SEWAK M. Deep Q network (DQN), double DQN, and dueling DQN: a step towards general artificial intelligence [M]. Singapore: Springer, 2019.
[本文引用: 1]
[15]
ZENG Y, XU X, JIN S, et al Simultaneous navigation and radio mapping for cellular-connected UAV with deep reinforcement learning
[J]. IEEE Transactions on Wireless Communications , 2021 , 20 (7 ): 4205 - 4220
DOI:10.1109/TWC.2021.3056573
[本文引用: 1]
[16]
LUO C, JIN L, SUN Z MORAN: a multi-object rectified attention network for scene text recognition
[J]. Pattern Recognition , 2019 , 90 : 109 - 118
DOI:10.1016/j.patcog.2019.01.020
[本文引用: 1]
[17]
DE BLASI S, KLÖSER S, MÜLLER A, et al KIcker: an industrial drive and control Foosball system automated with deep reinforcement learning
[J]. Journal of Intelligent and Robotic Systems , 2021 , 102 (1 ): 107
[本文引用: 1]
[18]
HE G, LIU T, WANG Y, et al. Research on Actor-Critic reinforcement learning in RoboCup [C]// World Congress on Intelligent Control and Automation . Dalian: IEEE, 2006: 205.
[本文引用: 1]
[19]
WAN K F, GAO X G, HU Z J, et al. Robust motion control for UAV in dynamic uncertain environments using deep reinforcement learning [EB/OL]. [2021-05-20]. https://www.mdpi.com/2072-4292/12/4/640.
[本文引用: 1]
[20]
YANG Q, ZHU Y, ZHANG J, et al. UAV air combat autonomous maneuver decision based on DDPG algorithm [C]// 2019 IEEE 15th International Conference on Control and Automation . Edinburgh: IEEE, 2019.
[本文引用: 1]
[21]
WAN K, GAO X, HU Z, et al Robust motion control for UAV in dynamic uncertain environments using deep reinforcement learning
[J]. Remote Sensing , 2020 , 12 (4 ): 640
DOI:10.3390/rs12040640
[本文引用: 1]
[22]
SHIN S, KANG Y, KIM Y Reward-driven U-net training for obstacle avoidance drone
[J]. Expert Systems with Applications , 2019 , 143 : 113064
[本文引用: 2]
[23]
POLVARA R, PATACCHIOLA M, HANHEIDE M, et al. Sim-to-real quadrotor landing via sequential deep Q-networks and domain randomization [EB/OL]. [2021-05-20]. https://www.mdpi.com/2218-6581/9/1/8.
[本文引用: 1]
[24]
SHAH S, KAPOOR A, DEY D, et al AirSim: high-fidelity visual and physical simulation for autonomous vehicles
[J]. Field and Service Robotics , 2017 , 11 (1 ): 621 - 635
[本文引用: 1]
[25]
林传健, 章卫国, 史静平, 等 无人机跟踪系统仿真平台的设计与实现
[J]. 哈尔滨工业大学学报 , 2020 , 52 (10 ): 119 - 127
[本文引用: 1]
LIN Chuan-jian, ZHANG Wei-guo, SHI Jing-ping, et al Design and implementation of UAV tracking system simulation platform
[J]. Journal of Harbin Institute of Technology , 2020 , 52 (10 ): 119 - 127
[本文引用: 1]
[26]
LIU H, WU Y, SUN F Extreme trust region policy optimization for active object recognition
[J]. IEEE Transactions on Neural Networks and Learning Systems , 2018 , 29 (6 ): 2253 - 2258
DOI:10.1109/TNNLS.2017.2785233
[本文引用: 1]
[27]
WANG Z, LI H, WU Z, et al A pretrained proximal policy optimization algorithm with reward shaping for aircraft guidance to a moving destination in three-dimensional continuous space
[J]. International Journal of Advanced Robotic Systems , 2021 , 18 (1 ): 1 - 9
[本文引用: 1]
[28]
WU Y, MANSIMOV E, GROSSE R B, et al Scalable trust-region method for deep reinforcement learning using Kronecker-factored approximation
[J]. Advances in Neural Information Processing Systems , 2017 , 30 (1 ): 5279 - 5288
[本文引用: 1]
[29]
BABENKO B, YANG M H, BELONGIE S. Visual tracking with online multiple instance learning [C]// IEEE Conference on Computer Vision and Pattern Recognition . Miami: IEEE, 2009.
[本文引用: 1]
[30]
D COMANICIU, RAMESH V, MEER P. Real-time tracking of non-rigid objects using mean shift [C]// IEEE Conference on Computer Vision and Pattern Recognition . Nice: IEEE, 2003.
[本文引用: 1]
[31]
HENRIQUES J F, CASEIRO R, MARTINS P, et al High-speed tracking with kernelized correlation filters
[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2015 , 37 (3 ): 583 - 596
DOI:10.1109/TPAMI.2014.2345390
[本文引用: 1]
[32]
KALAL Z, MIKOLAJCZYK K, MATAS J Tracking-learning-detection
[J]. IEEE Transactions on Software Engineering , 2011 , 34 (7 ): 1409 - 1422
[本文引用: 1]
3
... 无人机的运动目标跟踪技术被广泛应用于各个领域,如监视预警、探测救援、高空射击等[1 -4 ] . 对于无人机机动目标跟踪任务,我们应该寻求主动跟踪的解决方案,统一物体跟踪和运动控制2个子任务. 传统的无人机目标跟踪系统主要基于规则进行决策. 当面对复杂多变的场景时,规则构建复杂[5 -7 ] ,难以覆盖可能出现的场景. 随着人工智能技术在无人驾驶领域的应用,复杂的场景理解与决策均由神经网络来执行,不需要人为地制定规则,形成端到端的决策控制模型,即通过获取无人机及飞行场景的相关信息( 如飞行姿态、速度、障碍距离、环境图像等) ,经过神经网络的处理后,直接输出无人机运动控制信号. 端到端决策系统简单且性能良好,受到学术界和工业界的广泛关注[8 ] . ...
... 式中: $A、c、d、\lambda $ $ A > 0 $ $ c > 0 $ $ d > 0 $ $ \lambda > 0 $ . 式(7)表示当目标与无人机正面的距离为d 并表现出无旋转时,获得最大回报 $ A $ 图5 ). $ c $ [1 ] . 式(7)中,省略了时间步长下标. 由于虚拟环境提供的API能够访问感兴趣的内部状态,建立所需的奖励函数. 除了跟踪奖励以外,添加无人机稳定飞行奖励 $ {r_{{\text{ste}}}} $ $ {r_{{\text{cou}}}} $ [4 ] ,分别如下所示: ...
... 实验采用2个度量标准,即计算每一代(episode)的累积奖励(accumulated rewards, AR)和代的长度(episode length, EL)进行定量评估[1 ] . 实验结果如表3 、4 所示. 结果表明,设计的端到端主动跟踪器与模拟的传统跟踪器相比,性能提升明显,在多种任务中都能够对目标进行稳定且精确的跟踪. ...
2
... 式中: $ \bar {\boldsymbol{a}} $ $ \;\beta $ $ {\sigma _1} $ $ {{\boldsymbol{W}}_t} $ [3 ] . 考虑到转移模型对先前任务的确定性最优策略在新的任务场景中可能不适用,引入另一种高斯噪声来帮助无人机学习的自适应随机行为. 这一探索过程在迁移学习的初期尤为重要. 基于策略的优化行为通过混合噪声网络[3 ] 输出更新为 ...
... [3 ]输出更新为 ...
2
... 式中: $ \bar {\boldsymbol{a}} $ $ \;\beta $ $ {\sigma _1} $ $ {{\boldsymbol{W}}_t} $ [3 ] . 考虑到转移模型对先前任务的确定性最优策略在新的任务场景中可能不适用,引入另一种高斯噪声来帮助无人机学习的自适应随机行为. 这一探索过程在迁移学习的初期尤为重要. 基于策略的优化行为通过混合噪声网络[3 ] 输出更新为 ...
... [3 ]输出更新为 ...
Maneuvering target tracking of UAV based on MN-DDPG and transfer learning
7
2021
... 无人机的运动目标跟踪技术被广泛应用于各个领域,如监视预警、探测救援、高空射击等[1 -4 ] . 对于无人机机动目标跟踪任务,我们应该寻求主动跟踪的解决方案,统一物体跟踪和运动控制2个子任务. 传统的无人机目标跟踪系统主要基于规则进行决策. 当面对复杂多变的场景时,规则构建复杂[5 -7 ] ,难以覆盖可能出现的场景. 随着人工智能技术在无人驾驶领域的应用,复杂的场景理解与决策均由神经网络来执行,不需要人为地制定规则,形成端到端的决策控制模型,即通过获取无人机及飞行场景的相关信息( 如飞行姿态、速度、障碍距离、环境图像等) ,经过神经网络的处理后,直接输出无人机运动控制信号. 端到端决策系统简单且性能良好,受到学术界和工业界的广泛关注[8 ] . ...
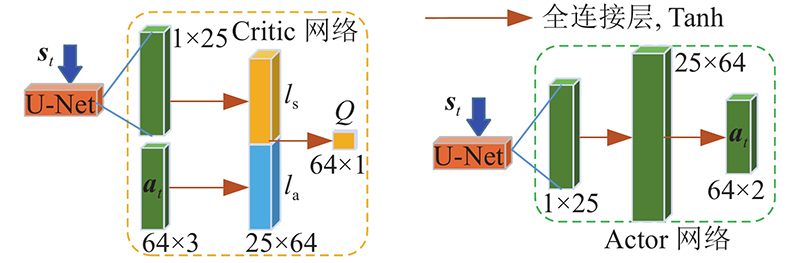
... DDPG算法是成熟的DRL算法,可以用于解决连续动作控制的问题. 该算法主要基于Actor-Critic框架组成,利用Actor-online网络 $ \;\mu $ $ {\boldsymbol{a}}_{t} = \mu \left( {{{\boldsymbol{s}}_t}\left| {{{\boldsymbol{\theta}\,} ^\mu }} \right.} \right) $ $ Q $ $ r_t = Q\left( {{{\boldsymbol{s}}_t},{{\boldsymbol{a}}_t}\left| {{{\boldsymbol{\theta}} ^Q}} \right.} \right) $ ${{\boldsymbol{\theta}\,} ^\mu }$ $ {{\boldsymbol{\theta}} ^Q} $ $\; \mu ' $ $ Q' $ [4 ] . 当更新Actor和Critic网络时,从经验重放缓冲区中取样 $ N $ $ \left[ {{{\boldsymbol{s}}_t},{{\boldsymbol{a}}_t},{r_t},{{\boldsymbol{s}}_{t + 1}}} \right] $
... 通过软更新策略[4 ] ,对 $ {{\boldsymbol{\theta}\,} ^{\mu '}} $ $ {{\boldsymbol{\theta}} ^{Q'}} $
... 式中: $ \tau $ [4 ] 可以表示为 ...
... 式中: $A、c、d、\lambda $ $ A > 0 $ $ c > 0 $ $ d > 0 $ $ \lambda > 0 $ . 式(7)表示当目标与无人机正面的距离为d 并表现出无旋转时,获得最大回报 $ A $ 图5 ). $ c $ [1 ] . 式(7)中,省略了时间步长下标. 由于虚拟环境提供的API能够访问感兴趣的内部状态,建立所需的奖励函数. 除了跟踪奖励以外,添加无人机稳定飞行奖励 $ {r_{{\text{ste}}}} $ $ {r_{{\text{cou}}}} $ [4 ] ,分别如下所示: ...
... 基于DDPG的连续动作空间学习的主要挑战是探索. 在无人机的训练过程中,随着目标轨迹和环境的变化,无人机需要探索新的策略来完成跟踪任务. 引入改进的MN-DDPG算法[4 ] ,该算法将高斯噪声和欧恩斯坦-乌伦贝克(OU)噪声混合在一起,对DDPG生成的确定性策略进行优化,指导无人机进行策略探索. 考虑到DRL将跟踪任务建模为序贯决策问题,根据无人机连续动作输出的特点,采用序列相关的Ornstein-Uhlenbeck(OU)随机过程为无人机应对不断变化的环境提供动作探索. 基于OU过程的噪声向量 $ {{\boldsymbol{N}}_{{\text{OU}}}} $
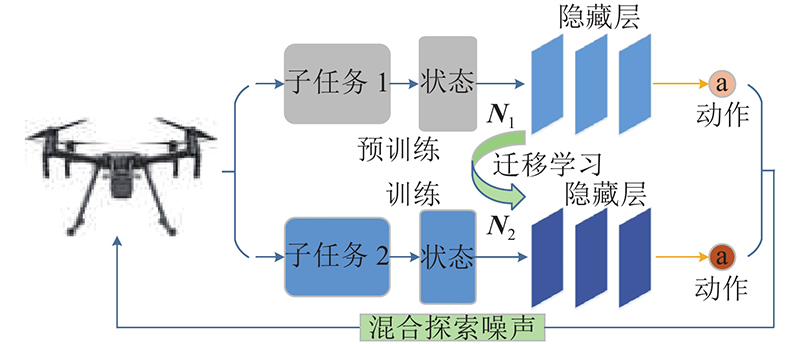
... 参考文献[4 ],讨论将迁移学习方法与DDPG相结合的过程. 本质上,该过程将跟踪任务连续分解为2个子任务,对跟踪任务进行双重训练. 为了帮助无人机逐步学习如何高效、稳定地跟踪目标,将无人机跟踪复杂机动目标的总体任务分解为2个简单的子任务:无人机对匀速直线运动目标的跟踪任务(子任务1)和无人机对复杂曲线运动目标的跟踪任务(子任务2). 如图6 所示为基于任务分解和双重训练的跟踪任务迁移学习. ...
多旋翼无人机目标跟踪系统设计
1
2019
... 无人机的运动目标跟踪技术被广泛应用于各个领域,如监视预警、探测救援、高空射击等[1 -4 ] . 对于无人机机动目标跟踪任务,我们应该寻求主动跟踪的解决方案,统一物体跟踪和运动控制2个子任务. 传统的无人机目标跟踪系统主要基于规则进行决策. 当面对复杂多变的场景时,规则构建复杂[5 -7 ] ,难以覆盖可能出现的场景. 随着人工智能技术在无人驾驶领域的应用,复杂的场景理解与决策均由神经网络来执行,不需要人为地制定规则,形成端到端的决策控制模型,即通过获取无人机及飞行场景的相关信息( 如飞行姿态、速度、障碍距离、环境图像等) ,经过神经网络的处理后,直接输出无人机运动控制信号. 端到端决策系统简单且性能良好,受到学术界和工业界的广泛关注[8 ] . ...
多旋翼无人机目标跟踪系统设计
1
2019
... 无人机的运动目标跟踪技术被广泛应用于各个领域,如监视预警、探测救援、高空射击等[1 -4 ] . 对于无人机机动目标跟踪任务,我们应该寻求主动跟踪的解决方案,统一物体跟踪和运动控制2个子任务. 传统的无人机目标跟踪系统主要基于规则进行决策. 当面对复杂多变的场景时,规则构建复杂[5 -7 ] ,难以覆盖可能出现的场景. 随着人工智能技术在无人驾驶领域的应用,复杂的场景理解与决策均由神经网络来执行,不需要人为地制定规则,形成端到端的决策控制模型,即通过获取无人机及飞行场景的相关信息( 如飞行姿态、速度、障碍距离、环境图像等) ,经过神经网络的处理后,直接输出无人机运动控制信号. 端到端决策系统简单且性能良好,受到学术界和工业界的广泛关注[8 ] . ...
基于Tiny-YOLOV3的无人机地面目标跟踪算法设计
0
2021
基于Tiny-YOLOV3的无人机地面目标跟踪算法设计
0
2021
基于非线性导引的多无人机协同目标跟踪控制
1
2019
... 无人机的运动目标跟踪技术被广泛应用于各个领域,如监视预警、探测救援、高空射击等[1 -4 ] . 对于无人机机动目标跟踪任务,我们应该寻求主动跟踪的解决方案,统一物体跟踪和运动控制2个子任务. 传统的无人机目标跟踪系统主要基于规则进行决策. 当面对复杂多变的场景时,规则构建复杂[5 -7 ] ,难以覆盖可能出现的场景. 随着人工智能技术在无人驾驶领域的应用,复杂的场景理解与决策均由神经网络来执行,不需要人为地制定规则,形成端到端的决策控制模型,即通过获取无人机及飞行场景的相关信息( 如飞行姿态、速度、障碍距离、环境图像等) ,经过神经网络的处理后,直接输出无人机运动控制信号. 端到端决策系统简单且性能良好,受到学术界和工业界的广泛关注[8 ] . ...
基于非线性导引的多无人机协同目标跟踪控制
1
2019
... 无人机的运动目标跟踪技术被广泛应用于各个领域,如监视预警、探测救援、高空射击等[1 -4 ] . 对于无人机机动目标跟踪任务,我们应该寻求主动跟踪的解决方案,统一物体跟踪和运动控制2个子任务. 传统的无人机目标跟踪系统主要基于规则进行决策. 当面对复杂多变的场景时,规则构建复杂[5 -7 ] ,难以覆盖可能出现的场景. 随着人工智能技术在无人驾驶领域的应用,复杂的场景理解与决策均由神经网络来执行,不需要人为地制定规则,形成端到端的决策控制模型,即通过获取无人机及飞行场景的相关信息( 如飞行姿态、速度、障碍距离、环境图像等) ,经过神经网络的处理后,直接输出无人机运动控制信号. 端到端决策系统简单且性能良好,受到学术界和工业界的广泛关注[8 ] . ...
基于深度强化学习的端到端无人驾驶决策
1
2020
... 无人机的运动目标跟踪技术被广泛应用于各个领域,如监视预警、探测救援、高空射击等[1 -4 ] . 对于无人机机动目标跟踪任务,我们应该寻求主动跟踪的解决方案,统一物体跟踪和运动控制2个子任务. 传统的无人机目标跟踪系统主要基于规则进行决策. 当面对复杂多变的场景时,规则构建复杂[5 -7 ] ,难以覆盖可能出现的场景. 随着人工智能技术在无人驾驶领域的应用,复杂的场景理解与决策均由神经网络来执行,不需要人为地制定规则,形成端到端的决策控制模型,即通过获取无人机及飞行场景的相关信息( 如飞行姿态、速度、障碍距离、环境图像等) ,经过神经网络的处理后,直接输出无人机运动控制信号. 端到端决策系统简单且性能良好,受到学术界和工业界的广泛关注[8 ] . ...
基于深度强化学习的端到端无人驾驶决策
1
2020
... 无人机的运动目标跟踪技术被广泛应用于各个领域,如监视预警、探测救援、高空射击等[1 -4 ] . 对于无人机机动目标跟踪任务,我们应该寻求主动跟踪的解决方案,统一物体跟踪和运动控制2个子任务. 传统的无人机目标跟踪系统主要基于规则进行决策. 当面对复杂多变的场景时,规则构建复杂[5 -7 ] ,难以覆盖可能出现的场景. 随着人工智能技术在无人驾驶领域的应用,复杂的场景理解与决策均由神经网络来执行,不需要人为地制定规则,形成端到端的决策控制模型,即通过获取无人机及飞行场景的相关信息( 如飞行姿态、速度、障碍距离、环境图像等) ,经过神经网络的处理后,直接输出无人机运动控制信号. 端到端决策系统简单且性能良好,受到学术界和工业界的广泛关注[8 ] . ...
Human-level control through deep reinforcement learning
1
2019
... 基于深度强化学习[9 ] 的研究方法是当前主流的端到端无人机控制决策方法,深度强化学习(deep reinforcement learning, DRL)通过智能体和环境之间的交互过程在线生成自适应策略[10 -11 ] ,在无人机运动规划领域表现良好[12 -14 ] . ...
Deep learning
1
2015
... 基于深度强化学习[9 ] 的研究方法是当前主流的端到端无人机控制决策方法,深度强化学习(deep reinforcement learning, DRL)通过智能体和环境之间的交互过程在线生成自适应策略[10 -11 ] ,在无人机运动规划领域表现良好[12 -14 ] . ...
Reinforcement learning, fast and slow
1
2019
... 基于深度强化学习[9 ] 的研究方法是当前主流的端到端无人机控制决策方法,深度强化学习(deep reinforcement learning, DRL)通过智能体和环境之间的交互过程在线生成自适应策略[10 -11 ] ,在无人机运动规划领域表现良好[12 -14 ] . ...
Path planning for UAV-mounted mobile edge computing with deep reinforcement learning
1
2020
... 基于深度强化学习[9 ] 的研究方法是当前主流的端到端无人机控制决策方法,深度强化学习(deep reinforcement learning, DRL)通过智能体和环境之间的交互过程在线生成自适应策略[10 -11 ] ,在无人机运动规划领域表现良好[12 -14 ] . ...
Playing a FPS Doom video game with deep visual reinforcement learning
0
2019
1
... 基于深度强化学习[9 ] 的研究方法是当前主流的端到端无人机控制决策方法,深度强化学习(deep reinforcement learning, DRL)通过智能体和环境之间的交互过程在线生成自适应策略[10 -11 ] ,在无人机运动规划领域表现良好[12 -14 ] . ...
Simultaneous navigation and radio mapping for cellular-connected UAV with deep reinforcement learning
1
2021
... 这些方法虽然已成功地应用于无人机目标跟踪任务中,但在建立决策模型之前,过分简化了无人机的飞行环境,将连续动作空间划分为有限的动作间隔,对无人机的姿态稳定性和跟踪精度有着重要的影响[15 -16 ] . ...
MORAN: a multi-object rectified attention network for scene text recognition
1
2019
... 这些方法虽然已成功地应用于无人机目标跟踪任务中,但在建立决策模型之前,过分简化了无人机的飞行环境,将连续动作空间划分为有限的动作间隔,对无人机的姿态稳定性和跟踪精度有着重要的影响[15 -16 ] . ...
KIcker: an industrial drive and control Foosball system automated with deep reinforcement learning
1
2021
... 为了实现无人机的连续动作控制,研究人员探索其他基于策略梯度的深度强化学习(DRL)算法. De Blasi等[17 ] 通过在Actor-Critic框架[18 ] 中引入DQN,提出高效、可行的深度确定性策略梯度(DDPG)算法,它可以将连续观测值直接映射到持续的行动. DDPG算法在无人机智能连续控制中得到越来越广泛的应用,但是现有的基于DDPG的无人机智能动作控制远远不够智能,解决方案往往由于确定性策略的产生而陷入局部最优. 现有基于DDPG算法的策略仅限于单个预定义的任务,很难推广到目标以随机轨迹运动的新任务. ...
1
... 为了实现无人机的连续动作控制,研究人员探索其他基于策略梯度的深度强化学习(DRL)算法. De Blasi等[17 ] 通过在Actor-Critic框架[18 ] 中引入DQN,提出高效、可行的深度确定性策略梯度(DDPG)算法,它可以将连续观测值直接映射到持续的行动. DDPG算法在无人机智能连续控制中得到越来越广泛的应用,但是现有的基于DDPG的无人机智能动作控制远远不够智能,解决方案往往由于确定性策略的产生而陷入局部最优. 现有基于DDPG算法的策略仅限于单个预定义的任务,很难推广到目标以随机轨迹运动的新任务. ...
1
... Wan等[19 ] 提出新的深度强化学习方法和鲁棒深度确定性策略梯度,用于开发控制器,使得无人机(unmanned aerial vehicle, UAV)在动态不确定环境中实现鲁棒飞行. Yang等[20 ] 提出新的架构,其中有监督的分割网络以奖励驱动的方式由Actor-Critic网络[21 -23 ] 所制作的标签来训练. ...
1
... Wan等[19 ] 提出新的深度强化学习方法和鲁棒深度确定性策略梯度,用于开发控制器,使得无人机(unmanned aerial vehicle, UAV)在动态不确定环境中实现鲁棒飞行. Yang等[20 ] 提出新的架构,其中有监督的分割网络以奖励驱动的方式由Actor-Critic网络[21 -23 ] 所制作的标签来训练. ...
Robust motion control for UAV in dynamic uncertain environments using deep reinforcement learning
1
2020
... Wan等[19 ] 提出新的深度强化学习方法和鲁棒深度确定性策略梯度,用于开发控制器,使得无人机(unmanned aerial vehicle, UAV)在动态不确定环境中实现鲁棒飞行. Yang等[20 ] 提出新的架构,其中有监督的分割网络以奖励驱动的方式由Actor-Critic网络[21 -23 ] 所制作的标签来训练. ...
Reward-driven U-net training for obstacle avoidance drone
2
2019
... 本文设计的端到端视觉感知-运动决策控制模型的2个学习过程是交互协作的,整个系统的学习过程可以分为环境探索及网络训练2部分. 训练好的运动控制模型包含以下2部分:1)以目标分割图的形式对场景进行视觉表示的模型;2)用于控制连续动作空间中的无人机的Actor-Critic强化学习模型. 运动控制决策模型的整体训练框架如图1 所示. Actor网络与Target-Actor网络用来输出动作,Critic网络与Target-Critic网络来计算action的值,经验回放池用来存储探索数据,Airsim是无人机运行的仿真交互环境,运动控制动作的奖励通过奖励函数来计算. U-Net分割网络的输出通过池化和矢量化过程输入到Actor网络[22 ] ,无人机接收Actor网络的输出并生成相应的飞行策略来跟踪目标. 在与环境的交互过程中,网络可以更新,无人机可以不断地学习和制定有效的顺序控制策略. ...
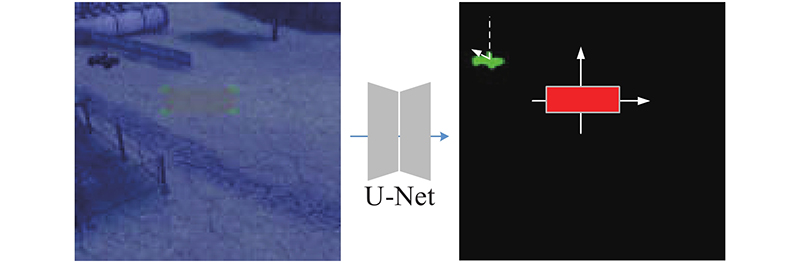
... 在 $ t $ $ {\dot v_t} $ $ {\dot \varphi _t} $ 图3 所示. 该网络将原始图像归一化为256×256×3像素,在最后一层使用Sigmoid函数输出256 × 256 ×1像素的分割特征图,包含对输入图像的奖励分割. 在训练阶段,U-Net、Actor和Critic都参与训练;在测试阶段,只使用U-Net和Actor-network,采用文献[22 ]方法初始化权重,将偏差设为0. ...
1
... Wan等[19 ] 提出新的深度强化学习方法和鲁棒深度确定性策略梯度,用于开发控制器,使得无人机(unmanned aerial vehicle, UAV)在动态不确定环境中实现鲁棒飞行. Yang等[20 ] 提出新的架构,其中有监督的分割网络以奖励驱动的方式由Actor-Critic网络[21 -23 ] 所制作的标签来训练. ...
AirSim: high-fidelity visual and physical simulation for autonomous vehicles
1
2017
... 基于Microsoft Airsim[24 ] 搭建无人机机动目标跟踪的仿真环境,生成虚拟世界,主要包括丛林和沙漠2个场景. 在这些场景中搭建包括道路、仓库、民房、车库等常规军事和民用建筑,设置车辆、人作为跟踪目标,在虚拟环境中训练无人机进行目标跟踪,如图7 所示. ...
无人机跟踪系统仿真平台的设计与实现
1
2020
... 在本文的实验中,模拟步长为0.1 s. 若无人机在规定时间内完成跟踪任务或目标超出摄像机的探测范围,则认为当前训练集的任务结束,重置模拟环境. 当经验回放缓冲区充满数据时,采用Adam优化算法对神经网络参数进行更新. 不同训练阶段的具体超参数设置如表1 所示. 混合噪声的相关参数用随机过程的学习率 $ \;\beta {\text{ = }}0.1 $ $ {\sigma _1}{\text{ = }}0.1 $ $ {\sigma _2}{\left( 0 \right)^2}{\text{ = }}0.3 $ $ \delta {\text{ = }}0.001 $ . 采用四自由度无人机模型,UAV飞行高度为 50 m,飞行加速度为[−5, 5] m/s2 ,起点坐标为(0,0),滚转角限制为[−5°, 5°],FVP 的分辨率设置为256 × 256,纵向和横向视场角均为80°[25 ] . ...
无人机跟踪系统仿真平台的设计与实现
1
2020
... 在本文的实验中,模拟步长为0.1 s. 若无人机在规定时间内完成跟踪任务或目标超出摄像机的探测范围,则认为当前训练集的任务结束,重置模拟环境. 当经验回放缓冲区充满数据时,采用Adam优化算法对神经网络参数进行更新. 不同训练阶段的具体超参数设置如表1 所示. 混合噪声的相关参数用随机过程的学习率 $ \;\beta {\text{ = }}0.1 $ $ {\sigma _1}{\text{ = }}0.1 $ $ {\sigma _2}{\left( 0 \right)^2}{\text{ = }}0.3 $ $ \delta {\text{ = }}0.001 $ . 采用四自由度无人机模型,UAV飞行高度为 50 m,飞行加速度为[−5, 5] m/s2 ,起点坐标为(0,0),滚转角限制为[−5°, 5°],FVP 的分辨率设置为256 × 256,纵向和横向视场角均为80°[25 ] . ...
Extreme trust region policy optimization for active object recognition
1
2018
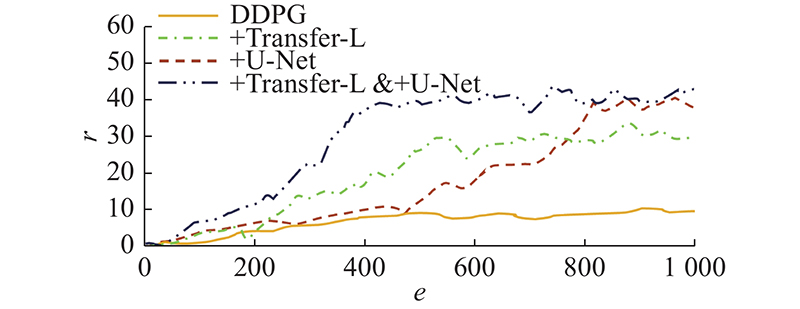
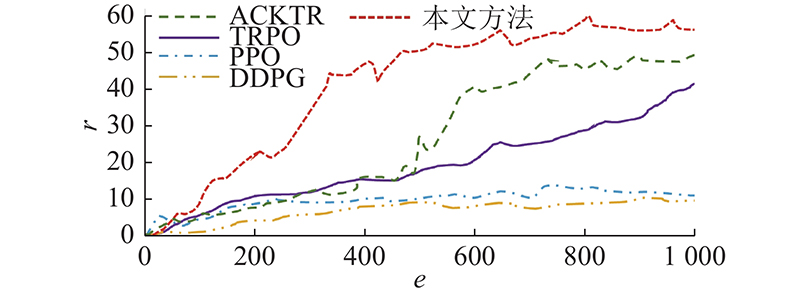
... 为了讨论本文方法较其他基于Actor-Critic的方法在给定目标跟踪任务上的性能,通过逐个替换Actor-Critic算法,开展对比试验. U-Net和奖励方案是相同的,对比算法为DDPG、TRPO[26 ] 、PPO[27 ] 和ACKTR[28 ] . ...
A pretrained proximal policy optimization algorithm with reward shaping for aircraft guidance to a moving destination in three-dimensional continuous space
1
2021
... 为了讨论本文方法较其他基于Actor-Critic的方法在给定目标跟踪任务上的性能,通过逐个替换Actor-Critic算法,开展对比试验. U-Net和奖励方案是相同的,对比算法为DDPG、TRPO[26 ] 、PPO[27 ] 和ACKTR[28 ] . ...
Scalable trust-region method for deep reinforcement learning using Kronecker-factored approximation
1
2017
... 为了讨论本文方法较其他基于Actor-Critic的方法在给定目标跟踪任务上的性能,通过逐个替换Actor-Critic算法,开展对比试验. U-Net和奖励方案是相同的,对比算法为DDPG、TRPO[26 ] 、PPO[27 ] 和ACKTR[28 ] . ...
1
... 将设计的跟踪模型和一些传统视觉跟踪模型在上述4个不同任务场景下进行性能比较,包括MIL[29 ] 、Meanshift[30 ] 、KCF[31 ] 及TLD[32 ] . 通过直接调用OpenCV的接口来实现以上算法,通过增加PID的模块来控制无人机飞行. ...
1
... 将设计的跟踪模型和一些传统视觉跟踪模型在上述4个不同任务场景下进行性能比较,包括MIL[29 ] 、Meanshift[30 ] 、KCF[31 ] 及TLD[32 ] . 通过直接调用OpenCV的接口来实现以上算法,通过增加PID的模块来控制无人机飞行. ...
High-speed tracking with kernelized correlation filters
1
2015
... 将设计的跟踪模型和一些传统视觉跟踪模型在上述4个不同任务场景下进行性能比较,包括MIL[29 ] 、Meanshift[30 ] 、KCF[31 ] 及TLD[32 ] . 通过直接调用OpenCV的接口来实现以上算法,通过增加PID的模块来控制无人机飞行. ...
Tracking-learning-detection
1
2011
... 将设计的跟踪模型和一些传统视觉跟踪模型在上述4个不同任务场景下进行性能比较,包括MIL[29 ] 、Meanshift[30 ] 、KCF[31 ] 及TLD[32 ] . 通过直接调用OpenCV的接口来实现以上算法,通过增加PID的模块来控制无人机飞行. ...