近年来,机器人因其对当今世界的重要性和应用的广泛性逐渐成为研究的热点. 由于技术的不断进步,对机器人的需求和提供的服务不断增加,人们针对不同的需求选择一系列环境传感器耦合在机器人上,用于执行复杂任务[1]. 触觉的产生是复杂且难以复现的生理过程,涉及皮肤深层及表皮的多种触觉感受器,机器人难以生成甚至理解这一感觉. 传感器的发展使得静态和无生命的物体能够具备像人类一样的感知能力,在如今智能机器人的发展中起着至关重要的作用[2]. 目前对触觉传感器用于物体识别的研究较多,Eguíluz等[3]提出递归多模态材料识别的方法,利用材料振动的频率响应和热特性进行识别. Yang等[4]将触觉和温度传感元件异质集成在柔性衬底上,以感知触觉. 本文选择PVDF(聚偏氟乙烯)材料制成的压电触觉传感器(下文以PVDF代称)来采集机器人原始触觉数据,经时频域处理后馈送至深度学习模型中. 目前在信号处理领域存在相关算法的尝试,如卷积神经网络(convolutional neural network, CNN)[5-9]、支持向量机(support vector machine, SVM)[10-13]、聚类算法[14-15]等.
本文采取2种网络模型来进行触觉识别,从实验结果来看,这2种方法都存在触感相似的材质分类混淆的问题,严重影响了识别结果. 在网络架构部分提出渐进式级联卷积神经网络,由2层独立训练的网络连接构成. 实验数据表明,该网络模型在同一数据集下的平均识别准确率有显著提升.
本文介绍了建立机器人触觉识别系统的过程,选取若干具有代表性的生活中常见物体作为识别对象,收集机器人手指触摸物体时传感器与材质摩擦产生的压电信号,经过去噪、去除异常值及标准化等操作后构建为数据集. 根据模型的分类结果进行分析反馈,设计对比测试,在不同方面对模型进行改进,得到较高的分类准确率,对机器人触觉的发展有重要意义.
1. 基于卷积神经网络的信号分类模型
1.1. 原始触觉数据获取与处理
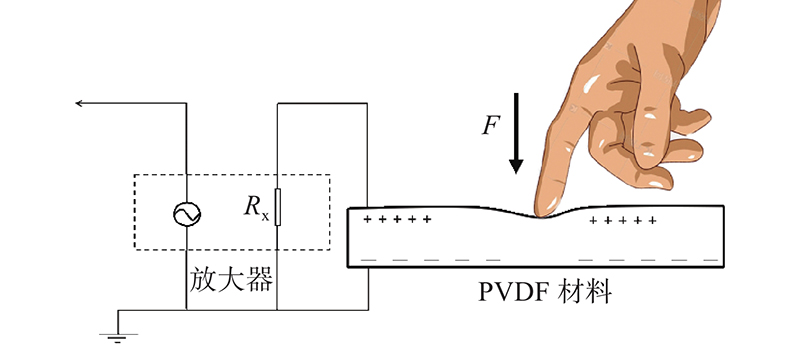
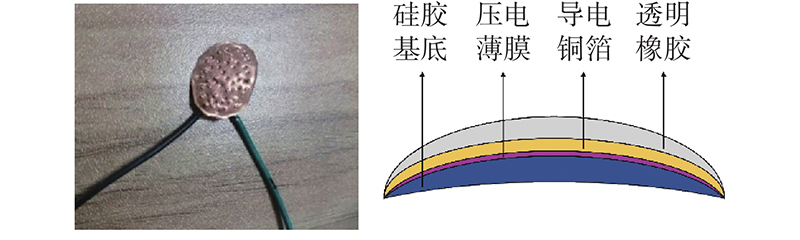
PVDF压电薄膜传感器具有韧性高、结构稳定、压电特性好等优点,能够记录薄膜表面的微小变化. 当PVDF受到法向方向的外力产生形变时,压电薄膜内部会出现极化效应,内部微单元会在表面细微纹理颗粒挤压的形变效应下造成表面电荷分布不均(PVDF压电薄膜的转换模型示意图见图1),产生与所受力相匹配的电荷信号. 此时,可将薄膜短暂视为电容器,可存储的电容量为
图 1
式中:
式中:
在后级采用电压放大模块对信号进行放大处理,使输出电压保持在固定的水平区间内,保证单片机能够识别采集的电压信号.
图 2
图 3
在确定实验所需的材质类型后,将每种材料裁成15 cm×5 cm尺寸的矩形,包裹在圆筒形卷轴外侧,用双面胶固定. 与常见的在材料上移动传感器来收集振动数据的方法不同,为了节省实验设备所占用的空间、控制传感器移动的速度及距离,将材料包裹在圆筒外围,通过电机匀速带动圆筒,使材质相对于传感器进行圆周运动,保证可以在有限的空间内收集高质量摩擦数据.
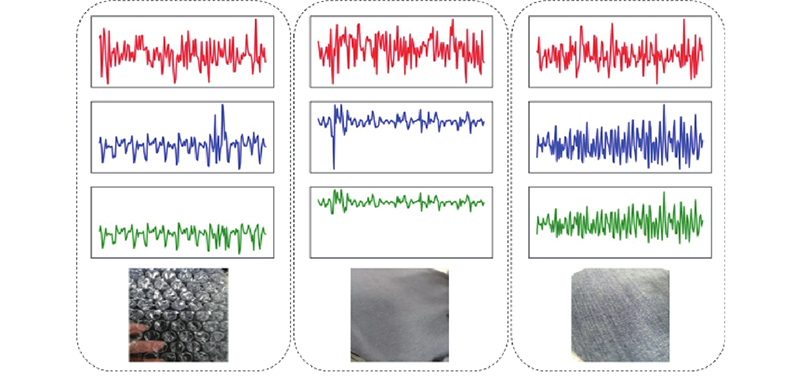
如图4所示为搭建的数据采集平台,为了保证数据的准确性与一致性,消除无关因素对数据的影响,机械手指与样本以固定的面积和压力接触. 圆筒转动时,手指匀速划过样本,传感器发生形变并输出电信号. 电机转速设置为30 r/min,传感器的采样率为1 kHz. 取1.8 s作为基础采样时间,每种材质的一个样本由1800个采样点构成,每种材质收集500组样本. 使用STM32F767IGT6 的 ADC 模块对采集到的信号进行模数转换后,得到原始触觉数据. 若将全部表征周期信号输入网络,则会造成特征维度过多,梯度收敛慢,识别不准确. 为了降低网络的输入规模,减轻计算负担,对时间序列进行处理. 触觉信号的采集过程中会出现2种主要干扰:原点漂移和振动噪音. 对触觉信号采取的主要处理方法如下. 1)使用双向线性数字滤波器进行去噪,在去除噪声的同时防止了数据的相位移动. 2)计算数据的统计性描述,开展数据的异常值分析,剔除与平均值的偏差超过标准差的3倍的异常值. 3)采用z-score方法标准化数据,将数据按比例缩放到零点附近. 选取3种代表性的材质, 原始数据、去噪后的数据、剔除异常值后的数据进行标准化的数据如图5所示.
图 4
图 5
图 6
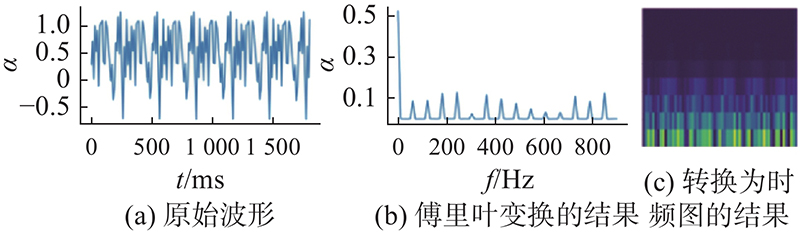
图 6 信息从时域到频域的转化
Fig.6 Transformation of information from time domain to frequency domain
1.2. 卷积神经网络结构
1.2.1. 1-D CNN的构建
图 7
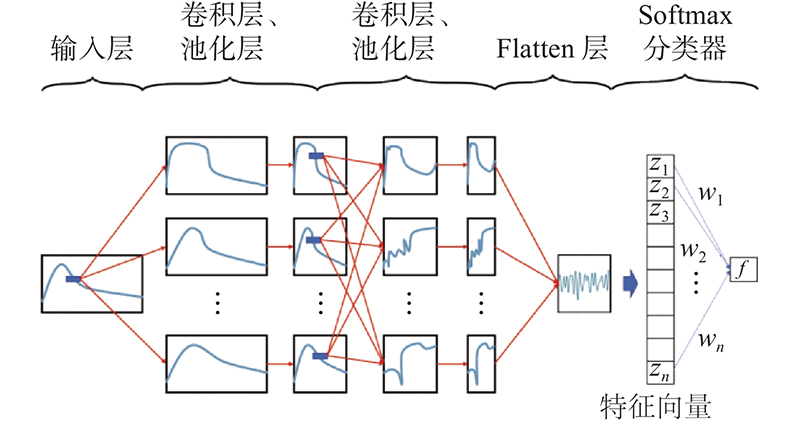
网络包含6个卷积层、3个池化层和连接Softmax分类器的全连接层. 所有卷积层由tanh函数激活. tanh函数将前一层输出的结果转换到 (−1,1)上. 比较大的负数无限接近于 −1,比较大的正数无限接近于1. 最大池化层输出先前卷积块的卷积结果的最大值. 输入层之后的每两个卷积层与池化层交替相连,每层的池化层抽取前一层神经元传播的二维映射. 通过BP算法进行训练. 输入层接受输入信号,将其完整地通过足够数量的卷积核进行前向传播,在最后一个池化的输出处估计决策向量.
在前向传播过程中,假设第
式中:
表 1 一维卷积神经网络参数设置
Tab.1
| 模块 | 参数 | 参数值 |
| 卷积层 | 卷积核维度 | 3×1×1 |
| 卷积层 | 卷积核步长 | 2 |
| 卷积层 | 卷积核个数 | 16 |
| 卷积层 | 卷积层激活函数 | tanh |
| 池化层 | 池化方式 | 最大池化 |
| 池化层 | 卷积核维度 | 3×1×1 |
| 池化层 | 卷积核步长 | 1 |
图 8
图 8 1-D CNN的分类结果混淆矩阵
Fig.8 Confusion matrix of classification results of 1-D CNN
1.2.2. 2-D CNN的构建
图 9
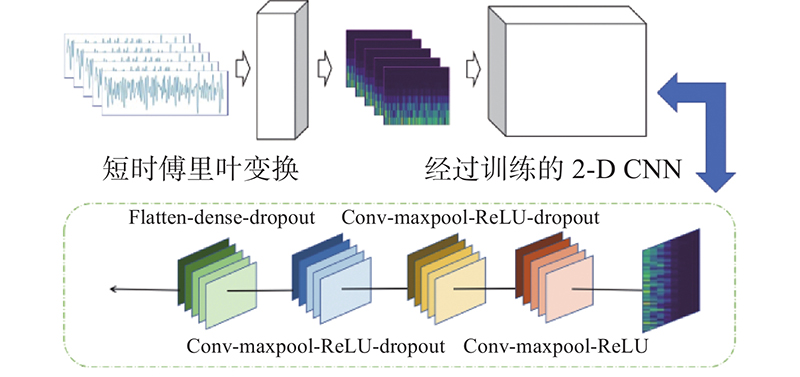
使用的网络由4个卷积层和2个最大池化层构成,卷积运算在图像处理领域中用于检测上一层的局部特征,如边缘检测、模糊处理. 在处理频谱图时,通过卷积和池化操作提取的特征,可以很容易地识别出该信号的调制模式. 池化过程通过将多个相似的特征合并,提高模型的可泛化性. 模型带有2个Dropout层,使网络在正向训练过程中以概率P丢弃一定的神经元,再次提高模型的泛化能力,防止过拟合. 结合时频分析和CNN这2个过程,综合它们的优点重新设计网络的拓扑结构.
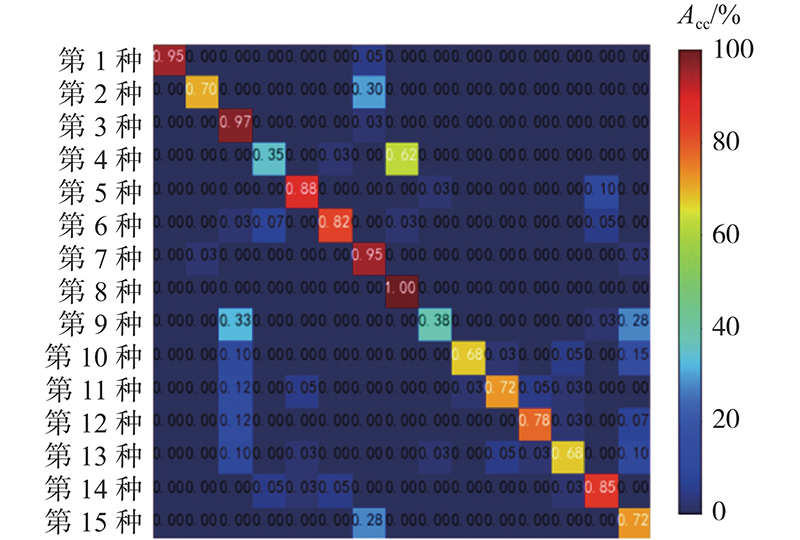
从图10的分类结果可以看出,与1-D CNN相比,输入更多信息的2-D CNN在分类效果上有着一定的提升,分类完全正确的类别数有一定提升,但对于易混淆的材料难以有效地区分.
图 10
图 10 2-D CNN的分类结果混淆矩阵
Fig.10 Confusion matrix of classification results of 2-D CNN
2. 基于级联神经网络的信号分类模型
针对上述工作中出现的相近材料易混淆的情况,提出渐进式的级联神经网络结构,由独立训练的2个网络相互连接构成,将待分类的15种材料进行预先的粗粒度归类. 第1层网络先将所有材料粗分类,抽取出截至Softmax层前的向量参数作为第2层网络的输入,对粗粒度归类方式及细粒度网络构成进行多次实验,构建分类效果最优的级联神经网络.
2.1. 粗粒度分类
对于所有的实验材料,共选择4种粗分类方式:由聚类算法进行的四分类、五分类及实验人员通过肉眼和常识判定较接近的四分类、五分类.
聚类的目标是识别形成同质化的样本集,在形成的聚类中,来自相同类别样本之间形成的距离(包括但不限于欧氏距离)度量最小,来自不同类别样本之间的相似度最小. 在分类好的集群上建模比在原始数据集上建模更加容易,因此预先使用聚类算法对某些特性上相似度较高的材料进行预分类,开展下一步分类,解决1.2.1节的混淆问题. 具有一定时间序列特性的聚类技术在诸多领域被证明十分有效[22-24],选择K-Medoids聚类算法. 设n个具有p个变量的对象被分成k (k < n)个簇,其中k是给定的. 根据选择的度量方法计算所有对象两两之间的距离,对于每一个对象
式中:
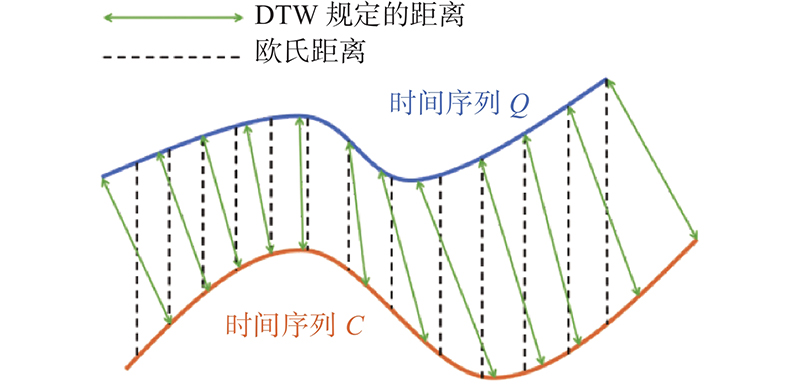
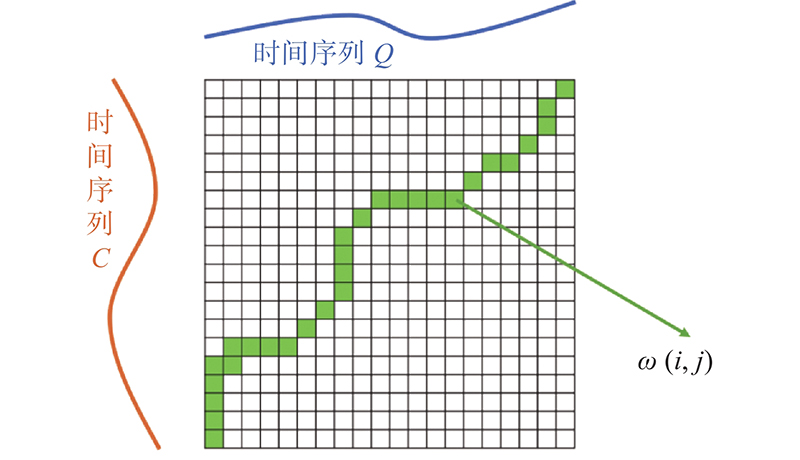
设2个长度不同的时间序列分别为C和Q,其中
式中:
图 11
图 11 欧氏距离和DTW距离度量方法的对比
Fig.11 Comparison of Euclidean distance and DTW distance measurement methods
DTW的表达式类似于动态规划的递推状态转移方程,根据要对比的信号生成代价矩阵. 矩阵中的每一个元素都代表Q和C中2个时间帧的对齐. DTW算法的目的是寻找出一条穿过整个矩阵的路径,如图12的点集所示. 绿色路径上的每一个点都可以视为2段时间序列的一次对齐.
图 12
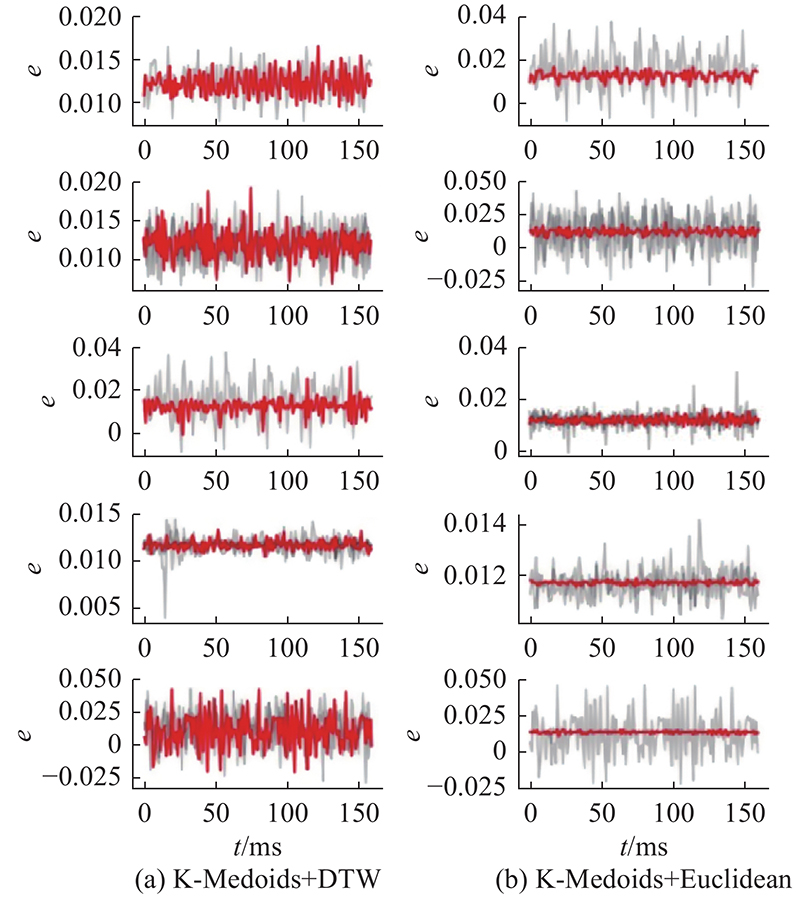
图13中,e为分离系数. 可以看出,采用欧氏距离度量时数据之间的距离普遍较大,耦合程度较差,聚类中心与轮廓相差较大,不能很好地代表所聚类的数据. 当采用DTW作为度量时,轮廓系数更优,相同类别的数据相似性更高.
考虑所有可能影响聚类结果的因素,从分类规则层面考虑了人主观和算法的差异,从分类结果上考虑了分类数量不同的区别. 根据这些材料在现实中的触感,将类别数 k 分别设置为4和5,在不同情况下实现K-Medoids聚类算法,分析维度压缩后的分类结果. 实验数据显示,不同的粗粒度归类下,人工和算法2种不同的方式分类准确率存在较大差异,如表2所示.
图 13
图 13 DTW 与欧氏距离的聚类结果比较
Fig.13 Comparison of clustering results between DTW and Euclidean distance
表 2 基于不同聚类方式的数据分类准确率比较
Tab.2
| 数据 | Acc/% |
| 人工分类(四分类) | 36.67 |
| 人工分类(五分类) | 57.74 |
| 算法分类(四分类) | 87.33 |
| 算法分类(五分类) | 99.44 |
2.2. 细粒度分类
选择此前的2-D CNN作为粗粒度分类模块,将2-D CNN的Flatten层参数提取出来输入到细分类网络中,用粗分类结果和原始标签共同指导第2层网络的训练. 由于粗分类已有较好的分类结果,第2层网络的主要意义是区分聚类算法所归类的极相似的材料.
在选择损失函数时,选择交叉熵损失函数(cross entropy)[28]. 使用Softmax函数,可以将拉平的特征向量转化成各分类结果的概率,在计算损失时需要计算输出概率和期望概率的差. 交叉熵函数可以有效地计算该数值,交叉熵越小,分类准确率越高. 在多分类中,交叉熵损失函数的表达式为
式中:
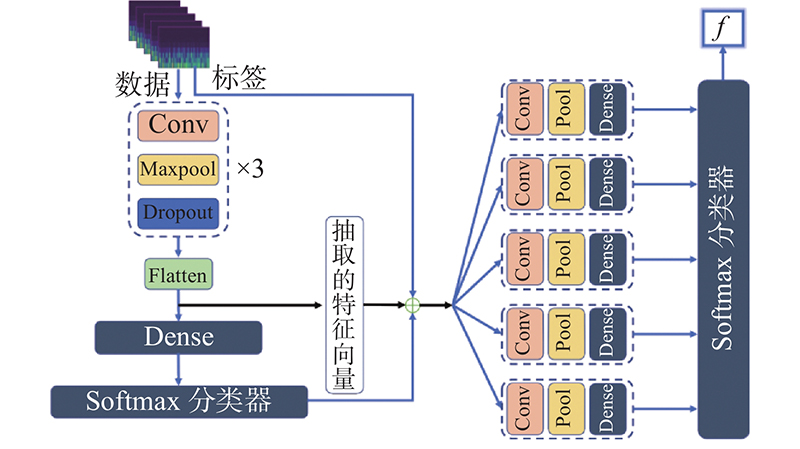
2层网络的总架构如图14所示.
图 14
图 14 级联神经网络的信号分类模型架构
Fig.14 Signal classification model architecture of cascaded neural networks
图 15
图 16
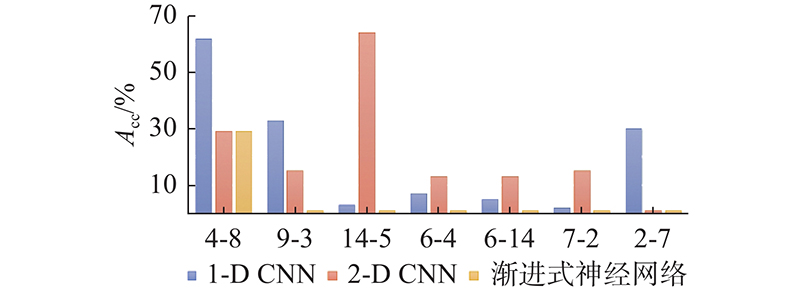
图 16 相似材质识别结果的量化分析
Fig.16 Quantitative analysis of similar material recognition results
3. 结果与讨论
提出的所有分类模型均由Python语言搭建,使用开源库TensorFlow[29],该库由Google为深度学习而开发. 训练CNN模型需要大量的计算能力和训练时间,实验装置包括配备了Intel i9 10900X的服务器, 64 GB的RAM、1TB SSD硬盘驱动器和2块Nvidia RTX 2080 TI GPU. 对输入数据进行分割,75%的数据用于训练,25%用于测试. 在训练过程中,使用10倍交叉验证.
根据PVDF优秀的压电特性,开发触觉传感器. 通过上位机与传感器的有机耦合,建立高度集成的硬件系统,对传感器的输入信号进行实时处理. 在数据处理部分,通过构建2个步骤的级联网络完成这一操作. 针对原始触觉信号设计CNN模型,研究该模型的性能. 通过开发的CNN模型解决相近材质易混淆的情况,提高检测性能. 将输入信号转换为时间和频率的二维图像数据.
采用的分类算法结果比较如表3所示. 可见,当粗分类数为5时,提出的分类方法在几乎所有的类别下都出现了100%的分类正确率,尤其在易混淆的材料上有着较高的分离度,较单步卷积神经网络模型有较大的提升.
表 3 不同算法对于整体数据的分类准确率
Tab.3
| 材质类型 | Acc/% | ||
| 1-D CNN | 2-D CNN | 渐进式模型 | |
| 百洁布 | 95.25 | 100 | 100 |
| 栅格文件袋 | 70.32 | 100 | 100 |
| 硬质纸板 | 97.54 | 90.02 | 90.03 |
| 泡沫塑料 | 35.26 | 57.44 | 71.44 |
| 无痕布 | 88.44 | 100 | 100 |
| 纹理布 | 82.47 | 100 | 93.66 |
| 硅胶片 | 95.52 | 100 | 100 |
| 塑料片 | 100 | 100 | 100 |
| 塑料栅格 | 38.33 | 62.15 | 100 |
| 粗糙胶带 | 68.10 | 100 | 100 |
| 柔软布 | 72.05 | 100 | 100 |
| 软牛仔裤 | 78.66 | 100 | 100 |
| 硬质布 | 68.38 | 100 | 100 |
| 硬牛仔裤 | 85.54 | 57.06 | 100 |
| 毛衣 | 72.80 | 100 | 100 |
| 平均准确率 | 76.57 | 91.11 | 97.01 |
4. 结 语
本文构建的渐进式分类模型的平均准确率为97.01%,保证机器人对于训练过的材料有极高的成功识别率,为下一步的交互控制夯实了基础. 本研究的优点是使用PVDF传感器与卷积神经网络结合的方式进行触觉识别,将训练于二维图像数据的流行模型的权重转移到对一维信号的分类中,打破了深度模型构建和训练阶段的约束,灵活地使用K-Medoids聚类算法,显示出较好的分类性能. 建立小型数据库,数据的重复处理导致机器人记忆了训练数据,仅能对已有的材质类型进行分类,对没有记录过的测试数据识别效果有待提升. 进一步的研究方向是利用该模型来帮助机器人学习从未触摸过的材质,反馈未知材质与数据库中已存在记录的相似程度,帮助机器人构建类人的触觉产生机理.
参考文献
A review on challenges of autonomous mobile robot and sensor fusion methods
[J].
A flexible thermal sensor based on PVDF film for robot finger skin
[J].DOI:10.1080/10584587.2019.1668687 [本文引用: 1]
Multimodal material identification through recursive tactile sensing
[J].DOI:10.1016/j.robot.2018.05.003 [本文引用: 1]
A 32×32 temperature and tactile sensing array using PI-copper films
[J].DOI:10.1007/s00170-009-1940-z [本文引用: 1]
One-dimensional CNN-based intelligent recognition of vibrations in pipeline monitoring with DAS
[J].
A 1D-CNN-spectrogram based approach for seizure detection from EEG signal
[J].
Real-time motor fault detection by 1-D convolutional neural networks
[J].
Convolutional neural networks for vibrational spectroscopic data analysis
[J].
High performance EEG signal classification using classifiability and the Twin SVM
[J].
EEG signal classification using universum support vector machine
[J].
Clustering technique-based least square support vector machine for EEG signal classification
[J].DOI:10.1016/j.cmpb.2010.11.014 [本文引用: 1]
Neural signal classification using a simplified feature set with nonparametric clustering
[J].DOI:10.1016/j.neucom.2009.07.013 [本文引用: 1]
Gradient-based learning applied to document recognition
[J].DOI:10.1109/5.726791 [本文引用: 1]
ImageNet classification with deep convolutional neural networks
[J].
Psychophysical dimensions of tactile perception of textures
[J].
One-dimensional convolutional neural networks for spectroscopic signal regression
[J].DOI:10.1002/cem.2977 [本文引用: 1]
Classification of arrhythmia by using deep learning with 2-D ECG spectral image representation
[J].DOI:10.3390/rs12101685 [本文引用: 1]
Clustering of time series data: a survey
[J].DOI:10.1016/j.patcog.2005.01.025 [本文引用: 1]
Smart homes for the elderly dementia sufferers: identification and prediction of abnormal behavior
[J].
The BOSS is concerned with time series classification in the presence of noise
[J].DOI:10.1007/s10618-014-0377-7 [本文引用: 1]
Time series clustering model based on DTW for classifying car parks
[J].DOI:10.3390/a13030057 [本文引用: 1]
A tutorial on the cross-entropy method
[J].DOI:10.1007/s10479-005-5724-z [本文引用: 1]