微夹持器是微操作系统的重要执行器,按其驱动方式的不同,可分为压电式[7]、电磁式[8]、电热式[9]、静电式[10]和形状记忆合金式[11]. 国内外学者在微夹持器的设计上已有众多成果,Hao等[12]基于PRRP型分布柔度式结构设计大行程且具有抗屈曲能力的微夹持器;Chen等[13]提出具有多级放大机构的非对称式微夹持器;吴志刚等[14]将Scott-Russell结构与平行四边形结构相结合,设计结构紧凑的微夹持器. 微定位平台是微操作系统实现精密定位的关键,其多采用压电陶瓷[15]或音圈电机[16]驱动. 林盛隆等[15]基于柔性直梁,设计具有高带宽的两自由度微定位平台;Awtar等[16]基于反向串联式双簧片结构,设计大行程且完全解耦的两自由度微定位平台;田延岭等[17]基于4-PP-E解耦并联机构,设计大行程且高承载的两自由度微定位平台. 综上所述,尽管国内外针对微夹持器和微定位平台的研究均取得了大量成果,但不难发现:1)微夹持器是微操作系统的重要执行器,其仅能实现夹持作用,难以实现精密定位;2)大行程、具有高定位精度的平台是实现微操作系统中微夹持器精密定位,增大微夹持器可达定位空间的关键.
本文设计新型大行程、解耦两平动柔性微定位平台,并将其与微夹持器相结合,可实现精密定位且具有较大定位空间的微定位夹持系统;建立系统静、动态特性的理论模型;以提高微定位夹持系统的静、动态特性为目标,对其进行参数优化;通过有限元验证理论模型的正确性,并根据理论与仿真结果,给出微夹持器的可达定位空间.
1. 结构设计
1.1. 大行程两平动微定位平台的结构设计
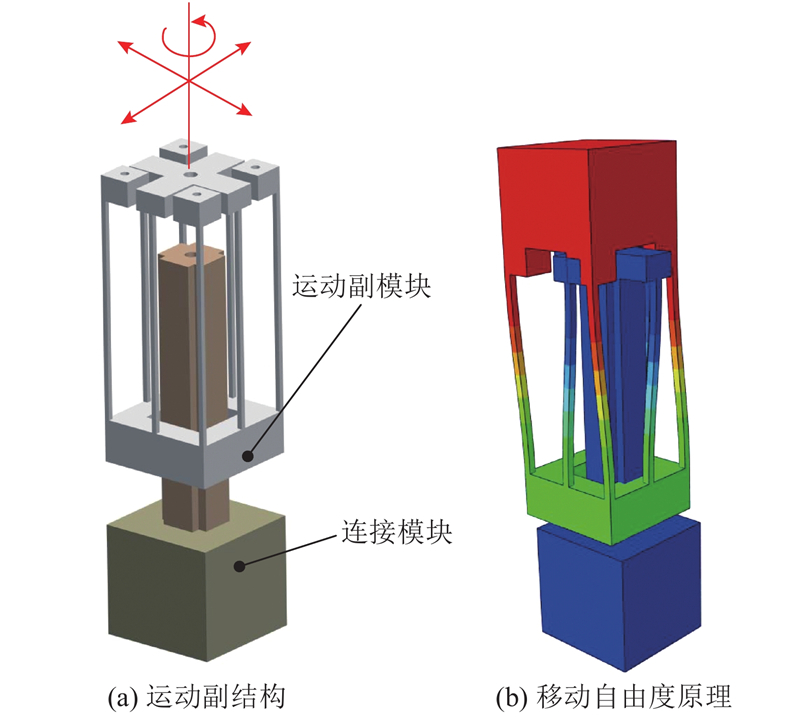
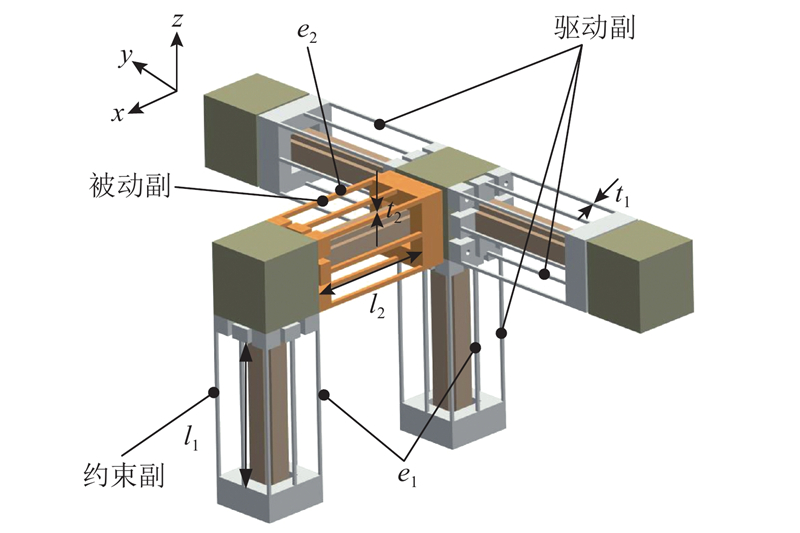
为了使微操作系统中微夹持器具有较大的可达定位空间与高定位精度,作为定位机构的两自由度平台需同时具有大的运动行程和良好的解耦特性. 基于自由度与约束空间拓扑法[18-19],提出2移1转(2 translation and 1 rotation,2T1R)型柔性运动副[20],结构如图1(a)所示. 该运动副由2组四杆结构串联而成,反向串联结构[16, 21]与均布柔度的细长杆单元既扩大了运动副的运动行程,又抵消了运动副移动变形时2组四杆结构产生的寄生运动,故该运动副利于实现平台的大行程解耦运动. 同时,该运动副结构紧凑、尺寸参数少、可实现模块化装配,其移动自由度原理如图1(b)所示. 此外,该运动副变形时无应力刚化效应[22],有利于简化平台理论建模的难度.
图 1
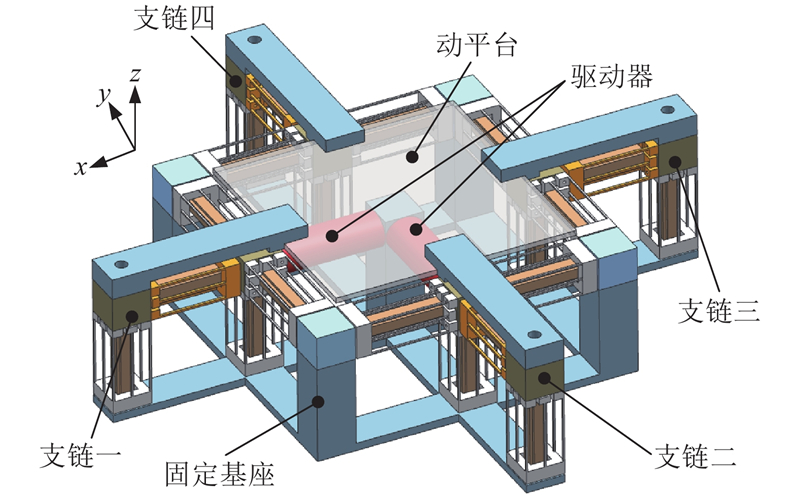
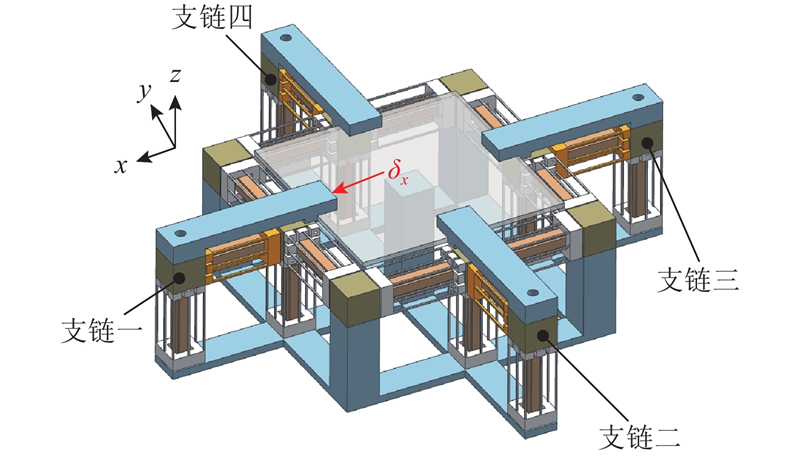
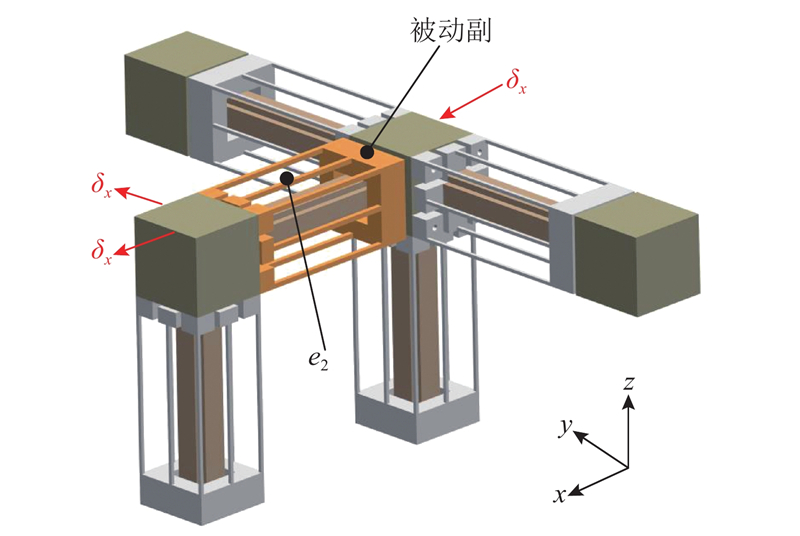
基于该运动副,设计如图2所示的新型大行程两平动微定位平台,其包括4个相同的柔性支链和固定基座,驱动器置于平台内部.
图 2
图 2 大行程两自由度微定位平台结构示意图
Fig.2 Structure diagram of 2-DOF micro-positioning platform
图 3
关于微定位平台的驱动方案,两自由度微定位平台采用驱动器可固定安装的并联式结构,且平台具有较大的运动行程,因此拟采用具有毫米级位移输出的音圈电机以实现平台驱动. 以平台x轴方向为例,当音圈电机单独沿支链一或支链三驱动副施加驱动位移时,动平台即可实现沿x轴的位移输出.
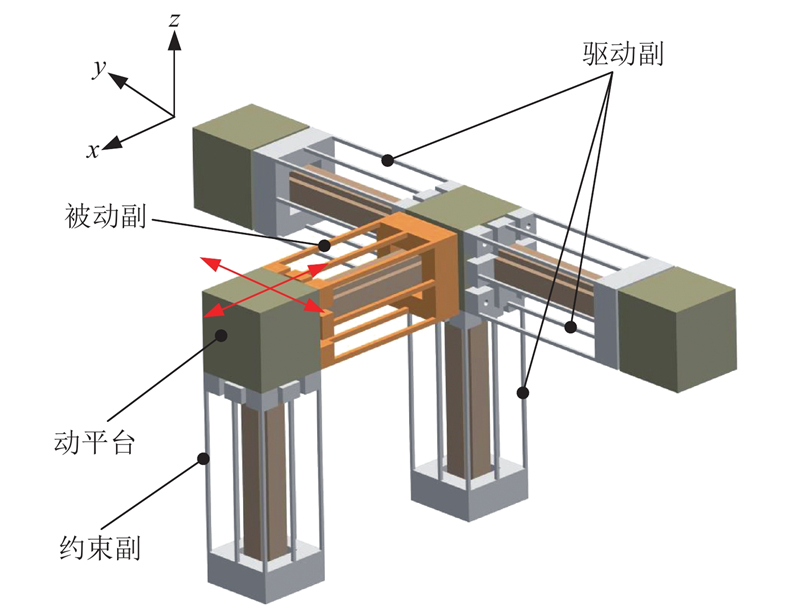
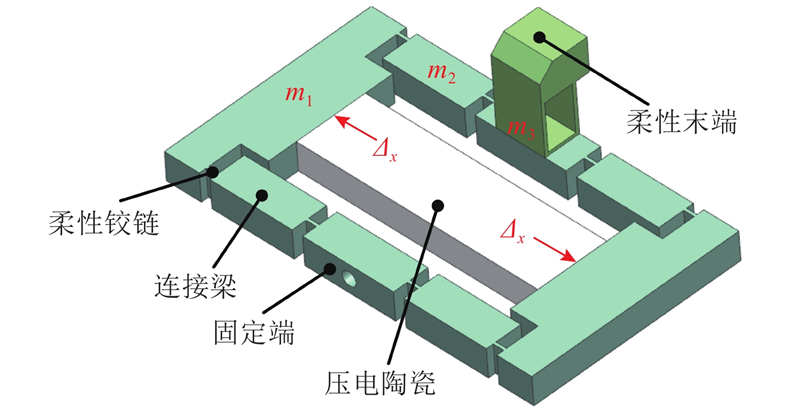
1.2. 微定位夹持系统结构设计
图 4
图 5
图 6
2. 静、动态特性分析
2.1. 静态特性理论分析
2.1.1. 微定位平台力−位移关系理论分析
平台为解耦对称结构,沿x、y轴方向特性完全相同,以x轴方向为研究对象,建立平台在x轴方向的力−位移关系模型. 通过建立单根细长杆单元的力−位移关系模型,可以得到平台整体在x轴方向的力−位移关系. 如图7所示,支链一中各运动副均为反向串联结构,其受力与变形为线性关系,其中细长杆ei(i=1,2)的刚度kei为
图 7
式中:E为杨氏模量,li、ti别为细长杆ei的长度、厚度. 则对应支链一中各运动副的刚度为
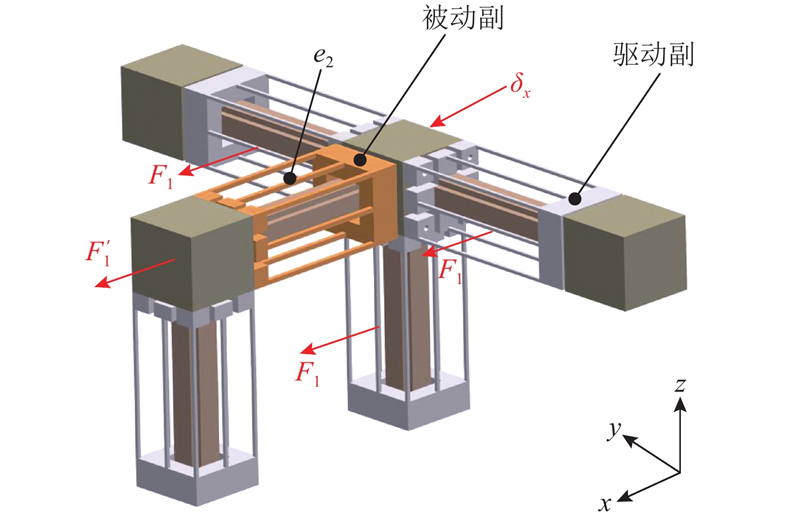
如图8所示,基于并联机构的运动学原理,当沿x轴方向支链一驱动副单独施加驱动位移δx时,支链一及支链三中驱动副与约束副、支链二及支链四中被动副与约束副均产生弹性变形,由此可得平台的输入刚度Kp,以及驱动力Fp与驱动位移δx之间的关系:
图 8
图 8 平台沿x轴方向驱动示意图
Fig.8 Schematic diagram of platform driving along x axis direction
2.1.2. 平台丢失运动分析
丢失运动是指平台输入、输出位移之间的差值,为了提升平台的定位精度,应减小平台的丢失运动. 驱动力作用支链下被动副的轴向变形是造成微定位平台丢失运动的主要原因. 如图9所示,当沿x轴方向支链一驱动副施加驱动位移δx时,该支链中驱动副与被动副所承受作用力F1与
因被动副为反向串联结构,2组四杆机构分别受到力
图 9
2.1.3. 平台屈曲分析
平台中承受压力的细长杆易发生压杆失稳现象,进而影响平台的静态性能,因此有必要分析平台屈曲. 同理,当沿x轴方向支链一驱动副施加驱动位移δx时,该支链中被动副承受轴向压力,被动副为反向串联结构,其中正向四杆机构承受压力,有压杆失稳风险. 选取其中细长杆e2进行屈曲分析,根据欧拉公式,细长杆e2可承受的临界压力Fcr为
式中:I2为细长杆e2的截面惯性矩.
2.1.4. 平台材料应力分析
其中弯曲应力σb与压缩应力σc分别为
式中:W2、A2分别为细长杆e2的抗弯截面系数、面积.
图 10
图 10 支链一中细长杆e2应力分析图
Fig.10 Stress analysis diagram of medium slender rods e2 in limb one
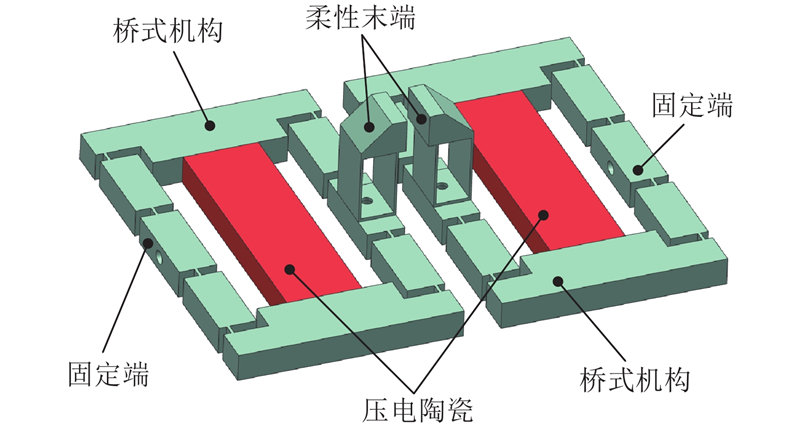
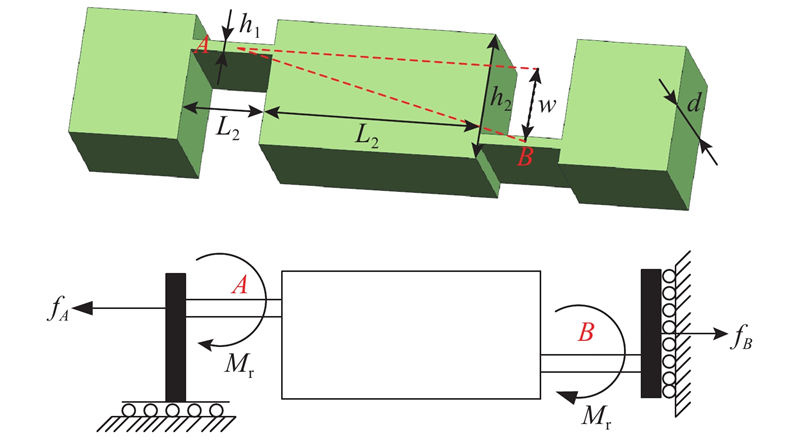
2.1.5. 微夹持器位移放大倍率分析
图 11
图 12
式中:w为2个柔性铰链的间距,fA、fB为刚性构件所受力,fx、Mr分别为柔性铰链所受力和力矩,Fgin为桥式结构的输入力.
用L1、L2分别表示柔性铰链和刚性连接梁的长度,基于胡克定律,柔性铰链和连接梁的伸长量分别为
基于欧拉−伯努利梁模型,柔性铰链和连接梁的弯曲应变能为
当驱动位移为Δx时,基于能量守恒定律,有:
联立式(15)~(19)可得:
基于桥式机构的刚度矩阵[27],柔性铰链和连接梁的拉伸刚度
式中:h1为柔性铰链的厚度,h2为刚性连接梁的厚度,d为桥式结构的宽度. 当d>10h1时,杨氏模量E应修正为平面模量E1,二者之间的关系为[21]
式中:v为材料的泊松比.
基于欧拉-伯努利梁模型,桥式机构的输出位移Δy为柔性铰链和连接梁的挠度之和,即:
联立式(20)和(23),可求得微夹持器的位移放大倍率Ramp为
式中:Δout为微夹持器沿x轴方向输出位移.
2.1.6. 微夹持器力−位移关系分析
力−位移关系是微夹持器的重要静态特性,建立微夹持器力−位移关系的理论模型,不仅可以为后续的实验控制奠定理论基础,还可以对夹持力进行定量分析以防止过载. 联立式(15)、(20),可求得到微夹持器的输入刚度Kg为
其中夹持力Fg的计算公式为[5]
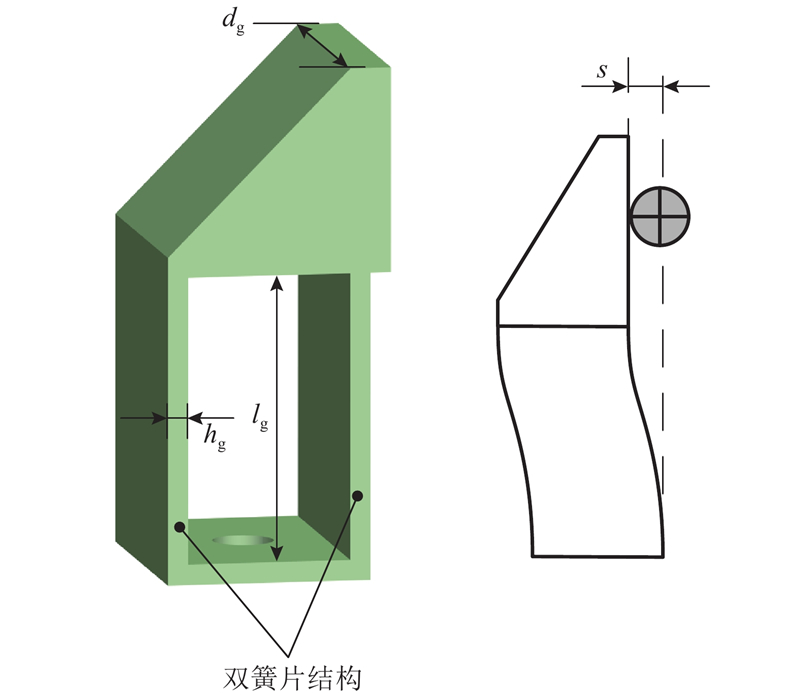
式中:dg、hg、lg分别为柔性末端簧片的厚度、宽度与长度. 联立式(25)~(27)可得微夹持器驱动力Fpzt与输入位移Δx、柔性末端横向位移s的关系式:
2.1.7. 微夹持器材料应力分析
为了证材料变形在弹性范围内,对微夹持器中柔性铰链进行材料应力分析,其最大应力σg为
其中Mg为
式中:W3、A3分别为柔性铰链的抗弯截面系数和截面面积.
2.2. 动态特性分析
2.2.1. 微夹持器模态分析
为了研究微夹持器的动态特性,对微夹持器进行模态分析. 如图11所示,取微夹持器的输入位移Δx为广义坐标p,则微夹持器的动能可以表示为
基于拉格朗日方程[28],微夹持器的等效质量Mge与等效刚度Kge分别为
式中:m1、m2、m3分别为微夹持器中各刚性部件的质量,J2为转动惯量. 微夹持器的固有频率为
2.2.2. 微定位平台模态分析
模态是微定位平台的固有振动特性. 为了直观地描述微定位平台结构参数与固有频率之间的关系,对微定位平台进行模态分析. 基于拉格朗日方程,微定位平台的等效质量与等效刚度为
式中:M1为平台发生弹性变形的柔性部件质量之和,M2为平台平动的刚、柔性部件质量之和. 式(34)的推导过程可参考文献[22]. 微定位平台的一阶固有频率为
3. 参数优化
上述理论分析未充分考虑微定位平台与微夹持器静、动态特性间的相互影响,因此建立微定位夹持系统的全局优化模型,以同时提高微定位夹持系统的静、动态特性. 选择AL-7075作为微定位平台与微夹持器的材料,其中E=7.17 GPa,v=0.33,屈服强度为503 MPa,密度为2 810 kg/m3. 微定位夹持系统的主要结构参数包括细长杆的长度ei和宽度l1、t1、l2、t2,柔性铰链的长度L1和厚度h1,刚性连接梁的长度L2,柔性铰链的间距w,基于式(6)、(10)、(24)、(25)、(33)、(35),取优化模型的设计变量为
其中设计变量的范围与初始值X0分别为
为了方便后续试验中驱动器选型,设定音圈电机与压电陶瓷的预期最大驱动位移分别为1 mm和0.01 mm,设定平台所需驱动力不超过100 N,微夹持器的输入刚度不超过6 N/μm. 同时,平台最大应力不应超过许用应力且不应发生屈曲现象,微夹持器最大应力不应超过许用应力. 为了提高微定位夹持系统的静、动态特性,优化时:1)减小平台的丢失运动;2)增加平台的一阶频率;3)增大微夹持器的位移放大倍率;4)增大微夹持器的工作频率. 基于上述,微定位夹持系统优化模型的目标函数与约束条件分别为
为了保证可靠性,设定安全系数k=2.
基于MATLAB中的fmincon和fgoalattain函数,采用目标规划法对微定位夹持系统进行多目标参数优化. 参数优化后微定位夹持系统的尺寸为196 mm×196 mm×51 mm,其主要结构参数如表1所示.
表 1 微定位夹持系统的结构参数
Tab.1
| 参数 | 数值/mm | 参数 | 数值/mm | |
| l1 | 26 | h1 | 0.4 | |
| t1 | 0.55 | L1 | 1.5 | |
| l2 | 22.19 | L2 | 11.78 | |
| t2 | 0.8 | w | 1.3 |
微定位夹持系统优化前后的静、动态特性如表2所示. 由表可知,优化后:1)微定位平台的固有频率提升25.3%,丢失运动减小25.2%;2)微夹持器的固有频率增加18.3%,位移放大倍率提升28.8%. 微定位夹持系统的静、动态特性均有较大提升,优化结果完全符合预期.
表 2 优化前后微定位夹持系统的静、动态特性
Tab.2
| 特征参数 | 优化前 | 优化后 | 优化率/% |
| fp | 40.84 Hz | 51.16 Hz | 25.3 |
| fg | 292.81 Hz | 346.27 Hz | 18.3 |
| δlost | 5.16 μm | 3.86 μm | −25.2 |
| Ramp | 15.22 | 19.61 | 28.8 |
4. 有限元仿真验证
为了验证所推导理论模型的正确性和优化模型的可行性,基于表1所确定的微定位夹持系统结构参数,运用Abaqus构建有限元分析模型,分别对微定位平台和微夹持器的静、动态特性进行有限元仿真验证.
4.1. 静态特性验证
4.1.1. 微定位平台静态特性验证
图 13
图 13 微定位平台x轴方向的静态性能有限元仿真
Fig.13 Finite element simulation of static performance for micro-positioning platform in x axis direction
图 14
图 14 微定位平台x轴方向静态性能验证
Fig.14 Static performance verification for micro-positioning platform in x axis direction
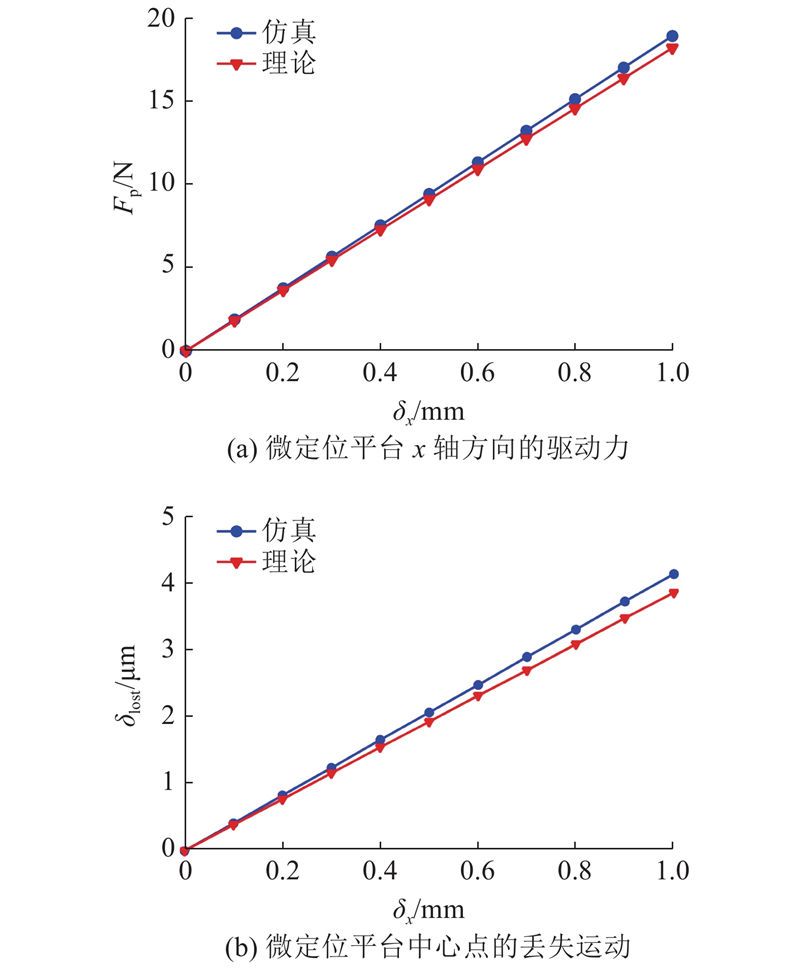
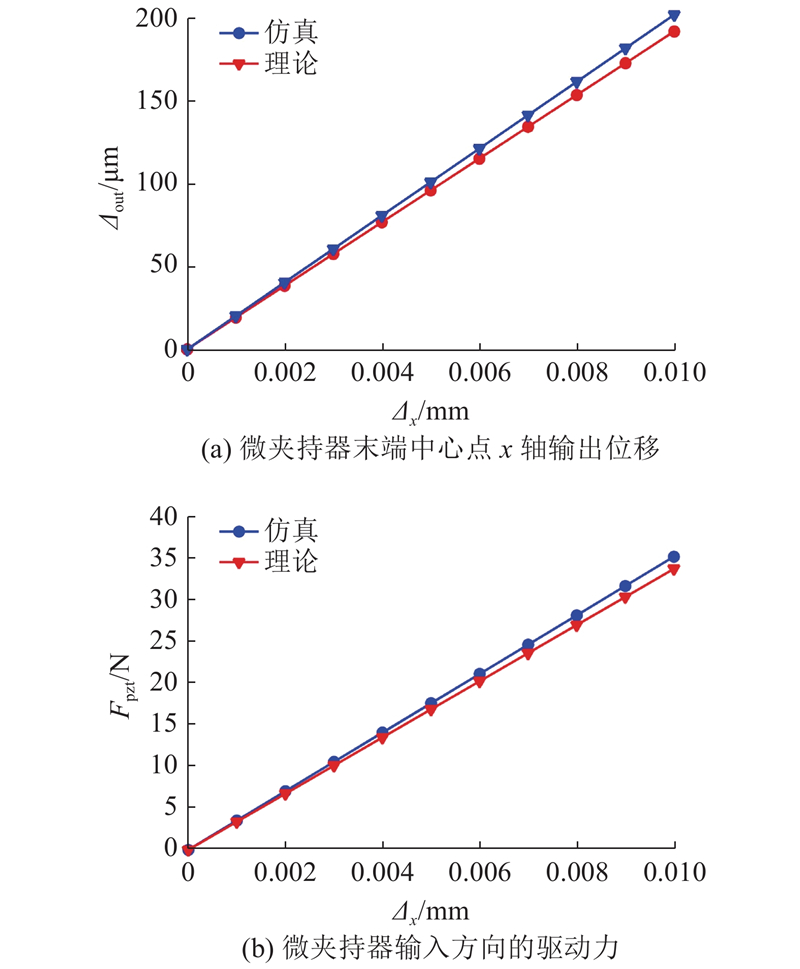
如图14(a)所示,在0~1 mm驱动位移δx内,基于式(7)微定位平台沿x轴方向驱动力Fp理论、仿真的最大值分别为18.22、19.24 N,理论值与仿真值的相对误差为0.2%~5.6%. 如图14(b)所示,在0~1 mm驱动位移δx内,基于式(10)微定位平台丢失运动δlost理论、仿真的最大值分别为3.86 μm、4.14 μm,理论值与仿真值的相对误差为0.1%~7.3%. 由图14仿真结果可知,平台支链一中细长杆e2所承受压力
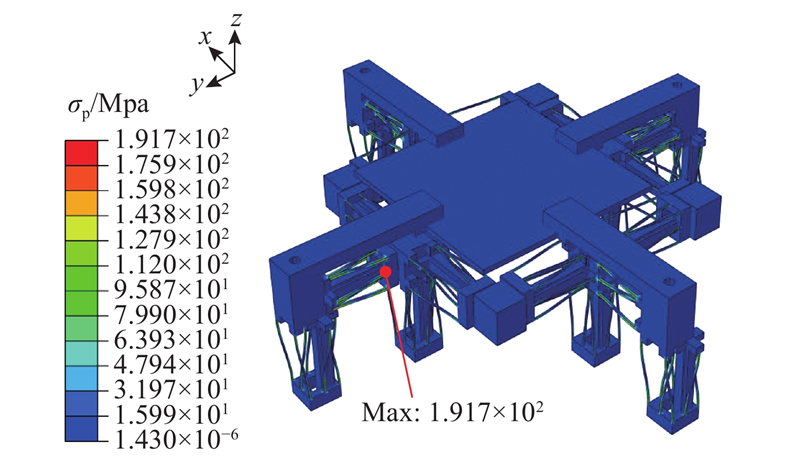
为了验证微定位平台的最大应力,如图15所示,沿x、y轴方向同时施加1 mm的驱动位移δx. 由仿真结果可知,支链一中细长杆e2所受最大应力σp的仿真值为191.7 Mpa. 基于式(12)可知对应最大应力σp的理论值为196.2 Mpa,理论值与仿真值的相对误差为2.3%,且理论值与仿真值均远小于材料许用应力,表明平台无应力失效风险.
图 15
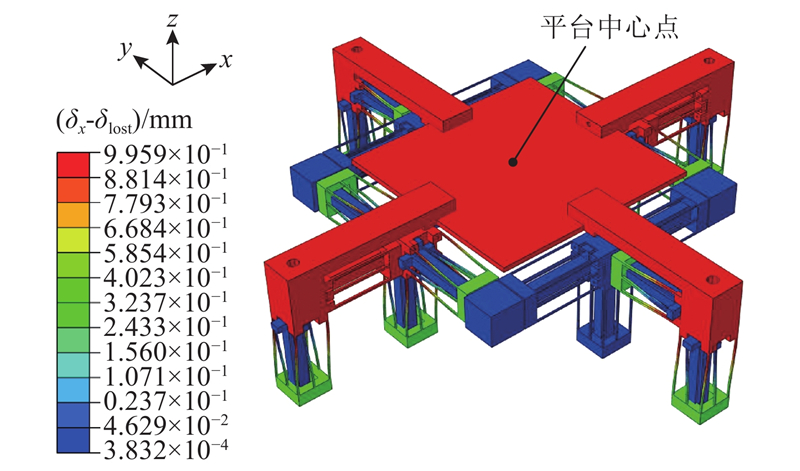
4.1.2. 微定位平台输入输出耦合仿真
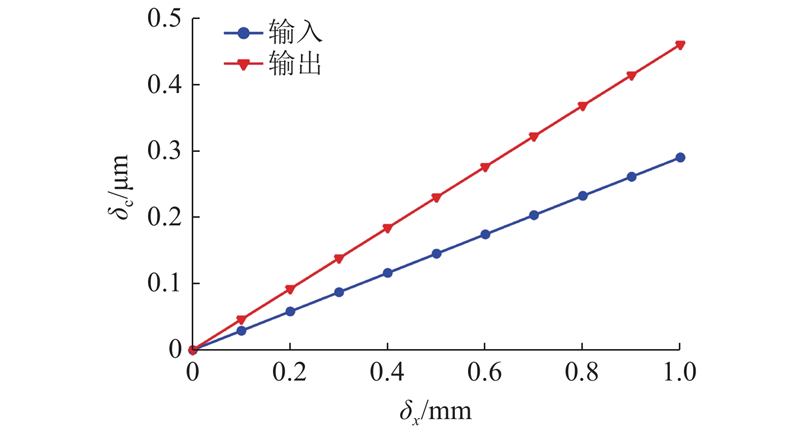
微定位夹持系统通过微定位平台实现微夹持器的精密定位,而解耦性能是影响平台精密定位能力的关键. 为了验证平台的解耦性能,分别对平台的输入输出耦合位移δc进行仿真.
图 16
图 16 微定位平台输入输出耦合仿真
Fig.16 Simulation of input and output coupling displacement for micro-positioning platform
结合仿真结果可知,在1 mm驱动位移内,微定位平台的丢失运动δlost仅占驱动位移δx的0.41%,且其输入输出完全解耦,表明微定位平台具备实现微定位夹持系统中微夹持器精密定位的能力.
4.1.3. 微夹持器静态特性验证
图 17
图 17 微夹持器的静态性能有限元仿真
Fig.17 Finite element simulation of static performance for micro-gripper
图 18
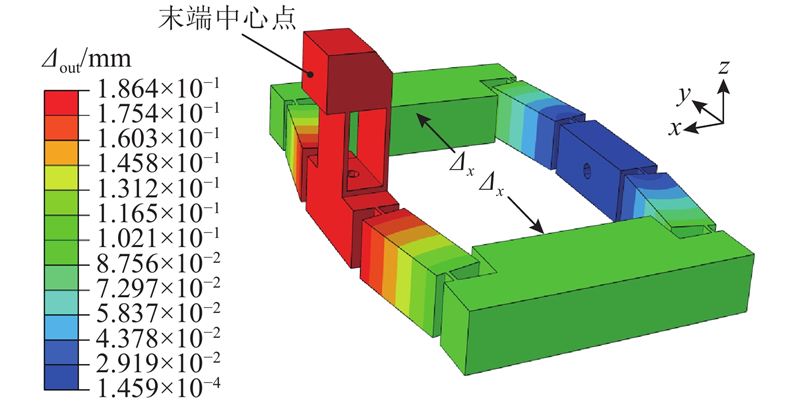
由图17所示仿真结果可知微夹持器中最大应力σg仿真值为93.4 MPa,基于式(29)可知对应最大应力σg理论值为89.2 MPa,理论值与仿真值的相对误差为4.7%,且理论值与仿真值均远小于材料许用应力,表明柔性铰链无应力失效风险.
4.2. 动态特性验证
4.2.1. 微夹持器固有频率验证
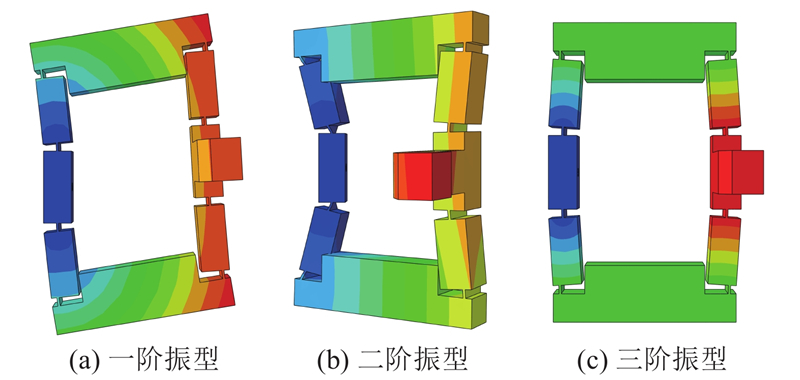
对微夹持器进行有限元模态分析,得到微夹持器的前3阶模态振型如图19所示,其中三阶振型为微夹持器位移输出方向的工作振型. 基于式(33)可知微夹持器工作频率的理论值、仿真值分别为346.27、360.42 Hz,理论值与仿真值的相对误差为4.1%.
图 19
4.2.2. 微定位平台固有频率验证
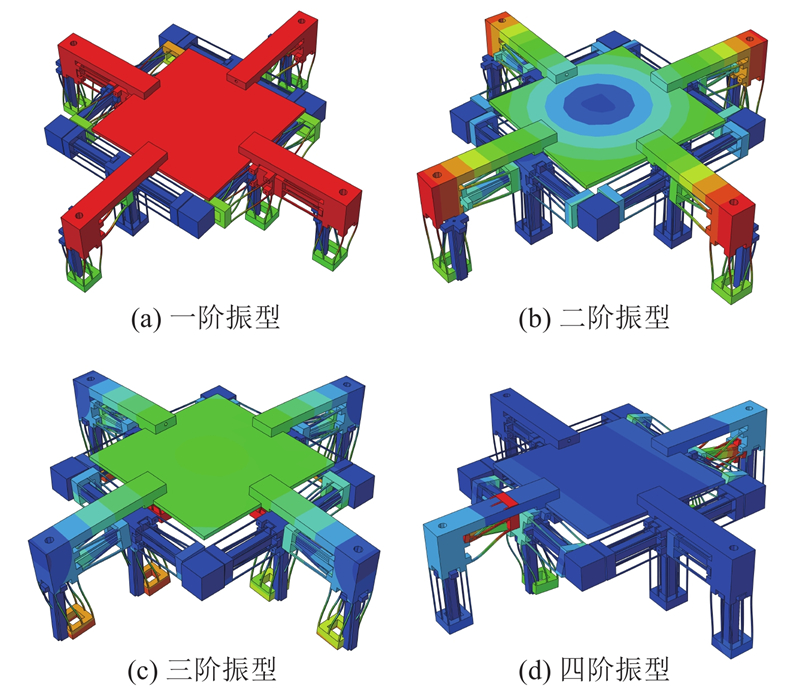
对微定位平台进行有限元模态分析,得到微定位平台的前4阶模态振型如图20所示,其中一阶振型为平台沿自由度方向的输出振型.
图 20
图 20 微定位平台的前4阶模态振型
Fig.20 First four modal shapes of micro-positioning platform
由仿真结果可知,微定位平台前4阶固有频率的仿真值分别为53.32、65.49、206.51、258.35 Hz. 基于式(35)可知微定位平台一阶固有频率理论值为51.16 Hz,理论值与仿真值的相对误差为4.2%,表明理论模型完全正确.
基于模态分析结果:1)微定位平台、微夹持器固有频率理论值与仿真值的相对误差均小于5%,理论模型完全正确;2)微定位平台与微夹持器动态特性间的相互影响还未深入研究,其在后续工作中还有待进一步完善.
5. 微夹持器可达定位空间分析
微夹持器可达定位空间是微定位夹持系统的重要性能指标. 微夹持器的可达定位空间,可通过分析微定位平台丢失运动δlost、微夹持器位移放大倍率Ramp得到.
以微夹持器柔性末端为研究对象,基于式(10)和(24),当微定位平台沿x、y轴方向驱动位移为δx、微夹持器驱动位移为Δx时,其在x-y平面上的可达定位空间为
图 21
6. 结 论
(1)提出新型大行程两自由度柔性微定位平台,并将其与微夹持器相结合,设计大行程两自由度柔性微定位夹持系统.
(2)建立微定位夹持系统静、动态特性的理论模型,并建立全局优化模型确定微定位夹持系统的最优参数,实现微定位夹持系统的参数优化.
(3)通过有限元仿真验证微定位夹持系统理论模型的正确性与优化模型的可行性,结果表明,微定位夹持系统中微夹持器在x、y轴方向分别具有[−1182.3,1182.3]、[−995.9,995.9] μm的可达定位空间.
(4)本文未对微定位夹持系统的样机制作与实验测试进行研究,其在后续工作中还有待进一步完善.
参考文献
微/纳传动平台的位移耦合分析
[J].DOI:10.3785/j.issn.1008-973X.2013.04.024 [本文引用: 1]
Displacement coupling analysis of micro/nano transmission platform
[J].DOI:10.3785/j.issn.1008-973X.2013.04.024 [本文引用: 1]
面向光学精密装配的微操作机器人
[J].DOI:10.3901/JME.2009.02.280 [本文引用: 1]
Micro operation robot for optical precise assembly
[J].DOI:10.3901/JME.2009.02.280 [本文引用: 1]
Modular soft robotic microdevices for dexterous biomanipulation
[J].DOI:10.1039/C8LC01200H [本文引用: 1]
具有高位移增幅特性的柔顺并联式x-y-θ微动平台
[J].
A parallel compliant x-y-θ micro-stage with the characteristic of high displacement magnification
[J].
Monolithically integrated two-axis microgripper for polarization maintaining in optical fiber assembly
[J].DOI:10.1063/1.4907551 [本文引用: 3]
柔性机构及其应用研究进展
[J].DOI:10.3901/JME.2015.13.053 [本文引用: 1]
State-of-art of compliant mechanisms and their applications
[J].DOI:10.3901/JME.2015.13.053 [本文引用: 1]
压电驱动微夹持器特性分析
[J].
Characteristic analysis of the microgripper driven by piezoelectric actuators
[J].
Design and static testing of a compact distributed-compliance gripper based on flexure motion
[J].DOI:10.1016/j.acme.2016.04.011 [本文引用: 1]
Design, closed-form modeling and analysis of SU-8 based electrothermal microgripper for biomedical applications
[J].DOI:10.1007/s00542-018-4059-z [本文引用: 1]
Design and analysis of a decoupled XY MEMS microgripper with integrated dual-axis actuation and force sensing
[J].DOI:10.1016/j.ifacol.2017.08.144 [本文引用: 1]
Performance of a two-way shape memory microgripper actuator
[J].DOI:10.1061/(ASCE)AS.1943-5525.0000857 [本文引用: 1]
Design of a monolithic double-slider based compliant gripper with large displacement and anti-buckling ability
[J].
Design of large-displacement asymmetric piezoelectric microgripper based on flexible mechanisms
[J].DOI:10.1016/j.npe.2019.11.001 [本文引用: 1]
压电精密驱动柔性微夹钳设计
[J].
Design of flexure micro-gripper precision-driven by piezoceramics
[J].
高带宽两自由度并联柔顺精密定位平台的优化设计与实验
[J].DOI:10.3788/OPE.20192708.1774 [本文引用: 3]
Optimal design and experiment of a high-bandwidth two-degree-of-freedom parallel nanopositioning stage
[J].DOI:10.3788/OPE.20192708.1774 [本文引用: 3]
Design of a large range XY nanopositioning system
[J].DOI:10.1115/1.4023874 [本文引用: 3]
音圈电机驱动的柔性定位平台设计与控制
[J].
Design and control of a flexible positioning stage driven by voice coil motors
[J].
Synthesis of multi-degree of freedom, parallel flexure system concepts via freedom and constraint topology (FACT) part I: principles
[J].DOI:10.1016/j.precisioneng.2009.06.008 [本文引用: 1]
Synthesis of multi-degree of freedom, parallel flexure system concepts via freedom and constraint topology (FACT) part II: practice
[J].DOI:10.1016/j.precisioneng.2009.06.007 [本文引用: 1]
3-PPP型柔性并联微定位平台的设计与分析
[J].
Design and analysis of a 3-PPP compliant parallel micro-positioning stage
[J].
基于应力刚化效应的动态特性可调微动平台设计新方法
[J].DOI:10.3901/JME.2015.23.153 [本文引用: 3]
A new design method of dynamic characteristics adjustable micro motion stage based on tension stiffening
[J].DOI:10.3901/JME.2015.23.153 [本文引用: 3]
Screw theory based methodology for the deterministic type synthesis of flexure mechanisms
[J].
Design, analysis and simulation of a novel 3-DOF translational micromanipulator based on the PRB model
[J].
On a simplified nonlinear analytical model for the characterisation and design optimisation of a compliant XY micro-motion stage
[J].DOI:10.1016/j.rcim.2017.05.012 [本文引用: 1]
Development of a piezoelectric actuator using a three-dimensional bridge-type hinge mechanism
[J].DOI:10.1063/1.1569411 [本文引用: 1]
Analytical modeling, optimization and testing of a compound bridge-type compliant displacement amplifier
[J].
Design and control of a multi-DOF micromanipulator dedicated to multiscale micromanipulation
[J].DOI:10.1088/1361-665X/aa8f73 [本文引用: 1]