<img src="https://www.zjujournals.com/gcsjxb/images/1006-754X/images/logo.png" class="img-responsive">

图1 大型深海AUV的总体布局

Fig.1 Overall layout of large deep-sea AUV

1.2　动力学模型

本文采用拉格朗日方程建立大型深海AUV的动力学模型，具体步骤如下^［8］：首先，在惯性坐标系下描述AUV的受力情况；然后，计算AUV的动能并对速度求导，获得其动量，并对动量关于时间求导，获取运动坐标系下AUV所受的合外力；最后，通过坐标变换将速度坐标系下AUV所受的水动力和水动力矩转换为运动坐标系下的。

1.2.1　坐标系构建

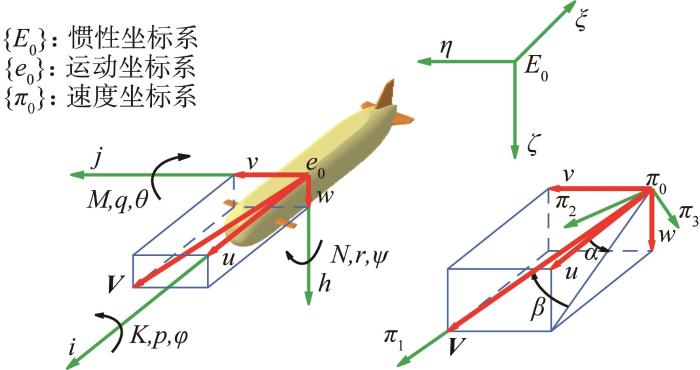
为便于分析大型深海AUV的运动和受力情况，建立相应的惯性坐标系、运动坐标系和速度坐标系，如图2所示，各坐标轴均按右手定则确定。其中，惯性坐标系原点E₀位于空间内某一点，η轴、ξ轴分别指向正北和正东，ζ轴指向地心为正向。运动坐标系以AUV的浮心为原点，i轴平行于艇体基线，指向艏部为正向；j轴平行于基线面，指向右舷为正向；h轴指向艇体底部为正向。速度坐标系也以AUV的浮心为原点，其各轴方向与AUV的攻角α和漂角β有关，由运动坐标系绕j轴旋转-α，再绕h轴旋转β后获得，其中π₁轴方向与AUV的速度方向一致。

图2

图2 大型深海AUV坐标系构建

Fig.2 Construction of coordinate system of large deep-sea AUV

令大型深海AUV的浮心在惯性坐标系中的空间位置向量 b = $[x y z]$ ^T，姿态角矩阵 Θ = $[φ θ ψ]$ ^T。在运动坐标系下，该AUV浮心处的速度为 V，角速度为 Ω，其沿3个坐标轴方向的分量分别为u、v、w和p、q、r；其所受外力 F 和力矩 M 沿3个坐标轴方向的分量分别为X、Y、Z和K、M、N。规定速度和力的方向与运动坐标系坐标轴方向一致，角速度和力矩的方向按右手定则判定。

大型深海AUV的速度和角速度在惯性坐标系与运动坐标系之间的变换关系为^［10］：

\{\begin{array}{l} \dot{b} = J_{1} V \\ \dot{Θ} = J_{2} Ω \end{array}

（1）

式中： J₁、 J₂分别为对应速度、角速度的变换矩阵。

令s=sin，c=cos，则变换矩阵 J₁和 J₂可表示为：

J_{1} = [\begin{matrix} c θ c ψ & s φ s θ c ψ - c φ s ψ & c φ s θ c ψ + s φ s ψ \\ c θ s ψ & c φ c ψ + s φ s θ s ψ & - s φ c ψ + c φ s θ s ψ \\ - s θ & s φ c θ & c φ c θ \end{matrix}]

（2）

J_{2} = [\begin{matrix} 1 & s φ t a n θ & c φ t a n θ \\ 0 & c φ & - s φ \\ 0 & s φ s e c θ & c φ s e c θ \end{matrix}]

（3）

由于惯性坐标系和运动坐标系均为正交坐标系，其之间的变换矩阵也为正交矩阵，故有：

{J_{1}}^{- 1} = {J_{2}}^{T}

（4）

1.2.2　受力分析

定义在惯性坐标系下大型深海AUV的动量为 p，动量矩为 π，令 τ =［ p π ］。根据质心运动定理和动量矩定理，惯性坐标系下大型深海AUV所受的力和力矩为：

\{\begin{array}{l} \dot{p} = (m_{1} + m_{2} - m_{0}) g h + \sum_{a = 1}^{m} f_{e x t a} \\ \dot{π} = \sum_{a = 1}^{m} r_{a} \times f_{e x t a} + r_{1} \times m_{1} g h + r_{2} \times m_{2} g h + \sum_{c = 1}^{n} τ_{e x t c} \end{array}

（5）

式中：m₁、m₂、m₀分别为大型深海AUV的固定质量、压载质量和排水质量；g为重力加速度； h 为运动坐标系h轴的单位方向向量； r₁、 r₂分别为固定质量块和压载质量块质心相对于运动坐标系原点e₀的矢径； f_ext_a 、 τ_ext_c 分别为大型深海AUV在惯性坐标系下所受的外力和外力矩； r_a 为惯性坐标系下 f_ext_a 的作用点相对于e₀的矢径。

为便于表示动能，令大型深海AUV在运动坐标系下的动量和动量矩矢量 η = $[P Π]$ ，通过变换矩阵 J₁将运动坐标系下的动量和动量矩矢量 η 转换为惯性坐标系下的 τ ：

\{\begin{array}{l} p = J_{1} P \\ π = J_{1} Π + b \times p \end{array}

（6）

对式（6）关于时间t求导，可得：

\{\begin{array}{l} \dot{p} = J_{1} (\dot{P} + Ω \times P) \\ \dot{π} = J_{1} (\dot{Π} + Ω \times Π + V \times P) + b \times \dot{p} \end{array}

（7）

联立式（5）和式（7），推导得到运动坐标系下大型深海AUV所受的力与力矩分别为：

\{\begin{array}{l} \dot{P} = P \times Ω + J_{1}^{T} (m_{1} + m_{2} - m_{0}) g h + J_{1}^{T} \sum_{a = 1}^{m} f_{e x t a} \\ \dot{Π} = Π \times Ω + P \times V + (m_{1} r_{1} + m_{2} r_{2}) \times J_{1}^{T} g h + \\ J_{1}^{T} [\sum_{a = 1}^{m} (r_{a} - b) \times f_{e x t a}] + J_{1}^{T} \sum_{c = 1}^{n} τ_{e x t c} \end{array}

（8）

由此可知，运动坐标系下大型深海AUV受到的广义力包含静力、水动力以及广义动量与广义速度的耦合项。整理后，式（8）可表示为：

\{\begin{array}{l} F = P \times Ω + J_{1}^{T} (m_{1} + m_{2} - m_{0}) g h + F_{e x t} \\ M = Π \times Ω + P \times V + (m_{1} r_{1} + m_{2} r_{2}) \times J_{1}^{T} g h + M_{e x t} \end{array}

（9）

其中：

\{\begin{array}{l} F_{e x t} = J_{1}^{T} \sum_{a = 1}^{m} f_{e x t a} \\ M_{e x t} = J_{1}^{T} [\sum_{a = 1}^{m} (r_{a} - b) \times f_{e x t a}] + J_{1}^{T} \sum_{c = 1}^{n} τ_{e x t c} \end{array}

1.2.3 动能求解

大型深海AUV的动能项主要涉及固定质量、压载质量和附加质量，下文将分别求解各质量块的动能。

为方便表述，根据向量叉乘特性，定义若向量 x = ${[x_{1} x_{2} x_{3}]}^{T}$ ，则其对应的叉乘矩阵 $\hat{x}$ 为：

\hat{x} = [\begin{matrix} 0 & - x_{3} & x_{2} \\ x_{3} & 0 & - x_{1} \\ - x_{2} & x_{1} & 0 \end{matrix}]

（10）

对于向量 x = ${[x_{1} x_{2} x_{3}]}^{T}$ 和 y = ${[y_{1} y_{2} y_{3}]}^{T}$ ，其叉乘具有如下性质：

x \times y = \hat{x} y

（11）

由于大型深海AUV的浮心与各质量块的质心不重合，则其浮心处的速度与各质量块质心处的速度并不相等。令 U =［ VΩ ］^T，则运动坐标系下固定质量块的质心相对于AUV浮心的速度 V₁和角速度 Ω₁可表示为：

\{\begin{array}{l} V_{1} = V + Ω \times r_{1} = V - r_{1} \times Ω = (E - {\hat{r}}_{1}) U \\ Ω_{1} = Ω \end{array}

（12）

式中： E 为单位矩阵。

则固定质量块的动能 $T_{1}$ 可表示为：

T_{1} = \frac{1}{2} m_{1} V_{1}^{2} + \frac{1}{2} I_{1} Ω_{1}^{2} = \frac{1}{2} U^{T} Γ_{1} U

（13）

其中：

Γ_{1} = [\begin{matrix} m_{1} E & - m_{1} {\hat{r}}_{1} \\ m_{1} {\hat{r}}_{1} & I_{1} - m_{1} {\hat{r}}_{1} {\hat{r}}_{1} \end{matrix}]

式中： I₁为固定质量块的转动惯量。

同理，压载质量块的动能 $T_{2}$ 可表示为：

T_{2} = \frac{1}{2} m_{2} V_{2}^{2} + \frac{1}{2} I_{2} Ω_{2}^{2} = \frac{1}{2} U^{T} Γ_{2} U

（14）

其中：

Γ_{2} = [\begin{matrix} m_{2} E & - m_{2} {\hat{r}}_{2} \\ m_{2} {\hat{r}}_{2} & I_{2} - m_{2} {\hat{r}}_{2} {\hat{r}}_{2} \end{matrix}]

式中： I₂为压载质量块的转动惯量。

另外，大型深海AUV在运动过程中会引起周围的水流加速，导致水流阻尼力增大。假设该AUV上下、左右对称，可得附加质量块的动能 $T_{3}$ 为：

T_{3} = \frac{1}{2} U^{T} Γ_{3} U

（15）

其中：

Γ_{3} = [\begin{matrix} m_{3} & C_{3} \\ C_{3}^{T} & I_{3} \end{matrix}] = [\begin{matrix} - X_{\dot{u}} & 0 & 0 & 0 & 0 & 0 \\ 0 & - Y_{\dot{v}} & 0 & 0 & 0 & - Y_{\dot{r}} \\ 0 & 0 & - Z_{\dot{w}} & 0 & - Z_{\dot{q}} & 0 \\ 0 & 0 & 0 & - K_{\dot{p}} & 0 & 0 \\ 0 & 0 & - M_{\dot{w}} & 0 & - M_{\dot{q}} & 0 \\ 0 & - N_{\dot{v}} & 0 & 0 & 0 & - N_{\dot{r}} \end{matrix}]

式中： m₃为附加质量矩阵； C₃为附加质量静矩； I₃为附加转动惯量； $X_{\dot{u}}$ 、 $Y_{\dot{v}}$ 、 $Z_{\dot{w}}$ 等为水动力系数。

联立式（13）至式（15），得到大型深海AUV的总动能T：

T = \frac{1}{2} U^{T} Γ_{1} U + \frac{1}{2} U^{T} Γ_{2} U + \frac{1}{2} U^{T} Γ_{3} U = \frac{1}{2} U^{T} Γ U

（16）

其中：

Γ = [\begin{matrix} (m_{1} + m_{2}) E + m_{3} & - m_{1} {\hat{r}}_{1} - m_{2} {\hat{r}}_{2} + C_{3} \\ m_{1} {\hat{r}}_{1} + m_{2} {\hat{r}}_{2} + C_{3}^{T} & I_{1} + I_{2} + I_{3} - m_{1} {\hat{r}}_{1} {\hat{r}}_{1} - m_{2} {\hat{r}}_{2} {\hat{r}}_{2} \end{matrix}]

1.2.4 动力学方程构建

对大型深海AUV总动能T关于速度 U 求导，可得到其动量和动量矩矢量 η，然后对 η 关于时间t求导，得到运动坐标系下其所受的合外力和合外力矩。在AUV运动过程中，其各质量块不发生变化，则可得其动力学模型为：

\dot{U} = Γ^{- 1} ([\begin{matrix} P \times Ω \\ Π \times Ω + P \times V \end{matrix}] + [\begin{matrix} J_{1}^{T} (m_{1} + m_{2} - m_{0}) g h \\ (m_{1} r_{1} + m_{2} r_{2}) \times J_{1}^{T} g h \end{matrix}] + [\begin{matrix} F_{e x t} \\ M_{e x t} \end{matrix}])

（17）

参考文献［11］，速度坐标系下大型深海AUV在运动过程中所受的黏性水动力 F_v和黏性水动力矩 M_v可表示为：

F_{v} = [\begin{matrix} - D \\ S \\ - L \end{matrix}] = [\begin{matrix} (K_{D 0} + K_{D} α^{2}) V^{2} \\ K_{β} β V^{2} \\ (K_{L 0} + K_{L} α) V^{2} \end{matrix}]

（18）

M_{v} = [\begin{matrix} M_{1} \\ M_{2} \\ M_{3} \end{matrix}] = [\begin{matrix} (K_{M Y} β + K_{p} p) V^{2} \\ (K_{M 0} + K_{M} α + K_{q} q) V^{2} \\ (K_{M Z} β + K_{r} r) V^{2} \end{matrix}]

（19）

式中：D为阻力；S为侧力；L为升力；M₁、M₂、M₃为黏性水动力矩分量；V为速度 V 对应的数值；K_D₀、K_D 、K_β 等均为黏性水动力系数。

将速度坐标系下大型深海AUV所受的黏性水动力 F_v和黏性水动力矩 M_v变换到运动坐标系下，则有：

\{\begin{array}{l} F_{h d} = R_{π e} F_{v} + F_{r} \\ M_{h d} = R_{π e} M_{v} + M_{r} \end{array}

（20）

其中：

R_{π e} = [\begin{matrix} c α c β & - c α s β & - s α \\ s β & c β & 0 \\ s α c β & - s α s β & c α \end{matrix}]

F_{r} = [\begin{matrix} X_{δ_{b} δ_{b}} u^{2} δ_{b}^{2} + X_{δ_{s} δ_{s}} u^{2} δ_{s}^{2} + X_{δ_{r} δ_{r}} u^{2} δ_{r}^{2} \\ Y_{δ_{r}} u^{2} δ_{r} \\ Z_{δ_{b}} u^{2} δ_{b} + Z_{δ_{s}} u^{2} δ_{s} \end{matrix}]

M_{r} = [\begin{matrix} 0 \\ M_{δ_{b}} u^{2} δ_{b} + M_{δ_{s}} u^{2} δ_{s} \\ N_{δ_{r}} u^{2} δ_{r} \end{matrix}]

式中： R_πe 为速度坐标系与运动坐标系之间的变换矩阵； F_r、 M_r分别为运动坐标系下鳍舵产生的力和力矩；δ_b、δ_s、δ_r分别为艏升降舵角、艉升降舵角和艉方向舵角； $X_{δ_{b} δ_{b}} 、$ $Y_{δ_{r}}$ 、 $Z_{δ_{b}}$ 等为水动力系数。

联立上文各式，可得运动坐标系下大型深海AUV所受的力与力矩在各方向上的分量，分别为：

\{\begin{array}{l} X = \sum_{σ = 1}^{2} \{m_{σ} [v r - w q + x_{σ} (q^{2} + r^{2}) - y_{σ} p q - z_{σ} p r]\} - \\ K_{β} β V^{2} c o s α s i n β + (K_{D 0} + K_{D} α) V^{2} c o s α c o s β - \\ (K_{L 0} + K_{L} α) V^{2} s i n α + {X_{δ_{s}}}_{δ_{s}} u^{2} δ_{s}^{2} + {X_{δ_{r}}}_{δ_{r}} u^{2} δ_{r}^{2} + \\ {X_{δ_{b}}}_{δ_{b}} u^{2} δ_{b}^{2} - (G - F_{B}) s i n θ \\ Y = \sum_{σ = 1}^{2} \{m_{σ} [w p - u r - x_{σ} p q + y_{σ} (p^{2} + r^{2}) - z_{σ} q r]\} + \\ (K_{D 0} + K_{D} α) V^{2} s i n β + K_{β} β V^{2} c o s β + Y_{δ_{r}} u^{2} δ_{r} + \\ (G - F_{B}) c o s θ s i n φ \\ Z = \sum_{σ = 1}^{2} \{m_{σ} [u q - v p - x_{σ} p r - y_{σ} q r + z_{σ} (p^{2} + q^{2})]\} + \\ (K_{L 0} + K_{L} α) V^{2} s i n α c o s β + (K_{L 0} + K_{L} α) V^{2} c o s α - \\ K_{β} β V^{2} s i n α s i n β + Z_{δ_{s}} u^{2} δ_{s} + (G - F_{B}) c o s θ c o s φ + \\ Z_{δ_{b}} u^{2} δ_{b} \\ K = \sum_{σ = 1}^{2} [(I_{y y σ} - I_{z z σ}) q r + m_{σ} y_{σ} (u q - v p) + m_{σ} z_{σ} (u r - w p)] + \\ (K_{M Y} β + K_{p} p) V^{2} c o s α c o s β - (K_{M Z} β + K_{r} r) V^{2} s i n α - \\ (K_{M 0} + K_{M} α + K_{q} q) V^{2} c o s α s i n β + \\ \sum_{σ = 1}^{2} G_{σ} (y_{σ} c o s θ c o s φ - z_{σ} c o s θ s i n φ) \\ M = \sum_{σ = 1}^{2} [(I_{z z σ} - I_{x x σ}) p r + m_{σ} x_{σ} (v p - u q) + m_{σ} z_{σ} (v r - w q)] + \\ (K_{M Y} β + K_{p} p) V^{2} s i n β + (K_{M 0} + K_{M} α + K_{q} q) V^{2} c o s β + \\ M_{δ_{b}} u^{2} δ_{b} + M_{δ_{s}} u^{2} δ_{s} - \sum_{σ = 1}^{2} P_{σ} (x_{σ} c o s θ c o s φ + z_{σ} s i n θ) \\ N = \sum_{σ = 1}^{2} [(I_{x x σ} - I_{y y σ}) p q + m_{σ} x_{σ} (w p - u r) + m_{σ} y_{σ} (w q - v r)] + \\ (K_{M Y} β + K_{p} p) V^{2} s i n α c o s β + (K_{M Z} β + K_{r} r) V^{2} c o s α - \\ (K_{M 0} + K_{M} α + K_{q} q) V s i n α s i n β + \\ \sum_{σ = 1}^{2} G_{σ} (x_{σ} c o s θ s i n φ + z_{σ} s i n θ) + N_{δ_{r}} u^{2} δ_{r} \end{array}

（21）

式中：G、F_B为大型深海AUV的重力和浮力；G₁、G₂为固定质量块、压载质量块的重力；x₁、y₁、z₁和x₂、y₂、z₂分别为固定质量块和压载质量块在惯性坐标系下的位置分量。

最后，确定相应的水动力系数后，即可得到完整的大型深海AUV动力学模型。

2 大型深海AUV的水动力系数计算

2.1　数值模拟计算方法

采用CFD软件计算大型深海AUV动力学模型中的水动力系数。为减少计算量，采用雷诺时均纳维‒斯托克斯（Navier-Stokes, N-S）方程作为控制方程^［12］。假设流体为不可压缩的连续介质，且不考虑热交换，则雷诺时均化后流体的平均质量和动量传输方程可表示为：

\frac{\partial ρ}{\partial t} + \nabla \cdot (ρ \bar{v}) = 0

（22）

\frac{\partial}{\partial t} (ρ \bar{v}) + \nabla \cdot (ρ \bar{v} \otimes \bar{v}) = - \nabla \cdot (\bar{p} Ε) + \nabla \cdot O + f_{b}

（23）

式中：ρ为流体密度； $\bar{v}$ 和 $\bar{p}$ 分别为流体的平均速度和平均压力； O 为黏性应力张量； f_b 为体积力的合力。

大型深海AUV的流体计算域及边界条件如图3所示。其中：计算域为92 m×40 m×40 m的长方体，右侧为压力出口边界，出口压力设定为0 Pa；其他侧面均为速度入口边界，入口速度设定为1.028 8 m·s^-1；AUV表面边界为壁面条件，艇体和鳍舵周围为局部加密区域。

图3

图3 大型深海AUV的流体计算域及边界条件

Fig.3 Fluid computational domain and boundary conditions of large deep-sea AUV

采用切割体网格生成器生成的六面体网格对大型深海AUV的流体计算域进行网格划分，并在壁面及其周围流场采取网格加密处理，边界层处加入8层棱柱网格以有效模拟近壁面处的流体流动。为了选取合适的网格基本尺寸，以尽可能少的网格数量获得较高的计算精度，使用7种不同的网格基本尺寸计算来流流速为1.028 8 m·s^-1工况下大型深海AUV直航运动时的阻力系数，其中湍流模型选择SST k-ω模型，求解器选择隐式不定常求解器，固定时间步长为0.05 s，计算结果如表1所示。表中：C_D 为阻力系数；∆C_D 为阻力系数的相对误差。

表1 大型深海AUV数值模拟的网格无关性验证结果

Table 1 Grid irrelevance verification results of numerical simulation of large deep-sea AUV

基本尺寸/m	网格数量/万个	C_D	∆C_D /%
0.88	152.0	0.117 33	-1.244
0.72	233.8	0.115 69	-1.418
0.68	271.7	0.114 82	-0.679
0.64	310.5	0.114 15	-0.587
0.60	358.0	0.112 91	-1.098
0.56	419.2	0.112 70	-0.186
0.52	508.2	0.113 09	0.345

从表1中可以看出，当网格基本尺寸小于0.72 m时，大型深海AUV直航运动时的阻力系数计算值的变化幅度较小。考虑到计算资源，最终选用网格基本尺寸为0.60 m进行数值模拟计算。

2.2　直航试验数值模拟

数值模拟时通过调整来流流速来改变大型深海AUV的运动速度。设置来流流速为0.257 2~2.057 6 m·s^-1，不同流速间隔为0.257 2 m·s^-1。采用CFD软件对8种来流流速工况下大型深海AUV的直航试验进行数值模拟，得到的阻力如表2所示。

表2 不同直航试验工况下大型深海AUV阻力的数值模拟结果

Table 2 Numerical simulation results of large deep-sea AUV resistance under different direct route test conditions

来流流速/m·s^-1	阻力D/N	来流流速/m·s^-1	阻力D/N
0.257 2	18.11	1.286 0	310.10
0.514 4	59.58	1.543 2	433.65
0.771 6	123.03	1.800 4	576.55
1.028 8	206.21	2.057 6	739.32

对表2中的直航阻力计算结果进行二次函数拟合，得到大型深海AUV直航运动时的阻力公式为：

D = 194.004 3 V^{2}

（24）

2.3　斜航试验数值模拟

设置来流流速为1.028 8 m·s^-1并保持不变，将大型深海AUV旋转一定的角度，计算不同斜航试验工况（攻角α，漂角β和舵角δ_b、δ_s、δ_r不同，如表3所示）下AUV所受的水动力，并通过最小二乘线性回归法拟合得到相应的水动力系数^［13］。

表3 大型深海AUV的斜航试验数值模拟工况设计

Table 3 Numerical simulation working condition design for oblique towing test of large deep-sea AUV

工况	参数
水平面	1）漂角变化：α=0°；β=0°，±2°，±4°，±6°，±8°，±10°，±12°，±14°和±16°；δ_b=δ_s=δ_r=0°
水平面	2）艉方向舵角变化：α=0°；β=0°；δ_b=δ_s=0°，δ_r=0°，±5°，±10°，±15°，±20°，±25°和±30°
垂直面	1）攻角变化：α=0°，±2°，±4°，±6°，±8°，±10°，±12°，±14°和±16°；β=0°；δ_b=δ_s=δ_r=0°
	2）艏升降舵角变化：α=0°；β=0°；δ_b=0°，±5°，±10°，±15°，±20°，±25°和±30°，δ_s=δ_r=0°
	3）艉升降舵角变化：α=0°；β=0°；δ_b=0°，δ_s=0°，±5°，±10°，±15°，±20°，±25°和±30°，δ_r=0°

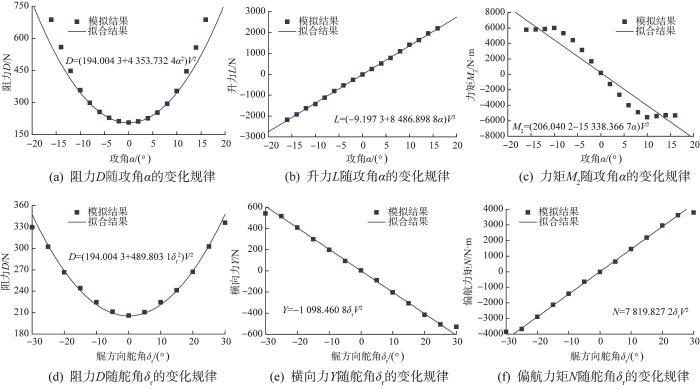
根据CFD模拟结果，得到大型深海AUV在斜航运动过程中所受力与力矩的变化规律及其拟合结果，如图4所示（部分结果）。

图4

图4 大型深海AUV斜航试验数值模拟结果（部分）

Fig.4 Numerical simulation results of oblique towing test of large deep-sea AUV (part)

2.4　悬臂水池试验数值模拟

悬臂水池试验数值模拟是指在相对静止的条件下以“静态”网格计算水动力，以避免大量的流域重建、网格划分等重复性工作。在该模拟过程中，须将惯性坐标系变换至运动坐标系。设大型深海AUV的切向运动速度为1.028 8 m·s^-1，使其绕不同半径作回转运动，利用CFD软件计算不同悬臂水池试验工况（攻角、漂角和角速度不同，如表4所示，表中R为回转半径，l_t为AUV艇体长度）下AUV所受的水动力，并通过最小二乘线性回归法拟合得到相应的水动力系数。

表4 大型深海AUV的悬臂水池试验数值模拟工况设计

Table 4 Numerical simulation working condition design of cantilever pool test of large deep-sea AUV

工况	参数
水平面	α=0°；β=-3°，0°，3°，6°，9°和12°；δ_b=δ_s=δ_r=0°；R=2.5l_t，5l_t，10l_t，15l_t，20l_t，30l_t，50l_t和-50l_t
垂直面	α=0°，±3°，±6°，±9°和±12°；β=0°；δ_b=δ_s=δ_r=0°；R=2.5l_t，5l_t，10l_t，15l_t，20l_t，30l_t，50l_t和-50l_t
空间	α=0°；β=0°，±2°，±4°，±6°，±8°，±10°，±12°，±14°和±16°；δ_b=δ_s=δ_r=0°；p=0 rad·s^-1；R=20l_t，30l_t，40l_t，50l_t，+∞和-50l_t

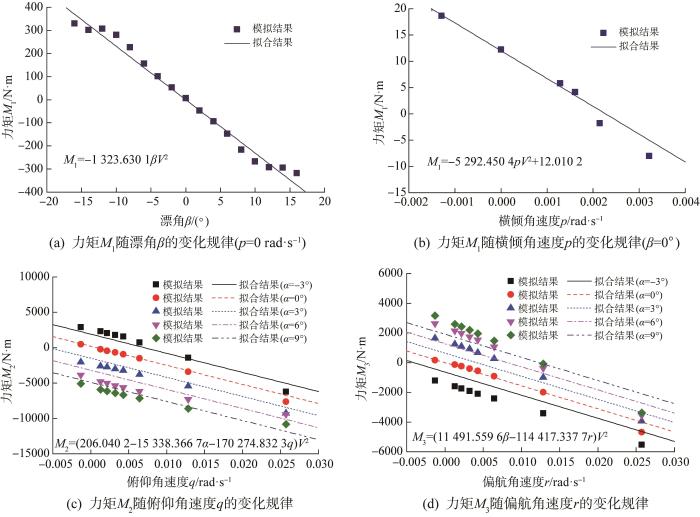
根据CFD模拟结果，得到大型深海AUV在悬臂回转运动过程中所受力与力矩的变化规律及其拟合结果，如图5所示（部分结果）。

图5

图5 大型深海AUV悬臂水池试验数值模拟结果（部分）

Fig.5 Numerical simulation results of cantilever pool test of large deep-sea AUV (part)

2.5　平面运动机构试验数值模拟

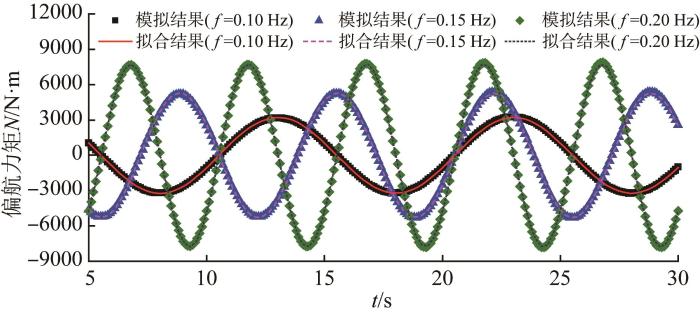
平面运动机构试验包含纯横荡运动、纯升沉运动、纯摇艏运动和纯俯仰运动四种运动。以大型深海AUV作纯横荡运动为例，利用CFD软件对其进行平面运动机构试验数值模拟，以求取加速度相关的水动力系数。

大型深海AUV的纯横荡运动参数设置如下：

\{\begin{array}{l} y = A s i n ω t \\ ψ = 0 ° \\ \dot{ψ} = 0 r a d \cdot s^{- 1} \\ v = \dot{y} = A ω c o s ω t \\ \dot{v} = - A ω^{2} s i n ω t \end{array}

（25）

式中：A、ω分别为大型深海AUV作横荡运动的振幅和圆频率。

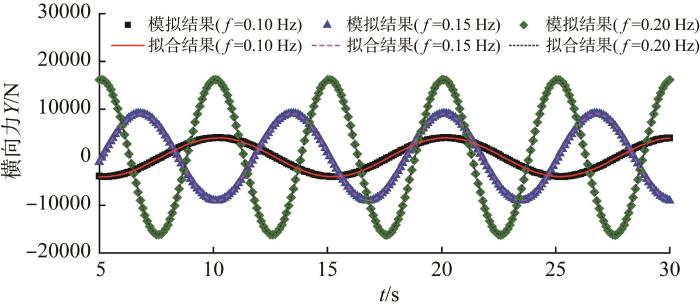
取振荡频率f=0.10，0.15和0.20 Hz，振幅A=0.2 m，大型深海AUV的纵向运动速度恒定为1.028 8 m·s^-1。利用CFD软件进行数值模拟，可得该AUV在纯横荡运动过程中所受的横向力和偏航力矩随时间的变化曲线及拟合结果，分别如图6和图7所示。

图6

图6 纯横荡运动过程中大型深海AUV所受横向力的变化规律

Fig.6 Variation law of lateral force of large deep-sea AUV during pure sway motion

图7

图7 纯横荡运动过程中大型深海AUV所受偏航力矩的变化规律

Fig.7 Variation law of yaw moment of large deep-sea AUV during pure sway motion

根据拟合结果可得，在纯横荡运动过程中，大型深海AUV所受的横向力和偏航力矩满足如下线性关系：

\{\begin{array}{l} Y = Y_{\dot{v}} \dot{v} + Y_{v} v + Y_{0} \\ N = N_{\dot{v}} \dot{v} + N_{v} v + N_{0} \end{array}

(26)

通过最小二乘线性回归法拟合得到不同振荡频率下大型深海AUV作纯横荡运动时的加速度相关水动力系数，如表5所示。

表5 不同振荡频率下大型深海AUV的加速度相关水动力系数拟合结果

Table 5 Fitting results of acceleration dependent hydrodynamic coefficient of large deep-sea AUV under different oscillation frequencies

振荡频率/Hz	$Y_{\dot{v}}$ /kg	$N_{\dot{v}}$ /kg·m
平均值	-5 838.787 5	-28 035.394 1
0.10	-6 695.222 8	-38 568.912 2
0.15	-5 514.450 4	-26 142.592 2
0.20	-5 306.689 4	-19 394.677 8

同理可得与纯升沉运动、纯摇艏运动、纯俯仰运动以及直航变速运动相关的大型深海AUV的加速度相关水动力系数。最终得到的大型深海AUV水动力系数计算结果如表6所示。

表6 大型深海AUV水动力系数计算结果

Table 6 Calculation results of hydrodynamic coefficient of large deep-sea AUV

水动力系数	量值
黏性水动力相关系数	$\begin{array}{l} K_{D_{0}} = - 194.004 3 k g / m \\ K_{D} = - 4 353.732 4 k g / (m \cdot r a d^{2}) \end{array}$
	$K_{β} = - 5 707.978 0 k g / (m \cdot r a d)$
	$\begin{array}{l} K_{L_{0}} = - 9.197 3 k g / m \\ K_{L} = - 8 486.898 8 k g / (m \cdot r a d) \end{array}$
黏性水动力矩相关系数	$\begin{array}{l} K_{M Y} = - 1 323.630 1 k g / r a d \\ K_{p} = - 5 292.450 4 k g \cdot s / r a d \end{array}$
	$\begin{array}{l} K_{M_{0}} = 206.040 2 k g \\ K_{M} = - 15 338.366 7 k g / r a d \\ K_{q} = - 170 274.832 3 k g \cdot s / r a d^{2} \end{array}$
	$\begin{array}{l} K_{M Z} = 11 491.559 6 k g / r a d \\ K_{r} = - 114 417.337 7 k g \cdot s / r a d^{2} \end{array}$
加速度相关系数	$\begin{array}{l} X_{\dot{u}} = - 2 707.241 4 k g \\ Y_{\dot{v}} = - 5 838.787 5 k g \\ Y_{\dot{r}} = 30 017.879 7 k g \cdot m / r a d \\ Z_{\dot{w}} = - 10 159.604 0 k g \\ M_{\dot{w}} = 42 912.398 6 k g \cdot m \\ M_{\dot{q}} = 444 749.939 5 k g \cdot m^{2} / r a d^{2} \\ N_{\dot{v}} = - 28 035.394 1 k g \cdot m \\ N_{\dot{r}} = - 269 033.762 9 k g \cdot m^{2} / r a d \end{array}$
舵角相关系数	$\begin{array}{l} {X_{δ_{b}}}_{δ_{b}} = - 799.853 6 k g / m \\ {X_{δ_{s}}}_{δ_{s}} = - 461.005 4 k g / m \\ {X_{δ_{r}}}_{δ_{r}} = - 489.803 1 k g / m \\ Y_{δ_{r}} = - 1 098.460 8 k g \cdot m / r a d^{2} \\ Z_{δ_{b}} = - 2 373.612 2 k g / (m \cdot r a d) \\ Z_{δ_{s}} = - 1 129.144 6 k g / (m \cdot r a d) \\ M_{δ_{b}} = 15 443.455 8 k g / r a d \\ M_{δ_{s}} = - 8 494.593 7 k g / r a d \\ N_{δ_{r}} = 7 819.812 8 k g / r a d \end{array}$

3 大型深海AUV无动力螺旋下潜运动仿真分析

3.1　运动仿真模型构建

基于所构建的动力学模型，利用MATLAB/Simulink和S函数建立大型深海AUV的六自由度运动仿真模型，如图8所示。该仿真模型共有6个控制参数：净负浮力W、重心纵向位移x_g、稳心高度z_g、艏升降舵角δ_b、艉升降舵角δ_s和艉方向舵角δ_r。采用Runge-Kutta（龙格‒库塔）法求解该AUV无动力螺旋下潜时的状态参数。

图8

图8 大型深海AUV的六自由度运动仿真模型

Fig.8 Six-degree-of-freedom motion simulation model of large deep-sea AUV

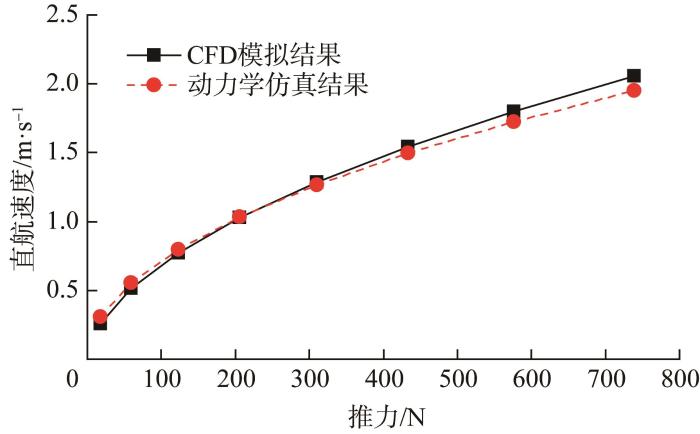
图9所示为给定推力条件下大型深海AUV直航速度的动力学仿真结果与CFD模拟结果对比，由图可知两者基本吻合。

图9

图9 不同推力下大型深海AUV的直航速度对比

Fig.9 Comparison of direct route speed of large deep-sea AUV under different thrusts

3.2　无动力螺旋下潜稳态特征分析

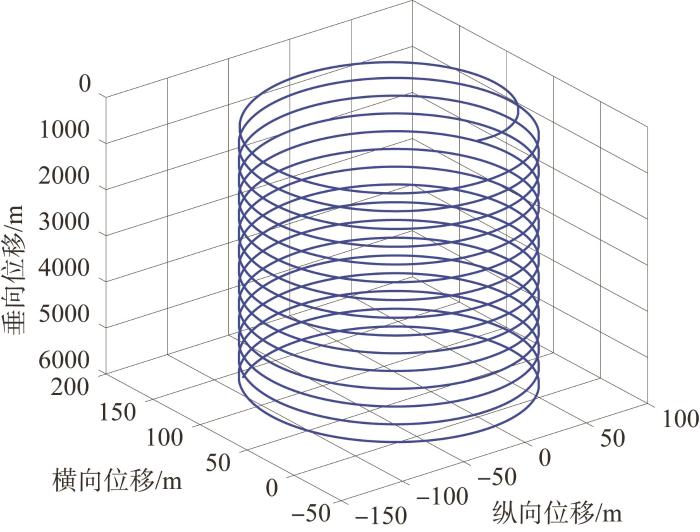
大型深海AUV主要依靠压载提供下潜动力，通过偏转艉方向舵产生横向力和偏航力矩，从而实现螺旋下潜。将该AUV的初始状态参数作置零处理，给定控制参数值：W=1 000 N，x_g=0.112 5 m，z_g=0.20 m，δ_b=0°，δ_s=0°，δ_r=20°，通过仿真得到其无动力螺旋下潜运动轨迹，如图10所示（对于垂向位移，规定下潜方向为正方向），各状态参数随时间的变化规律如图11所示。

图10

图10 大型深海AUV无动力螺旋下潜运动轨迹

Fig.10 Unpowered spiral diving trajectory of large deep-sea AUV

图11

图11 大型深海AUV无动力螺旋下潜状态参数随时间的变化规律

Fig.11 Variation law of state parameters of large deep-sea AUV unpowered spiral diving with time

由仿真结果可得，大型深海AUV在650 s后以恒定的速度和角速度作稳态螺旋下潜运动，各状态参数如下：纵向速度为1.550 6 m·s^-1，横向速度为-0.196 5 m·s^-1，垂向速度为0.069 8 m·s^-1，横倾角速度为0.006 8 rad·s^-1，纵倾角速度为0 rad·s^-1，偏航角速度为0.011 8 rad·s^-1，横倾角为0.437 5°，纵倾角为-29.977 2°，攻角为2.578 7°，漂角为-7.215 5°，螺旋回转直径为194.66 m，螺距为385.24 m，螺旋回转周期为461.95 s，下潜6 000 m深度用时7 273 s，约2.02 h。由此可以看出，当大型深海AUV稳态螺旋下潜时，除艏向角和位置分量外，其余各状态参数均为常数，则对应的水动力和水动力矩也为常数。

通过控制单一变量，可得大型深海AUV无动力螺旋下潜稳态参数与其静力配置参数之间的关系。

1）净负浮力变化。令100 N≤W≤2 500 N，x_g=0.112 5 m，z_g=0.20 m，δ_b=0°，δ_s=0°，δ_r=20°，通过仿真分析得到净负浮力对大型深海AUV无动力螺旋下潜稳态参数的影响，结果如图12所示（V_ζ 为惯性坐标系下AUV下潜速度沿ζ方向的分量，下文同）。由图可以看出，净负浮力作为大型深海AUV螺旋下潜的主要动力来源，决定了AUV的速度和角速度；净负浮力越大，AUV的螺旋回转直径越大，则下潜6 000 m深度的用时越短。

图12

图12 净负浮力对大型深海AUV无动力螺旋下潜稳态参数的影响

Fig.12 Influence of net negative buoyancy on unpowered spiral diving steady-state parameters of large deep-sea AUV

2）重心纵向位移变化。令0.010 0 m≤x_g≤0.200 0 m，W=1 000 N，z_g=0.20 m，δ_b=0°，δ_s=0°，δ_r=20°。通过仿真分析得到重心纵向位移对大型深海AUV无动力螺旋下潜稳态参数的影响，结果如图13所示。由图可以看出，在稳心高度不变的条件下，重心纵向位移主要影响AUV下潜过程的纵倾角；重心纵向位移越大，纵倾角越快，则垂向下潜速度越快，偏航角速度越大，下潜6 000 m深度的用时越短；螺旋回转直径随重心纵向位移的增加呈先增大后减小趋势。

图13

图13 重心纵向位移对大型深海AUV无动力螺旋下潜稳态的影响

Fig.13 Influence of longitudinal displacement of gravity center on unpowered spiral diving steady-state parameters of large deep-sea AUV

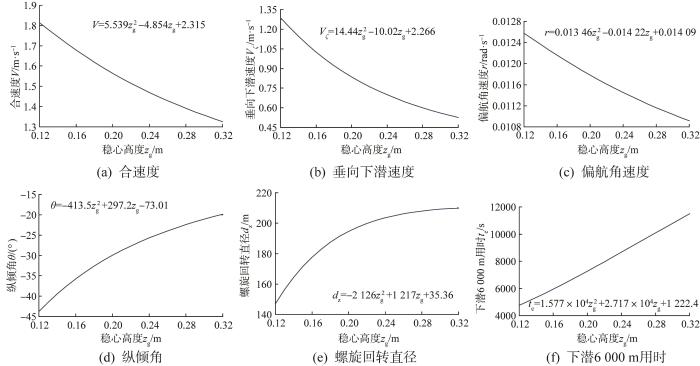
3）稳心高度变化。令0.12 m≤z_g≤0.32 m，W =1 000 N，x_g=0.112 5 m，δ_b=0°，δ_s=0°，δ_r=20°，通过仿真分析得到稳心高度对大型深海AUV无动力螺旋下潜稳态参数的影响，结果如图14所示。由图可以看出，稳心高度也主要影响AUV的纵倾角，稳心高度越大，纵倾角越小，则垂向下潜速度越慢，偏航角速度越慢，螺旋回转直径越大，下潜6 000 m深度的用时越长。

图14

图14 稳心高度对大型深海AUV无动力螺旋下潜稳态参数的影响

Fig.14 Influence of metacentric height on unpowered spiral diving steady-state parameters of large deep-sea AUV

4 大型深海AUV缩比样机水池试验

4.1　缩比样机

为验证大型深海AUV无动力螺旋下潜动力学仿真结果的正确性，设计了1∶10的缩比样机并开展水池试验。如图15所示，大型深海AUV缩比样机的排水质量为21 kg，正浮力小于0.1 N；长度为1.6 m，宽度为0.2 m，高度为0.2 m，艇体回转直径为0.225 m；浮心位于水平面方向上距艏部端面593.7 mm，垂直方向上距艇体中间平面3.45 mm处；重心位于水平面方向上距艏部端面593.7 mm，垂直方向上距艇体中间平面-3.629 mm处。

图15

图15 大型深海AUV缩比样机

Fig.15 Scaled-down prototype of large deep-sea AUV

如图15所示，大型深海AUV缩比样机的壳体为透水结构，结构件均采用3D打印，材料为光敏树脂；其电子舱为密封结构，两侧为铝合金密封法兰，舱体采用亚克力透明圆管，长度为0.60 m，内径为0.12 m，外径为0.13 m，舱内组件主要包括树莓派、姿态传感器、锂电池、电源管理板、旋钮防水开关和深度计等，用于获取缩比样机下潜过程中的姿态和深度信息，如图16所示。

图16

图16 大型深海AUV缩比样机的电子密封舱

Fig.16 Electronic sealed cabin of scaled-down prototype of large deep-sea AUV

4.2　水池试验

大型深海AUV缩比样机无动力螺旋下潜水池试验在中国科学院沈阳自动化研究所的试验水池内进行。试验水池的长度为90 m，宽度为25 m，深度为15 m，试验现场如图17所示。利用吊车将AUV缩比样机吊放至水面，牵引绳和安全绳与缩比样机顶部吊环连接，其长度均为14 m，将浮球与牵引绳连接后控制样机的最大下潜深度。充气橡皮艇上的操作人员负责脱钩和扶正调整缩比样机的初始状态，以防止缩比样机与池壁发生碰撞，从而威胁其安全。缩比样机脱钩释放后开始进行无动力螺旋下潜试验。

图17

图17 大型深海AUV缩比样机水池试验现场

Fig.17 Pool test site of scaled-down prototype of large deep-sea AUV

大型深海AUV缩比样机无动力螺旋下潜水池试验工况如表7所示，其中，艏、艉升降舵角均为0°，将不同净负浮力工况下选用的铅块依次固定在缩比样机前端底部距离浮心600，300，200和150 mm处。尽管该缩比样机在水平方向上保持重心位置不变，但随着净负浮力的增大，其稳心高度逐渐增大，因此4个试验工况下的重心纵向位移与稳心高度的比值逐渐减小。

表7 大型深海AUV缩比样机的无动力螺旋下潜水池试验工况

Table 7 Pool test conditions of scaled-down prototype of large deep-sea AUV unpowered spiral diving

工况参数	数值
净负浮力W/N	2.5，5.0，7.5，10.0
艉方向舵角δ_r/(°)	16，20，24

图18所示为净负浮力W=7.5 N，艉方向舵角δ_r=24°时大型深海AUV缩比样机的无动力螺旋下潜运动过程。从图中可以看出，该缩比样机可实现逆时针螺旋下潜运动，符合设计预期，由此验证了无动力螺旋下潜时的静力配置方案的可行性。

图18

图18 大型深海AUV缩比样机无动力螺旋下潜过程（ W=7.5 N， δ_r=24°）

Fig.18 Unpowered spiral diving process of scaled-down prototype of large deep-sea AUV （W=7.5 N，δ_r=24°）

当艉方向舵角δ_r =20°时，不同净负浮力下大型深海AUV缩比样机的下潜深度、偏航角速度、纵倾角和艏向角随时间的变化规律如图19所示。

图19

图19 不同净负浮力下大型深海AUV缩比样机无动力螺旋下潜状态参数随时间的变化规律（δ_r =20°）

Fig.19 Variation law of unpowered spiral diving state parameters of large deep-sea AUV scaled-down prototype with time under different net negative buoyancy （δ_r=20°）

从图19中可以看出，随着净负浮力的增大，大型深海AUV缩比样机的下潜速度增快，下潜11 m深度的用时缩短，但艏向角的变化幅度较小。随着重心纵向位移与稳心高度比值的减小，该缩比样机的纵倾角减小，且达到稳态运动状态所需的时间延长。

综上所述，大型深海AUV缩比样机无动力螺旋下潜状态参数的变化规律与动力学仿真结果基本一致。但从净负浮力为5.0 N的工况可以看出，当牵引绳和安全绳位置不当时，该缩比样机螺旋下潜时存在一定的干扰。此外，由于水池条件有限，该缩比样机的最大下潜深度为13 m，部分状态参数未达到稳定值，后续将在更深的水域内开展试验，以验证大型深海AUV无动力螺旋下潜的稳定性。

5 结论

1）基于拉格朗日方程推导了大型深海AUV的动力学模型，并利用CFD软件对其直航试验、斜航试验、悬臂水池试验和平面运动机构试验进行了数值模拟，并采用最小二乘线性回归法对模拟结果进行拟合，获得了动力学模型所需的水动力系数。

2）利用MATLAB/Simulink和S函数建立了大型深海AUV的六自由度运动仿真模型，并分析了净负浮力、重心纵向位置和稳心高度对其无动力螺旋下潜稳态参数的影响，可得：① 净负浮力作为大型深海AUV螺旋下潜时的主要动力来源，决定了AUV的速度和角速度；净负浮力和重心纵向位移与稳心高度的比值越大，AUV的垂向下潜速度越快，下潜6 000 m深度的用时越短。② 由于大型深海AUV体量较大，其纵倾角主要由重心纵向位移与稳心高度的比值决定，压载质量对其重心位置和转动惯量的影响可以忽略。

3）通过对比给定推力条件下大型深海AUV直航速度的动力学仿真结果和CFD模拟结果发现，两者吻合较好，验证了所建动力学模型的有效性。最后，通过设计了1∶10缩比样机并开展水池试验，进一步验证了动力学仿真结果的正确性。研究结果可为大型AUV无动力螺旋下潜时静力配置的工程设计和应用提供参考。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

蒋新松，封锡盛，王棣棠.水下机器人［M］.沈阳：辽宁科技出版社，2000：1-30.

JIANG

Xin-song

， FENG

Xi-sheng

， WANG

Di-tang

. Unamnned underwater vehicles［M］. Shenyang： Liaoning Science and Technology Press， 2000： 1-30.

[2]

钱东，唐献平，赵江.

UUV技术发展与系统设计综述

［J］. 鱼雷技术，2014，22（6）：401-414. doi：10.3969/j.issn.1673-1948.2014.06.001

DOI:10.3969/j.issn.1673-1948.2014.06.001 [本文引用: 1]

QIAN

Dong

， TANG

Xian-ping

， ZHAO

Jiang

Overview of technology development and system design of UUVs

［J］. Torpedo Technology， 2014， 22（6）： 401-414.

[3]

李硕，刘健，徐会希，等.

我国深海自主水下机器人研究现状

［J］.中国科学：信息科学，2018，48（9）：1152-1164.doi：10.1360/n112017-00264

Shuo

， LIU

Jian

， XU

Hui-xi

， et al.

Research status of autonomous underwater vehicles in China

［J］. Scientia Sinica Informationis， 2018， 48（9）： 1152-1164.

DOI:10.1360/n112017-00264 [本文引用: 1]

[4]

United States Navy.

Autonomous undersea vehicle requirement for 2025

［R］. Washington： United States Department of Defense， 2016.

[5]

顾建农，李启杰，高磊，等.

水下滑翔机运动特性建模与仿真

［J］.华中科技大学学报（自然科学版），2016，44（1）：76-80. doi：10.13245/j.hust.160116

Jian-nong

， LI

Qi-jie

， GAO

Lei

， et al.

Modeling and simulation for the motion performance of underwater glider

［J］. Journal of Huazhong University of Science and Technology （Nature Science Edition）， 2016， 44（1）： 76-80.

DOI:10.13245/j.hust.160116 [本文引用: 1]

[6]

孙秀军，王雷，桑宏强.

Petrel-Ⅱ 200水下滑翔机动力学建模及仿真

［J］.水下无人系统学报，2019，27（5）：480-487. doi：10.11993/j.issn.2096-3920.2019.05.002

DOI:10.11993/j.issn.2096-3920.2019.05.002 [本文引用: 1]

SUN

Xiu-jun

， WANG

Lei

， SANG

Hong-qiang

Dynamic modeling and simulation of underwater glider Petrel-Ⅱ 200

［J］. Journal of Unmanned Undersea Systems， 2019， 27（5）： 480-487.

[7]

于鹏垚，王天霖，甄春博，等.

水下滑翔机的稳态运动速度分析

［J］.哈尔滨工程大学学报，2018，39（11）：1767-1772. doi：10.11990/jheu.201705030

Peng-yao

， WANG

Tian-lin

， ZHEN

Chun-bo

， et al.

Analysis of the steady-state motion velocity of an underwater glider

［J］. Journal of Harbin Engineering University， 2018， 39（11）： 1767-1772.

DOI:10.11990/jheu.201705030 [本文引用: 1]

[8]

ZHANG

Shao-wei

， YU

Jian-cheng

， ZHANG

Ai-qun

， et al.

Sprialing motion of underwater gliders： modeling， analysis， and experiment results

［J］. Ocean Engineering， 2013， 60： 1-13. doi：10.1016/j.oceaneng.2012.12.023

[本文引用: 2]

[9]

CAO

Jun-jun

， CAO

Jun-liang

， YAO

Bao-heng

， et al.

Three dimensional model， hydrodynamics analysis and motion simulation of an underwater glider

［C］//OCEANS 2015-Genova， Genova， May 18-21， 2015. doi：10.1109/oceans-genova.2015.7271365

[10]

施生达

.潜艇操纵性［M］.北京：国防工业出版社，1995：10-231.

SHI

Sheng-da

. Submarine’s maneuverability［M］. Beijing： National Defense Industry Press， 1995： 10-231.

[11]

GRAVER

J G

Underwater gliders： dynamics， control and design

［D］. Princeton： Princeton University， 2005： 42-144.

[12]

SIEMENS.

STAR-CCM+ v13.02 user’s guide

［R］. Plano： Siemens PLM Software Inc.， 2018.

[13]

胡志强

海洋机器人水动力数值计算方法及其应用研究

［D］.北京：中国科学院大学，2013：33-71.

Zhi-qiang

Numerical calculation methods for hydrodynamics of unmanned marine vehicles and their application

［D］. Beijing： University of Chinese Academic of Sciences， 2013： 33-71.