浙江大学学报(工学版)

浙江大学学报(工学版), 2025, 59(8): 1574-1582 doi: 10.3785/j.issn.1008-973X.2025.08.003

机械工程、能源工程

基于三维视觉的软体机器人实时定位与控制

张弘,, 张学成, 王国强, 顾潘龙, 江楠

1. 浣江实验室 软体机器人与智能器件研究中心，浙江 诸暨 311800

2. 浙江大学 航空航天学院，浙江 杭州 310058

Real-time positioning and control of soft robot based on three-dimensional vision

ZHANG Hong,, ZHANG Xuecheng, WANG Guoqiang, GU Panlong, JIANG Nan

1. Center for Soft Machines and Smart Devices, Huanjiang Laboratory, Zhuji 311800, China

2. School of Aeronautics and Astronautics, Zhejiang University, Hangzhou 310058, China

收稿日期: 2024-06-13  

基金资助: 浣江实验室专项资助项目（128102-E52201/031）；浙江省自然科学基金资助项目（LGG21F030003, LGG20E050011）.

Received: 2024-06-13  

Fund supported: 浣江实验室专项资助项目（128102-E52201/031）；浙江省自然科学基金资助项目（LGG21F030003,LGG20E050011）.

作者简介 About authors

张弘（1990—），男，助理研究员，从事机器人及传感器技术的研究.orcid.org/0009-0006-1402-3109.E-mail：517180508@qq.com , E-mail：517180508@qq.com

摘要

针对软体机器人建模困难、控制稳定性差和精度低等问题，设计模块化气动软体机械臂平台，推导得到从驱动空间、虚拟关节空间到工作空间的位置正解模型. 根据实际结构参数的约束生成工作空间数据集，通过构建KD树的三维空间索引结构，有效地完成了位置逆解求解，极大地提高了求解速度. 采用提出的逆解筛选原则，在多个解中选取最优解，增强了气动软体机械臂的控制稳定性及精度. 为了提升机械臂末端的控制精度，开发结合深度学习与RANSAC算法的机械臂末端三维视觉实时定位算法，实现了机械臂末端位姿的闭环控制，与开环控制相比，实现了约4倍的精度提升.

关键词： 软体机械臂 ; KD树 ; 三维视觉 ; 深度学习 ; 运动学

Abstract

A platform for modular pneumatic soft robotic arm was designed, and a forward position model from the driving space, virtual joint space to the workspace was derived aiming at the problems of difficult modeling, poor control stability and low accuracy of soft robotic. The workspace data set was generated according to the actual structural parameter constraints. The position inverse solution was effectively completed by constructing the three-dimensional spatial index structure of KD tree. Then the solution speed was greatly improved. The proposed inverse solution selection principle was used to select the optimal solution from multiple solutions, which enhanced the control stability and accuracy of the pneumatic soft robotic arm. A real-time 3D visual positioning algorithm for the end of robotic arm combining deep learning and RANSAC algorithm was developed in order to improve the control accuracy of the end of the robot arm. Then closed-loop control of the end position and orientation of robotic arm was achieved, and about four times more precision improvement was achieved compared with open-loop control.

Keywords： soft robotic arm ; KD tree ; three-dimensional vision ; deep learning ; kinematics

PDF (2000KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

张弘, 张学成, 王国强, 顾潘龙, 江楠. 基于三维视觉的软体机器人实时定位与控制. 浙江大学学报(工学版)[J], 2025, 59(8): 1574-1582 doi:10.3785/j.issn.1008-973X.2025.08.003

ZHANG Hong, ZHANG Xuecheng, WANG Guoqiang, GU Panlong, JIANG Nan. Real-time positioning and control of soft robot based on three-dimensional vision. Journal of Zhejiang University(Engineering Science)[J], 2025, 59(8): 1574-1582 doi:10.3785/j.issn.1008-973X.2025.08.003

随着机器人学、仿生学和材料科学的高速发展，软体机器人作为新兴交叉领域获得了广泛的关注. 这类机器人借鉴生物仿生的原理，采用软材料制造，通过气压、流体、磁场、机械等驱动方式，能够模拟自然界中的章鱼触手、大象鼻子和蛇类等连续体软体结构. 该类机器人具有较高的灵活性及柔顺性，具有良好的负载能力和环境适应性，在医疗、航空航天、海洋开发及水下救援等领域展现出巨大的应用潜力[1-8].

在软体机器人的研究领域中，虽然针对结构设计和驱动方式的研究已经取得重要进展[9-11]，但由于软材料的固有柔顺性及多自由度和大尺度形变的特点，在软体机器人系统中建立精确的运动学模型并实施有效的动态控制，面临着不小的挑战. 针对这些挑战，Xu等[12-23]探索了多种建模及控制策略，实现了软体机器人在不同环境下的作业. Chen等[24]模拟脊椎动物的弯曲行为，设计气动软体致动器，通过建模及仿真实现了类似“C型”及“S型”的扭转运动，但是该软体致动器在弯曲及扭转的结构设计上有一些改进的空间. 张志远等[25]提出螺线构型的气动软体致动器，根据圆形、阿基米德螺线及对数螺线实现了3种结构设计，开展了气压与角度的关系解析，该研究中静力学的模型参数与气压的对应关系有待进一步的优化. 夏泽洋等[26]提出刚软混杂的机器人仿真耦合模型，通过气动软体致动器弯曲实验并与仿真结果对比，验证了耦合模型的有效性. 王昱欣等[27]提出软体机器人手眼视觉/形状混合控制的方法，结合深度无关交互矩阵自适应视觉控制，实现了软体机器人的形状控制. Muller等[28]在Festo的Bionic Soft Arm的基础上开发软体机械臂，通过结构设计及建立的滞后描述补偿模型来提高机器人的性能.

通过视觉闭环[29]对软体机器人进行引导及闭环控制是提高软体机器人控制能力的关键方法之一. 气动软体机器人的刚度差、建模困难的问题影响视觉引导及伺服下的控制性能，仿生视觉的“眼在手外”的环境遮挡及视觉靶点添加存在通用性的问题.

为了解决上述问题，本文设计使用视觉进行闭环的模块化气动软体机器人平台，将KD树查找策略引入到无模型的软体机器人位置逆解求解中，提出软体机器人逆解及路径选取方法. 结合自主开发的通用性强的深度学习位姿检测算法，提高了软体机器人的控制性能.

1. 软体机械臂系统

1.1. 软体机械臂的实验平台

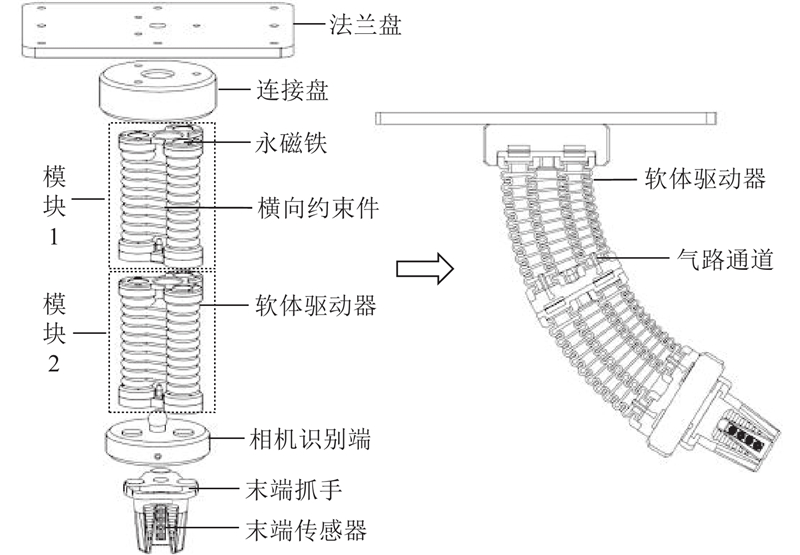
搭建气动软体机械臂的运动控制实验平台，如图1所示. 该系统由硬件、软件及软体机械臂组成. 其中，硬件部分包括深度相机、压电比例阀、压力传感器、正压气源装置、负压气源装置及单片机等. 软件部分为控制代码，采用Arduino及Python进行联合控制. 软体机械臂作为主要的研究对象，主要由模块1、模块2及末端抓手部分组成. 其中模块1及模块2均由3个软体驱动器及气路通道组成，详见1.2节.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   气动软体机械臂运动控制的实验平台

Fig.1   Experimental platform of pneumatic soft robotic arm motion control


实验平台中主要用到的硬件配置如表1所示.

表 1   机器人实验平台的主要硬件

Tab.1  Main hardware of robotic experimental platform

名称型号公司
压电比例阀VAB-B-26-D13FESTO
负压气源装置KVP8 PLUS-KB-SKamer
正压气源装置KZP-PFKamer
压力传感器DP-102APanasonic
调压阀AW2000-02SMC
单片机Arduino MEGA2560Arduino LLC
深度相机RealSense D435iIntel

新窗口打开| 下载CSV


采用深度学习算法进行特征识别，搭建软件系统所需的环境配置，如表2所示.

表 2   基于深度学习的算法开发环境配置

Tab.2  Development environment configuration of deep learning-based algorithm

名称型号版本
操作系统Ubuntu20.04
中央处理器英特尔Xeno-W2155
显卡英伟达QuadroP6000
Pytorch—1.12
Cuda—11.0
Python—3.8

新窗口打开| 下载CSV


1.2. 软体机械臂的结构及驱动原理

软体机械臂的结构如图2所示. 该系统主要由模块1和模块2构成，单个模块可以实现3个不同方向的弯曲运动，多个模块组合能够实现多维空间的运动. 每个模块主要由3个软体驱动器、横向约束件、磁铁连接端等组成，软体驱动器呈120°圆周放置，每个软体驱动器连接1根气管，每组模块需要3根气管.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   软体机械臂的结构图

Fig.2   Structural diagram of soft robotic arm


软体机械臂变形的原理如下. 当施加正压时，软体驱动器产生弹性形变而伸长，压力越大，伸长量越大；当施加负压时，软体驱动器被压缩，真空度越高，压缩程度越大. 如图3所示为软体驱动器变形的原理图. 如图3（a）所示为施加负压驱动器被压缩，如图3（b）所示为初始状态，如图3（c）所示为施加正压驱动器伸长.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   软体驱动器变形的原理图

Fig.3   Schematic of deformation of soft driver


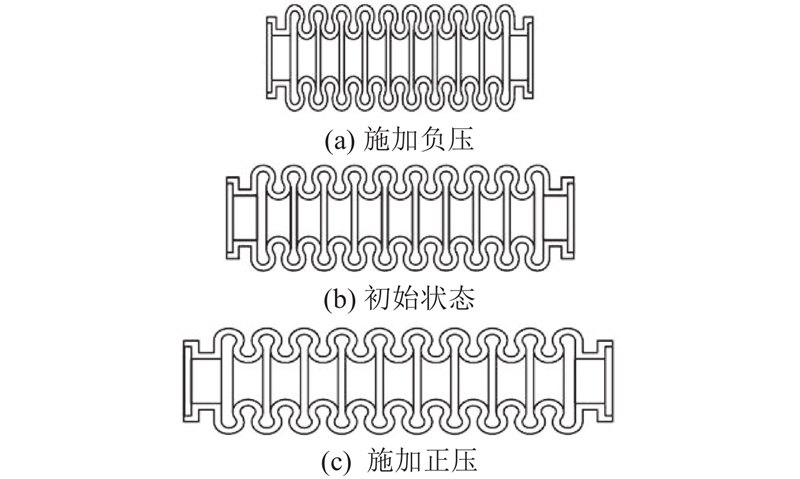
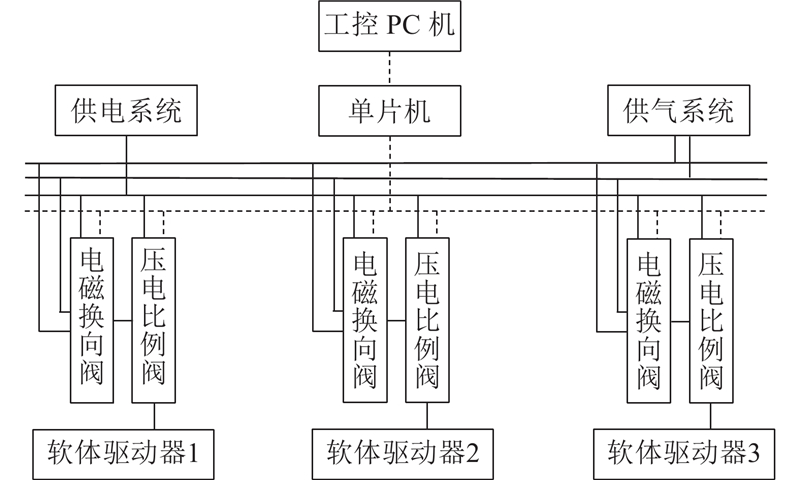
如图4所示为控制系统的电气逻辑图. 通过正压气源装置和负压气源装置分别供气，采用电磁换向阀进行正、负压输入的切换，输入气体经过压电比例阀在−100 kPa到100 kPa之间无极调压输出到软体驱动器中，驱动机械臂变形运动.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   控制系统的电气逻辑图

Fig.4   Electrical logic diagram of control system


软体机械臂的结构参数如表3所示.

表 3   软体机械臂的结构参数

Tab.3  Structure parameter of soft robotic arm

参数数值
软体驱动器个数6
最大负压(−96 kPa)条件下的长度/mm70
初始状态长度/mm103
最大正压(96 kPa)条件下的长度/mm195
永磁铁半径/mm7.5
连接盘半径/mm45
法兰盘尺寸/mm210×140×8
气管内径/mm2
横向约束件内径/mm12.5

新窗口打开| 下载CSV


2. 软体机械臂的建模

2.1. 软体机械臂的位置正解

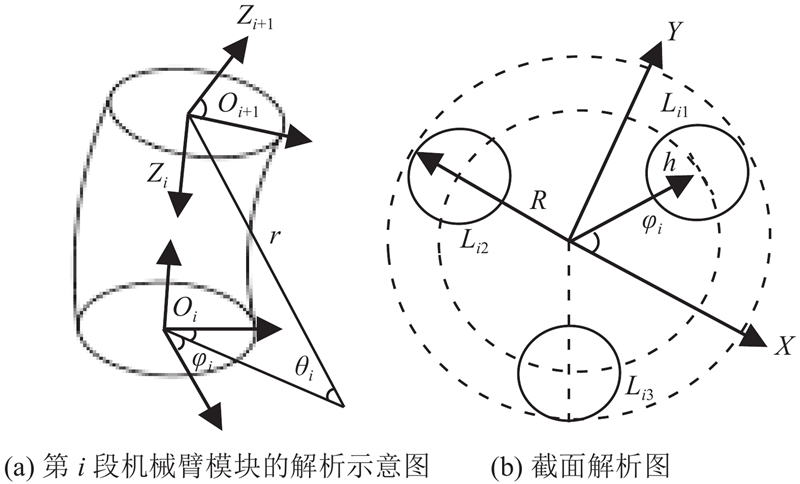
为了方便叙述，如图5所示，将机械臂模块i的第j个软体驱动器长度定义为$ {L}_{ij} $，输入的气压为$ {p}_{ij} $，机械臂模块i的偏转角定义为$ {\varphi }_{i} $，弯曲角定义为$ {\theta }_{i} $、曲率半径为$ {r}_{i} $. 假设在机械臂的控制过程中，机械臂模块的曲率半径$ {r}_{i} $和弯曲角$ {\theta }_{i} $满足常曲率圆弧关系.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   软体机械臂末端位置的正解解析示意图

Fig.5   Analytical schematic of forward kinematics for end position of soft robotic arm


图5中，坐标原点位于软体机械臂端面的圆心位置，Z轴垂直于端面，通过计算可以得到机械臂模块i的中心弧长$ {L}_{i{\mathrm{e}}} $：

$ {L}_{i{\mathrm{e}}}=\frac{{L}_{i1}+{L}_{i2}+{L}_{i3}}{3}. $

同时，可以得到$ {L}_{ij} $与弯曲角$ {\theta }_{i} $和偏转角$ {\phi }_{i} $有如下关系：

$ \left.\begin{array}{c}\dfrac{1}{{r}_{i}}=\dfrac{2\sqrt{{L}_{i1}^{2}+{L}_{i2}^{2}+{L}_{i3}^{2}-{L}_{i1}{L}_{i2}-{L}_{i1}{L}_{i3}-{L}_{i2}{L}_{i3}}}{{(L}_{i1}{+L}_{i2}+{L}_{i3})h},\\{\varphi }_{i}={\mathrm{arc}}{{\mathrm{tan}}}\left(\dfrac{{L}_{i2}+{L}_{i3}-2{L}_{i1}}{\sqrt{3}\left({L}_{i2}-{L}_{i3}\right)}\right),\\{\theta }_{i}=\dfrac{2\sqrt{{L}_{i1}^{2}+{L}_{i2}^{2}+{L}_{i3}^{2}-{L}_{i1}{L}_{i2}-{L}_{i1}{L}_{i3}-{L}_{i2}{L}_{i3}}}{3h}.\end{array} \right\} $

式中：$ {\theta }_{i}\in \left(-\text{π} ,\text{π} \right) $，$ {\varphi }_{i}\in \left(\mathrm{0,2}\text{π} \right) $，$ h $为同一横截面上软体驱动器中心到机械臂模块中心的距离. 将第i模块的参数模型汇总，如表4所示.表中，θ为绕Z轴的旋转角度，d为沿Z轴的平移距离，a为沿X轴的平移距离，α为绕X轴的旋转角度.

表 4   软体机械臂的D-H参数表

Tab.4  D-H parameter table of soft robotic arm

序号$ {\theta }_{} $$ {d}_{} $$ {a}_{} $$ {\alpha }_{} $
1$ {\varphi }_{i} $$ 0 $$ 0 $$ -\mathrm{\text{π} }/2 $
2$ {\theta }_{i}/2 $$ 0 $$ 0 $$ \mathrm{\text{π} }/2 $
3$ 0 $$ {(2{L}_{i{\mathrm{e}}}}/{{\theta }_{i})}\mathrm{sin}\left({{\theta }_{i}}/{2}\right) $$ 0 $$ -\mathrm{\text{π} }/2 $
4$ {\theta }_{i}/2 $$ 0 $$ 0 $$ \mathrm{\text{π} }/2 $
5$ -{\varphi }_{i} $$ 0 $$ 0 $$ 0 $

新窗口打开| 下载CSV


具体的位置正解求解过程如算法1所示.

算法1　位置正解求解

输入: 输入的气压为$ {p}_{ij} $

输出: 机械臂末端坐标$ \left(X,Y,Z\right) $

函数 位置正解

1）通过标定得到准确的软体驱动器伸长量与输入气压的关系：$ {L}_{ij}=f\left({p}_{ij}\right) $.

2）根据式(1)、(2)，求解各机械臂模块的虚拟关节变量：$ {\theta }_{i},{\varphi }_{i},{L}_{i{\mathrm{e}}}=g\left({L}_{ij}\right) $.

3）$ {{\boldsymbol{T}}}_{i}=h({\theta }_{i},{\varphi }_{i},{L}_{i{\mathrm{e}}}) $，其中$ {{\boldsymbol{T}}}_{i}$为软体机械臂模块i上下端面的齐次变换矩阵.

4）$ {\boldsymbol{E}}({{\boldsymbol{T}}}_{1},{{\boldsymbol{T}}}_{2})= {{\boldsymbol{T}}}_{1}{{\boldsymbol{T}}}_{2}$，其中$ {\boldsymbol{E}}({{\boldsymbol{T}}}_{1},{{\boldsymbol{T}}}_{2} )$为机械臂运用链式法则求出的总的齐次变换矩阵.

5）（X，Y，Z）从${\boldsymbol{E}}({{\boldsymbol{T}}}_{1},{{\boldsymbol{T}}}_{2} $)中提取.

结束函数

2.2. 利用KD树算法求逆解

2.2.1. 求解中多解情况

当面对气动软体机械臂多解选取的情况时，需要考虑机械臂本体在运动过程中存在运动滞后、运动稳定性较差的情况. 提出以下3种原则进行改善.

1）角度变化最小的原则. 当气动软体机械臂到达期望坐标点时，选取到达目标点角度变化最小的解作为最优解，优先选择靠近末端的关节进行运动.

2）弯曲角变化趋势变小的原则. 在角度变化过程中，优先选择角度变化减小的解.

3）偏转角共面及最大负压的原则. 尽量选择偏转角共面或偏转角度相差较小的解，同时尽量选取驱动器最大负压的解.

通过角度变化最小的原则，可以减小气动软体机械臂的运动滞后，加快机械臂的恢复稳定. 弯曲角变化趋势变小的原则主要是考虑到弯曲角变大时机械臂负载能力变差的情况. 通过偏转角共面及最大负压原则，能够尽可能地保证机械臂的刚度.

2.2.2. KD树算法

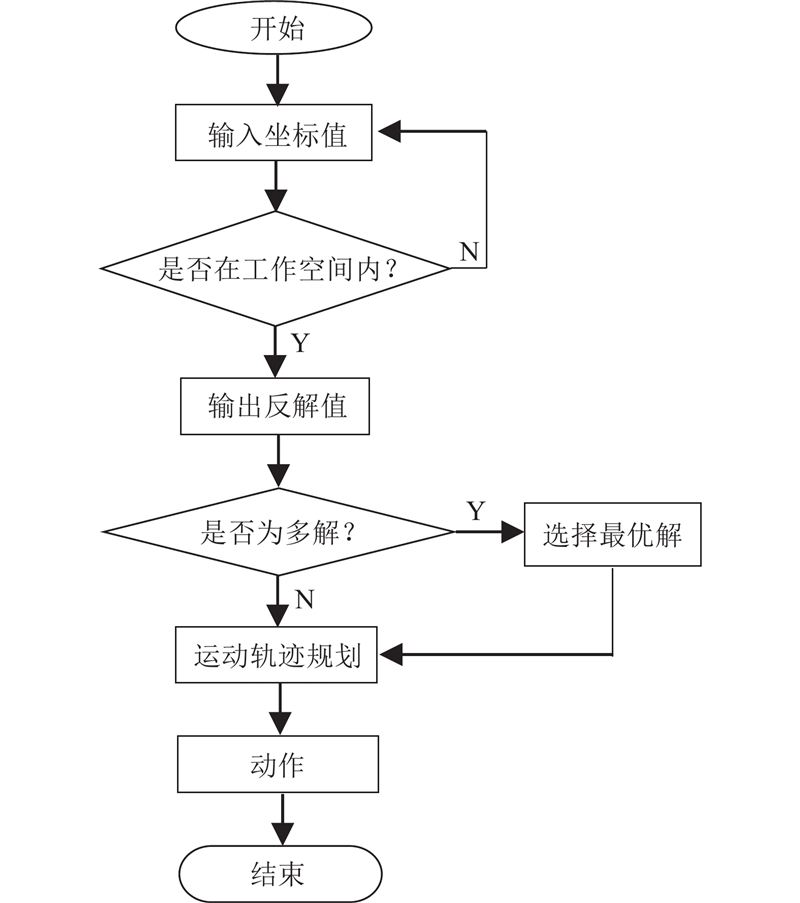
通过对软体机械臂运动学的求解，生成了大量的工作空间坐标点，将关节输入量与对应的坐标值保存至数据库. 当求机械臂位置逆解时，输入期望的末端坐标，并判断是否在工作空间内. 求解流程图如图6所示.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   软体机械臂的位置逆解求解流程图

Fig.6   Position inverse flow chart of soft robotic arm


当求解软体机械臂的位置逆解时，为了能够快速查找到合适的数据，与传统的遍历求解算法进行对比，如表5所示. 表中，tb为遍历用时，tk为KD树用时. 从表5可知，当处理相同数据量时，KD树的用时较短. KD树[30-32]是可以存储多维数据的二叉搜索算法，通过对数据的方差求解，能够对高维空间进行划分，最终搜索到目标节点.

表 5   不同数据量下逆解求解算法的性能对比

Tab.5  Performance comparison of inverse solving algorithm by different data volume

数据量tb/mstk/ms
50 00041.861.99
100 00084.822.98
150 000124.523.34
200 000167.033.55
250 000209.303.98

新窗口打开| 下载CSV


通过位置正解模型生成了大量的工作空间的点，将三维坐标点与虚拟关节角相匹配，并保存至数据库中. 求位置逆解时，将期望的三维坐标点代入数据库，利用KD树搜索最近点，在误差允许范围内取出点集，利用最小二乘法迭代得到位置逆解，求解流程如图7所示.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   KD树求位置逆解的简图

Fig.7   Schematic of KD tree position inverse solution


为了更加清晰地表示KD树求位置逆解的过程，部分代码如下所示.

算法2　KD树求位置逆解

输入: 目标点坐标$ \left(X,Y,Z\right) $

输出: 软体驱动器管腔压力$ {p}_{ij} $

函数　位置逆解

1）计算目标点坐标与数据集中候选点point的欧氏距离: dist = h( X, Y, Z, point).

2）假设精度要求为l，则: If dist < l

3）　　then 将该点加入点集points

4） Else

5）　　Continue

6） End if

7） 获取虚拟关节角: $ {\mathrm{angles}}=k\left({\mathrm{points}}\right) $.

8） 通过最小二乘法进行迭代，将上一步得到的角与当前位置得到的角作差，角度差: diff = O (angles).

9） 得到最小变化角度: $ {\mathrm{angle}}={\mathrm{min}}\left({\mathrm{diff}}\right) $.

10）得到管腔长度: $ {L}_{ij}={g}^{-1}\left({\mathrm{angle}}\right) $.

11）得到管腔压力$ :{p}_{ij}={f}^{-1}\left({L}_{ij}\right) $.

结束函数

3. 机械臂末端定位

为了提高软体机器人末端位姿检测的抗环境干扰能力及通用性，设计可安装在机械臂末端用于确定机械臂末端位姿的定位环. 该定位环可以嵌入至机器人的结构本身，不需要添加额外的特征点，保证不会受机械臂的运动产生视觉遮挡. 使用RealSense深度相机，可以实时获取目标图像及三维点云数据.

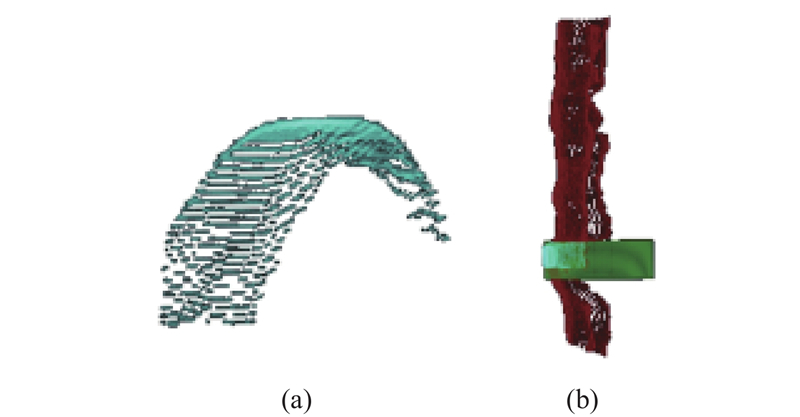
引入基于Yolact的深度学习算法，用于分离点云中的定位环部分的点云. 为了方便后续的定位环定位，使用体素滤波方法，对分割得到的点云进行预处理. 如图8所示，可以确保点云中的点在空间中均匀分布.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   定位环视觉识别的示意图

Fig.8   Schematic diagram of visual recognition of positioning ring


在获取定位环部分的点云后，利用基于RANSAC的算法，在定位环点云和真实CAD模型之间进行拟合，确定机械臂关节处的位姿.

在算法的运行过程中，从定位环的点云数据中拟合初始的定位环位姿，将剩余的数据代入拟合模型，将符合的点记为内点，不符合的点记为外点. 计算当前内点数在总点云数中的占比，并判断是否大于设定阈值. 若大于阈值，则模型较理想；若小于阈值，则判断随机采样的次数是否达到最大迭代次数. 若达到，则迭代结束；若没达到，则继续迭代，直至迭代结束.

对于最大迭代次数，设内点数在点云中的占比为$ t $，则$ t $可以表示为

$ t=\frac{{n}_{\mathrm{i}\mathrm{n}}}{{n}_{\mathrm{i}\mathrm{n}}+{n}_{\mathrm{o}\mathrm{u}\mathrm{t}}}. $

式中：$ {n}_{\mathrm{i}\mathrm{n}} $为内点数，$ {n}_{\mathrm{o}\mathrm{u}\mathrm{t}} $为外点数. 在计算模型使用$ N $个点的情况下，至少有一个点为外点的概率为

$ {P}_{\mathrm{o}\mathrm{u}\mathrm{t}}=1-{t}^{N}. $

式中：$ N $为每次随机采集点云的数量. $ {\left(1-{t}^{N}\right)}^{k} $为$ k $次迭代后都至少采样一个外点模型的概率，采样点数$ N $全部为内点的概率为

$ P=1-{\left(1-{t}^{N}\right)}^{k} . $

式中：$ P $为随机采样全为内点的概率. 对式（5）取对数，即理论迭代次数为

$ k={{\mathrm{lg}}}\;\frac{\left(1-P\right)}{{\mathrm{lg}}\;(1-{t}^{N})} . $

经过上述步骤，可以完成定位环点云的拟合. 经过拟合后，可以得到定位环，如图9所示. 如图9（a）所示为原始点云，如图9（b）所示为处理后的点云.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9   定位环点云的预处理图

Fig.9   Preprocessing diagram of point cloud of positioning ring


在相对静止状态下对定位环点云进行圆柱拟合后，随机提取30个圆柱中心. 为了验证实验的可靠性，在整个软体机械臂的工作空间内随机改变圆柱体位置10次，开展重复实验. 分别计算30个圆柱中心点的平均坐标及与真实坐标的方差，所有实验组别的拟合圆柱中心点与真实坐标的对比数据如表6所示，得到的方差均小于2 mm.

表 6   拟合坐标值与真实坐标值的对比

Tab.6  Comparison of fitted coordinates and true coordinates

组别真实坐标/mm拟合中心点平均坐标/mm方差/mm
2(2.5, −3, 470.4)(2.43, −2.41, 470.68)0.65
3(−10, −5, 440.4)(−10.61, −5.30, 440.24)0.70
4(1.5, −4.5, 471.2)(2.53, −3.93, 471.66)1.26
5(−15.4, −3.2, 456)(−14.79, −3.44, 455.27)0.98
6(2.6, −3.5, 469.8)(2.43, −3.93, 471.66)1.92
7(−15, −5, 458.4)(−16.01, −3.61, 458.05)1.75
8(2.8, −1.8, 469.7)(2.93, −2.41, 470.68)1.16
9(4, −3.5, 439.3)(4.44, −3.51, 439.24)0.45
10(−9.3, −5.3, 441)(−10.11, −5.30, 440.24)1.11

新窗口打开| 下载CSV


4. 实验结果及分析

4.1. 控制流程

通过视觉引导，对软体机械臂末端进行闭环控制. 使用9点标定法获取机械臂坐标系到相机坐标系的外参矩阵，然后获取10组每组包含9个具有对应关系的三维点后，利用最小二乘法求解相机到机械臂坐标系转换的外参矩阵.

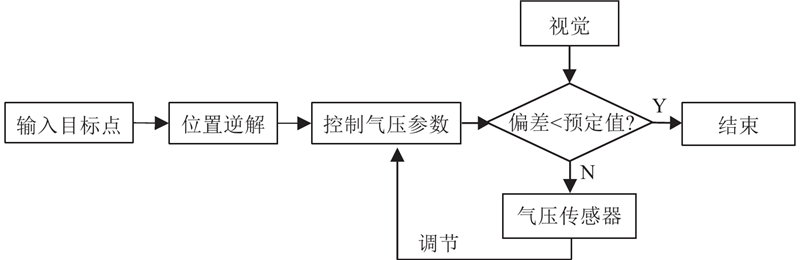
在完成标定后，将机械臂坐标系下的期望位姿转换到相机坐标系下进行闭环控制. 控制流程如下：根据输入的末端位姿信息，解算出各软体驱动器对应的输入气压，当机械臂末端到达目标点附近时，结合气压传感器调节压力变化，对目标点与视觉反馈的实际位置进行误差调节. 当误差在允许范围内时控制结束，控制流程如图10所示.

图 10

新窗口打开| 下载原图ZIP| 生成PPT

图 10   软体机械臂的闭环控制流程图

Fig.10   Closed-loop control flowchart of soft robotic arm


4.2. 软体机械臂的弯曲运动实验

测试软体机械臂进行弯曲动作时的开环机械臂精度，在模块1保持初始位姿（3个驱动器全为负压）的条件下，对模块2在不同弯曲角度下的位姿进行实验（偏转角为30°），实验结果如图11所示.

图 11

新窗口打开| 下载原图ZIP| 生成PPT

图 11   软体机械臂的弯曲运动示意图

Fig.11   Schematic diagram of bending motion of soft robotic arm


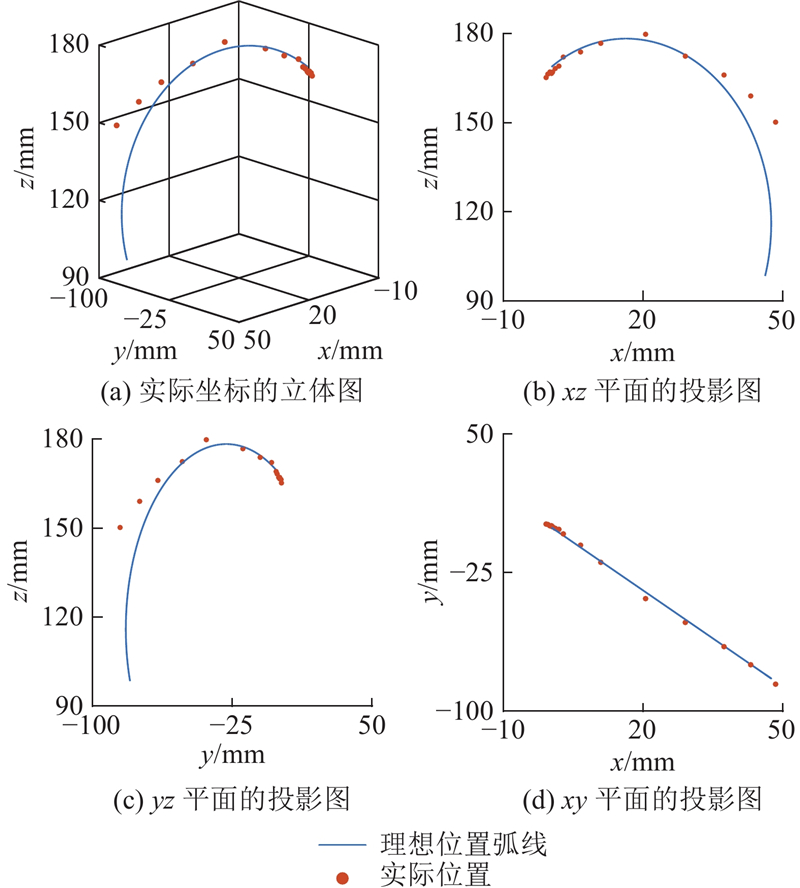
如图12所示为弯曲实验开环实际位置的坐标图. 可以看出，软体机械臂本身刚性较低，导致负载能力较差，随着弯曲角的增大，开环误差也逐步增大，经计算得到开环轨迹的平均误差为8.77 mm.

图 12

新窗口打开| 下载原图ZIP| 生成PPT

图 12   机械臂末端开环的弯曲运动轨迹

Fig.12   Trajectory of bending movement of robotic end in open-loop


在加入闭环后，开展了与图11相同的实验，机械臂的末端运动轨迹如图13所示. 经计算可知，期望位姿和实际位置的平均偏差为2.03 mm. 可以看出，加入视觉闭环，可以有效地降低机械臂运动的位置误差.

图 13

新窗口打开| 下载原图ZIP| 生成PPT

图 13   机械臂末端闭环的弯曲运动轨迹

Fig.13   Trajectory of bending movement of robotic end in closed-loop


为了展示弯曲运动加入闭环控制后末端的移动速度，在保持偏转角30°不变的情况下，分别探究软体机械臂的弯曲角从0°变化到30°、60°、90°及120°的运动时间，实验结果如表7所示. 表中，ts为运行时间，v为平均速度.

表 7   弯曲运动实验过程中的机械臂末端速度

Tab.7  End velocity of robotic arm during experiment of bending motion

θ2/(°)ts/sv/(rad·s−1)
0~301.190.44
0~601.420.74
0~901.580.99
0~1201.811.15

新窗口打开| 下载CSV


4.3. 软体机械臂的偏转运动实验

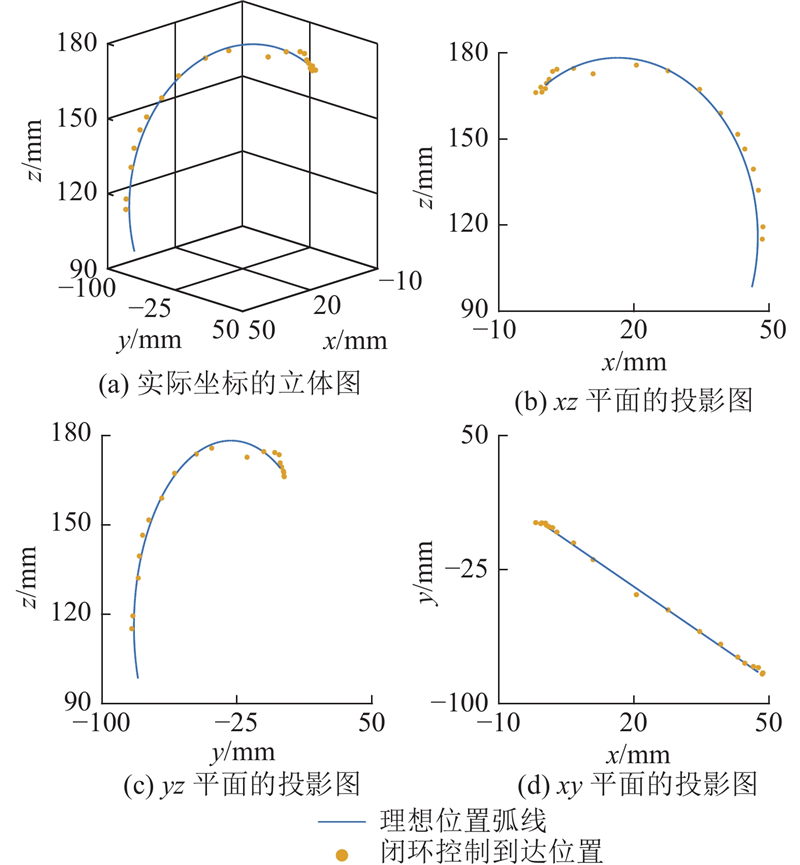
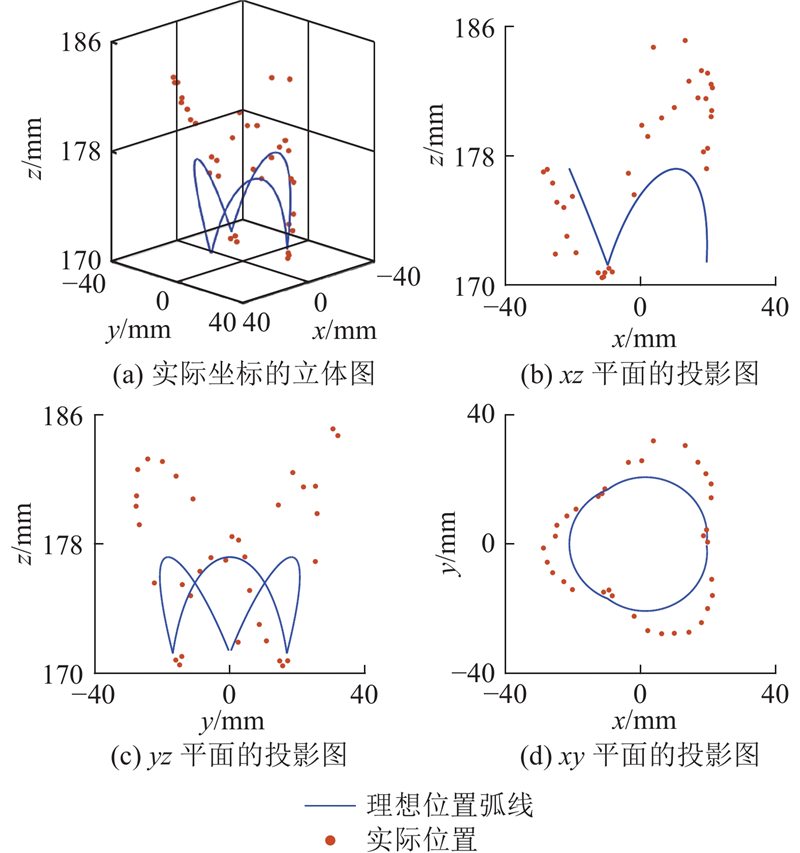
当选取模块2的弯曲角度为30°时，控制软体机械臂进行偏转一周的动作，记录机械臂末端的运动轨迹，实验结果如图14所示.

图 14

新窗口打开| 下载原图ZIP| 生成PPT

图 14   软体机械臂的偏转运动示意图

Fig.14   Schematic diagram of deflection of soft robotic arm


如图15所示为偏转实验开环实际位置的坐标图. 可知，在理想状态下，软体机械臂在转动时的轨迹呈周期性分布. 对通过相机捕获的末端数据与理想模型数据进行比较，得到平均偏差为6.63 mm. 采用视觉伺服对各点的位置误差进行调整，调整后的末端位置如图16所示.

图 15

新窗口打开| 下载原图ZIP| 生成PPT

图 15   机械臂末端的开环偏转运动轨迹

Fig.15   Trajectory of robotic end of deflection in open-loop


机械臂弯曲动作的末端位置精度从8.77 mm提高到2.03 mm，偏转动作的末端位置精度从6.63 mm提高到1.68 mm. 由此可见，经过视觉闭环控制调节后，机械臂末端的控制精度得到了显著提升.

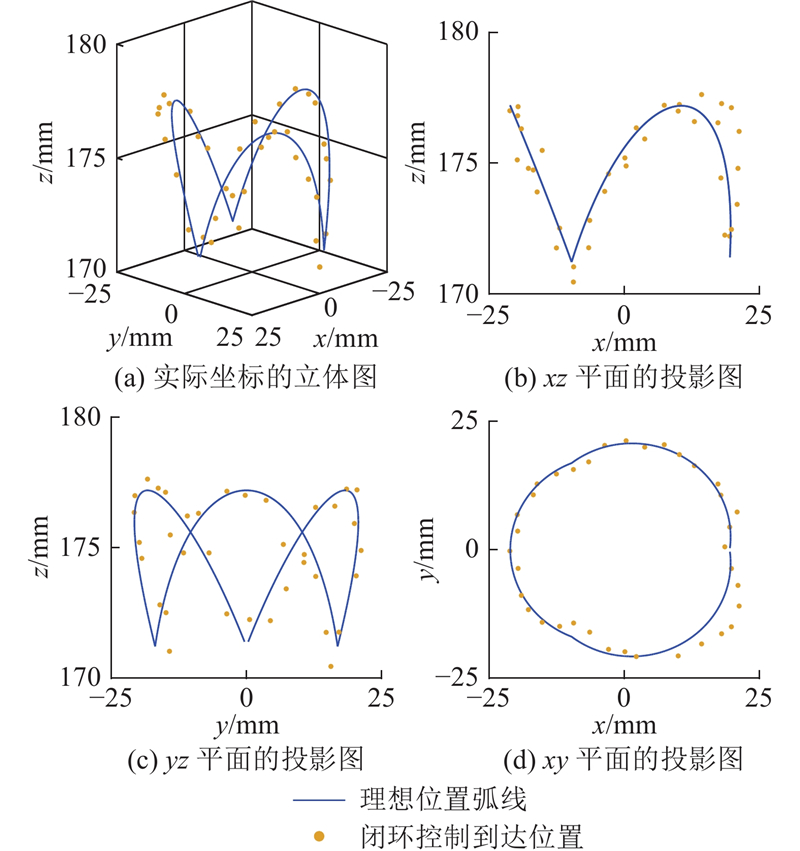
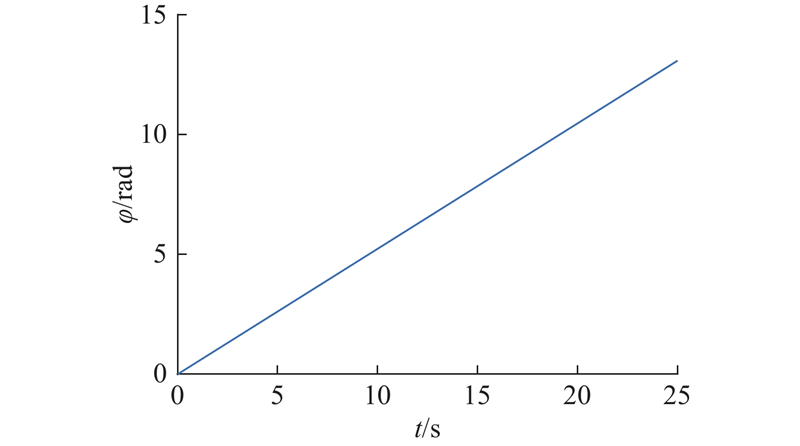
为了展示偏转运动加入闭环控制后的末端移动速度，在保持弯曲角为30°的情况下，探究偏转角从0°到360°的变化过程，偏转弧度与时间的关系如图17所示. 结果显示，机械臂末端能够保持近匀速运动，平均移动速度约为0.52 rad/s.

图 16

新窗口打开| 下载原图ZIP| 生成PPT

图 16   机械臂末端的闭环偏转运动轨迹

Fig.16   Trajectory of robotic end of deflection in closed-loop


图 17

新窗口打开| 下载原图ZIP| 生成PPT

图 17   偏转运动实验过程中的机械臂末端速度

Fig.17   End velocity of robotic arm during experiment of deflection


5. 结　语

本文搭建模块化气动软体机械臂系统，建立运动学模型，提出软体机械臂位置逆解多解的选取原则，提高了机械臂在运动过程中的稳定性. 将KD树数据解析算法应用于软体机械臂的位置逆解求解中，提高了运动求解的效率，满足了机械臂运动控制的实时性需求. 采用基于YOLACT的深度学习算法，开展定位环数据集的采集、点云信息处理及拟合，实现了机械臂末端位置坐标的实时获取. 通过视觉引导与闭环控制算法调节末端位置误差，显著提高了气动软体机械臂在运动过程中末端位置的控制精度. 在后续的工作中，将开展软体机械臂在核电站维护、电网检修、管道巡检等实际应用场景中的探索. 研究主要包括增加机构自由度构建更复杂的运动轨迹算法及存在外部干扰下的交互研究，完成指定的任务.

参考文献

LUAN H, WANG M, ZHANG Q, et al

Variable stiffness fibers enabled universal and programmable re-foldability strategy for modular soft robotics

[J]. Advanced Science, 2024, 11 (10): 2307350

DOI:10.1002/advs.202307350      [本文引用: 1]

郝天泽, 肖华平, 刘书海, 等

集成化智能软体机器人研究进展

[J]. 浙江大学学报: 工学版, 2021, 55 (2): 229- 243

HAO Tianze, XIAO Huaping, LIU Shuhai, et al

Research status of integrated intelligent soft robots

[J]. Journal of Zhejiang University: Engineering Science, 2021, 55 (2): 229- 243

ARACHCHIGE D, PERERA D, MALLIKARACHCHI S, et al

Soft steps: exploring quadrupedal locomotion with modular soft robots

[J]. IEEE Access, 2023, 11: 63136- 63148

DOI:10.1109/ACCESS.2023.3289156     

HUANG J D, ZHOU J S, WANG Z Y, et al

Modular origami soft robot with the perception of interaction force and body configuration

[J]. Advanced Intelligent Systems, 2022, 4 (9): 2200081

DOI:10.1002/aisy.202200081     

THURUTHEL T G, ANSARI Y, FALOTICO E, et al

Control strategies for soft robotic manipulators: a survey

[J]. Soft Robotics, 2018, 5 (2): 149- 163

DOI:10.1089/soro.2017.0007     

QU J T, XU Y N, LI Z K, et al

Recent advances on underwater soft robots

[J]. Advanced Intelligent Systems, 2024, 6 (2): 2300299

DOI:10.1002/aisy.202300299     

WANG S, SUN Z

Hydrogel and machine learning for soft robots' sensing and signal processing: a review

[J]. Journal of Bionic Engineering, 2023, 20 (3): 845- 857

DOI:10.1007/s42235-022-00320-y     

YIMING B, HAN Y, HAN Z, et al

A mechanically robust and versatile liquid-free ionic conductive elastomer

[J]. Advanced Materials, 2021, 33 (11): 2006111

DOI:10.1002/adma.202006111      [本文引用: 1]

SHAO X, CAI Y, YIN S, et al

Mechanics of interfacial delamination in deep-sea soft robots under hydrostatic pressure

[J]. Journal of Applied Mechanics, 2023, 90 (2): 021009

DOI:10.1115/1.4056214      [本文引用: 1]

TANG W, ZHANG Y, XU H, et al

Self-protection soft fluidic robots with rapid large-area self-healing capabilities

[J]. Nature Communications, 2023, 14 (1): 6430

DOI:10.1038/s41467-023-42214-5     

LI G, CHEN X, ZHOU F, et al

Self-powered soft robot in the Mariana Trench

[J]. Nature, 2021, 591 (7848): 66- 71

DOI:10.1038/s41586-020-03153-z      [本文引用: 1]

XU F, WANG H

Soft Robotics: morphology and morphology-inspired motion strategy

[J]. IEEE-CAA Journal of Automatica Sinica, 2021, 8 (9): 1500- 1522

DOI:10.1109/JAS.2021.1004105      [本文引用: 1]

VINOCOUR P E T, KOKUBU S, MATSUNAGA F, et al

Development of a dual function joint modular soft actuator and its evaluation using a novel dummy finger joint-soft actuator complex model

[J]. IEEE Robotics and Automation Letters, 2024, 9 (5): 4210- 4217

DOI:10.1109/LRA.2024.3376975     

SU M, XIE R, QIU Y, et al

Design, mobility analysis and gait planning of a leech-like soft crawling robot with stretching and bending deformation

[J]. Journal of Bionic Engineering, 2023, 20 (1): 69- 80

DOI:10.1007/s42235-022-00256-3     

DAS R, BABU S P M, VISENTIN F, et al

An earthworm-like modular soft robot for locomotion in multi-terrain environments

[J]. Scientific Reports, 2023, 13 (1): 1571

DOI:10.1038/s41598-023-28873-w     

ZHANG K, FAN Y, SHEN S

Tunable folding assembly strategy for soft pneumatic actuators

[J]. Soft Robotics, 2023, 10 (6): 1099- 1114

DOI:10.1089/soro.2022.0166     

LI G, WONG T W, SHIH B, et al

Bioinspired soft robots for deep-sea exploration

[J]. Nature Communications, 2023, 14 (1): 7097

DOI:10.1038/s41467-023-42882-3     

GONG Z, FANG X, CHEN X, et al

A soft manipulator for efficient delicate grasping in shallow water: modeling, control, and real-world experiments

[J]. International Journal of Robotics Research, 2021, 40 (1): 449- 469

DOI:10.1177/0278364920917203     

WAN Z, SUN Y, QIN Y, et al

Design, analysis, and real-time simulation of a 3D soft robotic snake

[J]. Soft Robotics, 2023, 10 (2): 258- 268

DOI:10.1089/soro.2021.0144     

FOKOU M R T, XIA Q, JIN H, et al

A soft robotic fish actuated by artificial muscle modules (SoRoFAAM-1)

[J]. Journal of Bionic Engineering, 2023, 20 (5): 2030- 2043

DOI:10.1007/s42235-023-00390-6     

HABICH T L, HAACK J, BELHADJ M, et al

SPONGE: open-source designs of modular articulated soft robots

[J]. IEEE Robotics and Automation Letters, 2024, 9 (6): 5346- 5353

DOI:10.1109/LRA.2024.3388855     

SHAN Y, ZHAO Y, YU H, et al

Design and grasping force modeling for a soft robotic gripper with multi-stem twining

[J]. Journal of Bionic Engineering, 2023, 20 (5): 2123- 2134

DOI:10.1007/s42235-023-00371-9     

ZHANG J, LI Y, KAN Z, et al

A preprogrammable continuum robot inspired by elephant trunk for dexterous manipulation

[J]. Soft Robotics, 2023, 10 (3): 636- 646

DOI:10.1089/soro.2022.0048      [本文引用: 1]

CHEN G, LIN T, LODEWIJKS G, et al

Design of an active flexible spine for wall climbing robot using pneumatic soft actuators

[J]. Journal of Bionic Engineering, 2023, 20 (2): 530- 542

DOI:10.1007/s42235-022-00273-2      [本文引用: 1]

张志远, 王松涛, 王学谦, 等

螺线型气动软体致动器设计与建模

[J]. 机器人, 2020, 42 (1): 10- 20

[本文引用: 1]

ZHANG Zhiyuan, WANG Songtao, WANG Xueqian, et al

Design and modeling of a spiral pneumatic soft actuator

[J]. Robot, 2020, 42 (1): 10- 20

[本文引用: 1]

夏泽洋, 陈君, 甘阳洲, 等

一种用于刚软混杂机器人仿真的耦合模型

[J]. 机器人, 2021, 43 (1): 29- 35

[本文引用: 1]

XIA Zeyang, CHEN Jun, GAN Yangzhou, et al

A coupled model for the simulation of rigid-soft hybrid robot

[J]. Robot, 2021, 43 (1): 29- 35

[本文引用: 1]

王昱欣, 王贺升, 陈卫东

软体机器人手眼视觉/形状混合控制

[J]. 机器人, 2018, 40 (5): 619- 625

[本文引用: 1]

WANG Yuxin, WANG Hesheng, CHEN Weidong

The hybrid eye-in-hand visual/shape control for soft robots

[J]. Robot, 2018, 40 (5): 619- 625

[本文引用: 1]

MULLER D, SAWODNY O

Modeling the soft bellows of the bionic soft arm

[J]. Ifac Papersonline, 2022, 55 (20): 229- 234

DOI:10.1016/j.ifacol.2022.09.100      [本文引用: 1]

徐璠, 王贺升

软体机械臂水下自适应鲁棒视觉伺服

[J]. 自动化学报, 2023, 49 (4): 744- 753

[本文引用: 1]

XU Fan, WANG Hesheng

Underwater adaptive robust visual servo for soft manipulator

[J]. Acta Automatica Sinica, 2023, 49 (4): 744- 753

[本文引用: 1]

CHENG D, XU R, ZHANG B, et al

Fast density estimation for density-based clustering methods

[J]. Neurocomputing, 2023, 532 (1): 170- 182

[本文引用: 1]

徐志博, 刘永生, 户盼茹

结合离群因子和K-means++聚类改进的点云去噪算法

[J]. 信息技术与信息化, 2023, (3): 21- 24

XU Zhibo, LIU Yongsheng, HU Panru

Improved denoising algorithm for point cloud based on outlier factor and K-means++ clustering

[J]. Information Technology and Informatization, 2023, (3): 21- 24

唐佳林, 林寿南, 周壮, 等

基于特征变换结合KD树改进ICP的快速点云配准方法

[J]. 计算机科学, 2023, 50 (Suppl.2): 248- 252

[本文引用: 1]

TANG Jialin, LIN Shounan, ZHOU Zhuang, et al

Fast point cloud registration method for improving ICP based on feature transformation combined with KD tree

[J]. Computer Science, 2023, 50 (Suppl.2): 248- 252

[本文引用: 1]

/

〈 〉