通常,点云配准技术的关键在于找到准确的点对匹配关系,以此为基础获取刚性变换的相应结果. Besl等[7]提出的迭代最近点算法(iterative closest point, ICP)是最经典的双视角点云配准算法,主要通过迭代进行最近邻匹配点对搜索和刚性变换优化2个步骤来完成配准任务,该算法虽然有效,但容易陷入局部最优解,且难以处理部分重叠的点云配准问题. 随着三维点云采集设备的持续发展,各种双视角点云配准方法逐渐被提出,大多数都是在传统ICP上进行改进与优化,因此依然隶属于“点到点”的配准模式. “点到点”配准模式存在2个弊端,一是通常须重复遍历所有的点云数据,这一过程可能会占用并消耗大量的计算资源,导致配准效率低下;二是一般情况下源点云和目标点云可能只有部分重叠,因此搜索到的最近邻匹配点对不一定重合,如不使用合适的过滤手段进行剔除,很可能会影响实际配准效果,甚至导致获得完全错误的刚性变换矩阵.
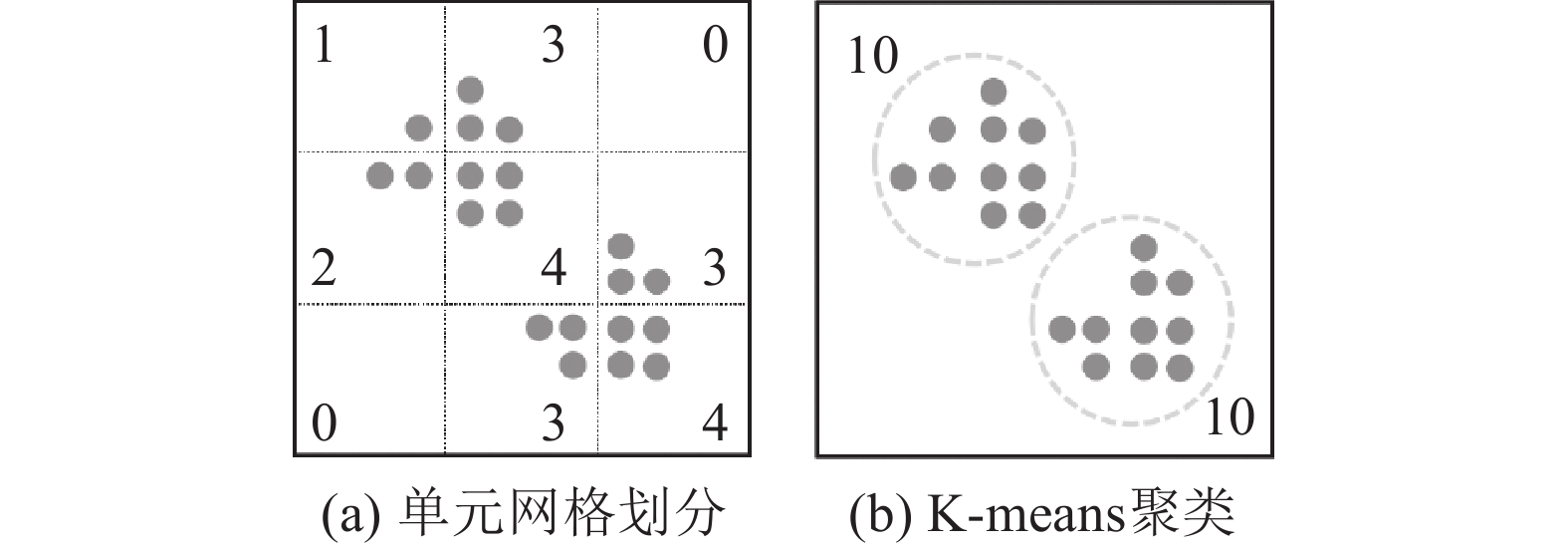
为了规避ICP变体算法或者说“点到点”配准算法的上述弊端,许多学者尝试对配准任务进行进一步定义与建模. 例如,Biber等[8]提出正态分布变换算法(normal distribution transform, NDT),利用正态分布拟合原始的二维点云数据,从而将最小化最近邻匹配点对距离问题转化为基于正态空间的源数据最大概率生成问题,因此隶属于“点到分布”的配准模式. 相较于传统ICP算法,该算法无须建立点对之间的显式连接、无须在每次迭代过程中重复搜索最近邻匹配点,因此即使在数据量较大的情况下也能有效降低计算的时间开销. 然而,这类“点到分布”的算法通常基于固定大小网格来实现空间划分,数据点的密度差异较悬殊,所得的正态分布不一定可靠,因此会影响最终的配准结果.
近年来,神经网络逐渐兴起,深度点云配准技术持续发展. Charles等[9]提出的PointNet将原始三维点云作为输入,利用神经网络获取点云的内部逻辑关系以提取嵌入特征,最终完成分类和分割的任务. 基于这一研究基础,许多学者尝试将深度网络应用在点云配准领域,提出各种各样的深度点云配准算法,有效解决了数据稀疏、不规则且无序的问题. 然而,这些算法一方面需要大量的数据集进行训练,其配准效果依赖数据集的数量和质量;另一方面,这些算法虽然在多数情况下能够求解合适的刚性变换结果,但在处理纹理精细的特定模型或者真实场景时,往往难以取得理想的性能表现.
针对上述问题,提出基于正态分布相似性的双视角点云配准方法. 该方法的优势包括:1)利用K-means算法为源点云和目标点云分别生成若干正态分布聚簇,将传统“点到点”配准问题转化为“分布到分布”配准问题,有效提升配准任务的效率;2)利用正态分布之间的Kullback-Leibler(KL)散度来计算数据属于重叠部分的权重概率,以此为基础弱化不可靠的数据区域,从而有效完成部分重叠的点云配准任务,保证配准结果精度;3)算法将刚性变换配准结果映射到李代数求解器进行求解,相较于传统NDT算法所使用的牛顿求解器,具有更强的原理性和实现性.
1. 相关研究工作
1.1. 基于“点到点”的配准算法
基于传统ICP的点云配准算法往往关注最近邻匹配点对之间的拟合,隶属于“点到点”的配准模式. 为了提升配准精度,Chetverikov等[10]引入重叠百分比参数来裁剪非重叠的数据区域,提出能在一定程度上解决部分重叠配准问题的裁剪迭代最近点算法(trimmed iterative closest point, TrICP);Bouaziz等[11]提出稀疏迭代最近点算法(sparse iterative closest point, SpICP),以稀疏表示理论为基础,利用稀疏lp范数来改进ICP的鲁棒性,但其引入增广拉格朗日函数,计算成本大大增加. 为了提升配准速度,Pavlov等[12]将安德鲁加速器与传统ICP框架进行结合,提出安德鲁加速算法(iterative closest point with Anderson acceleration, AAICP). Zhang等[13]在此基础上引入威尔斯函数鲁棒误差度量,进一步提升了配准效率,也在一定程度上降低了算法对异常值的敏感性. 这类算法耗时较少,但在面对部分重叠配准时,精度提升依然有限. 除此之外,许多同样基于传统ICP的“点到点”配准方法[14-17]也被提出,分别针对局部收敛问题、粗配准问题和异常值问题等进行尝试与探索,有一定改进,但是难以实现效率和精度的统一,且在处理部分重叠配准任务时稳定性较差.
1.2. 基于“点到面”的配准算法
依靠“点到点”配准模式搜索到的最近邻匹配点对较难实现真实重叠,因此部分学者在“点到面”的配准上进行探索. 例如,Chen等[18]最先通过最小化点到面之间的距离来完成点云配准任务,该方法的优势在于能够允许点云数据在平坦区域进行滑动,迭代次数更少且收敛更快,缺陷是依然需要良好的刚性变换初始值. 点到面的度量通常使用非线性最小二乘法进行求解,然而一些研究[19]发现,当初始位姿估计较好时,可以将点到面的度量转化为线性优化问题,从而进一步提升算法性能. Rusinkiewicz[20]提出对称迭代最近点算法(symmetrical iterative closest point, SmICP),利用对称目标函数来实现对于光滑模型或部分重叠模型的精确配准;Li等[21]引入自适应鲁棒损失来优化对称点到面的距离度量,进而提出鲁棒性对称迭代最近点算法(robust symmetrical iterative closest point, RSICP). 这些算法往往能扩宽收敛域,提升收敛速度,但须依赖法向量估计的质量,且每次迭代耗时较长.
1.3. 基于概率模型的配准算法
基于概率模型的配准算法通常隶属于“点到分布”或“分布到分布”的配准模式. 这类算法在配准过程中利用概率分布来拟合实际的点云数据,通常能够容忍噪声值或异常值的存在,效率较高. Magnusson等[22]提出三维NDT算法,将目标点云空间划分为若干规则单元体素网格,并利用网格当中的数据计算对应正态分布的均值和协方差矩阵,从而将点云配准问题转化为最大化源数据的概率生成问题. 耗时大幅降低,但规则化的体素划分致使每个网格中数据数量差异过大,最终的配准结果会受到影响. Stoyanov等[23]在此基础上,将“点到分布”转化为“分布到分布”的配准问题,尝试为源点云和目标点云分别生成三维NDT模型,进而求解能使2个模型尽可能拟合的最优刚性变换结果. 然而该算法依然平等看待每一个正态分布,没有考虑潜在的非重叠数据区域,因此精度表现不佳.
1.4. 基于深度网络的配准算法
深度配准的基本思想是学习点云内部的逻辑结构,从而将低维数据映射为高维嵌入特征,以便完成“特征到特征”的配准任务. Aoki等[24]将Lucas & Kanade算法引入PointNet网络,提出具有迭代递归能力的PointNetLK框架;Wang等[25]提出深度最近点算法(deep closest point, DCP),利用动态图卷积[26]和注意力机制求取最终的刚性变换配准结果;Yuan等[27]提出第1个基于学习且利用概率模型来完成配准任务的深度高斯混合模型网络(deep Gaussian mixture model, DeepGMR),该算法的优势在于无须依赖初始刚性变换矩阵,可以在任意姿态位置将点云数据进行对齐. 上述深度配准方法的性能相较传统配准方法而言有了一定程度上的改进,但它们依然难以处理部分重叠配准问题. 为此,一些面向部分重叠的配准网络[28-29]被提出,在重叠点检测和异常特征掩码等方面给出了解决思路. 然而,这些方法虽然有效,但需要大量的、高质量的数据集进行训练,且难以应对纹理精细的特定模型,在精配准方面的表现可能还不如传统算法.
综上所述,目前大部分的配准算法在本质上依然隶属于“点到点”的配准模式,耗时较长且不一定能有效解决部分重叠的配准问题;部分配准算法采用“点到面”、“点到分布”之类的技术手段,但它们往往难以实现效率和精度的统一. 为此,本研究设计基于正态分布相似性的双视角点云配准方法.
2. 基于正态分布相似性的配准方法
2.1. 模型建立
规定源点云和目标点云可以分别用
式中:
图 1
令
式中:
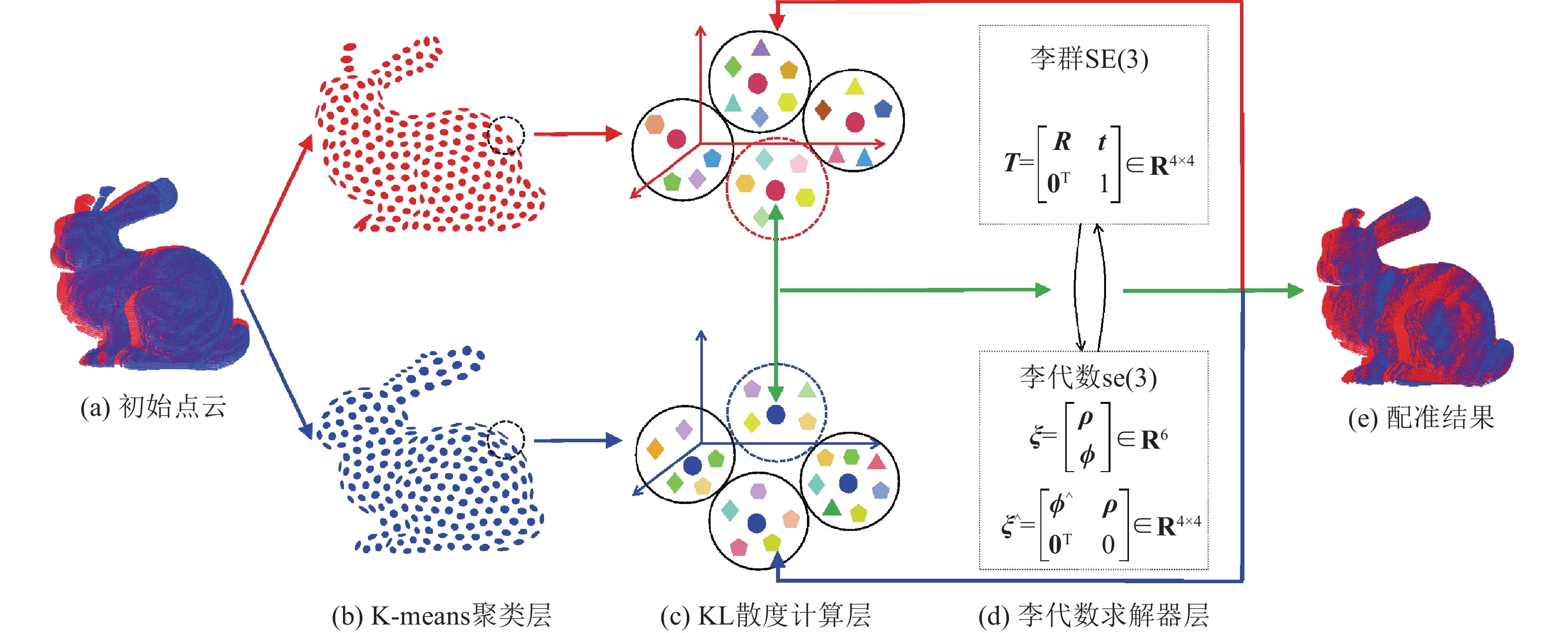
为了优化求解式(2),采用如图2所示的配准策略. 图中,初始点云当中的蓝色部分表示源点云,红色部分表示目标点云. 整个算法框架共分为3层,其中K-means聚类层并不参与算法整体的大循环,但会通过内部迭代来生成稳定的聚簇结果和对应的正态分布参数集;KL散度计算层和李代数求解器层则作为整体共同参与算法的整个迭代过程,直至达到大循环次数阈值上限或相邻2次配准结果没有明显区别,再输出最终的刚性变换矩阵.
图 2
图 2 基于正态分布相似性的双视角点云配准方法示意图
Fig.2 Diagram of pair-wise point cloud registration method based on normal distribution similarity
2.2. 任务求解
由式(2)可知,在利用李代数求解器优化配准结果前,需要2类关键信息:第1类信息是正态分布参数集合
给定初始刚性变换以及2帧点云各自的初始聚簇中心,规定h表示K-means聚类层的内部迭代次数,H表示KL散度计算层和李代数求解器层的整体迭代次数. 基于正态分布相似性的双视角点云配准方法步骤如下.
2.2.1. K-means聚类层
利用K-means聚类算法为源点云和目标点云分别生成若干正态聚簇,并利用其中的数据计算对应的均值和协方差矩阵.
1)为每个源数据
2)利用新一轮的聚簇结果,为每个正态分布更新其均值信息:
式中:
3)重复上述环节直至h达到阈值上限或聚簇均值稳定,略去上下标h,利用最终的聚簇信息为每个正态分布求解其对应的协方差矩阵:
注意,K-means聚类层的上述步骤须分别应用在源点云和目标点云,在此之后,即可得到它们各自的正态分布组件参数
2.2.2. KL散度计算层
利用聚簇均值之间的空间距离来搜索最近邻匹配正态分布,并计算它们的KL散度,以此作为识别非重叠区域的依据.
1)为每个源正态分布
2)在获取最近邻匹配分布的基础上,求解两者的KL散度,以描述它们的数据相似性:
式中:D表示正态分布维度,等于点云的坐标维度3;
3)计算最近邻正态分布匹配对的权重系数,以判断其属于真实重叠的可靠性:
式(2)所需的正态分布参数集信息以及相似性权重系数信息全部求解完毕.
2.2.3. 李代数求解器层
将最终的求解过程映射至李代数空间,获取新一轮刚性变换结果.
为了便于书写,后续求解过程略去下标
式中:
式中:
式中:
式中:
综上,在K-means聚类层获取正态分布参数集的基础上,重复迭代KL散度计算层和李代数求解器层,直至整体大循环次数H达到其阈值上限或相邻2次求解得到的刚性变换矩阵没有明显差异,即可输出最终结果.
2.3. 算法实现和复杂度分析
规定h和H的阈值上限都为200. 在此基础上,本研究所提的基于正态分布相似性的双视角点云配准方法的具体实现如算法1所示.
算法1 基于正态分布相似性的双视角点云配准方法
输入:源点云X,目标点云Y,初始旋转矩阵和平移矩阵,
X和Y各自的初始聚簇中心
1) 初始化h=1,H=1;
Repeat:
2) 令h=h+1;
3) 根据式(3)~(5),分别为源点云和目标点云生成正态分布参数集;
Until:h大于200或前后2次聚簇均值不再发生变化;
Repeat:
4) 令H=H+1;
5) 根据式(6)搜索最近邻匹配正态分布;
6) 根据式(7)、(8)计算最近邻正态分布的相似性权重;
7) 根据式(11)计算李代数求解器相关参数;
8) 根据式(10)、(12)优化新一轮刚性变换配准结果;
Until:H大于200或前后2次配准结果没有明显变化;
输出:最优旋转矩阵R和平移矩阵t
在对所提方法进行复杂度分析之前,作出以下假设:1)待配准的2帧点云所包含的数据量不会相差太大,统一用N表示;2)待配准的2帧点云数据分布密度相对均匀,因此其对应的正态分布聚簇数量不会相差太大,统一用K表示.
2.3.1. 算法的时间复杂度分析
基于上述假设,所提方法的时间复杂度如表1所示,具体分析如下.
表 1 双视角点云配准方法的时间复杂度
Tab.1
| 所属模块 | 具体操作 | 时间复杂度 |
| K-means聚类 | 建立k-d树 | |
| K-means聚类 | 更新聚簇并计算正态参数 | |
| KL散度计算 | 搜索最近邻匹配正态分布 | |
| KL散度计算 | 计算KL散度并生成权重 | |
| 李代数求解器 | 优化新一轮刚性变换 |
1) K-means聚类层. 为源点云当中的K个聚簇中心建立k-d树,复杂度为
2) KL散度计算层. 为源点云的每一个正态分布搜索其在目标点云空间的最近邻匹配,复杂度为
3) 李代数求解器层. 求解过程相当于遍历所有正态组件参数,整体复杂度为
2.3.2. 算法的空间复杂度分析
令D表示输入数据的维度,结合上述假设,可知2帧点云各自占用的空间大小为
1) K-means聚类层. 该层的目标是更新簇中心和协方差矩阵,两者所占用的空间大小直接关系于正态聚簇个数K,因此复杂度可以分别表示为
2) KL散度计算层. 该层的任务是求解最近邻匹配正态分布聚簇之间的相似性权重,对应的空间复杂度与正态分布数量呈线性相关,因此可以直接表示为
3) 李代数求解器层. 该层直接利用上述环节所获取的正态参数集信息和相似性权重信息来优化刚性变换配准结果,期间没有大量额外空间须被耗用,因此复杂度用
基于正态分布相似性的双视角点云配准方法空间复杂度如表2所示. 本研究输入点云的维度D=3,所提方法的空间复杂度与K可以看作线性关系,而K一般又远小于点云数据量N,因此所提方法空间复杂度整体较低.
表 2 双视角点云配准方法的空间复杂度
Tab.2
| 所属模块 | 具体操作 | 空间复杂度 |
| K-means聚类 | 建立k-d树 | |
| K-means聚类 | 求解正态分布聚簇中心 | |
| K-means聚类 | 求解正态分布协方差矩阵 | |
| KL散度计算 | 计算KL散度并生成权重 | |
| 李代数求解器 | 优化新一轮刚性变换 |
3. 实验结果
为了验证本研究所提出的基于正态分布相似性的双视角点云配准方法的性能,使用4个斯坦福数据集[32](Bunny、Armadillo、Buddha、Dragon)进行消融实验、精度实验、效率实验等. 4个数据集包含的点云帧数分别为10、12、15和15,每帧点云平均拥有的数据量分别为
将本研究所提方法与其他8种较流行的算法进行对比,具体包括TrICP[10]、NDT[22]、SpICP[11]、SmICP[20]、AAICP[13]、刚性变换一致(rigid transformation consensus, RTC)算法[16]、镜像迭代(mirrored iterative closest point, MICP)算法[17]、RSICP[21],所有测试均在Matlab R2021a上实现. 如无特殊说明,在实验过程中,将对同一数据集的相邻2帧点云两两配准,最终求解指标的平均值以说明不同算法的性能. 所用的精度指标包括平均均方根误差RMSE和总体配准成功率SR,定义如下:
式中:F表示数据集两两配准的总次数,具体为该数据集的点云帧数减去1;
对于待配准的某特定数据集,指标RMSE能够反映方法对不同重叠百分比下的各相邻帧进行配准时的平均精确度,而指标SR能够反映方法在配准过程中保持良好性能的稳定性.
3.1. 参数选择
本研究所提方法的参数K,表示源点云或目标点云的正态分布聚簇个数. 一般而言,这个数量难以直接估计,但可以通过确定每个分布平均包含的数据量进行反推. 令
图 3
图 3 正态分布聚簇内平均数据量不同时的配准结果
Fig.3 Registration results with different mean data volume within normal distribution clusters
3.2. 精度和效率实验
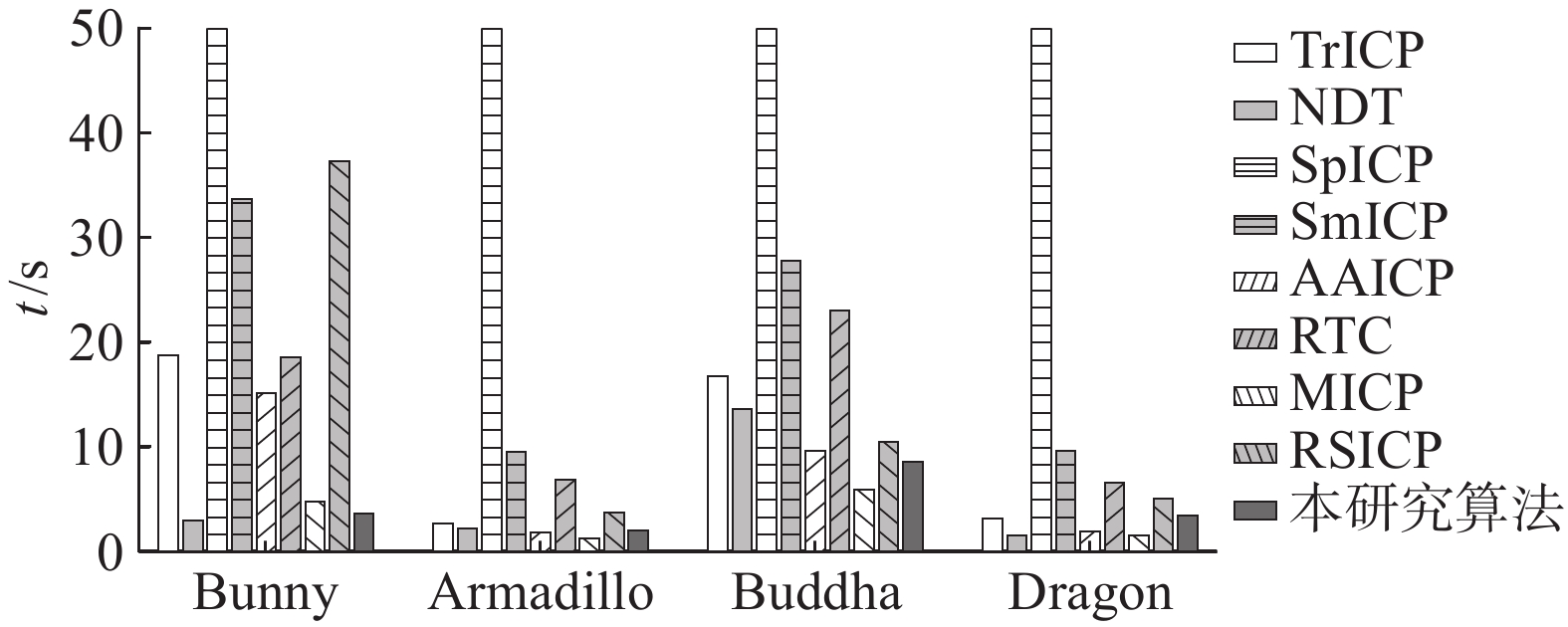
在刚性变换的真值结果中加入随机扰动,以生成初始配准参数. 在斯坦福的不同数据集上对各种算法进行测试,所用指标包括平均均方根误差RMSE、平均配准成功率SR、平均配准用时t. 配准结果如表3所示. 表中,粗体表示配准中的最优值,下划线表示次优值,Initial表示未使用任何配准方法. 为了便于观察差异,如图4所示给出了用不同方法配准Bunny第2、3帧和Dragon第12、13帧的结果示意图,这些点云数据之间的重叠率约为65%. 图中,RP表示经配准后2帧点云的拟合度,颜色越偏蓝色表示算法越能处理部分重叠的点云配准任务,越偏红色表示处理能力越差. 此外,为了进一步说明不同方法的运行效率,如图5所示给出了它们在不同数据集上配准的平均用时示意.
表 3 不同方法在4个数据集上的精度结果对比
Tab.3
| 配准方法 | Bunny | Armadillo | Buddha | Dragon | |||||||
| RMSE | SR | RMSE | SR | RMSE | SR | RMSE | SR | ||||
| Initial | — | — | — | — | |||||||
| TrICP | 2.759 4 | 0.78 | 1.00 | 0.64 | 0.93 | ||||||
| NDT | 0.00 | 0.00 | 0.50 | 0.00 | |||||||
| SpICP | 0.56 | 0.91 | 0.21 | 0.57 | |||||||
| SmICP | 0.22 | 1.00 | 1.00 | 0.86 | |||||||
| AAICP | 0.11 | 1.00 | 1.00 | 0.93 | |||||||
| RTC | 0.56 | 0.73 | 0.86 | 0.79 | |||||||
| MICP | 0.44 | 1.00 | 0.249 6 | 1.00 | 0.93 | ||||||
| RSICP | 0.56 | 1.00 | 1.00 | 0.335 2 | 1.00 | ||||||
| 本研究方法 | 1.00 | 0.161 9 | 1.00 | 1.00 | 1.00 | ||||||
图 4
图 4 不同方法配准结果的颜色渐变示意图
Fig.4 Color gradient illustration of registration results of different methods
图 5
图 5 不同双视角点云配准方法的运行时间对比
Fig.5 Comparison of relative runtime of different pair-wise point cloud registration methods
TrICP、SpICP、AAICP和MICP都是对传统ICP的改进,隶属于“点到点”配准模式. TrICP主动引入重叠百分比参数来预测重叠部分,虽然有效,但依然仅仅利用点对之间的空间距离来完成配准任务,一旦非重叠区域面积增大或更加精细复杂,很可能因陷入大量迭代而致使效率和精度同时下降. SpICP基于稀疏表示理论来增强算法整体的鲁棒性,但由于引入了增广拉格朗日函数,算法效率处于对比当中的最差. AAICP将安德鲁加速算法引入传统ICP框架,效率得到有效提升;此外,该算法基于威尔斯函数设计了鲁棒性误差度量,来避免噪声值和异常值的不利影响,但其准确性同样依赖于真实重叠百分比. MICP在配准过程中须为数据建立可靠的邻域空间,算法本身非常高效,但最终的配准结果并不稳定,尤其是在真实重叠百分比较低时,其搜索的邻域空间往往并不可靠甚至完全错误,致使最终的配准精度大幅下降.
NDT和RTC都是基于概率的配准算法. NDT隶属于“点到分布”配准,非常高效,但须对点云空间进行单元体素划分,提前确定合适的网格大小,否则数据分布极不均匀,导致正态参数求解的偏差过大. RTC会为最近邻匹配点对分配一个后验概率,以指示其属于真实匹配的可能性大小,在本质上仍属于“点到点”配准,虽能在一定程度上解决部分重叠问题,但其本身须固定若干高斯参数,参数选取不当容易导致配准失败.
SmICP和RSICP虽然也是对ICP的改进,但将传统“点到点”转化为“点到面”配准,使用对称目标函数来尽可能优化点面距离,从而能够提升配准的精度. 此外,相较于SmICP,RSICP由于引入鲁棒性对称度量,既能拓宽收敛域又能提升收敛速度,因此整体性能会更强. 然而这类“点到面”的算法都须估计法向量,在迭代过程中可能会耗用更多时长,且在处理像Bunny数据集这样的低重叠配准任务时,其度量结果可能会出现较大的偏差,致使配准完全失败.
综上所述,相较于其他方法,本研究所提方法有性能上的优势,能兼顾效率和精度. 具体来说,算法采用“分布到分布”配准技巧,能够避免频繁对所有数据进行遍历迭代,耗时大幅降低;算法利用最近邻正态分布之间的相似性来识别潜在的非重叠区域,从而能有效完成部分重叠配准任务,提升配准精度.
3.3. 鲁棒性实验
为了验证本研究所提方法对于数据异常值的鲁棒性,为斯坦福各个数据集分别添加信噪比SNR为50、25 dB的高斯噪声. 此外,为了保证公平性,所有方法在实验过程中须对同一数据集的相邻2帧进行两两配准,最终求解平均均方根误差RMSE作为该数据集的一次实验数据,在此基础上对该数据集独立重复进行共计30次实验后求取实验数据均值. 最终的实验结果如表4所示,其中指标RMSE以“平均值±标准差”的形式进行表示,粗体部分表示对比中的最优值,下划线部分表示对比中的次优值. 由实验结果可知,在加入高斯噪声后,不同方法的配准精度都会出现一定程度的扰动,且噪声越剧烈,扰动的幅度可能越大. 在相同的噪声水平下,本研究所提方法能保持相对更稳定的配准效果. 一方面,该算法利用K-means进行正态聚类和参数求解,灵活性和可靠性较高,即使出现噪声值或异常值,其正态分布拟合也不会出现较大波动,配准所用的均值和协方差矩阵信息相对稳定;另一方面,该算法使用基于KL散度的权重系数来识别非重叠的数据区域,能够将配准的注意力集中在真实重叠部分,从而规避异常数据的影响,进一步提升配准过程的鲁棒性.
表 4 不同高斯噪声(50、25 dB)下的配准结果
Tab.4
| 配准方法 | SNR/dB | RMSE | |||
| Bunny | Armadillo | Buddha | Dragon | ||
| TrICP | 50 | ||||
| 25 | |||||
| NDT | 50 | ||||
| 25 | |||||
| SpICP | 50 | ||||
| 25 | |||||
| SmICP | 50 | ||||
| 25 | |||||
| AAICP | 50 | ||||
| 25 | |||||
| RTC | 50 | ||||
| 25 | |||||
| MICP | 50 | ||||
| 25 | |||||
| RSICP | 50 | ||||
| 25 | |||||
| 本研究方法 | 50 | ||||
| 25 | |||||
NDT和RTC均以高斯概率模型为基础进行配准. NDT使用规则单元来划分正态分布,一旦噪声数据增加,固定网格的数据信息变化相对剧烈,因此正态参数求解误差增大,方法的鲁棒性下降. RTC为每一对最近邻匹配点计算其是否属于“真实匹配”的后验概率,而在噪声数据较多时,点对的概率评估可靠性势必会受到影响,致使最终的配准结果波动幅度较大.
TrICP、SpICP、SmICP、AAICP、MICP和RSICP均为基于ICP的改进算法. 其中,TrICP和MICP能够将注意力放在数据的重叠区,对于异常信息有一定的过滤和清除作用,因此具有一定的鲁棒性,但当高斯噪声加剧时,这种识别能力可能会受到一定影响. SpICP和AAICP都在传统“点到点”配准目标函数的基础上进行改进和优化,前者使用lp范数替换原先的l2范数,后者引入基于威尔斯函数的鲁棒性误差度量,都能在一定程度上增强配准结果的稳定性. SmICP和RSICP均采用“点到面”的方式对点云数据进行配准,能够有效规避“点到点”配准的信息度量误差,且两者都使用对称型目标函数来降低算法对于噪声数据的敏感程度. 然而,这些算法虽然在其他数据集上有较好的配准表现,但在处理像Bunny数据集这样重叠百分比极低的数据时依然容易出现剧烈的精度偏移.
3.4. 消融实验
本研究所提方法因隶属“分布到分布”配准而拥有较高的效率,因引入由KL散度推导的相似性权重系数而拥有较好的精度. 从这2个要素出发,可以设计以下实验:1)“点到分布”+“无相似性权重”(P2DNDT),即将K-means聚类层只应用在目标点云,将配准问题转化为源数据的概率生成和最大问题,中间不涉及KL散度计算,但利用李代数求解器对结果进行求解;2)“分布到分布”+“无相似性权重”(D2DNDT),即配准任务不包含KL散度计算层,除此之外的过程皆与本研究所提方法一致. 须注意,由于KL散度计算须面向“分布到分布”,不能设计“点到分布”+“有相似性权重”的实验. 最终的消融实验结果如表5所示,用于比较的实验指标包括平均均方根误差RMSE、平均配准用时t和整体配准成功率SR. 表中,粗体表示结果中的最优值. 由实验结果可知,D2DNDT的效率略高于所提方法的,这是因为其无须经过KL散度计算层处理,但其也因此无法对非重叠区域进行识别,配准精度大幅下降. 与之相比,P2DNDT须遍历所有源数据点,信息较为全面可靠,因此在精度方面会有一定保障,但依然低于本研究所提方法的,且该算法须重复遍历源点云当中的所有数据,会消耗大量的时间.
表 5 在不同数据集上消融实验的结果
Tab.5
| 数据集 | Initial | P2DNDT | D2DNDT | 本研究方法 | |||||||||
| RMSE | RMSE | t /s | SR | RMSE | t /s | SR | RMSE | t /s | SR | ||||
| Bunny | 19.75 | 0.33 | 3.99 | 0.33 | 3.74 | 1.00 | |||||||
| Armadillo | 14.58 | 0.91 | 1.64 | 0.82 | 2.33 | 1.00 | |||||||
| Buddha | 42.88 | 1.00 | 4.35 | 1.00 | 9.47 | 1.00 | |||||||
| Dragon | 15.99 | 1.00 | 1.93 | 0.71 | 3.56 | 1.00 | |||||||
3.5. 真实场景实验
为了进一步论证所提算法的性能,在真实数据集GazeboS和GazeboW[33]上测试,两者各包含约30帧的点云,每帧点云含3~5万个数据,这些数据由配备扫描仪的机器人采集得到. 如表6所示为不同方法对2个数据集相邻2帧两两配准后的实验结果. 表中,粗体表示结果中的最优值,下划线表示结果中的次优值. 可以看出,除了NDT之外,多数算法都能得到精度相对良好的配准结果,这是因为点云数据是由机器人沿二维闭合路径按照较小的视角变化采集得到的,相邻2帧的重叠百分比较高,因此它们的配准精度均较高. 整体来看,本研究所提方法在精度上相较于TrICP、SmICP、AAICP等算法具有明显的优势;在2个数据集上精度分别排名第2的RSICP算法和SpICP算法,其平均配准效率均落后于本研究所提方法,其中,RSICP的效率不足本研究所提方法的60%,而SpICP的效率甚至不足1%. 综上所述,本研究所提方法在真实环境场景配准方面也具有较好的应用潜力.
表 6 在真实场景数据集上的配准结果
Tab.6
| 配准方法 | GazeboS | GazeboW | |||||
| RMSE | t /s | SR | RMSE | t /s | SR | ||
| Initial | — | — | — | — | |||
| TrICP | 13.88 | 0.84 | 2.83 | 1.00 | |||
| NDT | 2.85 | 0.26 | 1.97 | 0.63 | |||
| SpICP | 0.77 | 0.019 6 | 402.32 | 1.00 | |||
| SmICP | 34.42 | 0.74 | 17.37 | 0.97 | |||
| AAICP | 5.77 | 0.71 | 2.29 | 1.00 | |||
| RTC | 5.66 | 0.74 | 1.94 | 1.00 | |||
| MICP | 2.24 | 0.71 | 1.54 | 0.93 | |||
| RSICP | 26.04 | 0.93 | 7.88 | 0.97 | |||
| 本研究方法 | 9.48 | 0.90 | 4.25 | 1.00 | |||
4. 结 论
(1)所提算法通过引入K-means聚类策略,将传统“点到点”配准模式转化为“分布到分布”的配准问题,不仅规避了传统正态分布变换规则划分体素单元致使数据不均的弊端,也有效保证了配准任务的整体效率.
(2)为了解决部分重叠配准任务,所提算法引入相似性权重对非重叠区域进行识别. 方法利用均值之间的距离来搜索最近邻匹配分布,并在此基础上计算KL散度,散度越小,意味2个分布越相似,为它们赋予权重则越高. 经过这一环节处理,可以有效提升配准结果的精度.
(3)在公开数据集上的结果表明,相较于目前主流的基于ICP或“点到点”配准的算法,所提方法能够在兼顾效率的同时提升配准结果的精度,且可以有效容忍噪声的存在,在真实数据集上也表现出了良好的适应能力和应用能力.
(4)尽管所提方法在性能上有一定优势,但也存在待改进的方面. 由于方法更适合用于庞杂精细模型的双视角配准任务,因此如何将其应用至深度网络进行嵌入特征分析,或如何将其应用至多视角点云配准,将成为后续工作的重点.
参考文献
Evaluation of the ICP algorithm in 3D point cloud registration
[J].DOI:10.1109/ACCESS.2020.2986470 [本文引用: 1]
Global-PBNet: a novel point cloud registration for autonomous driving
[J].DOI:10.1109/TITS.2022.3153133 [本文引用: 1]
基于灰度相似性的激光点云与全景影像配准
[J].
Registration of laser point cloud and panoramic image based on gray similarity
[J].
三维场景点云理解与重建技术
[J].DOI:10.11834/jig.230004 [本文引用: 1]
Scene point cloud understanding and reconstruction technologies in 3D space
[J].DOI:10.11834/jig.230004 [本文引用: 1]
A method for registration of 3-D shapes
[J].DOI:10.1109/34.121791 [本文引用: 1]
Sparse iterative closest point
[J].DOI:10.1111/cgf.12178 [本文引用: 2]
Fast and robust iterative closest point
[J].
Go-ICP: a globally optimal solution to 3D ICP point-set registration
[J].DOI:10.1109/TPAMI.2015.2513405 [本文引用: 1]
Improved iterative closest point (ICP) 3D point cloud registration algorithm based on point cloud filtering and adaptive fireworks for coarse registration
[J].DOI:10.1080/01431161.2019.1701211
Point set registration via rigid transformation consensus
[J].DOI:10.1016/j.compeleceng.2022.108098 [本文引用: 1]
面向缺失点云配准的镜像迭代最近点算法
[J].DOI:10.7652/xjtuxb202307019 [本文引用: 2]
Mirrored iterative closest point algorithm for missing point cloud registration
[J].DOI:10.7652/xjtuxb202307019 [本文引用: 2]
Object modelling by registration of multiple range images
[J].DOI:10.1016/0262-8856(92)90066-C [本文引用: 1]
A symmetric objective function for ICP
[J].
Robust symmetric iterative closest point
[J].DOI:10.1016/j.isprsjprs.2022.01.019 [本文引用: 2]
Scan registration for autonomous mining vehicles using 3D-NDT
[J].DOI:10.1002/rob.20204 [本文引用: 2]
Dynamic graph CNN for learning on point clouds
[J].
Efficient registration of multi-view point sets by K-means clustering
[J].DOI:10.1016/j.ins.2019.03.024 [本文引用: 1]
3DMNDT: 3D multi-view registration method based on the normal distributions transform
[J].DOI:10.1109/TASE.2022.3225679 [本文引用: 1]
Challenging data sets for point cloud registration algorithms
[J].DOI:10.1177/0278364912458814 [本文引用: 1]