模型参考自适应控制(model reference adaptive control, MRAC)基于参考模型实时修正控制系统的指令信号,使控制器按照预设的自适应机制实现参数自适应,达到控制误差最小化的目的[9-11]. Piippo等[12]提出基于矢量控制的模型参考自适应永磁同步电机无速度传感器方案,利用q轴电流信息得到实际转速,具备一定的动静态性能. 王庆龙等[13]提出基于双滑模模型参考自适应系统的永磁同步电机无传感器控制策略,分别建立电机自身模型和电机电流模型,通过滑模算法获得位置信息. 在MRAC理论方面,Anderson等[14]针对控制系统匹配不确定性和参数不确定性的非线性动力系统,提出新的MRAC自适应律,在控制系统的跟踪误差和控制输入约束条件下,极大程度提高了跟踪误差收敛的速率. Kamalifar等[15]提出基于状态反馈的鲁棒模型自适应控制方法,在MRAC基础上增加了鲁棒控制器,使得控制系统的收敛速度、精度和鲁棒性都得到改善. Mishra等[16]提出以视觉传感器(未知非线性系统)信号为输入量的自适应控制器设计方法,用于AGV路径跟踪,使每组驱动电机获得良好的稳态性能.
MRAC针对控制系统参数不确定性问题,给出了优良的解决方案,但是其应用并未普及,重要的原因是MRAC中参数估计的计算过程复杂,参考模型的选取难度大. 考虑到路况复杂、载荷变化大及驱动轮间负载分布不均衡等因素,本研究以麦克纳姆轮AGV为对象,将MRAC应用于AGV伺服系统,探究AGV在运动过程中的动、静态性能.
1. AGV控制系统
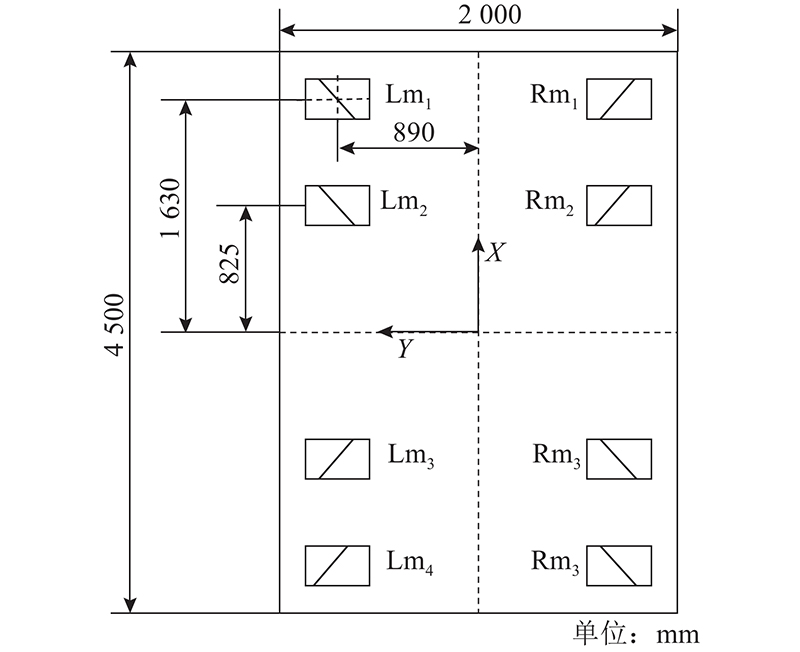
如图1所示,麦克纳姆轮AGV的车体为背负式结构,主要包括车架、麦克纳姆轮、铅酸电池组、电气控制柜、声光报警器及安全防撞传感器等. AGV驱动是整个系统的核心部件之一,优良的伺服控制性能是AGV获得较高定位精度及动态性能的关键. 8组呈对称式分布的伺服电机协同工作,通过减速器带动麦克纳姆轮,使车体实现包括直行、斜行、原地回转等在内的多种复杂运动. 车体自重为2 t,最大负载为5 t. 理论上每台伺服电机承受1/8的负载;在实际运行中,由于路况及负载是变化的,导致运动模型的控制参数不确定,从而影响控制系统性能.
图 1
如图2所示,AGV控制系统硬件由铅酸电池组提供动力电源,嵌入式PC来自德国倍福公司,基于EtherCAT总线拓扑8组伺服电机的驱动器,ADS通信协议以及I/O信号集成了外部传感器和输入输出设备(如触摸屏、遥控器、防撞传感器等).
图 2
2. 基于MRAC的AGV伺服系统
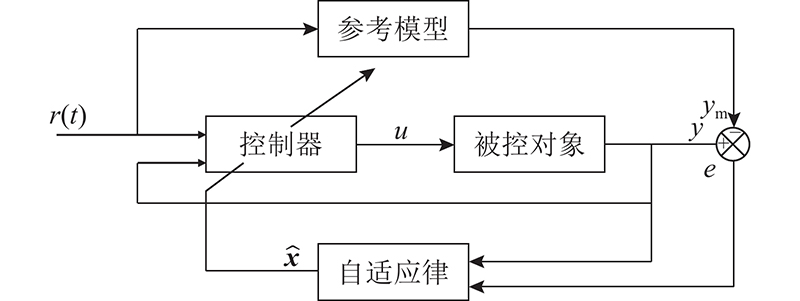
2.1. MRAC原理
图 3
2.2. AGV驱动系统运动模型
永磁同步电机在dq坐标系下的数学模型包括电压方程、磁链方程、转矩方程和运动方程,共4个部分[22].
电压方程为
式中:
磁链方程为
式中:
采用磁场分量
式中:
运动方程为
式中:
忽略伺服电机磁饱和,当
式中:s为拉普拉斯算子,
驱动器放大电路采用PWM可逆功率放大器,根据工程近似处理原则,将三相逆变器视作纯滞后的放大环节,简化成一阶惯性环节,定义
机械传递环节有减速器,视作比例环节,定义i为减速比;伺服电机将麦克纳姆轮的旋转运动转换为平台的直线运动,定义D为轮子的外包络圆直径,将轮子视作积分环节,因此机械传递环节的传递函数为
电机等效转动惯量
综上所述,建立AGV单个驱动系统输出的直线位移与电机输入电压间的传递函数为
电机工作在不超过2 000 r/min的低频段,因此对以上传递函数进行降阶处理,设置成标准二阶系统,一方面降低系统自身的复杂程度,另一方面减少参考模型的计算量. AGV驱动系统的各个参数如表1所示,将数据代入式(11),得到AGV单个驱动系统在空载(
表 1 AGV驱动系统运动模型参数
Tab.1
| 参数 | 数值 | 参数 | 数值 | |
| i | 50 | J1/(kg·m2) | 5.93×10−4 | |
| D/mm | 425 | J2/(kg·m2) | 7.23×10−4 | |
| Kc/(V·A) | 31.416 | Ke/(V·s) | 4.24 | |
| τc/ms | 0.725 | L/mH | 3.47 | |
| Ki | 30 | R/Ω | 18.5 | |
| τi /ms | 0.5 | np | 10 |
2.3. 参考模型
自适应过程是基于参考模型与实际控制系统输出间的相对误差实现的,参考模型的选择必须兼顾自适应系统自身性能和实际控制系统的性能要求. 由于参考模型与实际模型阶数相同,系统输出响应调整时间小于0.15 s,选择二阶系统作为参考模型的传递函数为
式中:
2.4. 控制律与自适应律
根据AGV实际驱动系统的传递函数,结合式(12)和MRAC原理,得到驱动系统在空载时的二阶相伴线性控制方程为
由于负载具有不确定性,假设在未知负载作用下的系数为
根据参考模型的传递函数式(14)和MRAC原理,得到式(14)的二阶相伴线性控制方程为
MRAC的目的是选取合适的控制律和自适应律,使控制对象的输出跟踪以上参考模型的输出. 选取辅助变量,时域信号
式中:
由于
结合式(16)、(18)、(20),消去
可以看出,为了使实际模型跟踪参考模型输出,
代入式(21),得到
令
定义广义误差向量
针对广义误差向量
式中:
假设
且
李雅普诺夫函数在大范围渐进稳定,即
并且
由式(29),可以求得
由于系数
代入式(32)后得到自适应律的参数表达式为
赫尔维茨多项式系数由实验测得,其中
2.5. 低通滤波器
伺服控制系统在受到外部高频信号干扰,或者控制环参数设置不合理的情况下,很容易引起驱动系统剧烈振动,甚至会对机械传动部件造成致命损伤.
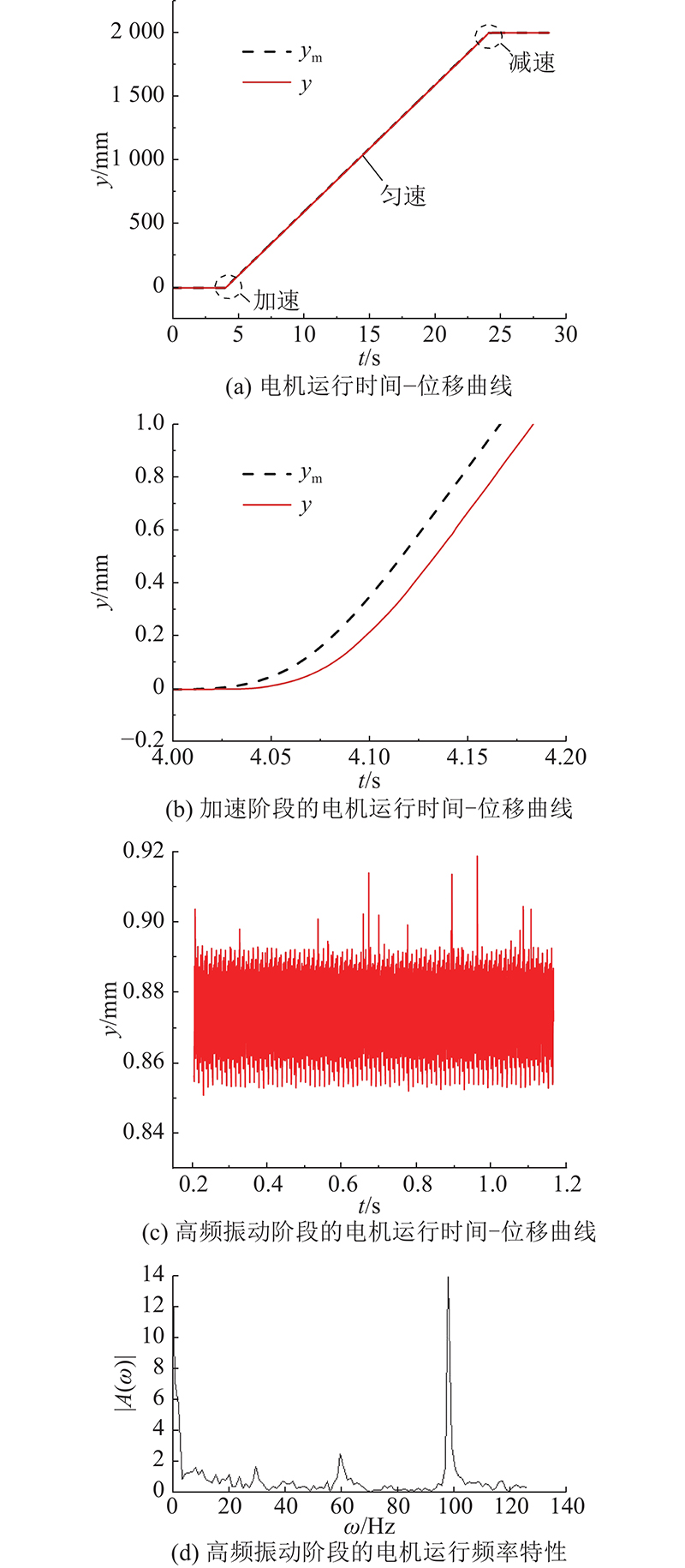
AGV驱动系统引入MRAC之后,为了获得较快的伺服电机收敛速度,通常选取相对较大的增益矩阵
图 4
图 4 采用模型参考自适应控制的电机位移特性
Fig.4 Motor displacement characteristics with model reference adaptive control
式中:
3. AGV运动控制实验
图 5
图 6
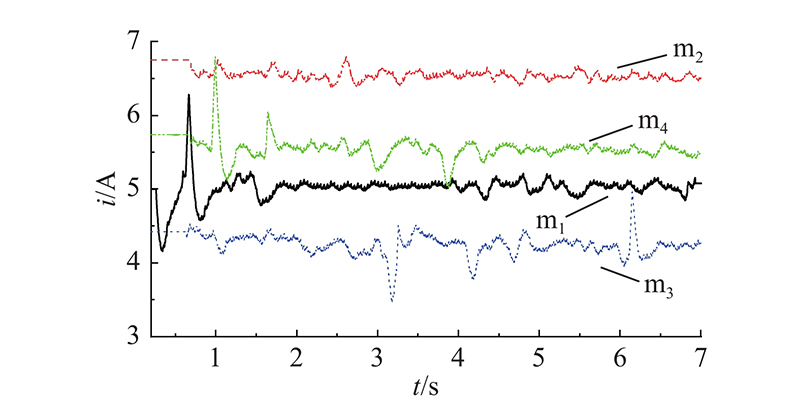
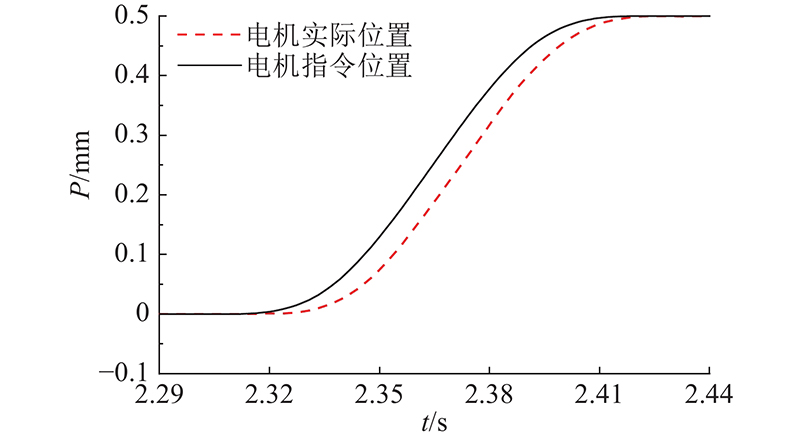
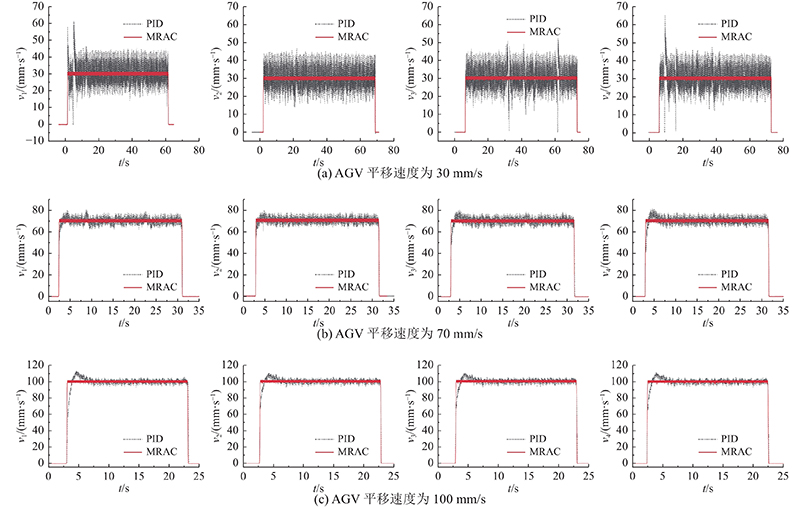
传统PID和MRAC这2种控制方法均可以在TwinCAT软件中实现. 车体加载负载为3 t,加上自重,总计负载为5 t. 实验路面可见凹凸起伏的不平整区域,会造成冗余驱动的电机组产生负载不均的现象. 如图7所示为4组电机(编号分别为m1、m2、m3、m4)在该路径下的实际运行电流. 可以看出,电机间的实际运行电流最大差异为2 A,m1、m4受负载影响较大,有1.5 A的波动,折算成扭矩,为4.96 N·m. 如图8所示为采用MRAC的驱动电机阶跃信号响应特性(幅值为0.5 mm). 图中,P为电机运动位移,伺服电机在[2.305 , 2.425] s完成阶跃响应,上升时间为0.12 s,超调量与稳态误差为零,满足参考模型设计指标. 选取平移速度分别为30、70、100 mm/s的AGV,记录8组电机中的外侧4组在2种控制方法下的实际速度(折算成线速度)v1、v2、v3、v4,结果如图9所示. PID控制方法的参数(如摩擦力、阻尼测量,频率响应测试)由伺服系统软件自动整定,再经过三环控制理论计算,进行适当优化. 可以看出,当AGV在低速模式下(平移速度为30 mm/s)时,4个轮子自身的速度波动较大,最大有50%的超调,车体有轻微抖动. 在行驶过程中,受到路面不平整和电机间相互作用的影响,伺服电机的实际速度出现明显的波动. 在MRAC控制下,4个轮子的速度波动为6.5%,路面不平整带来的不利影响有所抑制. 当平移速度增加到70 mm/s时,PID控制方法的速度波动下降到17%,但是AGV仍然受到路况影响,速度产生突变,并且电机的稳态误差为1.8 mm. MRAC方法下的4组速度波动误差为5%,没有受到速度增加和路面不平整因素的影响. 当平移速度达到100 mm/s时,PID控制方法的速度波动为12%,但是受到路面状况的影响比较大. MRAC方法将4组速度稳定在100 mm/s,波动为3%,电机自身的稳态误差不超过1.8 mm.
图 7
图 8
图 9
图 9 不同AGV平移速度时驱动电机的响应速度
Fig.9 Drive motor speed response at different speeds of AGV
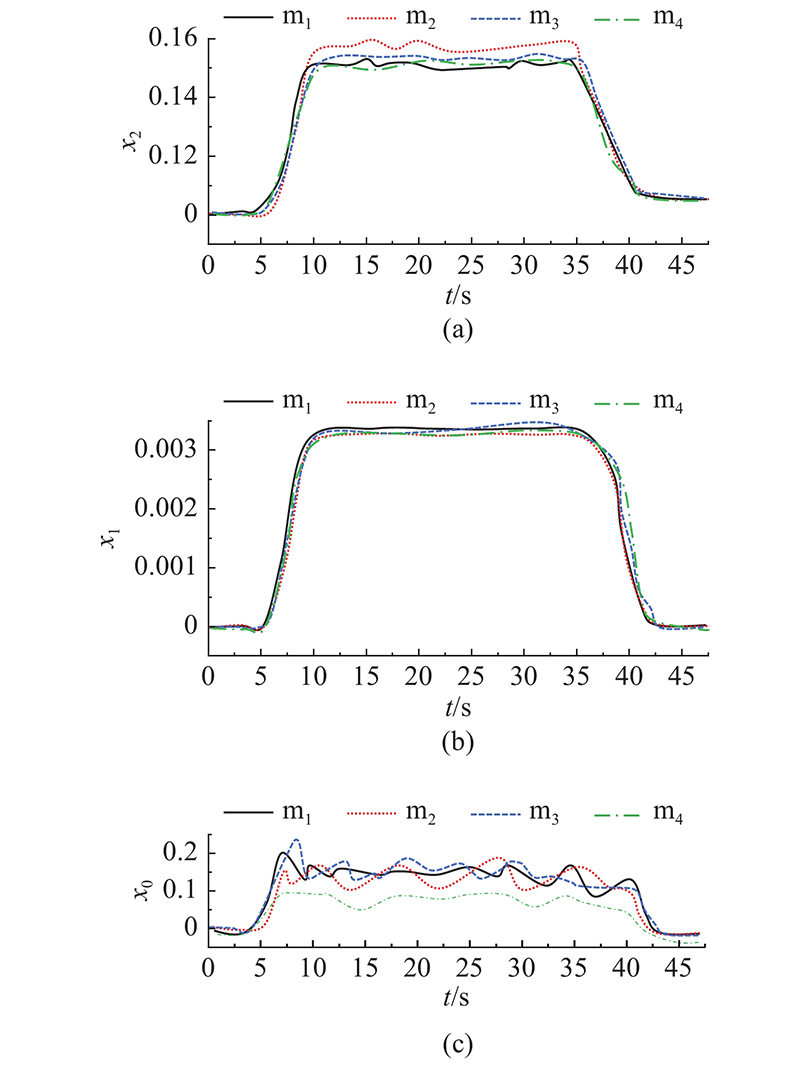
如图10所示为AGV在固定路径平移速度为100 mm/s时,4组电机的自适应参数
图 10
图 10 4组电机在AGV平移速度100 mm/s时的自适应参数调整曲线
Fig.10 Adaptive parameter adjustment curve of four motors at AGV speed of 100 mm/s
表 2 采用模型参考自适应控制的AGV停车精度测试结果
Tab.2
| mm | |||||||
| Pt | Pa | Pt | Pa | Pt | Pa | ||
| 0 | 0.02 | 4 000 | 4 001.24 | 8 000 | 8 002.89 | ||
| 1 000 | 1 000.69 | 5 000 | 5 001.77 | 9 000 | 9 003.12 | ||
| 2 000 | 2 000.75 | 6 000 | 6 002.21 | 10 000 | 10 003.51 | ||
| 3 000 | 3 000.96 | 7 000 | 7 002.22 | —— | —— | ||
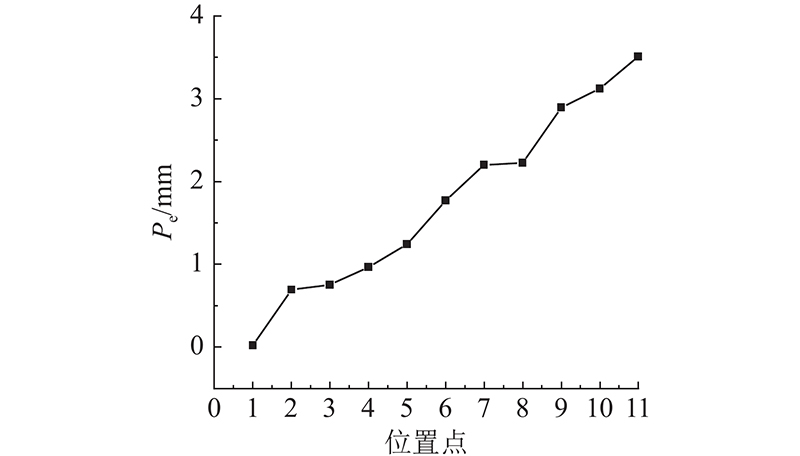
图 11
图 11 采用模型参考自适应控制的AGV定位误差测试结果
Fig.11 Results of AGV positioning error at model reference adaptive control method
4. 结 论
(1)设计基于MRAC的8驱麦克纳姆轮AGV运动控制系统,利用李雅普诺夫稳定理论求解MRAC控制律和自适应律,消除AGV在运行过程中由于负载不均引起的控制参数不确定性对系统控制性能的影响.
(2)分析基于MRAC的AGV控制系统在电机运行过程中的位移振动信号,设计二阶巴特沃兹低通滤波器,有效消除由于较大自适应增益参数引起的电机高频振荡,保证了AGV系统稳定运行.
(3)将MRAC应用于AGV系统。实验结果表明,与传统PID控制方法相比,MRAC方法下的AGV电机速度波动不超过3%,车体最大停车误差为3.6 mm.
参考文献
轮式移动机器人研究综述
[J].DOI:10.3969/j.issn.1001-3881.2009.08.079 [本文引用: 1]
A review of wheeled mobile robots
[J].DOI:10.3969/j.issn.1001-3881.2009.08.079 [本文引用: 1]
Kalman filter sensor fusion for Mecanum wheeled automated guided vehicle localization
[J].
麦克纳姆轮驱动的移动机器人自适应滑模控制器设计
[J].DOI:10.3969/j.issn.1000-2758.2018.04.004 [本文引用: 1]
Design of adaptive sliding mode controller for mobile robot driven by Mecanum
[J].DOI:10.3969/j.issn.1000-2758.2018.04.004 [本文引用: 1]
Inertial navigation system for an automatic guided vehicle with Mecanum wheels
[J].DOI:10.1007/s12541-012-0048-9 [本文引用: 1]
Geometry and kinematics of the Mecanum wheel
[J].DOI:10.1016/j.cagd.2008.07.008 [本文引用: 1]
磁导航AGV控制系统的设计与实现
[J].DOI:10.3969/j.issn.1001-9944.2014.03.002 [本文引用: 1]
Design and implementation of the magnetic navigation AGV control system
[J].DOI:10.3969/j.issn.1001-9944.2014.03.002 [本文引用: 1]
Robust adaptive fuzzy control for a class of uncertain nonaffine nonlinear systems with unknown control directions
[J].DOI:10.1177/01423312211015114 [本文引用: 1]
模型参考模糊自适应控制
[J].
Model reference fuzzy adaptive control
[J].
永磁同步电机的模型参考自适应反步控制
[J].DOI:10.3321/j.issn:1001-0920.2008.03.022
Model reference adaptive backstepping control of permanent magnet synchronous motors
[J].DOI:10.3321/j.issn:1001-0920.2008.03.022
Robustness analysis of discrete-time indirect model reference adaptive control with normalized adaptive laws
[J].DOI:10.1007/s11633-010-0518-4 [本文引用: 1]
Analysis of an adaptive observer for sensorless control of interior permanent magnet synchronous motors
[J].DOI:10.1109/TIE.2007.911949 [本文引用: 1]
永磁同步电机矢量控制双滑模模型参考自适应系统转速辨识
[J].DOI:10.13334/j.0258-8013.pcsee.2014.06.010 [本文引用: 1]
Double sliding-mode model reference adaptive system speed identification for vector control of permanent magnet synchronous motors
[J].DOI:10.13334/j.0258-8013.pcsee.2014.06.010 [本文引用: 1]
Novel model reference adaptive control laws for improved transient dynamics and guaranteed saturation constraints
[J].DOI:10.1016/j.jfranklin.2021.06.020 [本文引用: 1]
Design of robust model reference adaptive controller for a wider class of nonlinear systems
[J].DOI:10.1007/s40998-021-00451-8 [本文引用: 1]
定位器模型参考自适应控制系统设计
[J].
Model reference adaptive control system design of localizer
[J].
Sensorless speed control of PMSM based on MRAC using active power
[J].
数控交流伺服系统三环整定及应用
[J].
Parameter tuning and application of the three loops in a NC servo system
[J].
Modeling and simulation of all-electric propulsion system with three-closed loop control
[J].DOI:10.3233/JCM-204432 [本文引用: 1]
采用id=0的永磁同步电机矢量控制系统MATLAB/Simulink仿真
[J].
Vector control with id=0 simulation of PMSM based on MATLAB/Simulink
[J].
某型运动平台三环控制系统设计与仿真
[J].
Design and simulation of a three-loop control system for a certain motion control
[J].