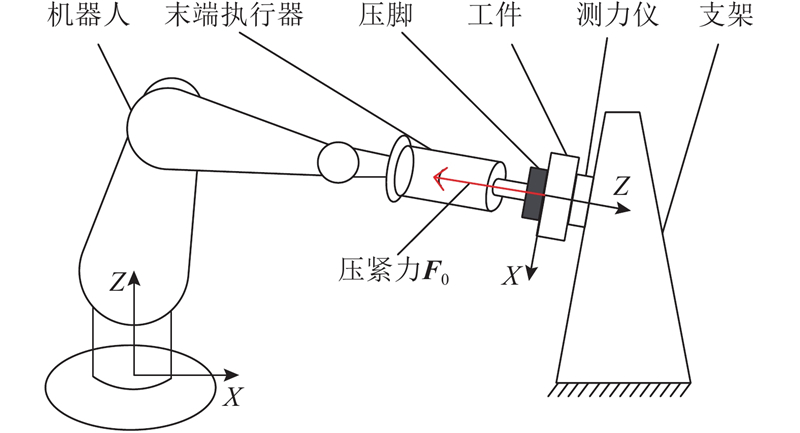
在机器人运行过程中,由于存在负载变形、几何误差、关节磨损、热误差等原因,其绝对定位精度往往只有2~3 mm. 对此,实验室前期已对机器人自动化制孔中绝对定位误差进行分析研究,提出多种补偿方法用于提高机器人制孔定位精度,但均未考虑压脚压紧后产生的二次定位误差[9-11]. 机器人在压脚压紧力作用下的变形会导致末端执行器压脚产生轴向变形和滑移变形. 其中轴向变形导致制孔过程中锪窝深度产生偏差,而滑移变形造成制孔定位误差. 针对轴向变形,费少华等[12]提出通过基于压脚位移反馈的补偿技术进行窝深控制. 对于滑移变形,Olsson等[13]利用6自由度力/力矩传感器,通过外力控制回路和相应的干扰补偿方案来控制压脚水平方向的力始终小于压脚与工件之间的最大静摩擦力,从而抑制压脚滑移. 然而该方法只能用于特定的加工系统,且须构建复杂的控制系统,在工业中的应用性相对较低. 考虑到机器人受力变形与其刚度密切相关,因此,解决这个问题的可行方法是根据机器人刚度模型对其变形进行离线预测和补偿. 为了实现该方法,首先须对机器人系统进行刚度建模以及相应的关节刚度辨识.
在机器人刚度建模方面,Salisbury[14]最早提出机器人刚度模型. 在此基础上,Chen等[15]通过引入补充刚度矩阵,提出增强型刚度模型,促进机器人刚度建模的发展. Dumas等[16]在对6自由度关节式工业机器人进行关节刚度辨识时发现,增强型刚度模型中的补充刚度矩阵在大多数情况下都可以忽略. Bu等[17]在研究机器人刚度特性时,为了简化计算而忽略末端的旋转变形和所受扭矩,将传统刚度模型简化为只有位移和力之间的关系,并通过与完整刚度模型下的实验变形进行对比,证明该简化刚度模型的有效性. 在机器人关节刚度辨识方面,大量学者基于各自的刚度模型和方法进行关节刚度辨识,但多数采用在机器人末端悬挂重物的加载方式,实验的难度和危险性较大[18-20]. 曲巍崴等[21]在对装有末端执行器的工业机器人系统进行关节刚度辨识时,将测力仪测得的压脚作用力作为机器人所受外载,简化关节刚度辨识的实验装置,但由于未考虑压脚与工件之间的摩擦力,导致实验结果存在误差.
本研究以机器人刚度分析为基础,提出适用于绝大多数机器人制孔系统的变形预测和离线补偿方法,用于进一步提高机器人制孔系统的定位精度. 以装有末端执行器的KUKA KR600型机器人为研究对象,建立机器人运动学模型,通过研究机器人末端平移变形与压脚压紧力的关系,建立压脚压紧力作用下的机器人刚度模型;通过基于L-M算法的机器人关节刚度辨识实验获取其关节刚度,并规划实验验证关节刚度的准确性;运用该机器人刚度模型对机器人滑移变形进行预测并补偿. 通过补偿前、后机器人制孔位置误差对比,证明该补偿方法能有效提高机器人末端定位精度.
1. 机器人运动学建模
表 1 KUKA KR600机器人MOD_DH参数表
Tab.1
| i | ai−1 / mm | αi−1/(°) | di / mm | θi/(°) |
| 1 | 0 | 0 | 1045 | 0 |
| 2 | 500 | 90 | 0 | 90 |
| 3 | 1300 | 0 | 0 | 0 |
| 4 | −55 | 90 | 1025 | 0 |
| 5 | 0 | −90 | 0 | 0 |
| 6 | 0 | 90 | 290 | −180 |
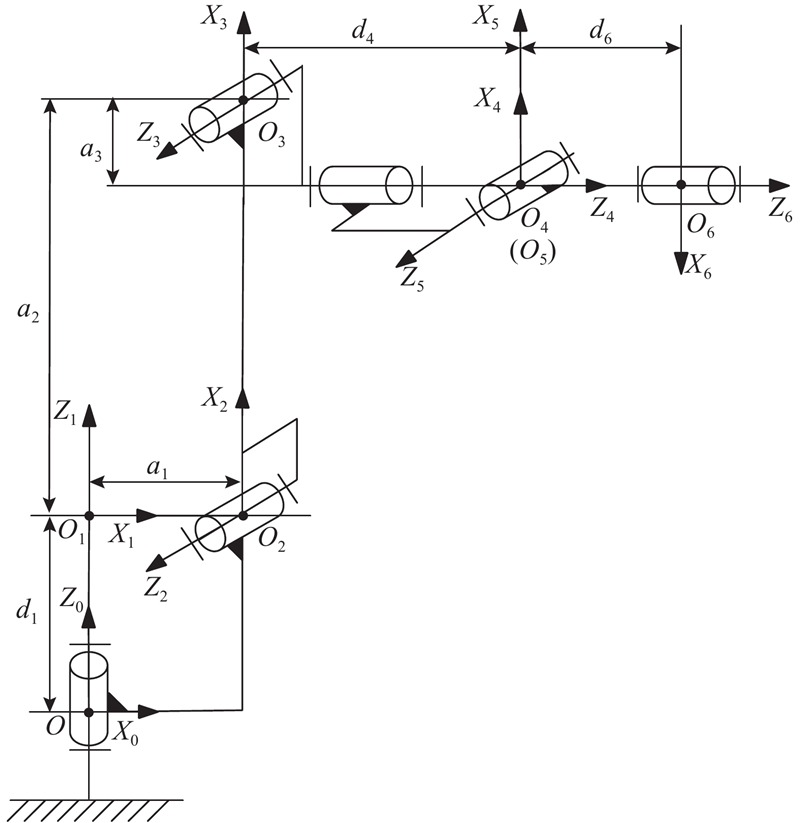
图 1
由文献[22]可知,相邻坐标系{Oi-1}和{Oi}之间的齐次变换矩阵为
式中:
将各坐标系之间的齐次变换矩阵顺序相乘,即可得到机器人末端坐标系相对于基坐标系的变换矩阵,即机器人运动学方程为
至此,完成机器人MOD_DH运动学模型建立,为后续机器人刚度分析奠定基础.
为了验证该运动学模型的正确性,将表1中6个关节转角参数代入机器人运动学方程,得到机器人末端在基坐标系下的位姿矩阵:
图 2
2. 压脚约束下的机器人刚度模型
机器人刚度主要反映机器人在外力作用下抵抗变形的能力,机器人刚度模型则表示外力与机器人变形之间对应的数值关系. 在机器人制孔中,末端执行器压脚产生的压紧力使机器人发生变形,导致压脚与工件表面发生相对滑移而产生滑动摩擦力,从而进一步影响机器人的变形情况. 因此,对于有压脚约束的机器人刚度模型应综合考虑压脚压紧力和摩擦力对机器人变形产生的影响.
Salisbury[14]最早建立机器人关节刚度和笛卡尔刚度的映射关系:
式中:
由式(4)可以求出机器人在笛卡尔空间下的刚度,进而得到传统机器人刚度模型:
式中:
由文献[17]可知,机器人制孔时所受的扭矩及其末端的旋转变形可以忽略不计,因此本研究主要研究机器人平移变形与外力(不含力矩)之间的关系. 假设机器人所受力矩和旋转变形均为零,则式(5)可以写为
式中:
将柔度矩阵
式中:
结合式(6)、(7),可以得到机器人平移变形和所受外力之间的关系,即简化后的传统机器人刚度模型:
式中:
在机器人制孔前,末端执行器压脚垂直压紧工件表面,产生压紧力
图 3
由式(8)可以求得机器人在初始压紧力作用下的理论末端变形
式中:
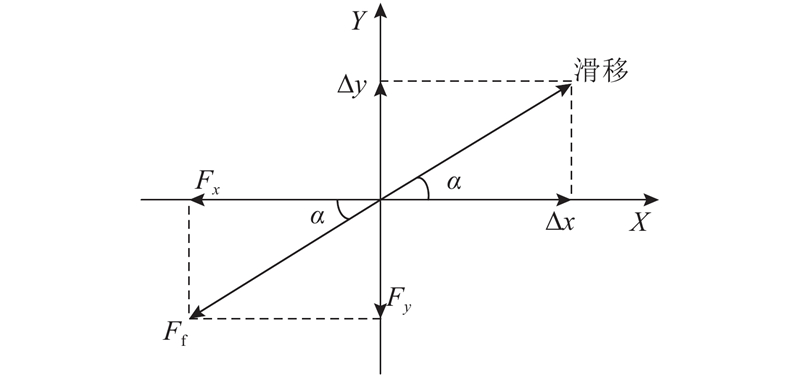
滑动摩擦力的方向与滑移方向相反,如图4所示. 将其沿X、Y方向分解后,可以得到
式中:
图 4
图 4 滑移及其滑动摩擦力示意图
Fig.4 Schematic diagram of sliding movement and sliding friction
结合式(8)~(10)可以得到滑动摩擦力:
因此,压脚压紧状态下的机器人末端作用力为
由
综合式(8)、(13),可以得到压脚约束下的机器人刚度模型为
式中:
至此,压脚约束下的机器人刚度模型建立完成. 由式(13)可知,压脚作用力随机器人位姿变化而变化,因此利用传统机器人刚度模型预测不同位姿下的变形须测得所有位姿下的压脚作用力,无法在工程中实际应用. 利用式(14)所表示的机器人刚度模型只须测得压脚压紧力
3. 基于L-M算法的机器人关节刚度辨识
由第2章的机器人刚度模型可知,压脚约束下的机器人平移柔度矩阵
3.1. 基于L-M算法的关节刚度辨识原理
由压脚约束下的机器人刚度模型可以得到
式中:
由式(15)可知,机器人在压脚压紧力作用下产生的变形
在不同机器人位姿
式中:
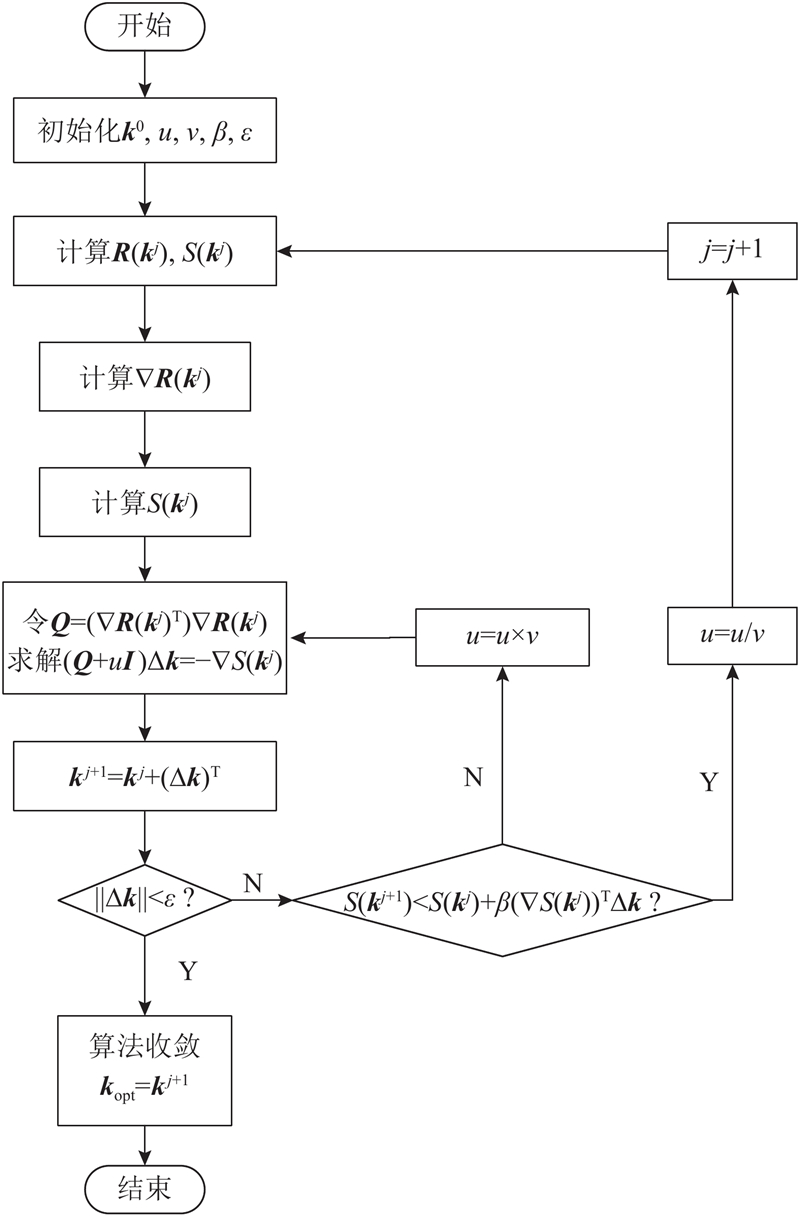
L-M算法求解关节刚度的算法流程如图5所示,具体步骤如下:1)选定初值
图 5
3.2. 关节刚度辨识实验
如图6所示为关节刚度辨识实验系统,由KUKA KR600机器人、工件、带有气缸压脚系统的末端执行器、Kistler 9257B测力仪和Leica LTD640激光跟踪仪等组成,其中工件的材料为铝合金,压脚的材料为45钢.
图 6
表 2 5种不同的机器人位姿
Tab.2
| 位姿 | θ1 /(°) | θ2 /(°) | θ3 /(°) | θ4 /(°) | θ5 /(°) | θ6 /(°) |
| 1 | 0.64 | 119.15 | −34.44 | 68.03 | 0.92 | 119.85 |
| 2 | 0.45 | 118.01 | −35.21 | 34.76 | 1.42 | 152.13 |
| 3 | 0.38 | 118.90 | −34.98 | 18.30 | 1.90 | 169.56 |
| 4 | 0.25 | 119.65 | −33.11 | 69.97 | 0.41 | 125.88 |
| 5 | 2.10 | 119.43 | −32.76 | 121.23 | 3.04 | 65.74 |
表 3 5种不同的压脚压紧力
Tab.3
| P / MPa | F0 / N | P / MPa | F0 / N | |
| 0.2 | 798.4 | 0.5 | 1996.8 | |
| 0.3 | 1181.6 | 0.6 | 2325.0 | |
| 0.4 | 1608.6 | − | − |
3.3. 关节刚度求解
在由刚度辨识实验获得25组实验数据后,利用L-M算法求解KUKA KR600机器人的关节刚度. 1)根据式(16)编写目标函数的Matlab程序,程序中包含实验所用的机器人位姿、压脚压紧力、机器人末端变形的计算值和实测值等;2)确定优化变量
因此,机器人的各关节刚度k1、k2、k3、k4、k5、k6分别为1.324×1010、1.028×1010、8.109×109、4.820×109、4.603×109、4.601×109 N·mm/rad.
4. 机器人滑移离线补偿
在获得KUKA KR600机器人关节刚度后,通过式(14)计算得到任意位姿下的机器人末端理论变形,从而对机器人制孔中的压脚滑移现象进行离线补偿. 通过关节刚度验证实验和压脚滑移变形补偿实验证明该补偿方案能有效提高机器人制孔定位精度.
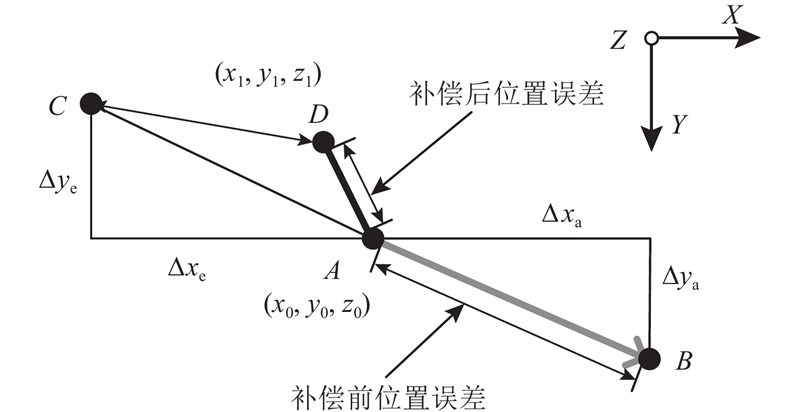
压脚滑移变形补偿原理如图7所示. 图中,点A为理论位置,在未补偿情况下,机器人末端受压紧力作用滑移到点B处,即补偿前位置误差为
图 7
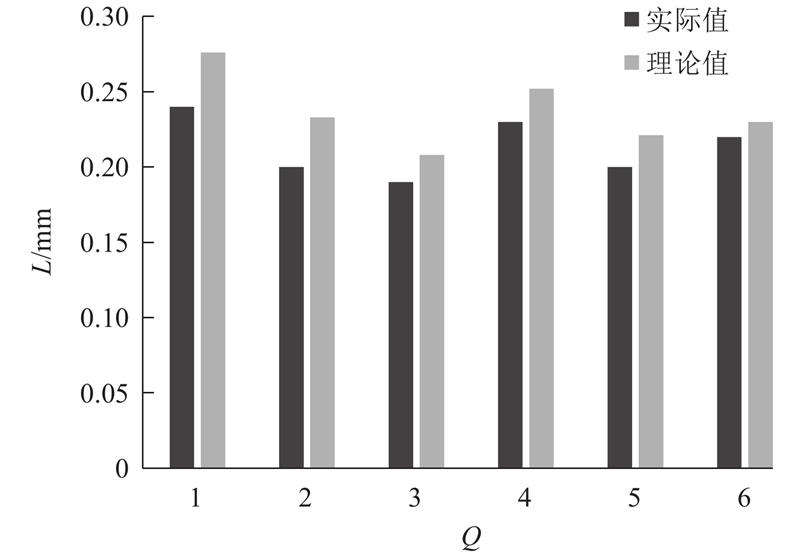
表 4 机器人6组位姿下末端滑移变形
Tab.4
| 组别 | 位姿 | 实际滑移/mm | 理论滑移/mm | |||||
| θ1/(°) | θ2/(°) | θ3/(°) | θ4/(°) | θ5/(°) | θ6/(°) | |||
| 1 | −51.18 | 85.00 | −7.05 | −85.00 | 49.95 | −99.25 | 0.24 | 0.28 |
| 2 | −49.36 | 86.27 | −14.49 | −77.03 | 49.40 | −102.94 | 0.20 | 0.24 |
| 3 | −47.69 | 86.15 | −21.44 | −67.37 | 50.83 | −101.28 | 0.19 | 0.21 |
| 4 | −45.80 | 83.41 | −2.40 | −92.21 | 53.61 | −95.40 | 0.23 | 0.25 |
| 5 | −43.80 | 87.20 | −16.84 | −67.88 | 51.61 | −121.12 | 0.20 | 0.22 |
| 6 | −42.21 | 94.21 | −9.60 | −85.02 | 42.88 | −99.00 | 0.23 | 0.24 |
图 8
图 8 压脚滑移补偿实验系统
Fig.8 Experimental system for compensation of pressure foot’s sliding movement
图 9
在验证完关节刚度的正确性后,参考上述6组位姿下的机器人理论末端滑移变形,分别对6个点的理论坐标进行补偿,而后操作机器人定位到补偿后的坐标下,在压紧压脚后,机器人末端受力滑移,测得此时的机器人末端位置,并与理论坐标相比,从而得到补偿后的位置误差,如表5所示. 表中,(x0,y0,z0)为理论位置,(x1,y1,z1)为补偿后的最终位置,[(x1−x0)2+(y1−y0)2]1/2为补偿后位置误差.
表 5 补偿后的机器人位置误差
Tab.5
| 组别 | (x0,y0,z0)/mm | (x1,y1,z1)/mm | [(x1−x0)2+(y1− y0)2]1/2/mm |
| 1 | (1294.89,−1256.59,2052.25) | (1294.92,−1256.54,2052.25) | 0.06 |
| 2 | (1293.29,−1177.33,1957.45) | (1293.30,−1177.31,1957.45) | 0.02 |
| 3 | (1293.18,−1112.40,1854.43) | (1293.13,−1112.39,1854.43) | 0.05 |
| 4 | (1437.22,−1143.03,2086.54) | (1437.18,−1143.04,2086.54) | 0.04 |
| 5 | (1380.01,−1026.21,1972.66) | (1379.98,−1026.25,1972.67) | 0.05 |
| 6 | (1342.29,−952.12,2187.55) | (1342.22,−952.09,2187.55) | 0.08 |
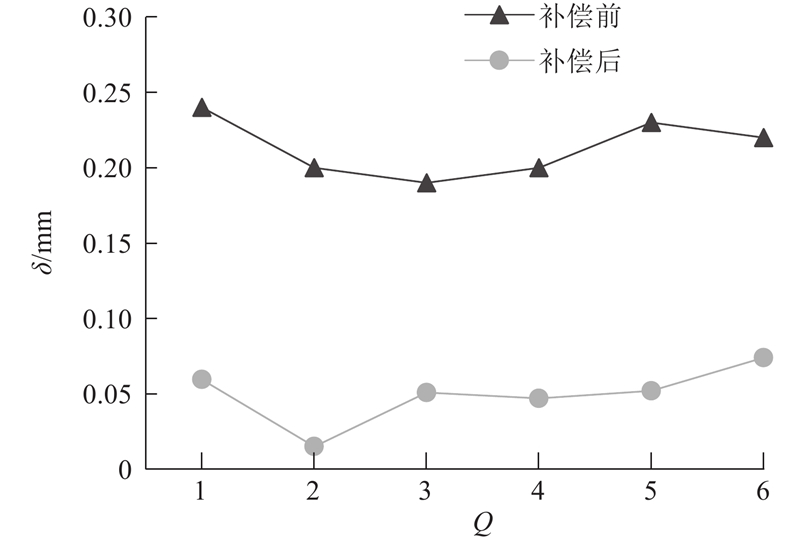
将上述6组位姿下的机器人滑移变形补偿前、后的位置误差进行对比,如图10所示. 图中,δ为位置误差. 可以发现,采用本研究所述方法补偿机器人的滑移变形后,平均位置误差由原先的0.22 mm降低到0.05 mm.
图 10
5. 结 论
(1)建立压脚约束下的机器人刚度模型,综合考虑压脚压紧力和摩擦力对机器人变形的影响,用于对机器人滑移变形进行预测和补偿.
(2)提出基于L-M算法的机器人关节刚度辨识方法,并采用测力仪测得的压脚作用力作为机器人所受外载,简化关节刚度辨识的实验装置.
(3)基于压脚约束下的机器人刚度模型,提出机器人滑移变形预测和补偿方法,使机器人制孔的平均位置误差由0.22 mm降为0.05 mm,提高机器人末端定位精度.
(4)在进行机器人关节刚度辨识实验时,由于测力仪面积较小且机器人相对工装无法移动,实验所选的机器人位姿较接近,由此计算的关节刚度可能存在一定误差,后续研究可以通过在机器人底部安装导轨或AGV车的方式,扩大实验中机器人的位姿变化.
参考文献
机器人自动化制孔系统
[J].
Robotic automatic drilling system
[J].
Stability of lateral vibration in robotic rotary ultrasonic drilling
[J].
Modelling of robotic drilling
[J].DOI:10.1016/j.procir.2017.03.246 [本文引用: 1]
Stiffness-oriented posture optimization in robotic machining applications
[J].DOI:10.1016/j.rcim.2015.02.006 [本文引用: 1]
新型工业机器人结构设计及其全域刚度预估方法
[J].
Structure design and global stiffness prediction method of a novel industrial robot
[J].
Chatter in machining processes: a review
[J].DOI:10.1016/j.ijmachtools.2011.01.001 [本文引用: 1]
机器人精镗飞机交点孔的颤振分析与识别
[J].
Chatter analysis and identification in robotic fine boring of aircraft intersection holes
[J].
机器人技术在航空工业中的应用
[J].DOI:10.3969/j.issn.1671-833X.2009.04.001 [本文引用: 1]
Applications of robotics in the aerospace industry
[J].DOI:10.3969/j.issn.1671-833X.2009.04.001 [本文引用: 1]
机器人辅助飞机装配制孔中位姿精度补偿技术
[J].
Pose accuracy compensation technology in robot-aided aircraft assembly drilling process
[J].
机器人自动制孔中绝对定位误差的分析与补偿
[J].
Analysis and compensation for absolute positioning error of robot in automatic drilling
[J].
Measurement error analysis and accuracy enhancement of 2D vision system for robotic drilling
[J].DOI:10.1016/j.rcim.2013.09.014 [本文引用: 1]
基于压脚位移补偿的机器人制孔锪窝深度控制
[J].
Countersink depth control of robot drilling based on pressure foot displacement compensation
[J].
Cost-efficient drilling using industrial robots with high-bandwidth force feedback
[J].DOI:10.1016/j.rcim.2009.01.002 [本文引用: 1]
Conservative congruence transformation for joint and cartesian stiffness, matrices of robotic hands and fingers
[J].DOI:10.1177/02783640022067201 [本文引用: 1]
Joint stiffness identification of six-revolute industrial serial robots
[J].DOI:10.1016/j.rcim.2011.02.003 [本文引用: 2]
Stiffness analysis and optimization in robotic drilling application
[J].
工业机器人大负载刚度辨识及误差补偿研究
[J].
Research of the stiffness identification and error compensationof industrial robot under heavy load
[J].
A new methodology for joint stiffness identification of heavy duty industrialrobots with the counterbalancing system
[J].DOI:10.1016/j.rcim.2018.03.001 [本文引用: 1]
机器人加工系统刚度性能优化研究
[J].
Research on the stiffness performance for robot machining systems
[J].
An algorithm for least-squares estimation of nonlinear parameters
[J].