运营铁路隧道治理专用凿毛装置的设计与运动学分析

doi:10.3785/j.issn.1006-754X.2025.05.117

运营铁路隧道治理专用凿毛装置的设计与运动学分析

周扬^,¹, 易勇², 罗舟², 宁智¹, 尹来容^,^,¹

1.长沙理工大学机械与运载工程学院，湖南长沙 410114

2.中国中铁五局集团有限公司，湖南长沙 410000

Design and kinematic analysis of special scabbling device for operational railway tunnel maintenance

ZHOU Yang^,¹, YI Yong², LUO Zhou², NING Zhi¹, YIN Lairong^,^,¹

1.College of Mechanical and Vehicle Engineering, Changsha University of Science & Technology, Changsha 410114, China

2.China Railway No. 5 Engineering Group Co. , Ltd. , Changsha 410000, China

通讯作者: 尹来容（1984—），男，教授，博士生导师，博士，从事机械设计理论与工程装备开发研究，E-mail: yinlairong@hotmail.com，https://orcid.org/0000-0002-8562-3148

收稿日期: 2025-02-28 修回日期: 2025-04-29

基金资助:

国家自然科学基金面上项目. 52175003

中国中铁股份有限公司科技研究开发计划重点课题（2022-重点-10）

湖南省科技创新领军人才项目. 2024RC1054

Received: 2025-02-28 Revised: 2025-04-29

作者简介 About authors

周　扬（2000—），男，硕士生，从事工程装备开发研究，E-mail:zhou_yang0412@163.com , E-mail：zhou_yang0412@163.com

摘要

针对运营铁路隧道治理天窗期短、人工凿毛效率低及定向专用设备缺乏等问题，基于隧道整治施工需求开发了一种隧道治理专用的凿毛装置。首先，根据凿毛作业要求确定了凿毛装置的结构为机械臂结合剪叉式提升架，并适配设计了固定连接型与铰接型凿毛机构。然后，通过改进D-H（Denavit-Hartenberg）参数法建立了凿毛装置运动学模型，开展了正、逆运动学分析，并采用蒙特卡洛法求解了凿毛装置的工作空间。最后，对凿毛装置的作业过程进行了运动轨迹规划分析，利用五次多项式插值法进行关节空间点到点轨迹规划，并利用基于S形加减速控制算法的平面圆弧插补方法进行笛卡儿空间指定路径规划。结果表明，所设计的凿毛装置的整体结构及工作空间符合设计要求，且运动性能良好；通过运动轨迹规划分析有效地减少了凿毛装置作业过程中的运动冲击与振动，保证了凿毛作业的安全性。研究结果为后续的凿毛装置实物样机制造与凿毛作业试验提供了理论基础。

关键词： 铁路隧道 ; 凿毛装置 ; S形加减速控制算法 ; 运动学分析 ; 运动轨迹规划

Abstract

In response to the issues of the short window period for tunnel maintenance in operational railway, the low efficiency of manual scabbling, and the lack of directional specialized equipment, a dedicated scabbling device for tunnel maintenance has been developed based on the construction requirements of tunnel renovation. Firstly, according to the scabbling operation requirements, the structure of the scabbling device was determined as a robotic arm combined with a scissor lift frame, and the fixed-connection and articulated scabbling mechanisms were designed. Then, the kinematic model of the scabbling device was established by improved D-H (Denavit-Hartenberg) parameter method for forward and inverse kinematic analyses, and the workspace of the scabbling device was solved by using the Monte Carlo method. Finally, the motion trajectory planning analysis for the scabbling device operation process was performed. The fifth-degree polynomial interpolation method was applied for the point-to-point trajectory planning in joint space, and the planar circular interpolation method based on the S-curve acceleration and deceleration control algorithm was used for the designated path planning in Cartesian space. The results showed that the overall structure and workspace of the designed scabbling device met the design requirements, and this device performed well in terms of motion. Through the motion trajectory planning analysis, the motion impact and vibration during the scabbling device operation process were effectively reduced, which ensured the safety of the scabbling operation. The research results provide a theoretical foundation for the subsequent physical scabbling device prototype manufacturing and scabbling operation testing.

Keywords： railway tunnel ; scabbling device ; S-curve acceleration and deceleration control algorithm ; kinematic analysis ; motion trajectory planning

PDF (4814KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

周扬, 易勇, 罗舟, 宁智, 尹来容. 运营铁路隧道治理专用凿毛装置的设计与运动学分析[J]. 工程设计学报, 2025, 32(5): 708-719 doi:10.3785/j.issn.1006-754X.2025.05.117

ZHOU Yang, YI Yong, LUO Zhou, NING Zhi, YIN Lairong. Design and kinematic analysis of special scabbling device for operational railway tunnel maintenance[J]. Chinese Journal of Engineering Design, 2025, 32(5): 708-719 doi:10.3785/j.issn.1006-754X.2025.05.117

随着我国交通基础设施建设的持续发展，我国已成为世界上隧道数量最多、最复杂、发展最快的国家^[1]。截至2023年底，我国铁路运营里程已达159 000 km，其中投入运营的铁路隧道为18 573座，总长为23 508 km，占铁路运营里程的14.8%^[2]。我国隧道建设正处于高速发展阶段，现已成为超级隧道大国，但同时也是铁路隧道病害最为严重的国家之一^[3]。对于已建成的运营铁路隧道，因受限于以前的勘察技术、设计标准以及施工工艺水平，随着服役时间的增加，在地质、环境、气候以及反复载荷的共同影响下，隧道结构普遍会出现渗漏水、衬砌裂损或腐蚀及隧底翻浆冒泥等病害^[4-6]。一旦上述病害导致隧道结构质量问题超出允许范围，隧道将无法继续使用。因此，为延长隧道的服役寿命，需对隧道病害进行整治处理^[7-8]。根据铁路工务部门对现有隧道病害类型的相关统计，现阶段我国隧道病害以严重渗漏水、衬砌腐蚀裂损、仰拱和铺底变形损坏为主，占总体隧道病害的75%以上^[9]。在对上述常见隧道病害进行整治施工时，需先对原有的衬砌表面进行凿毛处理，再进行喷射混凝土或喷涂防水层作业。现阶段，隧道凿毛作业自动化程度较低，主要依靠工人手持风镐或电镐并配合作业平台进行凿毛作业，存在凿毛效率低、凿毛效果难以保证、工人劳动强度大、作业环境恶劣及施工安全难以保障等问题。

目前，针对隧道机械化施工^[10-11]和隧道病害检测^[12-14]的研究较多，而对于隧道病害整治设备的研究仍比较少。为提高隧道病害的整治效率，许多学者针对隧道整治机械化施工设备开展了一系列研究。高菊茹等^[15]通过对隧道病害整治设备的发展进行分析，提出需从设计源头控制隧道病害发生。为解决人工手持混凝土切割机作业效率低下、劳动强度大等问题，施芸等^[16]研发了一套智能切槽机器人系统，张龙等^[17]提出了组合式刀具一次切削成槽的隧道衬砌钢拱架安装槽开槽方法，刘璟铮^[18]设计了一种隧道衬砌切割机械臂。针对隧道凿毛设备的开发，张龙等^[19]通过将整治设备安置在小型挖掘机的机械臂末端来实现机械化凿毛作业，但由于挖掘机的结构尺寸较大，并不适用于铁路隧道衬砌凿毛。李荆等^[20]采用层次分析法和TRIZ理论（发明问题解决理论）对铁路隧道病害治理台车方案进行了设计，通过集成二次衬砌破除、钢拱架安装以及凿毛作业功能的机械臂，实现了运营铁路隧道套衬施工中钢拱架安装和凿毛作业的机械化，但集成式治理台车的整体尺寸和重量过大。

综上，现有的机械化凿毛设备大多为挖掘机机械臂加装凿毛机构或隧道病害整治机械化集成式台车，无法用于天窗期短的铁路隧道病害治理场景，且目前针对铁路隧道专用机械化凿毛设备的研究较少。因此，针对运营铁路隧道治理天窗期短、人工凿毛效率低及凿毛质量难以保证等问题，研制一种专用的凿毛装置，对实现凿毛作业自动化、加快隧道整治效率和减轻工人劳动强度等具有重要意义。基于此，本文根据施工工艺要求，开发了一种结构为机械臂结合剪叉式提升架并搭配固定连接型与铰接型两类凿毛机构的运营铁路隧道治理专用凿毛装置。基于改进D-H（Denavit-Hartenberg）参数法对凿毛装置进行正、逆运动学分析，并采用蒙特卡洛法求解其工作空间。最后，利用五次多项式插值法和基于S形加减速控制算法的平面圆弧插补方法对凿毛装置的作业过程进行运动轨迹规划，并对其工作空间和性能进行分析，旨在为后续的实物样机制造和凿毛作业试验提供理论依据。

1 运营铁路隧道凿毛装置设计

1.1　凿毛装置设计要求

1.1.1　凿毛装置工作空间确定

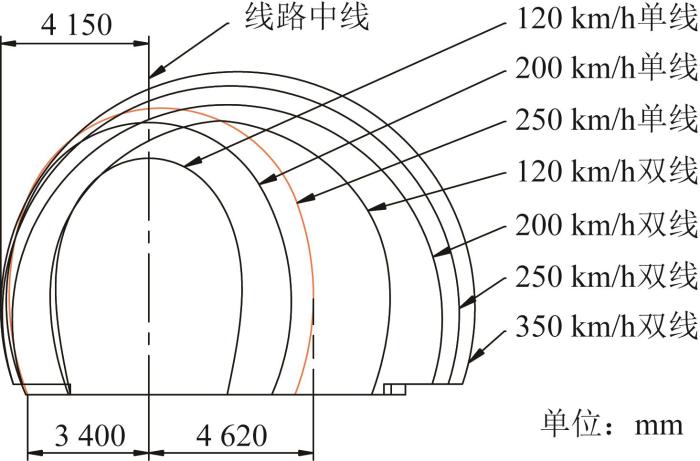
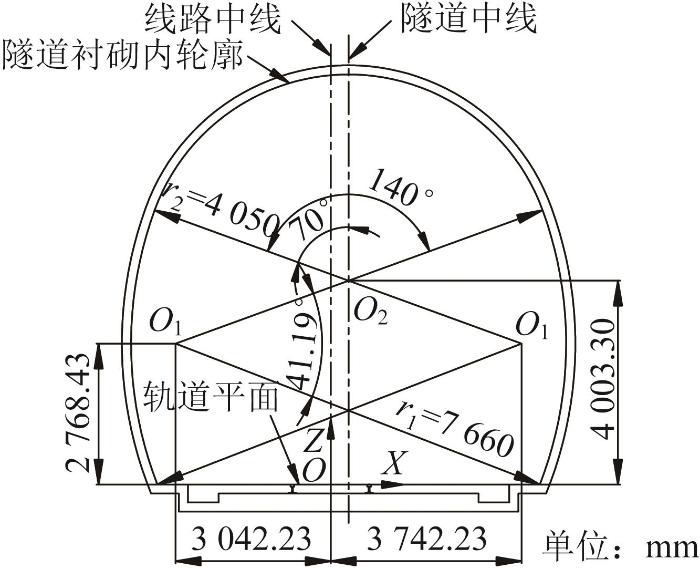
凿毛装置的主要功能是对运营铁路隧道边墙及拱部既有衬砌表面进行凿毛处理。为使凿毛装置的工作空间覆盖多类隧道，对各类隧道衬砌内轮廓结构进行对比分析。不同运行时速条件下各类隧道衬砌的内轮廓结构如图1所示^[21]。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 各类隧道衬砌内轮廓结构

Fig.1 Internal profile structures of various tunnel linings

120 km/h单双线隧道衬砌内轮廓到线路中线的距离与其余隧道相比差异较大，单靠一类凿毛装置难以满足各类隧道衬砌内轮廓的凿毛作业需求。当不考虑120 km/h单双线隧道时，其余隧道衬砌内轮廓到线路中线的距离为3 400~4 620 mm，这恰好为250 km/h单线隧道对应距离的变化范围，故以250 km/h单线隧道为凿毛装置工作空间的设计依据。

1.1.2　凿毛装置整体设计要求

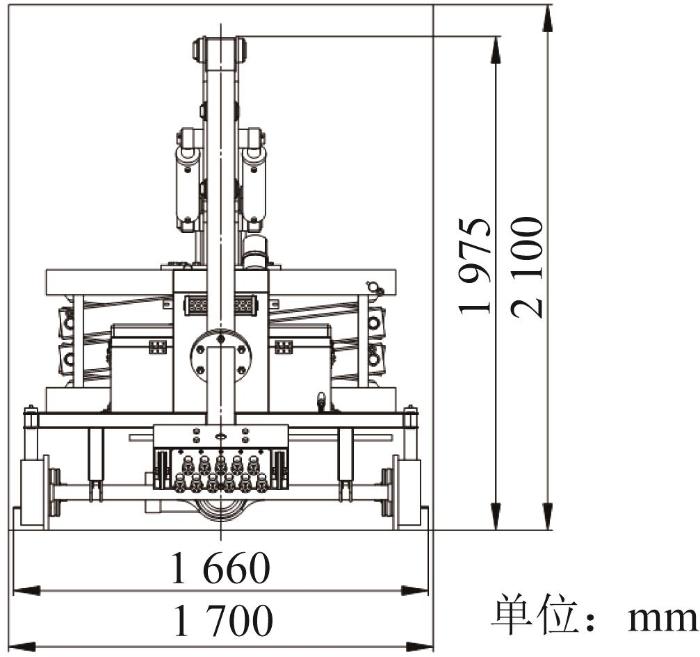
根据隧道整治的现场施工需求，为便于工人运输凿毛装置以及缩短施工准备时间，凿毛装置整体需从隧道斜井支洞内的安全防护门进入隧道内部，以进行凿毛作业。根据Q/CR 700—2019《隧道防护门》^[22]，常用隧道安全防护门的门扇通行尺寸为1.7 m×2.1 m（宽×高），故凿毛装置整体结构尺寸应满足图2所示条件。此外，凿毛装置需由工人运送至隧道内部，故其整体重量不宜过大。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 凿毛装置整体结构尺寸

Fig.2 Overall structural dimensions of scabbling device

综上，凿毛装置的整体设计要求如下：

1）凿毛装置折叠收拢后的整体结构尺寸应在1.7 m×2.1 m（宽×高）范围内。

2）凿毛装置可实现以线路中线为基准、凿毛距离变化范围为3 400~4 620 mm的工作空间，且可满足250 km/h单线隧道衬砌内轮廓垂直凿毛作业全覆盖的要求。

3）在满足使用需求的情况下，凿毛装置整体重量应尽量小。

1.2　凿毛装置结构设计

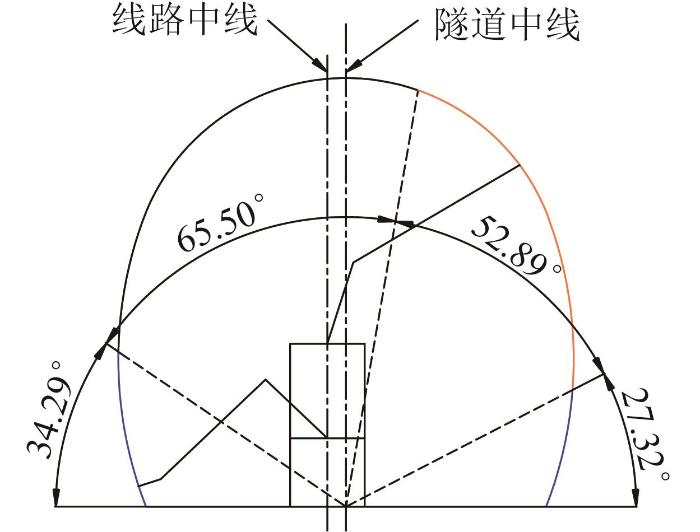
由上述设计要求可知，凿毛装置整体结构尺寸受安全防护门的限制，不宜过大，但其工作空间的高度较高；此外，凿毛装置末端须与待凿毛表面垂直，以保证凿毛作业质量。因此，采用机械臂结合剪叉式提升架的结构，通过提升架来实现高度调节，并设计固定连接型与铰接型凿毛机构，以在实现垂直凿毛作业的同时保证凿毛装置整体结构尺寸较小。对于隧道底部凿毛距离较短的左侧34.29°、右侧27.32°区域，采用铰接型凿毛装置以实现垂直凿毛作业，其余区域采用固定连接型凿毛装置。凿毛装置的工作空间划分如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 凿毛装置工作空间划分

Fig.3 Workspace division of scabbling device

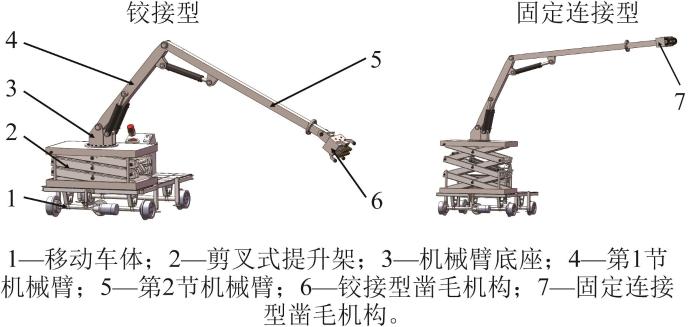
鉴于只需对隧道衬砌表面进行凿毛，在隧道左右两侧分别采用1台凿毛装置进行凿毛作业。这种作业方式不仅能提高凿毛效率，还无需配备回转机构，从而减小了凿毛装置的整体重量。所设计的凿毛装置主要由移动车体、剪叉式提升架、机械臂和凿毛机构组成，其三维模型如图4所示。为提高凿毛装置在作业过程中的整体稳定性，在其移动车体的四周设置支撑腿。在凿毛装置移动过程中，需收拢机械臂以使凿毛装置整机的重心位于车轮倾覆线范围内。待凿毛装置运动至指定的凿毛位置后，先将支撑腿打开，使其与地面接触并形成稳定支撑，随后进行凿毛作业，以此减少凿毛作业过程中产生的振动和冲击对凿毛装置稳定性的影响，从而保证凿毛作业的安全性。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 凿毛装置三维模型

Fig.4 Three-dimensional model of scabbling device

2 凿毛装置运动学建模与分析

2.1　运动学模型构建

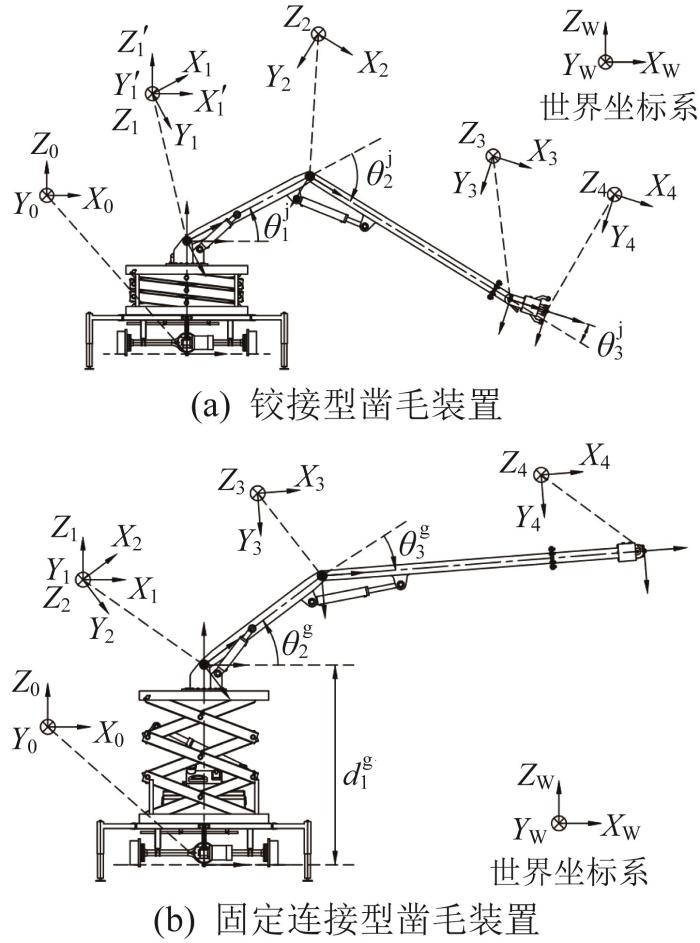
凿毛装置包括左侧和右侧两类作业位姿。在对左、右侧作业位姿下的凿毛装置进行运动学分析时，只有关节变量的取值范围发生变化，故本文以右侧作业位姿为例进行运动学分析。因铰接型凿毛装置只对隧道底部凿毛，其剪叉式提升架始终处于收拢状态，则2种类型的凿毛装置均为三自由度运动机构。其中，铰接型凿毛装置含3个转动关节，固定连接型凿毛装置含1个移动关节和2个转动关节。对凿毛装置三维模型进行简化处理，结合改进D-H参数法分别建立2种凿毛装置的连杆坐标系，如图5所示。图中：坐标系{0}为凿毛装置的基坐标系，坐标系{4}为凿毛装置的末端坐标系。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 凿毛装置连杆坐标系

Fig.5 Linkage coordinate systems of scabbling device

图5(a)中， $θ_{1}^{j}$ 、 $θ_{2}^{j}$ 、 $θ_{3}^{j}$ 为铰接型凿毛装置的3个关节变量；图5(b)中， $d_{1}^{g}$ 、 $θ_{2}^{g}$ 、 $θ_{3}^{g}$ 为固定连接型凿毛装置的3个关节变量。根据凿毛装置的连杆坐标系及其三维模型参数，可得铰接型和固定连接型凿毛装置各关节的D-H参数，分别如表1和表2所示。表中： $α_{i - 1}$ 表示连杆扭转角， $a_{i - 1}$ 表示连杆长度， $d_{i}$ 表示连杆偏距， $θ_{i}$ 表示关节角度。

表1 铰接型凿毛装置的D-H参数

Table 1 D-H parameters of articulated scabbling device

连杆i	$α_{i - 1}^{j}$ /(°)	$a_{i - 1}^{j}$ /mm	$d_{i}^{j}$ /mm	$θ_{i}^{j}$ /(°)
1	-90	0	$d_{1}^{j}$	$θ_{1}^{j}$ （-110.95~-15.75）
2	0	$a_{1}^{j}$	0	$θ_{2}^{j}$ （0~88.25）
3	0	$a_{2}^{j}$	0	$θ_{3}^{j}$ （-30~11）
4	0	$a_{3}^{j}$	0	0

新窗口打开| 下载CSV

表2 固定连接型凿毛装置的D-H参数

Table 2 D-H parameters of fixed-connection scabbling device

连杆i	$α_{i - 1}^{g}$ /(°)	$a_{i - 1}^{g}$ /mm	$d_{i}^{g}$ /mm	$θ_{i}^{g}$ /(°)
1	0	0	$d_{1}^{g}$ （1 300~3 730）	0
2	-90	0	0	$θ_{2}^{g}$ （-110.95~-15.75）
3	0	$a_{2}^{g}$	0	$θ_{3}^{g}$ （0~88.25）
4	0	$a_{3}^{g}$	0	0

新窗口打开| 下载CSV

表1中： $a_{1}^{j}$ 表示第1节机械臂的长度， $a_{1}^{j}$ =1 600 mm； $a_{2}^{j}$ 表示第2节机械臂和铰接型凿毛机构不可转动部分长度的总和， $a_{2}^{j}$ =2 710 mm； $a_{3}^{j}$ 表示铰接型凿毛机构可转动部分的长度， $a_{3}^{j}$ =440 mm； $d_{1}^{j}$ 表示机械臂底座与第1节机械臂的铰接中心点到轨道平面的距离， $d_{1}^{j}$ =1 300 mm。表2中， $a_{2}^{g}$ 表示第1节机械臂的长度， $a_{2}^{g}$ =1 600 mm； $a_{3}^{g}$ 表示第2节机械臂和固定连接型凿毛机构长度的总和， $a_{3}^{g}$ =3 500 mm。

2.2　正运动学求解

正运动学求解是指在已知各连杆关节变量和几何参数的情况下，通过变换矩阵求解机器人末端执行器相对于基坐标系的位姿。在改进D-H参数法中，连杆坐标系{i}相对于连杆坐标系{i-1}的齐次变换矩阵 ${}_{i}^{i - 1} T$ 可表示为^[23]：

{}_{i}^{i - 1} T = [\begin{matrix} c o s θ_{i} & - s i n θ_{i} & 0 & a_{i - 1} \\ s i n θ_{i} c o s α_{i - 1} & c o s θ_{i} c o s α_{i - 1} & - s i n α_{i - 1} & - d_{i} s i n α_{i - 1} \\ s i n θ_{i} s i n α_{i - 1} & c o s θ_{i} s i n α_{i - 1} & c o s 1 α_{i - 1} & d_{i} c o s α_{i - 1} \\ 0 & 0 & 0 & 1 \end{matrix}]

(1)

通过将各连杆坐标系间的变换矩阵 ${}_{i}^{i - 1} T$ 连续相乘的方式，可得到末端坐标系相对于基坐标系的变换矩阵：

{}_{n}^{0} T = {}_{1}^{0}T {}_{2}^{1}T \dots {}_{n - 2}^{n - 1}T {}_{n - 1}^{n}T

(2)

将表1和表2中的D-H参数分别代入式(1)和式(2)，可得铰接型凿毛装置的正运动学方程，表示为：

{}_{4}^{0}^{j} = [\begin{matrix} c_{123}^{j} & - s_{123}^{j} & 0 & p_{x}^{j} \\ 0 & 0 & 1 & 0 \\ - s_{123}^{j} & - c_{123}^{j} & 0 & p_{z}^{j} \\ 0 & 0 & 0 & 1 \end{matrix}]

(3)

其中：

p_{x}^{j} = 440 c_{123}^{j} + 2 710 c_{12}^{j} + 1 600 c_{1}^{j}

p_{z}^{j} = 1 300 - 2 710 s_{12}^{j} - 1 600 s_{1}^{j} - 440 s_{123}^{j}

s_{123}^{j} = s i n (θ_{1}^{j} + θ_{2}^{j} + θ_{3}^{j})

c_{123}^{j} = c o s (θ_{1}^{j} + θ_{2}^{j} + θ_{3}^{j})

s_{12}^{j} = s i n (θ_{1}^{j} + θ_{2}^{j})

c_{12}^{j} = c o s (θ_{1}^{j} + θ_{2}^{j})

s_{1}^{j} = s i n θ_{1}^{j}

c_{1}^{j} = c o s θ_{1}^{j}

固定连接型凿毛装置的正运动学方程为：

{}_{4}^{0}^{g} = [\begin{matrix} c_{23}^{g} & - s_{23}^{g} & 0 & p_{x}^{g} \\ 0 & 0 & 1 & 0 \\ - s_{23}^{g} & - c_{23}^{g} & 0 & p_{z}^{g} \\ 0 & 0 & 0 & 1 \end{matrix}]

(4)

其中：

p_{x}^{g} = 3 500 c_{23}^{g} + 1 600 c_{2}^{g}

p_{z}^{g} = d_{1}^{g} - 3 500 s_{23}^{g} - 1 600 s_{2}^{g}

s_{23}^{g} = s i n (θ_{2}^{g} + θ_{3}^{g})

c_{23}^{g} = c o s (θ_{2}^{g} + θ_{3}^{g})

s_{2}^{g} = s i n θ_{2}^{g}

c_{2}^{g} = c o s θ_{2}^{g}

2.3　逆运动学求解

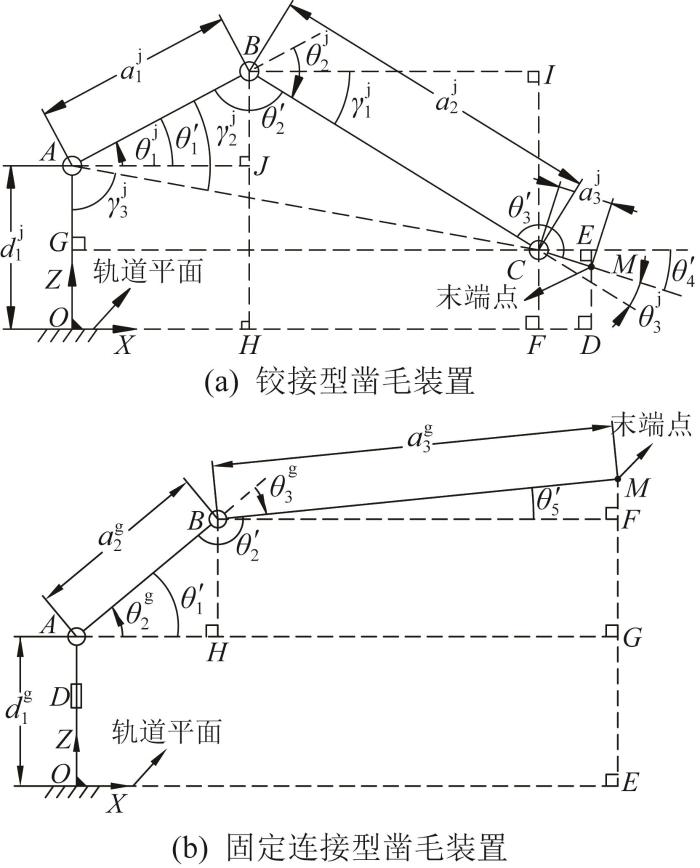
逆运动学求解是指在已知机器人末端位姿的情况下，求解各连杆的关节变量。凿毛装置为平面串联三自由度系统，其逆运动学方程为欠定方程组。为准确表示该逆运动学方程，需引入凿毛机构与待凿毛表面垂直的约束条件。考虑到几何法具有求解简单、直观的特点，适用于自由度较少的情况，本文采用几何法求解逆运动学方程^[24-25]。2种凿毛装置各连杆的几何关系如图6所示。为方便计算，以凿毛装置移动车体中心线与轨道平面的交点为原点建立坐标系O-XYZ，坐标系O-XYZ与上文的基坐标系{0}重合。图中： $θ_{4}^{'}$ 和 $θ_{5}^{'}$ 表示凿毛机构斜率角，规定 $θ_{4}^{'}$ 和 $θ_{5}^{'}$ 位于水平线以上时为正。凿毛机构与待凿毛表面垂直的约束条件为：凿毛机构斜率角等于待凿毛表面法线与水平线间的夹角。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 凿毛装置各连杆的几何关系

Fig.6 Geometric relationships of each linkage of scabbling device

为便于几何法求解，引入正向角 $θ_{1}^{'}$ 、 $θ_{2}^{'}$ 、 $θ_{3}^{'}$ ，各转动关节变量满足以下关系式：

\{\begin{array}{l} θ_{1}^{j} = θ_{2}^{g} = - θ_{1}^{'} \\ θ_{2}^{j} = θ_{3}^{g} = π - θ_{2}^{'} \\ θ_{3}^{j} = θ_{3}^{'} - π \end{array}

(5)

对铰接型凿毛装置进行逆运动学求解，根据图6(a)，在关节点C处，由△CEM可得：

x_{C}^{j} = x_{M}^{j} - a_{3}^{j} c o s θ_{4}^{'}

(6)

z_{C}^{j} = z_{M}^{j} - a_{3}^{j} s i n θ_{4}^{'}

(7)

式中：x_C 、z_C 和x_M 、z_M 分别为点C、点M的坐标。

在关节点B处，由△AJB和△BIC可得：

z_{B}^{j} = d_{1}^{j} + a_{1}^{j} s i n θ_{1}^{'}

(8)

z_{B}^{j} - z_{C}^{j} = a_{2}^{j} s i n γ_{1}^{j}

(9)

式中：x_B 、z_B 为点B的坐标。

由图6(a)中的几何关系可知：

γ_{1}^{j} = π - θ_{1}^{'} - θ_{2}^{'}

(10)

联立式(8)至(10)，可得：

\begin{array}{l} z_{C}^{j} = d_{1}^{j} + (a_{1}^{j} - a_{2}^{j} c o s θ_{2}^{'}) s i n θ_{1}^{'} - \\ a_{2}^{j} c o s θ_{1}^{'} s i n θ_{2}^{'} \end{array}

(11)

先求解 $θ_{3}^{'}$ ，由几何关系可知：

θ_{3}^{'} = π - (γ_{1}^{j} + θ_{4}^{'}) = θ_{1}^{'} + θ_{2}^{'} - θ_{4}^{'}

(12)

然后求解 $θ_{2}^{'}$ ，根据余弦定理，基于△ABC和△AGC进行求解，并联立式(6)和式(7)，可得：

θ_{2}^{'} = a r c c o s (b_{1}, b_{2})

(13)

其中：

\{\begin{array}{l} b_{1} = (a_{1}^{j})^{2} + (a_{2}^{j})^{2} - (d_{1}^{j} - z_{M}^{j} + a_{3}^{j} s i n θ_{4}^{'})^{2} - \\ (x_{M}^{j} - a_{3}^{j} c o s θ_{4}^{'})^{2} \\ b_{2} = 2 a_{1}^{j} a_{2}^{j} \end{array}

接着求解 $θ_{1}^{'}$ ，由几何关系可知：

c o s θ_{1}^{'} = s i n γ_{2}^{j} c o s γ_{3}^{j} + s i n γ_{3}^{j} c o s γ_{2}^{j}

(14)

根据正弦定理和余弦定理，基于△BAC和△AGC进行求解，并联立式(6)和式(7)，可得：

θ_{1}^{'} = a r c c o s (b_{3}, b_{4})

(15)

其中：

\{\begin{array}{l} b_{3} = 2 a_{1}^{j} a_{2}^{j} s i n θ_{2}^{'} (d_{1}^{j} - z_{M}^{j} + a_{3}^{j} s i n θ_{4}^{'}) + \\ (x_{M}^{j} - a_{3}^{j} c o s θ_{4}^{'}) [(a_{1}^{j})^{2} + (x_{M}^{j} - a_{3}^{j} c o s θ_{4}^{'})^{2} + \\ (d_{1}^{j} - z_{M}^{j} + a_{3}^{j} s i n θ_{4}^{'})^{2} - (a_{2}^{j})^{2}] \\ b_{4} = 2 a_{1}^{j} [(x_{M}^{j} - a_{3}^{j} c o s θ_{4}^{'})^{2} + (d_{1}^{j} - z_{M}^{j} + a_{3}^{j} s i n θ_{4}^{'})^{2}] \end{array}

最后将式(5)分别代入式(12)、式(13)和式(15)，可得铰接型凿毛装置的逆运动学方程：

\{\begin{array}{l} θ_{1}^{j} = - a r c c o s (b_{5}, b_{4}) \\ θ_{2}^{j} = π - a r c c o s (b_{1}, b_{2}) \\ θ_{3}^{j} = - θ_{1}^{j} - θ_{2}^{j} - θ_{4}^{'} \end{array}

(16)

其中：

\begin{array}{l} b_{5} = 2 a_{1}^{j} a_{2}^{j} s i n θ_{2}^{j} (d_{1}^{j} - z_{M}^{j} + a_{3}^{j} s i n θ_{4}^{'}) + \\ (x_{M}^{j} - a_{3}^{j} c o s θ_{4}^{'}) [(a_{1}^{j})^{2} + (x_{M}^{j} - a_{3}^{j} c o s θ_{4}^{'})^{2} + \\ (d_{1}^{j} - z_{M}^{j} + a_{3}^{j} s i n θ_{4}^{'})^{2} - (a_{2}^{j})^{2}] \end{array}

同理，对固定连接型凿毛装置进行逆运动学求解。根据图6(b)，在关节点B处，由△BFM可得：

x_{B}^{g} = x_{M}^{g} - a_{3}^{g} c o s θ_{5}^{'}

(17)

先求解 $θ_{1}^{'}$ ，根据△AHB并结合式(17)，可得：

θ_{1}^{'} = a r c c o s (\frac{x_{M}^{g} - a_{3}^{g} c o s θ_{5}^{'}}{a_{2}^{g}})

(18)

然后求解 $θ_{2}^{'}$ ，由几何关系可知：

θ_{2}^{'} = π + θ_{5}^{'} - θ_{1}^{'}

(19)

接着求解 $d_{1}^{g}$ ，由△AHB和△BFM可得：

d_{1}^{g} = z_{M}^{g} - a_{2}^{g} s i n θ_{1}^{'} - a_{3}^{g} s i n θ_{5}^{'}

(20)

最后，将式(5)分别代入式(18)至(20)，可得固定连接型凿毛装置的逆运动学方程：

\{\begin{array}{l} d_{1}^{g} = z_{M}^{g} + a_{2}^{g} s i n θ_{2}^{g} - a_{3}^{g} s i n θ_{5}^{'} \\ θ_{2}^{g} = - a r c c o s (\frac{x_{M}^{g} - a_{3}^{g} c o s θ_{5}^{'}}{a_{2}^{g}}) \\ θ_{3}^{g} = - θ_{2}^{g} - θ_{5}^{'} \end{array}

(21)

2.4　工作空间分析

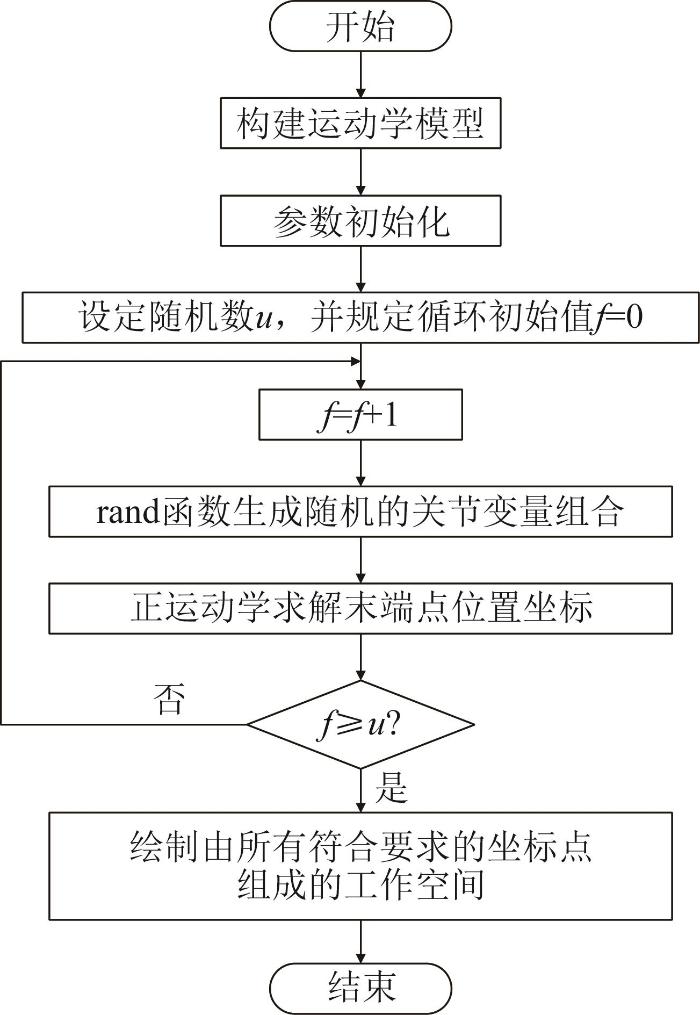
凿毛装置的工作空间是指凿毛机构中的凿毛头末端所能到达的所有点的集合，计算工作空间是验证和衡量凿毛装置工作范围的基础。本文采用蒙特卡洛法来求解凿毛装置的工作空间，具体流程如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 基于蒙特卡洛法的凿毛装置工作空间求解流程

Fig.7 Solution process for workspace of scabbling device based on Monte Carlo method

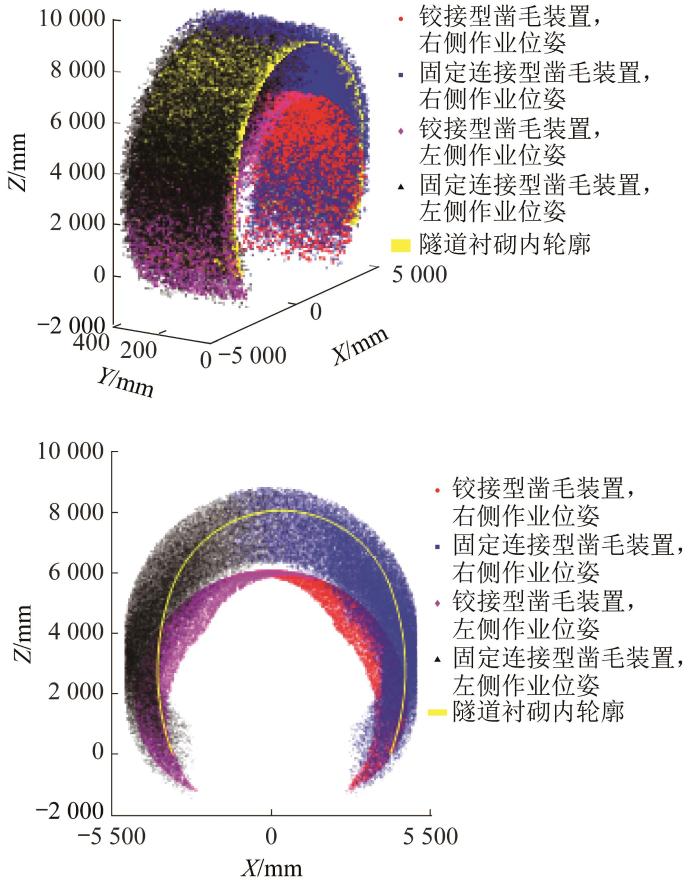
考虑到凿毛装置的作业位姿分为左、右侧两种情况，且具有2种类型的凿毛机构，需分别求解各类凿毛装置的工作空间，再合并得到凿毛装置的完整工作空间。根据凿毛装置的正运动学方程以及各关节变量的变化范围，利用MATLAB软件进行仿真计算，得到凿毛装置的工作空间，如图8所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 凿毛装置工作空间

Fig.8 Workspace of scabbling device

由图8可知，凿毛装置在X方向上的运动范围为-5 040~5 040 mm，在Z方向上的运动范围为-1 500~8 820 mm；Y方向为隧道纵深方向，凿毛装置单次凿毛的纵深距离由凿毛机构的宽度决定，为400 mm。结果表明，凿毛装置的工作空间可完全覆盖250 km/h单线隧道衬砌内轮廓，满足设计要求，验证了凿毛装置结构设计的合理性和可行性。

3 凿毛装置运动轨迹规划

3.1　运动轨迹整体规划

为使凿毛装置沿隧道衬砌内轮廓表面按指定路径进行凿毛作业，并避免因人工操作而导致凿毛装置与隧道表面发生碰撞，需对凿毛作业过程进行运动轨迹规划。以隧道右侧凿毛作业为例，250 km/h单线隧道衬砌内轮廓结构尺寸如图9所示。在凿毛装置运动轨迹规划中，须满足凿毛机构与待凿毛表面垂直的约束条件。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 250 km/h单线隧道衬砌内轮廓结构尺寸

Fig.9 Internal profile structure dimensions of single-track tunnel lining for 250 km/h

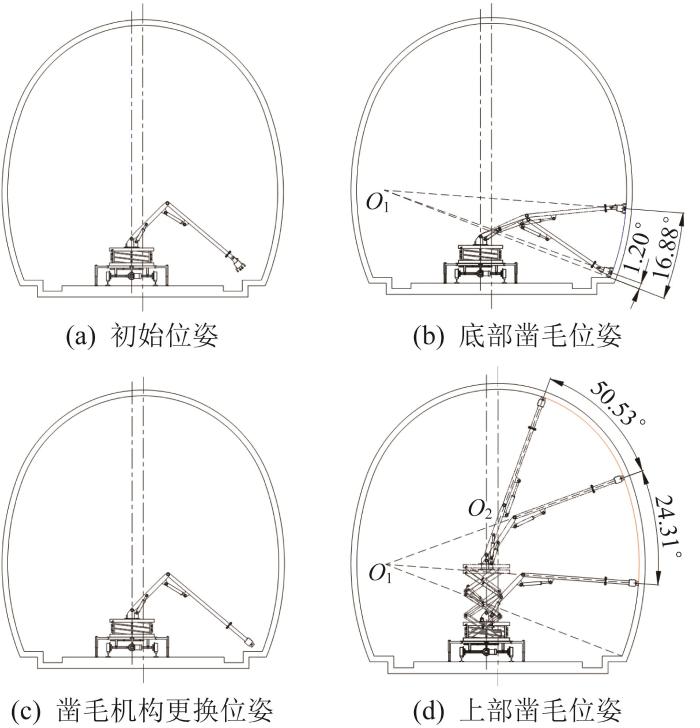
凿毛作业过程主要包括4个关键位姿，分别为初始位姿、底部凿毛位姿、凿毛机构更换位姿以及上部凿毛位姿，如图10所示。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 凿毛作业关键位姿

Fig.10 Key postures of scabbling operation

根据图10，可将凿毛作业过程细分为以下几个阶段：

1）第1阶段：铰接型凿毛装置由初始位姿运动至底部凿毛位姿。

2）第2阶段：铰接型凿毛装置沿隧道底部圆弧形指定路径进行凿毛，因受限于铰接型凿毛机构支撑轮结构，隧道最底部1.2°区域需采用人工凿毛。

3）第3阶段：铰接型凿毛装置由底部凿毛位姿运动至凿毛机构更换位姿。

4）第4阶段：凿毛装置暂停运动，人工更换凿毛机构。

5）第5阶段：固定连接型凿毛装置由凿毛机构更换位姿运动至上部凿毛位姿。

6）第6阶段：固定连接型凿毛装置沿隧道上部圆弧形指定路径进行凿毛。

凿毛装置运动轨迹规划是指针对隧道衬砌内轮廓表面整个断面的凿毛作业过程进行轨迹规划。第2阶段和第6阶段中凿毛机构均沿指定路径运动，需在笛卡儿空间中进行指定路径规划；而其余阶段对凿毛机构末端的运动轨迹并无严格要求，可在关节空间中进行点到点轨迹规划。待完成当前整个断面的凿毛作业后，凿毛装置通过移动车体沿隧道轴线方向运动至下一个待凿毛的隧道衬砌工作断面处。

3.2　关节空间点到点轨迹规划

为保证凿毛装置的运动轨迹曲线连续、变化平稳，并避免因速度、加速度突变而产生运动冲击和振动，采用五次多项式插值法进行关节空间轨迹规划，通过6个约束条件保证始末位置的速度、加速度为0^[26]。五次多项式插值轨迹规划方程如下：

\{\begin{array}{l} q (t) = c_{0} + c_{1} t + c_{2} t^{2} + c_{3} t^{3} + c_{4} t^{4} + c_{5} t^{5} \\ \dot{q} (t) = c_{1} + 2 c_{2} t + 3 c_{3} t^{2} + 4 c_{4} t^{3} + 5 c_{5} t^{4} \\ \ddot{q} (t) = 2 c_{2} + 6 c_{3} t + 12 c_{4} t^{2} + 20 c_{5} t^{3} \end{array}

(22)

式中： $q (t)$ 为运动轨迹末端点的位移，c₁、c₂、c₃、c₄、c₅为各阶次系数。

设上述轨迹规划方程的约束条件为： $q (t_{0}) = q_{0}$ 、 $q (t_{m}) = q_{m}$ 、 $\dot{q} (t_{0}) = {\dot{q}}_{0}$ 、 $\dot{q} (t_{m}) = {\dot{q}}_{m}$ 、 $\ddot{q} (t_{0}) = {\ddot{q}}_{0}$ 、 $\ddot{q} (t_{m}) = {\ddot{q}}_{m}$ 。其中， $t_{0}$ 表示起始时刻， $t_{m}$ 表示终止时刻。则各系数的解为：

\{\begin{array}{l} c_{0} = q_{0}, c_{1} = {\dot{q}}_{0} \\ c_{2} = \frac{{\ddot{q}}_{0}}{2}, c_{3} = \frac{k_{1}}{2 (t_{m} - t_{0})^{3}} \\ c_{4} = \frac{k_{2}}{2 (t_{m} - t_{0})^{4}}, c_{5} = \frac{k_{3}}{2 (t_{m} - t_{0})^{5}} \end{array}

(23)

其中：

\{\begin{array}{l} k_{1} = 20 (q_{m} - q_{0}) - (8 {\dot{q}}_{m} + 12 {\dot{q}}_{0}) (t_{m} - t_{0}) - \\ (3 {\ddot{q}}_{0} - {\ddot{q}}_{m}) (t_{m} - t_{0})^{2} \\ k_{2} = 30 (q_{0} - q_{m}) + (14 {\dot{q}}_{m} + 16 {\dot{q}}_{0}) (t_{m} - t_{0}) + \\ (3 {\ddot{q}}_{0} - 2 {\ddot{q}}_{m}) (t_{m} - t_{0})^{2} \\ k_{3} = 12 (q_{m} - q_{0}) - (6 {\dot{q}}_{m} + 6 {\dot{q}}_{0}) (t_{m} - t_{0}) - \\ ({\ddot{q}}_{0} - {\ddot{q}}_{m}) (t_{m} - t_{0})^{2} \end{array}

在凿毛作业过程中，需在关节空间中进行点到点轨迹规划的第1、第3、第5阶段的运动信息如表3所示。

表3 关节空间点到点轨迹规划的运动信息

Table 3 Motion information for point-to-point trajectory planning in joint space

运动阶段	轨迹点	关节位置/(°)或mm			关节速度/[(°)/s]或(mm/s)			关节加速度/[(°)/s²]或(mm/s²)			对应时刻/s
运动阶段	轨迹点	$θ_{1}^{j}$ （ $d_{1}^{g}$ ）	$θ_{2}^{j}$ （ $θ_{2}^{g}$ ）	$θ_{3}^{j}$ （ $θ_{3}^{g}$ ）	${\dot{θ}}_{1}^{j}$ （ ${\dot{d}}_{1}^{g}$ ）	${\dot{θ}}_{2}^{j}$ （ ${\dot{θ}}_{2}^{g}$ ）	${\dot{θ}}_{3}^{j}$ （ ${\dot{θ}}_{3}^{g}$ ）	${\ddot{θ}}_{1}^{j}$ （ ${\ddot{d}}_{1}^{g}$ ）	${\ddot{θ}}_{2}^{j}$ （ ${\ddot{θ}}_{2}^{g}$ ）	${\ddot{θ}}_{3}^{j}$ （ ${\ddot{θ}}_{3}^{g}$ ）	对应时刻/s
第1阶段	1	-45	85	11	0	0	0	0	0	0	0
	2	-24.18	52.73	11	3	1	0	-1	1	0	10
	3	-19.49	53.94	-14.47	0	0	0	0	0	0	15
第3阶段	1	-24.02	18.20	10.13	0	0	0	0	0	0	49.61
	2	-26.09	21.35	11	-2	4	0	-0.8	2.5	0	55
	3	-45	85	11	0	0	0	0	0	0	65
第5阶段^①	1	1 300	-45	85	0	0	0	0	0	0	75
第5阶段^①	2	1 300	-46.27	50.57	0	0	0	0	0	0	90

① 第5阶段凿毛机构固定连接，对应关节变量变为 $d 1 g$ （单位为mm）、 $θ 2 g$ 、 $θ 3 g$ 。

新窗口打开| 下载CSV

3.3　笛卡儿空间指定路径规划

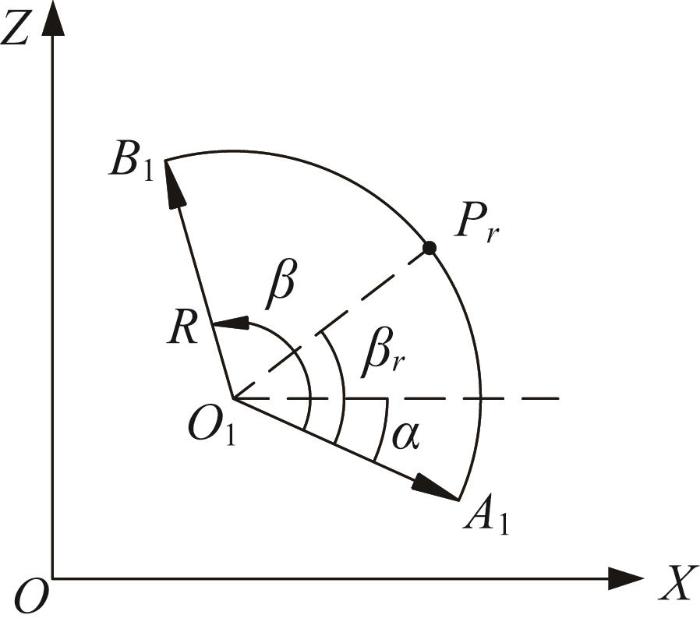
在凿毛作业过程中，笛卡儿空间中的指定路径为平面圆弧形。平面圆弧插补示意如图11所示，圆弧A₁B₁按逆时针旋转， $β$ 表示圆弧圆心角； $α$ 表示圆弧起始角度，当位于水平轴线以下时，圆弧起始角度 $α$ 为负； $β_{r}$ 为圆弧上某一插值点 $P_{r}$ 所对应的圆弧圆心角；R为圆弧半径。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 平面圆弧插补示意

Fig.11 Planar circular interpolation diagram

传统的平面圆弧插补属于等距插补，无法对始末位置的速度、加速度进行控制；而基于S形加减速控制算法的平面圆弧插补可在实现指定运动轨迹规划的同时，保证沿运动轨迹的速度、加速度曲线连续且无阶跃，以及始末位置的速度、加速度为0。因此，本文采用基于S形加减速控制算法的平面圆弧插补方法进行笛卡儿空间指定路径规划。

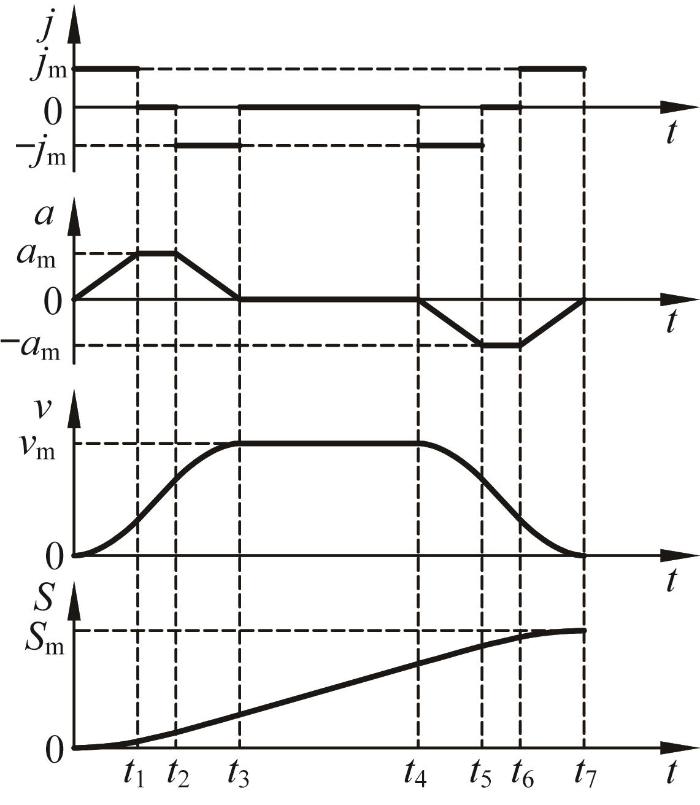
S形加减速曲线由7个运动阶段组成，如图12所示。其中：j为加加速度，a为加速度，v为速度，S为位移；j_m为最大加加速度，-j_m为最大减减速度， $a_{m}$ 为最大加速度，- $a_{m}$ 为最大减速度， $v_{m}$ 为最大速度，S_m为总位移^[27-28]。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 S形加减速曲线

Fig.12 S-shaped acceleration and deceleration curve

设 $t_{h}$ (h=1, 2,…, 7)为各阶段过渡点对应的时刻， $T_{h}$ (h=1, 2, …, 7)为各阶段的持续时间。为简化表达式，定义 $τ_{h} = t - t_{h - 1}$ (h=1, 2, …, 7)表示将各阶段起始时刻看作时间零点的局部时间，对加速度随时间变化的函数关于时间求2次积分，可得位移随时间变化的函数表达式，具体如下：

S (t) = \{\begin{array}{l} \frac{1}{6} j_{m} τ_{1}^{3}, 0 \leq t \leq t_{1} \\ S_{1} + \frac{1}{2} j_{m} T_{1}^{2} τ_{2} + \frac{1}{2} a_{m} τ_{2}^{2}, t_{1} \leq t \leq t_{2} \\ S_{2} + (\frac{1}{2} j_{m} T_{1}^{2} + a_{m} T_{2}) τ_{3} + \frac{1}{2} a_{m} τ_{3}^{2} - \frac{1}{6} j_{m} τ_{3}^{3}, t_{2} \leq t \leq t_{3} \\ S_{3} + v_{m} τ_{4}, t_{3} \leq t \leq t_{4} \\ S_{4} + v_{m} τ_{5} - \frac{1}{6} j_{m} τ_{5}^{3}, t_{4} \leq t \leq t_{5} \\ S_{5} + (v_{m} - \frac{1}{2} j_{m} T_{5}^{2}) τ_{6} - \frac{1}{2} a_{m} τ_{6}^{2}, t_{5} \leq t \leq t_{6} \\ S_{6} + (v_{m} - \frac{1}{2} j_{m} T_{5}^{2} - a_{m} T_{6}) τ_{7} - \frac{1}{2} a_{m} τ_{7}^{2} + \frac{1}{6} j_{m} τ_{7}^{3}, t_{6} \leq t \leq t_{7} \end{array}

(24)

其中：

\{\begin{array}{l} S_{1} = \frac{1}{6} j_{m} T_{1}^{3} \\ S_{2} = S_{1} + \frac{1}{2} j_{m} T_{1}^{2} T_{2}^{} + \frac{1}{2} a_{m} T_{2}^{2} \\ S_{3} = S_{2} + (\frac{1}{2} j_{m} T_{1}^{2} + a_{m} T_{2}) T_{3} + \frac{1}{2} a_{m} T_{3}^{2} - \frac{1}{6} j_{m} T_{3}^{3} \\ S_{4} = S_{3} + v_{m} T_{4} \\ S_{5} = S_{4} + v_{m} T_{5} - \frac{1}{6} j_{m} T_{5}^{3} 、 \\ S_{6} = S_{5} + (v_{m} - \frac{1}{2} j_{m} T_{5}^{2}) T_{6} - \frac{1}{2} a_{m} T_{6}^{2} \end{array}

因S形加减速曲线呈左右对称分布，故各阶段的持续时间满足以下关系：

\{\begin{array}{l} T_{1} = T_{3} = T_{5} = T_{7} = \frac{a_{m}}{j_{m}} \\ T_{2} = T_{6} = \frac{v_{m}}{a_{m}} - \frac{a_{m}}{j_{m}} \\ T_{4} = \frac{S_{m} - 2 S_{3}}{v_{m}} \end{array}

(25)

为保证S形加减速曲线满足标准的七段式运动规律，则每个阶段的持续时间均需大于0，即最大加加速度j_m、最大加速度a_m以及最大速度v_m之间需满足以下约束条件：

\{\begin{array}{l} \frac{v_{m}}{a_{m}} - \frac{a_{m}}{j_{m}} > 0 \\ S_{m} - [\frac{(j_{m} v_{m} - a_{m}^{2}) v_{m}}{j_{m} a_{m}} + \frac{2 a_{m} v_{m}}{j_{m}}] > 0 \end{array}

(26)

对位移曲线进行归一化处理，即可得到归一化因子 $λ$ 关于时间的表达式：

λ (t) = \frac{S (t)}{S_{m}}

(27)

最后，通过归一化因子 $λ$ 对圆弧圆心角 $β$ 进行插值处理，可得插值点 $P_{r}$ 的坐标随时间变化的函数：

\{\begin{array}{l} x_{P_{r}} (t) = x_{O_{1}} + R c o s (α + λ (t) β) \\ z_{P_{r}} (t) = z_{O_{1}} + R s i n (α + λ (t) β) \end{array}

(28)

在凿毛作业过程中，在笛卡儿空间中进行指定路径规划的第2、第6阶段的运动信息如表4所示。

表4 笛卡儿空间指定路径规划的运动信息

Table 4 Motion information for specified path planning in Cartesian space

运动阶段

最大加加速度

j_{m}

/[(°)/s³]

最大加速度a_m/

[(°)/s²]

最大速度v_m/

[(°)/s]

圆弧起始角度

α

/(°)

圆弧圆心角

β

/(°)

第2阶段

0.2

0.25

0.5

-19.99

15.68

第6阶段

0.2

0.25

1.0

-4.31

24.31

0.2

0.40

1.0

20.00

50.53

新窗口打开| 下载CSV

3.4　运动轨迹规划仿真分析

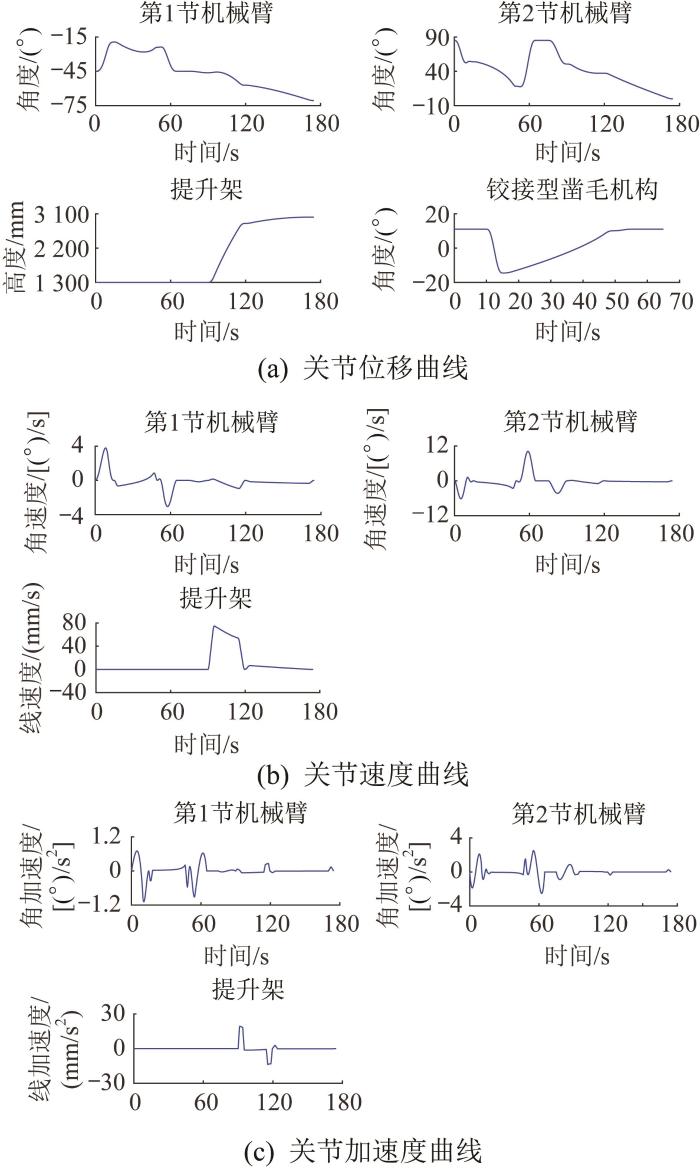
根据所建立的凿毛装置正逆运动学方程和运动轨迹规划中各阶段的运动信息，在MATLAB软件中编制相应程序，对凿毛装置进行运动轨迹规划仿真分析。隧道右侧凿毛作业过程中凿毛装置各关节的运动学参数随时间的变化曲线如图13所示。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 凿毛装置各关节的运动学参数变化曲线

Fig.13 Variation curves of kinematic parameters of each joint in scabbling device

因铰接型凿毛机构无驱动，在凿毛作业中靠支撑轮与隧道弧面的接触进行转动角度调节，故只需分析其转动角度是否在允许范围内即可，对角速度、角加速度并无运动学约束。结合图13、表1和表2可知，凿毛装置各关节的位置变化范围均在结构设计允许范围内，第1节、第2节机械臂的最大转动速度分别约为3.79 (°)/s和10.16 (°)/s，提升架移动的最大速度约为74.70 mm/s，第1节、第2节机械臂转动的最大角加速度分别约为1.09 (°)/s²和2.52 (°)/s²，提升架移动的最大加速度约为19.37 mm/s²。在整个凿毛作业过程中，凿毛装置各关节的位移曲线连续光滑且变化平稳，速度、加速度曲线均无阶跃情况发生，这可有效减少运动冲击和振动，表明该凿毛装置的运动特性良好。

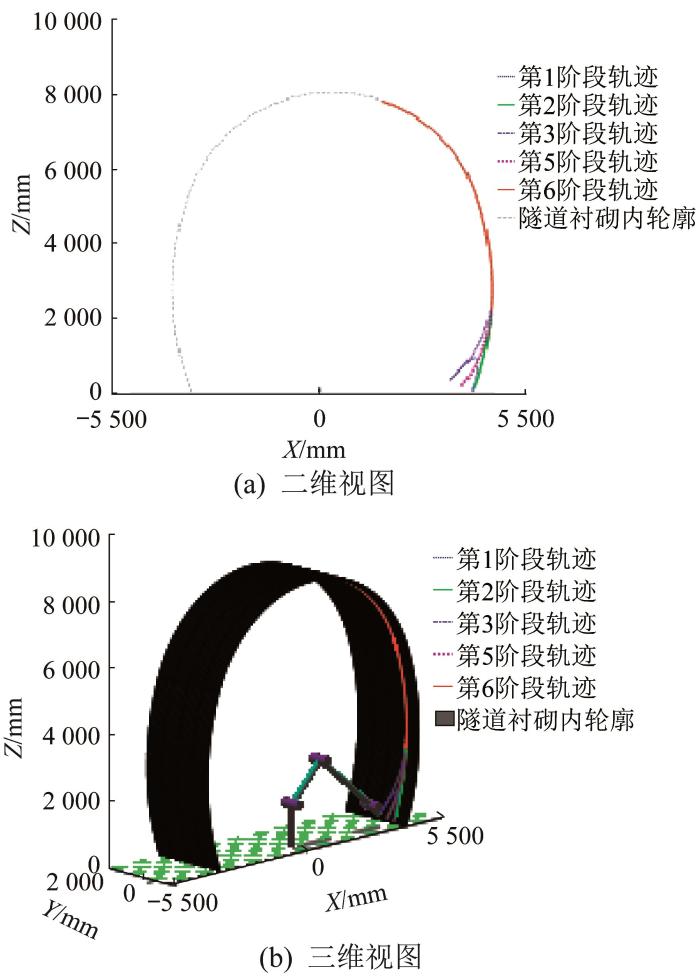
隧道右侧凿毛作业过程中凿毛装置末端的运动轨迹如图14所示。由图14可知，各阶段的运动轨迹曲线光滑连续，且采用笛卡儿空间指定路径规划的第2阶段和第6阶段的末端运动轨迹与隧道衬砌内轮廓基本完全重合；在其余采用关节空间点到点轨迹规划的各阶段，凿毛装置末端在到达指定位置的运动过程中不会与隧道衬砌内轮廓发生碰撞。由此可知，采用五次多项式插值法和基于S形加减速控制算法的平面圆弧插补方法分别进行关节空间点到点轨迹规划和笛卡儿空间指定路径规划，可满足凿毛装置作业过程的运动规划需求，保证了凿毛作业的安全性。

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 凿毛装置末端的运动轨迹

Fig.14 Motion trajectory at the end of scabbling device

4 结论

1）凿毛装置采用机械臂结合剪叉式提升架的结构，并搭配固定连接型与铰接型两类凿毛机构，从而实现在保证隧道全覆盖垂直凿毛作业的同时确保凿毛装置的总体尺寸和重量较小。

2）对凿毛装置进行了运动学分析，采用改进D-H参数法建立了其运动学模型，利用变换矩阵求解了正运动学方程，并利用几何法求解了逆运动学方程，最后利用蒙特卡洛法求解了工作空间。结果表明，凿毛装置的工作空间能完全覆盖250 km/h单线隧道衬砌内轮廓且能实现全隧道垂直凿毛作业，说明该凿毛装置满足设计要求，验证了其结构设计的合理性和可行性。

3）运动轨迹规划仿真结果表明，在凿毛装置的整个凿毛作业过程中，其各关节的位移、速度、加速度曲线均连续光滑且变化平稳。利用S形加减速控制算法可有效解决凿毛装置在第2和第6阶段出现的末端运动轨迹始末位置处速度、加速度阶跃的问题，从而有效减少了凿毛作业过程中的运动冲击与振动。结果表明，所设计的凿毛装置运动特性良好，其可沿隧道衬砌内轮廓进行垂直凿毛作业，且非凿毛状态下不会与隧道衬砌内轮廓发生碰撞，满足凿毛作业要求，这可为后续的实物样机制造与凿毛作业试验提供理论基础。

本文链接：https：//www.zjujournals.com/gcsjxb/CN/10.3785/j.issn.1006-754X.2025.05.117

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

李喆，江媛，姜礼杰，等.

我国隧道和地下工程施工技术与装备发展战略研究

［J］. 隧道建设（中英文）， 2021， 41（10）： 1717-1732.