现代机器人的研究始于20世纪中期。随着人类对自然界生物结构的深入了解,仿生机器人得到快速发展[1 -3 ] 。跳跃机器人[4 -6 ] 作为仿生机器人的一种,除了具有良好的运动性能外,还具有较好的越障能力和避险能力[7 -8 ] ,能更好地适应复杂地形,因此被广泛应用于探测[9 -10 ] 、救援救灾[11 -13 ] 、航空航天[14 ] 及军事[15 ] 等诸多领域。
当前,国内外学者对跳跃仿生机器人进行了许多研究。如:Haldane等[16 ] 设计了一种仿夜猴小型跳跃机器人Salto,其跳跃高度可达1 m,同时具有良好的连续跳跃能力;Klemm等[17 ] 设计了一种能适应复杂路面的两轮跳跃机器人,利用视觉传感技术使其拥有了更好的避障功能;Chen等[18 ] 设计了一种爆炸腿跳跃机器人,利用气动系统实现了其高爆炸性跳跃;李静等[19 ] 设计了一种仿婴猴单腿弹跳机器人,利用双闭环反馈控制系统控制机器人腿部关节,实现了机器人的连续稳定性跳跃和跳跃高度最大化;袁振宇[20 ] 设计了一种仿猫跳跃机器人,机器人利用弹簧机构的充能、储能、释能实现跳跃;高峰[21 ] 利用燃爆驱动方式设计了一种仿蛙软体跳跃机器人,采用自适应权重微粒子群优化算法求解机器人跳跃姿态的最优解,实现了最高跳跃60 cm、最远跳跃140 cm的目标。
为了提高跳跃机器人的跳跃能力,增大其向上跳跃高度和向前跳跃距离,作者根据跳蛛的外形结构特点,设计了仿跳蛛跳跃机器人(以下简称机器人)的整体结构。通过对跳蛛运动机理的分析,提出了一种弹射装置与腿部关节相互配合的复合式跳跃方式,并通过仿真和模型实验验证了复合式跳跃运动的合理性。
1 跳蛛和机器人的结构与跳跃原理
1.1 跳蛛的整体结构
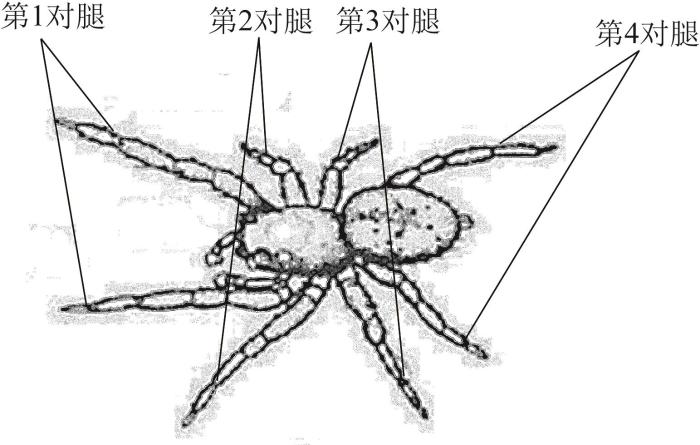
跳蛛属于蜘蛛目跳蛛科,全球约有3 000种。跳蛛由头部、躯干和腿部组成,大部分跳蛛的体长约为15 cm。跳蛛的运动能力很出色,不仅可以快速移动,还可以跳跃。其跳跃高度最高可以达到自身体长的十余倍,配合其敏锐的观察力,可以迅速扑杀猎物和躲避危险。跳蛛共有4对腿,如图1 所示,每对腿有不同的作用。从头部两侧开始按顺序排列,第1对腿的主要作用是抓取和携带物体,同时具有感知周围环境的功能;第2对腿具有辅助和支撑作用;第3对腿用于跳跃和移动,以实现其跳跃运动和躲避危险;第4对腿的作用与第2对腿类似,主要是辅助跳跃和移动。
图1
图1
跳蛛腿分布示意图
Fig.1
Schematic diagram of leg distribution of jumping spider
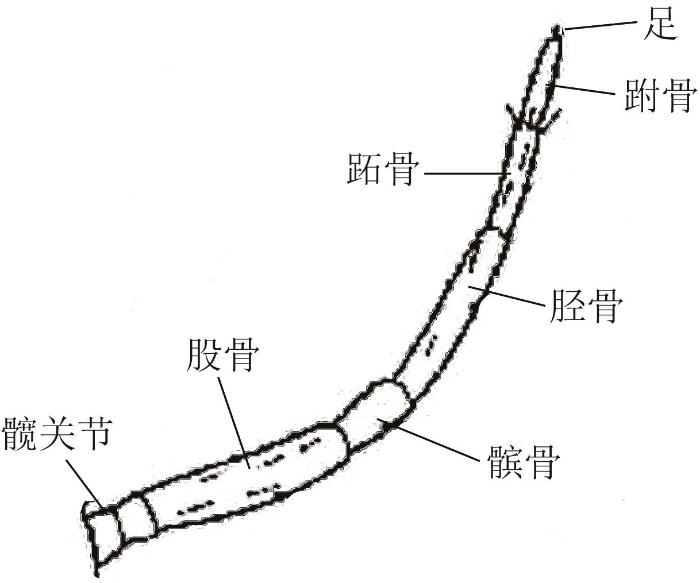
跳蛛的每条腿分别由髋关节、股骨、髌骨、胫骨、跖骨和跗骨等组成,如图2 所示。腿部关节包括股节、膝节、胫节、跖节和跗节。
图2
图2
跳蛛腿的组成
Fig.2
Composition of leg of jumping spider
1.2 跳蛛的跳跃机理
跳蛛在跳跃时主要依靠腿部伸张而带动身体协同运动。当跳蛛准备跳跃时,腿部向内弯曲收缩,作起跳准备;在进行跳跃时,其膝节和跗节没有伸肌,因此躯干部分的大部分血液流向腿部,这时其腿部相当于一个充满压力的液压缸,血流压力快速升高,并通过腿部各个关节的配合,使8条腿快速伸张,将身体发射出去,完成一次跳跃过程。跳蛛跳跃过程如图3 所示。
图3
图3
跳蛛跳跃过程
Fig.3
Jumping process of jumping spider
跳蛛具有良好的跳跃性能和移动性能,从结构上看其跳跃和移动两种行为具有不错的兼容性,同时腿部关节的适度舒张可以对起跳、腾空、着陆起到良好的平衡作用。
1.3 机器人结构与跳跃原理
通过观察和分析跳蛛的腿部结构与运动发现,对跳蛛跳跃起主要作用的是第2、第3和第4对腿,其利用腿部伸张将身体发射出去而实现跳跃动作。由此可知,在设计跳跃机器人时可以将弹射能量直接存储在机身上,结合腿部伸张完成机器人的跳跃运动。
根据以上分析,将机器人腿部设计为3对腿的结构,每对腿对应一对步足。为了简化机器人模型,将其腿部关节、连杆进行简化,将髌骨与胫骨合并成膝-胫连杆,跖骨与跗骨合并成跗骨连杆并在其中端设置弹簧减震装置。上述连杆与髋部连杆、股骨连杆共同组成机器人腿部的四杆结构。同时,设计了一种弹射装置,不仅可以帮助机器人完成跳跃动作,还可以增大机器人跳跃的高度和距离。跗骨连杆中的弹簧减震装置如图4 所示。
图4
图4
弹簧减震装置
Fig.4
Spring damping device
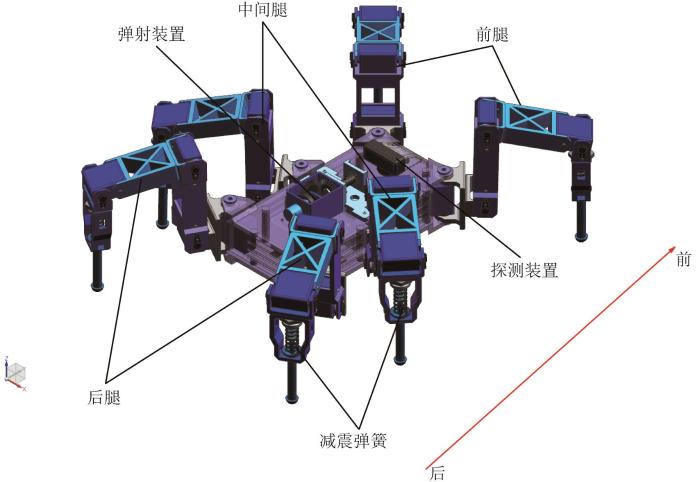
利用UG三维建模软件建立机器人整体模型,如图5 所示。机器人主体基座上端装有探测装置,探测装置前端装有照明装置以辅助探测工作,6条机械腿分布在基座两端,弹射装置安装在机身中部。
图5
图5
机器人整体模型
Fig.5
Overall model of robot
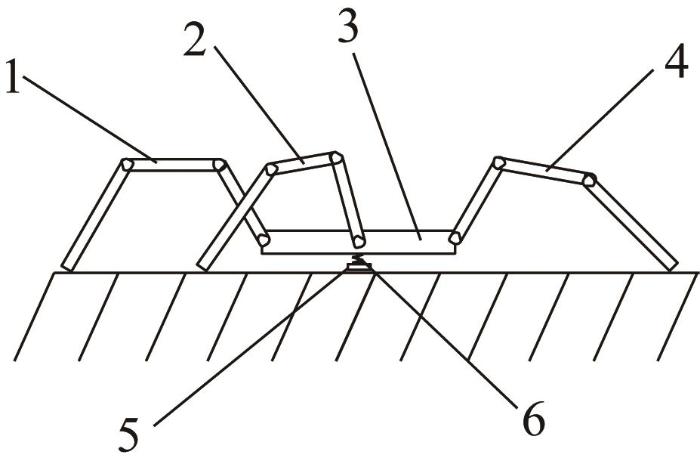
基于跳蛛利用腿部伸张将身体发射出去的运动方式,采用腿部关节、连杆与弹射装置协同配合的复合运动方式来实现机器人的跳跃运动。机器人结构简图如图6 所示。
图6
图6
机器人结构简图
1—后腿;2—中间腿;3—机身;4—前腿;5—弹射装置;6—储能弹簧。
Fig.6
Schematic diagram of robot structure
机器人包含了机身、前腿、中间腿、后腿、弹射装置和储能弹簧。腿部连杆间通过旋转运动副连接,利用舵机驱动运动副旋转,来调整腿部姿态并驱动连杆转动;腿部末端的跗骨连杆与地面接触而形成相互作用,提供机器人实现跳跃运动所需的反作用力。弹射装置内部有储能弹簧,通过压缩弹簧形成一部分能量积累;在释放弹簧储能时,弹射装置下端与地面相互作用而形成反作用力。利用腿部连杆与地面作用产生的反作用力和弹射装置释放能量而与地面产生的反作用力,实现机器人的跳跃运动。
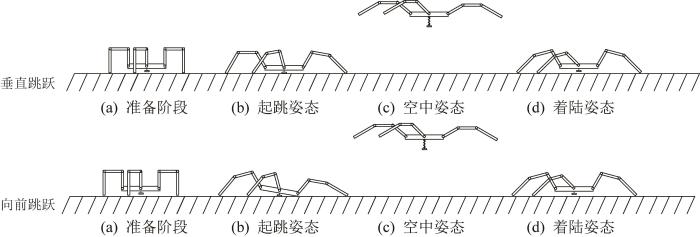
通过调整机器人起跳前的姿态,可以实现其垂直跳跃和向前跳跃。在腾空阶段,通过调整腿部连杆间的角度实现机身平衡,保证机器人在跳跃过程中的稳定性;在着陆时,通过调整腿部姿态并利用腿部末端的减震弹簧来实现机器人平稳落地。机器人跳跃过程如图7 所示。
图7
图7
机器人跳跃过程
Fig.7
Jumping process of robot
在垂直跳跃时,机器人起跳姿势为:机身保持水平,3条腿髋关节的角度保持不变,调节腿关节与水平方向成60°,膝关节与水平方向成20°,跗关节与垂直方向成50°。
在向前跳跃时,起跳姿势为:机身向前倾斜10°,3条腿髋关节的角度保持不变,调节前腿腿关节与竖直方向成29°,中间腿腿关节与竖直方向成35°,后腿腿关节与竖直方向成53.5°,前腿膝关节与水平方向成35°,中间腿膝关节与水平方向成25°,后腿膝关节与水平方向成38.5°,前腿跗关节与水平方向成40°,中间腿跗关节与竖直方向成9.9°,后腿跗关节与竖直方向成22°。
2 机器人腿部运动学与动力学分析
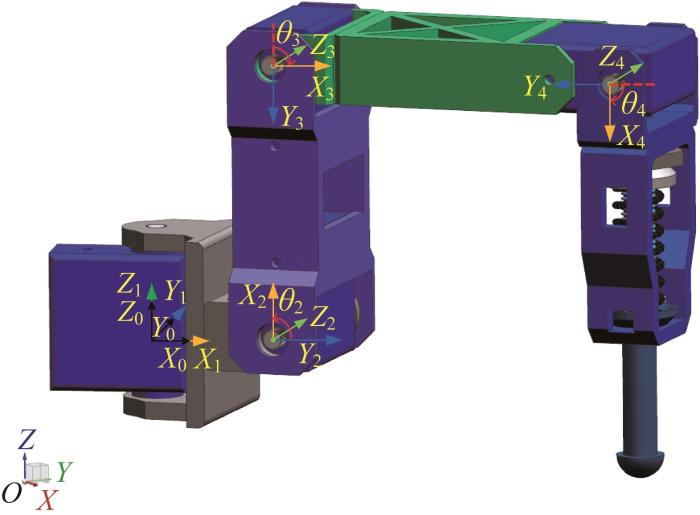
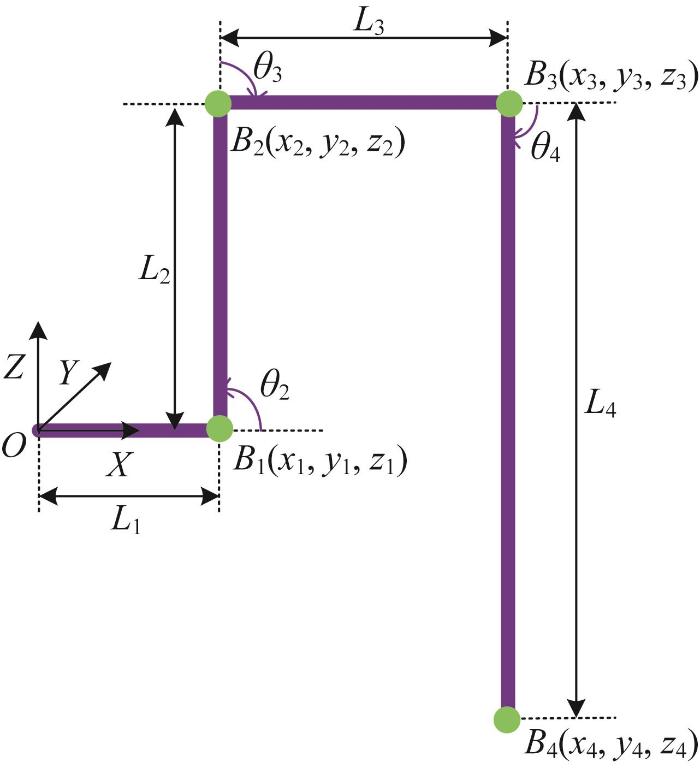
对机器人腿部进行运动学分析,有助于调整机器人的起跳姿态、空中姿态和着陆姿态,协调腿部连杆角度变化与弹射装置能量释放时机的配合,以保证机器人具有足够的运动空间和稳定的姿态。需确定其腿部末端的位置和姿态。根据前文对跳蛛运动机理的分析可知,机器人腿部结构包括髋部连杆1、股骨连杆2、膝-胫连杆3和跗骨连杆4等四部分,其长度分别为L 1 、L 2 、L 3 和L 4 ,缓冲装置安装在跗骨连杆处。首先利用MD-H(modified Denavit-Hartenberg,改进DH)法确定机器人腿部坐标系,如图8 所示。
图8
图8
机器人腿部坐标系示意
Fig.8
Schematic of robot leg coordinate system
根据上述D-H坐标系并结合机器人腿部的结构尺寸,整理后得出机器人腿部各个关节的D-H参数,如表1 所示。表中:αi -1 为连杆绕Z轴的转角;ai -1 为连杆在X 向的长度;θi 为关节转角;di 为连杆沿Z 向的平移量;i =1, 2, 3, 4,表示连杆。
根据上述D-H模型参数并通过坐标变换分析,可以得到每个旋转关节的坐标变换通式:
i - 1 i = c o s θ i - s i n θ i 0 a i - 1 c o s α i - 1 s i n θ i c o s α i - 1 c o s θ i - s i n α i - 1 - d i s i n α i - 1 s i n α i - 1 s i n θ i s i n α i - 1 c o s θ i c o s α i - 1 d i c o s α i - 1 0 0 0 1
M 4 P = L 4 0 0 1 T
根据坐标变换通式和D-H模型参数,可以确定M 点相对于基础坐标系O -XYZ 的姿态坐标为:
M 0 T = T 4 0 P M 4 = L 2 C 1 C 2 + L 3 C 1 C 23 + L 4 C 1 C 234 L 2 S 1 C 2 + L 3 S 1 C 23 + L 4 S 1 C 234 - L 2 S 2 - L 3 S 23 - L 4 S 234 1 = M 0 P x M 0 P y M 0 P z 1
C 23 = C 2 C 3 - S 2 S 3 , S 23 = C 2 S 3 - S 2 C 3
C 234 = C 2 C 34 - S 2 S 34 , S 234 = C 2 S 34 - S 2 C 34
机器人在跳跃时利用其与地面接触产生的反作用力迅速跃起,由式(3)可知机器人末端M 点X 、Y 、Z 方向的坐标如下:
X = L 2 C 1 C 2 + L 3 C 1 C 23 + L 4 C 1 C 234 Y = L 2 S 1 C 2 + L 3 S 1 C 23 + L 4 S 1 C 234 Z = - L 2 S 2 - L 3 S 23 - L 4 S 234
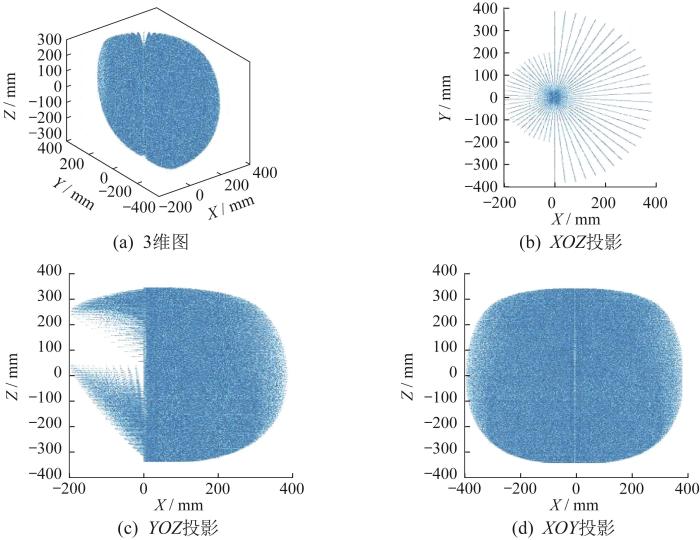
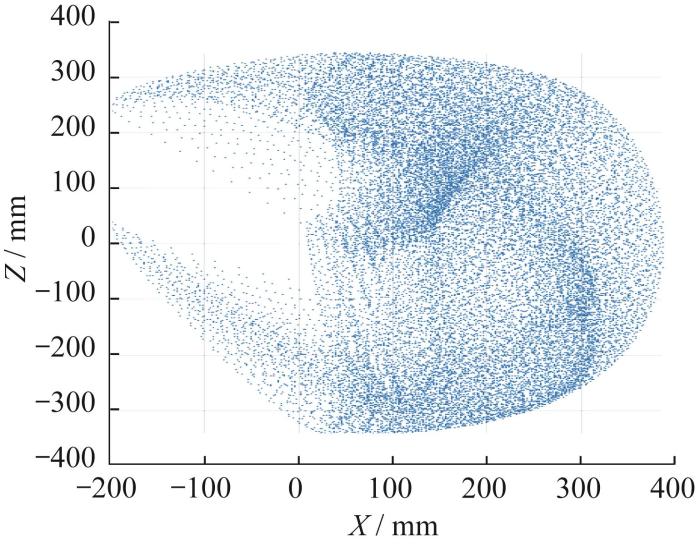
针对机器人腿部髋关节运动和不运动两种情况,利用MATLAB软件对机器人腿部的工作空间进行分析。根据上述得到的机器人腿部末端姿态坐标,将腿关节、膝关节转动角度设置为( - π / 2 , π / 2 ) ( - 3 π / 4 , π / 2 ) ( - π / 2 , π / 2 ) 图9 所示。当髋部关节不参与运动,即转动角度为0时,机器人腿部工作空间如图10 所示。
图9
图9
髋关节运动时机器人腿部工作空间
Fig.9
Working space of robot leg with hip joint movement
图10
图10
髋关节不运动时机器人腿部工作空间
Fig.10
Working space of robot leg without hip joint movement
根据上述运动学分析,可得到机器人关节角θi 的雅可比矩阵为:
J ( θ ) = ∂ X ∂ θ 1 ∂ X ∂ θ 2 ∂ X ∂ θ 3 ∂ X ∂ θ 4 ∂ Y ∂ θ 1 ∂ Y ∂ θ 2 ∂ Y ∂ θ 3 ∂ Y ∂ θ 4 ∂ Z ∂ θ 1 ∂ Z ∂ θ 2 ∂ Z ∂ θ 3 ∂ Z ∂ θ 4
机器人腿部动力学简化模型如图11 所示。假定各连杆的质心Bi 位于连杆末端,其坐标为(xi , yi , zi )。
图11
图11
机器人腿部动力学简化模型
Fig.11
Simplified dynamics model of robot leg
由拉格朗日动力学方程可以确定产生使机器人跃起的反作用力时,腿部关节所产生的力矩τi ,用拉格朗日动力学方程表示为;
τ i = d d t ∂ L ∂ θ ˙ i - ∂ L ∂ θ i = d d t ∂ E K ∂ θ ˙ i - ∂ E K ∂ θ i + ∂ W G ∂ θ i
τ 1 = ( m 1 L 1 2 + m 2 L 2 2 C 2 2 + m 3 L 3 2 C 23 2 + m 4 L 4 2 C 234 2 ) θ ¨ 1
τ 2 = ( m 2 L 2 2 + m 3 L 3 2 + m 4 L 4 2 ) θ ¨ 2 + 1 2 m 2 L 2 2 s i n ( 2 θ 2 ) + m 3 L 3 2 C 23 S 23 + m 4 L 4 2 C 234 S 234 θ ˙ 1 2 + m 2 g L 2 C 2 + m 3 g ( L 3 C 23 + L 2 C 2 ) + m 4 g ( L 4 C 234 + L 3 C 23 + L 2 C 2 )
τ 3 = ( m 3 L 3 2 + m 4 L 4 2 ) θ ¨ 3 + ( m 3 L 3 2 C 23 S 23 + m 4 L 4 2 C 234 S 234 ) θ ˙ 1 2 + m 3 g L 3 C 23 + m 4 g ( L 4 C 234 + L 3 C 23 )
τ 4 = m 4 L 4 2 θ ¨ 3 + m 4 L 4 2 C 234 S 234 θ ˙ 1 2 + m 4 g L 4 C 234
式中:m 1 、m 2 、m 3 、m 4 分别为髋部连杆、股骨连杆、膝-胫连杆、跗骨连杆的质量。
3 机器人弹射装置设计
3.1 传动机构设计
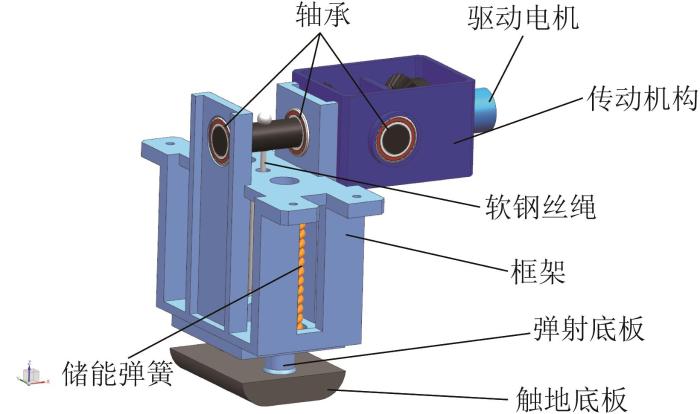
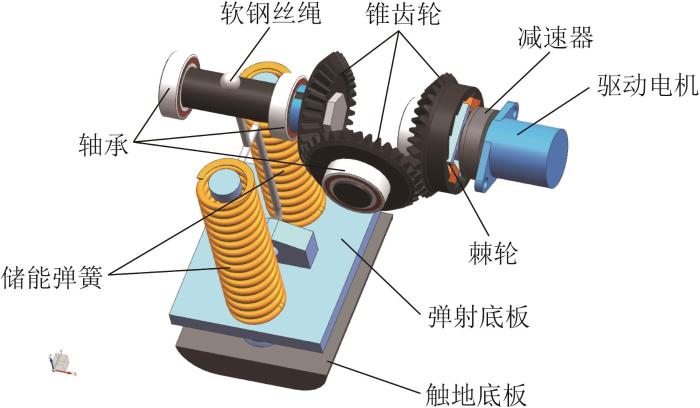
机器人弹射装置的结构如图12 所示。弹射装置利用弹簧储能和释能的方式,并采用棘轮作为压缩和释放弹簧的传动机构之一。传动机构的结构如图13 所示。由驱动电机和减速器提供适合的驱动力矩,棘轮与锥齿轮相连,锥齿轮末端装有旋转杆,旋转杆通过软钢丝绳拉动弹射底板以实现弹簧压缩储能,当弹射底板与框架接触,储能完成,电机停止输出力矩。由于棘轮的存在,储存的弹性势能被完全释放,与机器人腿部连杆的运动相互配合而完成机器人跳跃运动。
图12
图12
机器人弹射装置结构
Fig.12
Structure of ejection device of robot
图13
图13
弹射装置传动机构结构
Fig.13
Structure of transmission mechanism of ejection device
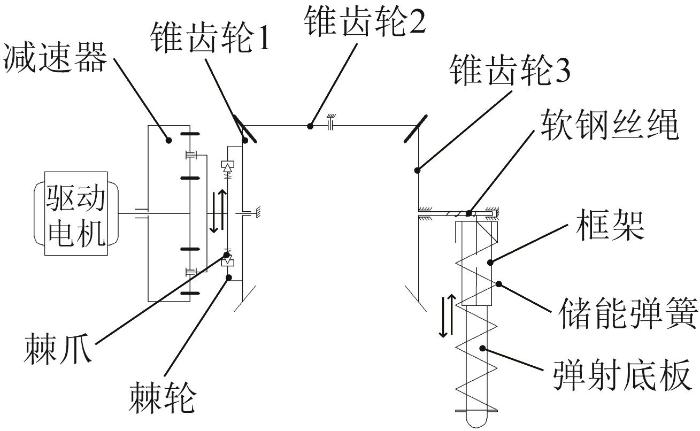
弹射装置的传动如图14 所示。传动机构由电机驱动,电机和减速器输出所需要的力矩,棘轮和2个锥齿轮以1∶1∶1的传动比将力矩输出到锥齿轮3;旋转杆通过软钢丝绳缠绕将弹射底板向上拉动使储能弹簧储能,当达到机器人跳跃所需的能量后,电机停止驱动,储能弹簧释能,能量通过锥齿轮反馈到棘轮处。由于棘轮具有单向传递力矩的功能,这部分返回的能量不会对电机造成伤害。
图14
图14
弹射装置传动示意图
Fig.14
Schematic diagram of transmission of ejection device
3.2 储能弹簧设计
通过分析可知,机器人跳跃所需的初始动能由弹射装置提供一部分。机器人垂直跳跃高度设计为0.5 m以上。依据设计目标,预估机器人质量为2.4 kg,其主要部件的参数如表2 所示。根据能量守恒定律,在一个孤立的系统中,总能量始终保持不变。
在理想条件下,弹簧压缩的弹性势能E 0 将完全转化为机器人起跳所需的初始动能E K ,再由动能完全转化机器人整体的重力势能E G ,由此可算得机器人跳跃所需的能量为:
E 0 = E K = E G = 11.76 J (11)
弹簧能量利用率η 弹 最高可达80%,齿轮传动效率η 齿 为90%~95%,因此机器人起跳所需的初始能量E 1 为:
E 1 = E 0 η 弹 η 齿 2 = 16.29 J (12)
预设弹簧压缩长度为45 mm,则所需的弹簧刚度k 0 为:
k 0 = 2 E 1 ( 45 m m ) 2 ≈ 16.09 N / m m (13)
根据结构设计,采用2个储能弹簧,所以单个弹簧的刚度k 1 =k 2 =8.045 N/mm。弹簧弹力F 弹 为:
F 弹 = k 1 × Δ x = 362.03 N (14)
选取中径D =12 mm、线径d =2 mm、支撑圈数量n =1圈、有效圈数量为11圈、自由长度为100 mm的非标弹簧,则其刚度k 为:
k = G d 4 8 D 3 n = 8.312 N / m m (15)
通过计算可知,所选择弹簧的刚度大于理论刚度,因此该弹簧符合要求。
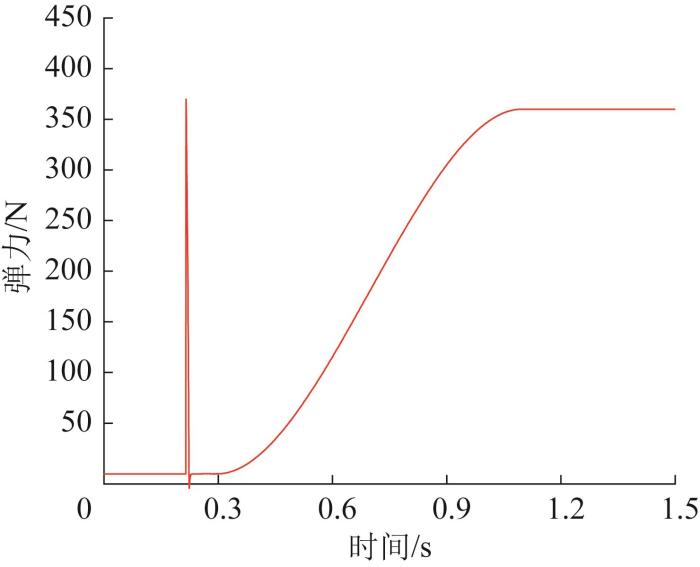
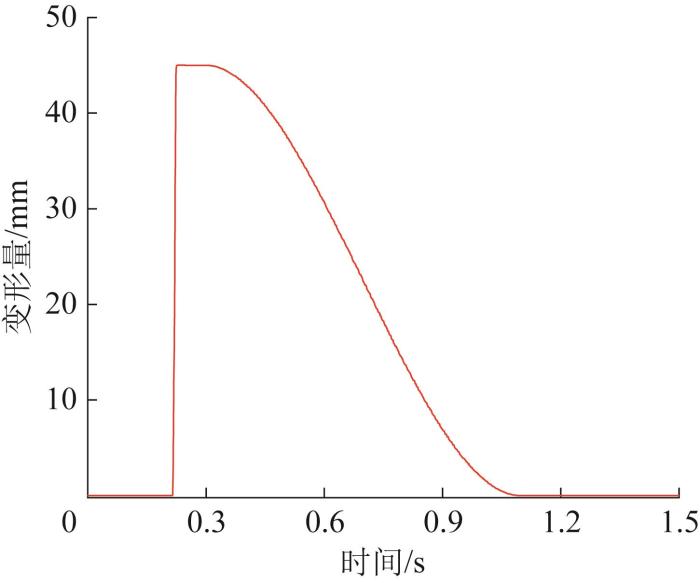
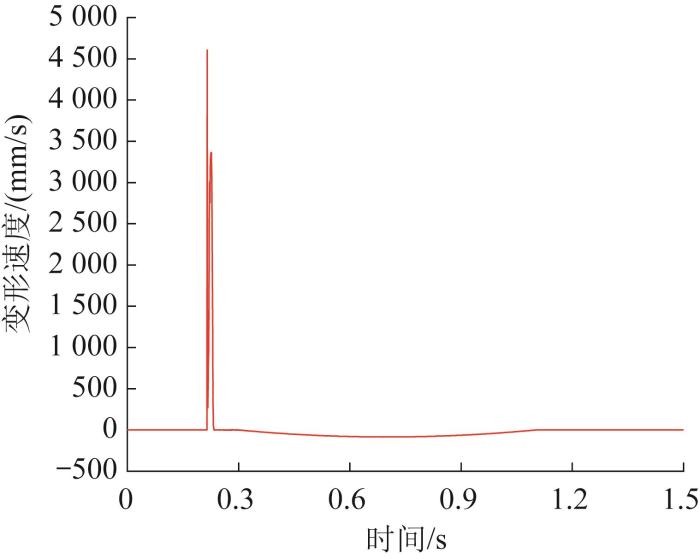
根据设计,机器人从初始姿态到起跳再落地这一完整的跳跃过程用时1.5 s,具体为:0—0.3 s为调整阶段,0.3—1.1 s为跳跃阶段,1.1—1.5 s为着陆阶段。根据胡克定律并结合ADAMS运动仿真,在整个跳跃过程中,弹簧弹力的变化如图15 所示,弹簧变形量的变化如图16 所示,弹簧变形速度的变化如图17 所示。
图15
图15
弹簧弹力曲线
Fig.15
Curve of spring elasticity
图16
图16
弹簧变形量曲线
Fig.16
Curve of spring deformation
图17
图17
弹簧变形速度曲线
Fig.17
Curve of spring deformation speed
根据上述计算和仿真结果,对所选弹簧的刚度取整为8.0 N/mm,则通过计算可知,当变形量为45 mm时,弹簧弹力为360 N。仿真前设置弹簧预紧力360 N,则弹射装置在释放和压缩完成时弹簧弹力的大小与理论计算值基本吻合。弹簧变形量和变形速度仿真值与理论值相差不到0.1%,均在合理范围内。
4 机器人运动控制系统设计
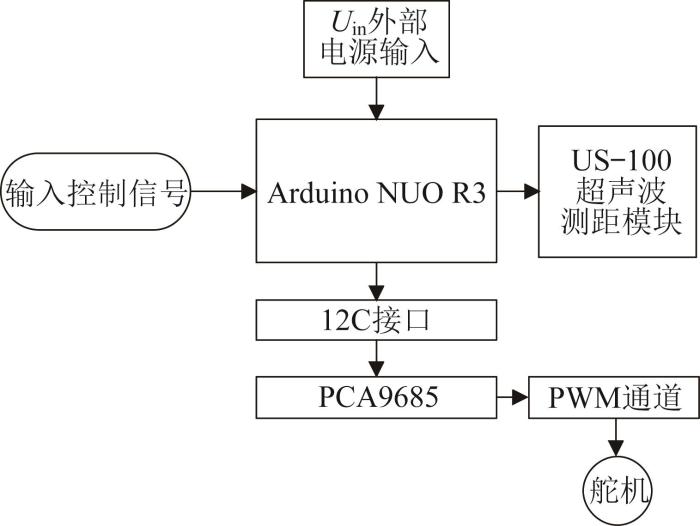
机器人的运动控制主要包括起跳前的姿态调整、跳跃时的姿态变换和着陆时的姿态控制,包括对腿部各关节角度和速度的控制以及对弹射装置释放时间的控制。其运动控制系统的硬件结构如图18 所示。
图18
图18
机器人运动控制系统硬件结构
Fig.18
Hardware structure of motion control system of robot
利用Arduino平台实现对机器人的运动控制。机器人控制系统的硬件主要包括Arduino NUO R3开发板、PCA9685 16路舵机驱动板块、舵机和测距仪等。通过Arduino平台设计舵机的旋转角度和运动时间,通过数据线将数据输入Arduino NUO R3开发板,并通过连接线传输到PCA9685 16路舵机驱动板块,与舵机驱动板块连接的舵机接收到信号后实现旋转;测距模块则通过连接线与开发板连接,在信号传递后测量跳跃高度。
5 机器人跳跃仿真分析
为了实现机器人腿部关节与弹射装置更好的配合,对跳蛛跳跃运动进行深入分析。跳蛛在起跳时,第3对、第4对步足向后摆动而瞬间蹬地,第2对步足瞬间抬起;在跳跃时,第1对步足抬起,但不参与跳跃。在这一过程中,第3对步足相对于其他步足最后离开地面,这进一步说明了第3对步足是跳蛛跳跃的主要运动步足。跳蛛跳跃时的腿部姿态如图19 所示。
图19
图19
跳蛛跳跃时的腿部姿态
Fig.19
Leg postures of jumping spider with jumping
利用UG三维软件对机器人建模,并将模型导出为.xt格式文件,然后导入ADAMS动力学仿真软件进行运动仿真。在导入前将机器人髋关节角度设置完成,因此在ADAMS环境下髋关节的变化角度为0。
5.1 垂直跳跃
机器人垂直跳跃过程包括起跳、弹射、上升、上升至最高点、下降和着陆等6个阶段,如图20 所示。
图20
图20
机器人垂直跳跃仿真过程
Fig.20
Simulation process of robot's vertical jump
在垂直跳跃过程中,机器人腿部关节角度的设置如表3 所示。
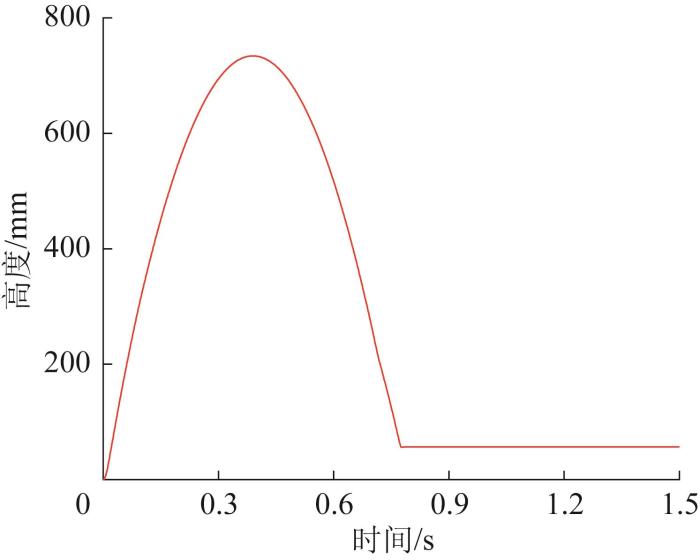
仿真中,步足1和步足4腿关节、膝关节的运动时间为0.01 s,跗关节从0变化为50°/-50°的时间为0.01 s,从50°/-50°变化为-30°/30°的时间为0.5~0.8 s;其余步足腿关节、膝关节的运动时间为0.1 s,跗关节从0变化为50°/-50°的时间为0.1 s,从50°/-50°变化为-30°/30°的时间为0.5~0.8 s。仿真得到机器人垂直跳跃时质心的高度、速度和加速度曲线,如图21 至图23 所示。
图21
图21
机器人垂直跳跃时质心高度曲线
Fig.21
Height curve of mass center with robot's vertical jump
图22
图22
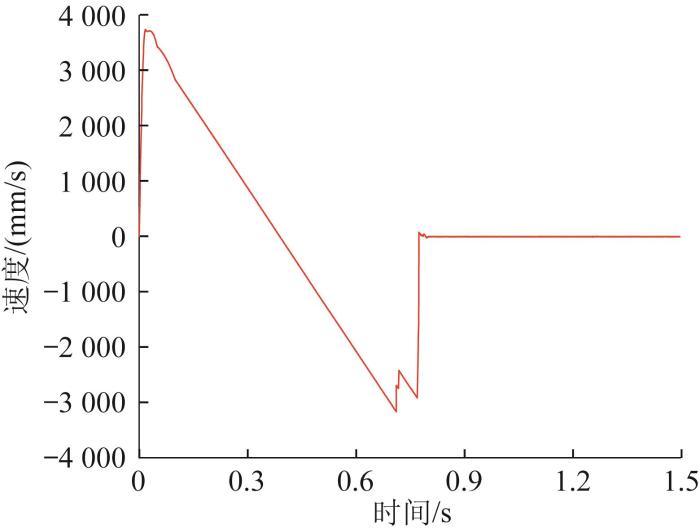
机器人垂直跳跃时质心速度曲线
Fig.22
Velocity curve of mass center with robot's vertical jump
图23
图23
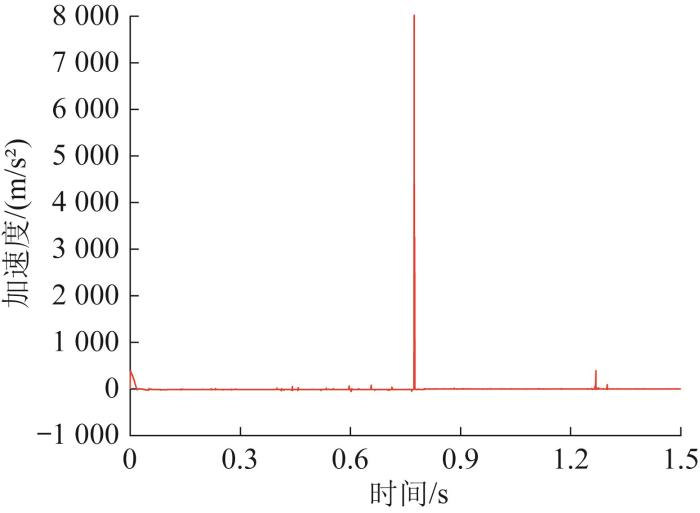
机器人垂直跳跃时质心加速度曲线
Fig.23
Acceleration curve of mass center with robot's vertical jump
由图21 可知,机器人质心高度最高可达734.117 6 mm,而预期高度为500 mm,可见机器人垂直跳跃高度完全达到了目标值。
由图22 可知:在起跳阶段,机器人质心速度突然提高,当上升到最高点时速度下降为0;在下降阶段,机器人进行反方向加速,在接触地面后,由于跗骨连杆有缓冲弹簧,在缓冲弹簧的作用下,其整体速度逐渐下降至0。
如图23 所示,由于弹簧的缓冲作用,机器人在起跳和着陆受到冲击时有小幅跳动,其质心加速度产生了突变。
5.2 向前跳跃
机器人向前跳跃过程包括起跳姿态调整、弹射、上升至最高点、下降、着陆姿态调整和着陆等6个阶段,如图24 所示。
图24
图24
机器人向前跳跃仿真过程
Fig.24
Simulation process of robot's forward jump
在向前跳跃过程中,机器人腿部关节角度的设置如表4 所示。
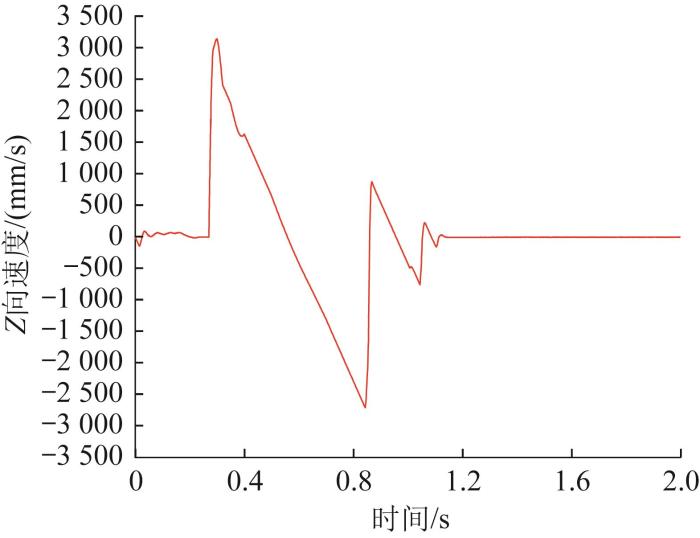
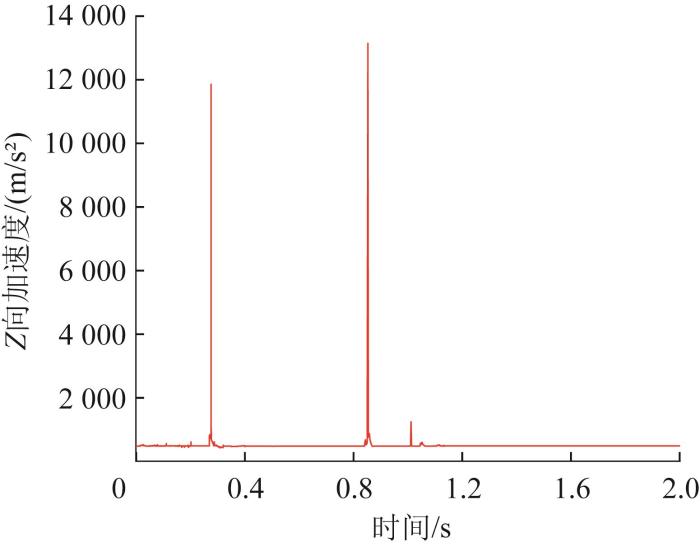
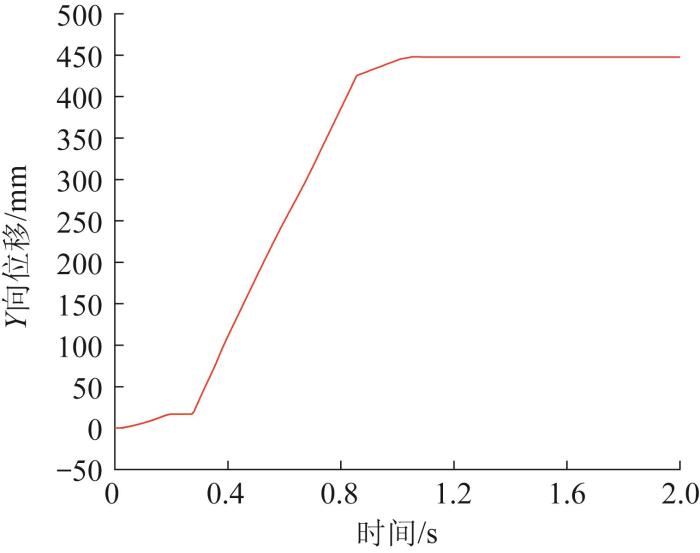
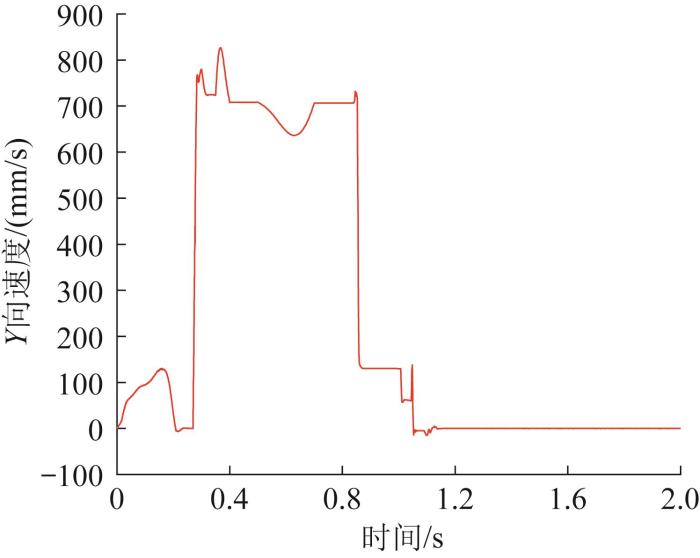
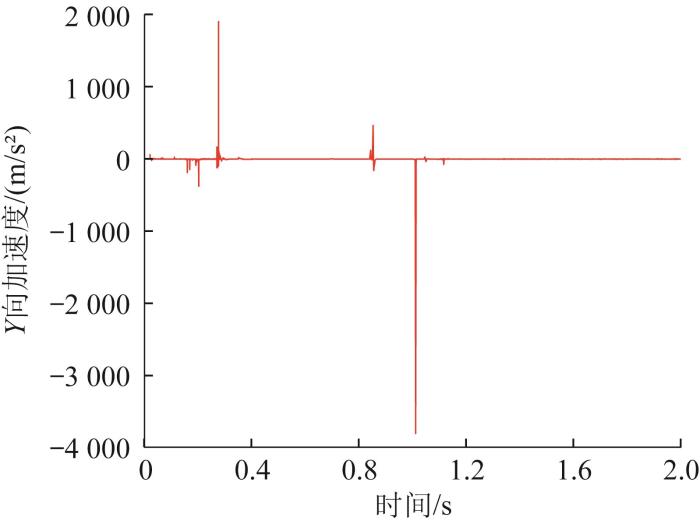
同理,仿真中,步足1腿关节的运动时间分别为0~0.2、0.5~0.7 s,膝关节的运动时间分别为0~0.2、0.5~0.7 s,跗关节的运动时间分别为0~0.2、0.27~0.30 s、0.5~0.7 s;步足2腿关节的运动时间分别为0~0.2、0.28~0.32、0.5~0.7 s,膝关节的运动时间分别为0~0.2、0.35~0.40、0.5~0.7 s,跗关节的运动时间分别为0~0.1、0.28~0.32、0.5~0.7 s;步足3腿关节的运动时间分别为0~0.2、0.28~0.32、0.5~0.7 s,膝关节的运动时间分别为0~0.2、0.35~0.40、0.5~0.7 s,跗关节的运动时间分别为0~0.2、0.28~0.32、0.5~0.7 s;步足4与步足1的运动同步,步足5与步足2的运动同步,步足6与步足3的运动同步。仿真得到机器人向前跳跃时质心位移、速度和加速度曲线,如图24 至图30 所示。其中,Z 向为垂直向上方向,Y 向为水平方向。
图25
图25
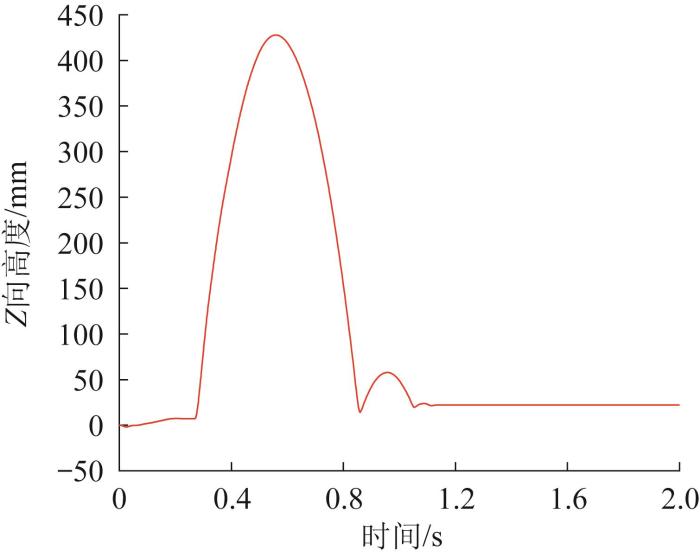
机器人向前跳跃时质心 Z
Fig.25
Z -direction displacement curve of mass center with robot's forward jump
图26
图26
机器人向前跳跃时质心 Z
Fig.26
Z -direction velocity curve of mass center with robot's forward jump
图27
图27
机器人向前跳跃质心 Z
Fig.27
Z -direction acceleration curve of mass center with robot's forward jump
图28
图28
机器人向前跳跃时质心 Y
Fig.28
Y -direction displacement curve of mass center with robot's forward jump
图29
图29
机器人向前跳跃时质心 Y
Fig.29
Y -direction velocity curve of mass center with robot's forward jump
图30
图30
机器人向前跳跃质心 Y
Fig.30
Y -direction acceleration curve of mass center with robot's forward jump
由图25 可知:机器人经过0.27 s后开始起跳,约0.33 s后达到最高点,此后机器人开始下降,2 s后接触地面;由于弹簧的缓冲作用,机器人接触地面后有小幅度的跳跃运动,然后逐渐稳定。
如图26 和图27 所示,由于机器人接触地面后仍有小幅度的跳跃运动,着陆后机器人的速度有相应的变化,加速度在机器人起跳和着陆时发生了突变。
如图28 所示,在与跳跃高度变化相同的时间段,机器人向前跳跃的距离也发生了变化。
如图29 所示,机器人在跳跃过程中腿部关节角度时刻发生着变化,影响着机器人向前运动的速度,因此机器人向前运动的速度总在变化。
如图30 所示,在机器人加速起跳和着陆冲击时,其向前运动的加速度发生突变。
通过仿真可知,机器人向前跳跃时,能达到的最大高度为425.900 5 mm,最大向前距离为447.641 7 mm,跳跃过程中的加速度突变属于正常现象。
6 机器人跳跃实验
利用3D打印技术制作机器人弹射装置和腿部模型,如图31 所示。模型整体高度为19.5 cm,全部伸展后长度为86.6 cm,质量为901.3 g。
图31
图31
机器人弹射装置和腿部模型
Fig.31
Ejection device and leg model of robot
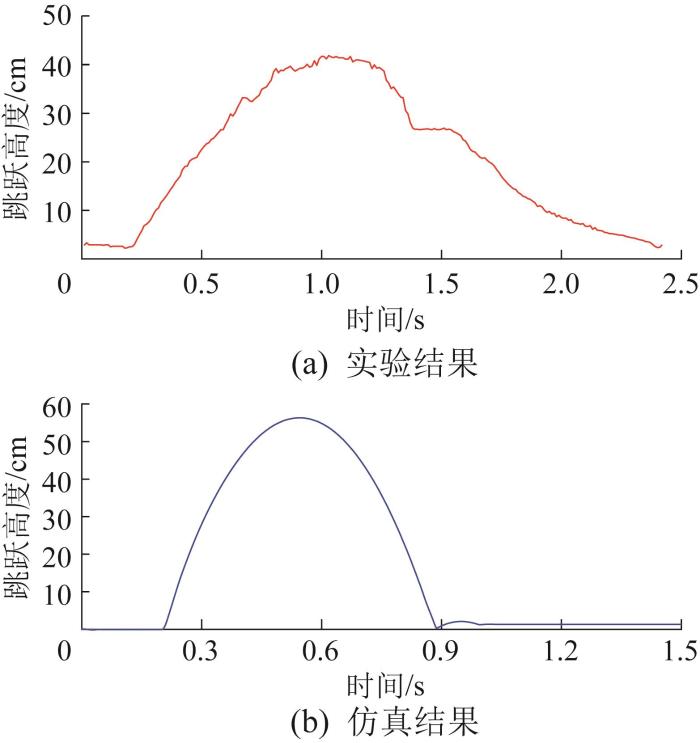
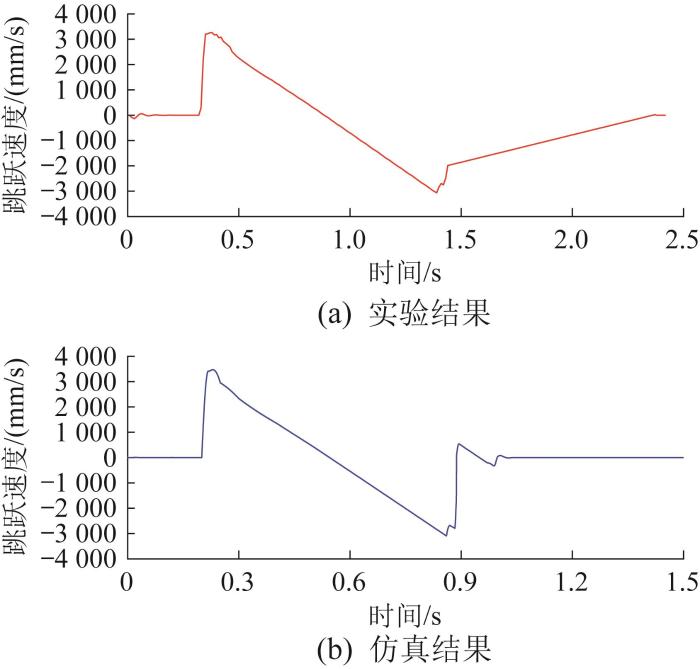
采用Arduino平台的硬件控制方案进行模型控制,利用US-100超声波测距模块进行测距并采集跳跃速度。将采集到的跳跃高度和速度与仿真结果进行对比,如图32 和图33 所示。由图32 可知,跳跃高度的实验结果与仿真结果存在一定的误差,原因是:实验时选用的弹簧的刚度与仿真时弹簧刚度有些许误差,控制线板的杜邦线排布影响了模型跳跃运动,同时外界噪音影响了超声信号的发出和收集。结果表明,实验与仿真得到的机器人高度与速度曲线总体的变化趋势基本一致,即这种复合式跳跃的方式是合理的。
图32
图32
机器人跳跃高度实验与仿真结果的对比
Fig.32
Comparison between experimental results and simulation results of robot jumping height
图33
图33
机器人跳跃速度实验与仿真结果的对比
Fig.33
Comparison between experimental results and simulation results of robot jumping velocity
模型跳跃姿态如图34 所示,与图7 所示跳跃过程中的姿态基本吻合,进一步说明基于弹射装置的复合式跳跃方式是可行的。
图34
图34
模型跳跃姿态
Fig.34
Jumping postures of model
7 结 论
1)通过观察跳蛛的跳跃过程,分析了跳蛛跳跃的运动机理。结合仿生机械学原理,设计了一种腿部带有被动减震装置的仿跳蛛跳跃机器人。利用MD-H法进行机器人腿部运动学建模,利用MATLAB软件确定了腿部的工作空间,采用拉格朗日法进行机器人腿部动力学建模,并得出其关节力矩。
2)根据跳蛛的跳跃过程,在机器人机身上设置了弹射装置。利用能量守恒定律和胡克定律对弹射装置的弹簧进行分析,得出了弹簧压缩及释放时的弹力、变形量和变形速度。提出了一种弹射装置与腿部运动相结合的复合运动方式,实现了机器人跳跃,并完成了其控制系统的设计。
3)利用UG软件进行机器人三维建模,并将模型导入ADAMS软件进行仿真。对机器人垂直跳跃和向前跳跃进行仿真分析,得出机器人垂直跳跃时最大高度达734.117 6 mm,向前跳跃时最大向前距离为447.641 7 mm,并通过模型实验验证了该复合运动方式的可行性。
参考文献
View Option
[1]
简珣 仿生机器人研究综述及发展方向
[J]. 机器人技术与应用 , 2022 (3 ): 17 -20 .
[本文引用: 1]
JIAN X Review and development direction of bionic robot research
[J]. Robot Technique and Application , 2022 (3 ): 17 -20 .
[本文引用: 1]
[2]
张建 , 周俊杰 , 苑士华 , 等 水陆两栖仿生机器人构形、运动机理及建模控制综述
[J]. 机器人 , 2023 , 45 (3 ): 367 -384 .
ZHANG J ZHOU J J YUAN S H et al Review of configuration, motion mechanism, modeling and control of amphibious bionic robots
[J]. Robot , 2023 , 45 (3 ): 367 -384 .
[3]
CUI Z A LI L WANG Y H et al Review of research and control technology of underwater bionic robots
[J]. Intelligent Marine Technology and Systems , 2023 , 1 (1 ): 7 .
[本文引用: 1]
[4]
[本文引用: 1]
MO X J GE W J REN Y F et al Design of locust-inspired eight-bar jumping robot based on take-off stability
[J]. Journal of Mechanical Engineering , 2023 , 59 (5 ): 41 -52 .
DOI:10.3901/jme.2023.05.041
[本文引用: 1]
[5]
MO X J GE W J ZHAO D L et al Review: research status of miniature jumping robot
[J]. Journal of Mechanical Engineering , 2019 , 55 (15 ): 109 -123 .
DOI:10.3901/jme.2019.15.109
[6]
ZHANG C ZOU W MA L P et al Biologically inspired jumping robots: a comprehensive review
[J]. Robotics and Autonomous Systems , 2020 , 124 : 103362 .
[本文引用: 1]
[7]
WANG W P WANG Y J FANG C et al Designing and analyzing for a bar linkage obstacle-surmounting robot with the same phase in all the wheels
[J]. IOP Conference Series: Materials Science and Engineering , 2018 , 382 : 042062 .
[本文引用: 1]
[8]
[本文引用: 1]
NIU L Z DING L GAO H B et al Review of actuation, modeling and simulation in soft-legged robot
[J]. Journal of Mechanical Engineering , 2021 , 57 (19 ): 1 -20 .
DOI:10.3901/jme.2021.19.001
[本文引用: 1]
[9]
CAO L J KONG T G ZHOU M Research on structure design and control method of underwater exploration robot
[J]. Procedia Computer Science , 2022 , 208 : 216 -222 .
[本文引用: 1]
[10]
孙俊凯 , 孙泽洲 , 辛鹏飞 , 等 深空着陆探测足式机器人发展综述
[J]. 中国机械工程 , 2021 , 32 (15 ): 1765 -1775 .
[本文引用: 1]
SUN J K SUN Z Z XIN P F et al Review on development of legged robots for deep space landing exploration
[J]. China Mechanical Engineering , 2021 , 32 (15 ): 1765 -1775 .
[本文引用: 1]
[11]
ARUNKUMAR V RAJASEKAR D AISHWARYA N A review paper on mobile robots applications in search and rescue operations
[J]. Advances in Science and Technology , 2023 : 65 -74 .
[本文引用: 1]
[12]
侯英 , 桂亚鹏 , 王建暖 救援机器人仿生造型设计
[J]. 机械设计 , 2019 , 36 (6 ): 145 .
HOU Y GUI Y P WANG J N Bionic modeling design of rescue robot
[J]. Journal of Machine Design , 2019 , 36 (6 ): 145 .
[13]
CHEN W CHENG H ZHANG W C et al Modeling and invariably horizontal control for the parallel mobile rescue robot based on PSO-CPG algorithm
[J]. Robotica , 2023 , 41 (11 ): 3501 -3523 .
[本文引用: 1]
[14]
王小涛 , 张震 , 崔宇新 , 等 月面六足机器人机构设计与行走控制方法综述
[J]. 载人航天 , 2023 , 29 (2 ): 264 -275 .
[本文引用: 1]
WANG X T ZHANG Z CUI Y X et al Review on mechanism design and walking control method of lunar hexapod robot
[J]. Manned Spaceflight , 2023 , 29 (2 ): 264 -275 .
[本文引用: 1]
[15]
单东升 , 何亚磊 一种六足军用机器人行走机构的设计与优化
[J]. 装甲兵工程学院学报 , 2018 (3 ): 72 -76 .
[本文引用: 1]
SHAN D S HE Y L Design and optimization of hexapod walking mechanism for military robot
[J]. Journal of Academy of Armored Force Engineering , 2018 (3 ): 72 -76 .
[本文引用: 1]
[16]
HALDANE D W PLECNIK M M YIM J K et al Robotic vertical jumping agility via series-elastic power modulation
[J]. Science Robotics , 2016 , 1 (1 ): eaag2048 .
[本文引用: 1]
[17]
KLEMM V MORRA A SALZMANN C et al Ascento: a two-wheeled jumping robot
[C]//2019 International Conference on Robotics and Automation . New York : IEEE , 2019 : 7515 -7521 .
[本文引用: 1]
[18]
CHEN Y F GAMBOA-GONZALEZ A WEHNER M et al Explosive legged robotic hopping: energy accumulation and power amplification via pneumatic augmentation
[EB/OL].(2023-12-10 )[2024-10-08 ]. .
URL
[本文引用: 1]
[19]
李静 , 李贵 , 孙伟 , 等 仿婴猴单腿弹跳机器人结构设计与实现
[J]. 机械传动 , 2023 , 47 (11 ): 43 -48 , 85 .
[本文引用: 1]
LI J LI G SUN W et al Structural design and implementation of simulating galago senegalensis monkey single-leg jumping robots
[J]. Journal of Mechanical Transmission , 2023 , 47 (11 ): 43 -48 , 85 .
[本文引用: 1]
[20]
袁振宇 仿猫跳跃机器人机构设计及仿真分析
[D]. 沈阳 : 沈阳工业大学 , 2020 .
[本文引用: 1]
YUAN Z Y Mechanism design and simulation analysis of cat jumping robot
[D]. Shenyang : Shenyang University of Technology , 2020 .
[本文引用: 1]
[21]
高峰 基于燃爆驱动的仿蛙软体跳跃机器人设计及实验研究
[D]. 哈尔滨 : 哈尔滨工业大学 , 2021 .
[本文引用: 1]
GAO F design and experiment of a frog-inspired soft jumping robot driven by combustion
[D]. Harbin : Harbin Institute of Technology , 2021 .
[本文引用: 1]
仿生机器人研究综述及发展方向
1
2022
... 现代机器人的研究始于20世纪中期.随着人类对自然界生物结构的深入了解,仿生机器人得到快速发展[1 -3 ] .跳跃机器人[4 -6 ] 作为仿生机器人的一种,除了具有良好的运动性能外,还具有较好的越障能力和避险能力[7 -8 ] ,能更好地适应复杂地形,因此被广泛应用于探测[9 -10 ] 、救援救灾[11 -13 ] 、航空航天[14 ] 及军事[15 ] 等诸多领域. ...
仿生机器人研究综述及发展方向
1
2022
... 现代机器人的研究始于20世纪中期.随着人类对自然界生物结构的深入了解,仿生机器人得到快速发展[1 -3 ] .跳跃机器人[4 -6 ] 作为仿生机器人的一种,除了具有良好的运动性能外,还具有较好的越障能力和避险能力[7 -8 ] ,能更好地适应复杂地形,因此被广泛应用于探测[9 -10 ] 、救援救灾[11 -13 ] 、航空航天[14 ] 及军事[15 ] 等诸多领域. ...
水陆两栖仿生机器人构形、运动机理及建模控制综述
0
2023
水陆两栖仿生机器人构形、运动机理及建模控制综述
0
2023
Review of research and control technology of underwater bionic robots
1
2023
... 现代机器人的研究始于20世纪中期.随着人类对自然界生物结构的深入了解,仿生机器人得到快速发展[1 -3 ] .跳跃机器人[4 -6 ] 作为仿生机器人的一种,除了具有良好的运动性能外,还具有较好的越障能力和避险能力[7 -8 ] ,能更好地适应复杂地形,因此被广泛应用于探测[9 -10 ] 、救援救灾[11 -13 ] 、航空航天[14 ] 及军事[15 ] 等诸多领域. ...
基于起跳稳定性的仿蝗虫八杆跳跃机器人设计
1
2023
... 现代机器人的研究始于20世纪中期.随着人类对自然界生物结构的深入了解,仿生机器人得到快速发展[1 -3 ] .跳跃机器人[4 -6 ] 作为仿生机器人的一种,除了具有良好的运动性能外,还具有较好的越障能力和避险能力[7 -8 ] ,能更好地适应复杂地形,因此被广泛应用于探测[9 -10 ] 、救援救灾[11 -13 ] 、航空航天[14 ] 及军事[15 ] 等诸多领域. ...
基于起跳稳定性的仿蝗虫八杆跳跃机器人设计
1
2023
... 现代机器人的研究始于20世纪中期.随着人类对自然界生物结构的深入了解,仿生机器人得到快速发展[1 -3 ] .跳跃机器人[4 -6 ] 作为仿生机器人的一种,除了具有良好的运动性能外,还具有较好的越障能力和避险能力[7 -8 ] ,能更好地适应复杂地形,因此被广泛应用于探测[9 -10 ] 、救援救灾[11 -13 ] 、航空航天[14 ] 及军事[15 ] 等诸多领域. ...
Biologically inspired jumping robots: a comprehensive review
1
2020
... 现代机器人的研究始于20世纪中期.随着人类对自然界生物结构的深入了解,仿生机器人得到快速发展[1 -3 ] .跳跃机器人[4 -6 ] 作为仿生机器人的一种,除了具有良好的运动性能外,还具有较好的越障能力和避险能力[7 -8 ] ,能更好地适应复杂地形,因此被广泛应用于探测[9 -10 ] 、救援救灾[11 -13 ] 、航空航天[14 ] 及军事[15 ] 等诸多领域. ...
Designing and analyzing for a bar linkage obstacle-surmounting robot with the same phase in all the wheels
1
2018
... 现代机器人的研究始于20世纪中期.随着人类对自然界生物结构的深入了解,仿生机器人得到快速发展[1 -3 ] .跳跃机器人[4 -6 ] 作为仿生机器人的一种,除了具有良好的运动性能外,还具有较好的越障能力和避险能力[7 -8 ] ,能更好地适应复杂地形,因此被广泛应用于探测[9 -10 ] 、救援救灾[11 -13 ] 、航空航天[14 ] 及军事[15 ] 等诸多领域. ...
软体足式机器人驱动、建模与仿真研究综述
1
2021
... 现代机器人的研究始于20世纪中期.随着人类对自然界生物结构的深入了解,仿生机器人得到快速发展[1 -3 ] .跳跃机器人[4 -6 ] 作为仿生机器人的一种,除了具有良好的运动性能外,还具有较好的越障能力和避险能力[7 -8 ] ,能更好地适应复杂地形,因此被广泛应用于探测[9 -10 ] 、救援救灾[11 -13 ] 、航空航天[14 ] 及军事[15 ] 等诸多领域. ...
软体足式机器人驱动、建模与仿真研究综述
1
2021
... 现代机器人的研究始于20世纪中期.随着人类对自然界生物结构的深入了解,仿生机器人得到快速发展[1 -3 ] .跳跃机器人[4 -6 ] 作为仿生机器人的一种,除了具有良好的运动性能外,还具有较好的越障能力和避险能力[7 -8 ] ,能更好地适应复杂地形,因此被广泛应用于探测[9 -10 ] 、救援救灾[11 -13 ] 、航空航天[14 ] 及军事[15 ] 等诸多领域. ...
Research on structure design and control method of underwater exploration robot
1
2022
... 现代机器人的研究始于20世纪中期.随着人类对自然界生物结构的深入了解,仿生机器人得到快速发展[1 -3 ] .跳跃机器人[4 -6 ] 作为仿生机器人的一种,除了具有良好的运动性能外,还具有较好的越障能力和避险能力[7 -8 ] ,能更好地适应复杂地形,因此被广泛应用于探测[9 -10 ] 、救援救灾[11 -13 ] 、航空航天[14 ] 及军事[15 ] 等诸多领域. ...
深空着陆探测足式机器人发展综述
1
2021
... 现代机器人的研究始于20世纪中期.随着人类对自然界生物结构的深入了解,仿生机器人得到快速发展[1 -3 ] .跳跃机器人[4 -6 ] 作为仿生机器人的一种,除了具有良好的运动性能外,还具有较好的越障能力和避险能力[7 -8 ] ,能更好地适应复杂地形,因此被广泛应用于探测[9 -10 ] 、救援救灾[11 -13 ] 、航空航天[14 ] 及军事[15 ] 等诸多领域. ...
深空着陆探测足式机器人发展综述
1
2021
... 现代机器人的研究始于20世纪中期.随着人类对自然界生物结构的深入了解,仿生机器人得到快速发展[1 -3 ] .跳跃机器人[4 -6 ] 作为仿生机器人的一种,除了具有良好的运动性能外,还具有较好的越障能力和避险能力[7 -8 ] ,能更好地适应复杂地形,因此被广泛应用于探测[9 -10 ] 、救援救灾[11 -13 ] 、航空航天[14 ] 及军事[15 ] 等诸多领域. ...
A review paper on mobile robots applications in search and rescue operations
1
2023
... 现代机器人的研究始于20世纪中期.随着人类对自然界生物结构的深入了解,仿生机器人得到快速发展[1 -3 ] .跳跃机器人[4 -6 ] 作为仿生机器人的一种,除了具有良好的运动性能外,还具有较好的越障能力和避险能力[7 -8 ] ,能更好地适应复杂地形,因此被广泛应用于探测[9 -10 ] 、救援救灾[11 -13 ] 、航空航天[14 ] 及军事[15 ] 等诸多领域. ...
Modeling and invariably horizontal control for the parallel mobile rescue robot based on PSO-CPG algorithm
1
2023
... 现代机器人的研究始于20世纪中期.随着人类对自然界生物结构的深入了解,仿生机器人得到快速发展[1 -3 ] .跳跃机器人[4 -6 ] 作为仿生机器人的一种,除了具有良好的运动性能外,还具有较好的越障能力和避险能力[7 -8 ] ,能更好地适应复杂地形,因此被广泛应用于探测[9 -10 ] 、救援救灾[11 -13 ] 、航空航天[14 ] 及军事[15 ] 等诸多领域. ...
月面六足机器人机构设计与行走控制方法综述
1
2023
... 现代机器人的研究始于20世纪中期.随着人类对自然界生物结构的深入了解,仿生机器人得到快速发展[1 -3 ] .跳跃机器人[4 -6 ] 作为仿生机器人的一种,除了具有良好的运动性能外,还具有较好的越障能力和避险能力[7 -8 ] ,能更好地适应复杂地形,因此被广泛应用于探测[9 -10 ] 、救援救灾[11 -13 ] 、航空航天[14 ] 及军事[15 ] 等诸多领域. ...
月面六足机器人机构设计与行走控制方法综述
1
2023
... 现代机器人的研究始于20世纪中期.随着人类对自然界生物结构的深入了解,仿生机器人得到快速发展[1 -3 ] .跳跃机器人[4 -6 ] 作为仿生机器人的一种,除了具有良好的运动性能外,还具有较好的越障能力和避险能力[7 -8 ] ,能更好地适应复杂地形,因此被广泛应用于探测[9 -10 ] 、救援救灾[11 -13 ] 、航空航天[14 ] 及军事[15 ] 等诸多领域. ...
一种六足军用机器人行走机构的设计与优化
1
2018
... 现代机器人的研究始于20世纪中期.随着人类对自然界生物结构的深入了解,仿生机器人得到快速发展[1 -3 ] .跳跃机器人[4 -6 ] 作为仿生机器人的一种,除了具有良好的运动性能外,还具有较好的越障能力和避险能力[7 -8 ] ,能更好地适应复杂地形,因此被广泛应用于探测[9 -10 ] 、救援救灾[11 -13 ] 、航空航天[14 ] 及军事[15 ] 等诸多领域. ...
一种六足军用机器人行走机构的设计与优化
1
2018
... 现代机器人的研究始于20世纪中期.随着人类对自然界生物结构的深入了解,仿生机器人得到快速发展[1 -3 ] .跳跃机器人[4 -6 ] 作为仿生机器人的一种,除了具有良好的运动性能外,还具有较好的越障能力和避险能力[7 -8 ] ,能更好地适应复杂地形,因此被广泛应用于探测[9 -10 ] 、救援救灾[11 -13 ] 、航空航天[14 ] 及军事[15 ] 等诸多领域. ...
Robotic vertical jumping agility via series-elastic power modulation
1
2016
... 当前,国内外学者对跳跃仿生机器人进行了许多研究.如:Haldane等[16 ] 设计了一种仿夜猴小型跳跃机器人Salto,其跳跃高度可达1 m,同时具有良好的连续跳跃能力;Klemm等[17 ] 设计了一种能适应复杂路面的两轮跳跃机器人,利用视觉传感技术使其拥有了更好的避障功能;Chen等[18 ] 设计了一种爆炸腿跳跃机器人,利用气动系统实现了其高爆炸性跳跃;李静等[19 ] 设计了一种仿婴猴单腿弹跳机器人,利用双闭环反馈控制系统控制机器人腿部关节,实现了机器人的连续稳定性跳跃和跳跃高度最大化;袁振宇[20 ] 设计了一种仿猫跳跃机器人,机器人利用弹簧机构的充能、储能、释能实现跳跃;高峰[21 ] 利用燃爆驱动方式设计了一种仿蛙软体跳跃机器人,采用自适应权重微粒子群优化算法求解机器人跳跃姿态的最优解,实现了最高跳跃60 cm、最远跳跃140 cm的目标. ...
Ascento: a two-wheeled jumping robot
1
2019
... 当前,国内外学者对跳跃仿生机器人进行了许多研究.如:Haldane等[16 ] 设计了一种仿夜猴小型跳跃机器人Salto,其跳跃高度可达1 m,同时具有良好的连续跳跃能力;Klemm等[17 ] 设计了一种能适应复杂路面的两轮跳跃机器人,利用视觉传感技术使其拥有了更好的避障功能;Chen等[18 ] 设计了一种爆炸腿跳跃机器人,利用气动系统实现了其高爆炸性跳跃;李静等[19 ] 设计了一种仿婴猴单腿弹跳机器人,利用双闭环反馈控制系统控制机器人腿部关节,实现了机器人的连续稳定性跳跃和跳跃高度最大化;袁振宇[20 ] 设计了一种仿猫跳跃机器人,机器人利用弹簧机构的充能、储能、释能实现跳跃;高峰[21 ] 利用燃爆驱动方式设计了一种仿蛙软体跳跃机器人,采用自适应权重微粒子群优化算法求解机器人跳跃姿态的最优解,实现了最高跳跃60 cm、最远跳跃140 cm的目标. ...
Explosive legged robotic hopping: energy accumulation and power amplification via pneumatic augmentation
1
... 当前,国内外学者对跳跃仿生机器人进行了许多研究.如:Haldane等[16 ] 设计了一种仿夜猴小型跳跃机器人Salto,其跳跃高度可达1 m,同时具有良好的连续跳跃能力;Klemm等[17 ] 设计了一种能适应复杂路面的两轮跳跃机器人,利用视觉传感技术使其拥有了更好的避障功能;Chen等[18 ] 设计了一种爆炸腿跳跃机器人,利用气动系统实现了其高爆炸性跳跃;李静等[19 ] 设计了一种仿婴猴单腿弹跳机器人,利用双闭环反馈控制系统控制机器人腿部关节,实现了机器人的连续稳定性跳跃和跳跃高度最大化;袁振宇[20 ] 设计了一种仿猫跳跃机器人,机器人利用弹簧机构的充能、储能、释能实现跳跃;高峰[21 ] 利用燃爆驱动方式设计了一种仿蛙软体跳跃机器人,采用自适应权重微粒子群优化算法求解机器人跳跃姿态的最优解,实现了最高跳跃60 cm、最远跳跃140 cm的目标. ...
仿婴猴单腿弹跳机器人结构设计与实现
1
2023
... 当前,国内外学者对跳跃仿生机器人进行了许多研究.如:Haldane等[16 ] 设计了一种仿夜猴小型跳跃机器人Salto,其跳跃高度可达1 m,同时具有良好的连续跳跃能力;Klemm等[17 ] 设计了一种能适应复杂路面的两轮跳跃机器人,利用视觉传感技术使其拥有了更好的避障功能;Chen等[18 ] 设计了一种爆炸腿跳跃机器人,利用气动系统实现了其高爆炸性跳跃;李静等[19 ] 设计了一种仿婴猴单腿弹跳机器人,利用双闭环反馈控制系统控制机器人腿部关节,实现了机器人的连续稳定性跳跃和跳跃高度最大化;袁振宇[20 ] 设计了一种仿猫跳跃机器人,机器人利用弹簧机构的充能、储能、释能实现跳跃;高峰[21 ] 利用燃爆驱动方式设计了一种仿蛙软体跳跃机器人,采用自适应权重微粒子群优化算法求解机器人跳跃姿态的最优解,实现了最高跳跃60 cm、最远跳跃140 cm的目标. ...
仿婴猴单腿弹跳机器人结构设计与实现
1
2023
... 当前,国内外学者对跳跃仿生机器人进行了许多研究.如:Haldane等[16 ] 设计了一种仿夜猴小型跳跃机器人Salto,其跳跃高度可达1 m,同时具有良好的连续跳跃能力;Klemm等[17 ] 设计了一种能适应复杂路面的两轮跳跃机器人,利用视觉传感技术使其拥有了更好的避障功能;Chen等[18 ] 设计了一种爆炸腿跳跃机器人,利用气动系统实现了其高爆炸性跳跃;李静等[19 ] 设计了一种仿婴猴单腿弹跳机器人,利用双闭环反馈控制系统控制机器人腿部关节,实现了机器人的连续稳定性跳跃和跳跃高度最大化;袁振宇[20 ] 设计了一种仿猫跳跃机器人,机器人利用弹簧机构的充能、储能、释能实现跳跃;高峰[21 ] 利用燃爆驱动方式设计了一种仿蛙软体跳跃机器人,采用自适应权重微粒子群优化算法求解机器人跳跃姿态的最优解,实现了最高跳跃60 cm、最远跳跃140 cm的目标. ...
仿猫跳跃机器人机构设计及仿真分析
1
2020
... 当前,国内外学者对跳跃仿生机器人进行了许多研究.如:Haldane等[16 ] 设计了一种仿夜猴小型跳跃机器人Salto,其跳跃高度可达1 m,同时具有良好的连续跳跃能力;Klemm等[17 ] 设计了一种能适应复杂路面的两轮跳跃机器人,利用视觉传感技术使其拥有了更好的避障功能;Chen等[18 ] 设计了一种爆炸腿跳跃机器人,利用气动系统实现了其高爆炸性跳跃;李静等[19 ] 设计了一种仿婴猴单腿弹跳机器人,利用双闭环反馈控制系统控制机器人腿部关节,实现了机器人的连续稳定性跳跃和跳跃高度最大化;袁振宇[20 ] 设计了一种仿猫跳跃机器人,机器人利用弹簧机构的充能、储能、释能实现跳跃;高峰[21 ] 利用燃爆驱动方式设计了一种仿蛙软体跳跃机器人,采用自适应权重微粒子群优化算法求解机器人跳跃姿态的最优解,实现了最高跳跃60 cm、最远跳跃140 cm的目标. ...
仿猫跳跃机器人机构设计及仿真分析
1
2020
... 当前,国内外学者对跳跃仿生机器人进行了许多研究.如:Haldane等[16 ] 设计了一种仿夜猴小型跳跃机器人Salto,其跳跃高度可达1 m,同时具有良好的连续跳跃能力;Klemm等[17 ] 设计了一种能适应复杂路面的两轮跳跃机器人,利用视觉传感技术使其拥有了更好的避障功能;Chen等[18 ] 设计了一种爆炸腿跳跃机器人,利用气动系统实现了其高爆炸性跳跃;李静等[19 ] 设计了一种仿婴猴单腿弹跳机器人,利用双闭环反馈控制系统控制机器人腿部关节,实现了机器人的连续稳定性跳跃和跳跃高度最大化;袁振宇[20 ] 设计了一种仿猫跳跃机器人,机器人利用弹簧机构的充能、储能、释能实现跳跃;高峰[21 ] 利用燃爆驱动方式设计了一种仿蛙软体跳跃机器人,采用自适应权重微粒子群优化算法求解机器人跳跃姿态的最优解,实现了最高跳跃60 cm、最远跳跃140 cm的目标. ...
基于燃爆驱动的仿蛙软体跳跃机器人设计及实验研究
1
2021
... 当前,国内外学者对跳跃仿生机器人进行了许多研究.如:Haldane等[16 ] 设计了一种仿夜猴小型跳跃机器人Salto,其跳跃高度可达1 m,同时具有良好的连续跳跃能力;Klemm等[17 ] 设计了一种能适应复杂路面的两轮跳跃机器人,利用视觉传感技术使其拥有了更好的避障功能;Chen等[18 ] 设计了一种爆炸腿跳跃机器人,利用气动系统实现了其高爆炸性跳跃;李静等[19 ] 设计了一种仿婴猴单腿弹跳机器人,利用双闭环反馈控制系统控制机器人腿部关节,实现了机器人的连续稳定性跳跃和跳跃高度最大化;袁振宇[20 ] 设计了一种仿猫跳跃机器人,机器人利用弹簧机构的充能、储能、释能实现跳跃;高峰[21 ] 利用燃爆驱动方式设计了一种仿蛙软体跳跃机器人,采用自适应权重微粒子群优化算法求解机器人跳跃姿态的最优解,实现了最高跳跃60 cm、最远跳跃140 cm的目标. ...
基于燃爆驱动的仿蛙软体跳跃机器人设计及实验研究
1
2021
... 当前,国内外学者对跳跃仿生机器人进行了许多研究.如:Haldane等[16 ] 设计了一种仿夜猴小型跳跃机器人Salto,其跳跃高度可达1 m,同时具有良好的连续跳跃能力;Klemm等[17 ] 设计了一种能适应复杂路面的两轮跳跃机器人,利用视觉传感技术使其拥有了更好的避障功能;Chen等[18 ] 设计了一种爆炸腿跳跃机器人,利用气动系统实现了其高爆炸性跳跃;李静等[19 ] 设计了一种仿婴猴单腿弹跳机器人,利用双闭环反馈控制系统控制机器人腿部关节,实现了机器人的连续稳定性跳跃和跳跃高度最大化;袁振宇[20 ] 设计了一种仿猫跳跃机器人,机器人利用弹簧机构的充能、储能、释能实现跳跃;高峰[21 ] 利用燃爆驱动方式设计了一种仿蛙软体跳跃机器人,采用自适应权重微粒子群优化算法求解机器人跳跃姿态的最优解,实现了最高跳跃60 cm、最远跳跃140 cm的目标. ...