近年来,提高能源效率、降低材料成本和提升机器人结构紧凑性[1]推动了对轻量化机器人的需求,机器人的轻量化设计得到了广泛研究。爬杆机器人在高空杆上作业是一项重要的功能,这对机器人的负载提出了更高的要求。研究人员采用了大量的方法来使机器人在性能降低较小的同时实现轻量化。
目前,轻量化技术已成功应用于各个领域,如汽车、航空航天等领域。应用于机器人领域的2种典型的轻量化技术为:材料轻量化和结构轻量化。材料轻量化能够获得较为良好的减重效果,因此机器人轻量化首选材料轻量化,即在保证机器人零部件力学性能的基础上优先选取轻质材料,达到轻量化的目的。具有材料轻量化代表的是工业机器人四大家族之一的德国KUKA机器人公司,其研究设计的轻型机器人LWR-3[2]的躯干均采用轻型材料(碳纤维),负重比接近1∶1,是当今负重比较高的机器人。材料轻量化的优势是可直接替换原有质量较大的金属材料以获得良好的减重效果,但弊端是轻质材料的成本较高且耐磨性比金属材料差,零部件反复拆装时容易磨损甚至发生断裂,这给机器人的后期维护带来了极大困难。而结构轻量化弱化了材料轻量化的弊端,在减重的同时保证机器人零部件的综合力学性能不变,降低了机器人的运行能耗,从而使机器人的综合性能得到提升,该方法是当前应用最广泛的机器人轻量化方法之一。与材料轻量化相比,结构轻量化只改变材料分布方式,通过去除冗余材料的方式直接达到轻量化目的,具有计算速度快、准确性高和易实现等优势。
目前,常用的结构优化方法可归类为以下3种:尺寸优化、形状优化、拓扑优化[3]。这3种方法适用的设计阶段和应用场合有所区别。其中:尺寸优化是在不改变零部件形状和材料的情况下,对内部结构尺寸进行优化设计,其设计变量通常选择厚度、孔径和深度等,但是该方法忽略了结构的形状和连接性;形状优化是指确定零部件的拓扑结构(即孔的数量和位置),并优化每个孔的形状;拓扑优化是指在给定设计域内,基于施加的约束条件(通常为质量保留百分比、刚度和变形量等)对材料分布与结点连接方式进行优化,该方法只研究材料的最佳分布情况。与尺寸优化和形状优化相比,拓扑优化不仅允许更大的设计自由度,而且能改变材料的分布状态。因此,采用拓扑优化方法进行机器人结构优化设计具有更高的层次。
随着计算机软件技术的发展及结构优化理论的逐渐成熟,拓扑优化方法已被广泛应用于各类机器人的结构轻量化设计[4]。赖欣等[5]利用变密度拓扑优化法,先将爬壁机器人分成若干个零部件,再根据各零部件的受力情况逐个进行优化,解决了机器人自身质量过大、结构复杂等问题,达到了轻量化目的。结果表明,优化后爬壁机器人的整机质量从1.14 kg减小为0.58 kg,轻量化效果显著,且优化后结构更为精简,为后续的装配环节提供了操作空间。Tran等[6]采用拓扑优化方法对Delta机器人的上臂进行了设计,在保证机器人刚度和耐用性的同时节省了材料和成本,重新设计后上臂的总质量为0.23 kg,相较于重新设计前减小了48.8%。Chu等[7]提出了一种以机器人结构的变形量、振动频率、质量为约束条件的多目标拓扑优化方法,优化后的机器人在实现减重的同时减小了整体变形量,提高了固有频率。黄永平等[8]利用变密度拓扑优化法对建筑重载机器人的主体结构进行了优化,使得其大臂的质量减小了29.6%,小臂的质量减小了33.4%,并进一步通过动力学仿真实验分析得到,优化后机器人的能耗明显改善。综上所述,拓扑优化方法非常适用于机器人的结构优化设计。
为实现爬杆机器人的结构紧凑和轻量化设计,克服其垂直爬杆困难等问题,笔者以自制仿尺蠖爬杆机器人为研究对象,以质量最小与柔度最小为目标函数,以3种运动步态的实际极限工况为边界约束条件,采用ANSYS Workbench软件对机器人关键零部件的结构进行变密度拓扑优化设计。同时,对优化后的机器人进行力学性能校验,以验证其减重降耗效果以及综合性能提升效果。
1 拓扑优化数学方法与分析过程
1.1 变密度拓扑优化问题的目标函数及约束
一般来说,基于连续体的变密度拓扑优化问题的基本数学模型包含目标函数、边界条件约束和设计变量。基于线性静力有限元分析的变密度拓扑优化问题的一般公式可以描述为:
式中:
在上述广义描述中,可以考虑各种目标和约束,包括柔度、应力、频率和位移等。
1.2 变密度拓扑优化数学模型
拓扑优化[9]的目的是在满足一定约束条件的前提下,根据载荷的分布方式将材料最佳地分布在约束支撑位置,使得结构性能达到最优。拓扑优化的一般流程为:根据定义的设计变量以及优化目标构建优化目标函数,在满足约束的条件下进行迭代求解,获得最优解后停止迭代。
式中:
本文以质量最小和柔度最小作为目标函数[17],以应力条件和载荷为边界约束条件,建立基于SIMP变密度法的结构拓扑优化数学模型:
式中:
2 爬杆机器人动力学分析与结构优化
2.1 爬杆机器人拓扑优化流程
本文以5-DOF(degree of freedom,自由度)串联爬杆机器人为研究对象。该机器人由2个夹持器、3个T关节(由摆动件和连接座组成)和2个I关节串联组成,其结构如图1所示。
图1
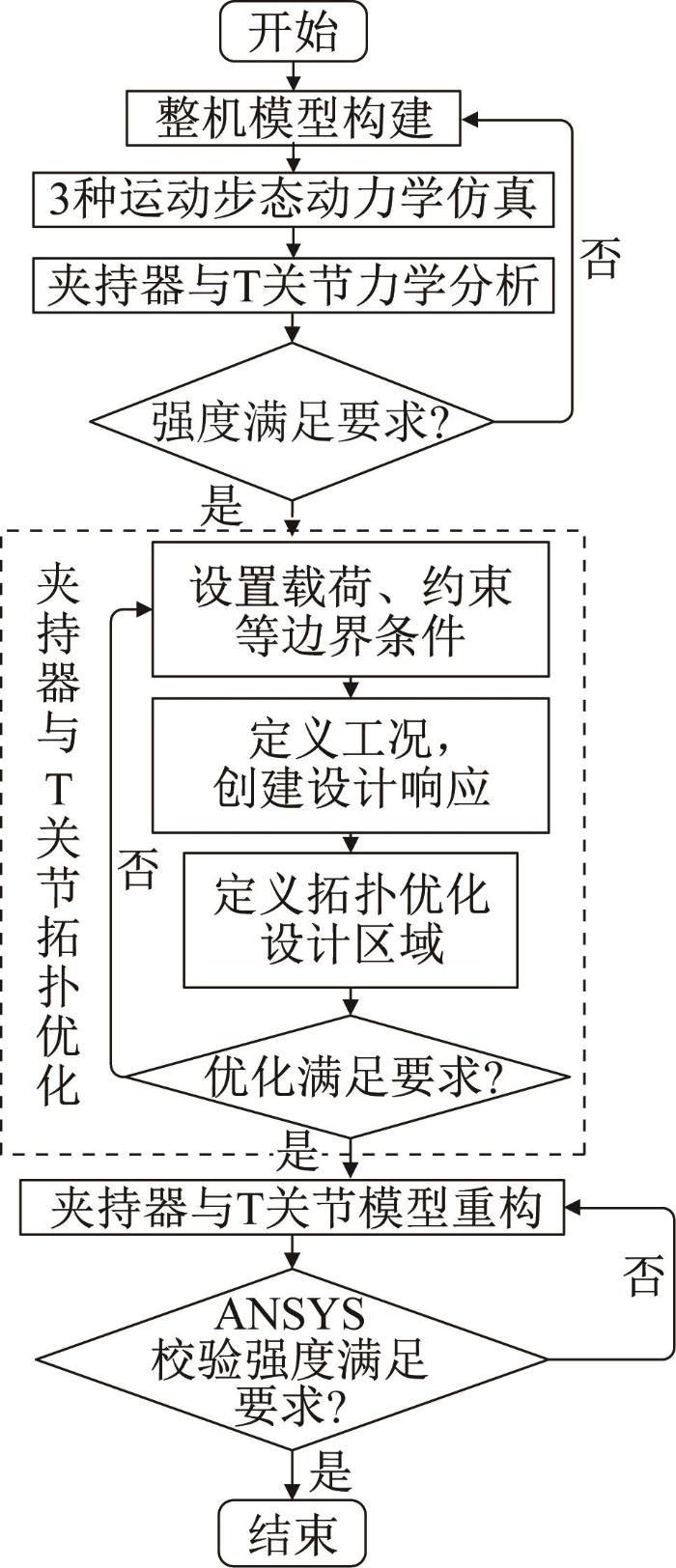
经分析,爬杆机器人主要靠夹持器与T关节支撑。选取负载最大的零部件(夹持器和T关节)作为优化对象,采用SIMP变密度拓扑优化方法对爬杆机器人进行结构优化,具体流程如图2所示。
图2
图2
基于SIMP变密度法的爬杆机器人拓扑优化流程
Fig.2
Topology optimization process of pole-climbing robot based on SIMP variable density method
根据图2,基于SIMP变密度法的爬杆机器人拓扑优化的主要步骤如下:
1)根据爬杆机器人各零部件的连接关系,在三维软件中建立机器人整机三维模型。
2)在ADAMS软件中对爬杆机器人的3种运动步态进行动力学仿真,分析其主要零部件在极限运动工况下的受力情况,获得极限工况信息。
3)根据极限工况信息,在ANSYS Workbench软件中对夹持器及T关节设置边界约束条件并进行力学分析,以得到所受的载荷、扭矩、等效应力和变形量的分布情况,从而确定这2个零部件是否可以进行拓扑优化。
4)利用SIMP变密度法对夹持器及T关节进行拓扑优化,并根据拓扑优化结果,对原夹持器及T关节的模型进行改进,并重新建立新的模型。
5)在ANSYS Workbench软件中对优化后的夹持器及T关节进行结构强度校核,判断其是否满足要求:若不满足,则根据拓扑优化结果重新对结构进行改进;若满足,则视新结构为最终设计方案。
2.2 ADAMS动力学仿真
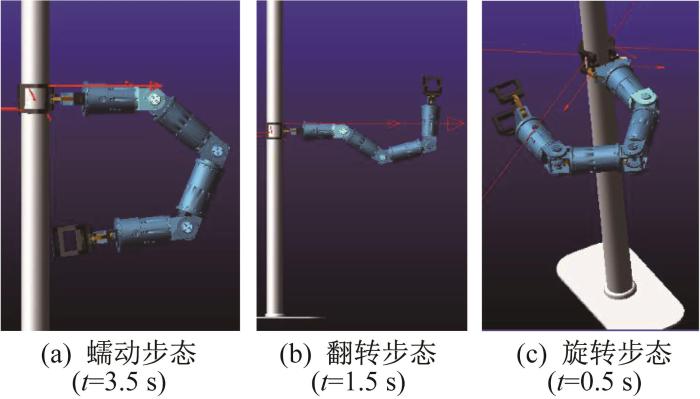
根据爬杆机器人的机构特点,设计3种运动步态,分别为蠕动步态、翻转步态和旋转步态,如图3所示。由于爬杆机器人(整机质量为13.60 kg)主要在高空环境中进行作业,其外部负载主要来自自身重量。利用ADAMS软件对爬杆机器人的3种运动步态进行动力学仿真,得到这3种运动步态下夹持器和T关节分别在t=3.5,1.5,0.5 s时的受力较大,即机器人运行的极限工况。
图3
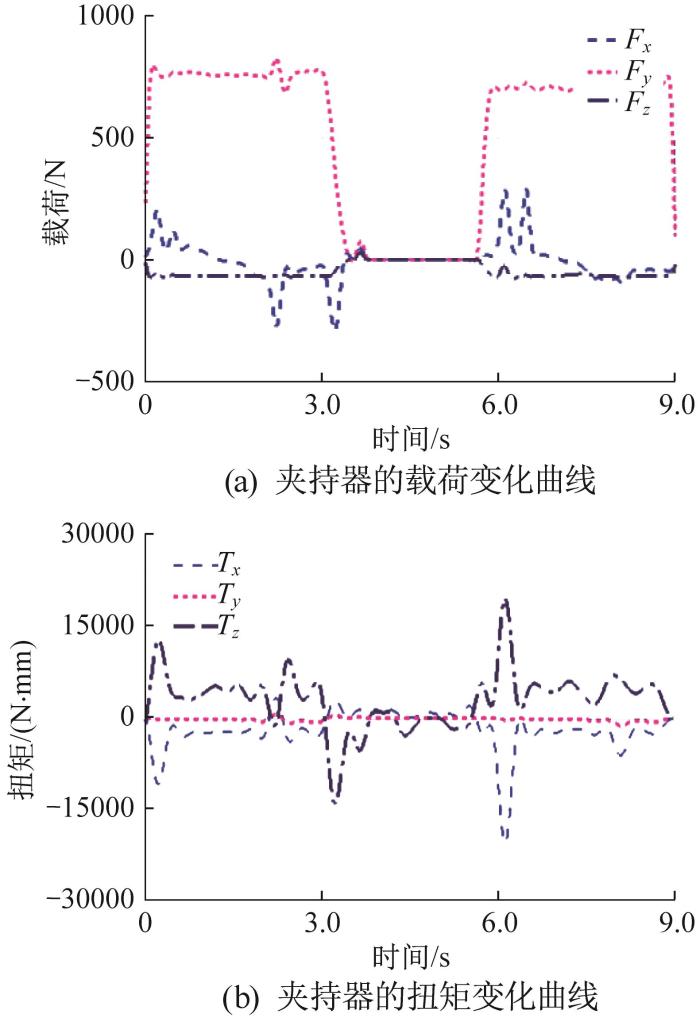
在爬杆机器人攀爬过程中,各夹持器和T关节均受到1个六维力(
图4
图5
图5
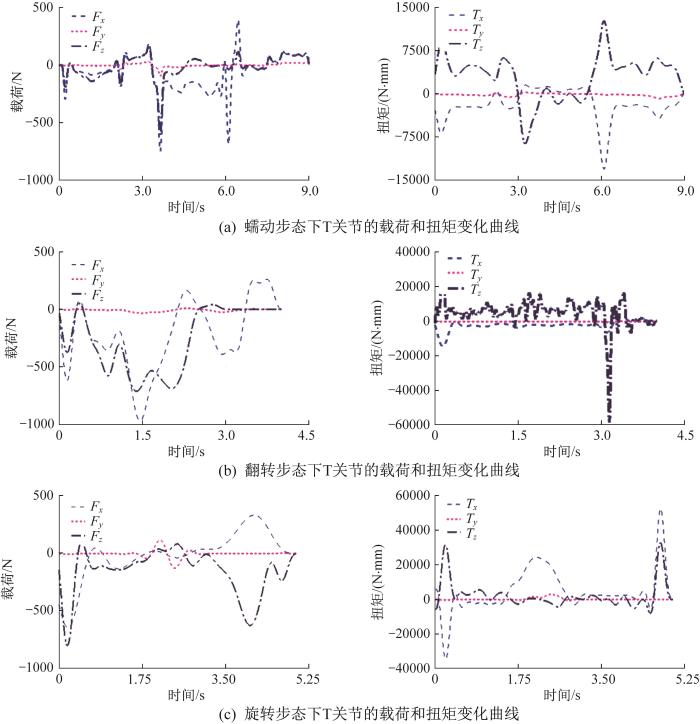
不同运动步态下T关节的载荷和扭矩变化曲线
Fig.5
Load and torque change curves of T-joint under different motion gaits
2.3 ANSYS有限元分析
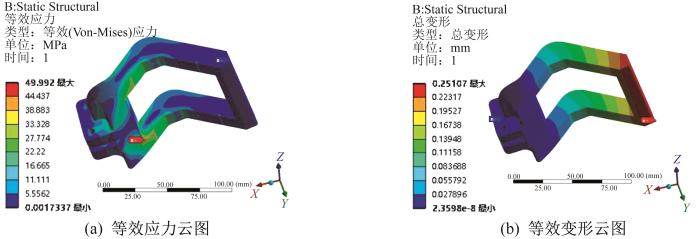
利用ANSYS Workbench软件中的Static Structual模块对爬杆机器人的夹持器和T关节进行静力学分析[19]。将通过ADAMS动力学仿真得到的翻转步态极限工况下的载荷、扭矩施加在夹持器的实际接触位置处。在实际工作过程中,夹持器的接触为点或线接触。为模拟真实工况,在ANSYS Workbench软件中将夹持器前端的2个销孔作固定支撑;根据夹持器在实际夹持工况下所受的载荷,可将其接触类型视为线接触;在前处理中,在夹持接触面处添加2条辅助直线,用于载荷施加。通过运算求解,得到该极限工况下夹持器的等效应力及等效变形云图,结果如图6所示。由图6(a)可知,夹持器的最大等效应力主要分布于夹持器两端连接处,为49.992 MPa;对应的最大等效变形主要集中在夹持器末端,为0.25 mm。
图6
图6
夹持器等效应力及等效变形云图
Fig.6
Cloud maps of equivalent stress and equivalent deformation of gripper
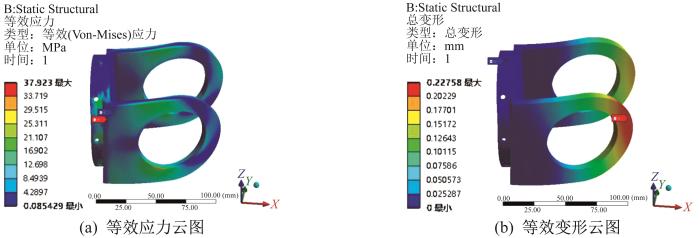
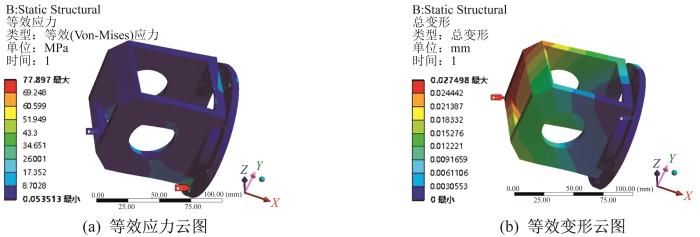
在分析T关节摆动件时,根据实际工况将摆动件前端的固定孔作固定支撑,在轴承孔处施加由ADAMS动力学仿真得到的翻转步态极限工况下的载荷及扭矩。通过运算求解,得到该极限工况下T关节摆动件的等效应力及等效变形云图,结果如图7所示。由图7可知,T关节摆动件的最大等效应力为37.923 MPa;等效变形集中在T关节摆动件末端处,最大值为0.23 mm。同理,按照ADAMS动力学仿真结果,将T关节连接座前端的螺丝定位孔固定,并在轴承孔处施加翻转步态极限工况下的载荷及扭矩。通过求解运算,得到该极限工况下T关节连接座的等效应力及等效变形云图,结果如图8所示。由图8可知,T关节连接座的等效应力集中在定位孔周边,最大值为77.897 MPa,因此建议增加此部位的定位孔,以减少应力集中;等效变形同样集中在T关节连接座末端远处,最大值为0.03 mm。
图7
图7
T关节摆动件的等效应力及等效变形云图
Fig.7
Cloud maps of equivalent stress and equivalent deformation of T-joint swinging component
图8
图8
T关节连接座的等效应力及等效变形云图
Fig.8
Cloud maps of equivalent stress and equivalent deformation of T-joint connection seat
本文爬杆机器人的夹持器及T关节均选用航空金属材料7075-T6铝合金,其密度为2.85 g/cm3,泊松比为0.33,屈服强度为504 MPa。综合上文的ANSYS有限元仿真结果可知,夹持器及T关节的最大等效应力远小于材料的屈服强度,因此可对其进行SIMP变密度拓扑优化。
2.4 结构优化分析
通过前文对爬杆机器人运行工况的综合分析,可知夹持器和T关节这2个关键零部件承受了大部分的载荷(包括自身重力以及负载)。基于爬杆机器人的ADAMS模型,利用ANSYS Workbench软件对夹持器和T关节进行SIMP变密度拓扑优化,优化目标是在体积约束下使柔度最小。按照约束条件,对设计变量进行寻优求解,求解器选用典型的优化准则法;设求解器最优迭代数为200次,最小相对密度为0.001,计算精度为0.15%。
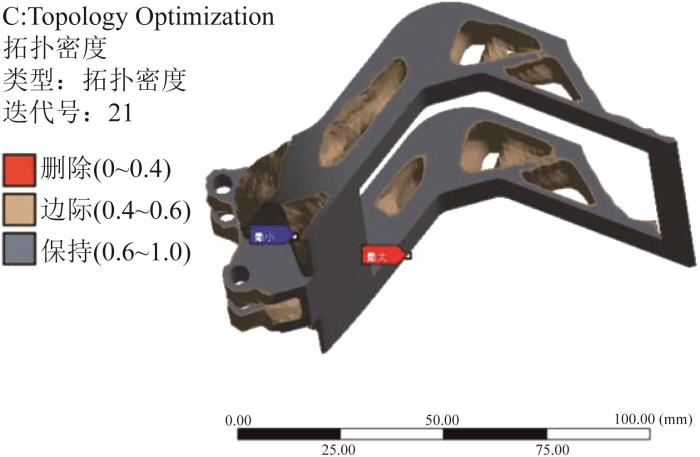
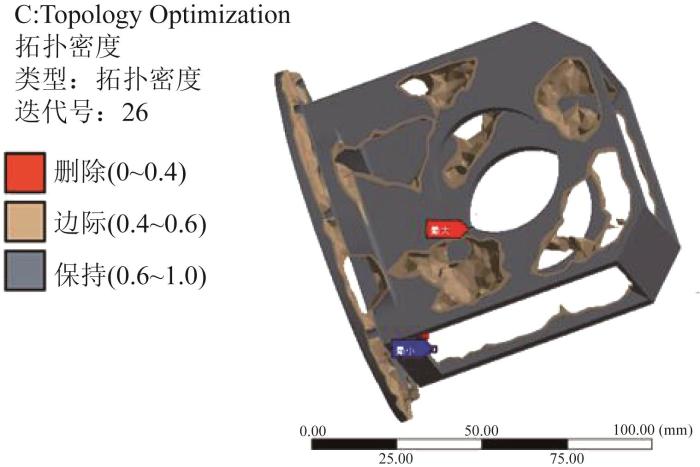
根据实际夹持工况,在Topology Optimization模块中设置优化区域为夹持器的整个材料区域,选择夹持面和支撑夹持器的2个销孔为优化排除域,响应约束设置为以质量最小为目标,保留质量百分比设置为45%。材料相对密度在0~1内变化,当相对密度接近1时,表明材料应保留;相反,当相对密度接近0时,表明材料可被去除。通过21次迭代计算,得到夹持器的变密度拓扑优化结果,如图9所示。
图9
图10
图11
图11
T关节摆动件拓扑优化云图
Fig.11
Topology optimization cloud map of T-joint swinging component
图12
图12
T关节连接座拓扑优化云图
Fig.12
Topology optimization cloud map of T-joint connection seat
图13
图14
3 爬杆机器人结构优化结果分析
图15
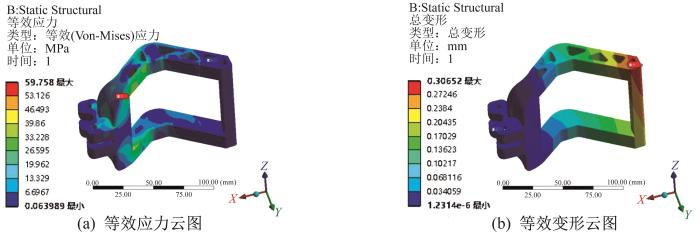
图15
优化后夹持器的等效应力及等效变形云图
Fig.15
Cloud maps of equivalent stress and equivalent deformation of optimized gripper
表 1 优化前后夹持器的质量和力学性能对比
Table 1
| 优化前后 | 质量/kg | 最大等效 应力/MPa | 最大等效变 形量/mm |
|---|---|---|---|
| 变化率/% | -28.6 | 19.5 | |
| 优化前 | 0.35 | 49.992 | 0.25 |
| 优化后 | 0.25 | 59.758 | 0.32 |
图16
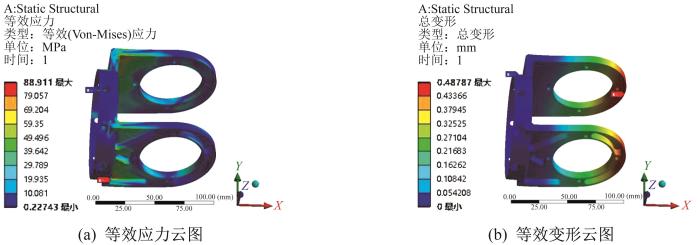
图16
优化后T关节摆动件的等效应力及等效变形云图
Fig.16
Cloud maps of equivalent stress and equivalent deformation of optimized T-joint swinging component
表2 优化前后T关节摆动件的质量和力学性能对比
Table 2
| 优化前后 | 质量/kg | 最大等效 应力/MPa | 最大等效变形量/mm |
|---|---|---|---|
| 变化率/% | -40.7 | 134.4 | |
| 优化前 | 0.27 | 37.923 | 0.23 |
| 优化后 | 0.16 | 88.911 | 0.49 |
图17
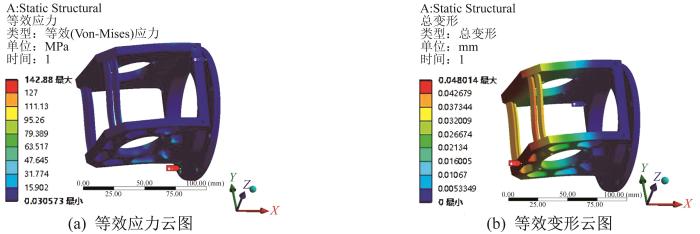
图17
优化后T关节连接座的等效应力及等效变形云图
Fig.17
Cloud maps of equivalent stress and equivalent deformation of optimized T-joint connection seat
表3 优化前后T关节连接座的质量和力学性能对比
Table 3
| 优化前后 | 质量/kg | 最大等效 应力/MPa | 最大等效变形量/mm |
|---|---|---|---|
| 变化率/% | -32.4 | 83.4 | |
| 优化前 | 0.34 | 77.897 | 0.03 |
| 优化后 | 0.23 | 142.880 | 0.05 |
上述拓扑优化结果表明,在保证结构强度的前提下,采用SIMP变密度拓扑优化方法可显著减小爬杆机器人的质量,并提高其综合性能。
4 实验验证
根据拓扑优化结果,重新设计爬杆机器人的夹持器和T关节,并完成加工和装配。最后,在自制的攀爬实验平台上测试爬杆机器人的性能,对其质量和能耗等进行对比。优化后爬杆机器人的质量为12.57 kg,相较于优化前减小了7.6%。
4.1 爬杆机器人能耗仿真实验
图18
图18
优化后爬杆机器人的能耗仿真模型
Fig.18
Energy consumption simulation model of optimized pole-climbing robot
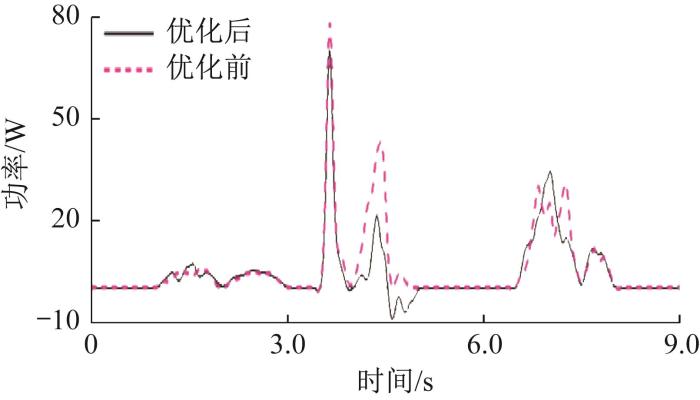
图19
图19
优化前后爬杆机器人能耗仿真结果
Fig.19
Simulation results of energy consumption of pole- climbing robot before and after optimization
4.2 爬杆机器人样机能耗实验
在爬杆机器人样机中,采用型号为QDD Pro-PR60-100-90的谐波减速电机,其额定扭矩为47 N·m,输出功率为147 W。使用STM32VET6主控板接收QT5.9.0版本的上位机指令并通过CAN(controller area network,控制器局域网)接口接收电机的驱动信号。在攀爬实验平台上开展爬杆机器人样机能耗实验(以蠕动步态工况为例),如图20所示。结果表明,蠕动步态符合仿生学设计,步态较柔顺,该步态下夹持器夹持稳定,未出现上下滑落现象。
图20
图20
爬杆机器人样机蠕动步态能耗实验
Fig.20
Energy consumption experiment on peristaltic gait of pole-climbing robot prototype
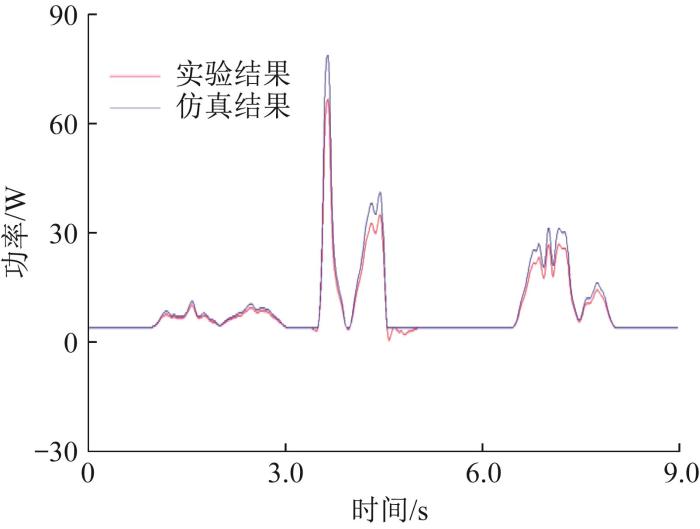
由于缺乏有效的能耗测量方案,本文通过读取爬杆机器人各关节电机内置函数值,并利用单片机将其转换为电压数据发送到上位机,经MATLAB软件处理得到功率曲线,结果如图21所示。由于能耗仿真实验中采用step函数来添加驱动,爬杆机器人的仿真轨迹与实际轨迹存在差异,故其关节电机功率的仿真结果与实验结果不完全吻合,但从总体上看,两者的相对误差在允许范围内,验证了仿真结果的正确性,表明优化后机器人可实现能耗降低的目标。
图21
图21
爬杆机器人能耗的仿真结果与实验结果对比
Fig.21
Comparison of simulation results and experimental results of energy consumption of pole-climbing robot
5 结 论
本文以自行开发的仿尺蠖爬杆机器人为研究对象,对其结构的拓扑优化进行分析。实验结果表明,所采用的SIMP变密度拓扑优化方法对机器人结构优化有显著效果。主要研究过程及结论如下:
1)构建了爬杆机器人的动力学模型,通过ADAMS软件仿真得到了该机器人在3种运动步态极限工况下的载荷和扭矩,为机器人结构拓扑优化的边界条件设置提供了基本依据。
2)利用ANSYS Workbench软件对爬杆机器人的力学性能进行有限元分析,得到了夹持器和T关节的等效应力和等效变形分布情况。
3)根据有限元分析结果,采用SIMP变密度拓扑优化方法对夹持器和T关节进行拓扑优化,去除了冗余材料,从而实现爬杆机器人的轻量化和间接提高负载自重比的目标,并通过实验验证了爬杆机器人可在减小质量的同时降低能耗。
本文研究方法可为高空爬杆机器人的结构优化设计提供参考。
参考文献
General design criteria for manipulators
[J].
A tool for the evaluation of human lower arm injury: approach, experimental validation and application to safe robotics
[J].
复杂机械结构拓扑优化若干问题研究
[D].
Study on topology optimization of complex mechanics structure
[D].
结构拓扑优化方法及其机器人轻量化应用现状及发展
[J].
Current situation and improving trends of structural topology optimization method and the corresponding application in robot light-weight design
[J].DOI:10.3969/j.issn.1009-9492.2018.11.034 [本文引用: 1]
爬壁机器人变密度拓扑优化吸附结构研究
[J].
Research on adsorption structure of wall climbing robot with variable density topology optimization
[J].DOI:10.13433/j.cnki.1003-8728.20200336 [本文引用: 1]
Design of Delta robot arm based on topology optimization and generative design method
[C]//
Multi-objective topology optimization for industrial robot
[C]//
基于拓扑优化的起重机转台的轻量化设计
[J].
Lightweight design of the crane turntable based on topology optimazation
[J].DOI:10.3969/j.issn.1009-9492.2022.10.051 [本文引用: 1]
基于双向渐进结构优化法的柔性机构设计
[J].
Design of compliant actuation mechanisms by evolutionary structural optimization method
[J].DOI:10.3901/jme.2021.19.004 [本文引用: 1]
Generating optimal topologies in structural design using a homogenization method
[J].
Optimal shape design as a material distribution problem
[J].
非均匀 Winkler 弹性地基上变厚度矩形板自由振动的 DTM 求解
[J].
Free vibration analysis for rectangular plates with variable thickness resting on a non-uniform Winkler elastic foundation by DTM
[J].DOI:10.7511/jslx20170217002 [本文引用: 1]
Eigenvalue topology optimization of structures using a parameterized level set method
[J].
Topology optimization of a constrained layer damping plate coupled with an acoustical cavity
[J].
An alternative interpolation scheme for minimum compliance topology optimization
[J].
连续体结构的拓扑优化设计
[J].
Topological optimization design for continuum structures
[J].DOI:10.6052/1000-0992-2004-4-J2003-111 [本文引用: 1]
工业机器人的结构分析与优化
[J].
Structural analysis and optimization of industrial robot
[J].DOI:10.3969/j.issn.1000-565X.2013.09.021 [本文引用: 1]