浙江大学学报(工学版)

浙江大学学报(工学版), 2025, 59(11): 2248-2258 doi: 10.3785/j.issn.1008-973X.2025.11.003

机械工程、能源工程

多约束人机协作U型拆卸线问题建模与优化

陈海烨,, 张则强,, 梁巍, 郭磊, 段淇耀

1. 西南交通大学 轨道交通运维技术与装备四川省重点实验室，四川 成都 610031

2. 西南交通大学唐山研究院，河北 唐山 063000

Modeling and optimization of human-robot collaborative U-shaped disassembly line problem with multi-constraint

CHEN Haiye,, ZHANG Zeqiang,, LIANG Wei, GUO Lei, DUAN Qiyao

1. Technology and Equipment of Rail Transit Operation and Maintenance Key Laboratory of Sichuan Province, Southwest Jiaotong University, Chengdu 610031, China

2. Tangshan Institute, Southwest Jiaotong University, Tangshan 063000, China

通讯作者: 张则强，男，教授. orcid.org/0000-0001-8781-3618. E-mail: zhangzq@home.swjtu.edu.cn

收稿日期: 2024-10-30  

基金资助: 国家自然科学基金资助项目(52375268, 52342505, 72401239); 教育部人文社会科学研究规划基金资助项目(23YJA630139); 河北省自然科学基金资助项目(E2024105031); 四川省自然科学基金资助项目(2025ZNSFSC0425, 2024NSFSC1048, 2024ZHCG0059).

Received: 2024-10-30  

Fund supported: 国家自然科学基金资助项目(52375268,52342505,72401239);教育部人文社会科学研究规划基金资助项目(23YJA630139);河北省自然科学基金资助项目(E2024105031);四川省自然科学基金资助项目(2025ZNSFSC0425,2024NSFSC1048,2024ZHCG0059).

作者简介 About authors

陈海烨（2001—），男，硕士生，从事智能制造优化的研究.orcid.org/0009-0008-0456-3632.E-mail：1627508814@qq.com , E-mail：1627508814@qq.com

摘要

针对现有人机协作拆卸线研究中未同时考虑人机任务时间差异和任务属性约束，且未将机器人购置成本考虑在人机协作长期成本中的问题，结合U型拆卸线，提出多约束人机协作拆卸线平衡问题. 以工作站数量、空闲时间均衡指标和长期成本为目标函数，构建考虑人机任务属性、人机任务时间、AND/OR优先关系等多种问题特征约束的U型拆卸线整数规划模型. 提出改进混合克隆模拟退火算法，设计双层编码、解码和考虑问题特性的变异和交叉操作. 引入克隆操作增强算法的局部搜索能力，通过两阶段退火加快算法的收敛速度. 应用Gurobi软件求解中小规模问题，与算法的求解结果进行对比，验证了模型和算法的正确性和有效性. 通过分别计算和对比不同模式拆卸线的成本随拆卸线预估运行时间的变化情况，验证了该模型具有柔性拆卸线规划的优点.

关键词： U型拆卸线平衡问题 ; 人机协作拆卸线 ; 改进混合克隆模拟退火算法 ; 整数规划模型 ; 多目标优化

Abstract

A multi-constrained human-robot collaborative disassembly line balancing problem was proposed for U-shaped disassembly lines in order to address the issues that existing studies on human-robot collaborative disassembly lines neither simultaneously consider differences in human and robotic task time and task attribute constraint, nor incorporate robot procurement costs into the long-term costs of collaboration. An integer programming model for the U-shaped disassembly line was constructed, with the objectives of minimizing the number of workstations, the idle time balancing index, and the long-term cost. Constraints considering various problem characteristics, including human-robot task attributes, human-robot task time, and AND/OR precedence relations were incorporated. An improved hybrid clonal simulated annealing algorithm was proposed. Double-layer encoding and decoding were designed, along with mutation and crossover operations specifically considering the problem characteristics. Cloning operations were introduced to enhance the local search capability of the algorithm, and a two-stage annealing process was implemented to accelerate convergence speed. Gurobi software was applied to solve small and medium-scale problems, and the results were compared with those obtained by the algorithm to verify the correctness and effectiveness of the model and algorithm. The cost variations of different disassembly line modes with the estimated operational time of the disassembly line were calculated and compared. Results demonstrate that the proposed model possesses the advantage of agile disassembly line planning.

Keywords： U-shaped disassembly line balancing problem ; human-robot collaborative disassembly line ; improved hybrid clone selection simulated annealing algorithm ; integer programming model ; multi-objective optimization

PDF (1077KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

陈海烨, 张则强, 梁巍, 郭磊, 段淇耀. 多约束人机协作U型拆卸线问题建模与优化. 浙江大学学报(工学版)[J], 2025, 59(11): 2248-2258 doi:10.3785/j.issn.1008-973X.2025.11.003

CHEN Haiye, ZHANG Zeqiang, LIANG Wei, GUO Lei, DUAN Qiyao. Modeling and optimization of human-robot collaborative U-shaped disassembly line problem with multi-constraint. Journal of Zhejiang University(Engineering Science)[J], 2025, 59(11): 2248-2258 doi:10.3785/j.issn.1008-973X.2025.11.003

随着工业自动化的发展，电子产品的更新换代速度不断加快，与之而来的是对资源的更大需求量和对环境的更大压力[1]. 再制造企业考虑到生产资源紧缺，面向大量寿命终止(end of life, EOL)产品提供生产服务. 废旧产品的拆卸是再制造中的关键环节，因此解决拆卸线平衡问题(disassembly line balancing problem, DLBP)对实际再制造发展具有重大意义.

自Gungor等[2]提出DLBP后，大量学者开展了广泛的研究. DLBP可以根据不同线型进行分类. Guo等[3]考虑随机任务时间，构建随机直线拆卸线平衡问题模型. Zhu等[4]建立并行拆卸线平衡问题模型，设计混合群变邻域搜索算法进行求解. U型拆卸线较其他线性具有工作站数量少、占地面积小、运行柔性强等优点. U型拆卸线工作站可以执行进口端或出口端任务的特点，增大了U型拆卸线平衡问题(U-shaped disassembly line balancing problem, UDLBP)的求解难度. Wang等[5]以利润为目标构建UDLBP，Wu等[6]构建多产品部分拆卸UDLBP. 上述研究中的数学模型均为概念模型，无法求得精确解，因此不能讨论模型的正确性.

人机协作拆卸线可以结合工人处理复杂任务的能力和机器人高效及处理危险操作的特点[7]. Hartono等[8]考虑机器人拆解过程中的环境和经济效益，设计改进哈里斯鹰算法进行求解. Lou等[9]提出考虑人机工程学的人机混合拆卸单元的拆卸顺序规划方法. 张则强等[10]建立不同站间操作者的并行DLBP模型，但未区分2种操作者间的任务属性差异. Wu等[11]通过人机协作的方式解决废弃动力电池拆解的问题，但未考虑不同操作者工作时间差异对任务分配的影响. Guo等[12]将人机协作拆卸线成本作为目标函数进行求解，但未计算工作站待机成本和拆卸线运行长期成本. 国际机器人联合会根据共同活动的程度将人机协作分为4种类型，包括共存、顺序协作、协作和响应式协作[13]. 本研究侧重于共存类型，单个机器人或工人只能被分配到单个工作站.

由于DLBP的NP-hard属性[14]，利用启发式方法和精确方法求解大规模问题较困难，多采用元启发式方法[15]求解DLBP. 脱阳等[16]设计樽海鞘群算法，求解可变时间双边机器人DLBP. 模拟退火算法[17] (simulated annealing, SA)是模拟材料退火这一物理过程的算法，具有良好的全局搜索能力. 克隆算法(clonal selection algorithm, CSA)是免疫算法(immune algorithm, IA)的一种[18]，可以有效地搜索复杂优化问题的解空间. 混合克隆模拟退火算法[19]结合2种算法的优点，以获得更好的求解效果.

本文针对问题的特点，提出改进混合克隆模拟退火算法(improved hybrid clone selection simulated annealing algorithm, IHCSSA). 引入克隆操作，增强算法的局部搜索能力，结合Pareto[20]多目标方法对问题进行求解，筛选非劣解前沿.

1. 人机协作UDLBP

1.1. 问题描述

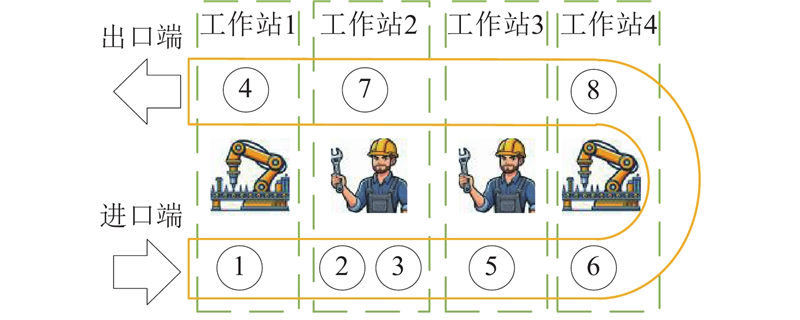
人机协作U型拆卸线的示意图如图1所示. 为了防止工作站中多操作者之间的干涉影响，每个工作站中只分配一个操作者. 根据任务属性的不同，危险任务只能分配到机器人工作站中执行，复杂任务只能分配到工人工作站中执行，机器人操作者和工人操作者都可以完成普通任务.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   人机协作U型拆卸线的示意图

Fig.1   Schematic diagram of human-robot collaborative U-shaped disassembly line


为了便于UDLBP模型的建立，提出以下模型假设. 1）拆卸产品单一，且组成完整，无部件缺失. 2）拆卸优先关系已知，拆卸任务时间已知，拆卸成本已知，任务属性已知. 3）忽略操作者的移动时间.

1.2. 数学模型

对于目标函数，最小化目标

$ {{F}} = \min \left\{ {{{{f}}_1},{{{f}}_2},{{{f}}_3}} \right\}. $

其中包含3个子目标.

$ {f_1} = \sum\limits_{n = 1}^N {\sum\limits_{l = 1}^2 {{z_{ln}}} } . $

式（2）表示最小化开启工作站数目. 式中：l表示操作者，l = 1表示操作者为人，l = 2表示操作者为机器人，n表示工作站的序号，zln 为二进制变量，zln = 1表示第n个工作站开启且操作者为l，否则zln = 0. 单个拆卸产品在整条拆卸线中的总拆卸时间与拆卸线工作站数量呈正相关，随着工作站数量的减少，拆卸产品在整条拆卸线中的总拆卸时间减少，故最小化工作站数量，提高拆卸线效率，减小拆卸线作业长度和占地面积.

$ {f_2} = {\sum\limits_{n = 1}^N {\left( {\sum\limits_{l = 1}^2 {{z_{ln}}} C - \sum\limits_{i = 1}^N {\sum\limits_{m = 1}^2 {\sum\limits_{l = 1}^2 {t_i^lx_i^{mln}} } } } \right)} ^2}. $

式（3）表示拆卸线空闲时间均衡指标. 式中：C表示节拍时间；i、j表示任务序号；m表示U型拆卸线的进出口端，m = 1表示进口端，m = 2表示出口端；$ {\mathit{t}}_{\mathit{i}}^{\mathit{l}} $表示操作者为l时任务i的拆卸时间， $ {x}_{i}^{mln} $为二进制变量， $ {x}_{i}^{mln}=1 $表示任务i分到了操作者为l的第n个工作站的m侧，否则$ {x}_{i}^{mln}=0 $. 该目标旨在使各工作站负载均衡，避免各工作站因为任务分配不均产生拥挤或堵塞的情况.

$ {f_3} = {C_{\mathrm{r}}}\sum\limits_{n = 1}^N {{z_{ln}}} +D G {C_{\mathrm{d}}}. $

式（4）表示拆卸线长期成本，其中包括机器人购置成本和拆卸线运营成本，拆卸线运营成本表示为每件EOL产品拆卸成本与拆卸线运行时间内拆卸总件数的乘积. 式中：Cr为单位机器人的购置成本，D为拆卸线的运行天数，G为每日拆卸线拆卸的总零件数，

$ \begin{split} {C_{\mathrm{d}}} =& \sum\limits_{n = {\text{1}}}^N \Bigg( \sum\limits_{i = {\text{1}}}^N {\sum\limits_{m = {\text{1}}}^{\text{2}} {\sum\limits_{l = {\text{1}}}^{\text{2}} {c_i^lx_i^{mln}} } } + \sum\limits_{l = {\text{1}}}^2 {z_{ln}}Cc_{\mathrm{r}}^l -\\ &\sum\limits_{i = {\text{1}}}^N {\sum\limits_{m = {\text{1}}}^{\text{2}} {\sum\limits_{l = {\text{1}}}^{\text{2}} {t_i^lx_i^{mln}} } } c_{\mathrm{r}}^l \Bigg) . \end{split}$

式（5）表示每件EOL产品的成本，其中包括分配不同操作者的各工作站的工作成本和待机成本. 式中：$ {c}_{i}^{l} $为操作者为l时任务i的成本， $ {c}_{{\mathrm{r}}}^{l} $为工作站操作者为l时的待机成本.

约束条件如下.

$ \sum\limits_{n = 1}^N {\sum\limits_{m = 1}^2 {\sum\limits_{l = 1}^2 {x_i^{mln}} } } = 1;\; i \in N. $

$ \sum\limits_{i = 1}^N {\sum\limits_{m = 1}^2 {(x_i^{m1n})} } \leqslant M {z_{1n}};\; n \in N. $

$ \sum\limits_{i = 1}^N {\sum\limits_{m = 1}^2 {(x_i^{m2n})} } \leqslant M(1 - {z_{1n}});\; n \in N. $

$ \sum\limits_{l = 1}^2 {{z_{ln}}} \leqslant 1;\; n \in N. $

$ \sum\limits_{m = 1}^2 {\sum\limits_{n = 1}^N {x_i^{m1n}} = 1;\; i \in {{K}}} . $

$ \sum\limits_{m = 1}^2 {\sum\limits_{n = 1}^N {x_i^{m2n}} = 1;\; i \in {{H}}} . $

$ \sum\limits_{i = 1}^N {\sum\limits_{m = 1}^2 {\sum\limits_{l = 1}^2 {t_i^lx_i^{mln}} \leqslant C\sum\limits_{l = 1}^2 {{z_{ln}}} ;\; n \in N} } . $

$ \begin{split} &\sum\limits_{n = 1}^N {\sum\limits_{l = 1}^2 {\Big[ n\left( {x_i^{1ln} - x_j^{1ln}} \right)+ \left( {2N - n} \right)\left( {x_i^{2ln} - x_j^{2ln}} \right)\Big] } } \leqslant 0;\\ &{{{\mathrm{TP}}}}_{ij} = 1. \\[-1pt]\end{split}$

$ \begin{split} &\sum\limits_{n = 1}^N {\sum\limits_{l = 1}^2 { \Big[ n(x_i^{1ln} - x_j^{1ln})+ (2N - n)(x_i^{2ln} - x_j^{2ln})\Big] } } \leqslant M(1 - {y_{ij}});\;\\ &{{{\mathrm{TP}}}}_{ij} = - 1. \\[-1pt]\end{split}$

$ \sum\limits_{i \in {\rm{O}}{{\rm{R}}_j}}^{} {{y_{ij}} \geqslant 1} ;\; j \in \left\{ {j|{\rm{TP}}_{ij} = - 1} \right\}. $

$ \sum\limits_{i = 1}^N {\sum\limits_{m = 1}^2 {\sum\limits_{l = 1}^2 {x_i^{mln}} \geqslant \sum\limits_{l = 1}^2 {{z_{ln}}} } ;\; n \in N} . $

$ \sum\limits_{l = 1}^2 {{z_{ln}}} \geqslant \sum\limits_{l = 1}^2 {{z_{ln+1}}} ;\;n \in \left[ {1,N - 1} \right]. $

式中：TP为优先关系矩阵，每个任务必须且仅能分配到一个工作站的一端；N为拆卸任务总数和最大工作站数；M为很大的正数；K为复杂任务集合；H为危害任务集合；yij为二进制变量，yij = 1表示任务i是任务j的OR紧前任务且任务i在任务j前完成，否则yij = 0. 式（6）表示任务分配约束. 式（7）~（9）表示每个工作站只能分配一种操作者. 式（10）表示具有复杂属性的任务必须分配到操作者为人的工作站. 式（11）表示具有危害属性的任务必须分配到操作者为机器人的工作站. 式（12）表示节拍时间约束，各工作站进出口端的任务总时间不超过节拍时间. 式（13）表示AND优先关系约束，具有AND优先关系的紧前任务必须在紧后任务之前完成. 式（14）、（15）表示OR优先关系约束，具有OR优先关系的紧前任务至少有一个在紧后任务前完成. 式（16）表示工作站开启约束，当拆卸任务分配至工作站n时，工作站n必须开启. 式（17）表示工作站顺序开启约束，工作站的开启必须按序进行.

2. 改进混合克隆模拟退火算法

混合克隆模拟退火算法的基本思想是通过模拟退火算法进行全局搜索，找到较好的解，使用克隆算法在该解附近进行局部搜索，进一步优化解. 对于多目标问题，该算法采用改进Metropolis准则，接受新解的概率为

$ P = \left\{ {\begin{gathered} {1,\exists m,f_m^{\rm{new}} < f_m^{\rm{cur}}}; \\ \displaystyle \prod\limits_{m = 1}^M \exp \left( { - \frac{{f_m^{\rm{new}} - f_m^{\rm{cur}}}}{T}} \right), \forall m,\; f_m^{\rm{new}} > f_m^{\rm{cur}}. \\ \end{gathered}} \right. $

式中：$f_m^{{\text{new}}}$为新解的第m个目标函数值，$f_m^{{\text{cur}}}$为当前解的第m个目标函数值.

在模拟退火算法中，通过冷却调度对温度进行调整，模拟退火算法常用的冷却调度方法为指数冷却，如下所示：

$ T = {\alpha ^{{\mathrm{gen}}}}{T_{\mathrm{s}}}. $

式中：α为降温系数，T为当前温度，Ts为初始温度，gen为算法迭代次数.

2.1. 编码

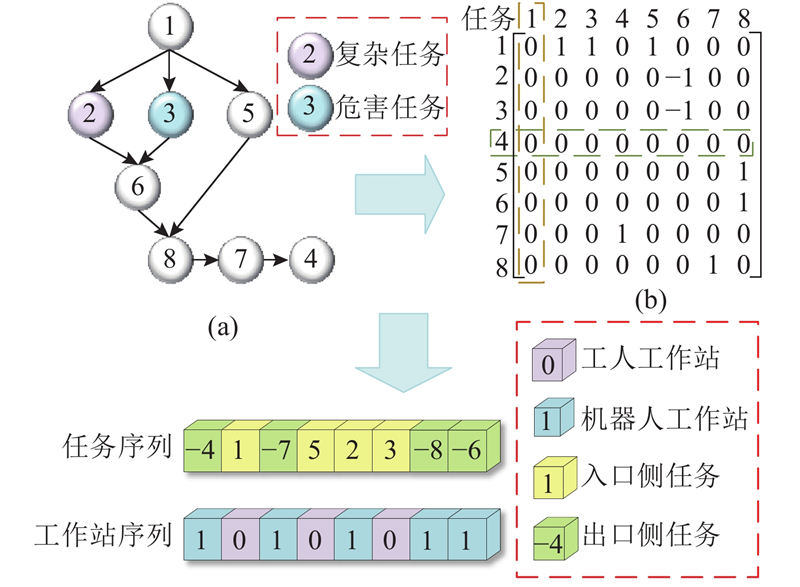
DLBP将拆卸任务分配到各工作站时，需要满足一系列约束，如任务优先关系约束、节拍时间约束和任务属性约束等.

编码过程如图2所示. “AND优先关系”在图2(a)中用实线表示，“OR优先关系”在图2(b)中用虚线表示. 为了便于算法计算，将拆卸任务的优先关系图转化为优先关系矩阵TP(见图2(b)). 该矩阵由0、1、−1组成，当任务i是任务j的且优先任务时，矩阵的第i行第j列元素为1，当任务i是任务j的或优先任务时，矩阵的第i行第j列元素为−1，否则为0.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   IHCSSA编码过程的示意图

Fig.2   Schematic diagram of IHCSSA encoding process


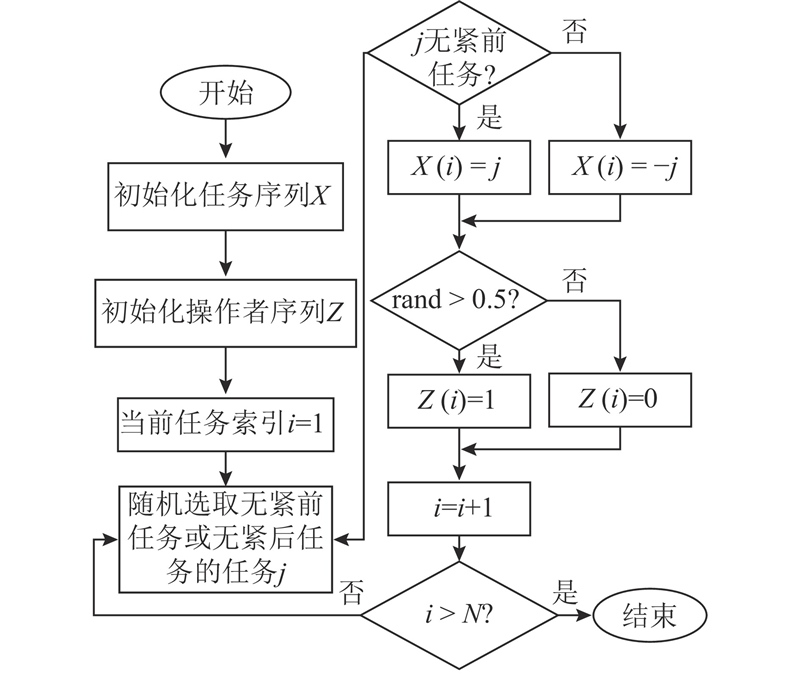
在任务序列的编码过程中，随机选择无紧前或无紧后任务的拆卸任务进行分配. 当该任务为无紧前任务的拆卸任务时，将任务分配到U型拆卸线入口侧，任务序号为正数；当该任务为无紧后任务时，将任务分配到U型拆卸线出口侧，任务序号为负数. 之后更新TP矩阵，重复上述操作直到任务序列中包含全部拆卸任务. 考虑到各工作站的操作者不同，为了增大解空间范围，采用双层编码，利用随机二进制数对工作站序列进行编码. 编码流程如图3所示. 其中，N为最大任务数.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   IHCSSA编码的流程图

Fig.3   Flowchart of IHCSSA encoding


2.2. 解码

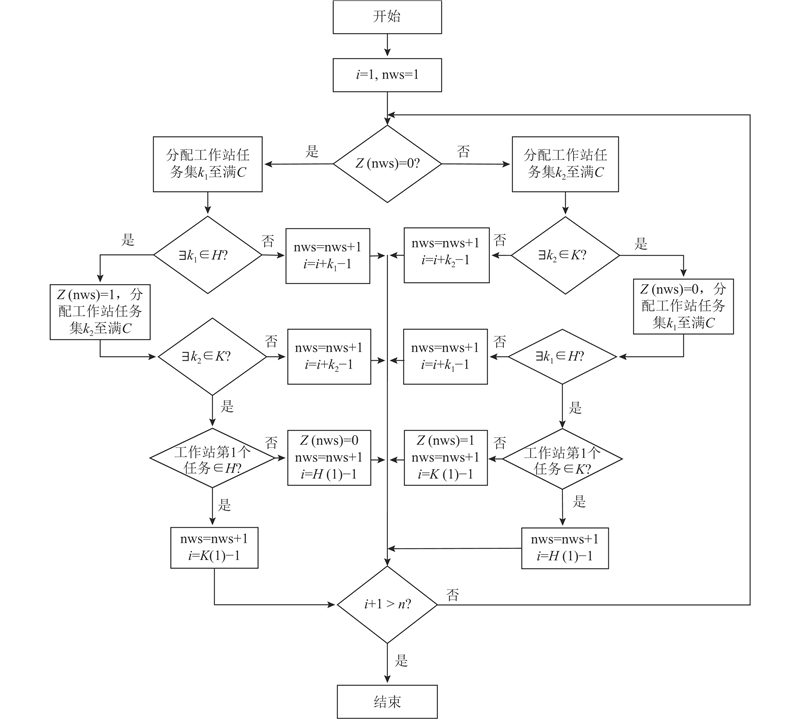
提出可更改操作者序列的解码方法：在开启新工作站后，按照操作者序列分配操作者并分配拆卸任务至满工作站节拍时间约束. 若所有分配的任务无属性冲突，则开启新工作站，继续分配剩余任务. 若分配至工作站的任务中有属性冲突任务，则改变工作站操作者，分配拆卸任务至满工作站节拍约束，并重新检查分配的任务有属性冲突. 若重新分配后的所有任务无属性冲突，则更新操作者序列并开启新工作站继续分配剩余任务. 若重新分配后的所有任务有属性冲突，则检查分配的第一个任务与原操作者是否有属性冲突. 若无冲突，则按照原操作者序列分配操作者，分配任务至冲突任务的前一任务并开启新工作站. 若有冲突，则改变当前工作站操作者，重复上述操作. 具体操作如图4所示. 其中，i为当前分配任务的索引，nws表示开启工作站的索引, k1和k2表示可分配进工作站的任务集，Z为操作者序列.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   IHCSSA解码的流程图

Fig.4   Flowchart of IHCSSA decoding


2.3. 变异操作

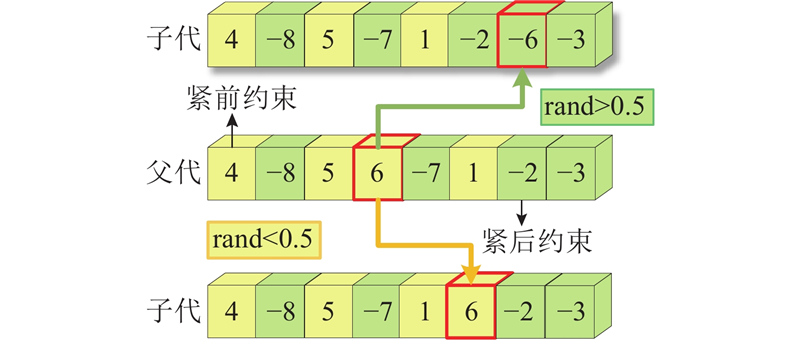
选取任务序列种群中的个体X作为父代，开展单点变异操作. 考虑本文所采用的正数和负数相间的任务序列和或优先关系，提出可改变任务进出口端的变异操作. 随机选取父代序列中的一点作为变异点，判断紧前紧后任务在进出口端的位置. 当紧前紧后任务不在同一端时，变异点随机插入可插入位置且可变换进出口端；当紧前紧后任务在同一端时，变异点随机插入可插入位置但不可变换进出口端. 若变异点无可插入位置，则重新选择变异点. 变异过程如图5所示.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   指数冷却阶段变异操作的示意图

Fig.5   Schematic diagram of index cooling stage variation operation


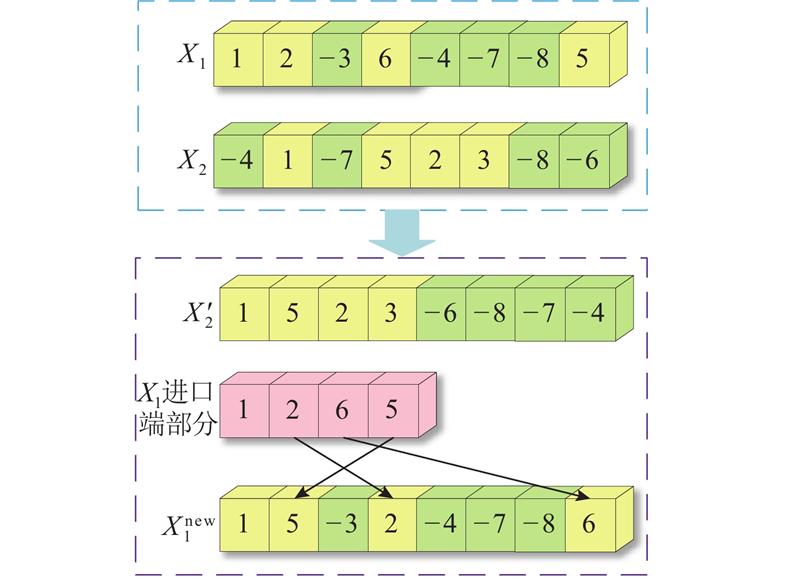
2.4. 交叉操作

将变异操作的结果X1和X2作为父代进行交叉操作. 将父代X2按照任务执行顺序重新排列为$X_2^{'}$，先随机选取X1进口端或出口端，再从对应序列中随机选取某段连续部分，按照$X_2^{'}$进行映射排列后重新放回X1中得到子代$X_1^{{\mathrm{new}}} $，$X_1^{{\mathrm{new}}} $交叉操作完成后进行优先关系检查. 若不符合优先关系，则重新操作. 具体的操作过程如图6所示.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   交叉操作的示意图

Fig.6   Schematic diagram of crossover operation


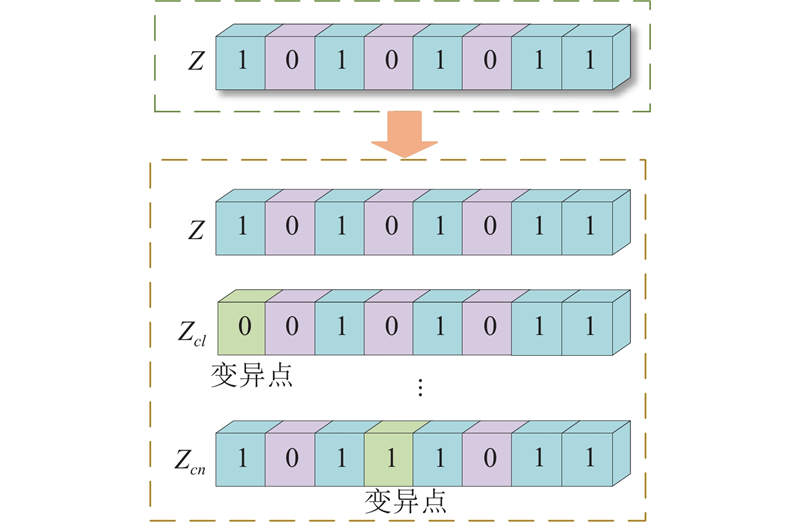
2.5. 克隆操作

针对该问题采用任务序列与操作者序列双层编码的特点，为了扩大解空间，将进行交叉变异后的两序列进行克隆操作，保持任务序列不变，随机翻转操作者序列中的变异点位. 考虑到实际工作站数量远小于任务数量，翻转操作者点位的选取采用轮盘赌的方式，较大概率地选取靠前工作站位置. 具体的操作过程如图7所示.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   IHCSSA克隆操作的示意图

Fig.7   Schematic diagram of IHCSSA cloning operation


2.6. 两阶段降温操作

传统的降温操作采用指数冷却方法，指数冷却存在当温度较低时冷却速度较慢，算法收敛时间长的问题. 提出两阶段降温方法：当前温度大于设定温度时采用式（19）的指数冷却方法，当前温度不大于设定温度时采用式（20）的线性冷却方法，提高了算法的收敛速度.

$ {T_1} = T - \Delta T,\;T \leqslant {T_0} . $

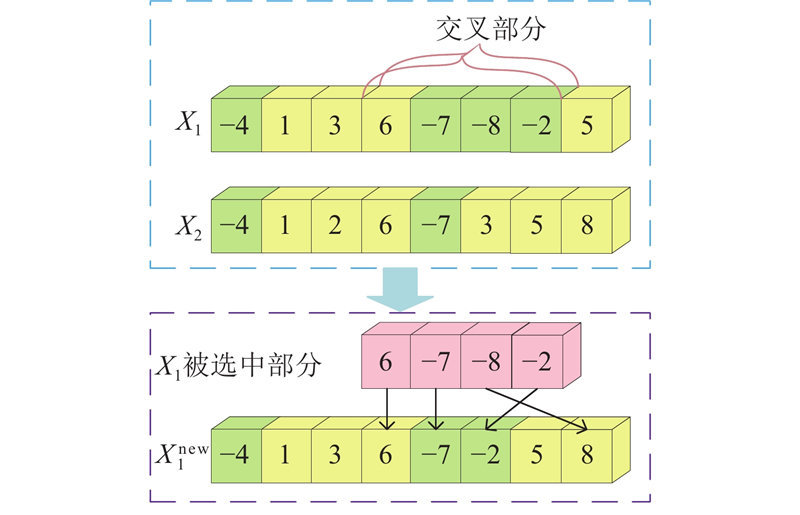
式中：T1为降温后温度；$\Delta T $为固定降温；T0为预设温度，当前温度小于T0时采用式（20）的线性冷却方法.

2.7. 线性冷却阶段的变异和交叉操作

线性冷却阶段的变异采用三点变异方式，随机选择3个拆卸任务，依次采用图5所示的变异操作进行随机变异. 线性冷却阶段的交叉采用可改变任务进出口端的交叉方法. 将变异操作的结果X1和X2作为父代进行交叉操作. 随机选取父代X1中的片段，将片段中与父代X2任务进出口端相同的任务放回序列X1中，依次检查剩余任务是否可以改变进出口端. 若该任务可以改变进出口端，则按照优先关系约束，将可以改变进出口端的任务随机插入另一端合理位置中，否则将任务随机插入原进出口端合理位置中，具体的操作方式如图8所示.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   线性冷却阶段交叉操作的示意图

Fig.8   Schematic diagram of cross operation in linear cooling stage


2.8. 种群更新机制

本文算法的目的是求解多目标问题，当进行算法迭代和外部档案存储时会产生大量的非劣解. 若将其全部进行迭代，则会大幅降低算法的运行效率. 采用Pareto方法，对解集进行处理. 当2个个体满足式（21）时，称个体1支配个体2.

$ \left. {\begin{array}{*{20}{c}} {{f_i}\left( {{X_1},{Z_1}} \right) \leqslant {f_i}\left( {{X_2},{Z_2}} \right),\forall {f_i} \in F}; \\ {{f_j}\left( {{X_1},{Z_1}} \right) < {f_j}\left( {{X_2},{Z_2}} \right),\exists {f_j} \in F} .\end{array}} \right\} $

式中：Xi和Zi分别为个体i的任务序列和工作站序列. 对于外部档案筛选，考虑到算法的收敛速度，采用NSGA-II拥挤距离机制[21].

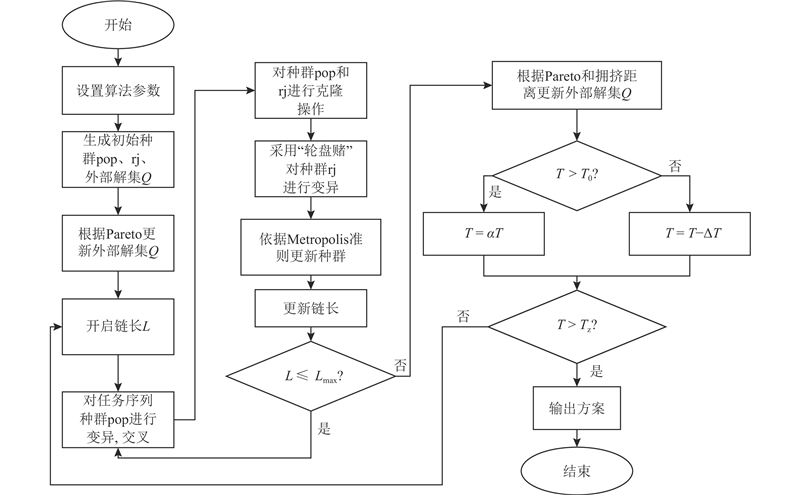
2.9. 算法流程

算法的具体流程如下所示.

输入：算法参数 X、Z、TP、KB

1.生成空外部档案Q，T = Ts

2.按种群规模p生成初始任务种群pop和操作者种群rj

3.计算目标函数值并根据Pareto更新外部档案

4.while T ≥ Tz //迭代过程

5. 　for L = 1 to Lmax //开启链长

6. 　　if T > T0

7. 　　　对pop执行交叉操作和变异操作

8. 　　else

9. 　　　对pop执行快速冷却交叉和变异操作

10. 　　end if

11. 　　对pop和rj执行克隆操作，并对rj采用轮盘赌的策略进行变异

12. 　　根据Metropolis准则更新种群

13. 　end for

14. 　根据Pareto更新Q

15. 　if T > T0

16.　　 T = αT

17. 　else

18. 　　T = T − ΔT.

19. 　end if

20.end while

其中，KB为任务信息矩阵，Tz为最终温度，Lmax为最大链长.

该算法的流程如图9所示.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9   IHCSSA算法的流程图

Fig.9   Flow chart of IHCSSA algorithm


3. 算例验证

3.1. 中小规模算例验证

为了验证所提模型的正确性，本文的运行环境如下：Windows 11系统，AMD Ryzen 7 6800H CPU，3.20 GHz，16 GB内存，应用Gurobi10.0.2精确求解器计算文献[22]的小规模算例P8和文献[4]的中规模算例P25. 应用MATLAB 2021a求解上述算例，与精确求解器进行对比. 利用IHCSSA算法求解小规模算例，算法参数如下：Ts = 10， Tz = 1，α = 0.9，T0 = 5，p = 30，Lmax = 10，克隆数v = 10， C = 40 s. 求解中规模的算法参数如下: C = 86 s, Ts = 20，Tz = 1，α = 0.95，T0 = 5，Lmax = 15，v = 10，p = 100. 机器人的购置成本为65 000 元. 假设拆卸线运行时每天拆卸产品的数量为160，预计产线运行时间为50 d. 考虑到在待机状态下机器人工作站的电能消耗较大，两算例中的工人和机器人的待机成本均分别为单位时间0.003 元和0.005 元. 表1和表2中，t1、t2分别为人和机器人的执行时间；“−”表示由于任务属性，该操作者无法操作.

表 1   P8算例的拆卸信息

Tab.1  Disassembly information of P8 example

任务t1, t2/sc1, c2/元任务t1, t2/sc1, c2/元
114, 100.70, 0.30514, 150.70, 0.45
220, —1.00, —615, 110.75, 0.33
3—, 8—, 0.24710, 120.50, 0.36
420, 141.00, 0.42813, 110.65, 0.33

新窗口打开| 下载CSV


表 2   P25算例的拆卸信息

Tab.2  Disassembly information of P25 example

任务t1, t2/sc1, c2/元任务t1, t2/sc1, c2/元
147, 332.35, 0.991420, 221.00, 0.66
2—, 17—, 0.511525, 181.25, 0.54
310, 70.50, 0.211618, 130.90, 0.39
420, 141.00, 0.421718, 130.90, 0.39
516, 200.80, 0.60187, —0.35, —
620, 241.00, 0.721915, 170.75, 0.51
720, 141.00, 0.422010, 70.50, 0.21
8—, 53—, 1.59215, 40.25, 0.12
930, 211.50, 0.602225, 181.25, 0.54
107, —0.35, —2340, 282.00, 0.84
1115, 180.75, 0.5424—, 42—, 1.26
1210, 70.50, 0.212528, 201.40, 0.60
13—, 20—, 0.6———

新窗口打开| 下载CSV


Gurobi求解器与算法计算的结果对比如表3所示. 可知，对于中小规模问题，在合理的时间内Gurobi和算法均求得了各目标函数的最优解，这证明了本文模型的正确性和算法的有效性. 相较于精确求解器只能求解单目标最优解，利用IHCSSA算法可以同时求解多个目标函数，且可以求解出非单目标最优解的Pareto前沿解，这为拆卸线的设计提供了更多的选择.

表 3   Gurobi求解器与IHCSSA算法的求解结果对比

Tab.3  Comparison of Gurobi solver and IHCSSA solution result

P8精确解t/s改进混合克隆模拟退火算法t/s
f1f2f3f1f2f3
3——0.103451042720.32
—37—0.47337105024
——1005840.243136100584
P25精确解t/s改进混合克隆模拟退火算法t/s
f1f2f3f1f2f3
6——0.766235480811.71
—2—1919.9162359368
——31282411.4971321312824

新窗口打开| 下载CSV


将IHCSSA算法与文献[17, 18, 23]中的免疫算法IA、遗传算法NSGA-II和模拟退火算法SA进行对比，每种算法取前沿解中的10个解进行对比，对比结果如表4所示. 其中，加粗部分表示单目标最优解，下划线部分表示该解被其他算法解完全支配.

表 4   利用4种算法求解P25问题的结果

Tab.4  Result of four algorithms solving P25 problem

IANSGA-II
f1f2f3f1f2f3
6$\underline{{\rm{67}}}$355312648355512
6$\underline{{\rm{68}}}$3547606$\underline{{\rm{83}}}$355008
61153530086100354760
6$\underline{{\rm{189}}}$3512006101353328
62223501206$\underline{{\rm{157}}}$351728
62613495686$\underline{{\rm{173}}}$351200
7113031500871075317368
$\underline 7$1186314480$\underline 7$1263315560
71253313928$\underline 7$1355313928
$\underline 7$1374313200$\underline 7$1546313200
SAIHCSSA
f1f2f3f1f2f3
6$\underline{{\rm{66}}}$40692862359368
6$\underline{{\rm{89}}}$40584867358768
6105353328610358216
6135353008659355008
61423522806151351728
$\underline 7$$\underline{{\rm{828}}}$3197286163351200
78433191767764319728
7113431500871170314480
7127731392871318313200
$\underline 7$139031320071321312824

新窗口打开| 下载CSV


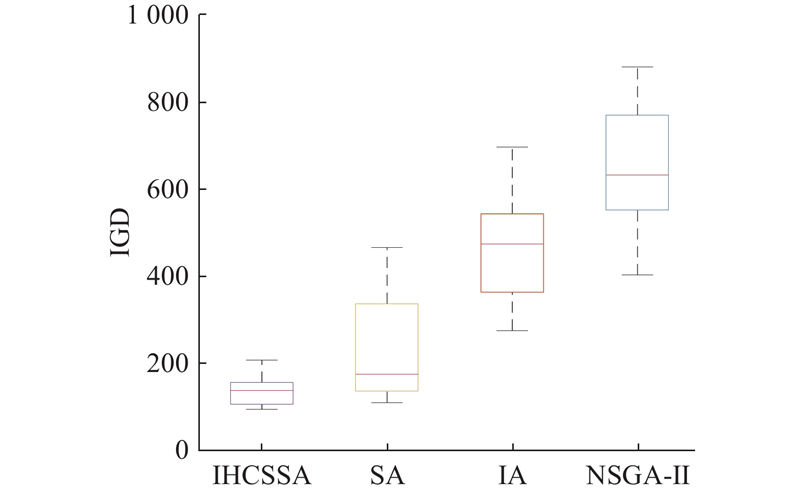
从算法多目标优化角度分析可知，在所对比的3种算法的求解结果中，IA算法有5个解被IHCSSA算法解完全支配，NSGA-II算法有6个解被IHCSSA算法解完全支配，SA算法有4个解被IHCSSA算法解完全支配，说明利用IHCSSA算法所求得的非劣解更逼近真实的Pareto前沿. 从算法的单目标求解效果分析可知，对于目标f1，利用4种算法均取得最优解，但对于目标f2和f3，利用IHCSSA算法求得最优解2和312824. 综上所述，IHCSSA算法无论是从多目标角度还是单目标角度都具有更好的求解性能.

IGD指标[24](inverted generational distance, IGD)是评价算法收敛性和多样性的多目标优化算法评价指标. IGD越低，说明算法的收敛性越好. 从图10可知，利用IHCSSA算法的计算结果的IGD值整体分布水平小于对比算法，说明IHCSSA算法的求解结果更加逼近理想解前沿，算法的求解性能和对解空间的搜索能力优于其他算法. IHCSSA算法的箱型宽度小于对比算法，说明算法的稳定性高.

图 10

新窗口打开| 下载原图ZIP| 生成PPT

图 10   利用4种算法求解P25结果的IGD指标箱型图

Fig.10   Box plot of IGD indicator for solving P25 result using four algorithms


3.2. 大规模实例验证

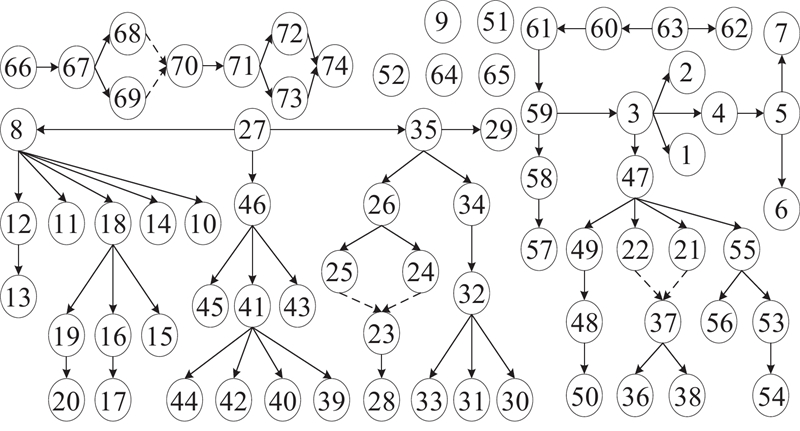
为了验证所提IHCSSA的优越性，将该算法应用于微波炉拆卸线中，该拆卸线具有74个拆卸任务，任务优先关系图如图11所示. 任务拆卸信息如表5所示. 模拟拆卸线一年工作200 d，每天拆卸数量为80台，节拍时间为40 s. 为了证明所提算法的优越性，与当前人机协作研究中较先进的多目标改进差分进化算法[25](multi-objective enhanced differential evolution algorithm, MEDE)、多目标混合跳蛙算法[3](multi-objective shuffled frog leaping algorithm, MSFL)和多目标改进教学优化算法[26](multi-objective modified teaching and learning optimization algorithm, MTLO)进行对比. 为了体现本研究所增加算子对原算法收敛性的影响，与无改进算子的SA算法进行计算对比.

图 11

新窗口打开| 下载原图ZIP| 生成PPT

图 11   P74实例的任务优先关系图

Fig.11   Precedence constraint graph of instance P74


表 5   P74实例的拆卸信息

Tab.5  Disassembly information for P74 instance

任务t1, t2/sc1, c2/元任务t1, t2/sc1, c2/元任务t1, t2/sc1, c2/元任务t1, t2/sc1, c2/元
12, 10.10, 0.03203, 20.15, 0.06393, 20.15, 0.06574, 30.20, 0.09
23, 20.15, 0.06213, —0.15, —403, 20.15, 0.06584, 20.20, 0.06
33, 10.15, 0.03223, 20.15, 0.06414, 30.20, 0.095912, 100.60, 0.30
44, 20.20, 0.06232, 10.10, 0.03425, —0.25, —604, 31.60, 0.93
53, 20.15, 0.06242, 10.10, 0.03433, 20.15, 0.06615, 50.25, 0.15
68, —0.40, —253, 10.15, 0.03449, 70.45, 0.21623, 20.15, 0.06
76, 50.30, 0.15262, 10.10, 0.03455, 40.25, 0.12634, 20.40, 0.18
83, 20.15, 0.06274, 40.20, 0.12462, 10.10, 0.03645, 40.10, 0.06
92, 20.10, 0.0628—, 11—, 0.33472, 10.10, 0.06654, 30.20, 0.09
1011, 90.55, 0.27297, 60.35, 0.18484, 20.20, 0.06664, 30.20, 0.09
118, —0.40, —304, 30.20, 0.09493, 10.15, 0.03673, 10.15, 0.03
124, 30.20, 0.09313, 20.15, 0.06502, 10.10, 0.036813, 110.65, 0.33
136, 50.30, 0.15325, 40.25, 0.12512, 10.10, 0.03697, —0.35, —
14—, 30.50, 0.27336, —0.25, —522, 10.10, 0.03705, 40.25, 0.12
153, 20.15, 0.06347, 50.35, 0.15533, 20.15, 0.06714, 30.20, 0.09
166, 60.30, 0.183512, 120.60, 0.36542, 10.10, 0.03726, 50.30, 0.15
176, 50.30, 0.15364, 30.20, 0.0955—, 2—, 0.06733, 20.15, 0.06
184, 30.20, 0.09375, 30.25, 0.09566, 50.30, 0.15744, 30.20, 0.09
1912, 100.60, 0.3038—, 5—, 0.15——————

新窗口打开| 下载CSV


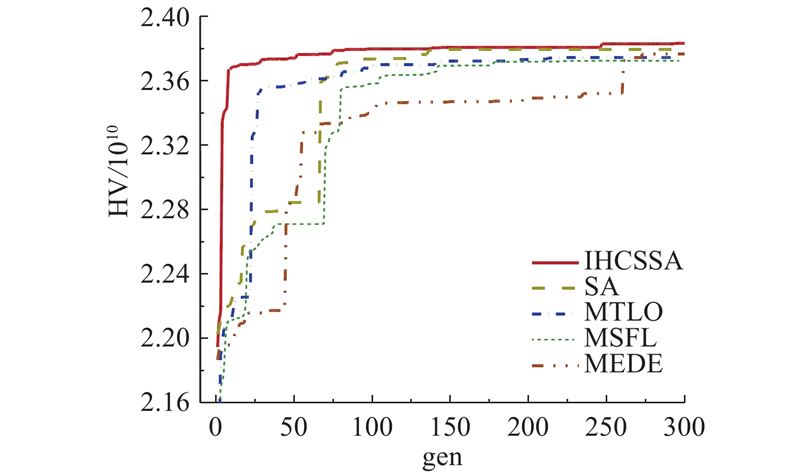
超体积指标[18](hypervolume, HV)常用来综合评价多目标智能算法求得的Pareto解集的收敛性. HV越高，说明解的收敛性和求解质量越好.

对于大规模问题，由于DLBP的NP-hard属性，精确求解器在有效时间内无法求得最优解. 为了评价IHCSSA算法的寻优能力和收敛性，将各算法运行300代，记录每代的HV值，绘制HV迭代图，如图12所示.

图 12

新窗口打开| 下载原图ZIP| 生成PPT

图 12   利用5种算法求解P74的HV迭代图

Fig.12   HV convergence plot of five algorithms on P74


从图12可以看出，在算法收敛速度方面，IHCSSA算法在开始迭代后HV值快速上升，当算法仅迭代到第9代时，HV指标达到2.367×1010，之后HV值基本达到平稳. 相较之下，SA收敛速度较慢，当迭代到第42代时，HV指标为2.284×1010，且之后出现了HV无增长的迭代期. 最终算法在第137代时才最终收敛. 说明所设计的克隆算子可以有效地增大原算法的收敛速度，使算法在迭代前期可以快速收敛. MTLO算法有着较优异的收敛速度，当算法迭代到第30代时可以快速收敛. 在算法寻优能力方面，IHCSSA算法的HV值最大，为2.382×1010，其次是SA算法的2.379×1010，MSFL算法最差仅为2.382×1010. 说明SA算法的整体迭代策略对解决该问题有着显著的效果. 综上分析可知，IHCSSA算法拥有SA算法的全局搜索性能，同时结合克隆算子加快了收敛速度，整体具有较好的搜索性能.

3.3. 动态人机协作方案规划的对比

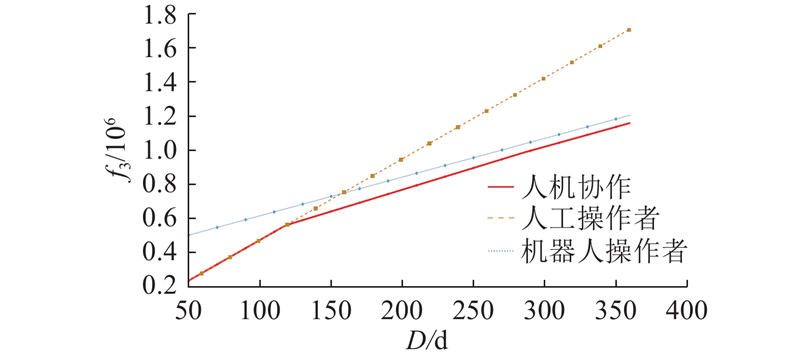
为了对比人机协作拆卸线与机器人和人工拆卸线对企业成本的影响，验证本文长期成本目标f3可对不同运行时长的拆卸线提供不同拆卸方案的优越性，解除上文P25问题中的任务属性约束，在其余条件不变的情况下，模拟拆卸线运行工作时间为50~360 d，根据不同的运行天数，运用Gurobi软件计算在该总运行天数下最优方案的成本目标，计算结果如图13所示. 其中，放大图为2类拆卸线在预计总运行117 d时最优方案的成本减去550 000时的对比图，左侧为人机协作拆卸线的拆卸方案，右侧为人工拆卸线方案.

图 13

新窗口打开| 下载原图ZIP| 生成PPT

图 13   不同操作者模式下的拆卸线运行成本

Fig.13   Operating cost of disassembly line under different operator mode


从图13可知，当预计运行总天数小于117 d时，由于机器人工作站较高的开启成本，人机协作拆卸线的最优方案未选用机器人工作站，成本与人工拆卸线相同，都低于机器人拆卸线. 当预计拆卸线运行天数为117 d时，人机协作拆卸线的最优方案为开启3个机器人工作站与3个工人工作站，工作站数量较人工拆卸线方案减少一个，且运行总成本降低624. 这说明当运行总天数不小于117 d时，机器人工作站有着较低的运行成本，总运行节省成本已超过原机器人工作站的开启成本，拆卸企业购置拆卸机器人会有更低的成本. 当拆卸线总运行时长大于159 d时，因为工人较高的雇佣费用，人工拆卸线最优方案的成本高于机器人拆卸线最优方案.

4. 结　语

本文提出考虑多约束的人机协作U型拆卸线，考虑人工操作者与机器人操作者任务属性的差异与工作时间的差异，同时考虑AND/OR优先关系，建立多目标数学模型. 采用Gurobi软件，对中小规模算例进行精确求解，验证了模型的正确性. 针对该问题，建立考虑工作站操作者差异的双层编码，设计适用于该问题的解码方法. 引入克隆算法中的克隆变异操作到模拟退火算法中. 通过与精确求解器结果的对比，验证了算法的正确性和高效性. 与传统算法对比求解结果的HV指标和IGD指标，验证了IHCSSA算法的优越性.

在未来的研究中，可以考虑加入更多其他的人机协作类型，如人机顺序协作、人机响应式协作模式. 本研究将继续在人机协作拆卸线领域从不同维度开展更深入的研究.

参考文献

XU X, LU Y, VOGEL-HEUSER B, et al

Industry 4.0 and Industry 5.0: inception, conception and perception

[J]. Journal of Manufacturing Systems, 2021, 61: 530- 535

DOI:10.1016/j.jmsy.2021.10.006      [本文引用: 1]

GUNGOR A, GUPTA S M

A solution approach to the disassembly line balancing problem in the presence of task failures

[J]. International Journal of Production Research, 2001, 39 (7): 1427- 1467

DOI:10.1080/00207540110052157      [本文引用: 1]

GUO X, FAN C, ZHOU M, et al

Human–robot collaborative disassembly line balancing problem with stochastic operation time and a solution via multi-objective shuffled frog leaping algorithm

[J]. IEEE Transactions on Automation Science and Engineering, 2024, 21 (3): 4448- 4459

DOI:10.1109/TASE.2023.3296733      [本文引用: 2]

ZHU L, ZHANG Z, GUAN C

Multi-objective partial parallel disassembly line balancing problem using hybrid group neighbourhood search algorithm

[J]. Journal of Manufacturing Systems, 2020, 56: 252- 269

DOI:10.1016/j.jmsy.2020.06.013      [本文引用: 2]

WANG W, GUO X, LIU S, et al. Multi-objective discrete chemical reaction optimization algorithm for multiple-product partial U-shaped disassembly line balancing problem [C]// IEEE International Conference on Systems. Melbourne: IEEE, 2021: 2322-2327.

[本文引用: 1]

WU K, GUO X, LIU S, et al. Multi-objective discrete brainstorming optimizer for multiple-product partial U-shaped disassembly line balancing problem [C]//33rd Chinese Control and Decision Conference. Kunming: IEEE, 2021: 305-310.

[本文引用: 1]

KHEIRABADI M, KEIVANPOUR S, CHINNIAH Y A, et al

Human-robot collaboration in assembly line balancing problems: review and research gaps

[J]. Computers and Industrial Engineering, 2023, 186: 109737

DOI:10.1016/j.cie.2023.109737      [本文引用: 1]

HARTONO N, RAMÍREZ F J, PHAM D T

A multiobjective decision-making approach for modelling and planning economically and environmentally sustainable robotic disassembly for remanufacturing

[J]. Computers and Industrial Engineering, 2023, 184: 109535

DOI:10.1016/j.cie.2023.109535      [本文引用: 1]

LOU S, TAN R, ZHANG Y, et al

Personalized disassembly sequence planning for a human-robot Hybrid disassembly cell

[J]. IEEE Transactions on Industrial Informatics, 2024, 20 (9): 11372- 11383

DOI:10.1109/TII.2024.3403254      [本文引用: 1]

张则强, 许培玉, 蒋晋, 等

站间操作者不同的并行拆卸线平衡问题优化

[J]. 浙江大学学报: 工学版, 2021, 55 (10): 1795- 1805

[本文引用: 1]

ZHANG Zeqiang, XU Peiyu, JIANG Jin, et al

Optimization of parallel disassembly line balancing problem with different operators between workstations

[J]. Journal of Zhejiang University: Engineering Science, 2021, 55 (10): 1795- 1805

[本文引用: 1]

WU T, ZHANG Z, YIN T, et al

Multi-objective optimisation for cell-level disassembly of waste power battery modules in human-machine hybrid mode

[J]. Waste Management, 2022, 144: 513- 526

DOI:10.1016/j.wasman.2022.04.015      [本文引用: 1]

GUO L, ZHANG Z, WU T, et al

Green and efficient-oriented human-robot hybrid partial destructive disassembly line balancing problem from non-disassemblability of components and noise pollution

[J]. Robotics and Computer-Integrated Manufacturing, 2024, 90: 102816

DOI:10.1016/j.rcim.2024.102816      [本文引用: 1]

CHUTIMA P, KHOTSAENLEE A

Multi-objective parallel adjacent U-shaped assembly line balancing collaborated by robots and normal and disabled workers

[J]. Computers and Operations Research, 2022, 143: 105775

DOI:10.1016/j.cor.2022.105775      [本文引用: 1]

丁力平, 谭建荣, 冯毅雄, 等

基于Pareto蚁群算法的拆卸线平衡多目标优化

[J]. 计算机集成制造系统, 2009, 15 (7): 1406- 1413

[本文引用: 1]

DING Liping, TAN Jianrong, FENG Yixiong, et al

Multiobjective optimization for disassembly line balancing based on Pareto ant colony algorithm

[J]. Computer Integrated Manufacturing Systems, 2009, 15 (7): 1406- 1413

[本文引用: 1]

郭磊, 张秀芬

多重故障驱动的再制造并行拆卸序列规划方法

[J]. 浙江大学学报: 工学版, 2020, 54 (11): 2233- 2246

[本文引用: 1]

GUO Lei, ZHANG Xiufen

Remanufacturing parallel disassembly sequence planning method driven by multiple failures

[J]. Journal of Zhejiang University: Engineering Science, 2020, 54 (11): 2233- 2246

[本文引用: 1]

脱阳, 张则强, 张裕, 等

考虑可变时间的双边机器人拆卸线平衡问题建模与优化

[J]. 计算机集成制造系统, 2023, 29 (12): 4073- 4088

[本文引用: 1]

TUO Yang, ZHANG Zeqiang, ZHANG Yu, et al

Modeling and optimization for two-sided robots disassembly line balancing problems considering variable time

[J]. Computer Integrated Manufacturing Systems, 2023, 29 (12): 4073- 4088

[本文引用: 1]

黄家骏, 腾来, 张朝杰, 等

基于模拟退火算法的I/Q不平衡校正

[J]. 浙江大学学报: 工学版, 2018, 52 (11): 2218- 2225

[本文引用: 2]

HUANG Jiajun, TENG Lai, ZHANG Chaojie, et al

I/Q imbalance calibration based on simulated annealing algorithm

[J]. Journal of Zhejiang University: Engineering Science, 2018, 52 (11): 2218- 2225

[本文引用: 2]

WU T, ZHANG Z, ZENG Y, et al

Techno-economic and environmental benefits-oriented human–robot collaborative disassembly line balancing optimization in remanufacturing

[J]. Robotics and Computer-Integrated Manufacturing, 2024, 86: 102650

DOI:10.1016/j.rcim.2023.102650      [本文引用: 3]

JIN X, DU H, HE W, et al. Optimizing the weights of neural networks based on antibody clonal simulated annealing algorithm [C]// Advances in Neural Networks. Berlin: Springer, 2004: 299-304.

[本文引用: 1]

ZHANG X, TIAN G, FATHOLLAHI-FARD A M, et al

A chance-constraint programming approach for a disassembly line balancing problem under uncertainty

[J]. Journal of Manufacturing Systems, 2024, 74: 346- 366

DOI:10.1016/j.jmsy.2024.03.014      [本文引用: 1]

YIN T, ZHANG Z, JIANG J

A Pareto-discrete hummingbird algorithm for partial sequence-dependent disassembly line balancing problem considering tool requirements

[J]. Journal of Manufacturing Systems, 2021, 60: 406- 428

DOI:10.1016/j.jmsy.2021.07.005      [本文引用: 1]

KALAYCI C B, GUPTA S M

A tabu search algorithm for balancing a sequence-dependent disassembly line

[J]. Production Planning and Control, 2014, 25 (2): 149- 160

DOI:10.1080/09537287.2013.782949      [本文引用: 1]

XU Z, HAN Y

Two sided disassembly line balancing problem with rest time of works: a constraint programming model and an improved NSGA II algorithm

[J]. Expert Systems with Applications, 2024, 239: 122323

DOI:10.1016/j.eswa.2023.122323      [本文引用: 1]

ZHOU B, BIAN J

A bi-objective salp swarm algorithm with sine cosine operator for resource constrained multi-manned disassembly line balancing problem

[J]. Applied Soft Computing, 2022, 131: 109759

DOI:10.1016/j.asoc.2022.109759      [本文引用: 1]

ZHANG Z, LIANG W, JI D, et al

Mixed integer programming and multi-objective enhanced differential evolution algorithm for human–robot responsive collaborative disassembly in remanufacturing system

[J]. Advanced Engineering Informatics, 2024, 62: 102895

DOI:10.1016/j.aei.2024.102895      [本文引用: 1]

ZHU L, CHEN Y, MUMTAZ J

Multi-objective human-robot collaborative disassembly line balancing considering components remanufacture demand and hazard characteristics

[J]. Computers and Industrial Engineering, 2024, 197: 110621

DOI:10.1016/j.cie.2024.110621      [本文引用: 1]

/

〈 〉