机器人技术在各种领域都有着广泛的应用，包括工业生产^[1]、食品加工^[2]、医疗卫生^[3]等. 相较于串联型机器人，并联机器人拥有响应速度更快、承载能力更高、无累计误差等优点. 复杂且多支链的结构导致其扰动具有多源性与不确定性，因此难以进行建模或优化. 实现高性能并联机器人的设计十分具有挑战性.

为了将制造与装配^[4]、振动^[5]、热变化^[6]、重力效应^[7]等多源混合不确定性纳入考虑范围，需要通过特殊建模方法或使用数值模拟技术，对这类不确定性扰动进行分析^[8]. 在完成建模后，可以通过多种优化设计方法对并联机器人进行参数优化设计. Mcdonald等^[9]研究缆绳驱动并联机器人的参数化设计方案，通过多种计算机辅助设计软件，实现运动学和静力学模拟及机器人工作轨迹的建模. Zaccaria等^[10]针对平面连续并联机器人的工作空间设计方法，提出基于逆几何静态问题的数值解析迭代计算方法. Khodaygan^[11]提出机械设计公差优化框架，提高机械装配的质量和系统性能的鲁棒性. 此外，预防性维保能够使机器人的动态性能退化在设计阶段被纳入考量^[12]. 预防性维保的主要思想是基于概率方法^[13]或模糊理论构建精度退化模型^[14]，对机器人系统的失效进行预测，从而在失效发生前进行防范.

目前，对不确定性优化设计方法的研究主要针对静态的优化设计，且大多研究未考虑基础设计的优劣. 针对动态退化预测，例如预测失效并实施预防性维修的研究未对维保策略的收益与优化方法进行深入讨论. 针对并联机器人多支链驱动导致干扰多源，扰动具有不确定性，造成机器人的性能对设计参数敏感，优化困难的问题，在Xu等^[15-16]研究的基础上，本文提出多源不确定混合扰动下的并联机器人降敏设计方法，研究并联机器人灵巧性能、定位性能与在役精度性能对设计参数的响应敏感程度，实现高性能并联机器人的定制化降敏设计.

并联机器人执行器的理想位姿由所有构件的尺寸参数及驱动件的驱动参数（即构件坐标参数）决定. 假设执行器的理想运动规律方程为

(1)$ {{{\boldsymbol {Z}}}}_{0}={{{ {f}}}}_{{\boldsymbol{Z}}_0}\left({{\boldsymbol{x}}},{{\boldsymbol{\lambda }}}\right). $

式中：$ {{{\boldsymbol {Z}}}}_{0} $为执行器的理想位姿参数，$ \boldsymbol{x} $为广义坐标参数，$ \boldsymbol{\lambda } $为尺寸参数.

执行器的实际运动规律与理想运动规律会产生一定的偏差，在存在多源不确定扰动的情况下，式（1）可以改写为

(2)$ {{\boldsymbol{Z}}}={{ {f}_{\boldsymbol{Z}}}}\left(\boldsymbol{x},\boldsymbol{\lambda },\boldsymbol{\xi }\right), $

(3)$ \boldsymbol{\xi }={\boldsymbol{\xi }}_{{\mathrm{s}}} \oplus {\boldsymbol{\xi }}_{{{\mathrm{d}}}}. $

式中：$ \boldsymbol{Z} $为执行器的实际位姿参数；$ {\boldsymbol{\xi }}_{{{\mathrm{s}}}} $为不确定性误差参数$ \boldsymbol{\xi } $的静态分量，即机器人在开始运行时刻的不确定性误差参数；$ {\boldsymbol{\xi }}_{{{\mathrm{d}}}} $为$ \boldsymbol{\xi } $的动态分量，即机器人在运行过程中的不确定性误差参数变化量；$ \oplus $表示逐元素相加.

将广义坐标参数与尺寸参数简化为综合输入参数$ \boldsymbol{\kappa } $，式（2）可以简化为

(4)$ \boldsymbol{Z}=f_{{\boldsymbol{Z}}}\left(\boldsymbol{\kappa }+\boldsymbol{\xi }\right). $

摄动法关注于主要因素并忽略一些次要因素的影响，使得这类复杂问题能够得到近似的解析解. 由于各不确定性误差参数相互独立，式（4）可以根据摄动理论展开为

(5)$ \boldsymbol{Z}=f_{{\boldsymbol{Z}}}\left(\boldsymbol{\kappa }\right)+\sum _{i=1}^{{N}_{\xi }}\frac{\partial {{\boldsymbol Z}}}{\partial {\kappa }_{i}}{\xi }_{i}+\frac{1}{2!}\sum _{j=1}^{{N}_{\xi }}\sum _{l=1}^{{N}_{\xi }}\frac{{\partial }^{2}{{\boldsymbol Z}}}{\partial {\kappa }_{j}\partial {\kappa }_{l}}{\xi }_{j}{\xi }_{l}+\cdots . $

式中：$ {N}_{\xi } $为独立误差源的总数. 一般可以假设不确定性误差为较小值，只保留一阶项并且舍去二阶及以上的高阶项，式（5）可以改写为

(6)$ \boldsymbol{Z}=f_{{\boldsymbol{Z}}}\left(\boldsymbol{\kappa }\right)+\sum _{i=1}^{{N}_{\xi }}\frac{\partial {{\boldsymbol Z}}}{\partial {\kappa }_{i}}{\xi }_{i}. $

将式（6）减去式（1），得到执行器实际位姿参数与理想位姿参数的偏差，即执行器误差传递方程：

(7)$ \Delta \boldsymbol{Z}={\boldsymbol{Z}}-{\boldsymbol{Z}}_{0}=f_{{\boldsymbol{Z}}}\left({\boldsymbol{\kappa }}\right)-{f_{{\boldsymbol{Z}}_{0}}}\left({\boldsymbol{\kappa}} \right)+\sum _{i=1}^{{N}_{\xi }}\frac{\partial {{\boldsymbol Z}}}{\partial {\kappa }_{i}}{\xi }_{i}. $

式中：$f_{{\boldsymbol{Z}}}\left(\boldsymbol{\kappa }\right)-{f_{{\boldsymbol{Z}}}}_{0}\left(\boldsymbol{\kappa }\right) $为在无任何扰动的情况下执行器实际设计位姿与理想位姿的偏差，称为设计误差，可以通过改进设计的方式对其进行抑制或消除. 在多源不确定性扰动下，并联机器人的误差传递方程为

(8)$ \Delta \boldsymbol{Z}=\sum _{i=1}^{{N}_{\xi }}\frac{\partial {{\boldsymbol Z}}}{\partial {\kappa }_{i}}{\xi }_{i}. $

从式（8）可知，执行器误差为$ \boldsymbol{\kappa } $及$ \boldsymbol{\xi } $的函数. $ \boldsymbol{\kappa } $可以进一步分为$ \boldsymbol{x} $和$ \boldsymbol{\lambda } $. $ \boldsymbol{\xi } $可以进一步分为$ {\boldsymbol{\xi }}_{{{\mathrm{s}}}} $和$ {\boldsymbol{\xi }}_{{{\mathrm{d}}}} $. 其中，广义坐标参数$ \boldsymbol{x} $主要受执行器位姿的影响，由确定工作任务后执行器的工作轨迹决定，因此不作为并联机器人优化设计的目标参数.

元启发式优化的优化搜索过程一般可以分为种群初始化、元启发式迭代策略及种群更新策略. 与使用简单的随机数生成器进行种群初始化相比，利用混沌映射技术能够生成分布更广泛的初始解，常见的有Logistic映射、Cubic映射、Tent映射等. 其中，Cubic混沌映射具有良好的混沌属性，表达式为

(9)$ {x}_{n+1}=\alpha {x}_{n}\left(1-{x}_{n}^{2}\right). $

式中：$ {x}_{n} $为(0, 1.0)的随机值，$ {x}_{n+1} $为混沌值，$ \alpha $为控制参数.

元启发式迭代策略通过启发式信息引导优化策略，从而使得算法具有避免局部最优和解决非凸问题的能力. 通过额外添加变异算法来优化迭代策略，可以提高算法找到全局最优的可能性. 柯西变异算法常被用于摆脱局部最优状态，表达式为

(10)$ c\left(\boldsymbol{x}\right)=\frac{1}{\text{π}}\left(\frac{1}{{\left(\boldsymbol{x}-{\boldsymbol{x}}_{0}\right)}^{2}+\gamma }\right). $

式中：$ {\boldsymbol{x}}_{0} $为分布中心，$ \gamma $为比例参数.

当优化目标从单一目标拓展到多目标时，需要引入具有多目标排序能力的方法，作为种群更新策略. 非支配排序方法能够有效地对多目标优化问题进行优劣比较，主要思路如下：计算通过寻找解空间中存在的那些不受任何剩余解支配的解，并将其汇总组成Pareto最优前沿. 多目标优化模型一般为

(11)$ \left.\begin{array}{l}{\mathrm{Find}}\;{\boldsymbol{X}}=[{x}_{1},{x}_{2},\cdots ,{x}_{n}]\in {{\bf{R}}}^{n},\\ {\mathrm{min}}\;f\left(\boldsymbol{X}\right)={\mathrm{min}}\;\left\{{{\mathrm{Obj}}}_{1},{{\mathrm{Obj}}}_{2},\cdots ,{{\mathrm{Obj}}}_{m}\right\};\\ {\mathrm{s.t.}}\;\;{{\mathrm{Res}}}_{1},{{\mathrm{Res}}}_{2},\cdots {,{\mathrm{Res}}}_{r}.\end{array}\right\} $

式中：$ \boldsymbol{X} $为设计变量参数，$ n $为设计变量个数，$ m $为优化目标个数，$ r $为约束条件个数，$ {{\mathrm{Obj}}}_{m} $为优化目标函数，$ {{\mathrm{Res}}}_{r} $为约束条件.

此外，对于同一支配等级下的候选解$ {{\boldsymbol{C}}}_{i}(i=\mathrm{1,2},\cdots , n $)，可以通过拥挤距离来排除那些过于接近的解：

(12)$ {D}_{{\mathrm{crowd}}}\left({{\boldsymbol{C}}}_{i}\right)=\sum _{o=1}^{m}\left(\frac{{{\mathrm{Obj}}}_{{o}}\left({{\boldsymbol{C}}}_{i+1}\right)-{{\mathrm{Obj}}}_{{o}}\left({{\boldsymbol{C}}}_{i-1}\right)}{{\mathrm{m}\mathrm{a}\mathrm{x}\;({\mathrm{Obj}}}_{{o}})-{\mathrm{m}\mathrm{i}\mathrm{n}\;({\mathrm{Obj}}}_{{o}})}\right). $

在复杂任务条件下，完整的任务流程可以分为多个有各自的优化目标靶区域偏向的子任务流程. 通过对优化目标函数进行多靶拆分与分域映射的改进，可以实现面向复杂任务的针对性优化. 此时，式（11）可以改写为

(13)$ \left.\begin{array}{l}{\mathrm{Find}}\;{\boldsymbol{X}}=[{x}_{1},{x}_{2},\cdots ,{x}_{n}]\in {{\bf{R}}}^{n},\\ \mathrm{min}\;f\left(\boldsymbol{X}\right)=\\ {\mathrm{min}}\;\left\{{{\mathrm{Obj}}}_{1},{R}_{1};{{\mathrm{Obj}}}_{2},{R}_{2};\cdots ;{{\mathrm{Obj}}}_{m},{R}_{m}\right\};\\ {\mathrm{s.t.}}\;\;{{\mathrm{Res}}}_{1},{{\mathrm{Res}}}_{2},\cdots {,{\mathrm{Res}}}_{r}.\end{array}\right\} $

式中：$ {[{\mathrm{Obj}}}_{i},{R}_{i}](i={1,2},\cdots ,m) $表示在特定子优化域所激活的靶目标.

设定并联机器人的尺寸参数为$ {\boldsymbol{P}}_{\rm{R}} $，驱动量为$ {\boldsymbol{Q}}_{\rm{R}} $，执行器位姿为$ {\boldsymbol{X}}_{\rm{R}} $，雅可比矩阵为$ \boldsymbol{J} $. 并联机器人的运动学方程为

(14)$ \dot{{\boldsymbol{X}}_{\rm{R}}}=\boldsymbol{J}({\boldsymbol{P}}_{\rm{R}},{\boldsymbol{Q}}_{\rm{R}},{\boldsymbol{X}}_{\rm{R}})\dot{{\boldsymbol{Q}}_{\rm{R}}}. $

式中：$ \dot{{\boldsymbol{Q}}_{\rm{R}}} $为驱动器速度，$ \dot{{\boldsymbol{X}}_{\rm{R}}} $为执行器速度. $ \boldsymbol{J} $随着机构的尺寸和位姿变化会发生改变，行数m为操作空间的自由度，列数n为关节空间的自由度.

关于并联机器人的工作能力，可以使用雅可比矩阵扩展灵巧性能、承载性能和刚度性能这3种性能评价指标：

(15)$ k=\frac{{\sigma }_{\mathrm{m}\mathrm{a}\mathrm{x}}\left(\boldsymbol{J}\right)}{{\sigma }_{\mathrm{m}\mathrm{i}\mathrm{n}}\left(\boldsymbol{J}\right)}, $

(16)$ {F}_{\max}={\sigma }_{\mathrm{m}\mathrm{a}\mathrm{x}}\left({\boldsymbol{J}}^{-1}\cdot {\left({\boldsymbol{J}}^{\mathrm{T}}\right)}^{-1}\right), $

(17)$ {D}_{\max}={\sigma }_{\mathrm{m}\mathrm{a}\mathrm{x}}\left(\boldsymbol{J} {\boldsymbol{J}}^{\mathrm{T}}\right). $

式中：$ {\sigma }_{\mathrm{m}\mathrm{a}\mathrm{x}}(\cdot ) $表示对矩阵求最大奇异值，$ {\sigma }_{\mathrm{m}\mathrm{i}\mathrm{n}}(\cdot ) $表示对矩阵求最小奇异值. 灵巧性能指标$ k $能够反映响应速度，承载性能指标$ {F}_{\max} $能够体现最大负载，刚度性能指标$ {D}_{\max} $表示最大变形量. 其中$ {F}_{\max} $和$ {D}_{\max} $仅须满足要求，$ k $将作为重点的优化目标.

将尺寸参数$ \mathit{\lambda } $作为设计变量，通过式（15）~(17）的性能指标拓展，式（13）可以改写成并联机器人的灵巧性能优化模型：

(18)$ \left.\begin{array}{l}\mathrm{F}\mathrm{i}\mathrm{n}\mathrm{d}\;\boldsymbol{X}=\boldsymbol{\lambda },\boldsymbol{\lambda }\in {{\bf{R}}}^{{N}_{\lambda }},\\ \mathrm{m}\mathrm{i}\mathrm{n}\;f\left(\boldsymbol{X}\right)=\left\{\begin{array}{l}\begin{array}{l}\mathrm{m}\mathrm{i}\mathrm{n}\;k\left(\boldsymbol{\lambda }\right)\;{\mathrm{in}}\;{R}_{k},\\ \mathrm{m}\mathrm{i}\mathrm{n}\;{-F}_{\max}\left(\boldsymbol{\lambda }\right)\;{\mathrm{in}}\;{R}_{{F}_{\max}},\end{array}\\ \begin{array}{l}\mathrm{m}\mathrm{i}\mathrm{n}\;{D}_{\max}\left(\boldsymbol{\lambda }\right)\;{\mathrm{in}}\;{R}_{{D}_{\max}},\\ \mathrm{m}\mathrm{i}\mathrm{n}\;\mathrm{\Delta }{{\boldsymbol{Z}}}\left(\boldsymbol{\lambda }\right)\;{\mathrm{in}}\;{R}_{\mathrm{\Delta }{{\boldsymbol{Z}}}};\end{array}\end{array}\right.\\ {\mathrm{s.t.}}\;\;{\boldsymbol{\lambda }}_{\mathrm{m}\mathrm{i}\mathrm{n}}\leqslant \boldsymbol{\lambda }\leqslant {\boldsymbol{\lambda }}_{\mathrm{m}\mathrm{a}\mathrm{x}}.\end{array}\right\} $

式中：$ {N}_{\lambda } $为设计变量的维数. 利用式（18）得到多个Pareto最优解，将所有的Pareto最优解作为候选解. 综合考虑不同优化目标对设计参数的敏感性，从候选解中选择低敏设计参数，实现灵巧性能对设计尺寸参数的降敏.

对于确定并联机器人的误差传递模型，可以对该模型的各个独立误差源进行分解：

(19)$ \Delta \boldsymbol{Z}={\boldsymbol{J}}_{{\mathrm{e}},1} {\xi }_{{\mathrm{s}},1}+{\boldsymbol{J}}_{{\mathrm{e}},2} {\xi }_{{\mathrm{s}},2}+\cdots +{\boldsymbol{J}}_{{\mathrm{e}},{N}_{\xi }} {\xi }_{{\mathrm{s}},{N}_{\xi }}. $

式中：$ {\boldsymbol{J}}_{{\mathrm{e}},i}=\partial \boldsymbol{Z}/\partial {\kappa }_{i} $，$ i=\mathrm{1,2},\cdots ,{N}_{\xi } $，其中$ {N}_{\xi } $为独立误差源的数量. 当同时有足够多数量的同种并联机器人时，并联机器人执行器误差的平方和为

(20)$ \begin{split} &{\Delta }{\boldsymbol{Z}}^{\left(1\right)}\odot {\Delta }{\boldsymbol{Z}}^{\left(1\right)}+{\Delta }{\boldsymbol{Z}}^{\left(2\right)}\odot {\Delta }{\boldsymbol{Z}}^{\left(2\right)}+\cdots +{\Delta }{\boldsymbol{Z}}^{\left({N}_{{\mathrm{s}}}\right)}\odot {\Delta }{\boldsymbol{Z}}^{\left({N}_{{\mathrm{s}}}\right)}=\\&{{\boldsymbol{J}}_{{\mathrm{e}},1}}\odot {{\boldsymbol{J}}_{{\mathrm{e}},1}}\left({{{\xi }_{{\mathrm{s}},1}}^{\left(1\right)}}^{2}+{{{\xi }_{{\mathrm{s}},1}}^{\left(2\right)}}^{2}+\cdots +{{{\xi }_{{\mathrm{s}},1}}^{\left({N}_{{\mathrm{s}}}\right)}}^{2}\right)+\cdots +\\&{{\boldsymbol{J}}_{{\mathrm{e}},{N}_{\xi }}}\odot {{\boldsymbol{J}}_{{\mathrm{e}},{N}_{\xi }}}\left({{{\xi }_{{\mathrm{s}},{N}_{\xi }}}^{\left(1\right)}}^{2}+{{{\xi }_{{\mathrm{s}},{N}_{\xi }}}^{\left(2\right)}}^{2}+\cdots +{{{\xi }_{{\mathrm{s}},{N}_{\xi }}}^{\left({N}_{{\mathrm{s}}}\right)}}^{2}\right)+\\&2{\sum _{k=1}^{{N}_{\xi }}}{\sum _{1\leqslant j\leqslant k}}\;{\sum _{m=1}^{{N}_{{\mathrm{s}}}}}\left({\boldsymbol{J}}_{{\mathrm{e}},j}\odot{\boldsymbol{J}}_{{\mathrm{e}},k}{{\xi }_{{\mathrm{s}},j}}^{\left(m\right)}{{\xi }_{{\mathrm{s}},k}}^{\left(m\right)}\right).\end{split} $

式中：$\odot $表示逐元素相乘，$ {N}_{{\mathrm{s}}} $为并联机器人的采样数量. 由于各误差源之间相互独立，当$ {N}_{{\mathrm{s}}} $足够大时，

(21)$ 2{\sum _{k=1}^{{N}_{\xi }}}{\sum _{1\leqslant j\leqslant k}}\;{\sum _{m=1}^{{N}_{{\mathrm{s}}}}}\left({{\boldsymbol{J}}}_{{\mathrm{e}},j}\odot {{\boldsymbol{J}}}_{{\mathrm{e}},k}{{\xi }_{{\mathrm{s}},j}}^{\left(m\right)}{{\xi }_{{\mathrm{s}},k}}^{\left(m\right)}\right)={\boldsymbol{0}}. $

将式（21）代入式（20），在等式两边除以$ {N}_{{\mathrm{s}}} $，可得

(22)$ {{{\bf{PE}}}}_{{\mathrm{out}}}\odot {{{\bf{PE}}}}_{{\mathrm{out}}}={{\sum_{i=1}^{{N}_{\xi }}}\left( {{{\boldsymbol{J}}_{{\mathrm{e}},i}}\odot {{\boldsymbol{J}}_{{\mathrm{e}},i}}} \right) \odot \left( {{\bf{PE}}_{{\mathrm{in}},i}}\odot{{\bf{PE}}_{{\mathrm{in}},i}}\right)} . $

式中：$ {\bf{PE}}_{{\mathrm{out}}} $为并联机器人执行器的输出概率误差，$ {\bf{PE}}_{{\mathrm{in}},i} $为第i个独立误差源的输入概率误差.

为了研究不同独立误差源对执行器输出误差的影响程度，需要构建评估指标来衡量这种影响. 假设并联机器人的执行器处于工作空间W中的某一位姿P时，定义该位姿下的局部误差敏感度$ {\boldsymbol{M}}_{{\boldsymbol{P}}} $为

(23)$ {\boldsymbol{M}}_{{\boldsymbol{P}}} \odot {{\bf{PE}}_{{\mathrm{in}},{\boldsymbol{P}}}} ={{\bf{PE}}_{{\mathrm{out}},{\boldsymbol{P}}}}. $

将局部误差敏感度扩展到整个工作空间中，可得并联机器人的全局误差敏感度：

(24)$ \boldsymbol{M}=\frac{\displaystyle \int {\boldsymbol{M}}_{{\boldsymbol{P}}}{\mathrm{d}}{W}}{{W}}. $

由于对式（24）直接进行求解较复杂，基于蒙特卡洛随机方法，可以在工作空间中选取$ {N}_{{\mathrm{M}}} $个采样点并计算局部误差敏感度. 当采样数量足够多时，可得全局误差敏感度的近似解：

(25)$ \boldsymbol{M}={{N}_{{\mathrm{M}}}^{-1}}{{\displaystyle\sum_{i=1}^{{N}_{{\rm{M}}}}}{{{\boldsymbol{M}}}}_{{\boldsymbol{P}}}^{(i)}}. $

式中：${{{\boldsymbol{M}}}}_{{\boldsymbol{P}}}^{(i)} $为第i个采样点的局部误差敏感度. 通过全局误差敏感度适当调整设计公差，可以实现定位性能的降敏设计.

由于磨损、松动、热变形、残余应力和振动等各种因素，机器人的精度会随着时间的推移而逐渐降低，表现为式（8）中的不确定性参数动态分量$ {{\boldsymbol{\xi}} }_{{\mathrm{d}}} $. 在机器人经过一段运行时间$ t $后，每个独立误差源都可能产生一定的精度退化：

(26)$ {{\boldsymbol{\xi}} }_{{\mathrm{d}}}={f}_{{\mathrm{d}}}\left(t,{\mu }_{i}\right). $

式中：$ {f}_{{\mathrm{d}}}(\cdot ) $为独立误差源的精度退化函数；$ {\mu }_{i} $为经历过$ i $次预防性维保后的精度退化因子，用以描述维保无法逆转的部件内部的老化过程. 将式（26）代入式（19），可得机器人的精度退化模型：

(27)$ \Delta\boldsymbol{Z}={\boldsymbol{J}}_{{\mathrm{e}}}\left({{\boldsymbol{\xi}} }_{{\mathrm{s}}}\ominus {{\boldsymbol{\xi}} }_{{\mathrm{d}}}\right). $

式中：$\ominus $表示逐元素相减.

预防性维保技术通过式（27）对机器人的失效进行预测，制定预防性维保策略需要考虑多种维保策略参数，如维保成本、维保阈值、预防性维保上限次数等. 预防性维保的成本$ {C}_{{\mathrm{m}}} $一般相较于失效后对相关部件进行替换的成本$ {C}_{{\mathrm{b}}} $低. 设定维保阈值为$ {e}_{\varepsilon } $，预防性维保上限次数为$ {N}_{{\mathrm{m}}} $，在经历过$ i $次预防性维保后，机器人的维保收益，即在役精度性能敏感性可以表示为

(28)$ {C}_{{\mathrm{e}}}=\frac{{\displaystyle\sum _{i=1}^{{N}_{{\mathrm{m}}}}}T({e}_{\varepsilon },{\mu }_{i})-{N}_{{\mathrm{m}}} {t}_{{\mathrm{m}}}}{{C}_{{\mathrm{m}}} {N}_{{\mathrm{m}}}+{C}_{{\mathrm{b}}}}. $

式中：$ T({e}_{\varepsilon },{\mu }_{i}) $为第i次预防性维保能够使机器人延长的使用寿命，其中${e}_{\varepsilon } $为维保阈值，$ {\mu }_{i} $为精度退化参数；$ {t}_{{\mathrm{m}}} $为单次预防性维保耗时；$ {C}_{{\mathrm{e}}} $为维保收益，表示单位成本下预防性维保能够使机器人延长的总使用寿命.

通过制定不同的维保策略，达到不同的维保效益，从而实现在役精度性能的降敏设计.

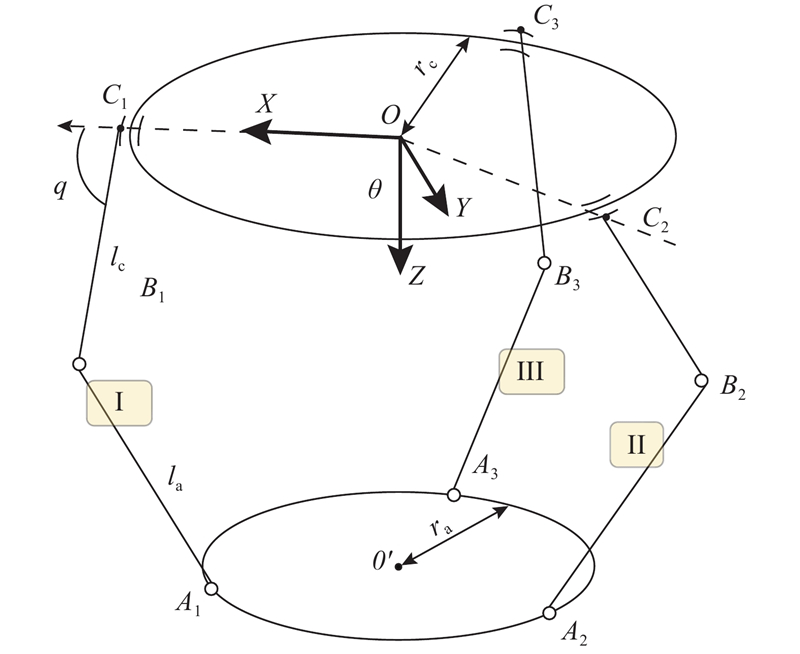
以图1所示的并联结构作为增材制造并联机器人的结构设计基础，介绍降敏设计方法的具体流程. 利用式（8），可以计算得到执行器的误差传递公式：

(29)$\left.\begin{array}{l}\Delta{\boldsymbol{Z}}=\left[\begin{array}{cc}{\boldsymbol{J}}_{{\mathrm{a}}}^{-1}\;\;-{\boldsymbol{J}}_{{\mathrm{a}}}^{-1}{\boldsymbol{J}}_{{\mathrm{b}}}\end{array}\right]\left[\begin{array}{l}\Delta {\boldsymbol{l}}_{{\mathrm{a}}}\\ \Delta \boldsymbol{V}\end{array}\right],\\{\boldsymbol{J}}_{{\mathrm{a}}} = \left[\begin{array}{l}{\boldsymbol{v}}_{1}^{{\mathrm{T}}}, {\boldsymbol{v}}_{2}^{{\mathrm{T}}}, {\boldsymbol{v}}_{3}^{{\mathrm{T}}}\end{array}\right]^{\mathrm{T}},\\{\boldsymbol{J}}_{{\mathrm{b}}} = \left[\begin{array}{cccccc}{\boldsymbol{v}}_{1}^{{\mathrm{T}}}& -{\boldsymbol{v}}_{1}^{{\mathrm{T}}}& {\boldsymbol{0}}& {\boldsymbol{0}}& {\boldsymbol{0}}& {\boldsymbol{0}}\\ {\boldsymbol{0}}& {\boldsymbol{0}}& {\boldsymbol{v}}_{2}^{{\mathrm{T}}}& -{\boldsymbol{v}}_{2}^{{\mathrm{T}}}& {\boldsymbol{0}}& {\boldsymbol{0}}\\ {\boldsymbol{0}}& {\boldsymbol{0}}& {\boldsymbol{0}}& {\boldsymbol{0}}& {\boldsymbol{v}}_{3}^{{\mathrm{T}}}& -{\boldsymbol{v}}_{3}^{{\mathrm{T}}}\end{array}\right] ,\\\Delta \boldsymbol{V}=\left[\begin{array}{l}\Delta {\boldsymbol{A}}_{1}^{m},\; \Delta {\boldsymbol{B}}_{1},\; \Delta {\boldsymbol{A}}_{2}^{m},\; \Delta {\boldsymbol{B}}_{2},\; \Delta {\boldsymbol{A}}_{3}^{m},\; \Delta {\boldsymbol{B}}_{3}\end{array}\right]^{\mathrm{T}}.\end{array} \right\}$

式中：$\Delta {{{\boldsymbol{l}}}}_a =\left[ \left| \overrightarrow{{{B}}_{{1}}{{A}}_{{1}}} \right|, \left| \overrightarrow{{{B}}_{{2}}{{A}}_{{2}}} \right| ,\; \left| \overrightarrow{{{B}}_{{3}}{{A}}_{{3}}} \right|\right]^{\mathrm{T}}$，$ {\boldsymbol{v}}_{i} $为$ \overrightarrow{{{B}}_{{i}}{{A}}_{{i}}} $的单位向量；上标$ m $为以执行器中心点$ {{O}{'}} $为中心的浮动坐标系中的坐标值，其余默认为以$ {O} $为中心的固定坐标系中的坐标值；上标T表示求转置矩阵.

根据设计经验对初始的设计尺寸进行假设，具体如下：固定平台半径$ {r}_{{\mathrm{c}}} $为90 cm，移动平台半径$ {r}_{\mathrm{a}} $为65 cm，主动臂长度$ {l}_{{\mathrm{c}}} $为125 cm，从动臂长度$ {{l}}_{\mathrm{a}} $为150 cm. 所有长度相关独立误差源的公差为0.1 mm，所有角度相关独立误差源的公差为0.001 rad.

打印任务流程大致可以分为执行器复位、执行调平程序和执行打印程序3大子任务. 分析打印任务的特点与分域映射的结果可知，$ {R}_{\mathrm{\Delta }{{ {\boldsymbol{Z}}}}} $与$ {R}_{{D}_{\max}} $重合，该部分为设计的最大可打印范围. $ {R}_{k} $与$ {R}_{{F}_{\max}} $重合，且其与$ {R}_{\mathrm{\Delta }{{{\boldsymbol{ Z}}}}} $或$ {R}_{{D}_{\max}} $的并集为整个工作空间，该部分为喷头快速移动的空间. 将整个执行器工作空间拆分成2个子区域，分别为快速移动区域$ {R}_{\mathrm{m}\mathrm{o}\mathrm{v}\mathrm{e}} $和精密打印区域$ {R}_{{\mathrm{print}}} $. 根据式（18）可知，并联机器人的灵巧性能优化模型可以改写为

(30)$ \left.\begin{array}{l}\mathrm{F}\mathrm{i}\mathrm{n}\mathrm{d}\;\boldsymbol{X}=\left[ \begin{array}{cc}\begin{array}{cc}{r}_{{\mathrm{c}}},& {r}_{{\mathrm{a}}},\end{array}& \begin{array}{cc}{l}_{{\mathrm{c}}},& {l}_{{\mathrm{a}}}\end{array}\end{array} \right]\in {{\bf{R}}}^{4},\\ \mathrm{m}\mathrm{i}\mathrm{n}\;f\left(\boldsymbol{X}\right) = \left\{\begin{array}{l}\mathrm{m}\mathrm{i}\mathrm{n}\left[\begin{array}{cc}\left\| {\mathrm{\Delta }\boldsymbol{Z}\left(\boldsymbol{\lambda }\right)} \right\|\;\; {D}_{\max}\left(\boldsymbol{\lambda }\right)\end{array}\right]\;{\mathrm{in}}\;{R}_{{\mathrm{print}}},\\ \mathrm{min}\left[\begin{array}{cc}k\left(\boldsymbol{\lambda }\right)\;\; {-F}_{\max}\left(\boldsymbol{\lambda }\right)\end{array}\right]\;{\mathrm{in}}\;{R}_{{\mathrm{move}}};\end{array}\right.\\ {\mathrm{s.t.}}\;\;\left[\mathrm{75,55,115,140}\right]\leqslant \boldsymbol{X}\leqslant \left[\mathrm{105,75,135,160}\right].\end{array}\right\} $

如表1所示为经过多靶分域尺寸优化后得到的Pareto最优解集，即并联机器人候选的最优设计参数及相应的适应度函数值. 在考虑不同优化目标对设计参数的敏感性后，选取第5组候选尺寸参数作为最终灵巧性能的降敏设计结果.

为了体现所提多靶分域尺寸优化相比其他经典优化算法的效果，选用粒子群优化(particle swarm optimization, PSO)算法对单一优化目标$ \mathrm{\Delta }{{\boldsymbol Z}} $进行优化，选用改进多目标遗传算法(nondominated sorting genetic algorithm-II, NSGA-II)对所有优化目标$ \mathrm{\Delta }{{\boldsymbol Z}} $、$ k $、$ {F}_{\max} $和$ {D}_{\max} $进行优化，结果如表2所示. 结果表明，相较于原始的设计变量，PSO方法能够在单一优化目标上取得最好的适应度结果，精度提高了3.78%，但是对灵巧性能造成了23.73%的极大负面影响. NSGA-II方法虽然对多种性能指标都有小幅度的优化，但由于未将特定任务域与目标进行关联，优化效果不明显. 利用多靶分域优化方法，能够较明显地提升多种性能指标，其中刚度性能的优化效果最明显，提升幅度达到了24.05%.

根据式(11)~(14)，可以得到并联机器人的概率误差模型. 分析图1所示并联机器人结构的不确定性误差来源，将其区分为17个独立误差源，分别为3个驱动杆的长度误差$ {\Delta l}_{{\mathrm{c}}} $、3个从动杆的长度误差$ {\Delta l}_{{\mathrm{a}}} $、3个驱动角度的误差$ \Delta q $、3个固定平台与驱动杆的连接铰点误差$ {\Delta \theta }_{{\mathrm{c}}} $、3个执行器与从动杆的连接铰点误差$ {\Delta \theta }_{{\mathrm{a}}} $、固定平台半径误差$ {\Delta r}_{{\mathrm{c}}} $及执行器半径误差$ {\Delta r}_{{\mathrm{a}}} $.

该并联机器人共具有17个独立误差源，将各个独立误差源分别进行编号，分别为：[$ {\Delta l}_{{\mathrm{a}}1},{\Delta l}_{{\mathrm{a}}2}, $${\Delta l}_{{\mathrm{a}}3},{\Delta l}_{{\mathrm{c}}1},{\Delta l}_{{\mathrm{c}}2},{\Delta l}_{{\mathrm{c}}3},\Delta {q}_{1},\Delta {q}_{2},\Delta {q}_{3},{\Delta \theta }_{{\mathrm{a}}1}, {\Delta \theta }_{{\mathrm{a}}2},{\Delta \theta }_{{\mathrm{a}}3},{\Delta \theta }_{{\mathrm{c}}1} $, $ {\Delta \theta }_{{\mathrm{c}}2},{\Delta \theta }_{{\mathrm{c}}3},{\Delta r}_{{\mathrm{a}}},{\Delta r}_{{\mathrm{c}}} $].

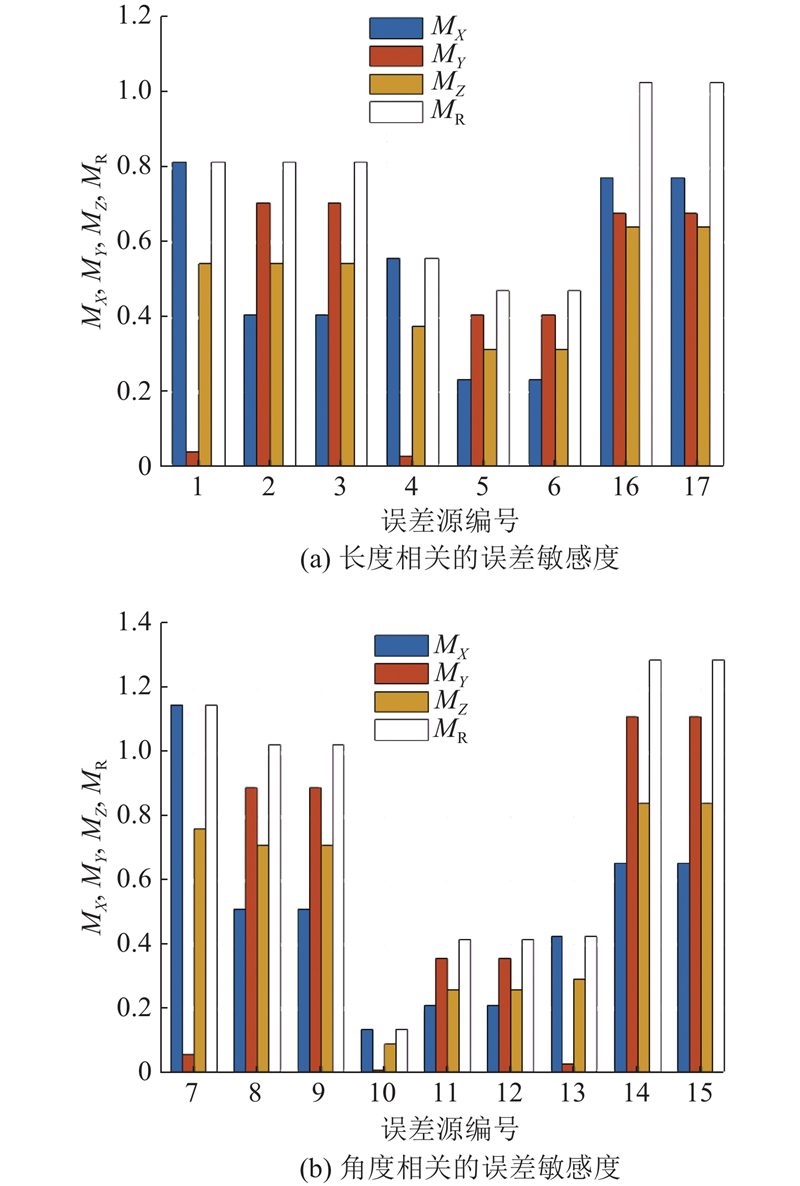
根据式（17）计算获得17个独立误差源在X、Y、Z 3个方向上的输出误差以及合成误差的误差敏感度M_X、M_Y、M_Z、M_R，按照长度相关或角度相关进行区分，结果如图2所示.

结果表明，不同的独立误差源对输出误差的影响差异很大. Delta机器人各驱动分支在设计上为严格空间对称分布，且驱动分支1布置在X轴上，因此驱动分支2和驱动分支3的误差源对输出误差的影响基本相同. 在实际中，由于受到装配误差的影响，各驱动分支不满足严格的对称条件，存在较小的差异. 对于X方向的误差敏感度，驱动分支1的影响较强. 驱动分支2和驱动分支3对Y方向输出误差的影响更大.

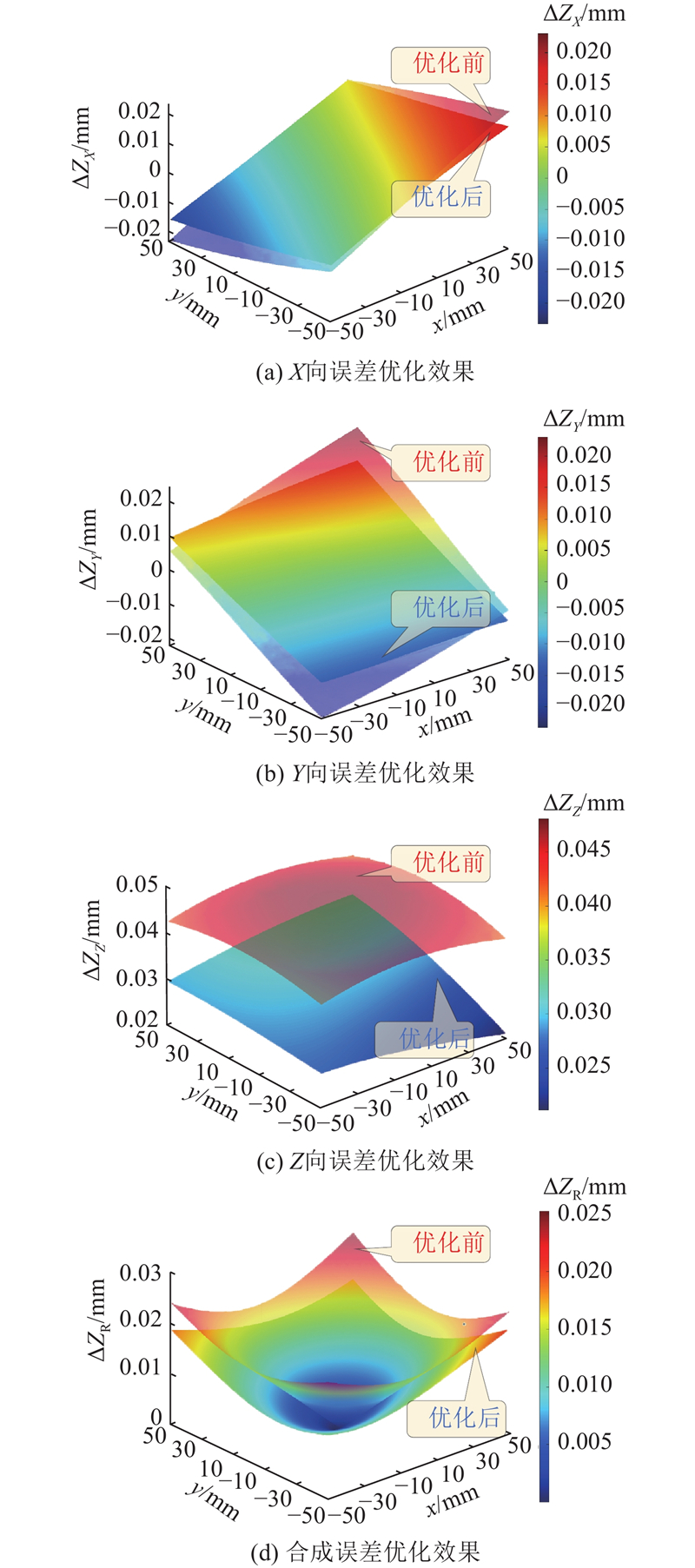
在获得机器人的误差敏感度后，可以通过将误差敏感度作为设计公差的分配权重，对机器人进行定位性能的降敏设计. 如图3所示为权重分配后的执行器误差分布图. 其中，$\Delta {{Z}_{X}} 、\Delta {{Z}_{Y}} 、\Delta {{Z}_{Z}} 、\Delta {{Z}_{{\mathrm{R}}}} $分别为X、Y、Z向误差及合成误差. 对于需要重点关注的合成误差，在原邻域内的最大值为0.025 2 mm，经过公差优化分配后最大值为0.020 9 mm，最大误差的抑制幅度达到17.06%.

将各个与误差敏感度关联较高的误差源设置更高的设计公差等级，将与误差敏感度关联较低的误差源设置更低的设计公差等级，从而在相同或更低的总成本下获得具有更高精度的支链驱动装备，结果如表3所示.

为了进一步增强并联机器人在服役过程中的可靠性，提高使用寿命，可以通过在役演化模型寻找最优维保策略，从而提高并联机器人的在役精度. 为了体现不确定性参数动态分量$ {{\boldsymbol{\xi}} }_{{\mathrm{d}}} $随着时间精度不断退化的过程，采用非线性Wiener过程来表征各个独立误差源的精度退化过程. 通过非线性Wiener过程描述精度退化的一般形式为

(31)$ {\xi }_{{\mathrm{d}}k}\left({\mathrm{NL}}\left(t\right)\right)=\mu_k {\mathrm{NL}}\left(t\right)+\sigma_k B\left({\mathrm{NL}}\left(t\right)\right). $

式中：$ \mu _k$为第k个误差源Wiener过程的漂移系数，$ \sigma _k$为第k个误差源Wiener过程的扩散系数，$ B $为标准的布朗运动过程，$ {\mathrm{NL}}\left(t\right) $为关于时间$ t $的非线性映射.

对误差源精度退化模型与在役精度性能敏感性模型的关键参数进行合理设定，如表4所示.

将表4的设定参数代入式(28)，可得维保收益为

(32)$ {C}_{{\mathrm{e}}}=\frac{{\displaystyle\sum_{i=1}^{{N}_{{\mathrm{m}}}}}T\left({e}_{\varepsilon },{\mu }_{i}\right)-0.5{N}_{{\mathrm{m}}}}{1\;200{N}_{{\mathrm{m}}}+5\;000}. $

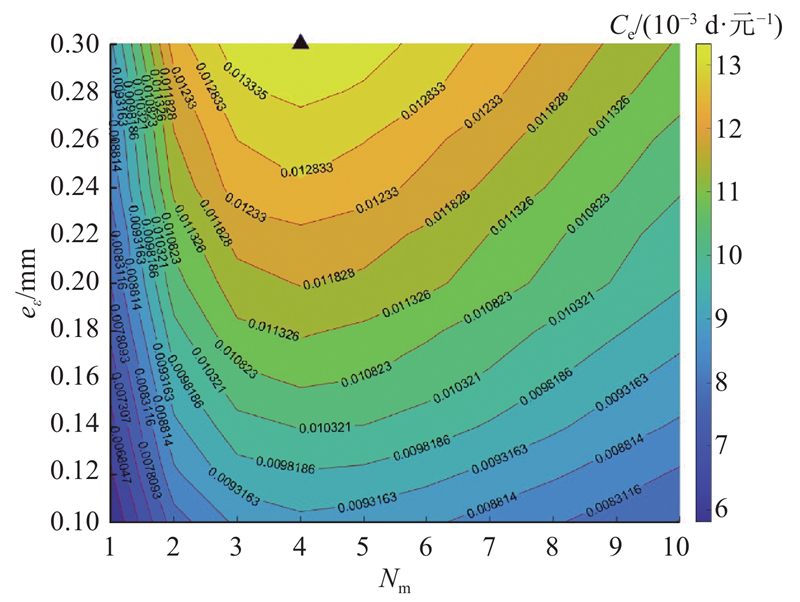
由于多次预防性维保无法完全逆转零件内部的老化过程，在经过设定的预防性维保上限次数后，机器人下一次将执行故障更换性维保. 利用式(32)可以得到Delta并联机器人的维保收益分布图，结果如图4所示. 可以看出，随着预防性维保上限次数$ {N}_{\mathrm{m}} $的增加，维保收益先增大后减小. 这是由于$ {N}_{\mathrm{m}} $过小将导致机器人快速进入故障更换性维保阶段，而成本远高于预防性维保. 当$ {N}_{{\mathrm{m}}} $过大时，由于零件内部的衰退已经到达较高的水平，后期的维保将快速失效，从而使得维保收益逐渐降低. 当设定$ {N}_{{\mathrm{m}}}=4,{e}_{\varepsilon }=0.3\;\mathrm{m}\mathrm{m} $时，本案例中的Delta并联机器人将拥有最高的维保收益，为0.013 8 d/元（图4中的黑色三角标记处）.

设定总体维保成本上限为15 000元，维保阈值为0.3 mm，维保策略参数中$ {N}_{{\mathrm{m}}} $分别为0、2、4或8，寿命对比如表5所示. 表5中，L_R为设计使用寿命. 结果表明，在总体维保成本为15 000元的前提下，实施在役精度性能降敏设计后，并联机器人的L_R可以延长2 016 d，且在同等维保成本下相较于普通维保方法（$ {N}_{{\mathrm{m}}} $=0）使用寿命的延长幅度达到104.36%，相较于采用高敏维保参数的预防性维保方法（$ {N}_{{\mathrm{m}}} $为2或8）使用寿命的延长幅度分别为12.82%和57.76%.

以面向高流速的止回阀阀体的增材制造为例，一般要求制造误差小于0.1 mm，以保证流型表面的精度. 并联机器人的结构设计决定了执行器的运动自由度，本文所研究的Delta型并联结构拥有空间三维平移自由度，可以实现增材制造所需的运动功能. 对于面向增材制造的并联机器人，主要关注执行器沿着所制造零件层切面轮廓上的运动精度，如图5（d）所示. 对于该止回阀阀体零件，在层切面轮廓上的最大合成误差出现在原理制造平台中心的轮廓边缘处，为0.023 2 mm，优化后的执行器误差满足设计精度的要求. 如图5（f）所示为增材制造并联机器人打印的止回阀阀体零件.

(1) 提出设计参数由尺寸参数与不确定性参数组成. 将不确定性参数区分为静态不确定性参数与动态不确定性参数，为后续降敏设计方法的研究和设计参数的对象分析奠定理论基础.

(2) 提出多靶拆分与分域映射技术，提高映射与变异改进的元启发式优化算法对复杂工作任务流程的适应性，实现机器人灵巧性能的降敏设计.

(3) 提出设计公差优化分配方法，实现机器人定位性能的降敏设计. 提出预防性维保策略调优方法，实现机器人在役精度性能的降敏设计. 以用于增材制造的并联机器人结构为例，说明降敏设计方法的实施流程.

未来将致力于将降敏设计方法推广到更多的场景，结合多传感器和通信技术进行动态维保策略的调整，实现机器人系统的高性能定制化设计.