经典控制理论为系统建模与分析提供了基础[4],使得以PID为代表的线性控制策略被广泛应用于各类电液伺服位置控制系统中[5-7]. 随着现代控制理论的发展,电液伺服系统的状态空间模型和非线性控制方法的研究取得显著进展[8],以反步法为基础的自适应控制[9]、鲁棒控制[10-11]策略被相继提出. PID控制策略虽然能够实现高精度的静态稳定控制,但动态响应能力有限;控制策略(如鲁棒自适应)虽然能够提高系统响应能力,但存在参数调节困难、依赖模型的缺陷. 在此背景下,韩京清[12]提出自抗扰控制(active disturbance rejection control, ADRC)策略,Gao[13]改进ADRC,发展出兼具调节参数少、鲁棒性强、控制精度高、不依赖模型等优点的线性自抗扰控制(linear active disturbance rejection control LADRC),为控制系统设计提供了新的方法.
1. 电液伺服系统线性自抗扰控制模型
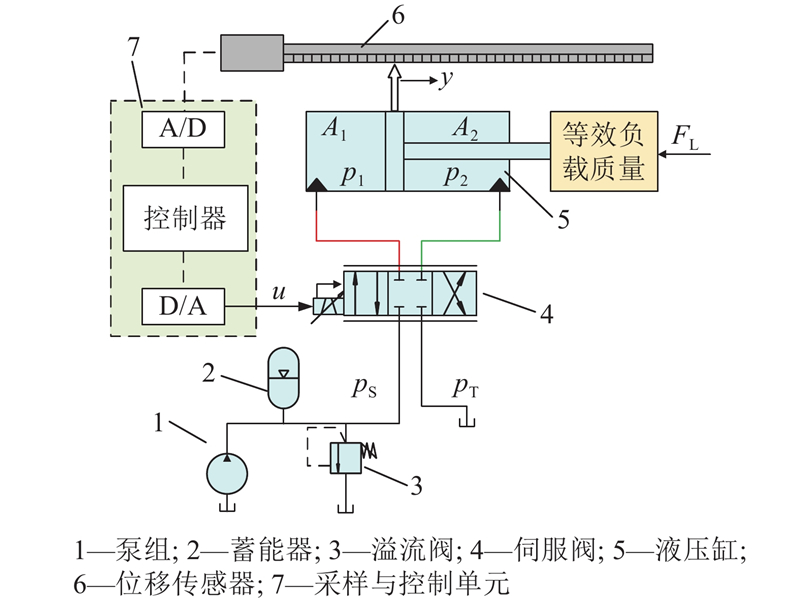
1.1. 阀控缸系统模型
图 1
式中:
式中:
式中:
1.2. 线性自抗扰控制器模型
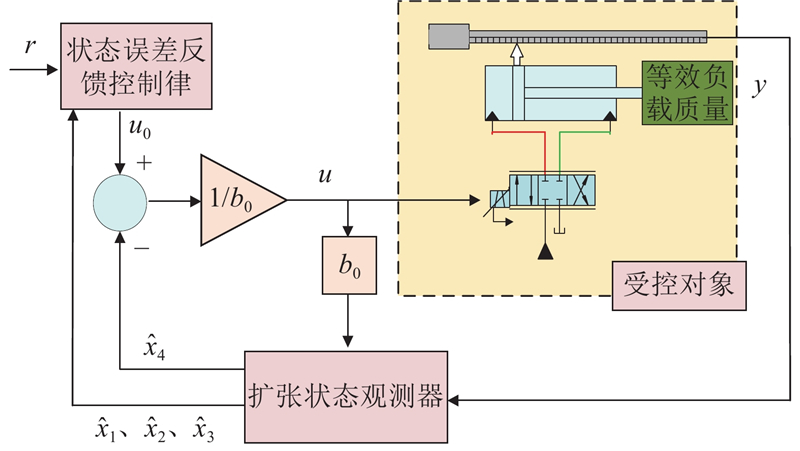
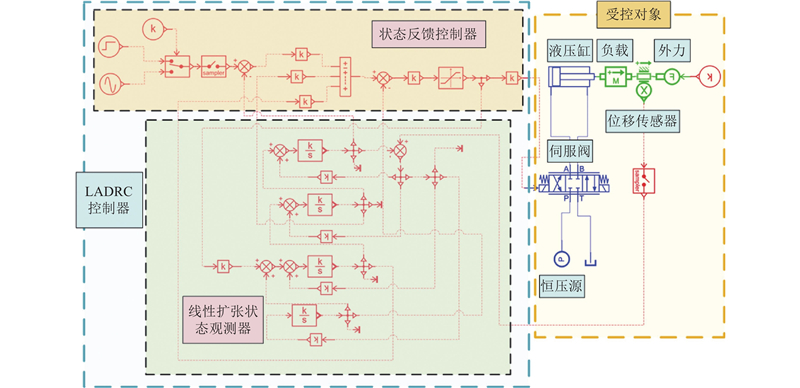
电液伺服系统线性自抗扰控制器结构如图2所示,
图 2
图 2 电液伺服系统线性自抗扰控制器结构
Fig.2 Structure of linear active disturbance rejection controller for electro-hydraulic servo system
式中:
对应线性扩张状态观测器(linear extended state observer,LESO)的形式为
式中:
式中:
LADRC的设计范式在理论上表明,提高控制器和观测器的带宽即可任意提升系统的动态响应能力,而名义控制增益
2. 系统频域分析
线性自抗扰控制器的结构不含非线性项,能够借助频域等效方法深入分析控制器特性. 联立式(6)、(7),求解控制器输出
对式(9)进行拉式变换,得到控制器输出
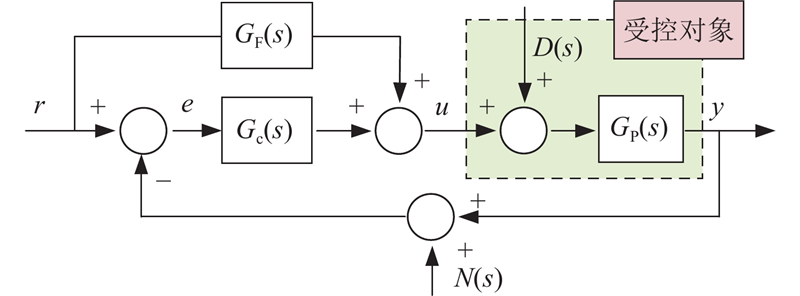
由式(1)、(11)将电液伺服线性自抗扰控制系统等效为如图3所示的频域模型,其中
图 3
图 3 线性自抗扰控制的控制框图
Fig.3 Control block diagram of linear active disturbance rejection control
则串联环节传递函数的表达式为
根据LADRC控制设计流程,
2.1. 串联校正环节频域特性
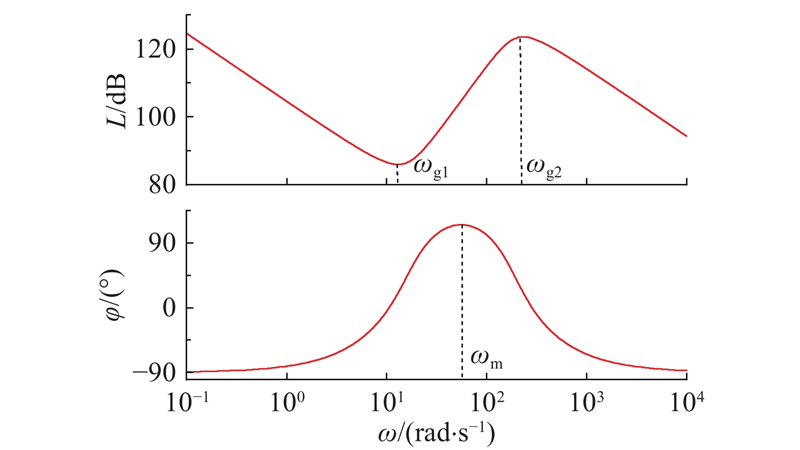
如图4所示为串联环节
图 4
式(15)中,零极点的解析解形式复杂,不便进行频域特性分析,由于系统的零点位置与极点位置分布集中,通过韦达定理求解拐点频率ωg1、ωg2以及相位峰值频率
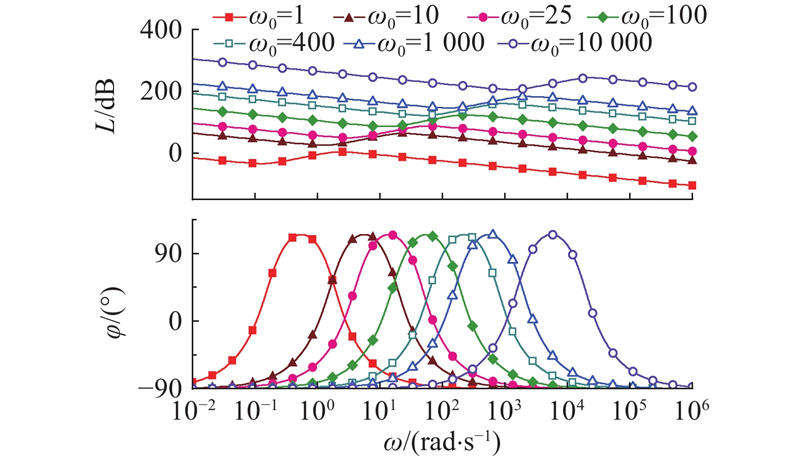
分别改变线性自抗扰控制器参数
图 5
图 5 观测器带宽对串联校正环节频域特性的影响
Fig.5 Effect of observer bandwidth on frequency-domain characteristics of cascade compensator
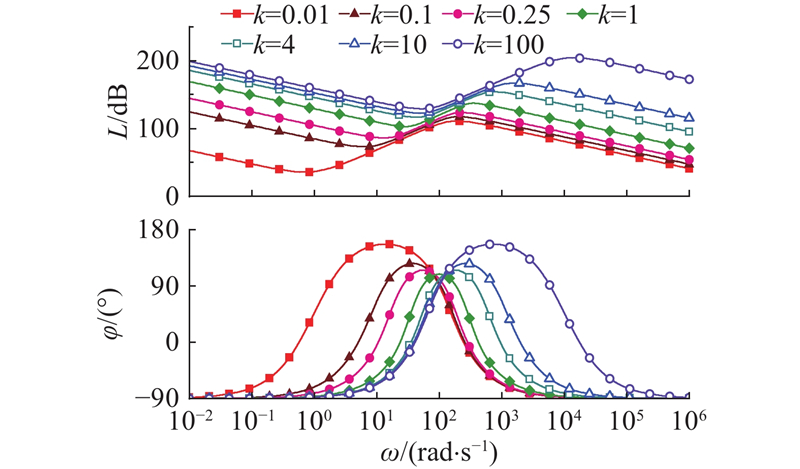
图 6
图 6 带宽系数对串联校正环节频域特性的影响
Fig.6 Effect of bandwidth factor on frequency-domain characteristics of cascade compensator
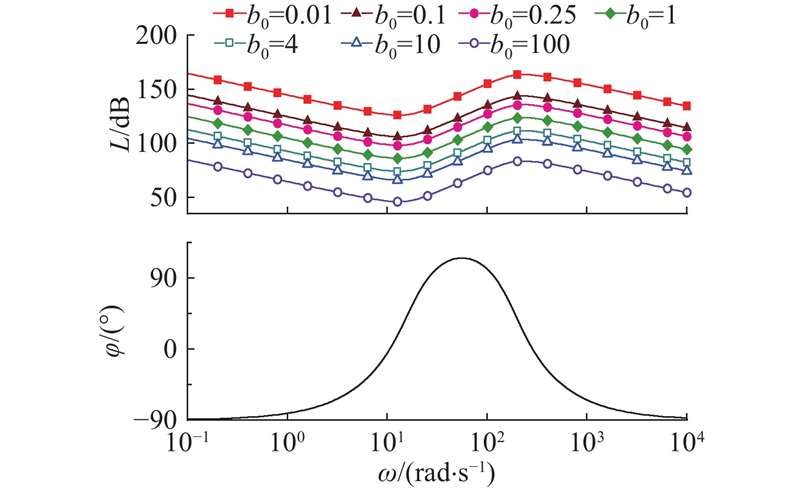
图 7
图 7 名义控制增益对串联校正环节频域特性的影响
Fig.7 Effect of nominal control gain on frequency-domain characteristics of cascade compensator
2.2. 闭环系统频域特性
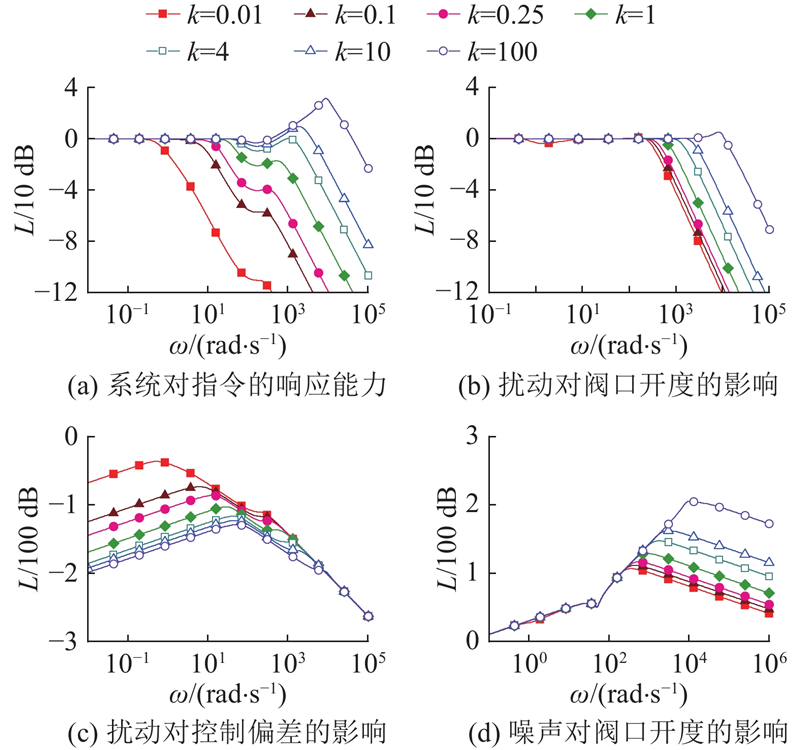
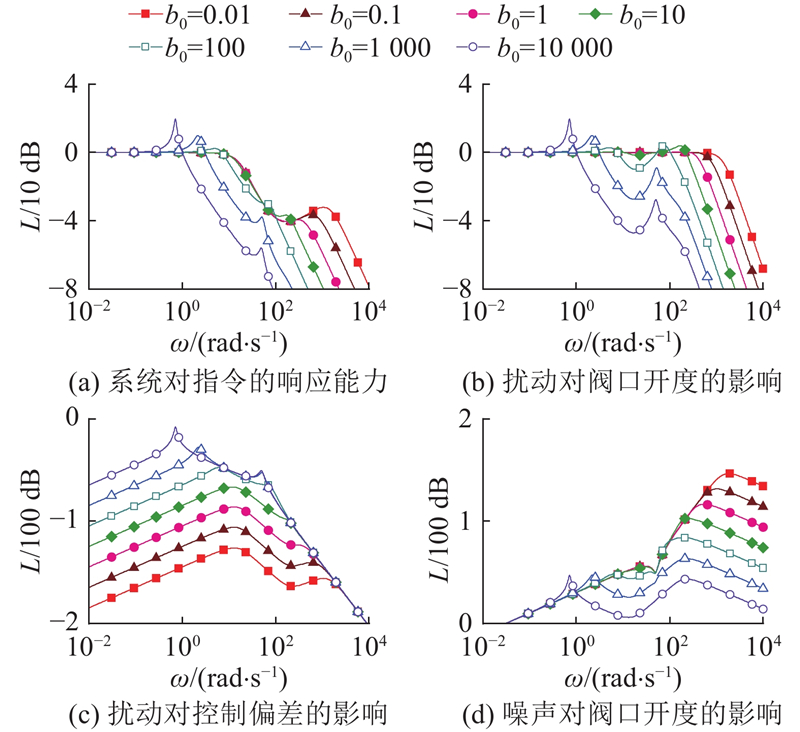
电液伺服系统对指令的响应能力、抗扰特性和抗噪特性是衡量LADRC性能的重要指标,研究LADRC各参数对闭环系统性能的影响规律能够为控制器参数设计提供有效指导. 单独调节
图 8
图 8 观测器带宽对闭环性能的影响
Fig.8 Effect of observer bandwidth on closed-loop performance
图 9
图 10
图 10 名义控制增益对闭环性能的影响
Fig.10 Effect of nominal control gain on closed-loop performance
2.3. 线性自抗扰控制的参数匹配设计
根据式(8),控制器带宽
2.3.1. 相位峰值频率大于液压固有频率
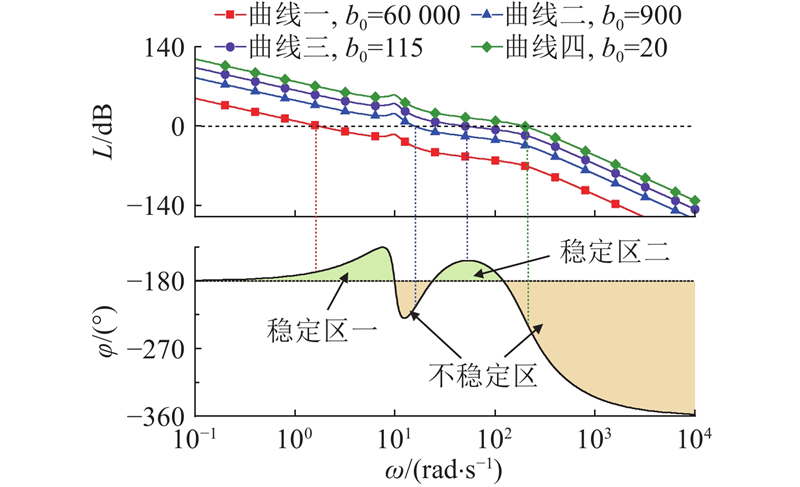
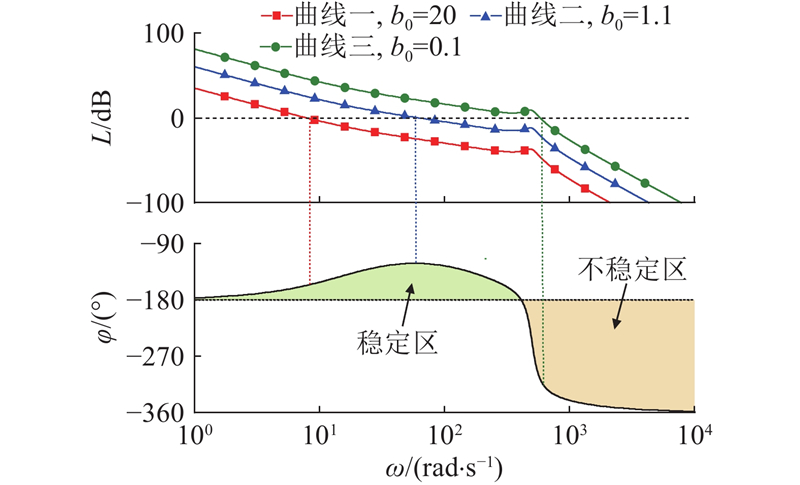
当
图 11
图 11 开环伯德图(相位峰值频率远大于液压固有频率)
Fig.11 Open-loop Bode plot with phase peak frequency much larger than hydraulic natural frequency
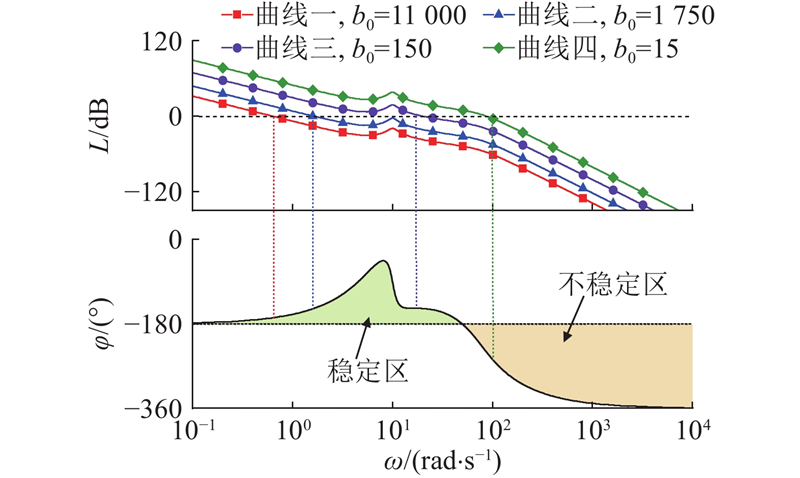
如图12所示,当
图 12
图 12 开环伯德图(相位峰值频率略大于液压固有频率)
Fig.12 Open-loop Bode plot with phase peak frequency silght larger than hydraulic natural frequency
矫正环节
为了实现开环传递函数在
2.3.2. 相位峰值频率小于液压固有频率
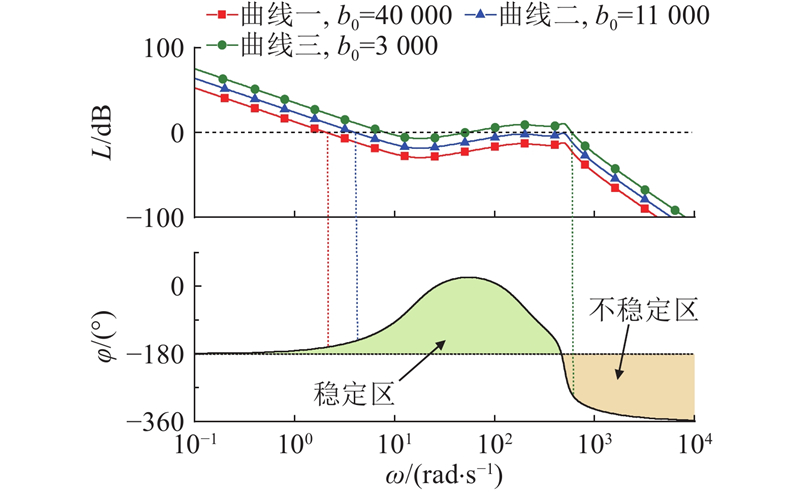
当
图 13
图 13 开环伯德图(相位峰值频率小于液压固有频率)
Fig.13 Open-loop Bode plot with phase peak frequency smaller than hydraulic natural frequency
串联环节
为了实现开环传递函数在
由于开环传递函数的幅频曲线在拐点频率之间具有正的斜率,幅频曲线无法在拐点频率之间完成负穿越,电液伺服系统的相位稳定裕度受到限制,三阶LADRC在此工况下难以有效改善电液伺服系统的动态性能. 降低LADRC控制器的阶数,使拐点频率之间具有负的斜率,能够提高系统的相位裕度,改善系统性能,一阶LADRC控制器结构为
一阶LADRC等效串联环节的拐点频率和相位峰值频率可以直接求解计算:
采用一阶LADRC控制器的电液伺服系统开环传递的伯德图如图14所示. 调节一阶LADRC的名义控制增益
图 14
图 14 一阶线性自抗扰控制系统开环伯德图
Fig.14 Open-loop Bode plot of first-order linear active disturbance rejection control system
3. 仿真与实验
液压固有频率的大小与系统的负载质量密切相关. 对于重载系统,液压固有频率通常低于所设计的相位峰值频率;对于小负载系统,液压固有频率较高,若设计的相位峰值频率过大,可能会激发噪声干扰,为此将相位峰值频率设计为低于液压固有频率. 开展仿真与实验研究,验证本研究理论分析结果与LADRC参数设计方法.
3.1. 仿真验证
搭建Amesim仿真模型如图15所示,对不同液压固有频率下LADRC的参数设计方法进行验证.
图 15
3.1.1. 小液压固有频率工况仿真
在小液压固有频率工况下的系统主要参数如表1工况一所示. 表中, D1为液压缸缸径,D2为液压缸杆径,l为液压缸行程. 工况一的系统液压固有频率约为15 rad/s,采样与控制周期为1 ms. 根据期望闭环性能设计
表 1 液压系统参数
Tab.1
| 工况 | m/ kg | D1/ mm | D2/ mm | l/ mm | Qch/ (L·min−1) | Δpch/ MPa | ps/ MPa |
| 一 | 200 | 120 | 100 | 0.5 | 25 | ||
| 二 | 350 | 100 | 50 | 280 | 200 | 0.5 | 2.5 |
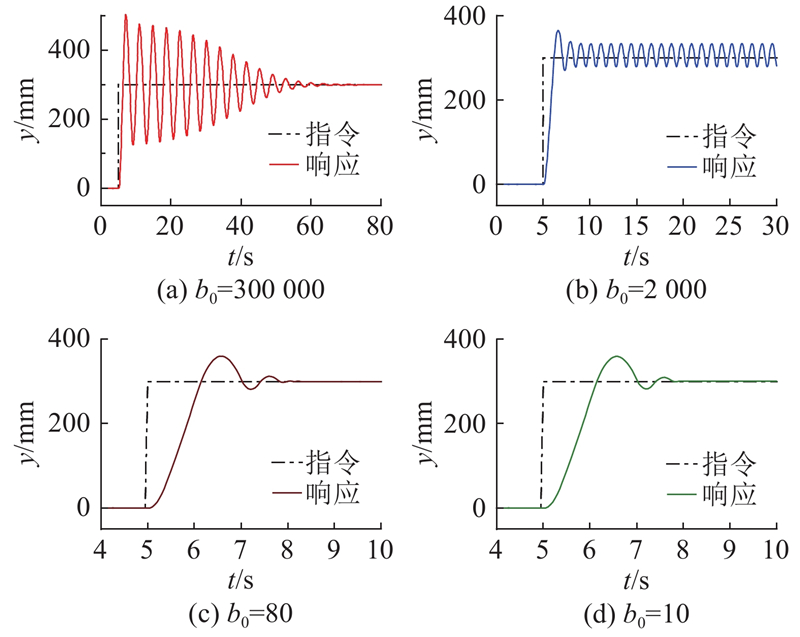
图 16
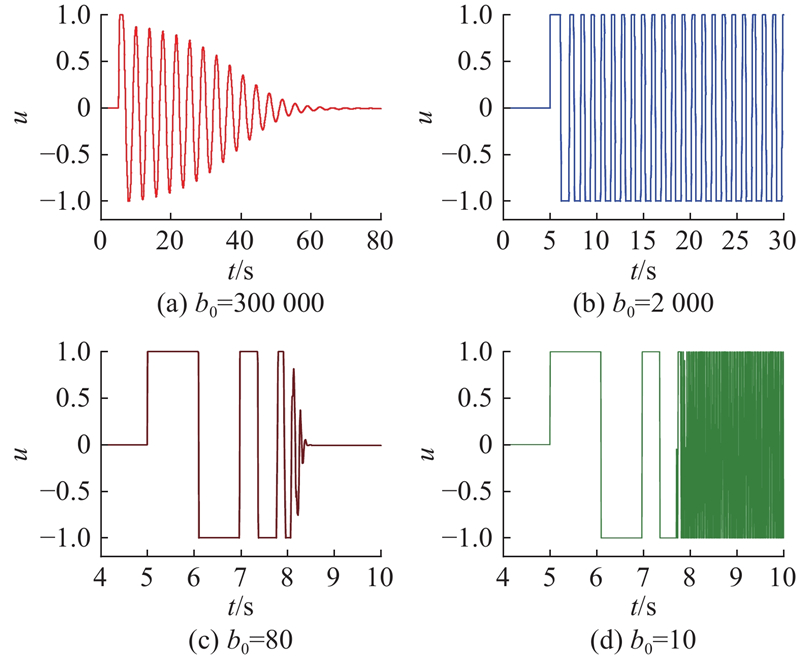
图 16 不同名义控制增益情况下的阶跃响应仿真
Fig.16 Simulation of step response for different nominal control gain cases
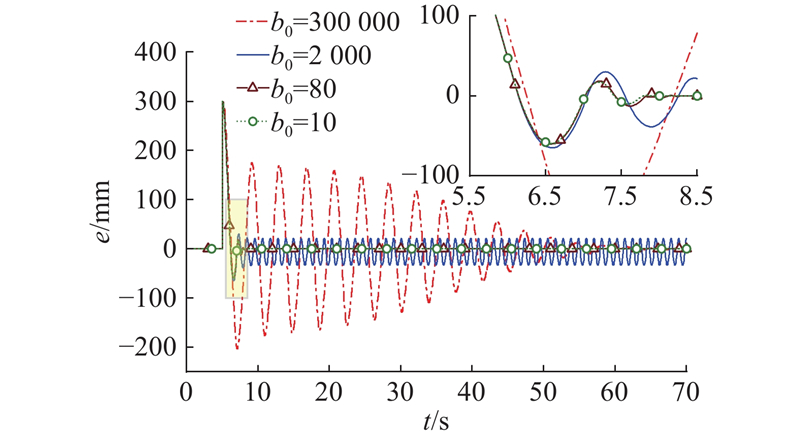
图 17
图 17 不同名义控制增益情况下的阶跃响应误差仿真
Fig.17 Simulation of step response error for different nominal control gain cases
图 18
图 18 不同名义控制增益情况下的阶跃响应阀口开度仿真
Fig.18 Simulation of spool opening for step response in different nominal control gain cases
图 19
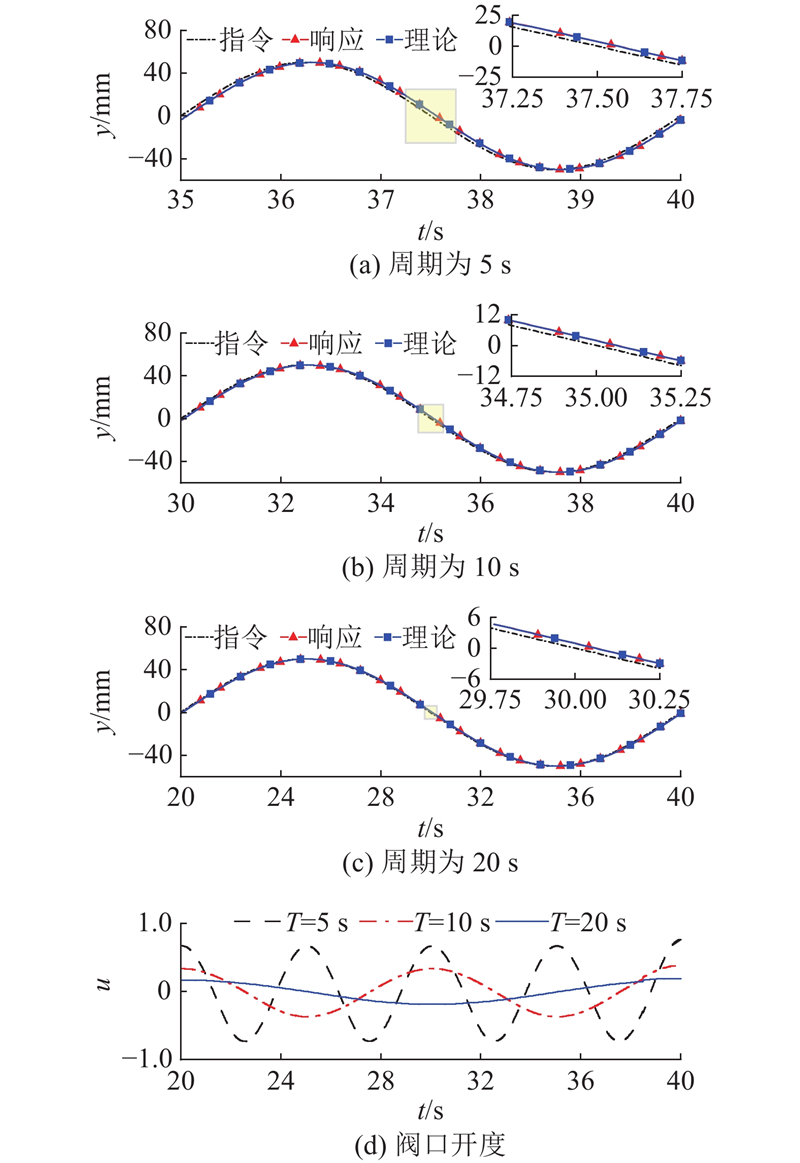
图 19 不同指令信号周期条件下的正弦响应与阀口开度仿真
Fig.19 Simulation of sinusoidal response and spool opening for different command signal period cases
图 20
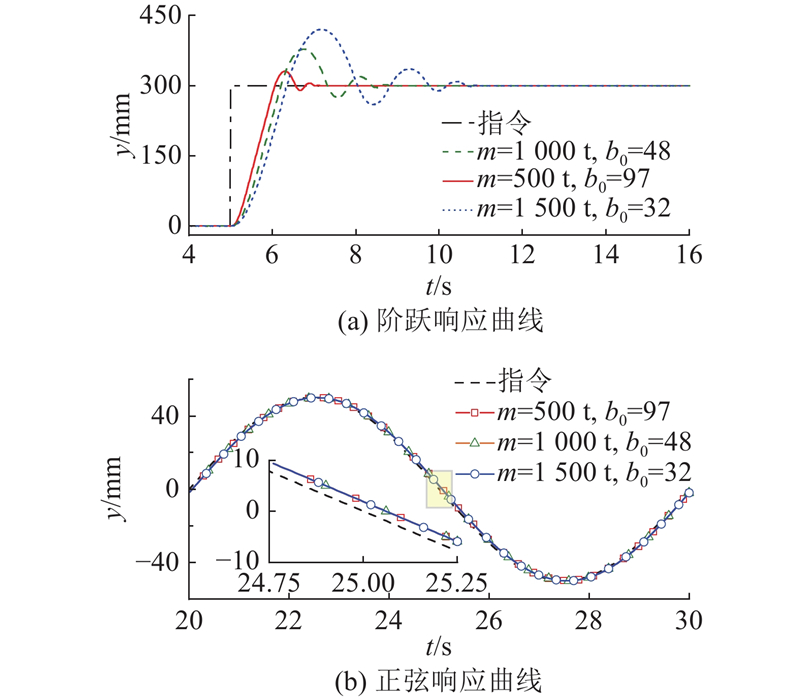
图 20 不同负载质量条件下的阶跃与正弦响应仿真
Fig.20 Simulation of step and sinusoidal response for different mass cases
3.1.2. 大液压固有频率工况仿真
大液压固有频率工况下系统主要参数如表1中工况二所示. 其中液压固有频率约为470 rad/s,根据期望闭环性能设计
图 21
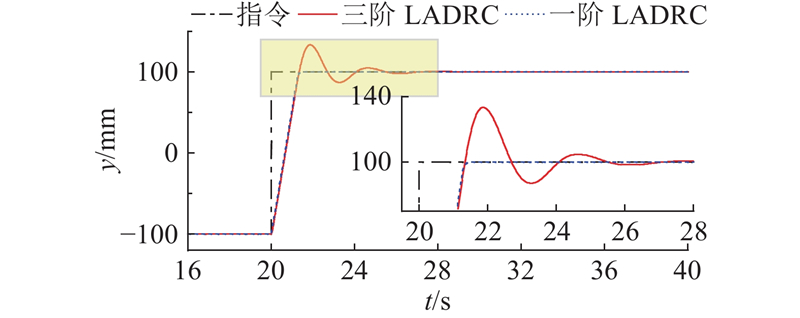
图 21 一阶与三阶线性自抗扰控制的阶跃响应对比仿真
Fig.21 Comparative simulation of step responses for first-order and third-order linear active disturbance rejection control
图 22
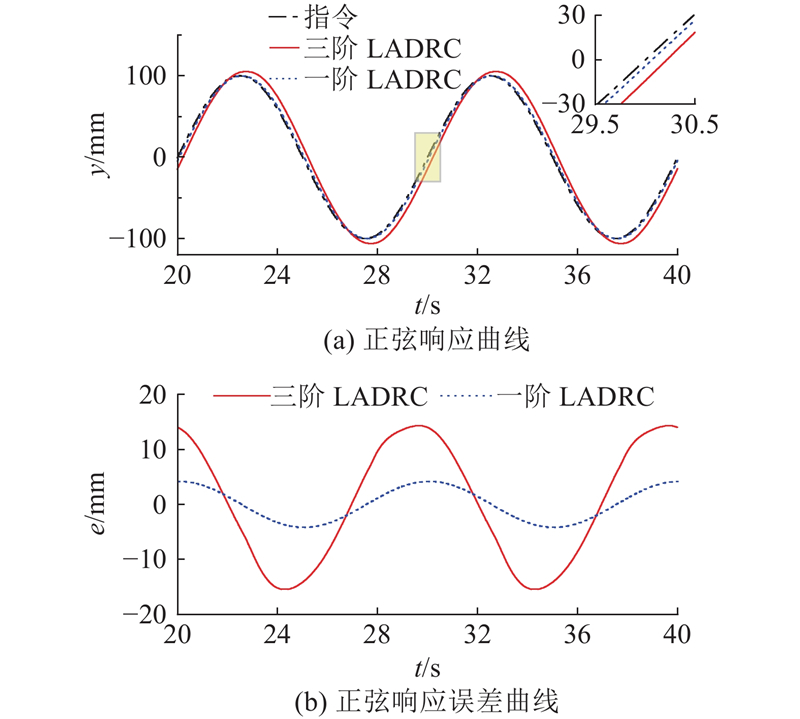
图 22 一阶与三阶线性自抗扰控制的正弦响应对比仿真
Fig.22 Comparative simulation of sinusoidal responses for first-order and third-order linear active disturbance rejection control
3.2. 实验验证
图 23
为了对比验证三阶及一阶LADRC对大液压固有频率系统的控制性能,设计
图 24
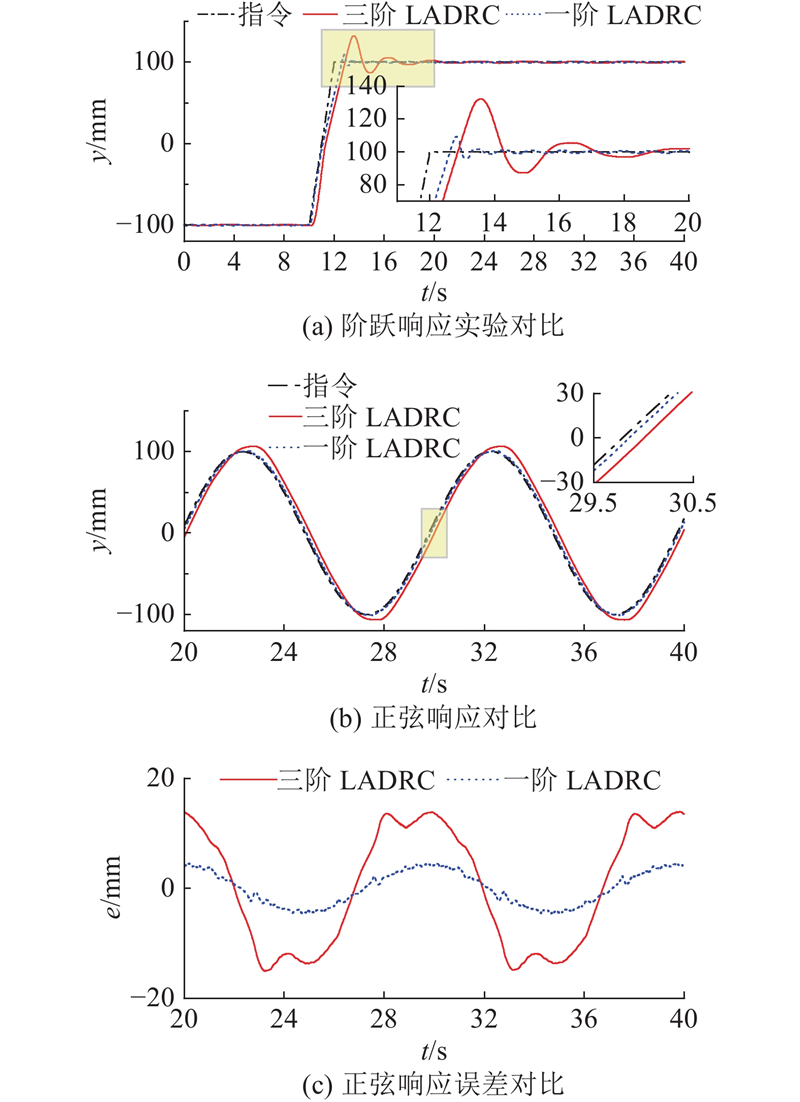
图 24 一阶与三阶线性自抗扰控制的跟踪响应对比实验
Fig.24 Experimental comparison of first-order and third-order linear active disturbance rejection control tracking responses
4. 结 语
本研究1)针对电液伺服系统LADRC参数难以整定的问题,推导线性自抗扰控制器的频域等效模型,从频域角度分析LADRC对电液伺服系统的校正机理. 2)分析LADRC参数对电液伺服系统闭环性能的影响,增大观测器带宽、增大带宽系数或减小名义控制增益会不同程度地提高系统对指令信号的响应能力和抗干扰能力,但会增加噪声对控制性能的影响,提高对伺服阀调节能力和响应速度的需求. 3)讨论不同液压固有频率下LADRC参数的匹配设计方法,仿真与实验结果表明,本研究提出的LADRC参数匹配设计方法能有效确保闭环系统的稳定性. 在液压固有频率较低的工况下,三阶LADRC控制能够有效改善液压系统响应性能. 在液压固有频率较高的工况下,一阶LADRC比三阶LADRC的控制性能更优. 本研究仅针对LADRC等效串联校正环节分析液压系统闭环性能和稳定性,未来将研究等效前馈校正环节对液压系统特性的影响,进一步指导LADRC控制器参数设计.
参考文献
Extended sliding mode observer-based robust tracking control scheme for electro-hydraulic servo systems
[J].
自抗扰控制技术
[J].
Auto disturbances rejection control technique
[J].
油液混合动力工程机械系统及控制策略研究综述
[J].
Overview of hydraulic hybrid engineering machinery system and control strategy
[J].
基于频域近似的线性系统自抗扰参数整定
[J].
盾构机液压系统研究进展综述
[J].
Review on research progress of related technologies of shield machine hydraulic system
[J].
Tuning of linear active disturbance rejection control via frequency domain approximation
[J].
飞机液压刹车系统的自激振动分析与抑制
[J].
Analysis and suppression for self-excited vibration of aircraft hydraulic braking system
[J].
阀控非对称缸频域建模
[J].DOI:10.3901/JME.2007.09.122 [本文引用: 1]
Modeling in frequency domain for valve controlled asymmetric hydraulic cylinders
[J].DOI:10.3901/JME.2007.09.122 [本文引用: 1]
阀控缸的非线性建模和分析
[J].
Valve control cylinder nonlinear modeling and analysis
[J].
On validation of extended state observer through analysis and experimentation
[J].DOI:10.1115/1.4005364 [本文引用: 1]
Research on the characteristics of electro-hydraulic position servo system of RBF neural network under fuzzy rules
[J].DOI:10.1038/s41598-024-64262-7
基于模糊PID的变幅液压控制系统
[J].
Variable amplitude hydraulic control system based on fuzzy PID
[J].
复合材料成形液压机自适应鲁棒运动控制
[J].
Adaptive robust motion control of composite material hydraulic press
[J].