在降低误差的方法中,误差补偿法具有成本较低且效率较高的特点,该方法包括4个步骤:运动学建模、参数测量、参数辨识、误差补偿.
误差参数测量为后续的误差补偿提供必要的数据. 双目视觉测量系统成本较低、可跟踪6自由度,但精度最高仅为0.1 mm,不适用于高精度场景[13]. 激光跟踪仪测量空间大,精度达10~100 μm,但成本较高[14]. 球杆仪实验成本相对较低且在精度方面可以达到1 μm[15]. Ferrarini等[16]用跟踪仪实验实现路径误差补偿. 黄鹏等[17] 提出加权点匹配法实现激光跟踪仪坐标转换. Jiang等[18]设计球杆仪“S”型轨迹简化误差辨识. 赵业和等[19]结合多种群竞争松鼠搜索算法规划最短时间轨迹. 上述研究均未考虑测量空间中定位误差的相似特性,该特性会导致运动轨迹偏差,影响测量结果准确性.
针对上述问题,本研究以六自由度工业机器人为对象开展测量轨迹规划及考虑测量不确定度的误差参数辨识研究,具体贡献如下:1) 提出空间圆弧测量轨迹与测量模型;2) 建立改进的飞蛾火焰优化逆运动学求解方法;3) 提出考虑不确定度的补偿参数量化嵌套算法.
1. 机器人运动学模型及求解
1.1. 基于POE的正向运动学模型
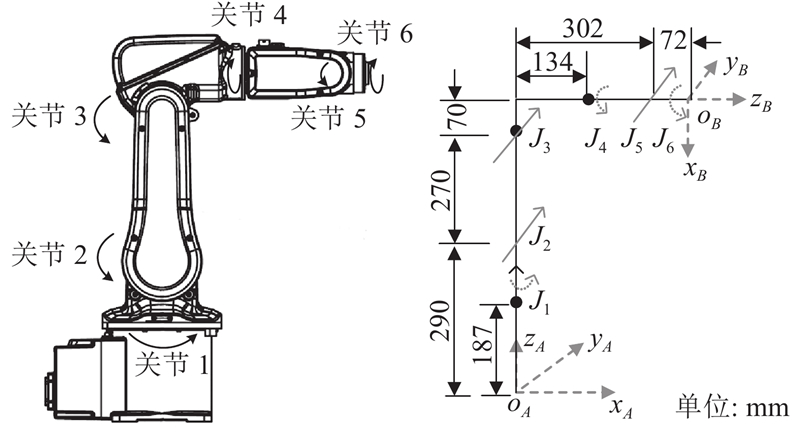
以6自由度工业机器人为研究对象,其零位构型及关节坐标系如图1所示.
图 1
基于POE模型对关节坐标系定义,z轴为关节轴线,x轴为相邻轴线公垂线,y轴依右手定则确定,原点为旋转关节中心. 图1中{A}为基础坐标系,{B}为工具坐标系,Ji (i=1,2,···,6)为旋转关节,箭头方向为旋转方向.
第i个旋转关节的关节旋量表达式如下:
式中:ωi为第i个旋转关节轴线方向的单位矢量,qi为第i个旋转关节的轴线位置矢量. 机器人正运动学使用的参数如表1所示.
表 1 机器人运动学建模使用参数
Tab.1
| i | ωi | qi |
| 1 | [0, 0, 1] | [0, 0, 187] |
| 2 | [0, 1, 0] | [0, 0, 290] |
| 3 | [0, 1, 0] | [0, 0, 560] |
| 4 | [1, 0, 0] | [134, 0, 630] |
| 5 | [0, 1, 0] | [302, 0, 630] |
| 6 | [1, 0, 0] | [374, 0, 630] |
机器人正向运动学模型表达式如下:
式中:gAB(0)为机器人初始位姿下末端工具坐标系对于基础坐标系的刚体变换矩阵,
式中:h为旋量的平移分量,当关节为旋转关节时,h=0,ωi =[ωiX, ωiY, ωiZ]T,||ωi||=1;
式(2)中的
式中:
由罗德里格斯公式可知,
式中:I为单位矩阵. 由此可得机器人运动学正解方程如下:
式中:R(θ)为机器人末端姿态矩阵,p(θ)为机器人末端位置矩阵.
将i=0代入式(7)中,即各关节变量理论值均为零时得到机器人处于零位时的刚体变换矩阵gAB(0)表达式如下:
1.2. 基于POE的运动学误差模型
表 2 误差模型参数对比
Tab.2
式中:w为平行度与垂直度误差.
表 3 误差参数影响率
Tab.3
| 误差参数 | ek/mm | eb/mm | ρ/% |
| Δωi | 0.563 | 0.552 | 1.95 |
| Δli | 0.563 | 0.395 | 29.84 |
| Δθi | 0.563 | 0.162 | 71.01 |
表 4 含有误差的机器人参数
Tab.4
| i | ||
| 1 | 187+Δl1 | 0+Δθ1 |
| 2 | 103+Δl2 | 0+Δθ2 |
| 3 | 270+Δl3 | 0+Δθ3 |
| 4 | 70+Δl4 | 0+Δθ4 |
| 5 | 134+Δl5 | 0+Δθ5 |
| 6 | 168+Δl6 | 0+Δθ6 |
在考虑误差的情况下,旋量的指数表达式如下:
由表4和式(11)可以得到基于POE模型的工业机器人误差模型:
式中:
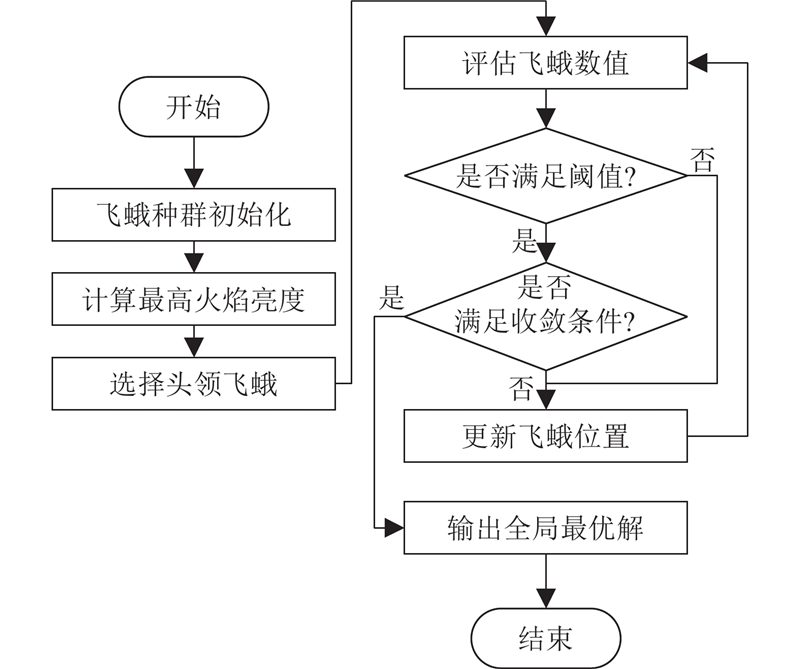
1.3. 基于MFO的运动学逆解
运动学逆解是在已知末端工具坐标系{B}相对于基础坐标系{A}的理论姿态矩阵
式中:Mi表示i个飞蛾,Fj表示第j个火焰,b为定义对数螺旋的常数,t为[−1.0, 1.0]的随机数. MFO算法的位置更新公式如下:
式中:M(i,j)为第i只飞蛾在维度j的位置,S(i,j)为适应度排序后的蛾群位置数组,参数D为第i只飞蛾在第j维度上对应火焰参数之间的绝对距离,T为位置更新随机参数. D和T的表达式分别如下:
式中:T0为[0,1.0]的随机数,A为线性递减参数.
式中:K为当前迭代次数,Kmax为最大迭代次数. 在对工业机器人进行逆解时,对已知的末端工具坐标系{B},相对于基础坐标系{A}构建期望目标矩阵
构建运动学逆解目标函数Rt,将姿态矩阵与位置矩阵进行拆分,目标函数如下:
式中:
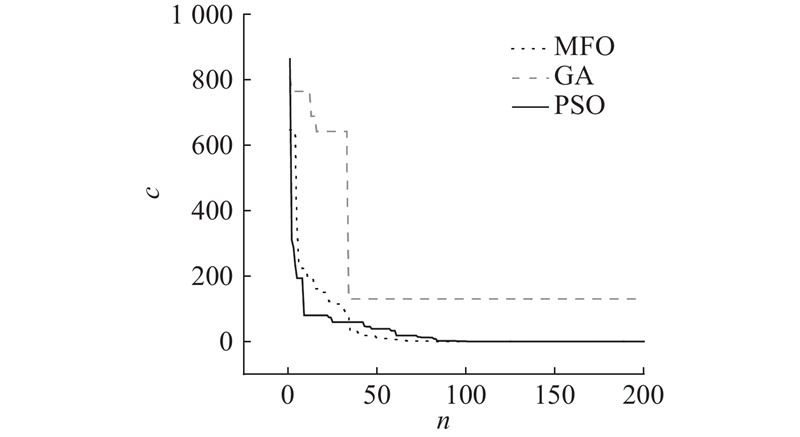
在使用MFO进行机器人逆解计算时,问题的维度为12,包含6个关节角度参数与6个连杆长度参数. 为了评估优化算法性能,对MFO算法、遗传算法(GA)和粒子群优化算法(PSO)进行比较,定义初始种群为500、最大迭代次数为200. 对比结果如图2所示. 其中,n为迭代次数,c为目标函数值. 可以看出,MFO算法在约50次迭代时达到收敛阈值,PSO需约80次,GA收敛性较弱. MFO迭代曲线平滑,较少陷入局部最优,在收敛速度和避免局部最优方面优于GA和PSO.
图 2
2. 基于球杆仪的测量轨迹设计
2.1. 变差函数表征的去冗余测量轨迹设计
通过分析机器人定位误差在笛卡尔和关节坐标空间中的空间相似性,推导测量轨迹,以降低采样点数据自相关性和样本偏差,提高样本精度. 在n自由度的机器人活动范围内,机器人定位误差的相似程度可以用变差函数表征:
式中:h为关节空间中2组关节的欧氏距离,作为关节分割量,即2组关节角度的广义距离;ΔP(θ+h)为距离坐标θ分割量为h时的定位误差.
变差函数值反映机器人定位误差空间相似度,值越小表明相似度越高. 假设在误差增量期望为0且方差平稳的条件下,变差函数值仅与关节输入增量相关. 不同关节分割量对误差相似性作用效果不同. 2组不同关节角度θ(i)与θ(j)关节分割量h表达式如下:
式中:
已知单侧测量轨迹关节输入,基于POE正运动学模型推导理论位置坐标. 给定随机误差参数
表 5 随机误差参数
Tab.5
| 1 | 0.4 365 | 0.0 007 |
| 2 | −0.4 578 | 0.0 024 |
| 3 | −0.0 429 | −0.0 044 |
| 4 | −0.0 616 | −0.0 048 |
| 5 | −0.4 143 | 0.0 047 |
| 6 | 0.0 126 | 0.0 051 |
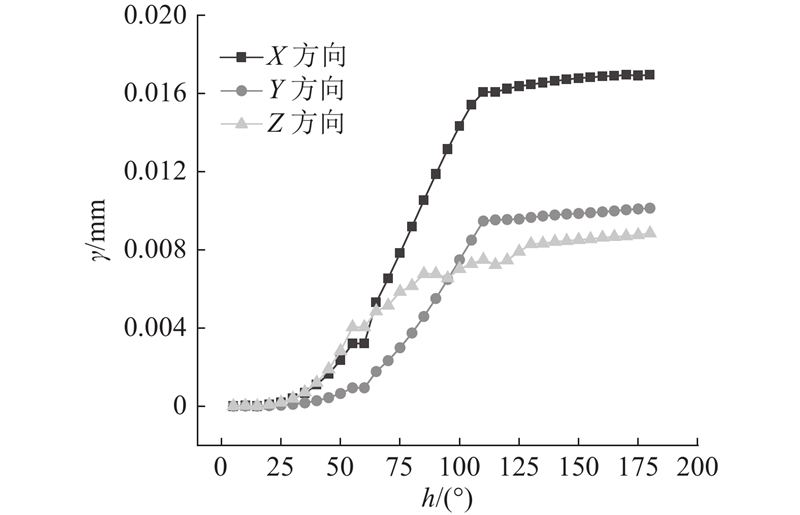
使用表5中的随机误差参数与式(23)计算每隔5°关节分割量的实验变差函数值
图 3
将误差信息不充分定义为测量时无法有效捕捉机械臂末端误差场全貌,导致误差分析信息不完整、无法代表真实误差分布或变动,难以充分反映完整测量空间内机械臂末端误差空间特征的现象. 所选轨迹测量误差范围小于随机误差范围,且误差场分布与完整空间差异较大,表明误差信息不充分. 这种局限性使得基于有限轨迹的误差分析会偏离实际,影响精度和有效性. 为了确保信息充分准确,须多轨迹全面反映误差特征.
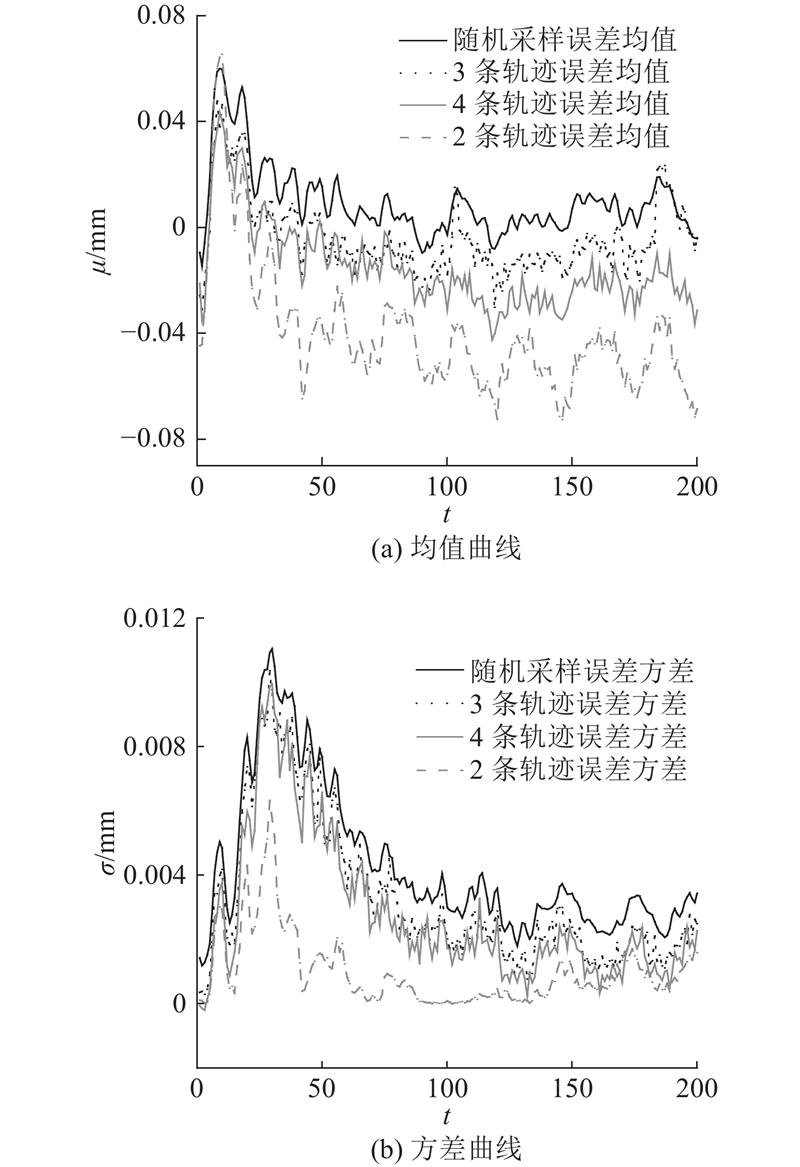
图 4
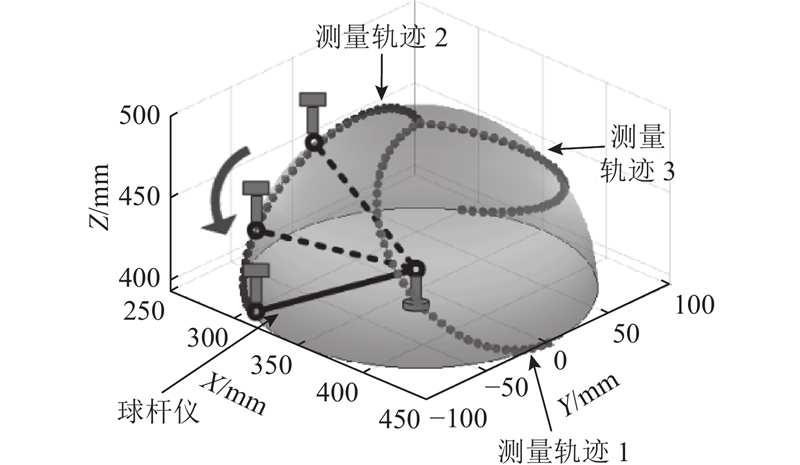
如图4(a)所示,采用随机采样方式测得的误差均值曲线,与使用3条轨迹进行测量所得到的误差均值曲线最为接近. 误差较低且稳定;采用2条和4条轨迹,误差较高且波动大,分别采用2条、3条、4条轨迹进行测量时,测得的误差均值变化率分别为5.77%、85.34%、15.19%. 图4(b)的方差分析呈现类似特征,采用随机采样方式测得的方差曲线,与使用3条轨迹进行测量所得到的方差曲线最接近,2、3、4条轨迹的方差变化率分别为61.76%、1.96%、4.91%. 以随机采样为参考,3条轨迹在控制误差方差方面表现最佳,能够有效降低不确定性;4条轨迹效果不稳定;2条轨迹表现最差,可能由信息不足导致. 综上所述,采用3条轨迹测量,误差信息更完备,离散程度低,测量更可靠. 3条测量轨迹的示意图如图5所示.
图 5
在3条轨迹上共取f个采样点,选择半球球心位置为球杆仪底座位置,在机器人按采样轨迹运动时,固定姿态不变,姿态矩阵R和位置误差矩阵p表达式分别如下:
设半球球心位置为(Xo, Yo, Zo),在实际情况中,球心位置存在偏差ΔXo、ΔYo、ΔZo,则球心实际坐标如下:
在使用球杆仪测量时,球杆仪末端在半球球面上移动,设球杆仪理论长度为Lt,实际测量长度为La,理论长度如下:
通过测量可得到f个包含误差参数的理论长度, Lt包含表4中的12个参数误差以及3个球心偏差量(ΔXo, ΔYo, ΔZo)共15个误差参数.
2.2. 轨迹圆弧插补算法
采用圆弧插补算法确定空间轨迹初始点位,随机选取不共线的3点(P1, P2, P3),其初始值为P1(x1, y1, z1),P2(x2, y2, z2),P3(x3, y3, z3),可以确定半径为r、圆心为o的圆弧,Pa、Pb的垂直平分面方程如下:
由式(28)可以求得P1与P2的垂直平分面方程和P2与P3的垂直平分面方程. 平面P1P2P3外接圆方程如下:
由式(28)、(29)可求得外接圆圆心o(x0, y0, z0),外接圆半径可由半径计算公式求得.
圆弧插补角度计算公式如下:
根据求得的圆心坐标、半径R以及插补角度可求得圆弧上点的坐标:
式中:ti为第i个点的线性插值参数.
3. 改进MFO误差参数辨识算法
当待辨识的误差参数趋于准确值时,球杆仪理论长度Lt趋近于测量值La,构建误差参数辨识的目标函数H,使目标函数值等于理论长度与实测长度的差且趋近于无穷小:
为了避免局部最优,加速误差参数辨识,位置更新公式如下:
式中:
图 6
使用Compute Unified Device Architecture (CUDA)对辨识算法进行加速,具体过程如下.
1)分离目标函数中计算(Xt−
2) 随机生成误差赋给步骤1)中的公式.
3) 计算结果导出至CPU,计算目标函数值,当接近0.02时收敛速度显著下降,表明逼近最优解. 函数值小于0.02时迭代停止.
4. 虑及不确定度的逆解补偿策略
4.1. 测量不确定度量化
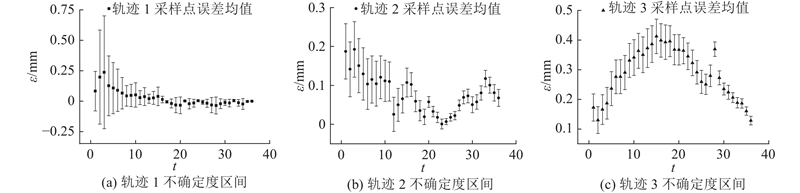
对于采样轨迹上的f个采样点进行多次测量求得各点的标准不确定度:
式中:
工业机器人定位误差符合正态分布,在95%的置信水平下,z=1.96.
4.2. 基于不确定度的嵌套补偿算法
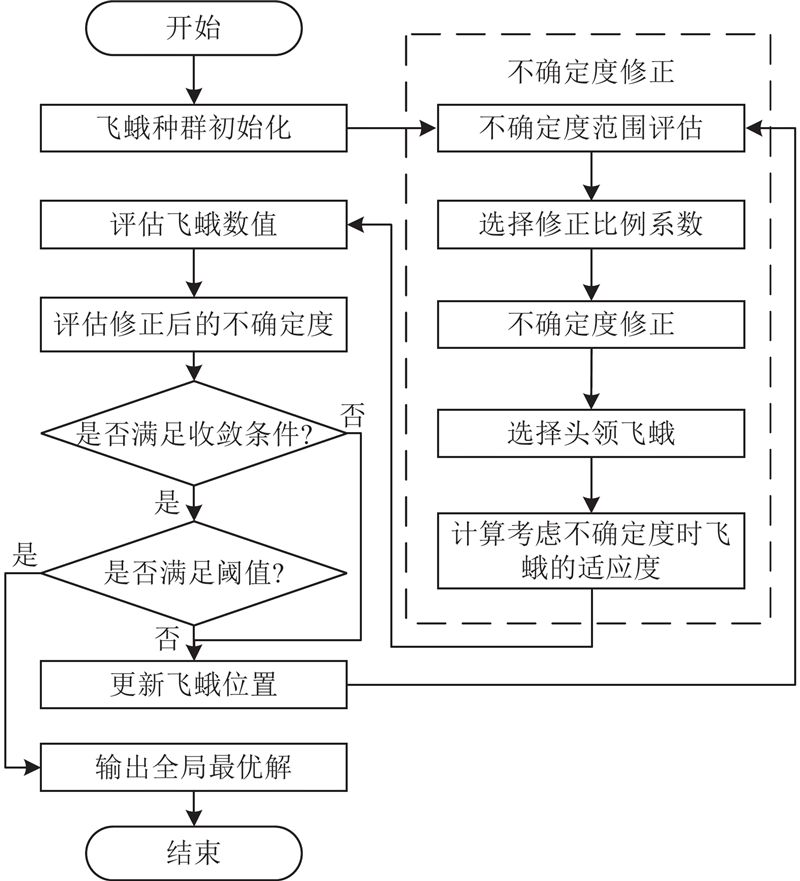
工业机器人重复定位误差及随机误差导致测量值具有不确定度,须对测量值进行动态修正,将测量值修正部分与辨识算法进行结合,获得修正后的误差辨识值,嵌套算法流程图如图7所示.
图 7
以采样点p为例,其不确定度范围为[−b, b],p点测量值为a,评估a并对参数c动态调节. 当a位于[−b,−b/2]或[b/2,b]时,c取2;当a位于(−b/2, b/4]或(b/4, b/2)时,c取4;当|a|小于b/4时,不修正. 修正后的测量值an表达式如下:
式中:a为初始测量值,
嵌套补偿算法首先进行种群初始化,并评估待辨识参数的不确定度范围. 根据式(36)修正待辨识参数的不确定度. 选择头领飞蛾并计算虑及不确定度的适应度. 最后,判断迭代过程是否满足收敛条件,以及修正后的待辨识参数是否符合修正判断条件,即目标函数值小于0.02且修正后的待辨识参数an的绝对值小于b/4.
5. 实验例证
实验中的ABB-IRB-120型机器人重复定位精度为±0.01 mm,额定负载为3 kg. 雷尼绍QC20-W球杆仪的测量半径为100 mm,理论球心坐标为:Xo =350,Yo =0,Zo =394,测量轨迹以5°为间隔均匀取点. 每条轨迹间隔取5个点用于轨迹绘制,如图8所示.
图 8
实验中机器人末端速度为30 mm/s,采样率为
图 9
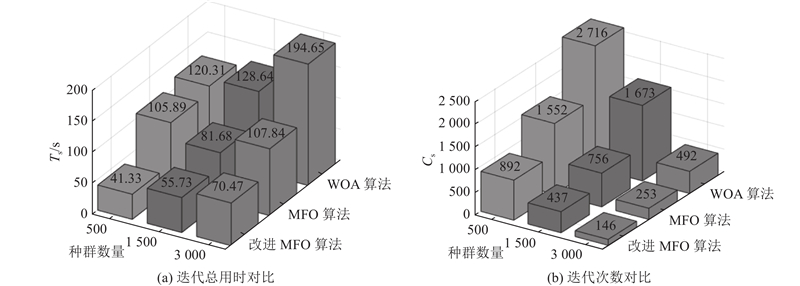
以最后一次测量结果作为补偿实验误差测量结果. 基于测量数据构建目标函数,分别用传统MFO、改进MFO和鲸鱼优化算法(WOA)进行10次迭代求解,比较总用时和迭代次数的平均值. 迭代条件为全局最优值小于0.02,种群数量分别为500、
图 10
图 10 不同种群数量下的算法迭代对比
Fig.10 Iterative comparison of algorithms with different population numbers
表 6 辨识及参数修正值
Tab.6
| 关节 | 误差辨识 | 不确定度误差辨识 | 参数修正 | 不确定度参数修正 | |||||||
| Δli/mm | Δθi/(°) | Δli/mm | Δθi/(°) | li/mm | θi/(°) | li/mm | θi/(°) | ||||
| 1 | −0.106 743 | 0.036 808 | −0.064 664 | 0.026 086 | 186.893 | 186.935 | 0.026 0 | ||||
| 2 | 0.051 048 | 0.015 275 | −0.060 463 | −0.020 891 | 103.051 | 102.940 | − | ||||
| 3 | 0.269 206 | −0.021 215 | 0.108 764 | 0.033 726 | 270.269 | − | 270.109 | ||||
| 4 | −0.263 183 | −0.166 136 | 0.158 623 | −0.140 743 | 69.736 | − | 70.158 | − | |||
| 5 | 0.070 808 | 0.071 966 | −0.028 081 | −0.211 071 | 134.071 | 133.972 | − | ||||
| 6 | 0.076 593 | 0.181 798 | 0.046 145 | 0.044 435 | 168.077 | 168.046 | |||||
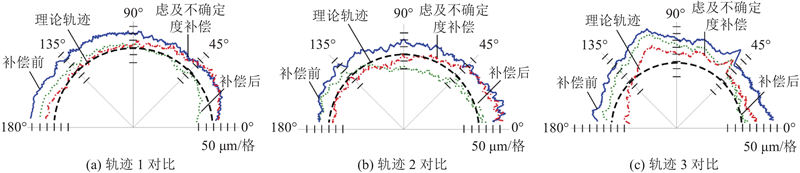
图 11
图 11 球杆仪测量轨迹补偿前后效果对比
Fig.11 Comparison of effects before and after measurement trajectory compensation of ball bar instrument
如表7所示为补偿效果对比. 其中,
表 7 考虑与不考虑不确定度补偿的机械臂轨迹误差及效率对比
Tab.7
| 轨迹 | 序号 | 不考虑不确定度补偿 | 虑及不确定度补偿 | |||
| 轨迹1 | 补偿前 | 99.431 | 104.559 | 99.431 | 104.559 | |
| 补偿后 | 44.217 | 54.909 | 41.328 | 50.623 | ||
| 55.55 | 47.48 | 58.69 | 51.58 | |||
| 轨迹2 | 补偿前 | 104.869 | 109.832 | 104.869 | 109.832 | |
| 补偿后 | 56.876 | 61.313 | 54.261 | 60.445 | ||
| 45.77 | 44.18 | 48.26 | 44.97 | |||
| 轨迹3 | 补偿前 | 179.795 | 184.411 | 179.795 | 184.411 | |
| 补偿后 | 93.141 | 102.967 | 83.685 | 91.950 | ||
| 48.19 | 45.29 | 53.45 | 50.14 | |||
为了验证所提出的精度校准方法在工业应用中的性能与效果,在ABB IRB 120工业机器人上进行实验,选用Ф2 mm HRC45 QXD球头铣刀,末端执行器转速为3 000 r/min,以铝合金材质棒料为加工对象. 加工叶轮工序如下. 1) 叶轮粗加工. 用球形铣刀铣削叶片间流道,从轮盖侧至轮毂侧逐步进行. 2) 叶轮精加工. 精修叶片表面及流道,确保型线精确、表面光滑,以减少阻力,提升效率. 3) 对叶轮进行外观修整,去除毛刺、锐角,确保叶轮表面质量.
使用三坐标测量机对补偿前后的叶轮半径、叶轮高度、叶片高度、上下平面平行度与平面度进行检测,实验现场及工件对比如图12所示. 检测结果显示,补偿前叶轮半径、叶片高度、叶轮高度、平行度、平面度各自的误差分别为0.086、0.109、0.093、0.015、0.008 mm;补偿后分别为0.054、0.069、0.066、0.009、0.005 mm. 尺寸误差平均减小32.3%,形位误差平均减小38.9%.
图 12
6. 结 论
针对提高工业机器人定位精度的问题,提出误差参数校正方法,并进行实验验证,本研究的主要结论如下.
(1)通过工业机器人关节与空间定位误差相似特性分析,设计了基于球杆仪的空间去冗余测量轨迹,实现了采样点的低相似性及去冗余测量.
(2) 建立了基于包围策略与猎物搜索机制的改进MFO优化逆解、辨识方法,改进的MFO算法相较于传统的飞蛾火焰优化算法与鲸鱼优化算法,收敛速率分别提升了42.46%、62.03%.
(3)构建了补偿参数嵌套算法并实现了辨识参数的不确定度修正. 实验结果表明,不考虑不确定度补偿,绝对平均误差相较于补偿前减少49.83%,均方根误差相较于补偿前减少45.65%;考虑不确定度补偿,绝对平均误差相较于补偿前减少53.47%,均方根误差相较于补偿前减少48.89%. 补偿后加工的叶轮尺寸误差相较于未补偿时加工的叶轮平均减小32.3%,形位误差相较于未补偿时加工的叶轮平均减小38.9%.
为了实现在线精度校准,后续将致力基于机器视觉的在线补偿策略研究,以实现工业机器人在复杂动态环境中定位精度的提升.
参考文献
基于粒子群优化神经网络的机器人精度补偿方法研究
[J].DOI:10.3969/j.issn.1004-132X.2013.02.007 [本文引用: 1]
Method of industrial robot accuracy compensation based on particle swarm optimization neural network
[J].DOI:10.3969/j.issn.1004-132X.2013.02.007 [本文引用: 1]
A technique to calibrate industrial robots with experimental verification
[J].DOI:10.1109/70.88114 [本文引用: 1]
Robot accuracy analysis based on kinematics
[J].DOI:10.1109/JRA.1986.1087054 [本文引用: 1]
Geometric calibration of industrial robots using enhanced partial pose measurements and design of experiments
[J].DOI:10.1016/j.rcim.2015.03.007 [本文引用: 1]
Kinematic modeling of six-axis industrial robot and its parameter identification: a tutorial
[J].DOI:10.20965/ijat.2021.p0599 [本文引用: 1]
Geometric error modeling of parallel manipulators based on conformal geometric algebra
[J].DOI:10.1007/s00006-018-0831-5 [本文引用: 1]
Review on kinematics calibration technology of serial robots
[J].DOI:10.1007/s12541-014-0528-1 [本文引用: 1]
基于POE模型的工业机器人运动学参数二次辨识方法研究
[J].DOI:10.6041/j.issn.1000-1298.2024.01.040 [本文引用: 1]
Quadratic identification method of kinematic parameters of industrial robots based on POE model
[J].DOI:10.6041/j.issn.1000-1298.2024.01.040 [本文引用: 1]
Kinematic and dynamic analysis of lower-mobility cooperative arms
[J].DOI:10.1017/S0263574714001039 [本文引用: 1]
A local POE-based self-calibration method using position and distance constraints for collaborative robots
[J].DOI:10.1016/j.rcim.2023.102685 [本文引用: 1]
Complete, minimal and continuous error models for the kinematic calibration of parallel manipulators based on POE formula
[J].DOI:10.1016/j.mechmachtheory.2017.11.003 [本文引用: 1]
A minimal POE-based model for robotic kinematic calibration with only position measurements
[J].DOI:10.1109/TASE.2014.2328652 [本文引用: 1]
Improvement of robot accuracy with an optical tracking system
[J].DOI:10.3390/s20216341 [本文引用: 1]
Real-time laser tracker compensation of robotic drilling and machining
[J].DOI:10.3390/jmmp4030079 [本文引用: 1]
A new method for measuring a large set of poses with a single telescoping ballbar
[J].DOI:10.1016/j.precisioneng.2012.12.001 [本文引用: 1]
A method for the assessment and compensation of positioning errors in industrial robots
[J].DOI:10.1016/j.rcim.2023.102622 [本文引用: 1]
激光跟踪仪三维坐标转换综合优化方法
[J].
Comprehensive optimization for three-dimensional coordinate transformation of laser tracker
[J].
Positioning error calibration of six-axis robot based on sub-identification space
[J].
基于多种群竞争松鼠搜索算法的机械臂时间最优轨迹规划
[J].
Time-optimal trajectory planning of manipulator based on multi-group competition squirrel search algorithm
[J].
A novel kinematic parameters calibration method for industrial robot based on Levenberg-Marquardt and differential evolution hybrid algorithm
[J].DOI:10.1016/j.rcim.2021.102165 [本文引用: 1]
Kinematic self-calibration method for dual-manipulators based on optical axis constraint
[J].
A robot calibration method using a neural network based on a butterfly and flower pollination algorithm
[J].DOI:10.1109/TIE.2021.3073312 [本文引用: 1]
Serial manipulator time-jerk optimal trajectory planning based on hybrid IWOA-PSO algorithm
[J].DOI:10.1109/ACCESS.2022.3141448 [本文引用: 1]
Time-optimal trajectory planning of serial manipulator based on adaptive cuckoo search algorithm
[J].DOI:10.1007/s12206-021-0638-5 [本文引用: 1]
Positioning error compensation of an industrial robot using neural networks and experimental study
[J].DOI:10.1016/j.cja.2021.03.027 [本文引用: 1]
Real-time trajectory position error compensation technology of industrial robot
[J].DOI:10.1016/j.measurement.2022.112418 [本文引用: 1]
基于扰动观测器的工业机器人高精度闭环鲁棒控制
[J].DOI:10.3901/JME.2022.14.062 [本文引用: 1]
High-precision closed-loop robust control of industrial robots based on disturbance observer
[J].DOI:10.3901/JME.2022.14.062 [本文引用: 1]
Accuracy compensation technology of closed-loop feedback of industrial robot joints
[J].
A novel method to identify DH parameters of the rigid serial-link robot based on a geometry model
[J].DOI:10.1108/IR-05-2020-0103 [本文引用: 1]
A kinematic modeling scheme of three-axis “Satcom-on-the-Move” antenna based on modified Denavit-Hartenberg method
[J].DOI:10.1051/jnwpu/20234130518 [本文引用: 1]
POE-based error modeling and multiple plane constraint-based parameter identification for the kinematic calibration of a 4-UPS/SPR parallel external fixator
[J].DOI:10.1016/j.apm.2024.05.031 [本文引用: 1]
A new calibration method for joint-dependent geometric errors of industrial robot based on multiple identification spaces
[J].DOI:10.1016/j.rcim.2021.102175 [本文引用: 1]