滑模控制是一种鲁棒非线性控制技术,因其收敛速度快、抗干扰、鲁棒性好等优点,广泛应用于空中作业机器人控制领域. 然而,传统的滑模控制只能保证渐近收敛到零,不能满足四旋翼子平台[6]的快速响应要求. 笔者[7]提出一种固定时间滑模控制器,与初始条件无关,保证收敛时间有界. 该控制器在保证系统稳定性的同时,获得了更快的收敛速度. 刘浩等[8]提出预定义时间滑模控制方法. 该方法离线设置稳定时间的上限,确保控制系统在指定的时间内达到稳定状态. 然而,预定义时间滑模控制引入了额外的无限控制增益项,导致实际应用时出现输入饱和问题. 为此,Yan等[9]提出一种显式时间稳定策略,有效地解决了输入饱和问题,减少了需要设计的控制器参数数量. 上述方法可以使误差在固定时间内收敛,在收敛速度方面具有优势. 然而,这些方法尚未针对空中作业机器人进行专门研究,且未充分考虑扰动存在的情况.
基于上述分析,提出一种空中作业机器人显式时间自适应控制(explicit-time adaptive control, ETAC)方法. 针对空中作业机器人轨迹跟踪控制问题,设计基于显式时间稳定策略的滑模控制器,确保系统能够在预定显式时间内快速收敛到零域,从而提升了控制精度和响应效率. 为了应对未知扰动带来的不确定性,控制器中集成了自适应神经网络,能够实时更新控制参数,确保系统的显式时间稳定性不受外界扰动的破坏,有效提高了系统的鲁棒性和抗干扰能力. 在真实环境下进行飞行实验,结果表明,该方法在精确性和稳定性方面具有优越的性能.
1. 控制对象建模
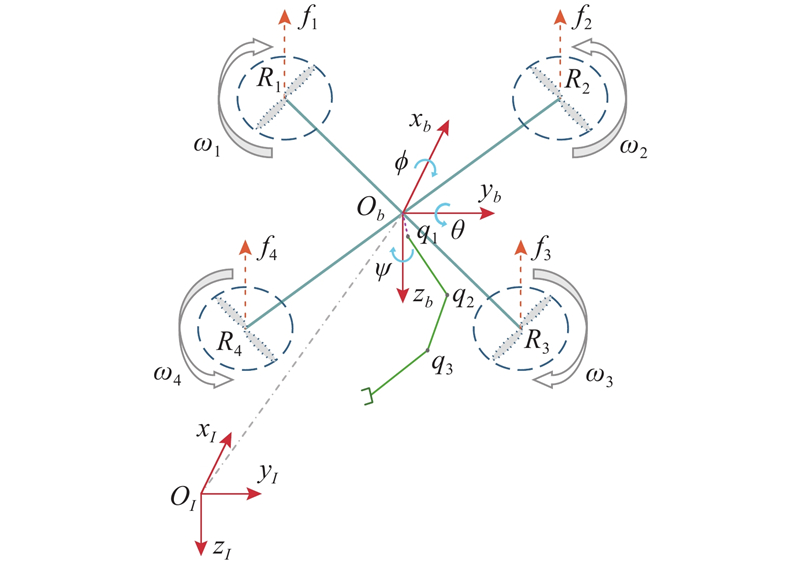
空中作业机器人结构如图1 所示. 令
图 1
图 1 空中作业机器人系统结构示意图
Fig.1 Schematic diagram of aerial manipulator system structure
假设空中作业机器人为对称结构,利用牛顿-欧拉方程建立的姿态动力学方程[13]为
式中:
为了提高计算效率,采用文献[14]提出的方法建立空中作业机器人解耦合模型,机械臂动力学模型为
式中:
空中作业机器人的机械手子系统在作业时,四旋翼飞行器需要处于悬停状态,此时机械臂对空中作业机器人机体产生1个力,导致重心不平衡[6]. 此时,可视为机械臂子系统产生了1个扰动项,其估计值为
式中:
结合式(4),使用
在实际的空中作业环境中,空中作业机器人会受到多种未知升力扰动的影响,这些扰动来源广泛,如复杂的气流变化、作业现场的局部强风、周围环境的温度梯度变化等. 这些未知升力扰动可能导致机器人飞行姿态不稳定,进而影响系统的整体稳定性. 因此,在建立模型时需要充分考虑这些扰动影响,并研究设计相应的鲁棒控制策略,以应对未知扰动对于系统稳定性的影响,保证空中作业机器人在不同工作状态中均具有良好性能.
空中作业机器人由4台电机驱动螺旋桨旋转,其中电机
式中:
空中作业机器人螺旋桨提供的升力
式中:
当空中作业机器人处于悬停状态时,各转子通常以近似相同的转速工作,从而产生对称的升力和相互抵消的反扭矩,使其保持静止的姿态. 假设4个旋翼安装得对称、平衡,其产生的总推力严格垂直向上且不会引入倾斜角度. 当
根据式(1)、(8),空中作业机器人的姿态动力学方程可以表示为
式中:
空中作业机器人的位置动力学方程为
式中:
空中作业机器人的位置动力学方程可以表示为
式中:
2. 控制器设计
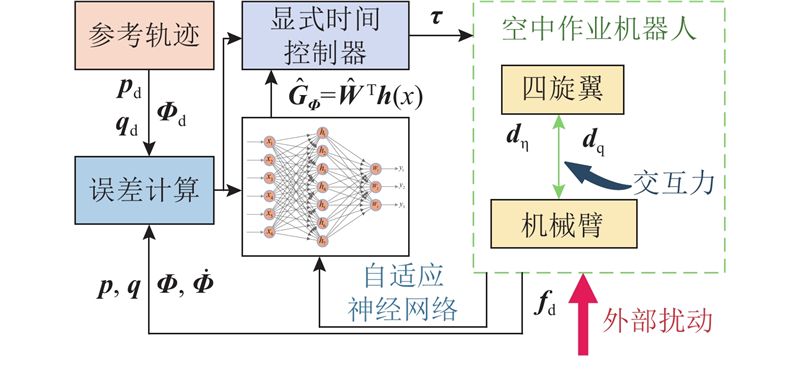
基于显式时间稳定策略设计滑模控制器,并采用自适应神经网络补偿参数不确定性和外界干扰,最后对空中机械手子系统进行稳定性分析. 空中作业机器人控制系统的结构框架如图2所示.
图 2
图 2 空中作业机器人控制结构框图
Fig.2 Control structure diagram of aerial manipulator system
2.1. 理论基础
根据建立的动力学模型,定义状态变量
式中:
定义空中作业机器人跟踪控制的期望姿态角为
对式(14)求导可得:
由于空中作业机器人的欠驱动特性,需要利用解耦合的方法在位置控制子系统中引入虚拟控制量. 位置控制子系统的虚拟控制量表示为
式中:
将位置控制子系统的虚拟控制输入作为姿态控制子系统的参考姿态角,以实现状态变量解耦合的目的. 此外,在实际控制中,由于缺乏速度反馈信息,需要引入虚拟控制量,间接求解出参考姿态角. 该方法将状态变量转换为传感器能够直接测量的物理量,以实现对于系统位置和姿态的有效控制. 参考姿态角可以表示为
空中机械手子系统存在建模不确定性和外界干扰问题,总不确定性项定义为
式中:
令
引理1[9] 考虑以下系统:
式中:
引理2[18] 对于 Lyapunov 函数
则称该系统是显式时间稳定的. 式中:
当
系统的收敛时间只与系统初始状态边界
2.2. 自适应神经网络设计
假设1 对于任何
式中:
引理3[22] 对于任意连续函数
式中:
式中:
本研究设计的自适应神经网络输入层的输入维数是6,隐藏层的节点数
式中:
神经网络的理想输出为
实际输出为
式中:
2.3. 显式时间控制器设计
根据引理1中的显式时间稳定策略,滑模面函数可以设计为如下形式:
式中:
对式(29)求导可得
为了加快系统收敛速度,设计如下形式的滑模收敛律:
式中:
根据式(30)和(31),显式时间自适应控制器可以设计为
式中:
根据上述原理,设计空中作业机器人位置子系统和机械臂子系统的控制器.
定理1 对于式(19)所示的系统误差模型,当选取滑模面(29)和收敛律(31)时,系统能够在全局范围内达到稳定状态,系统的姿态角跟踪误差和姿态角变化率误差能够在显式时间内收敛到零.
备注1 采用滑模控制原理设计控制器时,系统状态变化分为2个阶段:收敛阶段,滑模函数趋近于零;滑动阶段,系统误差趋近于零. 因此,需要分别分析每个阶段的稳定性和收敛时间.
证明 选择 Lyapunov 函数为
对
令
将式(26)中自适应权重更新率代入式(35)中,式(35)可以写为
根据假设1可知,神经网络具有很好的拟合能力,近似误差
根据式(22),可以计算得到系统在收敛阶段的收敛时间为
式中:
当系统处于滑动阶段时,
定义1个Lyapunov函数为
结合式(39)和引理2,可知系统的误差可以收敛到零,系统稳定.
根据式(22),可以算出系统在滑动阶段的收敛时间为
根据以上证明,系统是全局稳定的,且系统的总收敛时间
备注2 在实际控制系统设计中,通信延迟等问题使系统误差不能准确收敛到原点,而只能收敛到原点附近的1个邻域,但系统仍然满足显式时间稳定策略.
3. 仿真与飞行实验结果
对空中作业机器人进行数值仿真和物理飞行实验,以验证所提控制方法的有效性. 此外,与现有的先进控制方法进行对比实验.
3.1. 实验设置
3.1.1. 实验平台
采用的四轴无人机硬件由DJI F450机架、20 A电子调速器(electronic speed controller, ESC)、3S 4 300 mAh 45C LIPO电池、CFN 1045自锁桨叶和X2212 KV980电机组成. 自驾仪为PIXHAWK 2.4.8,长距离无线电(LORA)通信模块为LR900. 主控单片机接收姿态传感器传来的数据,通过无线通信模块发送到地面站. 地面站中的控制器计算出电机输出转速,并通过无线通信模块将转速信息发送给主控单片机,后者接收到目标转速后,将其转化为脉冲宽度调制(pulse width modulation, PWM)并发送给ESC. ESC根据接收到的PWM指令对电机转速进行闭环控制. 空中作业机器人实验平台如图3所示. 地面站控制器的采样频率为1 kHz,与传感器的处理速度同步.
图 3
3.1.2. 物理参数测量
在数值模拟和实物实验中,升力
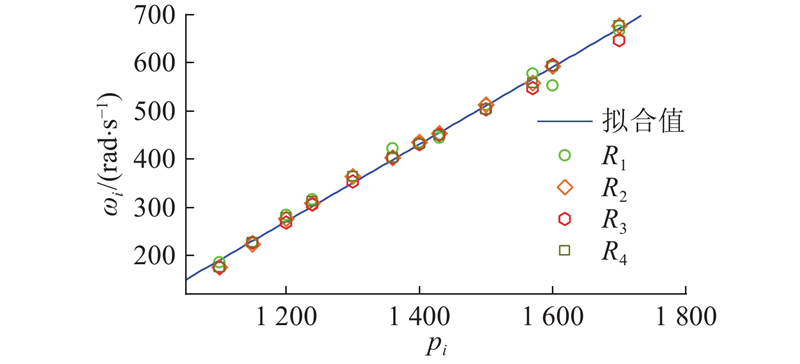
四旋翼无人机上的无刷直流电机由电子调速器驱动. 通过实验测量转速,得到电机转速
图 4
图 4 电机转速和输入PWM拟合实验结果
Fig.4 Fitting experimental results of motor speed and input PWM
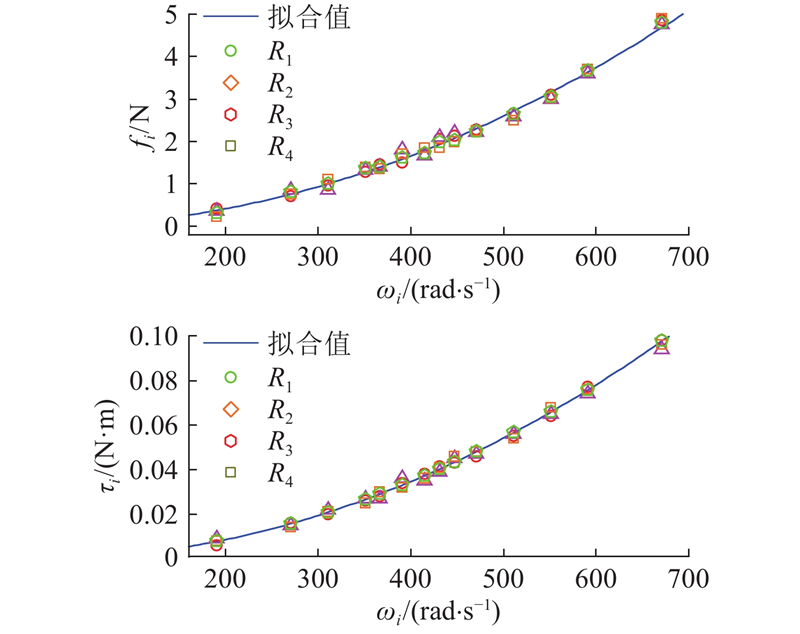
ETAC的输出为虚拟控制转矩,而在实际控制中需要控制电机转速. 为了得到虚拟控制转矩与电机转速的关系,利用张力计和电流表测量不同转速下的张力和转矩数据. 采用拟合方法得到系数
图 5
图 5 电机拉力系数与转矩系数拟合结果
Fig.5 Motor tension coefficient and torque coefficient fitting results
3.2. 数值仿真
对空中作业机器人轨迹跟踪控制进行数值仿真,以验证所提控制方法的理论正确性. 数值仿真在 MATLAB 2023b/Simulink 工具箱中进行.
空中作业机器人参考关节状态变量设置为
空中作业机器人初始关节角是0,其他状态变量设置为
自适应神经网络对系统集总扰动的估计效果如图6所示. 在该实验中,神经网络的学习率
图 6
图 6 自适应神经网络对集总不确定项的估计结果
Fig.6 Estimation results of lumped uncertainty terms using adaptive neural network
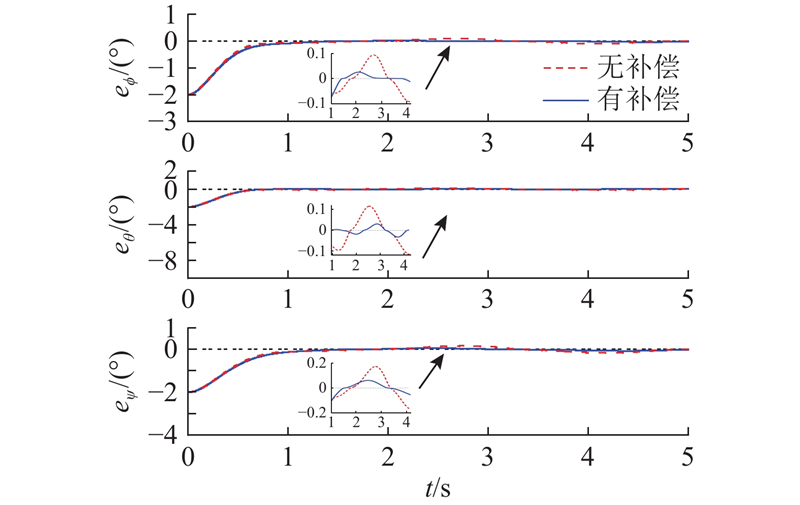
图7展示了ETAC方法中扰动补偿对系统控制性能的影响. 图中,
图 7
图 7 扰动补偿对系统控制性能的影响
Fig.7 Impact of disturbance compensation on system control performance
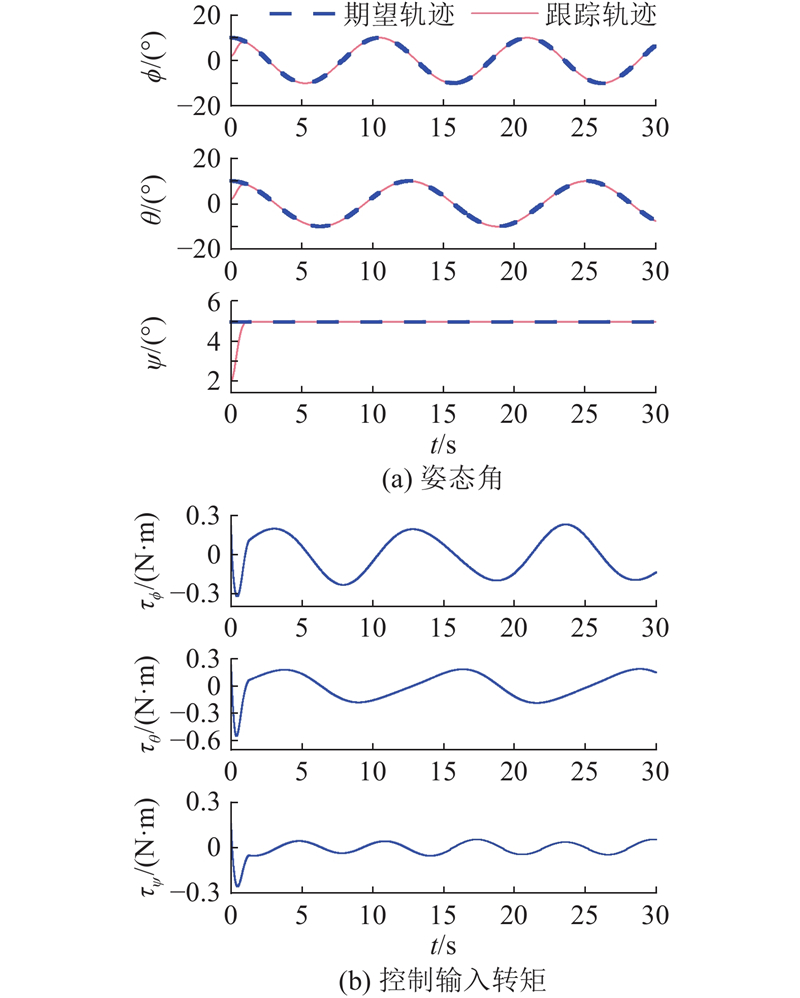
图 8
图 8 姿态跟踪控制的数值仿真结果
Fig.8 Numerical simulation results of attitude tracking control
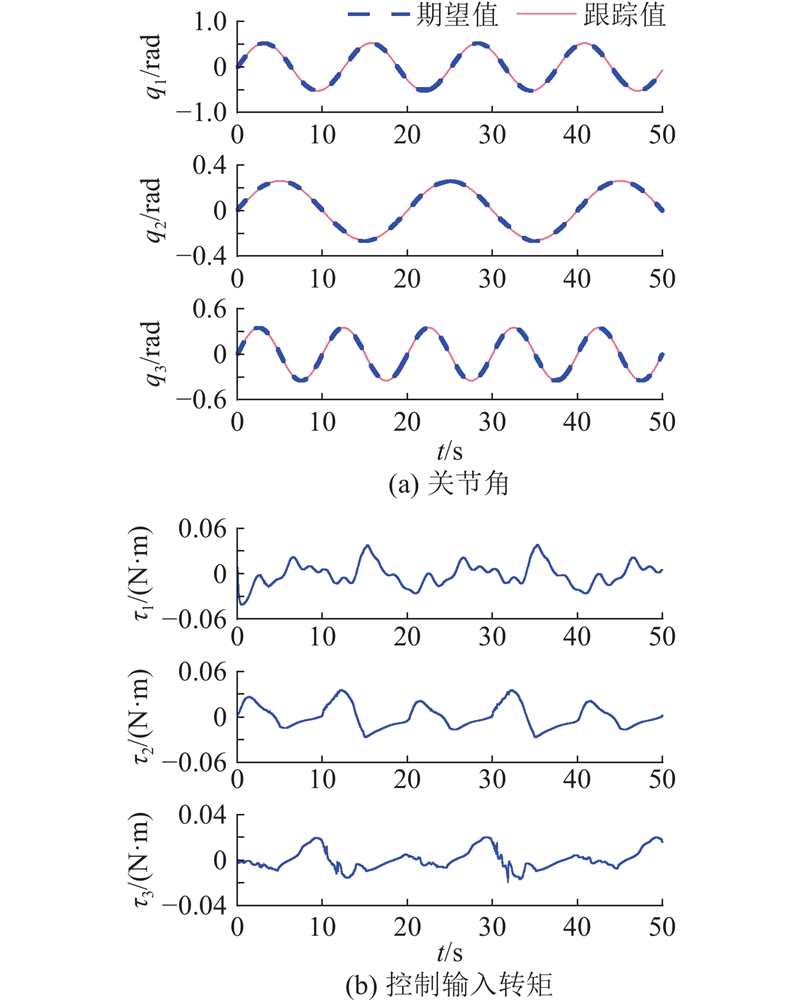
图 9
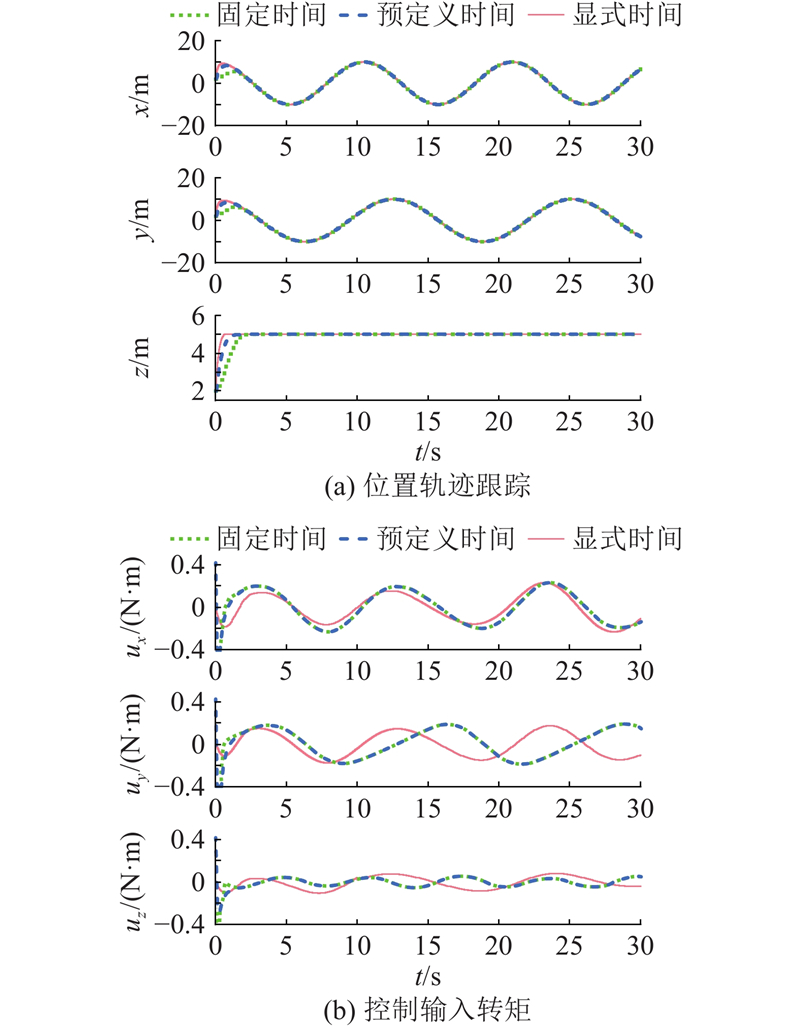
图 10
图 10 位置跟踪控制对比实验结果
Fig.10 Comparative experimental results of position tracking control
图 11
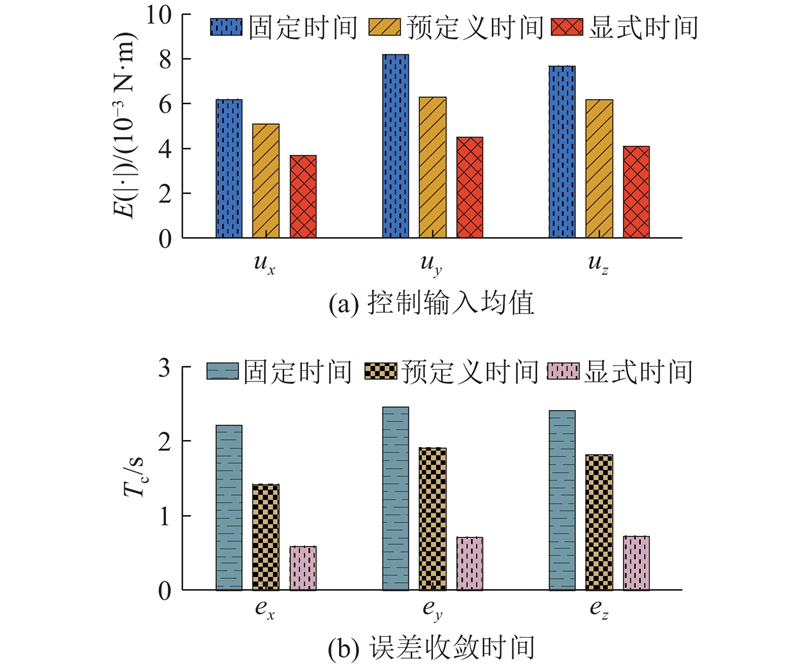
图 11 位置跟踪仿真实验量化结果
Fig.11 Quantitative results of position tracking simulation experiment
图 12
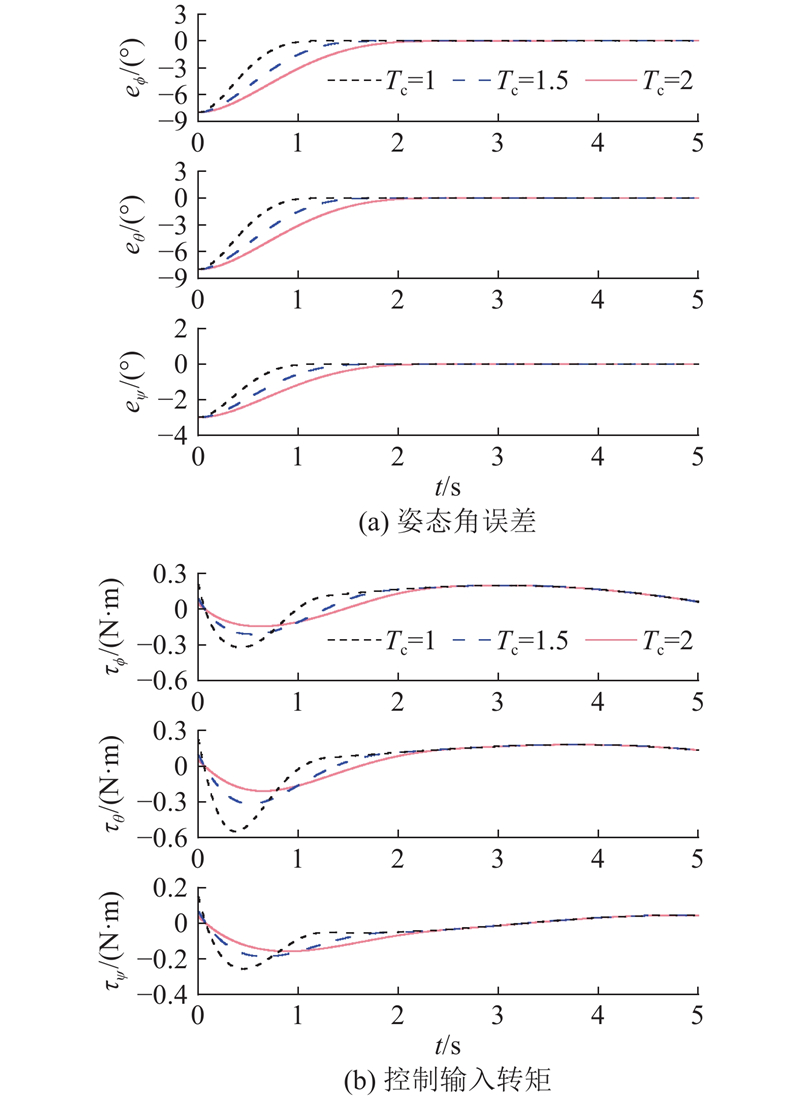
图 12 显式时间控制中不同收敛时间的性能对比
Fig.12 Performance comparison of different convergence times in explicit time control
3.3. 飞行实验
3.3.1. 姿态跟踪
设计1组飞行实验来验证所提控制方法的有效性,并与其他方法进行比较. 首先,在如图13所示的空中作业机器人实验平台上进行姿态跟踪飞行实验. 出于飞行安全的考虑,该实验平台将空中作业机器人固定在光滑的球面万向节上,以限制其位置变化. 空中作业机器人的3个关节被置零,以充分展示所提控制方法的控制性能.
图 13
图 13 空中作业机器人姿态跟踪实验装置
Fig.13 Attitude tracking experimental device of aerial manipulator system
飞行实验中采用的控制器参数和参考跟踪信号与数值仿真中采用的相同. 为了进一步验证ETAC方法的性能,与文献[24]提出的固定时间滑模控制(fixed time sliding mode control, FTSMC)方法和文献[21]中提出的预定义时间滑模控制(predefined time sliding mode control, PTSMC)方法进行对比实验,实验结果如图14所示. 可以看出3种方法都在短时间内取得了良好的姿态跟踪性能. 图14中(b)展示了空中作业机器人的姿态跟踪误差,具体数值结果如表1所示,表明提出的控制方法的姿态跟踪误差明显减小. 图14中(c)展示了控制输入转矩的对比结果. 可以看出,在跟踪同一参考轨迹时,ETAC方法的控制输入转矩较小,表明ETAC方法能够更好地跟踪参考轨迹,并将跟踪误差收敛到原点附近的1个邻域内. 在高动态快速响应和存在传感器信号干扰的实际飞行试验中,ETAC方法也获得了比其他方法更好的性能.
图 14
图 14 不同控制方法的空中作业机器人飞行实验对比结果
Fig.14 Comparative results of aerial manipulator flight experiments using different control methods
表 1 飞行实验中不同控制方法的定量比较
Tab.1
| 姿态角 | 控制方法 | RMSE/(°) | ||
| 滚转角 | FTSMC | 1.76 | 0.659 2 | 1.883 8 |
| PTSMC | 1.58 | 0.644 5 | 1.956 4 | |
| ETAC | 1.36 | 0.479 5 | 1.486 8 | |
| 俯仰角 | FTSMC | 2.27 | 0.764 8 | 1.853 6 |
| PTSMC | 1.85 | 0.523 1 | 1.611 8 | |
| ETAC | 1.80 | 0.397 2 | 1.096 4 | |
| 偏航角 | FTSMC | 1.89 | 0.512 9 | 1.847 7 |
| PTSMC | 1.35 | 0.384 1 | 1.161 8 | |
| ETAC | 1.22 | 0.256 1 | 0.923 9 |
3.3.2. 抗扰实验
图 15
图 15 空中作业机器人抗扰动飞行实验
Fig.15 Disturbance-rejection flight experiments of aerial manipulator
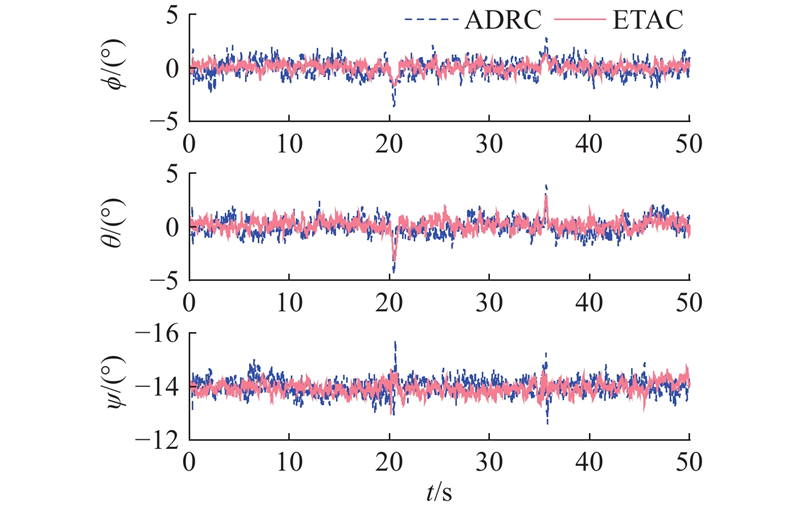
本次实验采用带激光测距的光流模块获取位置,在初始时刻空中作业机器人的
图 16
图 16 空中作业机器人抗扰动对比实验结果
Fig.16 Comparative experimental results of disturbance rejection of aerial manipulator
表 2 不同控制方法抗扰性能定量比较结果
Tab.2
| 姿态角 | 控制方法 | ||
| 滚转角 | ADRC | 0.747 7 | 2.768 5 |
| ETAC | 0.418 4 | 1.340 3 | |
| 俯仰角 | ADRC | 0.754 8 | 3.875 4 |
| ETAC | 0.588 0 | 3.012 3 | |
| 偏航角 | ADRC | 0.285 9 | 1.388 4 |
| ETAC | 0.222 9 | 1.062 1 |
4. 结 语
针对空中作业机器人轨迹跟踪控制中的挑战,提出了结合自适应神经网络与显式时间稳定策略的控制方法,重点解决了动力学模型中存在扰动和不确定性的问题. 研究结果表明,该方法能够在不依赖先验知识的条件下,自适应地逼近系统中的动态不确定性,并实现显式时间内的姿态收敛,同时具有较低的控制输入需求和较强的扰动抑制能力. 实际飞行实验验证了该方法在复杂工况下具有良好的稳定性和适应性,为空中作业机器人在任务执行过程中的高精度轨迹跟踪提供了理论支持与工程实践价值. 然而,本研究主要集中于部分自由度的轨迹跟踪控制,尚未涵盖全自由度的控制场景和空中抓取等复杂任务. 未来的研究将进一步探索空中作业机器人在全自由度跟踪控制和多任务协同作业中的潜力,推动其在多样化实际应用中的广泛发展.
参考文献
Control schemes for quadrotor UAV: taxonomy and survey
[J].
A novel robust observer-based nonlinear trajectory tracking control strategy for quadrotors
[J].
Robust adaptive backstepping neural networks fault tolerant control for mobile manipulator UAV with multiple uncertainties
[J].
Adaptive NN motion control and predictive coordinate planning for aerial manipulators
[J].
Fractional-order nonsingular terminal sliding mode control of a cable-driven aerial manipulator based on RBF neural network
[J].
Robust control based on adaptive neural network for the process of steady formation of continuous contact force in unmanned aerial manipulator
[J].
旋翼飞行机械臂固定时间滑模控制
[J].DOI:10.3969/j.issn.1671-637X.2024.01.011 [本文引用: 2]
Fixed-time sliding mode control of rotor flight manipulator
[J].DOI:10.3969/j.issn.1671-637X.2024.01.011 [本文引用: 2]
基于预定义时间的四旋翼滑模控制
[J].
Quadrotor sliding mode control based on predefined time
[J].
An explicit-time and explicit-accuracy control for a state-constrained nonstrict-feedback uncertain system based on adaptive fuzzy dynamic-approximation
[J].
Adaptive neural network backstepping control method for aerial manipulator based on coupling disturbance compensation
[J].
Low-complexity prescribed performance control for unmanned aerial manipulator robot system under model uncertainty and unknown disturbances
[J].
Composite disturbance rejection attitude control for quadrotor with unknown disturbance
[J].
Fuzzy-based fixed-time attitude control of quadrotor unmanned aerial vehicle with full-state constraints: theory and experiments
[J].
Redundancy-driven multi-task adaptive backstepping tracking control for aerial manipulators
[J].
Adaptive integral sliding mode control using fully connected recurrent neural network for position and attitude control of quadrotor
[J].
DDPG-based adaptive robust tracking control for aerial manipulators with decoupling approach
[J].
Predictor-based neural attitude control of a quadrotor with disturbances
[J].
1-order-smooth explicit-time nonsingular terminal sliding mode control of industrial cyber-physical systems against cyber-attacks
[J].
Neural adaptive sliding mode control for camera positioner quadrotor UAV
[J].
Adaptive sliding mode control for attitude stabilization with actuator saturation
[J].
Adaptive attitude control of a quadrotor using fast nonsingular terminal sliding mode
[J].
Observer-based adaptive neural networks control for large-scale interconnected systems with nonconstant control gains
[J].
RFlySim: automatic test platform for UAV autopilot systems with FPGA-based hardware-in-the-loop simulations
[J].
A novel fixed-time sliding mode control of quadrotor with experiments and comparisons
[J].
Active disturbance rejection attitude control for a dual closed-loop quadrotor under gust wind
[J].