[2]
SINGH R, REN J, LIN X A Review of deep reinforcement learning algorithms for mobile robot path planning
[J]. Vehicles , 2023 , 5 (4 ): 1423 - 1451
DOI:10.3390/vehicles5040078
[3]
ZHU K, ZHANG T Deep reinforcement learning based mobile robot navigation: a review
[J]. Tsinghua Science and Technology , 2021 , 26 (5 ): 674 - 691
DOI:10.26599/TST.2021.9010012
[4]
刘宇庭, 郭世杰, 唐术锋, 等 改进A*与ROA-DWA融合的机器人路径规划
[J]. 浙江大学学报: 工学版 , 2024 , 58 (2 ): 360 - 369
[本文引用: 1]
LIU Yuting, GUO Shijie, TANG Shufeng, et al Improved A* and ROA-DWA fusion for robot path planning
[J]. Journal of Zhejiang University: Engineering Science , 2024 , 58 (2 ): 360 - 369
[本文引用: 1]
[5]
YAN K, MA B Mapless navigation based on 2D LIDAR in complex unknown environments
[J]. Sensors , 2020 , 20 (20 ): 5802
DOI:10.3390/s20205802
[本文引用: 1]
[6]
ALI M, LIU L. GP-Frontier for local mapless navigation [C]//IEEE International Conference on Robotics and Automation . London: IEEE, 2023: 10047-10053.
[本文引用: 1]
[8]
朱威, 洪力栋, 施海东, 等. 结合优势结构和最小目标Q值的深度强化学习导航算法[J/OL]. 控制理论与应用, 2024, 41(4): 716-728 [2024-05-10]. http://kns.cnki.net/kcms/detail/44.1240.TP.20230223.1323.020.html.
[本文引用: 1]
ZHU Wei, HONG Lidong, SHI Haidong, et al. Deep reinforcement learning navigation algorithm combining advantage structure and minimum target Q value [J/OL]. Control Theory and Applications , 2024, 41(4): 716-728 [2024-05-10]. http://kns.cnki.net/kcms/detail/44.1240.TP.20230223.1323.020.html.
[本文引用: 1]
[10]
WANG C, WANG J, SHEN Y, et al Autonomous navigation of UAVs in large-scale complex environments: a deep reinforcement learning approach
[J]. IEEE Transactions on Vehicular Technology , 2019 , 68 (3 ): 2124 - 2136
DOI:10.1109/TVT.2018.2890773
[本文引用: 2]
[11]
CIMURS R, SUH I H, LEE J H Goal-driven autonomous exploration through deep reinforcement learning
[J]. IEEE Robotics and Automation Letters , 2021 , 7 (2 ): 730 - 737
[本文引用: 1]
[12]
KONG F, WANG Q, GAO S, et al B-APFDQN: a UAV path planning algorithm based on deep Q-network and artificial potential field
[J]. IEEE Access , 2023 , 11 : 44051 - 44064
DOI:10.1109/ACCESS.2023.3273164
[本文引用: 1]
[13]
李永迪, 李彩虹, 张耀玉, 等 基于APF-LSTM-DDPG算法的移动机器人局部路径规划
[J]. 山东理工大学学报: 自然科学版 , 2024 , 38 (1 ): 33 - 41
[本文引用: 2]
LI Yongdi, LI Caihong, ZHANG Yaoyu, et al Local path planning for mobile robots based on APF-LSTM-DDPG algorithm
[J]. Journal of Shandong University of Technology: Natural Science Edition , 2024 , 38 (1 ): 33 - 41
[本文引用: 2]
[15]
ZHANG Q, ZHANG L, MA Q, et al. The LSTM-PER-TD3 algorithm for deep reinforcement learning in continuous control tasks [C]//China Automation Congress . Chongqing: IEEE, 2023: 671-676.
[16]
TAN Y, LIN Y, LIU T, et al. PL-TD3: a dynamic path planning algorithm of mobile robot [C]//IEEE International Conference on Systems, Man, and Cybernetics . Prague: IEEE, 2022: 3040-3045.
[17]
HUANG B, XIE J, YAN J Inspection robot navigation based on improved TD3 algorithm
[J]. Sensors , 2024 , 24 (8 ): 2525
DOI:10.3390/s24082525
[本文引用: 1]
[18]
XIE L, WANG S, ROSA S, et al. Learning with training wheels: speeding up training with a simple controller for deep reinforcement learning [C]//IEEE International Conference on Robotics and Automation . Brisbane: IEEE, 2018: 6276-6283.
[本文引用: 1]
[19]
YU W, PENG J, QIU Q, et al. PathRL: an end-to-end path generation method for collision avoidance via deep reinforcement learning [C]// IEEE International Conference on Robotics and Automation . Yokohama: IEEE, 2024: 9278-9284.
[本文引用: 1]
[20]
户高铭, 蔡克卫, 王芳, 等 基于深度强化学习的无地图移动机器人导航
[J]. 控制与决策 , 2024 , 39 (3 ): 985 - 993
[本文引用: 1]
HU Gaoming, CAI Kewei, WANG Fang, et al Mapless navigation for mobile robots based on deep reinforcement learning
[J]. Control and Decision , 2024 , 39 (3 ): 985 - 993
[本文引用: 1]
[21]
金毅康. 移动机器人多机探索与路径规划算法研究[D]. 西安: 西安电子科技大学, 2020.
[本文引用: 1]
JIN Yikang. Research on multi-robot exploration and path planning algorithms for mobile robots [D]. Xi’an: Xidian University, 2020.
[本文引用: 1]
[22]
罗洁, 王中训, 潘康路, 等 基于改进人工势场法的无人车路径规划算法
[J]. 电子设计工程 , 2022 , 30 (17 ): 90 - 94
[本文引用: 1]
LUO Jie, WANG Zhongxun, PAN Kanglu, et al Path planning algorithm for unmanned vehicles based on improved artificial potential field method
[J]. Electronic Design Engineering , 2022 , 30 (17 ): 90 - 94
[本文引用: 1]
[23]
DOBREVSKI M, SKOČAJ D. Adaptive dynamic window approach for local navigation [C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Las Vegas: IEEE, 2020: 6930-6936.
[本文引用: 1]
[24]
DOBREVSKI M, SKOČAJ D. Dynamic adaptive dynamic window approach [J]. IEEE Transactions on Robotics , 2024, 40: 3068-3081.
[本文引用: 1]
[25]
ZHANG S, LI Y, DONG Q Autonomous navigation of UAV in multi-obstacle environments based on a deep reinforcement learning approach
[J]. Applied Soft Computing , 2022 , 115
[本文引用: 1]
[26]
张仪, 冯伟, 王卫军, 等 融合LSTM和PPO算法的移动机器人视觉导航
[J]. 电子测量与仪器学报 , 2022 , 36 (8 ): 132 - 140
[本文引用: 1]
ZHANG Yi, FENG Wei, WANG Weijun, et al Vision-based navigation of mobile robots integrating LSTM and PPO algorithms
[J]. Journal of Electronic Measurement and Instrumentation , 2022 , 36 (8 ): 132 - 140
[本文引用: 1]
Path planning for the mobile robot: a review
1
2018
... 随着智能与自动驾驶技术的迅速发展,基于深度强化学习的路径规划方法受到广泛关注. 导航任务是机器人智能的核心,但多数路径规划算法依赖先验地图,在地下探索、灾后救援、洞穴搜救等特殊环境下难以实现,因而无地图导航成为研究热点. 当前方法主要分为经典方法与深度强化学习方法. 经典算法如A*、Dijkstra和动态窗口法(DWA)已在机器人操作系统(ROS)中广泛实现,但存在计算开销大或易陷入局部最优的问题[1 -4 ] . 部分改进方法如基于间隙[5 ] 或高斯过程前沿方法[6 ] 虽然可以提升性能,但在感知稀疏或场景复杂时受限. ...
A Review of deep reinforcement learning algorithms for mobile robot path planning
0
2023
Deep reinforcement learning based mobile robot navigation: a review
0
2021
改进A*与ROA-DWA融合的机器人路径规划
1
2024
... 随着智能与自动驾驶技术的迅速发展,基于深度强化学习的路径规划方法受到广泛关注. 导航任务是机器人智能的核心,但多数路径规划算法依赖先验地图,在地下探索、灾后救援、洞穴搜救等特殊环境下难以实现,因而无地图导航成为研究热点. 当前方法主要分为经典方法与深度强化学习方法. 经典算法如A*、Dijkstra和动态窗口法(DWA)已在机器人操作系统(ROS)中广泛实现,但存在计算开销大或易陷入局部最优的问题[1 -4 ] . 部分改进方法如基于间隙[5 ] 或高斯过程前沿方法[6 ] 虽然可以提升性能,但在感知稀疏或场景复杂时受限. ...
改进A*与ROA-DWA融合的机器人路径规划
1
2024
... 随着智能与自动驾驶技术的迅速发展,基于深度强化学习的路径规划方法受到广泛关注. 导航任务是机器人智能的核心,但多数路径规划算法依赖先验地图,在地下探索、灾后救援、洞穴搜救等特殊环境下难以实现,因而无地图导航成为研究热点. 当前方法主要分为经典方法与深度强化学习方法. 经典算法如A*、Dijkstra和动态窗口法(DWA)已在机器人操作系统(ROS)中广泛实现,但存在计算开销大或易陷入局部最优的问题[1 -4 ] . 部分改进方法如基于间隙[5 ] 或高斯过程前沿方法[6 ] 虽然可以提升性能,但在感知稀疏或场景复杂时受限. ...
Mapless navigation based on 2D LIDAR in complex unknown environments
1
2020
... 随着智能与自动驾驶技术的迅速发展,基于深度强化学习的路径规划方法受到广泛关注. 导航任务是机器人智能的核心,但多数路径规划算法依赖先验地图,在地下探索、灾后救援、洞穴搜救等特殊环境下难以实现,因而无地图导航成为研究热点. 当前方法主要分为经典方法与深度强化学习方法. 经典算法如A*、Dijkstra和动态窗口法(DWA)已在机器人操作系统(ROS)中广泛实现,但存在计算开销大或易陷入局部最优的问题[1 -4 ] . 部分改进方法如基于间隙[5 ] 或高斯过程前沿方法[6 ] 虽然可以提升性能,但在感知稀疏或场景复杂时受限. ...
1
... 随着智能与自动驾驶技术的迅速发展,基于深度强化学习的路径规划方法受到广泛关注. 导航任务是机器人智能的核心,但多数路径规划算法依赖先验地图,在地下探索、灾后救援、洞穴搜救等特殊环境下难以实现,因而无地图导航成为研究热点. 当前方法主要分为经典方法与深度强化学习方法. 经典算法如A*、Dijkstra和动态窗口法(DWA)已在机器人操作系统(ROS)中广泛实现,但存在计算开销大或易陷入局部最优的问题[1 -4 ] . 部分改进方法如基于间隙[5 ] 或高斯过程前沿方法[6 ] 虽然可以提升性能,但在感知稀疏或场景复杂时受限. ...
基于路径规划和深度强化学习的机器人避障导航研究
1
2024
... 近年来,深度强化学习因硬件进步而得到快速发展[7 -8 ] . DQN、DDPG、PPO、TD3等算法通过强化策略学习显著提升导航的性能[9 -10 ] ,TD3引入双Q网络以减少高估偏差. 部分研究者结合深度强化学习与传统方法,如人工势场法[11 -13 ] ,增强经验学习能力. 引入LSTM网络[14 -17 ] 进一步提升对连续状态信息的处理能力,加速训练并提升泛化效果. Xie等[18 ] 在训练过程中使用简单控制器对深度强化学习模型进行引导,以达到提升样本质量的目的. ...
基于路径规划和深度强化学习的机器人避障导航研究
1
2024
... 近年来,深度强化学习因硬件进步而得到快速发展[7 -8 ] . DQN、DDPG、PPO、TD3等算法通过强化策略学习显著提升导航的性能[9 -10 ] ,TD3引入双Q网络以减少高估偏差. 部分研究者结合深度强化学习与传统方法,如人工势场法[11 -13 ] ,增强经验学习能力. 引入LSTM网络[14 -17 ] 进一步提升对连续状态信息的处理能力,加速训练并提升泛化效果. Xie等[18 ] 在训练过程中使用简单控制器对深度强化学习模型进行引导,以达到提升样本质量的目的. ...
1
... 近年来,深度强化学习因硬件进步而得到快速发展[7 -8 ] . DQN、DDPG、PPO、TD3等算法通过强化策略学习显著提升导航的性能[9 -10 ] ,TD3引入双Q网络以减少高估偏差. 部分研究者结合深度强化学习与传统方法,如人工势场法[11 -13 ] ,增强经验学习能力. 引入LSTM网络[14 -17 ] 进一步提升对连续状态信息的处理能力,加速训练并提升泛化效果. Xie等[18 ] 在训练过程中使用简单控制器对深度强化学习模型进行引导,以达到提升样本质量的目的. ...
1
... 近年来,深度强化学习因硬件进步而得到快速发展[7 -8 ] . DQN、DDPG、PPO、TD3等算法通过强化策略学习显著提升导航的性能[9 -10 ] ,TD3引入双Q网络以减少高估偏差. 部分研究者结合深度强化学习与传统方法,如人工势场法[11 -13 ] ,增强经验学习能力. 引入LSTM网络[14 -17 ] 进一步提升对连续状态信息的处理能力,加速训练并提升泛化效果. Xie等[18 ] 在训练过程中使用简单控制器对深度强化学习模型进行引导,以达到提升样本质量的目的. ...
基于深度Q网络的改进RRT路径规划算法
1
2021
... 近年来,深度强化学习因硬件进步而得到快速发展[7 -8 ] . DQN、DDPG、PPO、TD3等算法通过强化策略学习显著提升导航的性能[9 -10 ] ,TD3引入双Q网络以减少高估偏差. 部分研究者结合深度强化学习与传统方法,如人工势场法[11 -13 ] ,增强经验学习能力. 引入LSTM网络[14 -17 ] 进一步提升对连续状态信息的处理能力,加速训练并提升泛化效果. Xie等[18 ] 在训练过程中使用简单控制器对深度强化学习模型进行引导,以达到提升样本质量的目的. ...
基于深度Q网络的改进RRT路径规划算法
1
2021
... 近年来,深度强化学习因硬件进步而得到快速发展[7 -8 ] . DQN、DDPG、PPO、TD3等算法通过强化策略学习显著提升导航的性能[9 -10 ] ,TD3引入双Q网络以减少高估偏差. 部分研究者结合深度强化学习与传统方法,如人工势场法[11 -13 ] ,增强经验学习能力. 引入LSTM网络[14 -17 ] 进一步提升对连续状态信息的处理能力,加速训练并提升泛化效果. Xie等[18 ] 在训练过程中使用简单控制器对深度强化学习模型进行引导,以达到提升样本质量的目的. ...
Autonomous navigation of UAVs in large-scale complex environments: a deep reinforcement learning approach
2
2019
... 近年来,深度强化学习因硬件进步而得到快速发展[7 -8 ] . DQN、DDPG、PPO、TD3等算法通过强化策略学习显著提升导航的性能[9 -10 ] ,TD3引入双Q网络以减少高估偏差. 部分研究者结合深度强化学习与传统方法,如人工势场法[11 -13 ] ,增强经验学习能力. 引入LSTM网络[14 -17 ] 进一步提升对连续状态信息的处理能力,加速训练并提升泛化效果. Xie等[18 ] 在训练过程中使用简单控制器对深度强化学习模型进行引导,以达到提升样本质量的目的. ...
... 深度强化学习常需要大量训练数据的支持,基于实际硬件平台直接进行训练,可能会对硬件设备造成无法挽回的损坏. 在Gazebo构建Pioneer P3-DX机器人仿真环境,搭载激光雷达传感器,基于ROS Melodic实现算法设计和仿真验证. 网络训练平台为Ubuntu18.04,程序编写主要通过PyTorch完成. 系统内存为16 GB,处理器为Intel Core i5-12400F,显卡为RTX3060Ti、8 GB显存. 参考现有导航算法[10 ,12 -13 ] 的参数设定,针对DWA-LSTM TD3算法进行参数微调. 根据任务场景的复杂度,将每回合最大时间步调整为500步. 为了保证训练数据充足以降低过拟合风险,将经验池大小设置为${10^6}$ . 将策略噪声设置为0.2,提高策略网络的鲁棒性,最终的网络超参数设定如表1 所示. ...
Goal-driven autonomous exploration through deep reinforcement learning
1
2021
... 近年来,深度强化学习因硬件进步而得到快速发展[7 -8 ] . DQN、DDPG、PPO、TD3等算法通过强化策略学习显著提升导航的性能[9 -10 ] ,TD3引入双Q网络以减少高估偏差. 部分研究者结合深度强化学习与传统方法,如人工势场法[11 -13 ] ,增强经验学习能力. 引入LSTM网络[14 -17 ] 进一步提升对连续状态信息的处理能力,加速训练并提升泛化效果. Xie等[18 ] 在训练过程中使用简单控制器对深度强化学习模型进行引导,以达到提升样本质量的目的. ...
B-APFDQN: a UAV path planning algorithm based on deep Q-network and artificial potential field
1
2023
... 深度强化学习常需要大量训练数据的支持,基于实际硬件平台直接进行训练,可能会对硬件设备造成无法挽回的损坏. 在Gazebo构建Pioneer P3-DX机器人仿真环境,搭载激光雷达传感器,基于ROS Melodic实现算法设计和仿真验证. 网络训练平台为Ubuntu18.04,程序编写主要通过PyTorch完成. 系统内存为16 GB,处理器为Intel Core i5-12400F,显卡为RTX3060Ti、8 GB显存. 参考现有导航算法[10 ,12 -13 ] 的参数设定,针对DWA-LSTM TD3算法进行参数微调. 根据任务场景的复杂度,将每回合最大时间步调整为500步. 为了保证训练数据充足以降低过拟合风险,将经验池大小设置为${10^6}$ . 将策略噪声设置为0.2,提高策略网络的鲁棒性,最终的网络超参数设定如表1 所示. ...
基于APF-LSTM-DDPG算法的移动机器人局部路径规划
2
2024
... 近年来,深度强化学习因硬件进步而得到快速发展[7 -8 ] . DQN、DDPG、PPO、TD3等算法通过强化策略学习显著提升导航的性能[9 -10 ] ,TD3引入双Q网络以减少高估偏差. 部分研究者结合深度强化学习与传统方法,如人工势场法[11 -13 ] ,增强经验学习能力. 引入LSTM网络[14 -17 ] 进一步提升对连续状态信息的处理能力,加速训练并提升泛化效果. Xie等[18 ] 在训练过程中使用简单控制器对深度强化学习模型进行引导,以达到提升样本质量的目的. ...
... 深度强化学习常需要大量训练数据的支持,基于实际硬件平台直接进行训练,可能会对硬件设备造成无法挽回的损坏. 在Gazebo构建Pioneer P3-DX机器人仿真环境,搭载激光雷达传感器,基于ROS Melodic实现算法设计和仿真验证. 网络训练平台为Ubuntu18.04,程序编写主要通过PyTorch完成. 系统内存为16 GB,处理器为Intel Core i5-12400F,显卡为RTX3060Ti、8 GB显存. 参考现有导航算法[10 ,12 -13 ] 的参数设定,针对DWA-LSTM TD3算法进行参数微调. 根据任务场景的复杂度,将每回合最大时间步调整为500步. 为了保证训练数据充足以降低过拟合风险,将经验池大小设置为${10^6}$ . 将策略噪声设置为0.2,提高策略网络的鲁棒性,最终的网络超参数设定如表1 所示. ...
基于APF-LSTM-DDPG算法的移动机器人局部路径规划
2
2024
... 近年来,深度强化学习因硬件进步而得到快速发展[7 -8 ] . DQN、DDPG、PPO、TD3等算法通过强化策略学习显著提升导航的性能[9 -10 ] ,TD3引入双Q网络以减少高估偏差. 部分研究者结合深度强化学习与传统方法,如人工势场法[11 -13 ] ,增强经验学习能力. 引入LSTM网络[14 -17 ] 进一步提升对连续状态信息的处理能力,加速训练并提升泛化效果. Xie等[18 ] 在训练过程中使用简单控制器对深度强化学习模型进行引导,以达到提升样本质量的目的. ...
... 深度强化学习常需要大量训练数据的支持,基于实际硬件平台直接进行训练,可能会对硬件设备造成无法挽回的损坏. 在Gazebo构建Pioneer P3-DX机器人仿真环境,搭载激光雷达传感器,基于ROS Melodic实现算法设计和仿真验证. 网络训练平台为Ubuntu18.04,程序编写主要通过PyTorch完成. 系统内存为16 GB,处理器为Intel Core i5-12400F,显卡为RTX3060Ti、8 GB显存. 参考现有导航算法[10 ,12 -13 ] 的参数设定,针对DWA-LSTM TD3算法进行参数微调. 根据任务场景的复杂度,将每回合最大时间步调整为500步. 为了保证训练数据充足以降低过拟合风险,将经验池大小设置为${10^6}$ . 将策略噪声设置为0.2,提高策略网络的鲁棒性,最终的网络超参数设定如表1 所示. ...
好奇心蒸馏双Q网络移动机器人路径规划方法
1
2023
... 近年来,深度强化学习因硬件进步而得到快速发展[7 -8 ] . DQN、DDPG、PPO、TD3等算法通过强化策略学习显著提升导航的性能[9 -10 ] ,TD3引入双Q网络以减少高估偏差. 部分研究者结合深度强化学习与传统方法,如人工势场法[11 -13 ] ,增强经验学习能力. 引入LSTM网络[14 -17 ] 进一步提升对连续状态信息的处理能力,加速训练并提升泛化效果. Xie等[18 ] 在训练过程中使用简单控制器对深度强化学习模型进行引导,以达到提升样本质量的目的. ...
好奇心蒸馏双Q网络移动机器人路径规划方法
1
2023
... 近年来,深度强化学习因硬件进步而得到快速发展[7 -8 ] . DQN、DDPG、PPO、TD3等算法通过强化策略学习显著提升导航的性能[9 -10 ] ,TD3引入双Q网络以减少高估偏差. 部分研究者结合深度强化学习与传统方法,如人工势场法[11 -13 ] ,增强经验学习能力. 引入LSTM网络[14 -17 ] 进一步提升对连续状态信息的处理能力,加速训练并提升泛化效果. Xie等[18 ] 在训练过程中使用简单控制器对深度强化学习模型进行引导,以达到提升样本质量的目的. ...
Inspection robot navigation based on improved TD3 algorithm
1
2024
... 近年来,深度强化学习因硬件进步而得到快速发展[7 -8 ] . DQN、DDPG、PPO、TD3等算法通过强化策略学习显著提升导航的性能[9 -10 ] ,TD3引入双Q网络以减少高估偏差. 部分研究者结合深度强化学习与传统方法,如人工势场法[11 -13 ] ,增强经验学习能力. 引入LSTM网络[14 -17 ] 进一步提升对连续状态信息的处理能力,加速训练并提升泛化效果. Xie等[18 ] 在训练过程中使用简单控制器对深度强化学习模型进行引导,以达到提升样本质量的目的. ...
1
... 近年来,深度强化学习因硬件进步而得到快速发展[7 -8 ] . DQN、DDPG、PPO、TD3等算法通过强化策略学习显著提升导航的性能[9 -10 ] ,TD3引入双Q网络以减少高估偏差. 部分研究者结合深度强化学习与传统方法,如人工势场法[11 -13 ] ,增强经验学习能力. 引入LSTM网络[14 -17 ] 进一步提升对连续状态信息的处理能力,加速训练并提升泛化效果. Xie等[18 ] 在训练过程中使用简单控制器对深度强化学习模型进行引导,以达到提升样本质量的目的. ...
1
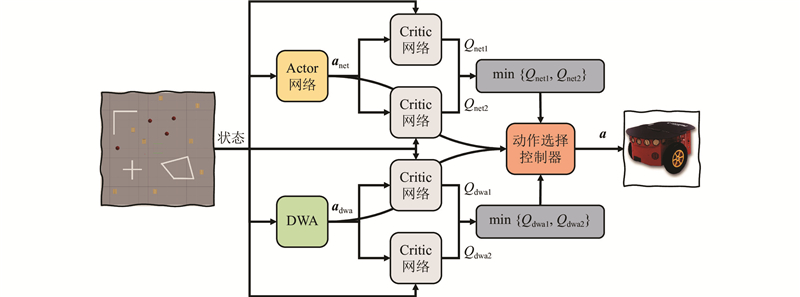
... 伴随深度强化学习的飞速发展,深度强化学习在无地图导航领域逐渐成为主流,然而深度强化学习方法需要进行大量的训练,该过程需要有足够多的优质数据才能训练出令人满意的模型[19 ] . 在无地图场景下导航无法获取最优的全局路径,仅依靠局部路径规划器无法实现高效导航[20 ] . 为了解决这些问题,结合神经网络的快速响应性和强鲁棒性[21 ] ,本文构建基于动态窗口法引导的TD3路径规划算法框架. 为了提升DWA局部路径规划算法在无地图环境下的表现,设计逃离机制,解决路径规划器易陷入局部最优的问题. 为了解决TD3算法训练速度慢、所需训练样本量大的问题,结合TD3算法与DWA,辅助TD3算法获得奖励更高的经验动作,以获得优质训练样本,加快算法的收敛进程. 引入LSTM网络,增强机器人对连续信息经验的学习能力,参考前序状态信息,进一步提升算法的训练效率,提高机器人的导航效果. ...
基于深度强化学习的无地图移动机器人导航
1
2024
... 伴随深度强化学习的飞速发展,深度强化学习在无地图导航领域逐渐成为主流,然而深度强化学习方法需要进行大量的训练,该过程需要有足够多的优质数据才能训练出令人满意的模型[19 ] . 在无地图场景下导航无法获取最优的全局路径,仅依靠局部路径规划器无法实现高效导航[20 ] . 为了解决这些问题,结合神经网络的快速响应性和强鲁棒性[21 ] ,本文构建基于动态窗口法引导的TD3路径规划算法框架. 为了提升DWA局部路径规划算法在无地图环境下的表现,设计逃离机制,解决路径规划器易陷入局部最优的问题. 为了解决TD3算法训练速度慢、所需训练样本量大的问题,结合TD3算法与DWA,辅助TD3算法获得奖励更高的经验动作,以获得优质训练样本,加快算法的收敛进程. 引入LSTM网络,增强机器人对连续信息经验的学习能力,参考前序状态信息,进一步提升算法的训练效率,提高机器人的导航效果. ...
基于深度强化学习的无地图移动机器人导航
1
2024
... 伴随深度强化学习的飞速发展,深度强化学习在无地图导航领域逐渐成为主流,然而深度强化学习方法需要进行大量的训练,该过程需要有足够多的优质数据才能训练出令人满意的模型[19 ] . 在无地图场景下导航无法获取最优的全局路径,仅依靠局部路径规划器无法实现高效导航[20 ] . 为了解决这些问题,结合神经网络的快速响应性和强鲁棒性[21 ] ,本文构建基于动态窗口法引导的TD3路径规划算法框架. 为了提升DWA局部路径规划算法在无地图环境下的表现,设计逃离机制,解决路径规划器易陷入局部最优的问题. 为了解决TD3算法训练速度慢、所需训练样本量大的问题,结合TD3算法与DWA,辅助TD3算法获得奖励更高的经验动作,以获得优质训练样本,加快算法的收敛进程. 引入LSTM网络,增强机器人对连续信息经验的学习能力,参考前序状态信息,进一步提升算法的训练效率,提高机器人的导航效果. ...
1
... 伴随深度强化学习的飞速发展,深度强化学习在无地图导航领域逐渐成为主流,然而深度强化学习方法需要进行大量的训练,该过程需要有足够多的优质数据才能训练出令人满意的模型[19 ] . 在无地图场景下导航无法获取最优的全局路径,仅依靠局部路径规划器无法实现高效导航[20 ] . 为了解决这些问题,结合神经网络的快速响应性和强鲁棒性[21 ] ,本文构建基于动态窗口法引导的TD3路径规划算法框架. 为了提升DWA局部路径规划算法在无地图环境下的表现,设计逃离机制,解决路径规划器易陷入局部最优的问题. 为了解决TD3算法训练速度慢、所需训练样本量大的问题,结合TD3算法与DWA,辅助TD3算法获得奖励更高的经验动作,以获得优质训练样本,加快算法的收敛进程. 引入LSTM网络,增强机器人对连续信息经验的学习能力,参考前序状态信息,进一步提升算法的训练效率,提高机器人的导航效果. ...
1
... 伴随深度强化学习的飞速发展,深度强化学习在无地图导航领域逐渐成为主流,然而深度强化学习方法需要进行大量的训练,该过程需要有足够多的优质数据才能训练出令人满意的模型[19 ] . 在无地图场景下导航无法获取最优的全局路径,仅依靠局部路径规划器无法实现高效导航[20 ] . 为了解决这些问题,结合神经网络的快速响应性和强鲁棒性[21 ] ,本文构建基于动态窗口法引导的TD3路径规划算法框架. 为了提升DWA局部路径规划算法在无地图环境下的表现,设计逃离机制,解决路径规划器易陷入局部最优的问题. 为了解决TD3算法训练速度慢、所需训练样本量大的问题,结合TD3算法与DWA,辅助TD3算法获得奖励更高的经验动作,以获得优质训练样本,加快算法的收敛进程. 引入LSTM网络,增强机器人对连续信息经验的学习能力,参考前序状态信息,进一步提升算法的训练效率,提高机器人的导航效果. ...
基于改进人工势场法的无人车路径规划算法
1
2022
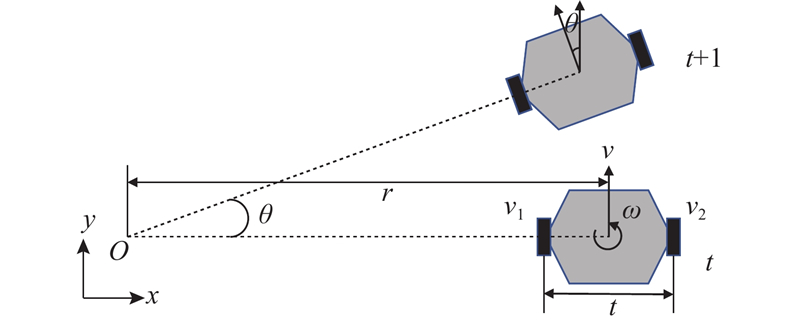
... 为了在DWA算法中进行线速度与角速度的评价,须建立机器人运动学的数学模型. 研究对象为双轮差速底盘机器人[22 ] (见图1 ). ...
基于改进人工势场法的无人车路径规划算法
1
2022
... 为了在DWA算法中进行线速度与角速度的评价,须建立机器人运动学的数学模型. 研究对象为双轮差速底盘机器人[22 ] (见图1 ). ...
1
... 动态窗口法具有决策延迟低、安全性高、多约束耦合能力强等优点,是高效且可靠的导航方法,因此将其与深度强化学习进行结合,提升导航性能. 动态窗口法需要在速度空间内对$ v $ $ \omega $ [23 ] . 由于机器人的固有特性和环境约束,速度空间会被限制在一定范围内. 速度空间的选取需要考虑其极限速度: ...
1
... 由于DWA作为局部路径规划算法,在无先验地图的情况下极易陷入局部最优. 针对该问题,在原始评级函数的基础上设计逃离机制. 评价函数的原理是在符合各种约束的速度空间中采样多组速度,模拟出一定时间内的轨迹[24 ] . 通过评价函数对这些轨迹进行评价,选出一条相对最优的轨迹和速度,评价函数的数学表达式如下: ...
Autonomous navigation of UAV in multi-obstacle environments based on a deep reinforcement learning approach
1
2022
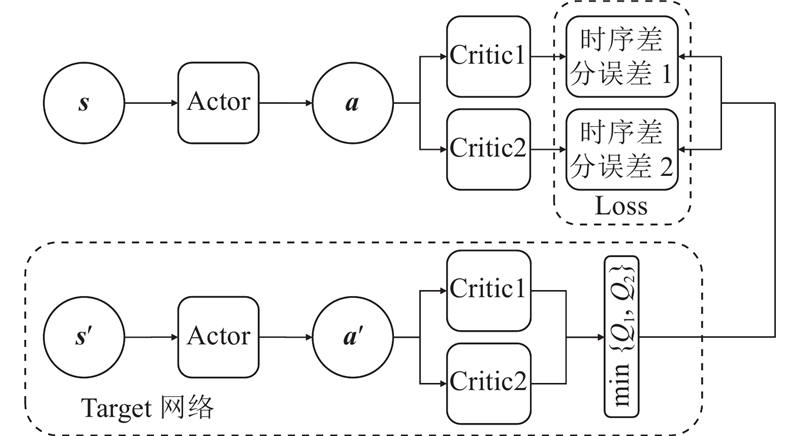
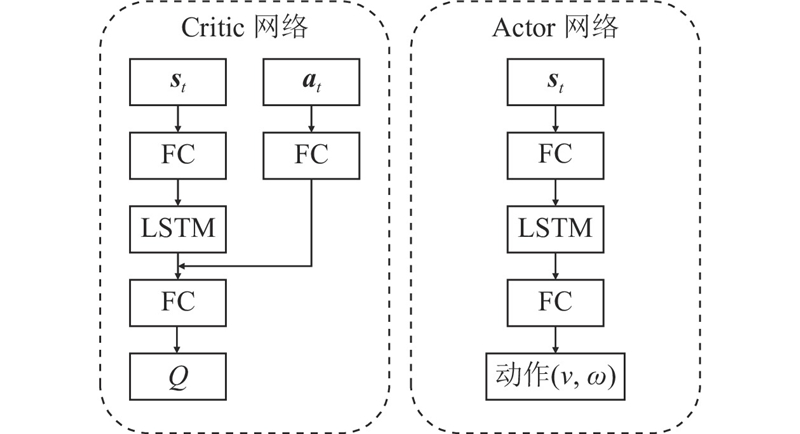
... 在TD3算法的训练过程中,网络从经验池中获取当前时刻的状态值、动作值、奖励值和$t+1$ $ \left( {{\boldsymbol{s}},{\boldsymbol{a}},r,{{\boldsymbol{s}}_{t+1}}} \right) $ $t+1$ [25 ] . 由2个Critic网络计算得到Q ,计算得到目标值$y$
融合LSTM和PPO算法的移动机器人视觉导航
1
2022
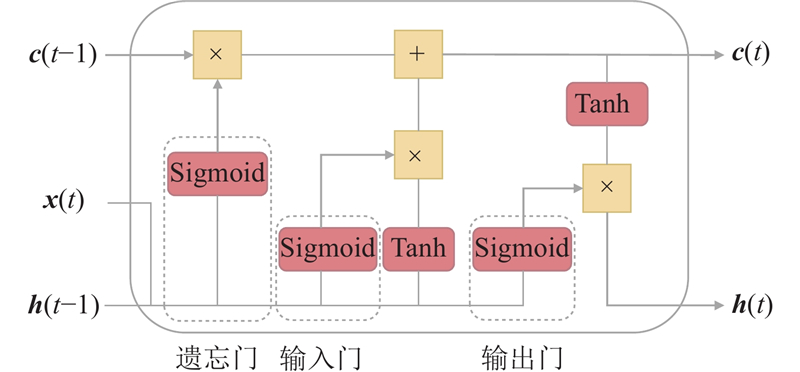
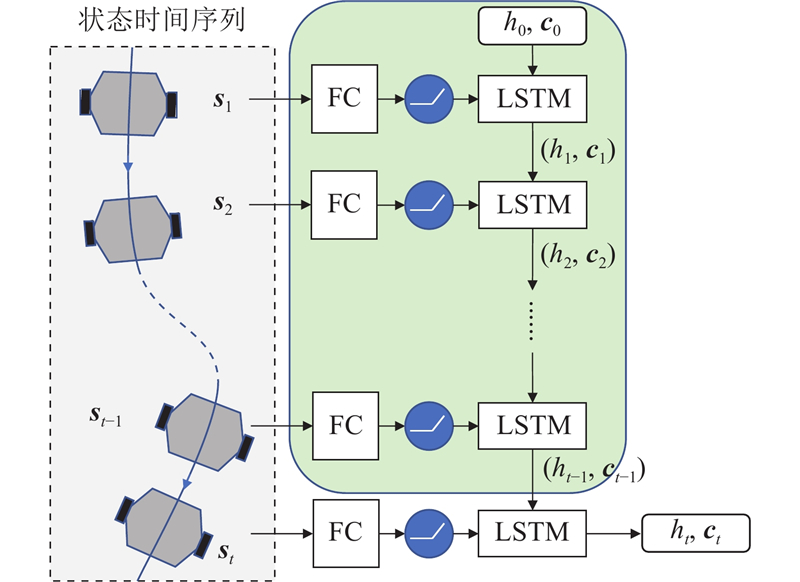
... 长短期记忆神经网络是RNN的衍生版本,具有特殊的网络结构,这种结构有利于避免RNN中长期依赖的问题. 在单个LSTM单元中,包括3个门结构,分别为遗忘门、记忆门与输出门. 其中遗忘门能够选择新输入信息${{\boldsymbol{x}}_t}$ ${{\boldsymbol{h}}_{t - 1}}$ ${{\boldsymbol{x}}_t}$ ${{\boldsymbol{h}}_{t - 1}}$ ${\boldsymbol{c}}$ [26 ] 如图4 所示. ...
融合LSTM和PPO算法的移动机器人视觉导航
1
2022
... 长短期记忆神经网络是RNN的衍生版本,具有特殊的网络结构,这种结构有利于避免RNN中长期依赖的问题. 在单个LSTM单元中,包括3个门结构,分别为遗忘门、记忆门与输出门. 其中遗忘门能够选择新输入信息${{\boldsymbol{x}}_t}$ ${{\boldsymbol{h}}_{t - 1}}$ ${{\boldsymbol{x}}_t}$ ${{\boldsymbol{h}}_{t - 1}}$ ${\boldsymbol{c}}$ [26 ] 如图4 所示. ...