种植牙技术是近几十年发展起来的一种治疗牙齿脱落的有效手术方法,长期使用效果较好,因此近些年来得到越来越多患者的选择[1]. 传统种植牙技术门槛较高,手术操作流程复杂,医生学习周期长,学习成本较高,对手术操作者提出很高的要求,非常不利于手术的推广. 在传统的种植牙手术过程中,术前医生会制定严谨的手术方案,通过手持种植牙钻进行骨钻孔,这难免引入人为误差,很难按照术前规划路径进行钻孔植入,医生的主观因素对手术精度和手术成功率影响较大[2-3]. 近些年来人工智能、CAD、CAM、3D打印等现代工程技术逐渐在医疗领域得到广泛应用,现代医学逐步迈向智能医疗、精准医疗的时代[4-5],手术机器人作为一种特殊的医疗器械受到越来越多的关注,因此研究出具有良好使用效果的种植牙手术机器人系统具有重要意义.
种植牙手术机器人系统相比较传统种植牙技术优势明显,手术过程更为客观,手术精度高,稳定性好,可以严格按照术前设计路径进行植入[6-7],并且大大降低了人力成本、经济成本、手术安全成本和医生的手术操作难度,有利于种植牙手术的推广.机器人末端执行器的运动规划作为口腔种植机器人系统的重要技术之一,对技术要求也越来越严格.为了确保机器人工作时的精度和效率,提高使用寿命,需要采用连续的轨迹规划策略. 机器人轨迹规划一般包括位置规划和姿态规划[8],基于现代计算几何算法的理论基础,机器人位置轨迹规划算法现在已经较为成熟,常用方法有多项式插值法、B样条插值法[9]、NURBS曲线[10]等. 姿态轨迹规划相对复杂,姿态的描述属于
机器人姿态常见的表示方法包括旋转矩阵、欧拉角、旋转向量、四元数等.旋转矩阵采用9个元素来描述姿态旋转,因为内存消耗较大并且计算复杂,所以很少直接用于实时性较高的姿态轨迹规划;欧拉角表示方便,仅使用3个元素,按照既定的旋转顺序绕坐标轴进行旋转,缺点在于存在万向节锁死问题即导致连续插补较为困难[11];旋转向量即旋转角度与单位转轴相乘的三维向量,简单直观、容易理解、插补效果较好,但有如下缺点:1)当旋转角度为0或
单位四元数具有提供平滑插值、避免万向节锁死等优点,被广泛应用于机器人末端的姿态规划中.目前广泛应用的姿态插补算法主要有Shoemake[16]提出的球面线性插值(spherical linear interpolation,SLERP)和球面立体插值(spherical and quadrangle,SQUAD).SLERP算法计算简单,可以高效地实现两姿态间的平滑插值.
当SLERP算法对多姿态进行插值时,轨迹在分段连接点处存在尖点不光滑,这会给机器人关节带来冲击和损害,因此SLERP算法不适合用于多姿态轨迹插值.为了实现多姿态间的平滑插值,Shoemake结合SLERP算法和Bézier曲线提出球面立体插值SQUAD算法. 该方法实现多姿态轨迹曲线的连续,但是仍难以满足机器人多姿态轨迹高阶平滑插值的需求,被认为是一个较为成熟的姿态插补算法.
为了进一步提高多姿态轨迹曲线的高阶平滑性,Kim等[17]通过类比欧氏空间中的样条曲线,提出
本研究开发一套自动化程度较高的种植牙手术机器人系统,介绍相关硬件设备及技术指标,对系统各空间坐标系转换进行分析. 针对现有四元数多姿态插值方法存在的高阶连续性差. 求解复杂等问题,基于四元数与旋转向量的关系,重点提出一种C2连续的多姿态平滑插值算法. 通过将单位四元数映射到三维空间中进行插值计算,大大减少计算难度,最后通过实验与其他已知姿态插值算法对比分析,验证所提算法的可行性和有效性.
1. 系统搭建
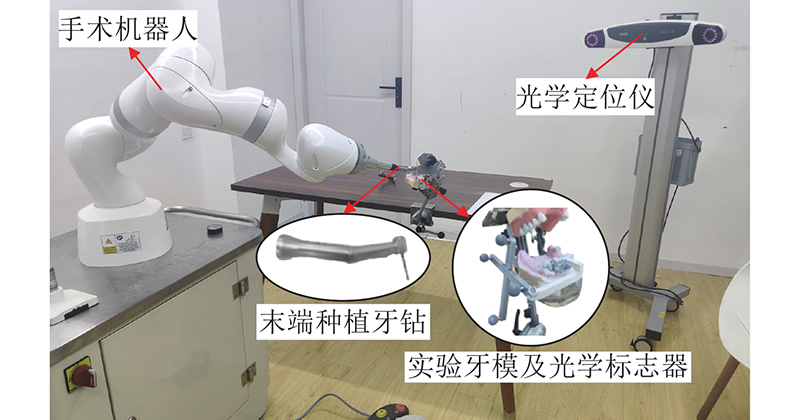
为了开发口腔种植机器人系统,对于种植手术的基本流程和需求进行阐述和分析,尽管市面上或研究中出现的种植系统不同,所遵循的种植牙手术基本原则是一致的. 广义的种植牙手术包含有术前设计、种植位点制孔、种植体植入、种植牙修复以及其他相关手术等流程. 本研究所开发的种植牙手术机器人系统重点在于种植位点制孔及种植体植入. 种植牙手术的核心要求是将种植体准确、安全、稳定地放置在术前设计的种植位点之上,并且在术后愈合中能够形成较为良好的骨结合,因此准确性和稳定性是影响手术成功的关键因素.根据口腔种植手术的需求,本研究基于光学定位技术开发一套自动化程度较高的种植牙手术机器人系统,该系统主要分为硬件与软件2个部分,硬件部分主要有主控计算机、机器人本体、机器人控制柜、末端执行器、视觉导航设备以及相关标志器.本系统选用的机器人为KUKA公司研发的LBR Med 7 R800医疗机器人,该机器人采用S-R-S (spherical-rotational-spherical)运动学结构,具有7个自由度,重量轻便,工作空间可以满足口腔种植手术的要求,具有精确、灵活、安全及灵敏等优点,主要性能参数如表1所示.
表 1 LBR Med 7 R800机器人性能参数
Tab.1
| 性能指标 | 参数 |
| 最大负载/kg | 7.0 |
| 轴数 | 7 |
| 定位精度/mm | ±0.1 |
| 转速精度/% | ±2.0 |
| 重量/kg | 25.5 |
| 防护等级 | IP54 |
表 2 Polaris Vega XT系统技术参数
Tab.2
| 技术指标 | 参数 |
| 定位误差/mm | 0.12 |
| 最大帧频/Hz | 250 |
| 平均延迟/ms | <4.00 |
| 视场范围/mm | 950~2 400 |
| 工具类型 | 被动式 |
| 工具最大数量/件 | 25 |
图 1
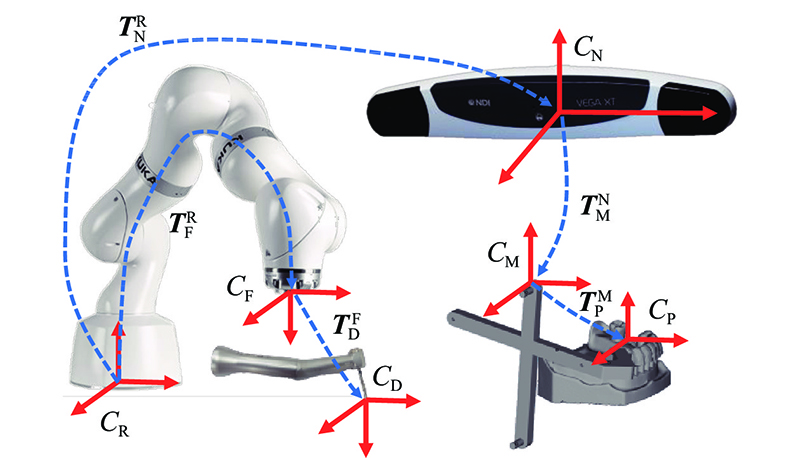
为了集成手术机器人系统,提高种植手术的准确性和精度,需要引入各坐标系以及明确各坐标系间的转换关系,手术机器人系统坐标系转换关系如图2所示. 该系统主要包含6个坐标系:机器人基坐标系
图 2
图 2 手术机器人系统坐标系转换关系
Fig.2 Coordinate system transformation relationship of surgical robot system
2. 多姿态轨迹平滑规划方法
种植牙手术对机器人末端姿态的精度及平滑性有着极高的要求,基于四元数与旋转向量的转换关系,提出一种
2.1. 基于旋转向量的四元数插值原理
选用旋转向量和四元数作为主要姿态插补和表示方法,并且对该方法的可行性做理论解释. 单位四元数的一般数学表达方式为
式中:
若是单位四元数
由式(2)不难看出单位四元数的对数运算与对应旋转向量之间的关系,即前者的虚部向量是后者的一半. 当对样条曲线取指数运算后,高阶连续性保持不变,因此可以在三维空间中对旋转向量进行插值运算,旋转向量对应的四元数将保持三维空间中所具有的连续性,由此实现在三维空间中对四元数进行高阶连续的姿态插值运算. 基于四元数与旋转向量之间的关系及优缺点,决定采用在三维空间中对旋转向量进行平滑插值,再映射回四元数空间,使用单位四元数进行姿态表示的方法. 在四元数
根据式 (3)将
2.2. 三次准均匀B样条曲线插值
均匀B样条曲线的特点是节点矢量均匀分布,B样条基函数在各节点区间内具有统一的表达式,使得计算处理起来简单方便,计算效率较高. 缺点是未保留Bézier曲线的端点几何性质,即均匀B样条曲线不再经过控制多边形的首末控制点. 为了获得更好的端点性质,采用三次准均匀B样条曲线用来构造平滑过渡曲线.
B样条曲线定义:
式中:
控制点与基函数一一对应,B样条基函数可由de Boor-Cox递推定义,曲线构造需要求解B样条曲线在端点处的一阶导数和二阶导数. 由于只关注B样条曲线端点处的导数计算,根据B样条曲线导数的基本性质求解,对于
由式(6)和(7)求得导数曲线的节点矢量和控制点,从而导数曲线方程为
导数曲线首末节点的重复度仍为次数加1,故导数曲线仍过首末控制点,则B样条曲线首末端点处的一阶导数和二阶导数为
2.3. 平滑过渡曲线构造
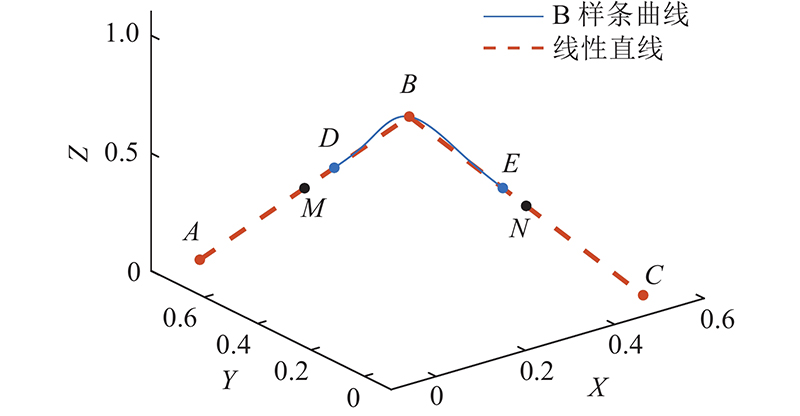
将单位四元数从
图 3
点
为了得到
由式(5)在点
式中:
关于过渡点
式中:l0为线段BD和BE的长度,l1为线段BM和BN长度的较小值,l0、l1均为中间变量.
再根据过渡点
由式(9)和 (10),带入式(14)得:
由式(12)和(15)共7个方程,求解出7个控制点,得到一条
3. 实验分析与验证
为了验证所提算法构造的姿态过渡曲线的平滑性,现以一组具体的关键姿态数据为例,如表3所示,其中,
表 3 关键姿态信息
Tab.3
| 序号 | | | | |
| | | | | |
| | | | | |
| | | | | |
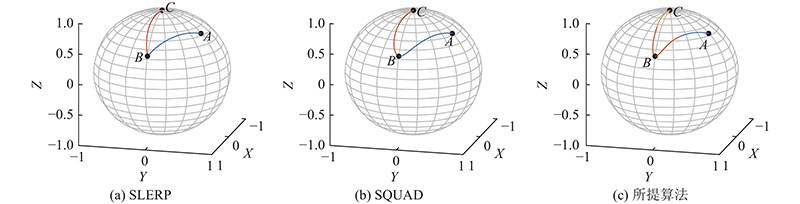
利用Hopf映射将单位四元数从
图 4
图 4 不同算法的四元数多姿态插值曲线
Fig.4 Quaternion multi-orientation interpolation curves for different algorithms
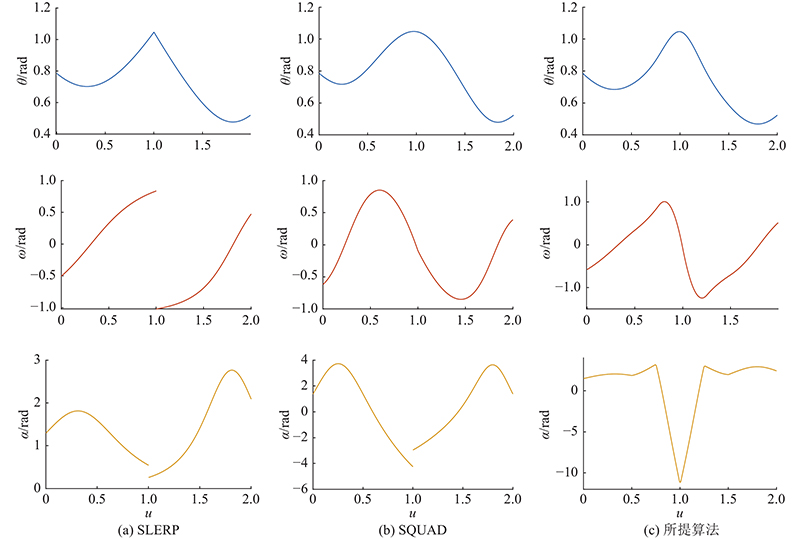
实验计算得到SLERP、SQUAD和所提方法3种插值算法在姿态插补过程中的旋转角度
图 5
图 5 多姿态插补过程中旋转角度、角速度和角加速度变化曲线
Fig.5 Augular, angular velocity and angular acceleration changing curves during multi-orientation interpolation
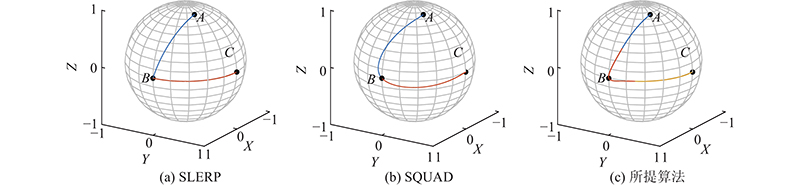
对3种插值方法的转轴矢量进行分析,如图6所示. 所提算法和SQUAD计算得到的转轴矢量曲线均是连续平滑的, SLERP方法的转轴矢量轨迹在连接点处存在明显的尖点不够平滑,故不适合用于机器人的多姿态插值计算.
图 6
图 6 不同算法的转轴矢量轨迹曲线
Fig.6 Rotation axis trajectory curves for different algorithms
为了比较不同姿态插值算法的实时性能,在Windows 10操作系统上使用Matlab计算平台进行测试,用3种姿态插值算法对给定不同数量的随机关键姿态进行插值计算,取插补步长
表 4 不同算法的计算时间
Tab.4
| 关键姿态数量 | | ||
| SLERP | SQUAD | 所提算法 | |
| 3 | 0.618 | 18.200 | 5.690 |
| 50 | 10.200 | 451.0 | 169.0 |
| 100 | 21.1 | 917.0 | 346.0 |
SLERP算法计算简单,在相同数量的关键姿态进行插值时,计算时间最短;SQUAD算法在计算控制点的过程中,涉及四元数的指数和对数运算,故计算时间结果最长;所提算法在三维空间中构造曲线,计算相对简单,故实时性能相比SQUAD算法有较大提升.
在算法的插值精度方面,由上节的理论分析可知,3种算法通过每一个给定的关键姿态. 在对相同的随机关键姿态进行插值时,表5比较不同插值方法所需总角位移
表 5 不同算法的总角位移
Tab.5
| 关键姿态数量 | | ||
| SLERP | SQUAD | 所提算法 | |
| 3 | 4.541 | 4.587 | 4.561 |
| 100 | 197.5 | 212.9 | 203.9 |
| 1000 | 2188 | 2468 | 2282 |
为了进一步验证所提多姿态平滑插值算法的合理性,实验利用机器人平台进行应用层面的测试. 与理论仿真一样,给定表3中的3个关键姿态,利用不同的四元数插值算法对姿态轨迹进行规划并且对机器人进行逆运动学求解;针对本系统中S-R-S构型的七自由度机器人逆解优化问题,采用臂角法得到逆解的封闭解,根据关节避限和避奇异的要求,构建目标函数进行求解,实现逆运动学最优解的选取,最终通过分析机器人笛卡尔空间欧拉角的变化情况来评价算法.
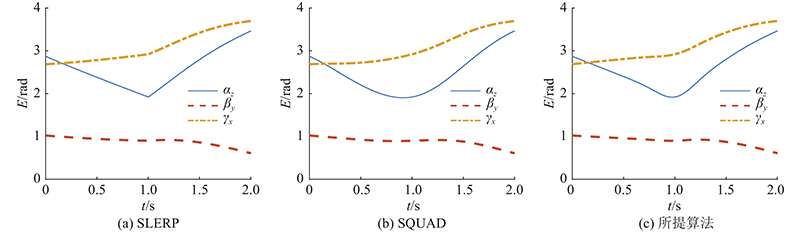
通过采集机器人末端相对于机器人基坐标系的欧拉角
图 7
图 7 不同算法的机器人笛卡尔空间欧拉角变化
Fig.7 Change of euler angles in robot Cartesian space for different algorithms
4. 结 论
针对传统种植牙技术门槛较高、手术操作流程复杂等缺点,本研究基于光学定位技术开发了一套种植牙手术机器人系统,介绍相关硬件设备及技术指标,并对系统空间坐标系转换等关键技术进行研究.针对手术机器人末端执行器姿态运动要求较高等特点,重点提出一种基于四元数和旋转向量的多姿态C2连续的平滑插值算法,通过在三维空间中采用线性插值与三次B样条曲线平滑拼接的方式实现对四元数C2连续的多姿态平滑插值.实验结果表明,所提多姿态插值算法相较于传统四元数插值算法SLERP和SQUAD具有C2连续性,并且计算量和所需的总角位移较小,在实时性能和运动效率方面优于SQUAD算法,更适用于机器人多姿态的轨迹规划.
参考文献
Long-term (10-year) dental implant survival: a systematic review and sensitivity meta-analysis
[J].DOI:10.1016/j.jdent.2019.03.008 [本文引用: 1]
Survival of dental implants at sites after implant failure: a systematic review
[J].DOI:10.1016/j.prosdent.2018.11.007 [本文引用: 1]
Risk factors related to late failure of dental implant: a systematic review of recent studies
[J].DOI:10.3390/ijerph17113931 [本文引用: 1]
Pilot study of a surgical robot system for zygomatic implant placement
[J].DOI:10.1016/j.medengphy.2019.07.020 [本文引用: 1]
Nanotechnology for modern medicine: next step towards clinical translation
[J].DOI:10.1111/joim.13254 [本文引用: 1]
Automatic robot-world calibration in an optical-navigated surgical robot system and its application for oral implant placement
[J].DOI:10.1007/s11548-020-02232-w [本文引用: 1]
An image-guided hybrid robot system for dental implant surgery
[J].DOI:10.1007/s11548-021-02484-0 [本文引用: 1]
An approach for smooth trajectory planning of high-speed pick-and-place parallel robots using quintic B-splines
[J].DOI:10.1016/j.mechmachtheory.2018.04.026 [本文引用: 1]
Perspectives on Euler angle singularities, gimbal lock, and the orthogonality of applied forces and applied moments
[J].DOI:10.1007/s11044-018-9620-0 [本文引用: 1]
基于四元数和B样条的机械手平滑姿态规划器
[J].
Smooth orientation planner for manipulators based on quaternion and B-spline
[J].
Kinematic modeling and control of a robot arm using unit dual quaternions
[J].DOI:10.1016/j.robot.2015.12.005 [本文引用: 1]
Smooth orientation interpolation using parametric quintic-polynomial-based quaternion spline curve
[J].DOI:10.1016/j.cam.2017.07.007 [本文引用: 1]
Animating rotation with quaternion curves
[J].DOI:10.1145/325165.325242 [本文引用: 1]
A general construction scheme for unit quaternion curves with simple high order derivatives
[J].
C2-continuous orientation trajectory planning for robot based on spline quaternion curve
[J].DOI:10.1108/AA-04-2017-050 [本文引用: 2]
C2-continuous orientation planning for robot end-Effector with B-Spline curve based on logarithmic quaternion
[J].
A practical algorithm for smooth interpolation between different angular positions
[J].
On the biharmonic and harmonic indices of the Hopf map
[J].DOI:10.1090/S0002-9947-07-03934-7 [本文引用: 1]