机电伺服系统具有结构简单、环保、高效的特点,被广泛应用于社会生产各个领域,如机械臂、精密转台、医疗仪器等. 随着社会需求的增加,机电系统工作环境日趋复杂,工作强度也越来越大,出现故障的几率也随之大大增加,而对产品可靠性的要求却与日俱增,因此故障检测与容错控制系统的设计就变得尤为重要.
故障检测方法可以大致分为2种:基于信号的故障检测和基于模型的故障检测. 基于信号的故障检测方法主要依赖数据测量与处理技术,根据提取的故障特征来判断是否发生故障[1],基于模型的故障检测方法则是利用冗余的系统解析模型输出与系统真实输出产生残差,来判别系统是否发生故障[2]. 基于模型的故障检测方法常用的模型有卡尔曼滤波器[3-4]、自适应滑模观测器[5-10]、未知输入观测器[11]等. 其中自适应滑模观测器因其自身的变结构,对噪声和干扰具有较强的鲁棒性,但敏感性也会相对下降.陶立权等[12]采用自适应滑模观测器直接检测故障信息,设定了故障的阈值检测故障,但是要求故障上界已知. 穆凌霞等[13]首先设计了一个辅助输出系统,再针对辅助输出系统设计了自适应滑模观测器,在此基础上进行了故障重构,但是其设计的自适应滑模观测器不能较好地区分扰动和故障,故障识别准确率不太高.
容错控制是基于系统故障检测、诊断和控制理论的非线性智能控制方法,可以分为被动容错控制和主动容错控制.其中,被动容错控制将系统故障看作干扰,利用鲁棒技术使控制器对故障发生与否不敏感[14-15],其结构简单、易于工程实现,但缺乏针对性,控制器设计较为保守;主动容错控制利用在线故障检测结果,进行针对性的控制器调节,使系统性能不受故障的影响或影响减小,因此可以恢复系统部分甚至全部控制性能. Gayaka等[16-18]做了大量而细致的工作,指出伺服系统的固有非线性、随环境及工况正常变化的参数不确定性及未建模干扰(不确定性非线性,如摩擦、外干扰)是基于模型的故障检测难于设计及难以应用于工程实践的原因,并提出了有针对性的故障检测策略,如间接自适应策略、鲁棒非线性观测器,获得了较好的理论分析结果,并在此基础上设计了容错控制器. 国内科研院校也在这个领域进行了积极的探索研究,Zhu等 [19]将故障分为传感器故障和作动器故障,将系统状态、传感器故障和执行器故障作为增维系统的状态变量,利用观测器的状态估计,对传感器和执行器实现故障重构,从而定位到故障发生的具体传感器或者执行器,并在此基础上设计了容错控制器,但即便如此,其本质上仍然是基于模型的故障检测及主动容错设计,在不明确系统参数变化的原因时,故障检测效果一般.
基于上述分析,针对可能发生故障的机电伺服系统,本研究提出基于自适应神经网络滑模观测器的快速终端滑模容错控制策略,提高了观测器在故障发生时的状态估计精度以及故障检测准确性. 观测器精度的提高保证了容错控制器的容错性能和控制精度.
1. 系统建模与问题描述
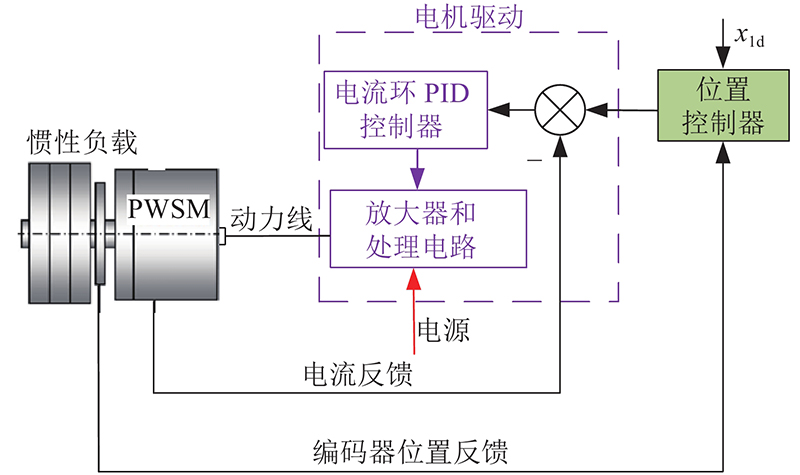
机电伺服作动系统主要由伺服驱动器及执行电机、机械传动机构、惯性负载、传感器(信号测量仪器:光电编码器或旋转变压器)、控制器以及其他的电气连接设备等部分组成,其系统组成如图1所示.
图 1
本研究以永磁同步电机作为机电控制系统的执行器,根据牛顿第二定律,建立永磁同步电机控制系统的数学模型:
式中:m为负载折算到电机端的转动惯量;y为电机位置输出量;ku为电机力矩系数;u为控制输入;B为作动器系统折算到电机的黏性阻尼系数;dn为未建模动态干扰;
式中:
将式(1)两边同时除以转动惯量
式中:
将式(3)转化为状态空间形式,选取系统状态变量x =[x1, x2]T = [y,
式(4)也可以写为
式中:
通过式(5),容易验证系统的参数矩阵A、C、D满足
式中:
由文献[14]可以证明式(6)与式(5)的不变零点相同.
经验证
假设1 故障
2. 自适应神经网络滑模观测器设计
观测器的设计是基于自适应滑模观测器,引入RBF神经网络,利用神经网络的逼近能力,准确估计故障,以获得更好的状态重构效果,思路如下.
对于辅助输出系统(式(6)),设计如下观测器:
式中:V1(t)为滑模变结构输入信号,
式中:
式中:
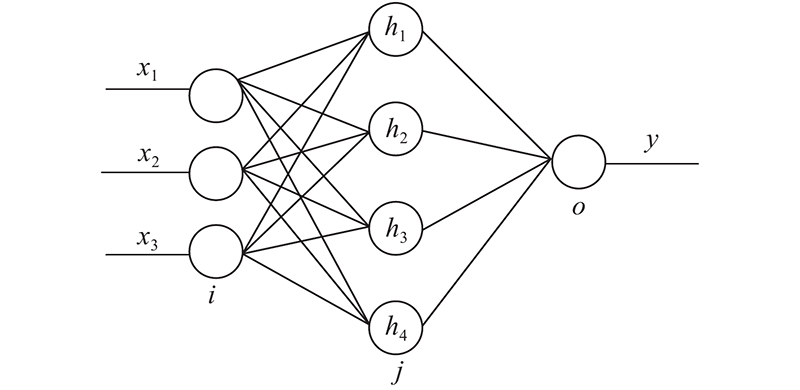
图 2
第1层为输入层,第2层为隐含层,第3层为输出层,激活函数采用高斯基函数
式中:
式中:
根据神经网络的特性,
引理1
定理1 对于满足假设1的观测器(式(8)),应用参数自适应率(式(10))以及权值更新率(式(11)),可以实现观测误差有界稳定.
证明 设计李雅普诺夫函数,定义神经网络的权值估计误差
易知,式(14)是正定的,对其求导可得
将式(12)代入式(15)中,得到
将式(10)、(13)代入式(16),可以推得
将式(7)、(9)代入式(17),得到
由于
设计
定义
式中:
令
式(21)可以化简为
当t趋于无穷,
由状态观测器的观测误差,定义如下残差
当传感器发生故障时,残差
3. 容错控制器设计
根据上述观测器的设计以及系统状态方程,控制器设计步骤如下.
1)定义滑模面
定义误差:
式中:
式中:
对滑模面求导,得到
将式(25)代入可得
定义
2)设计控制器
根据式(29)设计控制器:
式中:ua为前馈补偿项, us为鲁棒项.
3)设计参数自适应率.
将式(30)代入(29),得到
式中:
取自适应函数
式中:
一般根据客观条件,假设1中的
式中:
4)设计鲁棒项.
设计线性鲁棒项
式中:
取如下的非线性鲁棒项
由观测误差有界稳定可知,存在正常数
不等式(35)的证明如下:
同理可证:
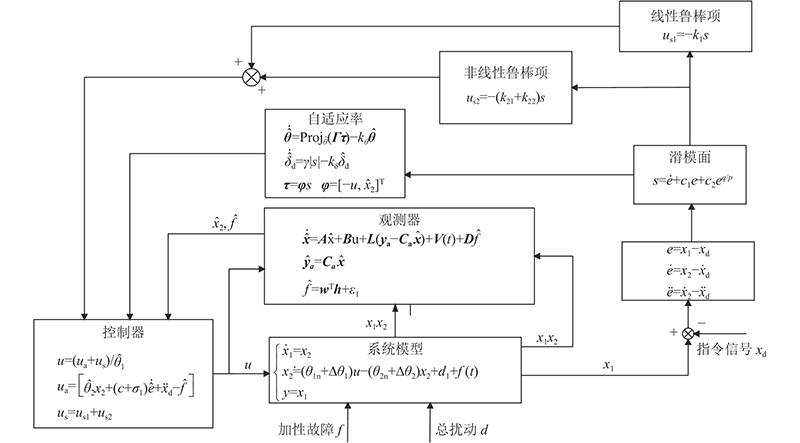
本节设计的总体控制策略结构,如图3所示.
图 3
定理2 对于辅助输出系统(式(6)),基于参数自适应率(式(32))和干扰上界自适应率(式(34))的控制器(式(30)),可以实现系统跟踪误差的有界稳定.
证明
设计李雅普诺夫函数:
根据式(29)、(32)、(34)可以证明,过程如下.
根据引理1,可证:
定义
故
有界稳定.
基于上述分析,所设计的容错控制器可以实现系统跟踪误差的有界稳定,所设计的基于自适应神经网络的滑模观测器可以很好地实现故障检测和状态估计.其中故障的估计,可以用于控制器前馈补偿项,以对故障进行补偿;状态的估计可以用于控制器的状态重构,从而实现主动容错控制.
4. 仿真与分析
为了验证所设计的快速终端滑模主动容错控制系统的有效性,对常见几种控制器的仿真结果进行比较分析,分别为PID控制器、普通快速终端滑模控制器、本研究设计的快速终端滑模主动容错控制器. 衡量跟踪精度的性能指标包括均值
为了验证本研究控制策略的有效性,系统给定信号
本研究想要呈现的是各控制器的最优控制性能对比图,由于各控制器的最优参数并不相同,参数选择会有所不同,参数如下.
1)PID控制器. PID控制器是工业控制中应用最广泛的控制器件,主要是由3个部分组成,包括比例环节kp、积分环节ki、微分环节kd. 3个参数各自功能不同,增加kp的值,可以加快响应速率,提高跟踪精度,但是太大会导致超调. 增加ki有利于减小系统的静态误差,以及在跟踪误差较小,kp系数调节效果不大时,能够进一步消除静态误差.增加系统的kd系数,会加快响应速度,减小系统的超调量,但是太大也会导致系统调节时间延长.根据实际工况下仿真的调试结果,系数选择如下:kp=100,ki=1,kd=2;
2)快速终端滑模控制器(fast terminal sliding mode,FTSM). 快速终端滑模是基于终端滑模进行改进的滑模控制器,在收敛速度上具有很大优势,快速终端滑模系统无论是在系统远离平衡位置还是接近平衡位置时,都能快速精确地收敛到平衡位置.根据实际工况下仿真的调试结果,各参数选择如下:
3)快速终端滑模主动容错控制器(fast terminal sliding mode active fault tolerant,FTSM_AFT). 快速终端滑模主动控制器,以RBF对故障的估计作为控制器前馈补偿项,重构控制器的结构,针对性较强,根据实际工况下仿真的调试结果,各参数选择如下:
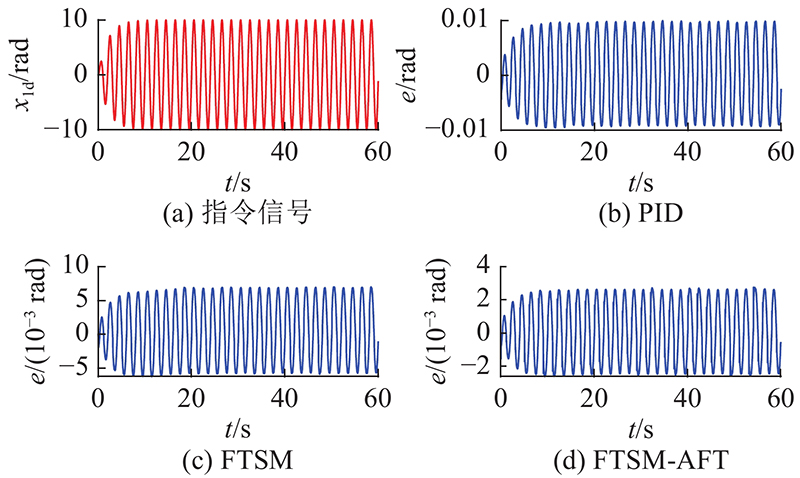
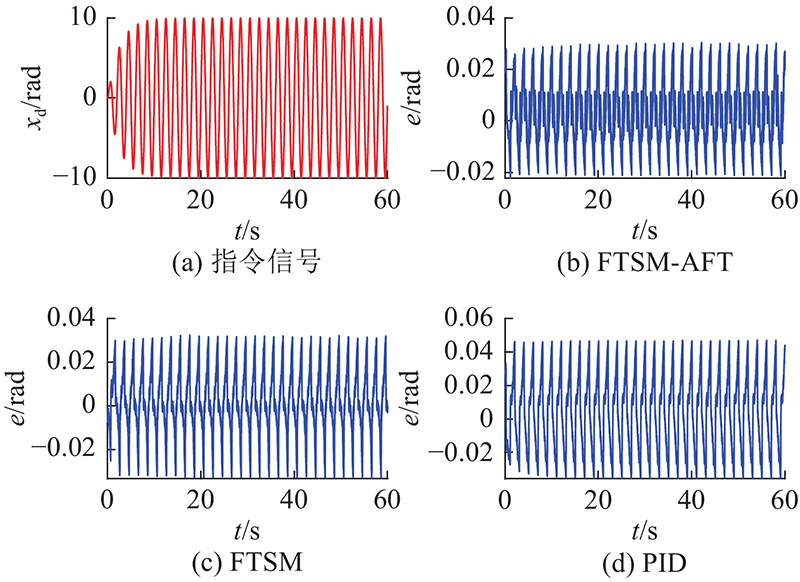
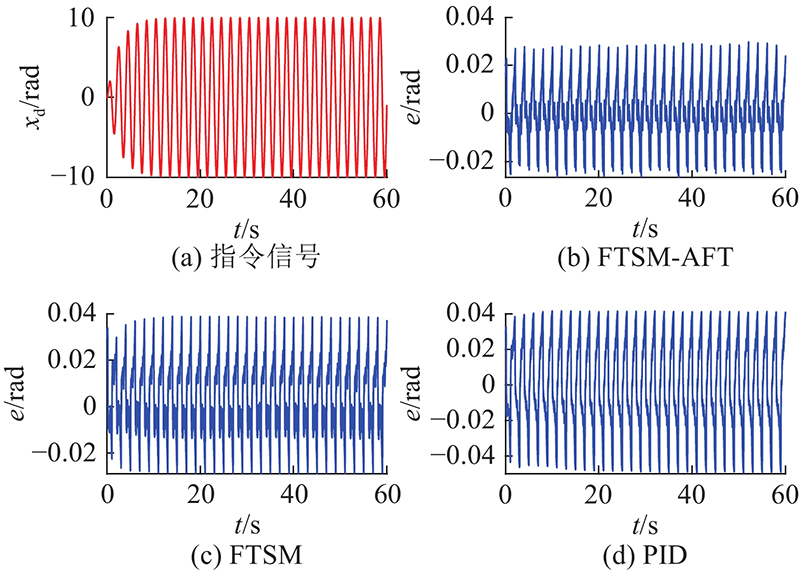
图 4
图 4 不同控制器位置指令的跟踪误差对比
Fig.4 Comparison of tracking errors of position commands of different controllers
图 5
图 6
图 7
表 1 各控制器性能指标
Tab.1
| 控制器 | Me/(°) | μ/(°) | σ/(°) |
| PID | 0.0105 | 0.0065 | 0.0032 |
| 快速终端滑模 | 0.0070 | 0.0043 | 0.0020 |
| 主动容错快速终端滑模 | 0.0028 | 0.0017 | 0.0010 |
由图5可以看出,参数估计值可以较快地收敛到真值,从而保证参数不确定性的补偿精度.针对系统中存在的非结构化不确定性设计了具有干扰上界自适应增益的鲁棒项加以克服. TSMC_AFT控制器在故障发生时利用神经网络对故障的估计值进行针对性的补偿,从而大大提高了控制精度.
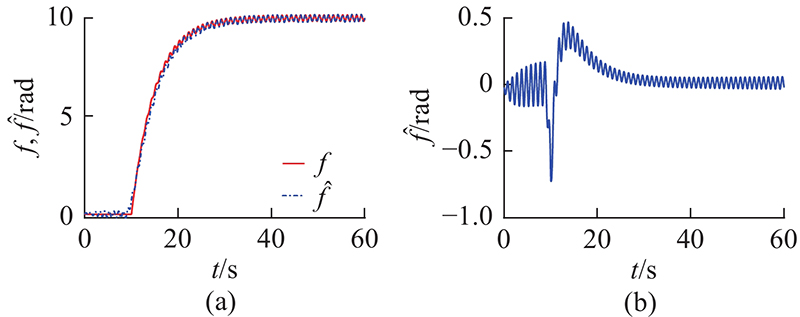
由图6可以看出,故障检测效果良好,这样就可以部分或者完全恢复系统在出现故障前的性能.
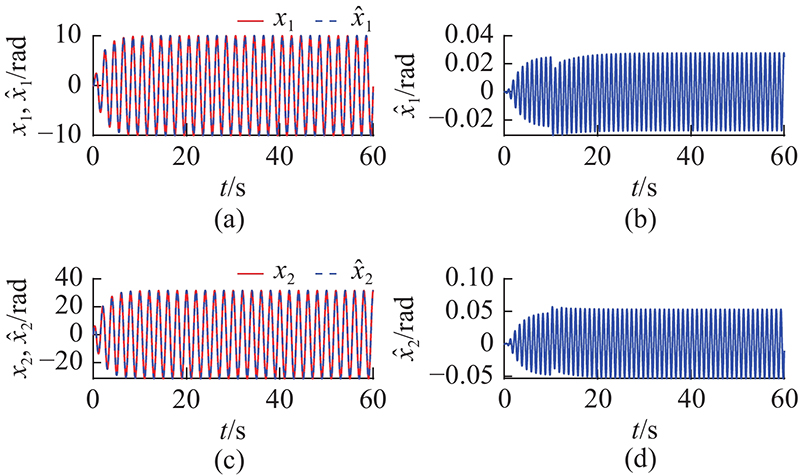
由图7可以看出,观测器通过故障补偿具有较好的状态估计性能,从而保证了基于状态重构的容错控制器的性能.而传统PID控制器则是依靠自身一定的鲁棒性克服故障和扰动,FTSM通过滑模变结构来克服故障和扰动,虽然比PID控制器性能有所提高,但相对于FTSM_AFT控制器由于缺少了针对性的补偿,性能依旧较差.
5. 实验与分析
为了进一步验证本研究提出的容错控制策略在实际工作场合的有效性,进行实验研究,并依旧与PID、快速终端滑模算法在控制精度和稳定性方面进行比较. 实验平台的结构如图8所示.该平台由底座、永磁同步电机运动系统(包括永磁同步电机、电动驱动器、旋转编码器、惯性板和联轴器)、电源、测控系统组成. 该测控系统包括监控软件和工控机.工控机配备实时操作系统,使用C语言编写控制程序. 工控机配有用于发送控制命令的16位数字/模拟(D/A)转换卡和用于采集光电编码器位置信息的16位采集卡. 控制周期为0.5 ms.系统速度由高精度位置信号的后向差产生. 同时,采用截止频率为50 Hz的二阶Butterworth滤波器对速度信号中的实测噪声进行抑制.
图 8
图 8 机电伺服控制实验平台结构图
Fig.8 Structure diagram of servo control experimental platform
实验环节采用3种控制器作对比,参考信号为
1)工况1. 仅存在加性故障
参数选择如下:
PID:
FTSM:
FTSM-AFT:
2)工况2. 存在加性故障
参数选择如下:
PID:
FTSM:
FTSM-AFT:
3)工况3. 存在加性故障信号
3种工况中f和d的设置和仿真中的设置是一样的.
参数选择如下.
PID:
FTSM:
FTSM-AFT:
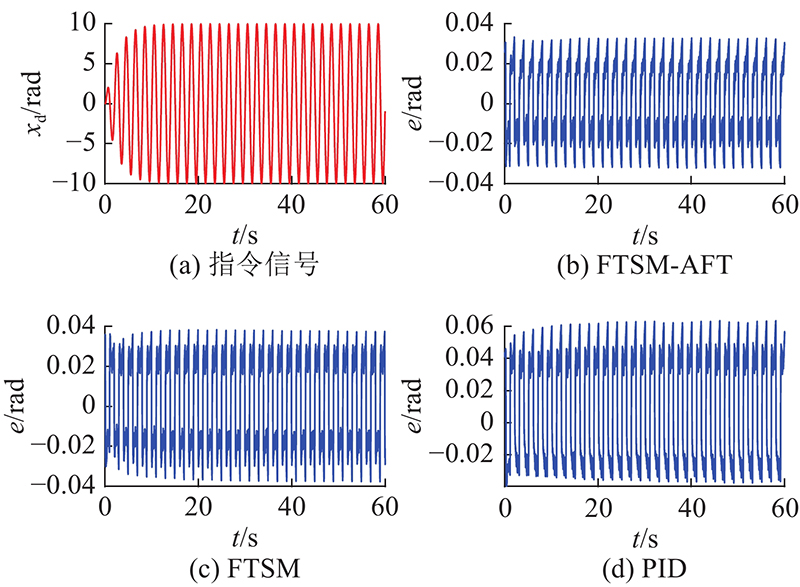
图 9
图 9 工况1下3种控制器跟踪误差对比
Fig.9 Comparison of tracking errors of three controllers under working condition one
图 10
图 10 工况2下3种控制器跟踪误差对比
Fig.10 Comparison of tracking errors of three controllers under working condition two
图 11
图 11 工况3下3种控制器跟踪误差对比
Fig.11 Comparison of tracking errors of three controllers under working condition three
表 2 工况1控制器性能指标
Tab.2
| 控制器 | Me/(°) | μ/(°) | σ/(°) |
| PID | 0.0472 | 0.0197 | 0.0121 |
| 快速终端滑模 | 0.0337 | 0.0114 | 0.0100 |
| 主动容错快速终端滑模 | 0.0306 | 0.0109 | 0.0081 |
表 3 工况2控制器性能指标
Tab.3
| 控制器 | Me/(°) | μ/(°) | σ/(°) |
| PID | 0.0416 | 0.0180 | 0.0108 |
| 快速终端滑模 | 0.0390 | 0.0140 | 0.0087 |
| 主动容错快速终端滑模 | 0.0299 | 0.0098 | 0.0084 |
表 4 工况3控制器性能指标
Tab.4
| 控制器 | Me/(°) | μ/(°) | σ/(°) |
| PID | 0.0636 | 0.0345 | 0.0121 |
| 快速终端滑模 | 0.0384 | 0.0228 | 0.0073 |
| 主动容错快速终端滑模 | 0.0334 | 0.0182 | 0.0063 |
6. 结 语
针对机电伺服系统故障检测准确率不高,系统容错性能不佳的问题,本研究提出了基于自适应神经网络滑模观测器的快速终端滑模的主动容错控制策略,提高了系统的的控制精度和容错性能,通过仿真和实验验证本研究所提控制策略的可行性.
本研究提出的方法还是有一定的局限性,由于系统故障较为复杂,为了方便研究仅对系统加性故障进行了研究,并且对故障进行了简单的建模,所以在适用范围上有一定的局限性. 下一步考虑将系统的乘性故障以及更加复杂的综合故障作为研究对象.
参考文献
基于声信号的故障检测方法在运载火箭上的应用
[J].DOI:10.3969/j.issn.1672-9374.2021.03.001 [本文引用: 1]
Application of fault detection method based on acoustic signal in launch vehicle
[J].DOI:10.3969/j.issn.1672-9374.2021.03.001 [本文引用: 1]
基于模型的风电机组偏航系统故障检测方法
[J].
Fault detection method for yaw system of wind Turbine based on model
[J].
基于卡尔曼滤波的卫星地基增强系统位置域完好性监测分析
[J].DOI:10.3969/j.issn.1671-1815.2018.26.038 [本文引用: 1]
Analysis on ground based augmentation system position domain integrity monitoring based on Kalman filtering
[J].DOI:10.3969/j.issn.1671-1815.2018.26.038 [本文引用: 1]
Extended sliding mode observer basedcontrol for Markovian jump linear systems with disturbances
[J].
Fault-tolerant individual pitch control using adaptive sliding mode observer
[J].
Adaptive rapid neural observer-based sensors fault diagnosis and reconstruction of quadrotor unmanned aerial vehicle
[J].
Adaptive sliding mode observer for nonlinear interconnected systems with time varying parameters
[J].
Adaptive SMO-based fault estimation for markov jump systems with simultaneous additive and multiplicative actuator faults
[J].
Adaptive sliding mode disturbance observer-based composite control with prescribed performance of space manipulators for target capturing
[J].
Bearing fault diagnosis by a robust higher-order super-twisting sliding mode observer
[J].DOI:10.3390/s18041128 [本文引用: 1]
基于鲁棒自适应滑模观测器的多故障重构
[J].DOI:10.13195/j.kzyjc.2015.0659 [本文引用: 1]
Design of the robust adaptive sliding mode observer for multiple fault reconstruction
[J].DOI:10.13195/j.kzyjc.2015.0659 [本文引用: 1]
基于自适应滑模观测器的航空发动机故障检测
[J].DOI:10.3969/j.issn.1006-9348.2019.12.014 [本文引用: 1]
Fault detection in aircraft engines based on adaptive sliding mode observer
[J].DOI:10.3969/j.issn.1006-9348.2019.12.014 [本文引用: 1]
自适应广义滑模观测器之状态估计和故障重构
[J].
State estimation and fault reconstruction from an adaptive descriptor sliding mode observer
[J].
基于自适应滑模观测器的不匹配非线性系统执行器故障重构
[J].DOI:10.7641/CTA.2014.30952 [本文引用: 3]
Adaptive sliding-mode observer for actuator fault reconstruction in nonlinear system with mismatched uncertainties
[J].DOI:10.7641/CTA.2014.30952 [本文引用: 3]
航天器故障诊断与容错控制技术研究综述
[J].DOI:10.3873/j.issn.1000-1328.2020.06.002 [本文引用: 1]
A review of fault diagnosis and fault-tolerant control techniques for spacecraft
[J].DOI:10.3873/j.issn.1000-1328.2020.06.002 [本文引用: 1]
Output feedback based adaptive robust fault tolerant control for a class ofuncertain nonlinear systems
[J].DOI:10.3969/j.issn.1004-4132.2011.01.005 [本文引用: 1]
Guaranteed cost fault-tolerant control for a class of uncertain linear system
[J].
Adaptive fault-tolerant attitude control for reentry vehicle involving actuator saturation
[J].DOI:10.1177/0954410018811715 [本文引用: 1]
Observer-based fault reconstructions and fault-tolerant control designs for uncertain switched systems with both actuator and sensor faults
[J].DOI:10.1049/iet-cta.2019.1051 [本文引用: 1]