触力觉感知技术是制约机器人技术发展与应用的核心瓶颈. 不同于视觉形式的感知信息，触力觉信息包含机器人与外部环境交互过程中的机械特性. 大量研究表明，基于触力觉的精准感知技术在人机协作^[1-2]、运动控制^[3]、医疗健康^[4-5]等领域都有广泛的应用. 现有的机器人触力觉感知技术存在维间串扰严重、灵敏度不足的问题^[6]，一些科研机构相继开展了新型触力觉感知技术的研究^[7-8].

在众多的新型触力觉感知装置中，基于弹性橡胶与霍尔器件构建的柔性触力觉感知装置因具有高灵敏、低迟滞、轻重量等优良特性，获得了学术界越来越多的关注. 该类型的感知装置在受到外部力刺激后输出对应的磁场信号，为了由磁场信号得到外部力刺激，Yan等^[9]通过设计特制的力给定装置采集大量训练数据，利用多层神经网络得到该映射关系. Wang等^[10]在考虑不同维度磁场信号拥有的强耦合特性的基础上，利用改进的最小二乘法建立从磁场信号到外部力刺激的映射关系. Tomo等^[11]通过对感知装置进行针对性结构设计降低磁场信号的耦合特性，利用线性拟合工具建立复杂度相对较低的映射关系. 上述研究所提出的方法虽然能够得到有一定适用性的映射关系，但是这些方法均依据数据驱动的黑箱模型. 在这种情况下，训练样本中的异常点对于最终的训练结果会产生较大影响，导致建立的映射关系鲁棒性较差、泛化性较弱，并且不具有可解释性. 利用这类黑箱模型建立的磁场−力映射关系在航空航天、精密加工、临床医疗等复杂交互场景下并不适用，也限制了基于弹性橡胶与霍尔器件构建的柔性触力觉感知装置的实际应用与大范围推广^[12].

为了克服黑箱模型的故有缺陷，建立具有高度可解释性的磁场−力映射关系，要解决的首要问题是解析计算弹性橡胶受力形变后产生的磁场. 基于Halbach阵列进行磁场解析计算的研究逐渐增多^[13]. Chen等^[14]利用二阶矢量势，推导由双层线式Halbach阵列组成的电动悬挂装置内部磁场的解析表达式，并利用有限元分析验证结果的正确性. Ladghem-Chikouche等^[15]利用精确子域模型，推导采用环式Halbach阵列磁化的同步电机内部磁场表达式. Tang等^[16]利用表面电流法，得到2个线式Halbach阵列间磁场的解析模型，并在此基础上通过虚功法得到阵列间的悬浮力. 以上研究虽然借助Halbach阵列得到了一些情形下的磁场解析表达式，但是所得到的表达式在触力觉感知领域并不适用.

针对上述问题，本研究设计带有凸起结构的柔性触力觉感知装置，基于环式Halbach阵列，提出解析计算感知装置内部磁场的方法，并且利用COMSOL Multiphysics进行磁场的有限元建模与仿真. 通过对仿真结果进行可视化表示与统计学分析，证明本研究所提方法在不同形变情形下的适用性.

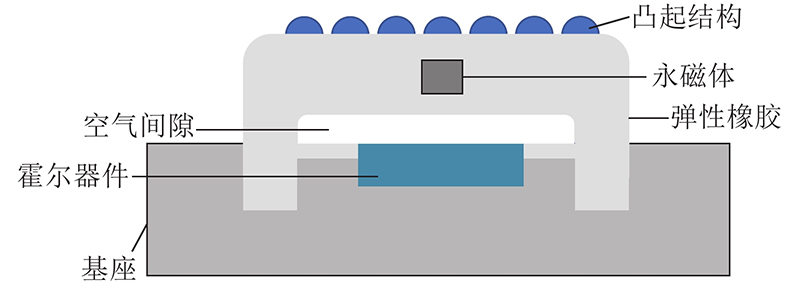
利用弹性橡胶与霍尔器件构建的柔性机器人触力觉感知装置结构示意图如图1所示. 弹性橡胶位于装置外侧，用于将外部多维度力刺激转换为多尺度位移量；永磁体嵌入弹性橡胶内部，用于将多尺度位移量转换为磁场变化量；霍尔器件固定在基座上，用于感知磁场变化量并输出. 在感知装置最外侧的半球形的凸起结构，使得弹性橡胶能够在受到外部力刺激时产生明显的形变，以提升感知灵敏度.可以看出，该柔性触力觉感知装置需要进行2个阶段的信息转换，最终以磁场变化量的形式输出信息. 解析表达这2个阶段的信息转换过程，对于建立高度可解释性的磁场−力映射关系，实现复杂交互环境下的机器人触力觉精准感知具有重要意义. 与第1阶段的信息转换过程可以依据理论较为完备的弹性力学进行求解不同，第2阶段由多尺度位移量到磁场变化量的信息转换过程可以依据的理论较少.

为了解析表达第2阶段的信息转换过程，本研究在假设感知装置中的永磁体依照Halbach阵列排布的基础上，提出柔性触力觉感知装置受力形变后中心处磁场的解析计算方法.

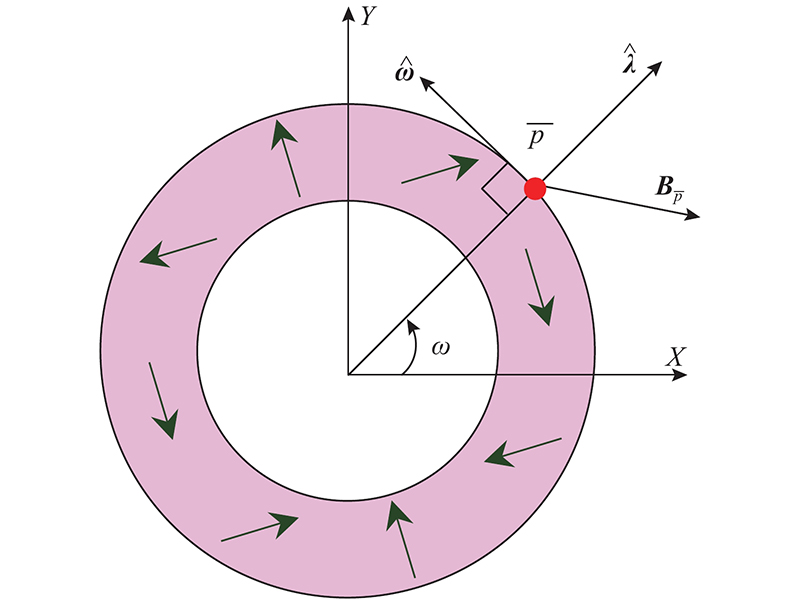
Halbach阵列是特殊的永磁体排布方式. 通过该方式排布永磁体，可以使得永磁体一侧磁场显著增强，另一侧磁场显著减弱. 按照几何特性进行分类，Halbach阵列可分为2个大类：线式、环式. 当在环式Halbach阵列中心建立如图2所示的坐标系时，可以将阵列上点 $ \stackrel{-}{p} $的磁场表示为

(1) $ {\boldsymbol{B}}_{\stackrel-{\boldsymbol{p}}}={B}_{\mathrm{r}}\left(\mathrm{cos}\; \left(\left(m-1\right)\left(\omega -\dfrac{\mathrm{{\text{π}} }}{2}\right)\right)\widehat{\boldsymbol{\lambda }}+ \mathrm{sin}\; \left(\left(m-1\right)\left(\omega -\dfrac{\mathrm{{\text{π}} }}{2}\right)\right)\widehat{\boldsymbol{\omega }}\right). 　 $

式中： $ {B}_{\mathrm{r}} $为永磁体的剩磁强度， $ m $为环式Halbach阵列的阶数， $ \omega $为点 $ \stackrel{-}{p} $与X坐标轴正方向所成的夹角， $\widehat{\mathit{\mathit{{\boldsymbol{\lambda}} }}}$为点 $ \stackrel{-}{p} $处径向方向的单位向量， $\widehat{\boldsymbol{{\boldsymbol{\omega }}}}$为点 $ \stackrel{-}{p} $处切向方向的单位向量^[17]. 当 $ m $的取值不同时，点 $ \stackrel{-}{p} $的磁场极化方向也不同. 为了便于后续的分析与推导，阵列内部的磁场应尽可能简化，本研究取 $ m= 2 $. 根据Halbach^[18]的推导，此时环式Halbach阵列在内部产生的磁感应强度为

(2) $ \begin{array}{c}{\boldsymbol{B}}_{\rm{i}}={B}_{\mathrm{r}}\mathrm{ln}\; \left(\dfrac{{r}_{\mathrm{o}}}{{r}_{\mathrm{i}}}\right)\widehat{\boldsymbol{x}}.\end{array} $

式中： $ {r}_{\mathrm{o}} $为环式Halbach阵列的外圆半径， $ {r}_{\mathrm{i}} $为环式Halbach阵列的内圆半径， $\widehat{\boldsymbol{{\boldsymbol{x}}}}$为 $ X $轴正方向的单位向量.

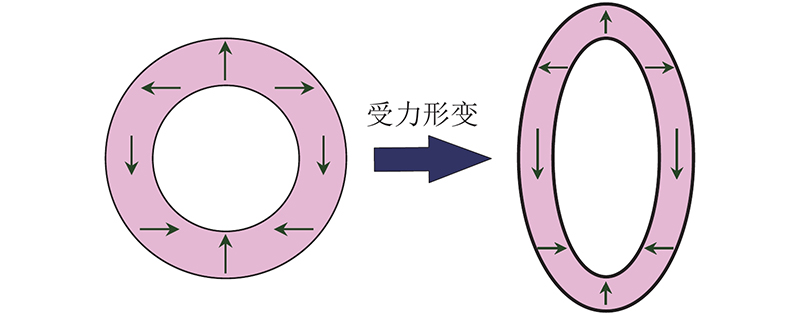
环式Halbach阵列产生的磁场具有轴向不变性，因此本研究简化空间3D环式Halbach阵列，只考虑平面2D情况. 此外，本研究假设包裹Halbach阵列的弹性橡胶在径向受到外部作用力后形变为椭圆形阵列，环式Halbach阵列受力形变的示意图如图3所示.

为了便于推导，对于阵列上点 $ \stackrel{-}{p} $、阵列内部点 $ {\stackrel{-}{p}}_{\mathrm{i}} $以及 $ {\stackrel{-}{p}}_{\mathrm{i}} $处的磁感应强度 $ \stackrel{-}{{\boldsymbol{B}}}\left({\stackrel{-}{p}}_{\mathrm{i}}\right) $均采用复数形式进行表达，即记：

(3) $ \begin{array}{c}\stackrel-{p}=x+{\rm{i}}y,\end{array} $

(4) $ \begin{array}{c}{\stackrel-{p}}_{\mathrm{i}}={x}_{\mathrm{i}}+{\rm{i}}{y}_{\mathrm{i}},\end{array} $

(5) $ \begin{array}{c}\stackrel-{{\boldsymbol{B}}}\left({\stackrel-{p}}_{\mathrm{i}}\right)={B}_{x}\left({\stackrel-{p}}_{\mathrm{i}}\right){\hat {\boldsymbol{x}}} +{B}_{y}\left({\stackrel-{p}}_{\mathrm{i}}\right){\hat {\boldsymbol{i}}}.\end{array} $

式中： $ {B}_{x}\left({\stackrel{-}{p}}_{\mathrm{i}}\right) $为点 $ {\stackrel{-}{p}}_{\mathrm{i}} $处磁感应强度大小的 $ X $轴分量， $ {B}_{y}\left({\stackrel{-}{p}}_{\mathrm{i}}\right) $为点 $ {\stackrel{-}{p}}_{\mathrm{i}} $处磁感应强度大小的 $ Y $轴分量， $ {\hat {\boldsymbol{i}}}$是虚轴正方向的单位向量. 通过后续的推导可知，磁感应强度的虚部被完全抵消，只保留实部，这与物理实际相符合.

由于永磁体按照2阶环式Halbach阵列排布，在形变前后，永磁体在垂直于XY平面的方向上均不产生极化. 根据文献[18]，有

(6) $ {\stackrel-{{\boldsymbol{B}}}}^{*}\left({\stackrel-{p}}_{\mathrm{i}}\right)=\dfrac{{\mu }_{0}}{2\mathrm{{\text{π}} }{\hat{{\boldsymbol{i}}}}}\iint \dfrac{j}{{\stackrel-{p}}_{\mathrm{i}}-\stackrel-{p}}\mathrm{d}x\mathrm{d}y,　 $

(7) $ \begin{array}{c}{\mu }_{0}j=\dfrac{\partial {B}_{\mathrm{r}y}}{\partial x}-\dfrac{\partial {B}_{\mathrm{r}x}}{\partial y},\end{array} 　 $

(8) $ \begin{array}{c}{B}_{\mathrm{r}x}={\mu }_{0}{H}_{\mathrm{c}x},\end{array} 　 $

(9) $ \begin{array}{c}{B}_{\mathrm{r}y}={\mu }_{0}{H}_{\mathrm{c}y}.\end{array} 　 $

式中： $ {\stackrel{-}{{\boldsymbol{B}}}}^{*}\left({\stackrel{-}{p}}_{\mathrm{i}}\right) $为 $ \stackrel{-}{{\boldsymbol{B}}}\left({\stackrel{-}{p}}_{\mathrm{i}}\right) $的复共轭， $ {\mu }_{0} $为真空磁导率， $ {B}_{\mathrm{r}x} $、 $ {B}_{\mathrm{r}y} $分别为点 $ \stackrel{-}{p} $处永磁体在 $ X $轴方向与 $ Y $轴方向的剩磁强度， $ {H}_{\mathrm{c}x} $、 $ {H}_{\mathrm{c}y} $分别为点 $ \stackrel{-}{p} $处永磁体在 $ X $轴方向与 $ Y $轴方向的矫顽力.

由二重积分的分部积分公式与安培环路定理有

(10) $\begin{split} {\stackrel-{{\boldsymbol{B}}}}^{*}\left({\stackrel-{p}}_{\mathrm{i}}\right)=& -\dfrac{{\mu }_{0}}{2\mathrm{{\text{π}} }{\hat{{\boldsymbol{i}}}}}\iint {H}_{\mathrm{c}y}{\left(\dfrac{1}{{\stackrel-{p}}_{\mathrm{i}}-\stackrel-{p}}\right)}^{2}\mathrm{d}x\mathrm{d}y+ \\ &\dfrac{{\mu }_{0}}{2\mathrm{{\text{π}} }} {\hat{{\boldsymbol{x}}}} \iint {H}_{\mathrm{c}x}{\left(\dfrac{1}{{\stackrel-{p}}_{\mathrm{i}}-\stackrel-{p}}\right)}^{2}\mathrm{d}x\mathrm{d}y.　 \end{split} $

记 ${\stackrel{-}{{\boldsymbol{B}}}}_{\mathrm{r}}={B}_{\mathrm{r}x} {\hat{{\boldsymbol{x}}}} +{B}_{\mathrm{r}y}{\hat{{\boldsymbol{i}}}}$，有

(11) $ {\bar {\boldsymbol{B}}^*}\left( {{{\bar p}_{\rm{i}}}} \right) = \displaystyle\sum\limits_{n = 1}^\infty {{{\bar {\boldsymbol{k}}}_n}} \bar p_{\rm{i}}^{n - 1}. $

(12) $ {\stackrel-{{\boldsymbol{k}}}}_{n}=\dfrac{n}{2\mathrm{{\text{π}} }}\iint \dfrac{{\stackrel-{{\boldsymbol{B}}}}_{\mathrm{r}}}{{\bar{p}^{n+1}}}\mathrm{d}x\mathrm{d}y.　 $

记 ${\stackrel{-}{{\boldsymbol{B}}}}_{\mathrm{r}}={B}_{\mathrm{r}}{e}^{\beta \left(\omega \right){\hat{{\boldsymbol{i}}}}},\stackrel{-}{p}=r{e}^{\mathrm{i}\varphi}$，其中 $ \beta \left(\omega \right) $为与 $ X $轴夹角为 $ \omega $的永磁体的极化方向， $ r $为阵列上一点 $ \stackrel{-}{p} $到坐标原点的距离. 考虑环式Halbach阵列的物理含义，有

(13) $ \begin{array}{c}\beta \left(\varphi \right)=\left(N+1\right)\omega .\end{array} 　 $

环式Halbach阵列的阶数由式(13)中的 $ N+1 $决定. 根据文献[19]，若

(14) $ {M}^{{'}}=\dfrac{M}{N}\geqslant 8. $

则 $ n\ne N $时， $ {\stackrel{-}{k}}_{n}\to 0 $. 其中 $ M $为阵列上极化方向符合式(13)的永磁体块数. 若式(14)成立，且点 $ {\stackrel{-}{p}}_{\mathrm{i}} $位于椭圆中心，考虑讨论的对象阶数为2，则将式(11)写成极坐标形式，有

(15) $ {\stackrel-{{\boldsymbol{B}}}}^{*}\left({\stackrel-{p}}_{\mathrm{i}}\right)=\dfrac{1}{2\mathrm{{\text{π}} }}{\int }_{0}^{2\mathrm{{\text{π}} }}\left({\int }_{{\rho }_{{\rm{i}}}}^{{\rho }_{{\rm{o}}}}\dfrac{{B}_{\mathrm{r}}}{r}\mathrm{d}r\right)\mathrm{d}\varphi{\hat{{\boldsymbol{x}}}} ,　 $

(16) $ {\rho }_{\mathrm{i}}=\dfrac{{b}_{\mathrm{i}}}{\sqrt{1-{\epsilon}_{\mathrm{i}}^{2}{\mathrm{cos}}^{2}\;\varphi }},　 $

(17) $ {\rho }_{\mathrm{o}}=\dfrac{{b}_{\mathrm{o}}}{\sqrt{1-{\epsilon}_{\mathrm{o}}^{2}{\mathrm{cos}}^{2}\;\varphi }}. $

式中： $ {b}_{\mathrm{i}} $、 $ {b}_{\mathrm{o}} $分别为内椭圆与外椭圆的半短轴， ${\epsilon}_{\mathrm{i}}$、 ${\epsilon}_{\mathrm{o}}$分别为内椭圆与外椭圆的离心率. 将式(16)、(17)代入式(15)并整理，有

(18) $ \begin{split} {\stackrel-{{\boldsymbol{B}}}}^{*}\left({\stackrel-{p}}_{\mathrm{i}}\right)=&\Bigg({B}_{\mathrm{r}}\mathrm{ln}\dfrac{{b}_{\mathrm{o}}}{{b}_{\mathrm{i}}}+\dfrac{{B}_{\mathrm{r}}}{2\mathrm{{\text{π}} }}{\int }_{0}^{2\mathrm{{\text{π}} }}(\mathrm{ln}\sqrt{1-{\epsilon}_{\mathrm{i}}^{2}{\mathrm{cos}}\;^{2}\omega }- \Bigg.\\ & \Bigg.\mathrm{ln}\sqrt{1-{\epsilon}_{\mathrm{o}}^{2}{\mathrm{cos}}^{2}\;\omega }){\rm{d}}\omega \Bigg) {\hat{{\boldsymbol{x}}}}. \end{split} 　 $

为了验证所提出的柔性触力觉感知装置内部磁场解析计算方法的正确性，在理论分析的基础上，借助COMSOL Multiphysics进行有限元仿真，通过比较不同形变程度下磁感应强度的仿真值与理论值，验证所提出方法的正确性.

构建模型须确定几何参数. 为了使得仿真结果与实际研究更加接近，通过查阅对应产品手册，并比较文献[9]~[11]构建的原型样机体积，选取环式Halbach阵列内、外圆半径分别为 ${r}_{{\rm{i}}}$=3.00 mm、 $ {r}_{{\rm{o}}} $=4.50 mm. 为了验证提出的计算方法在不同形变情况下的适用情况，以0.10 mm 为间隔，取形变量 $ d $∈[0.10,1.50] mm. 考虑到包裹永磁体的弹性橡胶在受到外加应力的情况下，具有体积不变性^[20]，得到的椭圆形阵列几何参数计算结果如表1所示. 表中， $ {a}_{\mathrm{i}}\mathrm{、}{a}_{\mathrm{o}} $分别为阵列形变后内椭圆与外椭圆的半长轴.

在模型中心构建椭圆形Halbach阵列，其中阵列的轴向长度为20 mm，几何参数按照表1所示数据依次选取. 在材料特性方面，选取阵列材料为钕铁硼 (NdFeB)的永磁体，其剩磁强度设置为1.41 T. 在完成椭圆形阵列的构建后，在其外部构建半径为40 mm，轴向长度为40 mm的实心圆柱. 圆柱材料选取为空气，相对磁导率设置为1.

理想的环式Halbach阵列要求环上任一点永磁体的极化方向均符合式(13)，这在实际制备与理论仿真中都是难以实现的. 如图4所示，本研究采用实际制备环式Halbach阵列时常用的分块法进行模型构建^[21]，即将Halbach阵列圆环等分为 $ N $个区域，每个区域使用1块永磁体，永磁体的极化方向通过将对应区域的坐标代入式(13)计算得到. 为了量化比较不同仿真精度下仿真值与理论值间的差异，将 $ N $从16到144，间隔16等分取点进行仿真.

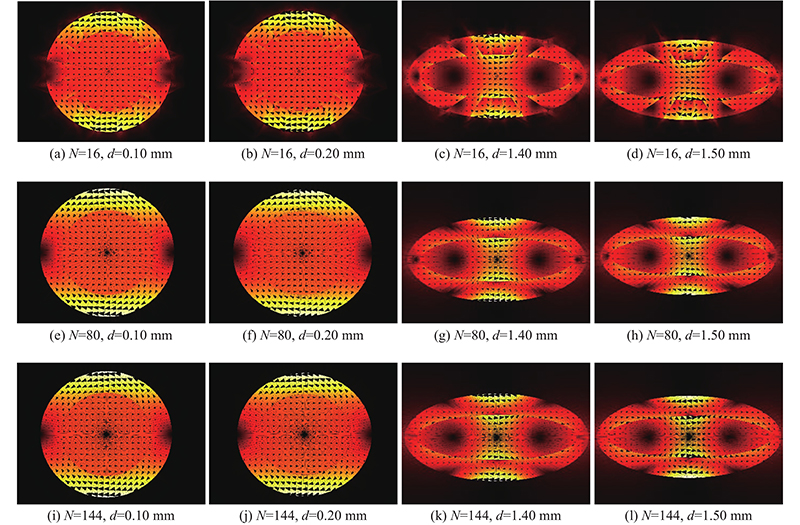
使用热力图对得到的仿真结果进行可视化显示，利用锥形体箭头表征磁感应强度的大小和方向. 当形变量 $ d $=0.10 、0.20、1.40、1.50 mm，分块数目 $ N $=16、80、144时的仿真结果如图5所示.

如表2所示，将不同压缩情况下，采用不同仿真精度时阵列中心处的磁感应强度仿真值 $ {B}_{\mathrm{c}} $列出，并基于式(18)计算得到对应情况下的理论值 $ {B}_{\mathrm{t}} $. 式(18)中被积函数的原函数不是初等函数，因此本研究取间隔为0.01，通过等分插值的方法得到磁感应强度的理论值. 由表2可知，随着仿真精度的不断提升，仿真值不断增大，且在15种压缩情况下，最小误差 $ {E}_{\mathrm{m}} $大多在 $ N $=144的情形下取得.

在不同形变情形下，将COMSOL内置的数值法与本研究所提方法在同一台计算机上运行并记录运行时间，结果如表3所示. 所使用计算机的中央处理器为英特尔Core i7-10700，主显卡为英伟达GTX 1050 Ti，运行内存为32 GB. 可知，本研究所提出方法的计算时间 $ {T}_{\mathrm{o}\mathrm{u}\mathrm{r}} $在所有情形下均显著低于数值法的计算时间T_num.

依据表2，绘制不同压缩情形下的仿真值散点图. 通过观察散点图，决定采用指数型函数拟合磁感应强度仿真值与分块数目间的关系，目标函数为

(19) $ \begin{array}{c}{B}_{\mathrm{c}}=b+l{k}^{N}\end{array} $

式中： $ b $、 $ l $、 $ k $为待拟合的参数，选取非线性最小二乘法进行参数拟合，待拟合参数的取值范围分别为 $ b\in \left[\mathrm{550,800}\right] $、 $ l\in \left[-\mathrm{100,0}\right] $、 $ k\in \left[\mathrm{0,2}\right] $. 拟合的具体结果及相应评价指标如表4所示. 表中， $ {R}^{2} $为决定系数， ${R}_{{\rm{A}}}^{2}$为校正决定系数， $ \mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E} $为均方根误差. 可知，15类压缩情况下的 $ {R}^{2} $与 ${R}_{{\rm{A}}}^{2}$均大于0.9900， $ \mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E} $均小于0.6000. 表明拟合曲线能够较好地反映仿真值与分块数目间的关系.

由图5可知，当压缩量从0.10 mm逐渐增大到1.50 mm时，中心处的磁感应强度大小有较明显增加，而方向几乎保持不变. 在对相应物理过程进行分析后认为，造成这一结果的原因可能是压缩量的增大使得阵列上的永磁体不断接近阵列中心，引起中心处磁感应强度的增大；Halbach阵列的特殊排布形式基本抵消了中心处 $ Y $轴方向的磁场分量，只保留了 $ X $轴方向的磁场分量，因此中心处的磁感应强度方向几乎不变.

由表2、4可知，随着仿真网络的不断细化，仿真值的增长幅度逐渐减小，并最终接近某一恒定值. 这一结论与仿真值会最终接近理论值的假设相符合，验证了公式推导与模型仿真的正确性. 然而，仿真值与理论值之间依然存在着差异. 在对公式推导和模型仿真的过程进行仔细分析后认为，主要有2个原因造成这种现象：1）在进行理论值求解时，采用等分插值的方法进行定积分计算，导致计算结果存在固有误差；2）在进行模型仿真时，使用分块法构建阵列，没有像理论推导中那样让椭圆环上永磁体的极化方向处处不同. 在后续的研究中，计划依据本研究所设计的结构制备实际样机，利用样机实测值对所提出方法进行进一步验证.

本研究设计了带有凸起结构的柔性触力觉感知装置，并基于环式Halbach阵列的磁场本构关系，推导了该装置在受力形变时，内部磁场的解析计算公式. 与常见的数值计算方法相比，本研究提出的磁场解析计算方法具有求解速度快、鲁棒性高、可解释性强等优势. 有限元仿真与统计学分析结果表明，本研究所提算法能够在不同情形下准确计算出感知装置中心处的磁场，能够为解决当前柔性触力觉感知装置面临的突出问题，实现复杂交互环境下的触力觉精准感知提供一定的参考作用. 限于加工精度与感测技术，本研究没有在实际场景下，检验所提出计算方法的适用性. 未来，计划将微加工技术与高精度磁场探测技术相结合，构建出感测装置的原理样机，并基于样机实测值对所提出的计算方法进行验证.