在机器人零部件完成加工和装配过程中,不可避免地会引入结构参数误差,机器人运动学校是保证其可靠及高精度运行的有效手段[1]. 对于校准问题的方法和理论,国内外学者对其作了大量研究. 最常见的方法是通过对机器人末端绝对定位二乘误差最小化来辨识结构参数误差[2-4]. 工业机器人在激光切割、弧焊等领域应用中,比如切割或焊接三维空间长方形,需要进行相对路点运动(如沿着X轴方向前进100 mm)[5-6]. 在这些应用中,前后2个位型的相对精度在一定程度上决定了机器人性能. 先前针对相对精度校准的研究主要是最小化前后2个位型的相对定位误差[7-8],忽视了相对定向精度对机器人性能的影响. 通过大量的机器人试验发现,如果机器人安装较长的工装,定向误差会经过工装放大到末端的定位误差[9]. 考虑姿态信息的校准是很有必要的. Xu 等[10]将机器人末端测量的多点位置建立坐标系,通过坐标系偏差计算绝对位姿残差,对残差进行优化. 位置与姿态误差的单位选择、坐标系建系策略都会直接影响校准效果及收敛性. 为了避免以上问题,本文通过最小化3个靶球对应的最大距离误差,可以同时提升相对定位及定向精度.
机器人校准问题可以视为一个非线性优化问题. 为了解决该问题,很多优化方法被提出,如高斯-牛顿法、莱文贝格-马夸特(LM)法、卡尔曼滤波法等. 由于能够快速收敛,高斯-牛顿法广泛地被应用于机器人校准,通常是最小化残差平方和[10]. LM法解决了高斯-牛顿法最优解搜索过程中矩阵运算可能存在的奇异问题[11]. 卡尔曼滤波法被用来减小测量及机器人重复性误差对辨识过程的影响[12]. 以上优化方法只能解决单目标优化问题,无法解决最小化3个靶球对应的最大距离误差这样的多目标优化问题. 本文使用二次序列规划(SQP)方法对极小极大问题进行求解,增加了校准过程鲁棒性,利用主二元算法在满足不等式约束条件下快速搜索到局部最优解.
1. 鲁棒的校准问题建模
1.1. 激光跟踪仪靶球-机器人系统
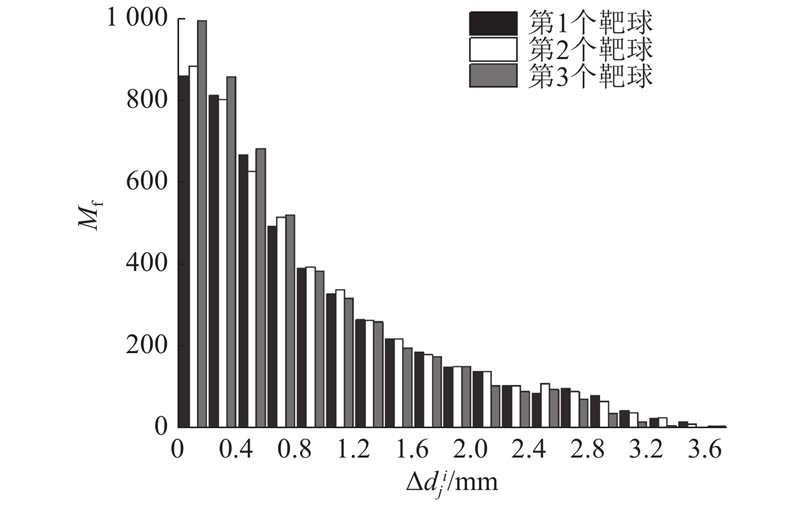
为了提升机器人的相对精度,首先需要通过高精度的测量设备测量和计算相应的指标. 如图1(a)所示,在机器人末端法兰盘上安装了3个可以原路反射激光的靶球,使用激光跟踪仪来测量这3个球心对应机器人末端的实际到达位置. 机器人每运动到一个位型,记录串联机器人各个关节轴的角度θ,同时测量能够反映机器人末端位姿信息的3个靶球位置.
图 1
1.2. 机器人前向与微分运动学
以一个n自由度的串联机器人为例,机器人末端中心点的位置和姿态可以表示为以下非线性关系:
映射f描述了关节空间中θ、机器人结构参数μ和笛卡尔空间的末端位置p、旋转矩阵R的关系. 如图1(a)所示,激光跟踪仪测量了安装在末端传感模块上的3个靶球,它们在工具坐标系下的坐标是未知的,记为ta、tb和tc. 测量点的名义坐标可以表示为
对式(2)两边求导,可得
式中:Jxi(i=a,b,c)是机器人末端定位误差-结构参数雅克比矩阵. 理想的状态是希望机器人末端实到位置与指令位姿一致. 由于机器人零部件在加工与制造过程中会引入结构参数与名义值的偏差,比如杆长、零位的偏差等,导致了机器人末端在笛卡尔空间中不均匀分布的误差.
1.3. 相对精度指标的定义
相对定位精度(即距离精度)描述了机器人准确地从当前位型到达下一位型的能力,其定义描述在标准ISO 9283中:
式中:
式中:正交矩阵R为末端工具坐标系从位型i变换到位型j的旋转矩阵. 指令相对姿态Ro到测量相对姿态Rm的微小姿态偏差可以视作三维刚体旋转变换. 根据Chasles定理可知,该刚体旋转变换可以通过绕单位向量轴的转动实现,∆o的物理意义是描述了刚体旋转变换绕空间单位轴旋转的角度,在一定程度上可以描述指令姿态与测量姿态的偏差[14]. 与相对定位精度一致,相对姿态精度的表示与参考系无关.
1.4. 相对位姿不变性的充分条件
如图1(a)所示,机器人末端传感模块包含3个测量点,描述了机器人末端的六维运动. 抽象地说,将末端传感模块视为笛卡尔空间中有6个自由度的三角形,每个位型对应一个这样的三角形. 将相对位姿不变性定义为任意2个不同位型对应的全等三角形相对位姿不变. 通过构建物理约束,可以使得由三角形与约束组成虚拟系统的内部自由度≤0,满足相对位姿不变性.
表 1 不同位型数对应虚拟机械系统自由度分析
Tab.1
| 位型数 | n | g | M | 位型数 | n | g | M | |
| 2 | 5 | 6 | 6 | 4 | 7 | 12 | 0 | |
| 3 | 6 | 9 | 3 | k | 3+k | 3k | 12−3k |
当位型总数≥4时,相对位姿不变性的充分条件是同一靶球在任意2个不同位型下的距离误差为0. 模型参数名义值计算距离与测量距离值之间总是存在偏差,通过最小化3个距离对应的最大偏差,在优化相对定位精度的同时,尽可能保障相对定向精度,避免了直接计算姿态误差可能引入的单位同质化问题与参考坐标依赖问题.
1.5. 校准问题的目标函数及约束
通过1.4节的分析可得,当位型数≥4时,同一靶球在任意2个不同位型下的距离误差为0,任意2个不同位型的相对位姿不变. 在实际情况中,由于机器人结构非线性误差的存在,末端距离误差不可能为0. 需要寻找一种策略,尽可能减小末端的距离误差,末端距离误差的平方和可以表示为
式中:∆d为距离误差序列;t为描述在工具坐标系下的3个靶球对应的名义坐标,
式中:tl(l=1,2,3)是2个靶球间的距离偏差,测量距离通过计算n个位型下对应测量距离的平均值得到,ε为由测量误差引入的不确定度. 对于优化问题,该非线性不等式约束可以重新写成
为了尽可能减小同一靶球在2个不同位型下的距离误差,同时保证机器人末端在2个不同位型下有较高的相对定位及定向精度,将目标函数定义为
式中:下标i表示安装在机器人末端的第i个靶球. 通过最小化3个靶球中最大的距离平方误差和,尽可能减少了机器人末端的距离误差,增加了校准过程的鲁棒性. 测量得到的机器人末端点位置坐标表示在测量坐标系下,若只通过距离误差的关系建立目标函数,则测量数据与参考系无关,在对机器人结构参数校准过程中不会引入从测量系到机器人基坐标系的坐标转换误差.
2. 校准问题的求解
2.1. 极小极大搜索算法的求解
由于极小极大搜索问题不是一个典型的凸优化问题,需要将其转换为二次序列规划(SQP)子问题才能更好地对原问题进行求解[16]. 极小极大问题可以等价为以下约束的极小化问题:
式中:x为在校准问题中待辨识的结构参数. 有以下关系
式(11)中描述的优化问题可以迭代生成二次序列规划子问题,该子问题是原校准问题的近似. SQP方法的核心思想是线性化原问题,对得到的线性近似问题设计具有快速局部收敛率的搜索方法. 由于Fi(x)是可微的,对于任何搜索方向∆x,方向导数为
式中:
近似的二次序列规划问题可以表示为
式中:λ为KKT条件的拉格朗日算子,λ≥0. 二次序列问题(15)的KKT条件可以推导为
运算符()+定义为
为了寻找迭代步长及算子(∆x,λ)的最优解,同时满足上述定义的KKT条件,使用主二元子梯度算法进行梯度方向的搜索:
式中:p为二次规划子问题的迭代次数. 迭代过程中KKT算子可以定义为
定义z=[∆x,λ]T,则搜索最优解z*的更新率为
式中:Tp∈T(zp),αp为迭代步长.
2.2. 目标函数及约束的梯度
直接给出式(10)中目标函数及约束条件的梯度解析式,能够使优化问题更快地收敛到最优解. 近似的二次序列规划问题(15)的目标函数梯度可以表示为
式中:海塞矩阵Hk可以通过BFGS方法得到;Fi(x)的梯度可以推导并表示为
图 2
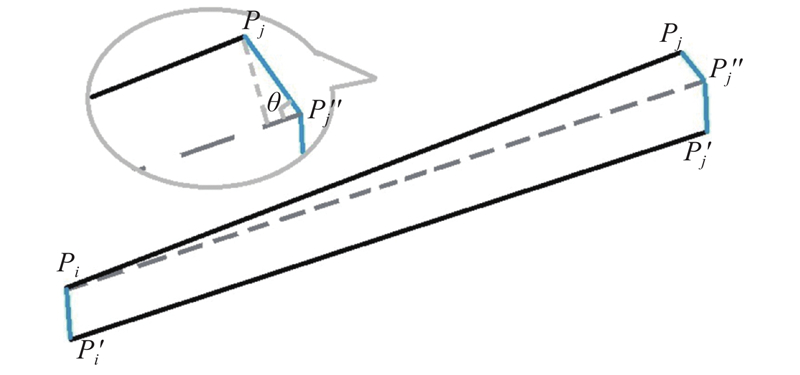
图 2 机器人末端两点间距离误差的线性近似
Fig.2 Linearization of distance errors between two end-points
式中:Pi及Pj分别为第i和第j个位型机器人末端实际到达并用激光跟踪仪测量的点,Pi'及Pj'为机器人末端名义计算点. 有以下向量关系式成立:
式中:∆pj和∆pi分别为机器人末端在点Pj和Pi处的绝对定位误差. 如图2所示,线段PiPj''与线段Pi'Pj'平行且等长,向量和距离之间有以下关系:
由于
通过上述分析,结合机器人运动学微分学理论,对式(27)两边求微分,可得式(23)中距离误差-结构参数雅克比矩阵的解析式为
二次序列规划问题不等式约束(15)的梯度可以表示为
物理约束c(x)的梯度可以推导为
2.3. 凸性及收敛性分析
由于机器人正解过程中包含非线性三角函数的乘积,对于校准问题(10),其目标函数是非凸的. 通过将原优化问题转换为近似的二次序列规划问题,可以证明得到的线性近似问题是凸的. 根据凸优化的理论可知,目标函数及约束条件是凸的须满足以下条件:
定义
由于海塞矩阵Hk是正定矩阵,有
证明了二次序列规划问题的目标函数是凸的. 同样地,可以证明约束条件是凸的. 对于凸优化问题,当迭代步长满足以下条件时可以证明其全局收敛到最优解[20]:
式中:ϒp为调节收敛率的比例因子. 对于校准原问题,由于SQP问题是对原问题的线性近似,原问题可以收敛到局部最小值.
2.4. 鲁棒的机器人运动学校准算法
对所有目标函数、约束条件及梯度进行初始化,然后对优化问题近似的二次规划子问题使用主二元子梯度算法寻找满足KKT条件的全局收敛解. 在子问题收敛后更新目标函数、约束条件及梯度,通过BFGS方法更新海塞矩阵. 在更新得到的解附近重新生成新的二次规划子问题,不断搜索直至原校准问题收敛.
算法:鲁棒的机器人运动学校准算法
输入:关节转角θ,名义结构参数x0,末端测量点pam、pbm和pcm.
输出:辨识的结构参数 x*.
初始化
∆d,Fi,▽Fi,C(x0),G(x0)<= =x0,H0
迭代过程
while x未收敛 do
∆x0=0,λ0=0.
while ∆x未收敛 do
主二元子梯度算法
end while
更新状态、约束、梯度和海塞矩阵:
xk+1=xk+∆xk,sk=∆xk,
end while
3. 实验结果分析
3.1. 六轴机器人实验结果分析
表 2 机器人IRB2600的名义DH参数
Tab.2
| 序号 | | | | |
| 1 | 150 | 445 | 0 | −90 |
| 2 | 900 | 0 | −90 | 0 |
| 3 | 150 | 0 | 0 | −90 |
| 4 | 0 | 938 | 0 | 90 |
| 5 | 0 | 0 | 180 | 90 |
| 6 | 0 | 200 | 0 | 0 |
图 3
图 4
表 3 不同校准方法对比
Tab.3
对比试验的结果如图5所示. 图中,da、db、dc分别为第1、2、3个靶球子在不同方法校准后的相对定位精度. 从图5可以看出,进行结构参数校准后所有方法均能明显提升相对精度. 基于距离误差的校准方法[7]和只考虑定位误差的方法[11]只对第1个靶球的对应指标进行优化,从图5(a)可以发现,这2个方法的第1个靶球对应相对定位精度指标优于考虑位姿的方法[10]. 对于第2个和第3个靶球对应的相对精度指标,基于距离误差的方法和只考虑定位误差的方法的相对定位精度都略差于本文提出的方法. 对于相对定向指标,这2个方法明显差于本文提出的方法. 对比考虑位姿的方法,同时考虑绝对定位与定向精度的方法[10]各项指标不及本文提出的方法. 为了更直观地反映各种方法的相对精度,不同方法的相对精度在不同特定区间内的概率分布如表4所示. 可以看出,本文提出的方法相对精度在接近0的区间内概率最高.
表 4 IRB2600相对精度在不同特定区间内频率分布
Tab.4
| 方法 | Δd1)/% | Δo/% | |||
| [0, 0.2] mm | [0, 0.4] mm | [0, 0.002] rad | [0, 0.004] rad | ||
| 注:1) 表示只列出3个靶球对应指标中最差的一项. | |||||
| 校准前 | 17.43 | 33.90 | 16.79 | 61.07 | |
| 本文方法 | 51.03 | 82.81 | 44.63 | 92.53 | |
| 文献[7]方法 | 50.63 | 80.59 | 29.62 | 82.32 | |
| 文献[10]方法 | 51.07 | 81.03 | 38.26 | 86.30 | |
| 文献[11]方法 | 49.21 | 79.66 | 28.34 | 76.73 | |
图 5
图 5 IRB2600不同方法校准前、后的相对精度分布
Fig.5 Relative positioning accuracy after calibration
各种方法对比的相对精度结果均方根与最大值如表5所示. 表中,RMSd、Δdmax分别为定位精度的均方根和最大值,RMSo、Δomax分别为定向精度的均方根和最大值. 使用提出的校准方法,相对定位及定向精度分别提升了67.98%和24.32%. 与其他方法相比,提出的方法相对于其他方法对相对精度的提升效果最好.
表 5 IRB2600不同方法的相对精度指标
Tab.5
| 方法 | RMSd1)/mm | Δdmax /mm | RMSo /rad | Δomax /rad |
| 注:1) 表示只列出3个靶球对应指标中最差的一项. | ||||
| 校准前 | 1.195 1 | 3.726 7 | 0.003 9 | 0.009 2 |
| 本文方法 | 0.293 2 | 1.193 4 | 0.002 5 | 0.007 4 |
| 文献[7]方法 | 0.318 4 | 1.413 8 | 0.003 1 | 0.008 5 |
| 文献[10]方法 | 0.312 8 | 1.488 1 | 0.002 9 | 0.008 4 |
| 文献[11]方法 | 0.332 3 | 1.589 7 | 0.003 3 | 0.009 0 |
3.2. 七轴机器人实验结果分析
表 6 IRB14000相对精度在不同特定区间内频率分布
Tab.6
| 方法 | Δd1)/% | Δo/% | |||
| [0, 0.3] mm | [0, 0.6] mm | [0, 0.005] rad | [0, 0.01] rad | ||
| 注:1) 表示只列出3个靶球对应指标中最差的一项. | |||||
| 校准前 | 3.37 | 7.01 | 2.30 | 12.48 | |
| 本文方法 | 71.39 | 94.79 | 63.96 | 99.84 | |
| 文献[7]方法 | 57.07 | 86.89 | 13.17 | 34.85 | |
| 文献[10]方法 | 65.82 | 92.18 | 30.10 | 86.08 | |
| 文献[11]方法 | 65.74 | 92.16 | 29.96 | 85.70 | |
表 7 IRB14000不同方法的相对精度指标
Tab.7
| 方法 | RMSd1)/mm | Δdmax /mm | RMSo /rad | Δomax /rad |
| 注:1) 表示只列出3个靶球对应指标中最差的一项. | ||||
| 校准前 | 5.560 9 | 13.519 | 0.023 3 | 0.044 5 |
| 本文方法 | 0.296 0 | 1.270 1 | 0.004 8 | 0.011 3 |
| 文献[7]方法 | 0.396 4 | 1.494 8 | 0.014 2 | 0.025 3 |
| 文献[10]方法 | 0.334 4 | 1.258 7 | 0.007 4 | 0.014 9 |
| 文献[11]方法 | 0.334 7 | 1.260 0 | 0.007 4 | 0.014 9 |
4. 结 语
本文提出基于相对精度指标的机器人结构参数校准方法. 该方法通过最小化3个靶球对应的最大距离误差来保证相对定位及定向精度. 为了求解非凸的极小极大问题,使用SQP方法对原校准问题进行近似,在增加了校准过程鲁棒性的同时,通过主二元子梯度算法在满足不等式约束条件下快速搜索到局部最优解. 该方法有以下优势:1)以距离误差的平方和作为目标函数,距离误差的计算与坐标系的选择无关,在参数辨识过程中不用考虑测量系与基坐标系的对齐问题;2)利用极小极大算法可以提升校准算法的鲁棒性;3)利用该方法可以同时提升相对定位及定向精度. 在进行校准及精度验证后,实验结果表明,六轴机器人IRB2600相对定位及定向精度分别提升了67.98%和24.32%,七轴机器人IRB14000分别提升了90.61%和74.61%.
参考文献
POE-based robot kinematic calibration using axis configuration space and the adjoint error model
[J].DOI:10.1109/TRO.2016.2593042 [本文引用: 1]
工业机器人视觉测量系统的在线校准技术
[J].
Online calibration of visualmeasurement system based on industrial robot
[J].
A minimal POE-based model for robotic kinematic calibration with only position measurements
[J].DOI:10.1109/TASE.2014.2328652 [本文引用: 1]
Manipulator motion planning for high-speed robotic laser cutting
[J].DOI:10.1080/00207540802070967 [本文引用: 1]
A distance error based industrial robot kinematic calibration method
[J].DOI:10.1108/IR-04-2014-0319 [本文引用: 6]
激光跟踪仪测量距离误差的机器人运动学参数补偿
[J].
Robot kinematic parameters compensation by measuring distance error using laser tracker system
[J].
A novel algorithm for robust calibration of kinematic manipulators and its experimental validation
[J].
Robot calibration using a 3D vision-based measurement system with a single camera
[J].DOI:10.1016/S0736-5845(01)00024-2 [本文引用: 6]
Online serial manipulator calibration based on multisensory process via extended Kalman and particle filters
[J].DOI:10.1109/TIE.2014.2314051 [本文引用: 1]
Stereo vision based autonomous robot calibration
[J].DOI:10.1016/j.robot.2017.04.001 [本文引用: 1]
关于重新建立空间机构自由度计算公式的探索
[J].DOI:10.3321/j.issn:0577-6686.2003.01.013 [本文引用: 1]
Exploration on re-establishing the calculation formula of degree of freedom for spatial mechanism
[J].DOI:10.3321/j.issn:0577-6686.2003.01.013 [本文引用: 1]
The BFGS method with exact line searches fails for non-convex objective functions
[J].DOI:10.1007/s10107-003-0421-7 [本文引用: 1]
Soving quasi-variational inequalities via their KKT-conditions
[J].
基于距离测量的机器人误差标定及参数选定
[J].
Robot error calibration based on distance measurement with parameter selection
[J].