微纳米定位技术在高精度显微、纳米光刻、超精密加工、微机电系统以及生物医学工程等诸多前沿领域中发挥着重要作用[1 -6 ] 。柔性机构基于柔性元件的弹性变形来传递运动,能够消除摩擦、机械间隙等机械不确定性[7 ] 。因此,现有的微纳米定位平台广泛采用柔性机构作为传动机构[8 ] 。
多自由度微纳米定位平台通常采用并联柔性机构来实现运动[9 -12 ] 。为了减少并联柔性机构各自由度间的耦合位移,通常需要加装柔性解耦机构,以实现各自由度方向上的运动解耦。当前,具有运动解耦功能的柔性机构主要应用于二自由度平动纳米定位平台,利用簧片梁沿其自身轴线方向上的较大刚度来实现2个自由度之间的解耦[13 -14 ] 。而针对旋转纳米运动的柔性解耦机构目前鲜有报道,多自由度并联柔性机构在实现独立旋转运动时仍面临较大挑战。在多自由度并联柔性机构中,旋转运动一般由多组直线支链同时驱动产生,如常见的平面XYθ 三自由度并联微定位平台。这类平台通常采用3-PPR和4-PPR构型[15 -17 ] ,其旋转运动并非独立驱动,与其他2个自由度间存在耦合,从而导致旋转中心容易发生漂移。
为解决上述问题,Li等[18 ] 将2组平行四边形机构分别进行正交组合和左右对称组合,形成了能够实现平面二自由度运动解耦的旋转运动解耦机构,但该解耦机构只能实现与平动自由度的解耦。为了扩展上述基于平行四边形机构正交组合的旋转运动解耦机构的应用范围,以实现对含平动在内的多个耦合自由度的解耦,本文尝试用圆弧梁替换原机构中的簧片梁,通过充分利用圆弧梁在各自由度方向上的柔度特性,设计一系列基于圆弧梁的旋转纳米运动柔性解耦机构。首先,对柔性解耦机构的构型进行介绍,并设计圆弧梁高度不同的柔性解耦机构;然后,通过柔度矩阵法对柔性解耦机构进行静力学建模并确定其尺寸参数,以获得其输出柔度;最后,通过有限元分析和实验相结合的方法对柔度理论模型的准确性进行验证,并比较各柔性解耦机构的解耦能力。
1 旋转纳米运动柔性解耦机构设计
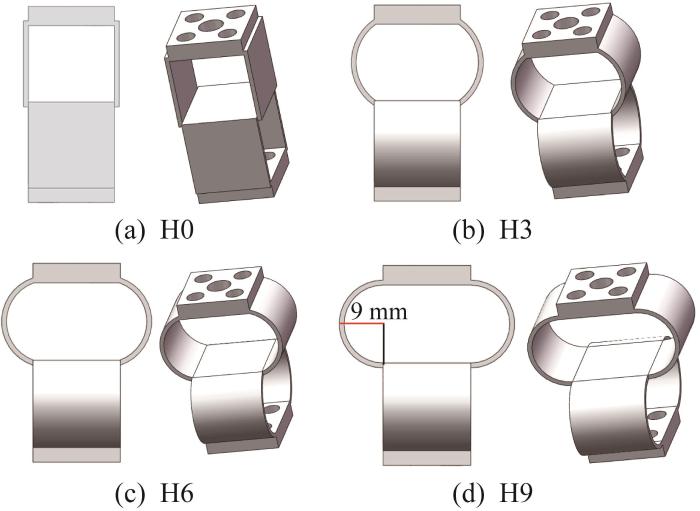
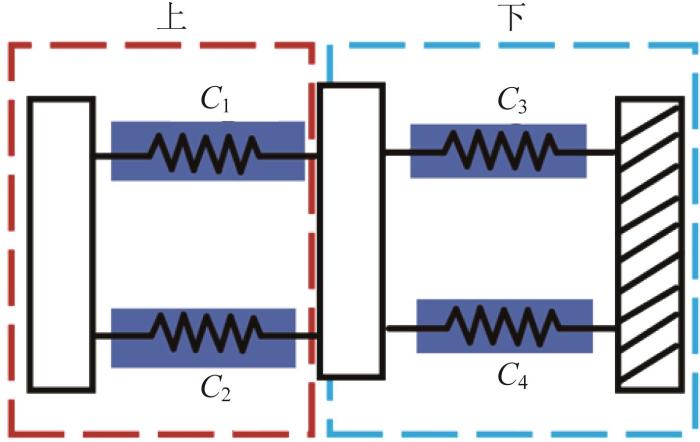
多自由度纳米定位平台的旋转运动由多组并联支链联合驱动,通常与其他方向的自由度存在严重耦合。为了提高旋转运动的精度,实现旋转运动与其他方向自由度的完全解耦,形成独立驱动的旋转运动模块,需要在旋转驱动机构后加入柔性解耦机构。旋转运动柔性解耦机构的基本构型如图1 (a)所示,由2组簧片梁式平行四边形机构正交组合而成,但该机构只能实现与平面X 、Y 方向上平动的解耦。为了解决这个问题,基于图1 (a)所示构型,将簧片梁替换为圆弧梁,形成圆弧梁高度不同的柔性解耦机构,如图1 (b)至(d)所示。为方便后续分析,根据圆弧梁高度来命名各机构。以图1 (d)所示机构为例,圆弧梁高度为9 mm,则该机构命名为H9,其余3个依次为H6、H3、H0(簧片梁可视作高度无限接近0的圆弧梁)。该柔性解耦机构由完全相同的上下两部分正交组成,每个部分由2个对称的圆弧梁组成,且上下两部分通过柔性簧片梁连接。
图1
图1
4 种柔性解耦机构的构型
Fig.1
Configurations of four flexible decoupling mechanisms
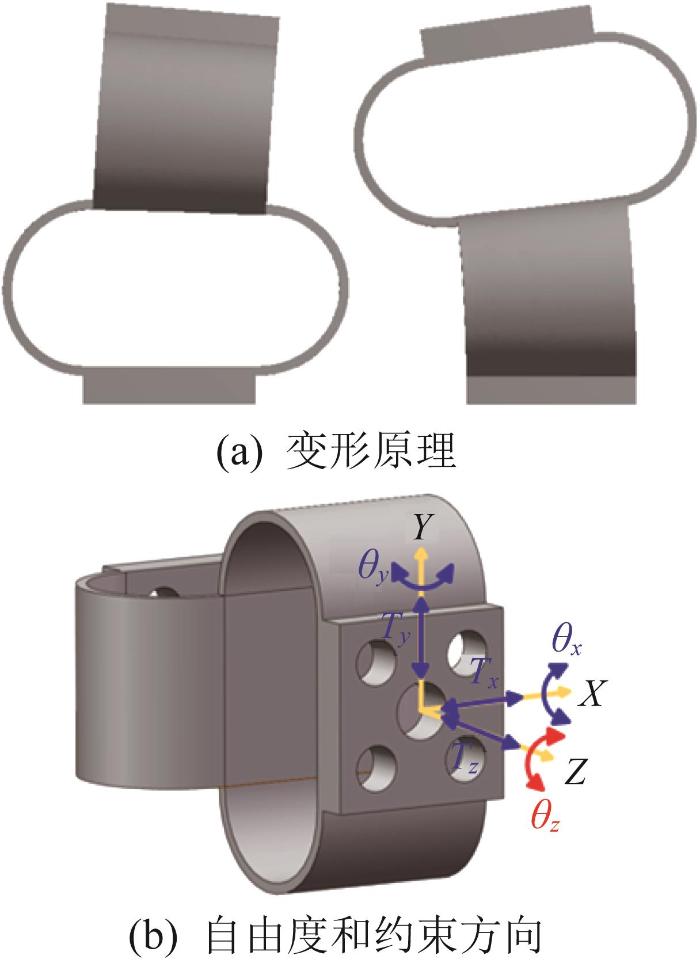
圆弧梁柔性解耦机构的变形原理如图2 所示。图中:蓝色部分表示机构在对应方向上的运动自由度,红色部分表示沿该方向的约束。由图2 可知,该机构的末端能够同时实现沿X、Y、Z 方向的移动和绕X、Y 轴的转动,以适应多自由度纳米定位平台末端位姿并实现其运动解耦。此外,该机构在绕Z 轴转动的方向上具有相对较高的刚度,使得该自由度方向成为柔性解耦机构的约束方向,如图2 (b)所示。值得注意的是,相较于含簧片梁式平行四边形机构的H0机构,H9等含圆弧梁的柔性解耦机构末端能够同时产生平移和弯曲变形,可实现其他5个自由度方向上的解耦运动,这也使多自由度纳米定位平台实现绕Z 轴方向的独立旋转运动成为可能,进而确保旋转扭矩的高效传递。
图2
图2
柔性解耦机构变形原理示意
Fig.2
Schematic of deformation principle of flexible decoupling mechanism
2 柔性解耦机构理论建模
2.1 局部坐标系下圆弧梁的内力向量
本文所设计的柔性解耦机构通过圆弧梁的变形来实现预期运动,故需对圆弧梁在外力作用下的变形情况进行分析。因受曲率及其他几何参数的影响,圆弧梁在外力作用下会产生轴向力、弯矩与扭矩的耦合效应。相比于簧片梁结构,圆弧梁的受力与变形较为复杂,且其柔度矩阵的求解过程较为繁琐。为了避免复杂微分方程的求解并简化计算过程,本节基于能量变分原理,省略形函数的引入,直接推导出圆弧梁柔度矩阵的显式表达式。
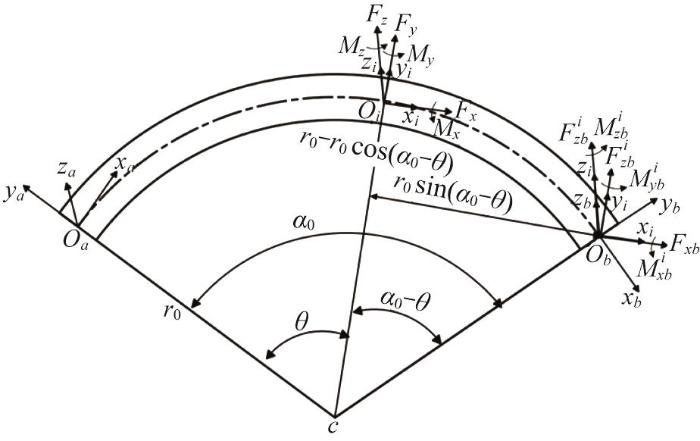
如图3 所示,在局部坐标系Oa -xa ya za 下,圆弧梁节点a 处的3个线位移分别为切向位移μa 、径向位移va 、横向位移wa ,3个角位移分别为扭转角θxa 、弯曲转角θya 、弯曲转角θza ,对应轴向力Fxa 、径向剪力Fya 、横向剪力Fza 、扭矩Mxa 、面外弯矩Mya 和面内弯矩Mza 。节点b 处的节点位移与节点力的定义与节点a 相同,其中节点力 F b
F b = F x b F y b F z b M x b M y b M z b T (1)
图3
图3
圆弧梁的局部坐标系和流动坐标系
Fig.3
Local coordinate system and mobile coordinate system of arc beam
在轴线上任意选择一节点i ,其对应的内力向量F i = F x F y F z M x M y M z T b 处构建与节点i 处坐标系方向相同的坐标系Oi -xi yi zi ,则节点b 在流动坐标系Oi -xi yi zi 下的力向量F b i F x b i F y b i F z b i M x b i M y b i M z b i T
F b i = T γ F b (2)
T γ = c o s γ s i n γ 0 0 0 0 - s i n γ c o s γ 0 0 0 0 0 0 1 0 0 0 0 0 0 c o s γ s i n γ 0 0 0 0 - s i n γ c o s γ 0 0 0 0 0 0 1
γ = α 0 - θ
式中: T γ Ob -xb yb zb 相对于流动坐标系Oi -xi yi zi 的变换矩阵,α 0 为圆弧梁的圆心角,θ 为节点a 处局部坐标系相对于点i 处流动坐标系的夹角。
将以点i 为起点、点b 为终点所表示的向量记作 i b ,则在流动坐标系Oi -xi yi zi 中向量 i b 可表示为:
i b = x i b y i b z i b = r 0 s i n γ - r 0 1 - c o s γ 0 (3)
F x + F x b i = 0 F y + F y b i = 0 F z + F z b i = 0 M x + M x b i + y i b F z b i = 0 M y + M y b i - x i b F z b i = 0 M z + M z b i + x i b F y b i + y i b F x b i = 0 (4)
F i = S γ F b i (5)
S γ = - 1 0 0 0 0 0 0 - 1 0 0 0 0 0 0 - 1 0 0 0 0 0 - y i b - 1 0 0 0 0 x i b 0 - 1 0 y i b - x i b 0 0 0 - 1
F i = H γ F b (6)
H γ = S γ T γ
2.2 圆弧梁的柔度建模
如图3 所示,当圆弧梁的a 端固定时,其应变能U 可表示为:
U = 1 2 ∫ 0 α 0 F i T D - 1 F i r 0 d θ (7)
D - 1 = d i a g E A x , G A y , G A z , G J x , E I y , E I z
式中:E 为弹性模量;G 为剪切模量;Ax 为圆弧梁的横截面积;f s 为圆弧梁横截面的剪切形状系数;Ay 、Az 为圆弧梁横截面的有效抗剪切面积,Ay =Az =Ax /fs ;Iy 、Iz 为圆弧梁横截面的惯性矩,Jx 为圆弧梁横截面的极惯性矩。
U = 1 2 F b T C F b (8)
C = r 0 ∫ 0 α 0 H γ T D - 1 H γ d γ
C = C x - F x C x - F y 0 0 0 C x - M z C y - F x C y - F y 0 0 0 C y - M z 0 0 C z - F z C z - M x C z - M y 0 0 0 C θ x - F z C θ x - M x C θ x - M y 0 0 0 C θ y - F z C θ y - M x C θ y - M y 0 C θ z - F x C θ z - F y 0 0 0 C θ z - M z (9)
式中:Cj 为各自由度方向上的柔度值,j 表示不同下标,如Cx-Fx、 Cy-Fy 和Cθz-Mz 分别表示柔性解耦机构沿X 轴平移方向、沿Y 轴平移方向以及绕Z 轴旋转方向的柔度。
C x - F x = r 0 τ 1 E A x + r 0 τ 2 G A y + r 0 3 2 τ 3 - τ 2 E I z C x - F y = C y - F x = - r 0 s i n 2 α 0 2 E A x + r 0 s i n 2 α 0 2 G A y + r 0 3 2 - 2 c o s α 0 - s i n 2 α 0 2 E I z C x - M z = C θ z - F x = - r 0 τ 3 E I z C y - F y = r 0 τ 2 E A x + r 0 τ 1 G A y + r 0 3 τ 2 E I z C y - M z = C θ z - F y = - r 0 2 1 - c o s α 0 E I z C z - F z = r 0 α 0 G A z + r 0 3 2 τ 3 - τ 2 G J x + r 0 3 s i n 2 τ 2 2 E I y C z - M x = C θ x - F z = - r 0 s i n α 0 - τ 1 G J x + r 0 2 τ 2 E I y C θ x - M y = C θ y - M x = - r 0 s i n 2 α 0 2 G J x + r 0 s i n 2 α 0 2 E I y C θ x - M x = r 0 τ 1 G J x + r 0 τ 2 E I y C θ z - M z = r 0 α 0 E I z C θ y - M y = r 0 τ 1 G J x + r 0 τ 2 G J x (10)
τ 1 = 2 α 0 + s i n 2 α 0 4
τ 2 = 2 α 0 - s i n 2 α 0 4
τ 3 = α 0 - s i n α 0
2.3 柔性解耦机构柔度建模
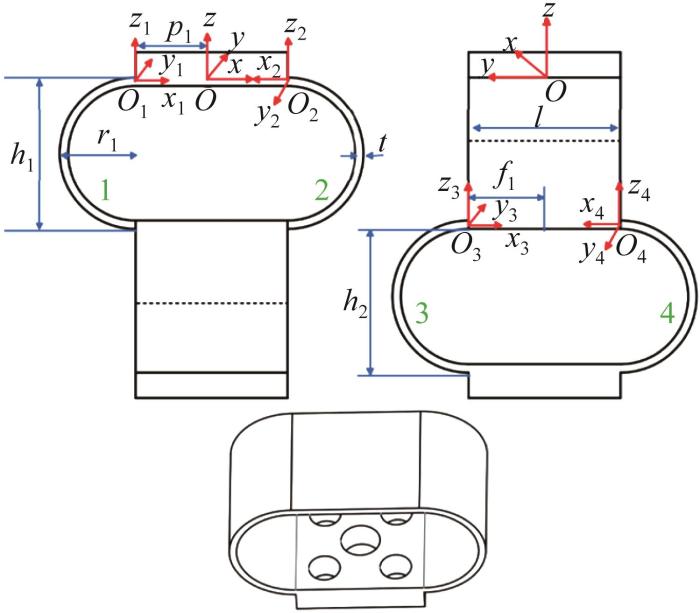
本文以柔性解耦机构H9为例进行柔度建模。柔性解耦机构H9的关键尺寸参数如图4 所示,以其工作平台的中心为原点建立全局坐标系O-xyz ,并在每个圆弧梁的输出端处建立局部坐标系On -xn yn zn (n =1, 2,…, 4)。
图4
图4
柔性解耦机构H9 的关键尺寸参数与坐标系
Fig.4
Key dimensional parameters and coordinate systems of flexible decoupling mechanism H9
如图4 所示,柔性解耦机构的上部分由圆弧梁1和圆弧梁2并联组成,下部分由圆弧梁3和圆弧梁4并联组成。基于此,构建柔性解耦机构的柔度模型,如图5 所示。图中:C 1 、C 2 、C 3 、C 4 为各圆弧梁的等效柔度。
图5
图5
柔性解耦机构柔度模型
Fig.5
Compliance model of flexible decoupling mechanism
结合图4 和图5 ,各圆弧梁在全局坐标系O-xyz 下的柔度矩阵C n O [19 ] :
C n O = T n O C n T n O T (11)
T n O = R n O S r n O R n O O R n O
式中: C n n 在其自身局部坐标系中的6×6柔度矩阵,具体表达式如式(9)所示;T n O On -xn yn zn 相对于全局坐标系O-xyz 的变换矩阵;R n O r n O On -xn yn zn 相对于全局坐标系O-xyz 的旋转矩阵和平移向量; S O
根据图4 所示的结构和几何尺寸,可得圆弧梁1对应的旋转矩阵和平移向量:
R 1 O = I r 1 O = - p 1 0 0 (12)
式中: I p 1 为圆弧梁输出端到工作平台中心的水平距离。
根据式(11),圆弧梁1在全局坐标系O - x y z C 1 O
C 1 O = T 1 O C 1 T 1 O T (13)
由于圆弧梁2与圆弧梁1对称,其在全局坐标系O - x y z C 2 O
C 2 O = R z π 0 0 R z π C 1 O R z π 0 0 R z π T (14)
由此可计算得到柔性解耦机构上部分在全局坐标系O - x y z C S O
C S O = C 1 O - 1 + C 2 O - 1 - 1 (15)
圆弧梁3在全局坐标系O - x y z C 3 O
C 3 O = T 3 O C 3 T 3 O T (16)
与式(16)中变换矩阵 T 3 O R 3 O r 3 O
R 3 O = R z π 2 r 3 O = 0 f 1 - h 1 (17)
式中:f 1 为圆弧梁输出端与工作平台中心在中间簧片梁上的投影距离,h 1 为圆弧梁输出端到工作平台中心的垂直距离。
同理,由于对称性,可以得到圆弧梁4在全局坐标系O - x y z C 4 O
C 4 O = R z π 0 0 R z π C 3 O R z π 0 0 R z π T (18)
联立式(16)与式(18),则可得到柔性解耦机构下部分在全局坐标系O-xyz 下的柔度矩阵C X O
C X O = C 3 O - 1 + C 4 O - 1 - 1 (19)
综上,整个柔性解耦机构在全局坐标系O - x y z C o O
C o O = C S O + C X O (20)
鉴于4个柔性解耦机构的设计原理和柔度建模方法相同,且其工作平台尺寸也完全相同,在对圆弧梁高度不同的柔性解耦机构进行柔度建模时,仅圆弧梁输出端的局部坐标系与全局坐标系的夹角不同,且这一夹角可通过简单的几何运算获得。因此,在得到柔性解耦机构H9的柔度矩阵后,保持建模过程不变,仅改变部分参数和坐标系转换角度,即可获得其他柔性解耦机构的柔度矩阵。
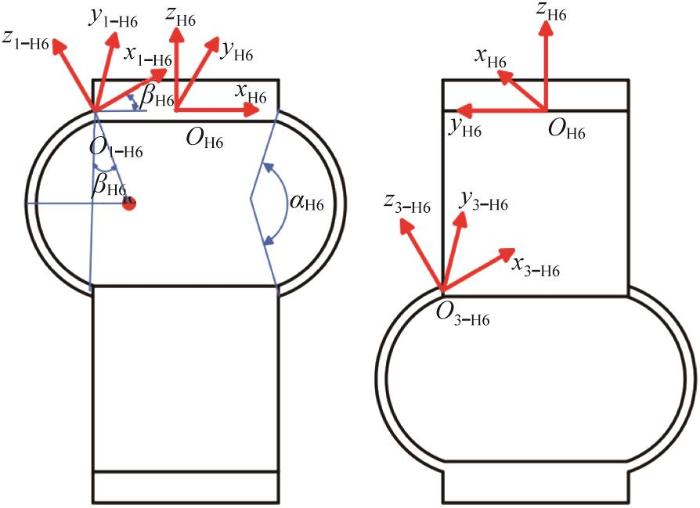
图6 所示为柔性解耦机构H6的坐标系,沿圆弧梁的切线方向为局部坐标系的x 轴,其与上部分平台的夹角即为局部坐标系相对于全局坐标系的旋转角度β H6 。因此,在计算柔性解耦机构H6中圆弧梁1的柔度时,基于柔性解耦机构H9中圆弧梁1的柔度矩阵C 1 O y 1-H6 轴旋转β H6 (即坐标系旋转到计算C 1 O C 1 O C 1 - H 6 O H 6
R 1 - H 6 O H 6 = R y H 6 β H 6 r 1 - H 6 O H 6 = [ 0 0 - h 1 ] (21)
图6
图6
柔性解耦机构H6 的坐标系建立
Fig.6
Coordinate system establishment of flexible decoupling mechanism H6
同样由于柔性解耦机构H6的上、下部分完全相同且上、下部分关于轴线对称,在计算柔性解耦机构H6中圆弧梁3的柔度矩阵时,基于柔度矩阵C 3 O z 1-H6 轴旋转π / 2
R 3 - H 6 O H 6 = R y H 6 β H 6 R z H 6 - π 2 r 3 - H 6 O H 6 = [ 0 - f 1 - h 1 ] (22)
同理,可计算得到柔性解耦机构H3中各圆弧梁的柔度矩阵。柔性解耦机构H0由簧片梁构成,簧片梁的柔度建模过程虽与圆弧梁不同,但机构整体的柔度建模过程与上文类似,故不再赘述。
3 柔性解耦机构有限元分析与实验测试
3.1 有限元分析
采用有限元分析软件ANSYS Workbench建立柔性解耦机构的有限元模型并进行静力学仿真分析,以验证上文所构建的柔度理论模型的准确性。柔性解耦机构的材料选择7075铝合金,其密度为2 810 kg/m3 ,杨氏模量为71 GPa,泊松比为0.33,屈服强度为455 MPa。圆弧梁和簧片梁的厚度均为1 mm。本文中4个柔性解耦机构的区别仅为圆弧梁高度不同,其余参数完全相同。经反复调整和计算,柔性解耦机构的尺寸参数如表1 所示。
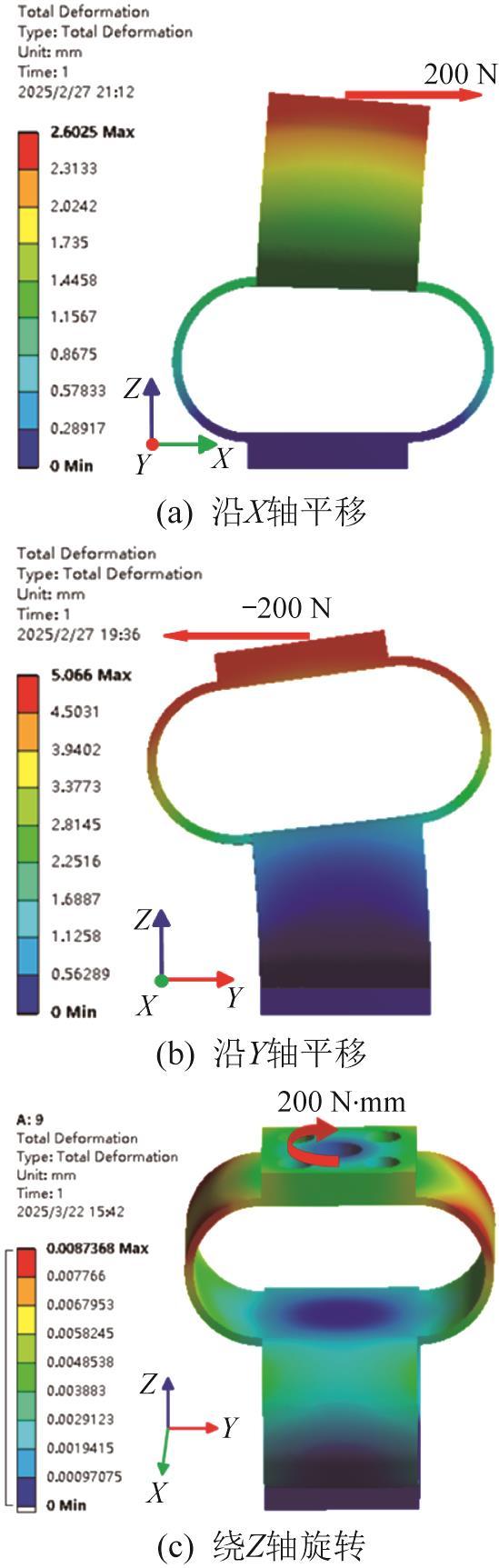
分别对4个柔性解耦机构进行静力学仿真分析,以计算其输出柔度。以柔性解耦机构H9为例,其静力学仿真结果如图7 所示。由图7 (a)和(b)可知,当分别对柔性解耦机构的上部分施加沿X 方向的200 N和沿Y 方向的-200 N输入力时,其沿X 方向产生了0.002 6 m的位移,沿Y 方向产生了0.005 1 m的位移,由此可得机构沿X 方向的输出柔度为1.3×10-5 m/N,沿Y 方向的输出柔度为2.55×10-5 m/N。由图7 (c)可知,当对柔性解耦机构施加绕Z 轴的200 N·mm力矩时,其产生了0.000 46 rad的转角,由此可得机构绕Z 轴旋转时的输出柔度为0.002 3 rad/(N·m),验证了其具有良好的扭矩传递性能。
图7
图7
柔性解耦机构H9 的静力学仿真结果
Fig.7
Statics simulation results of flexible decoupling mechanism H9
将柔性解耦机构各方向输出柔度的有限元仿真结果与理论计算结果进行对比,如表2 所示。
由表2 可知,各柔性解耦机构输出柔度的有限元仿真值与理论计算值的相对误差均在10%以内,验证了理论建模方法的准确性。
为了定量评估柔性解耦机构的解耦能力,本文定义了一个用于判断解耦能力的参数η
η = C x - F x + C y - F y 2 C θ z - M z (23)
解耦能力参数η 表示柔性解耦机构沿2个平移方向的柔度与扭转方向柔度的比值。η 值越大,表明机构在平移方向上具有较高的柔度,在扭转方向上具有较高的刚度,即能够在较小的转动位移损失下实现扭矩的高效传递和其他耦合方向上的运动。因此,η
基于式(23)对4个柔性解耦机构的解耦能力进行比较,结果如表3 所示。由表3 可知,柔性解耦机构H9的解耦能力参数η 最大,表明其解耦能力最强。从表3 中也可以看出,4个柔性解耦机构的解耦性能与两侧圆弧梁的高度成正比关系。
3.2 实验测试
为了进一步验证柔度理论模型的准确性,对4个柔性解耦机构进行实验测试[20 ] 。按照表1 所示的尺寸参数,加工4组柔性解耦机构并进行柔度测试实验。柔度测试包括平移方向和扭转方向的柔度测试,所用实验设备包括千分表、数显推力计和力矩扳手,如图8 所示。
图8
图8
柔性解耦机构柔度测试实验
Fig.8
Compliance test experiment for flexible decoupling mechanism
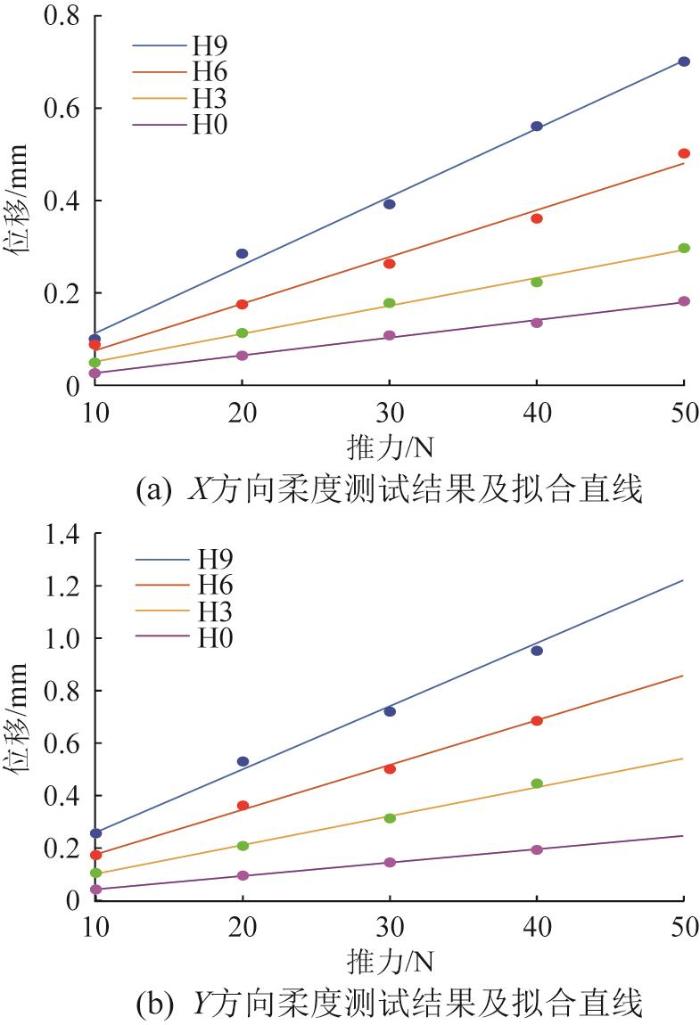
1)平移方向柔度测试。如图8 (a)所示,固定柔性解耦机构,将千分表放置在柔性解耦机构工作平台的中间,保持数显推力计与千分表始终处于同一直线,以确保测试精度。沿X 方向施加10~50 N的推力,每隔10 N记录柔性解耦机构所产生的位移以计算该方向的柔度,分别对4个柔性解耦机构进行测试。使用同样方法测量柔性解耦机构的Y 方向柔度。4个柔性解耦机构沿X 、Y 方向的平动柔度测试结果及拟合直线如图9 所示。
图9
图9
柔性解耦机构平动柔度实验结果
Fig.9
Experimental results of translational compliance for flexible decoupling mechanism
2)扭转方向柔度测试。如图8 (b)所示,固定柔性解耦机构,将千分表放置在柔性解耦机构工作平台的边角处,使用力矩扳手进行力矩输入。保持扳手水平并且输出恒定的6 N·m力矩,得到千分表位移后将其换算成相应的旋转角度,最终获得绕Z 轴方向的扭转柔度,实验结果如表4 所示。
由图9 和表4 所示的柔度测试实验结果可知,各柔性解耦机构沿各方向的输出柔度与有限元仿真和理论计算结果较为接近,相对误差均在10%以内。因此,4个柔性解耦机构的解耦能力参数η 也与表3 结果接近,即柔性解耦机构H9的解耦能力最佳。
4 结 论
为解决传统多自由度微纳米定位平台各运动方向间存在耦合效应和寄生运动的问题,本文设计了一种基于圆弧梁的柔性解耦机构。首先,对柔性解耦机构的构型和工作原理进行了介绍;然后,利用能量变分原理推导了圆弧梁的柔度理论模型,并利用该柔度模型对4个柔性解耦机构进行整体建模。最后,通过有限元分析和实验测试相结合的方法,对所构建的柔度理论模型的准确性进行了验证,得到各柔性解耦机构的输出柔度与理论计算结果的相对误差均在10%以内。在此基础上,定义了解耦能力参数,对柔性解耦机构的解耦能力进行了定量评价:柔性解耦机构的解耦能力与两侧圆弧梁的高度成正比,即机构H9具有最佳的解耦能力。本文所设计的柔性解耦机构在细胞操作与显微手术、超精密加工、芯片对准与封装等需要多自由度微纳米定位平台的场合下具有应用潜力。
参考文献
View Option
[1]
[本文引用: 1]
WANG C MENG X Y YU Y J et al High-accuracy characterization of areal micro-nano steps measured with optical microscopes
[J]. Optics and Precision Engineering , 2022 , 30 (6 ): 651 -658 .
DOI:10.37188/OPE.20223006.0651
[本文引用: 1]
[2]
XIAO R J XU M L SHAO S B et al Design and wide-bandwidth control of large aperture fast steering mirror with integrated-sensing unit
[J]. Mechanical Systems and Signal Processing , 2019 , 126 : 211 -226 .
[3]
刘昊 , 赖磊捷 大行程推拉电磁驱动微定位平台的内环阻尼与迭代学习控制
[J]. 机械科学与技术 , 2024 , 43 (7 ): 1238 -1243 .
LIU H LAI L J Inner loop damping and iterative learning control of a large stroke micro-positioning stage driven by push-pull electromagnetic actuators
[J]. Mechanical Science and Technology for Aerospace Engineering , 2024 , 43 (7 ): 1238 -1243 .
[4]
TEO T J YANG G L CHEN I M A large deflection and high payload flexure-based parallel manipulator for UV nanoimprint lithography: Part I. modeling and analyses
[J]. Precision Engineering , 2014 , 38 (4 ): 861 -871 .
[5]
ZHANG X LAI L J LI P Z et al Closed-loop inverse iterative learning control in frequency-domain for electromagnetic driven compliant micro-positioning platform
[J]. Optics and Precision Engineering , 2021 , 29 (9 ): 2149 -2157 .
DOI:10.37188/OPE.20212909.2149
[6]
[本文引用: 1]
WU J J LI Y Three-dimensional coordinate measurement of microstructures based on nano measuring machine
[J]. Optics and Precision Engineering , 2020 , 28 (10 ): 2252 -2259 .
DOI:10.37188/ope.20202810.2252
[本文引用: 1]
[7]
WANG P Y XU Q S Design of a flexure-based constant-force XY precision positioning stage
[J]. Mechanism and Machine Theory , 2017 , 108 : 1 -13 .
[本文引用: 1]
[8]
SHEN X ZHANG L QIU D M A lever-bridge combined compliant mechanism for translation amplification
[J]. Precision Engineering , 2021 , 67 : 383 -392 .
[本文引用: 1]
[9]
KANG S LEE M G CHOI Y M Six degrees-of-freedom direct-driven nanopositioning stage using crab-leg flexures
[J]. IEEE/ASME Transactions on Mechatronics , 2020 , 25 (2 ): 513 -525 .
[本文引用: 1]
[10]
YANG Z D LEE R HOPKINS J B Hexblade positioner: a fast large-range six-axis motion stage
[J]. Precision Engineering , 2022 , 76 : 199 -207 .
[11]
CHEN Y Z LAI L J LI P Z et al Full leaf-spring type spatial large-stroke parallel flexure micro-positioning stage and trajectory control
[J]. Optics and Precision Engineering , 2023 , 31 (18 ): 2675 -2686 .
DOI:10.37188/ope.20233118.2675
[12]
LAI L J GU G Y ZHU L M Design and control of a decoupled two degree of freedom translational parallel micro-positioning stage
[J]. Review of Scientific Instruments , 2012 , 83 (4 ): 045105 .
[本文引用: 1]
[13]
WU H T LAI L J ZHANG L Q et al A novel compliant XY micro-positioning stage using bridge-type displacement amplifier embedded with Scott-Russell mechanism
[J]. Precision Engineering , 2022 , 73 : 284 -295 .
[本文引用: 1]
[14]
XU Q S Design and development of a compact flexure-based XY precision positioning system with centimeter range
[J]. IEEE Transactions on Industrial Electronics , 2014 , 61 (2 ): 893 -903 .
[本文引用: 1]
[15]
LU S S YAN P ZHANG B Long stroke displacement measurement with reduced coupling error supporting high precision control of a beam flexure-based micro-stage
[J]. Review of Scientific Instruments , 2020 , 91 (7 ): 073701 .
[本文引用: 1]
[16]
YU H T ZHANG C YANG B et al The design and kinetostatic modeling of 3PPR planar compliant parallel mechanism based on compliance matrix method
[J]. Review of Scientific Instruments , 2019 , 90 (4 ): 045102 .
[17]
YANG M SUN M Y WU Z et al Design of a redundant actuated 4-PPR planar 3-DOF compliant nanopositioning stage
[J]. Precision Engineering , 2023 , 82 : 68 -79 .
[本文引用: 1]
[18]
LI H Y LIU Y J WANG Z P et al A constraint-flow based method of synthesizing XYθ compliant parallel mechanisms with decoupled motion and actuation characteristics
[J]. Mechanism and Machine Theory , 2022 , 178 : 105085 .
[本文引用: 1]
[19]
AL-JODAH A SHIRINZADEH B GHAFARIAN M et al Design, modeling, and control of a large range 3-DOF micropositioning stage
[J]. Mechanism and Machine Theory , 2021 , 156 : 104159 .
[本文引用: 1]
[20]
谢超 , 陈云壮 , 石光楠 , 等 正交簧片型大行程柔性球铰设计及柔度分析
[J]. 工程设计学报 , 2023 , 30 (5 ): 626 -633 .
[本文引用: 1]
XIE C CHEN Y Z SHI G N et al Design and compliance analysis of large stroke flexible ball hinge with orthogonal reeds
[J]. Chinese Journal of Engineering Design , 2023 , 30 (5 ): 626 -633 .
[本文引用: 1]
三维微纳米台阶高精度光学显微测量量化表征
1
2022
... 微纳米定位技术在高精度显微、纳米光刻、超精密加工、微机电系统以及生物医学工程等诸多前沿领域中发挥着重要作用[1 -6 ] .柔性机构基于柔性元件的弹性变形来传递运动,能够消除摩擦、机械间隙等机械不确定性[7 ] .因此,现有的微纳米定位平台广泛采用柔性机构作为传动机构[8 ] . ...
三维微纳米台阶高精度光学显微测量量化表征
1
2022
... 微纳米定位技术在高精度显微、纳米光刻、超精密加工、微机电系统以及生物医学工程等诸多前沿领域中发挥着重要作用[1 -6 ] .柔性机构基于柔性元件的弹性变形来传递运动,能够消除摩擦、机械间隙等机械不确定性[7 ] .因此,现有的微纳米定位平台广泛采用柔性机构作为传动机构[8 ] . ...
Design and wide-bandwidth control of large aperture fast steering mirror with integrated-sensing unit
0
2019
大行程推拉电磁驱动微定位平台的内环阻尼与迭代学习控制
0
2024
大行程推拉电磁驱动微定位平台的内环阻尼与迭代学习控制
0
2024
A large deflection and high payload flexure-based parallel manipulator for UV nanoimprint lithography: Part I. modeling and analyses
0
2014
电磁驱动柔顺微定位平台闭环频域逆迭代学习控制
0
2021
电磁驱动柔顺微定位平台闭环频域逆迭代学习控制
0
2021
基于纳米测量机的微结构三维坐标测量
1
2020
... 微纳米定位技术在高精度显微、纳米光刻、超精密加工、微机电系统以及生物医学工程等诸多前沿领域中发挥着重要作用[1 -6 ] .柔性机构基于柔性元件的弹性变形来传递运动,能够消除摩擦、机械间隙等机械不确定性[7 ] .因此,现有的微纳米定位平台广泛采用柔性机构作为传动机构[8 ] . ...
基于纳米测量机的微结构三维坐标测量
1
2020
... 微纳米定位技术在高精度显微、纳米光刻、超精密加工、微机电系统以及生物医学工程等诸多前沿领域中发挥着重要作用[1 -6 ] .柔性机构基于柔性元件的弹性变形来传递运动,能够消除摩擦、机械间隙等机械不确定性[7 ] .因此,现有的微纳米定位平台广泛采用柔性机构作为传动机构[8 ] . ...
Design of a flexure-based constant-force XY precision positioning stage
1
2017
... 微纳米定位技术在高精度显微、纳米光刻、超精密加工、微机电系统以及生物医学工程等诸多前沿领域中发挥着重要作用[1 -6 ] .柔性机构基于柔性元件的弹性变形来传递运动,能够消除摩擦、机械间隙等机械不确定性[7 ] .因此,现有的微纳米定位平台广泛采用柔性机构作为传动机构[8 ] . ...
A lever-bridge combined compliant mechanism for translation amplification
1
2021
... 微纳米定位技术在高精度显微、纳米光刻、超精密加工、微机电系统以及生物医学工程等诸多前沿领域中发挥着重要作用[1 -6 ] .柔性机构基于柔性元件的弹性变形来传递运动,能够消除摩擦、机械间隙等机械不确定性[7 ] .因此,现有的微纳米定位平台广泛采用柔性机构作为传动机构[8 ] . ...
Six degrees-of-freedom direct-driven nanopositioning stage using crab-leg flexures
1
2020
... 多自由度微纳米定位平台通常采用并联柔性机构来实现运动[9 -12 ] .为了减少并联柔性机构各自由度间的耦合位移,通常需要加装柔性解耦机构,以实现各自由度方向上的运动解耦.当前,具有运动解耦功能的柔性机构主要应用于二自由度平动纳米定位平台,利用簧片梁沿其自身轴线方向上的较大刚度来实现2个自由度之间的解耦[13 -14 ] .而针对旋转纳米运动的柔性解耦机构目前鲜有报道,多自由度并联柔性机构在实现独立旋转运动时仍面临较大挑战.在多自由度并联柔性机构中,旋转运动一般由多组直线支链同时驱动产生,如常见的平面XYθ 三自由度并联微定位平台.这类平台通常采用3-PPR和4-PPR构型[15 -17 ] ,其旋转运动并非独立驱动,与其他2个自由度间存在耦合,从而导致旋转中心容易发生漂移. ...
Hexblade positioner: a fast large-range six-axis motion stage
0
2022
全簧片式空间大行程并联柔性微定位平台及其轨迹控制
0
2023
全簧片式空间大行程并联柔性微定位平台及其轨迹控制
0
2023
Design and control of a decoupled two degree of freedom translational parallel micro-positioning stage
1
2012
... 多自由度微纳米定位平台通常采用并联柔性机构来实现运动[9 -12 ] .为了减少并联柔性机构各自由度间的耦合位移,通常需要加装柔性解耦机构,以实现各自由度方向上的运动解耦.当前,具有运动解耦功能的柔性机构主要应用于二自由度平动纳米定位平台,利用簧片梁沿其自身轴线方向上的较大刚度来实现2个自由度之间的解耦[13 -14 ] .而针对旋转纳米运动的柔性解耦机构目前鲜有报道,多自由度并联柔性机构在实现独立旋转运动时仍面临较大挑战.在多自由度并联柔性机构中,旋转运动一般由多组直线支链同时驱动产生,如常见的平面XYθ 三自由度并联微定位平台.这类平台通常采用3-PPR和4-PPR构型[15 -17 ] ,其旋转运动并非独立驱动,与其他2个自由度间存在耦合,从而导致旋转中心容易发生漂移. ...
A novel compliant XY micro-positioning stage using bridge-type displacement amplifier embedded with Scott-Russell mechanism
1
2022
... 多自由度微纳米定位平台通常采用并联柔性机构来实现运动[9 -12 ] .为了减少并联柔性机构各自由度间的耦合位移,通常需要加装柔性解耦机构,以实现各自由度方向上的运动解耦.当前,具有运动解耦功能的柔性机构主要应用于二自由度平动纳米定位平台,利用簧片梁沿其自身轴线方向上的较大刚度来实现2个自由度之间的解耦[13 -14 ] .而针对旋转纳米运动的柔性解耦机构目前鲜有报道,多自由度并联柔性机构在实现独立旋转运动时仍面临较大挑战.在多自由度并联柔性机构中,旋转运动一般由多组直线支链同时驱动产生,如常见的平面XYθ 三自由度并联微定位平台.这类平台通常采用3-PPR和4-PPR构型[15 -17 ] ,其旋转运动并非独立驱动,与其他2个自由度间存在耦合,从而导致旋转中心容易发生漂移. ...
Design and development of a compact flexure-based XY precision positioning system with centimeter range
1
2014
... 多自由度微纳米定位平台通常采用并联柔性机构来实现运动[9 -12 ] .为了减少并联柔性机构各自由度间的耦合位移,通常需要加装柔性解耦机构,以实现各自由度方向上的运动解耦.当前,具有运动解耦功能的柔性机构主要应用于二自由度平动纳米定位平台,利用簧片梁沿其自身轴线方向上的较大刚度来实现2个自由度之间的解耦[13 -14 ] .而针对旋转纳米运动的柔性解耦机构目前鲜有报道,多自由度并联柔性机构在实现独立旋转运动时仍面临较大挑战.在多自由度并联柔性机构中,旋转运动一般由多组直线支链同时驱动产生,如常见的平面XYθ 三自由度并联微定位平台.这类平台通常采用3-PPR和4-PPR构型[15 -17 ] ,其旋转运动并非独立驱动,与其他2个自由度间存在耦合,从而导致旋转中心容易发生漂移. ...
Long stroke displacement measurement with reduced coupling error supporting high precision control of a beam flexure-based micro-stage
1
2020
... 多自由度微纳米定位平台通常采用并联柔性机构来实现运动[9 -12 ] .为了减少并联柔性机构各自由度间的耦合位移,通常需要加装柔性解耦机构,以实现各自由度方向上的运动解耦.当前,具有运动解耦功能的柔性机构主要应用于二自由度平动纳米定位平台,利用簧片梁沿其自身轴线方向上的较大刚度来实现2个自由度之间的解耦[13 -14 ] .而针对旋转纳米运动的柔性解耦机构目前鲜有报道,多自由度并联柔性机构在实现独立旋转运动时仍面临较大挑战.在多自由度并联柔性机构中,旋转运动一般由多组直线支链同时驱动产生,如常见的平面XYθ 三自由度并联微定位平台.这类平台通常采用3-PPR和4-PPR构型[15 -17 ] ,其旋转运动并非独立驱动,与其他2个自由度间存在耦合,从而导致旋转中心容易发生漂移. ...
The design and kinetostatic modeling of 3PPR planar compliant parallel mechanism based on compliance matrix method
0
2019
Design of a redundant actuated 4-PPR planar 3-DOF compliant nanopositioning stage
1
2023
... 多自由度微纳米定位平台通常采用并联柔性机构来实现运动[9 -12 ] .为了减少并联柔性机构各自由度间的耦合位移,通常需要加装柔性解耦机构,以实现各自由度方向上的运动解耦.当前,具有运动解耦功能的柔性机构主要应用于二自由度平动纳米定位平台,利用簧片梁沿其自身轴线方向上的较大刚度来实现2个自由度之间的解耦[13 -14 ] .而针对旋转纳米运动的柔性解耦机构目前鲜有报道,多自由度并联柔性机构在实现独立旋转运动时仍面临较大挑战.在多自由度并联柔性机构中,旋转运动一般由多组直线支链同时驱动产生,如常见的平面XYθ 三自由度并联微定位平台.这类平台通常采用3-PPR和4-PPR构型[15 -17 ] ,其旋转运动并非独立驱动,与其他2个自由度间存在耦合,从而导致旋转中心容易发生漂移. ...
A constraint-flow based method of synthesizing XYθ compliant parallel mechanisms with decoupled motion and actuation characteristics
1
2022
... 为解决上述问题,Li等[18 ] 将2组平行四边形机构分别进行正交组合和左右对称组合,形成了能够实现平面二自由度运动解耦的旋转运动解耦机构,但该解耦机构只能实现与平动自由度的解耦.为了扩展上述基于平行四边形机构正交组合的旋转运动解耦机构的应用范围,以实现对含平动在内的多个耦合自由度的解耦,本文尝试用圆弧梁替换原机构中的簧片梁,通过充分利用圆弧梁在各自由度方向上的柔度特性,设计一系列基于圆弧梁的旋转纳米运动柔性解耦机构.首先,对柔性解耦机构的构型进行介绍,并设计圆弧梁高度不同的柔性解耦机构;然后,通过柔度矩阵法对柔性解耦机构进行静力学建模并确定其尺寸参数,以获得其输出柔度;最后,通过有限元分析和实验相结合的方法对柔度理论模型的准确性进行验证,并比较各柔性解耦机构的解耦能力. ...
Design, modeling, and control of a large range 3-DOF micropositioning stage
1
2021
... 结合图4 和图5 ,各圆弧梁在全局坐标系O-xyz 下的柔度矩阵C n O [19 ] : ...
正交簧片型大行程柔性球铰设计及柔度分析
1
2023
... 为了进一步验证柔度理论模型的准确性,对4个柔性解耦机构进行实验测试[20 ] .按照表1 所示的尺寸参数,加工4组柔性解耦机构并进行柔度测试实验.柔度测试包括平移方向和扭转方向的柔度测试,所用实验设备包括千分表、数显推力计和力矩扳手,如图8 所示. ...
正交簧片型大行程柔性球铰设计及柔度分析
1
2023
... 为了进一步验证柔度理论模型的准确性,对4个柔性解耦机构进行实验测试[20 ] .按照表1 所示的尺寸参数,加工4组柔性解耦机构并进行柔度测试实验.柔度测试包括平移方向和扭转方向的柔度测试,所用实验设备包括千分表、数显推力计和力矩扳手,如图8 所示. ...