随着机械臂架在工程领域的广泛应用,国内外学者对机械臂的力学特性进行了深入研究。如:赵斌等[4-7]利用Lagrange定理和虚功原理对机械臂的臂杆进行柔性处理,建立其非线性动力学方程,并通过仿真获得了在机械臂工作过程中各杆件的动态特性,但忽略了关节变形对机械臂运动的影响;张玉玲等[8]提出了臂杆刚度主动控制方法,减小了臂杆柔性变形带来的位移变化,提高了机械臂末端的定位精度和运动稳定性,但未对关节的刚度进行控制;王海等[9-11]为了避免在实际操作中影响机械臂的运动精度,建立了柔性机械臂关节的数值模型,利用MATLAB软件分析了机械臂运动轨迹,但未考虑臂杆变形对机械臂运动轨迹的影响;梁明轩等[12]基于“转子-扭簧”柔性关节模型,分析了不同关节刚度对机械臂固有频率的影响;Bilal等[13]建立了单连杆柔性关节机械臂的动力学模型,研究了具有参数不确定性的旋转柔性关节位置的确定方法;Kumar等[14]基于欧拉-伯努利梁和弹簧惯性系统描述了机械臂的运动轨迹,分析了关节运动和惯性耦合引起的机械臂的动态特性。
综上所述,现有对机械臂力学特性的研究中,大多只单独分析臂杆柔性或者关节柔性,很少同时考虑两者。为了使研究更加贴近实际工况,笔者以大行程、多自由度专用机械臂架为研究对象,以其末端执行器提取的钢丝绳重力为主要作用载荷,采用有限元分析方法和动力学分析方法对臂杆和主要铰接关节进行刚柔耦合分析,研究机械臂架更换钢丝绳时机械臂铰接关节的刚度对末端执行器位移的影响,及有/无钢丝绳作用对关节角位移和末端执行器位移的影响。
1 机械臂架结构
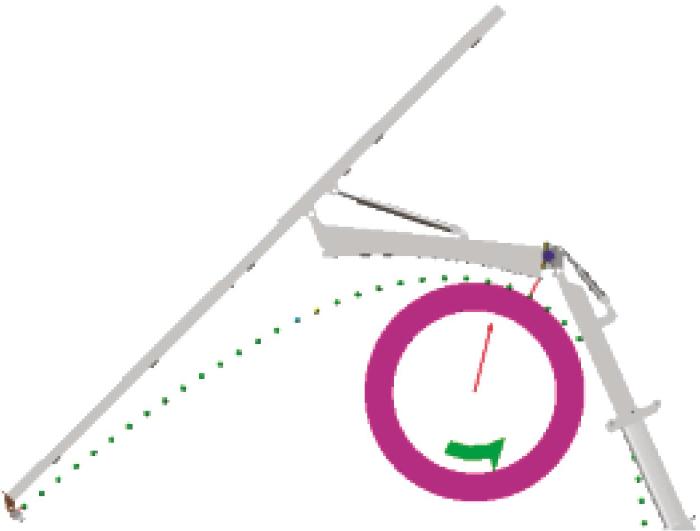
机械臂架作为更换电铲钢丝绳的关键设备,其结构是否合理将直接影响钢丝绳更换效率。机械臂架的结构如图1所示,其主要由回转机构、伸缩机构和更换机构等组成。通过各机构的相互配合完成回转、变幅、提升、抓取等动作,实现对电铲钢丝绳的更换。
图1
图2
图3
更换机构是抓取和更换钢丝绳的主要构件。更换机构的结构如图4所示,其主要由连接臂、一级变幅液压缸、二级变幅液压缸、弧形臂、伸缩小臂和末端执行器等组成,其中伸缩小臂由4节构成。当伸缩机构调整到合适位置后,一级变幅液压缸推动弧形臂搭扣天轮;二级变幅液压缸推动伸缩小臂变幅到合适位置;4节伸缩小臂由多级液压缸推动,完成伸展和缩回动作;伸缩小臂末端装有末端执行器,用于牵引钢丝绳,同时,小臂末端还装有摄像头,用于操控者观测。
图4
图4
更换机构结构
1—连接臂;2—一级变幅液压缸;3—二级变幅液压缸;4—弧形臂;5—伸缩小臂;6—末端执行器。
Fig.4
Structure of replacement mechanism
2 机械臂架运动仿真
机械臂架更换钢丝绳时,变幅液压缸推动铰接于回转台的伸缩机构。伸缩机构经变幅下落到电铲吊耳附近抓取钢丝绳,抓取完成后再经变幅上升到电铲天轮附近,其至合适位置后更换机构的弧形臂搭扣天轮,4节伸缩小臂经二级变幅液压缸推动至合适位置后依次伸缩,使钢丝绳沿天轮的绳槽方向被输送到电铲内部而完成钢丝绳一端的输送,然后重复此动作完成钢丝绳另一端的操作。在钢丝绳更换仿真时,对整个机械臂架的杆件进行柔性化,同时对伸缩机构与转台的铰接关节A、连接臂与连接板的铰接关节B、伸缩小臂与弧形臂的铰接关节C进行柔性化,分析不同关节刚度对末端执行器位移的影响及有/无钢丝绳作用对关节角位移和末端执行器位移的影响。
2.1 机械臂架运动约束的建立
根据多体动力学建模理论,采用Pro/E软件创建机械臂架三维实体模型,将它保存为X
表1 机械臂架运动副约束描述
Table 1
| 部件1 | 部件2 | 约束类型 | 约束自由度/个 |
|---|---|---|---|
| 转台 | 伸缩臂1 | 点线副 | 2 |
| 变幅液压缸筒 | 回转台 | 旋转副 | 5 |
| 变幅液压缸杆 | 伸缩大臂1 | 旋转副 | 5 |
| 伸缩大臂1 | 伸缩大臂2 | 移动副 | 5 |
| 伸缩大臂2 | 伸缩大臂3 | 移动副 | 5 |
| 伸缩大臂3 | 伸缩大臂4 | 移动副 | 5 |
| 伸缩大臂4 | 伸缩大臂5 | 移动副 | 5 |
| 一级变幅液压缸筒 | 连接臂 | 点线副 | 2 |
| 弧形臂 | 连接板 | 固定副 | 6 |
| 一级变幅液压缸杆 | 连接板 | 旋转副 | 5 |
| 二级变幅液压缸筒 | 弧形臂 | 点线副 | 2 |
| 二级变幅液压缸杆 | 伸缩小臂1 | 旋转副 | 5 |
| 弧形臂 | 伸缩小臂1 | 旋转副 | 5 |
| 伸缩小臂2 | 伸缩小臂1 | 移动副 | 5 |
| 伸缩小臂3 | 伸缩小臂2 | 移动副 | 5 |
| 伸缩小臂4 | 伸缩小臂3 | 移动副 | 5 |
图5
图5
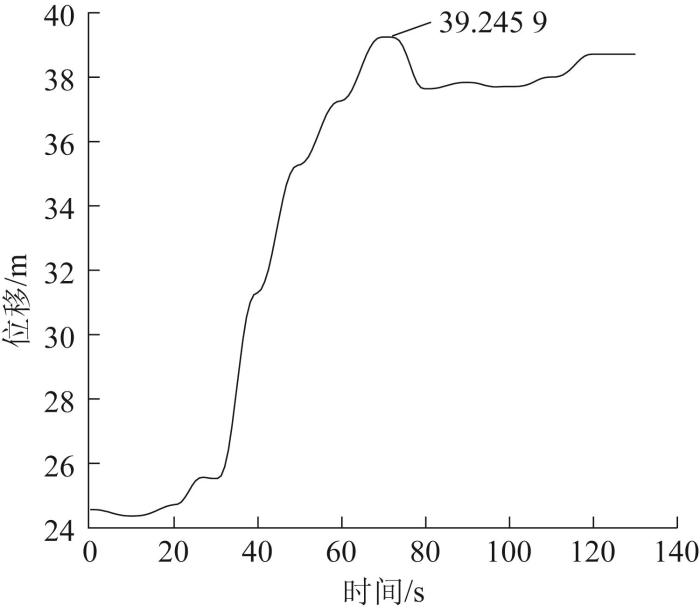
全刚体无钢丝绳状态下末端执行器的位移
Fig.5
End effector displacement in the state of complete rigid body without wire rope
图6
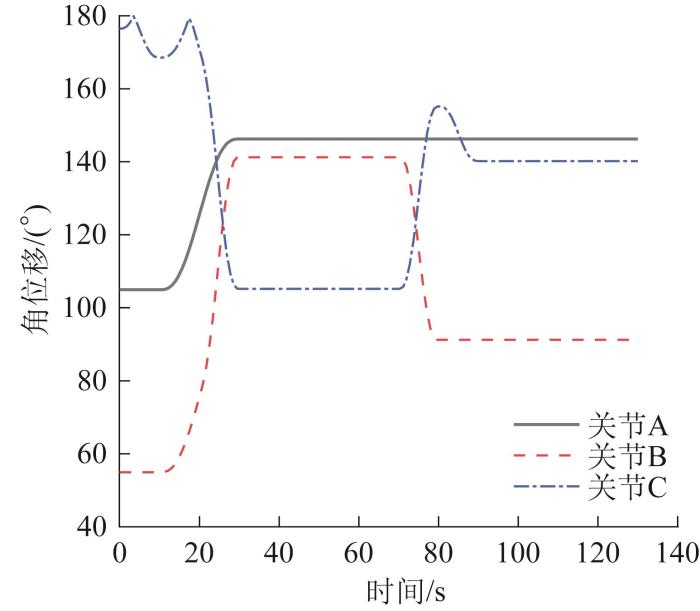
图6
全刚体无钢丝绳状态下关节角位移
Fig.6
Joint angular displacement in the state of full rigid body without wire rope
2.2 钢丝绳运动仿真
电铲的工作环境比较复杂,机械臂架会受到多种载荷同时作用。在机械臂架更换钢丝绳时以其末端执行器提取的钢丝绳重力为主要载荷,因此对钢丝绳运动进行仿真是十分必要的。
图7
表2 钢丝绳与天轮的接触参数
Table 2
| 参数 | 量值 |
|---|---|
| 接触刚度 | 1×108 N/m |
| 摩擦因数 | 0.6 |
| 摩擦速度 | 0.1 m/s |
表3 钢丝绳参数
Table 3
| 参数 | 量值 |
|---|---|
| 直径 | 90 mm |
| 密度 | 7 800 kg/m3 |
| 弹性模量 | 1.96×1011 Pa |
| 阻尼 | 0.3 kg/s |
图8
图9
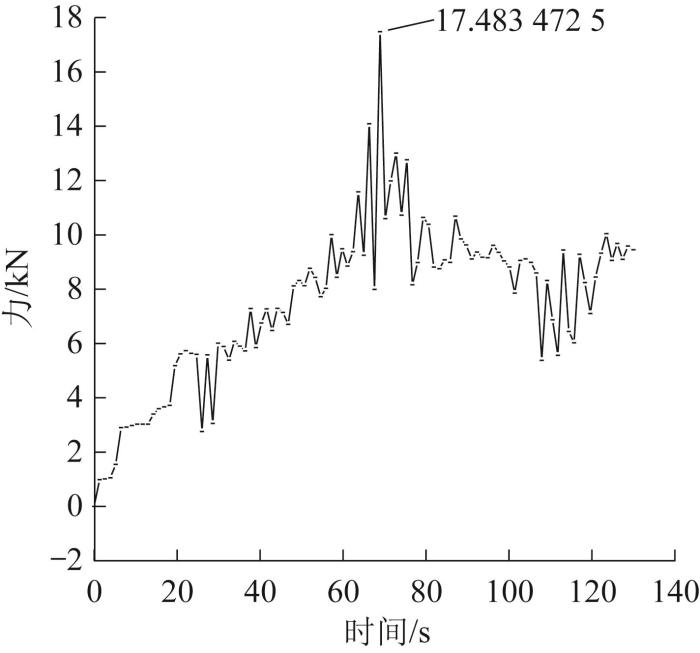
在更换过程中钢丝绳的张力变化如图10所示。在0 —70 s内被提取的钢丝绳上升至电铲天轮附近,随着所提取钢丝绳长度的增大,钢丝绳之间的张力逐渐变大,在与天轮接触前达到最大值17.483 472 5 kN。由于机械臂与天轮接触,钢丝绳发生抖动,此时其张力发生剧烈突变;钢丝绳完成搭扣后,张力逐渐缓慢变小,但由于抓取绳的长度继续增大,张力值仍大于提起钢丝绳的阶段。
图10
2.3 刚柔耦合模型的建立
为了更好地对机械臂架的运动进行实时、有效的预测和控制,利用ANSYS APDL软件生成机械臂架模态中性文件,并将其导入ADAMS进行刚柔耦合分析[18]。具体步骤如下:
1)创建模态中性文件。将在Pro/E中生成的X_T文件导入ANSYS APDL经典界面进行前处理,即进行单元类型选定、材料添加、网格划分、刚性区域和外连接点建立,并对伸缩机构、更换机构逐一柔化,每个部件建立2处刚性区域。采用智能划分的方法划分网格,网格密度定义为2。以伸缩小臂1为例,其刚性区域连接如图11所示。
图11
2)替换刚性模型。生成的模态中性文件mnf包含节点号、节点自由度和节点质量等信息。利用ADAMS软件打开创建的机械臂架刚体动力学bin文件,通过make flexible导入模态中性文件,替换原有的刚性部件。为了保证模型替换的准确性,在进行柔性化处理时须将模型整体导入。为了保证替换后的部件正常运动,柔性化后的部件须重新添加约束。
图12
图12
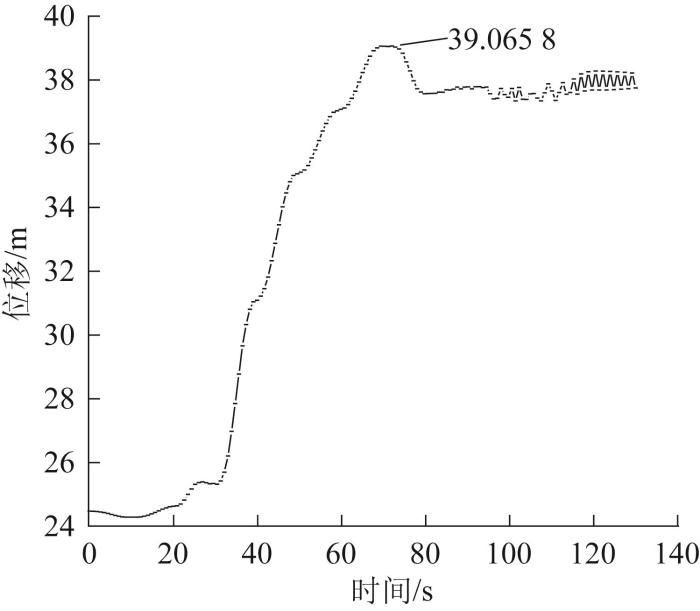
伸缩小臂柔化后末端执行器的位移
Fig.12
End effector displacement after flexing the telescopic forearm
图13
2.4 机械臂架动力学模型的建立
图14
式中:
式中:
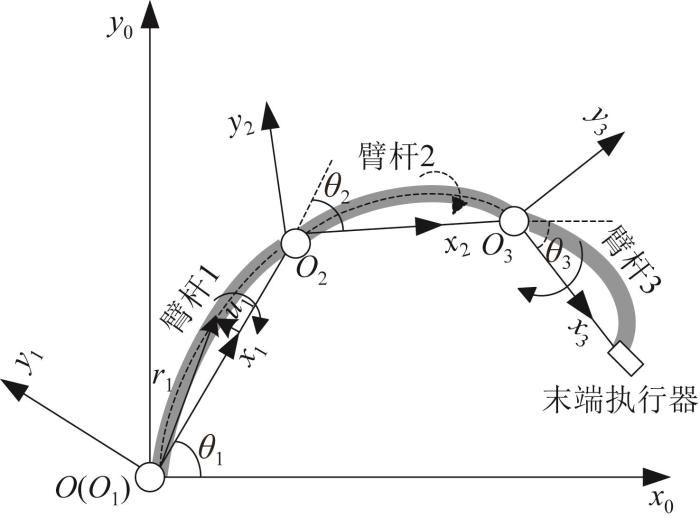
臂杆l的速度为:
反对称矩阵 A 为:
则臂杆1的速度也可以表示为:
臂杆1的动能T1为:
式中:
臂杆2的速度
式中:
臂杆3的速度为:
式中:
则机械臂架的总动能为:
机械臂架工作时产生的势能主要包括臂杆弯曲变形引起的应变能、臂杆变形引起的重力势能变化量和臂杆运动所产生的重力势能变化量,所以其势能U为:
式中:
将
式中:L为系统用各广义坐标 qj 和各广义速度 qj 表示的动能;
将第二类拉格朗日方程表示成动力学方程:
式中:
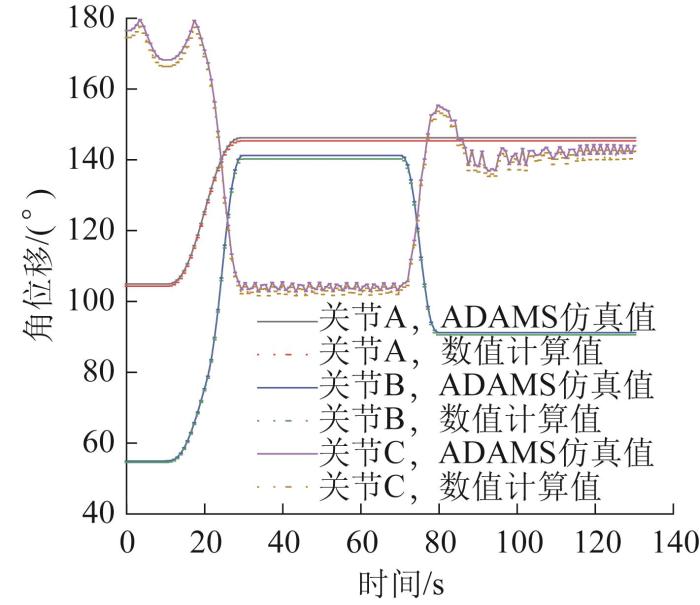
在驱动力已知的条件下,利用MATLAB软件求解关节A、B、C的角位移,并与通过ADAMS软件求解得到的角位移进行对比,结果如图15所示。
图15
由图15可知,通过数值计算与模型仿真得到的关节角位移之间的偏差较小,两者基本重合。产生偏差的原因是不同软件的计算精度不同,由此验证了所建机械臂架动力学模型的正确性。
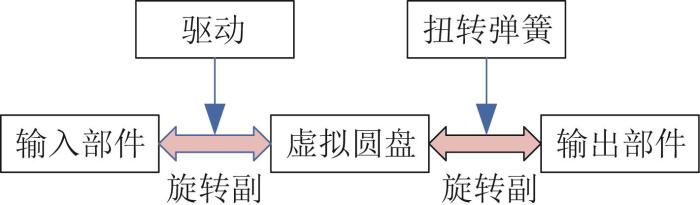
2.5 关节耦合
表4 关节约束
Table 4
| 部件1 | 部件2 | 约束类型 |
|---|---|---|
| 转台 | 圆盘A | 旋转副 |
| 圆盘A | 伸缩机构 | 旋转副 |
| 连接臂 | 圆盘B | 旋转副 |
| 圆盘B | 连接板 | 旋转副 |
| 弧形臂 | 圆盘C | 旋转副 |
| 圆盘C | 伸缩小臂 | 旋转副 |
图16
3 结果分析
3.1 不同关节刚度下末端执行器运动特性分析
为了研究关节刚度对钢丝绳更换稳定性的影响,运用控制变量法,在臂杆进行了柔性处理的前提下,分别对其中一个关节进行柔性处理,而其余两个关节为刚性连接,来分析末端执行器的位移变化。
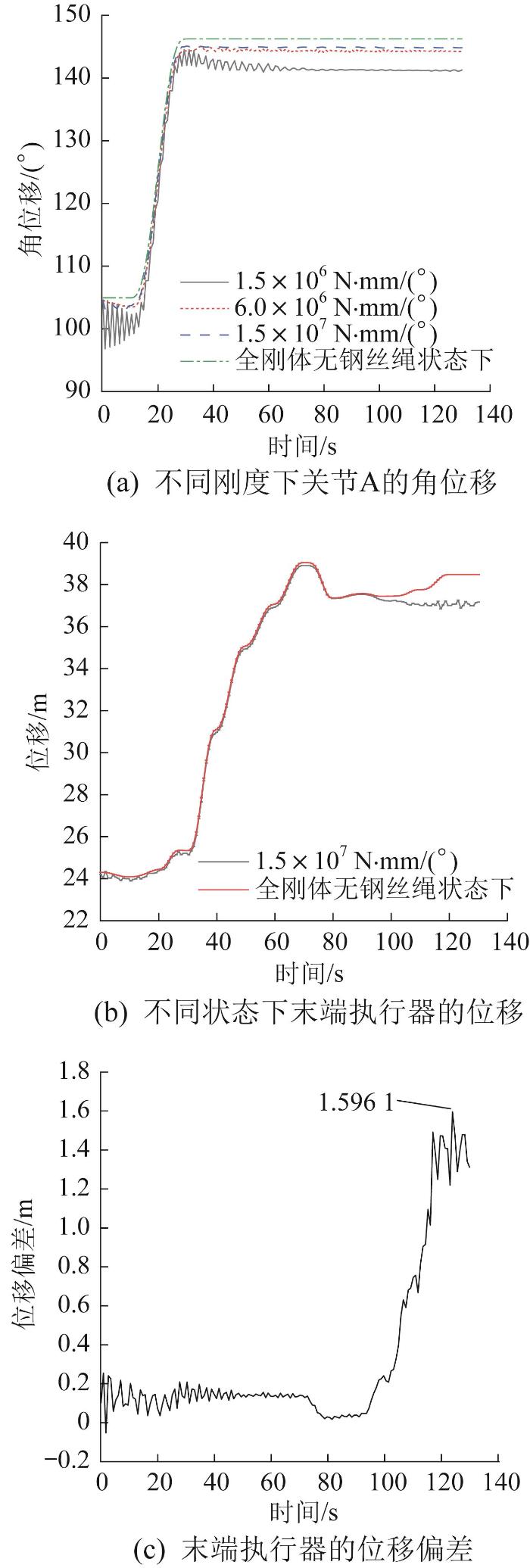
根据关节结构的工作特性,定义关节A的刚度系数分别为1.5×106,6.0×106,1.5×107 N·mm/(˚),对关节A进行柔性处理。关节A刚度对末端执行器位移的影响如图17所示。
图17
图17
关节A刚度对末端执行器位移的影响
Fig.17
Influence of joint A stiffness on end effector displacement
不同刚度下关节A的角位移如图17(a)所示。由图可知,当关节A的刚度系数为1.5×107 N·mm/(˚)时,机械臂架更换钢丝绳的过程较稳定,晃动程度较低,关节A的角位移与全刚体无钢丝绳状态较接近。
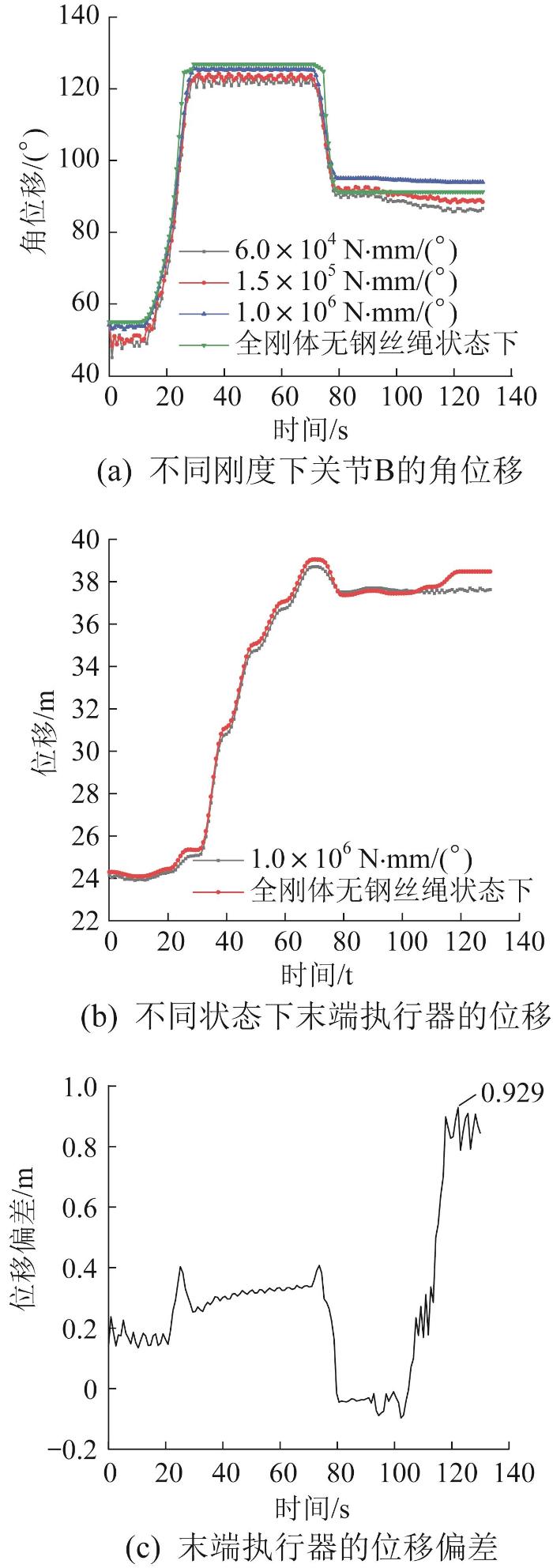
定义关节B的刚度系数分别6×104,1.5×105,1.0×106 N·mm/(˚),对关节B进行柔性处理。关节B刚度对末端执行器位移的影响如图18所示。
图18
图18
关节B刚度对末端执行器位移的影响
Fig.18
Influence of joint B stiffness on end effector displacement
不同刚度下关节B的角位移如图18(a)所示。由图可知:当关节B的刚度系数为1.0×106 N·mm/(˚)时,机械臂架的运动振幅较小,比较接近全刚体无钢丝绳状态;在20 —30 s和70 —80 s内进行了2次运动,分别实现了钢丝绳的提取和搭扣天轮。
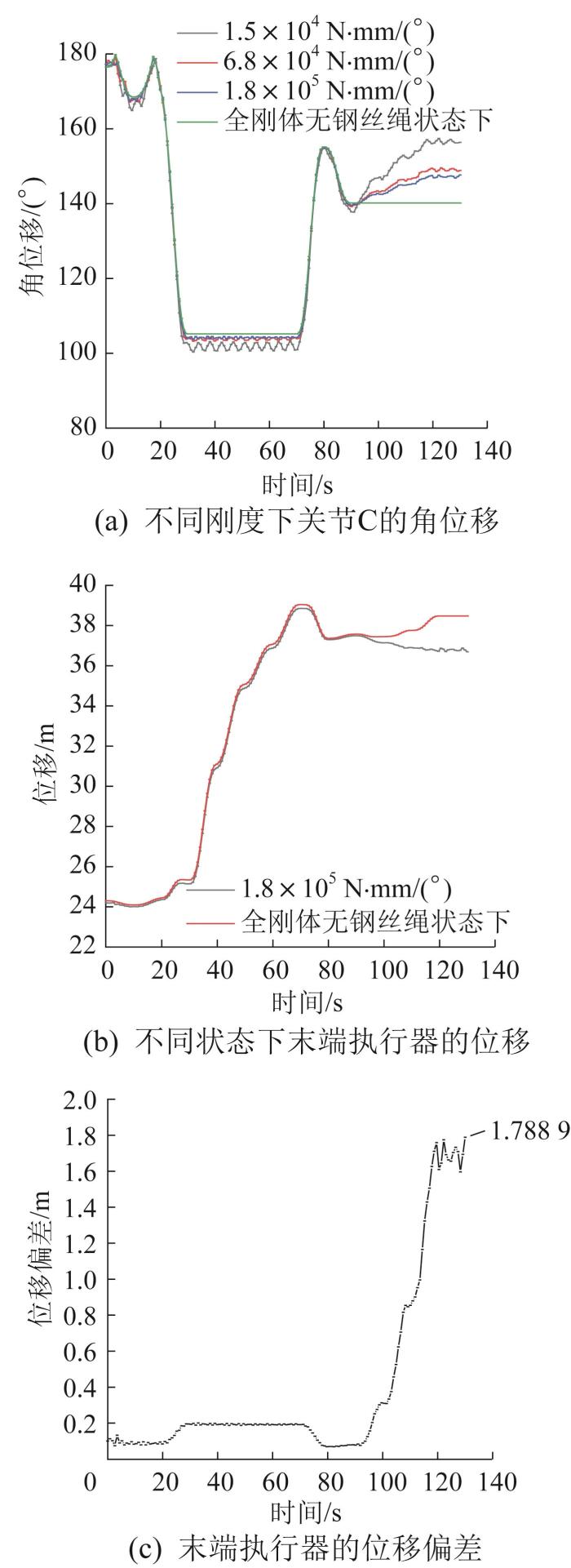
定义关节C的刚度系数分别1.5×104,6.8×104,1.8×105 N·mm/(˚),对关节C进行柔性处理。关节C刚度对末端执行器位移的影响如图19所示。
图19
图19
关节C刚度对末端执行器位移的影响
Fig.19
Influence of joint C stiffness on end effector displacement
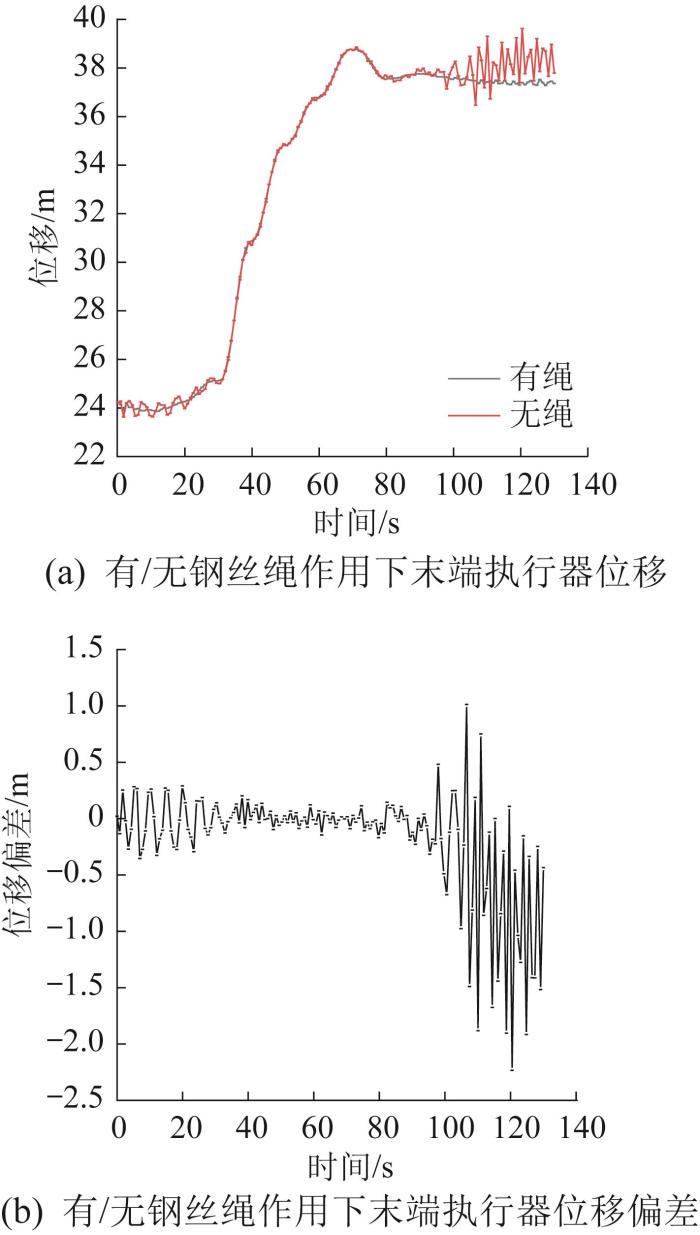
3.2 有/无钢丝绳作用对关节角位移和末端执行器位移的影响
图20
图20
有/无钢丝绳作用对关节角位移的影响
Fig.20
Influence on joint angular displacement with/without wire rope action
图21
图21
有/无钢丝绳作用对末端执行器位移的影响
Fig.21
Influence on end effector displacement deviation with/without wire rope action
4 结 论
1)采用有限元分析方法和动力学分析方法对机械臂架的臂杆和主要铰接关节进行柔性处理,并建立机械臂架动力学模型,以末端执行器提取的钢丝绳重力为主要作用载荷,来分析末端执行器的运动特性。
2)通过仿真发现,在较大的关节刚度系数下,机械臂架的运动状态趋近于全刚体无钢丝绳状态,关节C的刚度对末端执行器位移的影响最大,产生的关节位移偏差也最大。
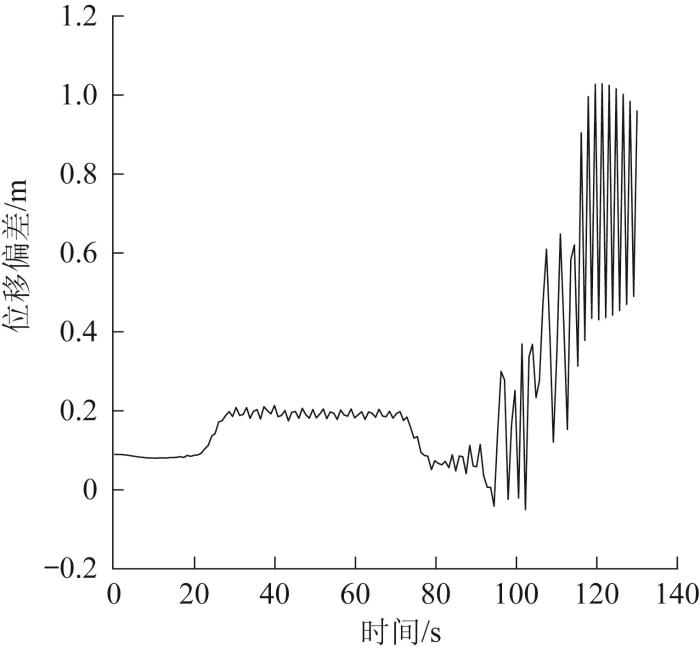
3)当关节A的刚度系数为1.5×107 N·mm/(˚)、关节B的刚度系数为1.0×106 N·mm/(˚)、关节C的刚度系数为1.8×105 N·mm/(˚)时,机械臂架空载运行时产生的关节角位移偏差及末端执行器位移偏差明显,而抓取钢丝绳时移偏差均较小,关节A角位移偏差最小,偏差最小值为0.590 2°。
4)本文为进一步研究机械臂架的工作稳定性及运动精度控制提供了参考。
参考文献
对电铲钢丝绳寿命计算及影响因素的探讨
[J].
Discussion on life calculation and influencing factors of electric shovel wire rope
[J].
对电铲钢丝绳寿命计算及影响因素的探讨
[J].
Discussion on life calculation and influencing factors of wire rope for electric shovel
[J].DOI:10.3969/j.issn.1008-0155.2019.15.062
矿用WK-10B型电铲装矿作业实时称重系统开发研究
[D].
Development and research of real-time weighing system for mine WK-10B electric shovel loading operation
[D].
基于三自由度挖掘机机械臂系统的刚柔耦合动力学分析
[D].
Dynamic analysis of rigid-flexible coup-ling based on three-degree-of-freedom excavator manipulator system
[D].
基于刚柔耦合的液压挖掘机机械臂非线性动力学研究
[J].
Nonlinear dynamical behavior analysis on rigid-flexible coupling mechanical arm of hydraulic excavator
[J].DOI:10.3969/j.issn.1000-3835.2014.01.011
柔性臂动力学建模与规划角加速度抑振研究
[J].
Flexible arm dynamics modeling and research on angular acceleration vibration suppression
[J].DOI:10.3969/j.issn.1001-3997.2022.06.054
大型柔性起重臂系统回转吊装刚柔耦合动力学模型
[J].
Rigid-flexible coupled dynamic model of a huge-type truckcrane's boom system during its slewing hoisting
[J].
机械臂臂杆刚度主动控制下的末端振动特性研究
[J].
Research on end vibration characteristics of the manipulator end under active control of arm stiffness
[J].
六自由度柔性关节机械臂的动力学分析
[J].
Dynamic analysis of a 6-DOF manipulators with flexible joints
[J].DOI:10.3969/j.issn.1004-132X.2016.08.018 [本文引用: 1]
考虑关节柔性的六自由度串联工业机器人动力学建模与末端抖动抑制
[D].
Dynamic modeling and terminal jitter suppression of a 6-DOFseries industrial robot considering joint flexibility
[D].DOI:10.1109/rcar52367.2021.9517338
柔性机械臂关节作动的振动抑制方法和原理性验证
[J].
Principle verification and joint-actuator method for vibration suppression of flexible manipulator
[J].
基于柔性多体动力学的机械臂结构优化设计
[J].
Structure optimization design of robot arm based on flexible multi-body dynamics
[J].DOI:10.3969/j.issn.1004-132X.2017.21.008 [本文引用: 1]
A jerk-bounded trajectory planning for rotary flexible joint manipulator: An experimental approach
[J].
Nonlinear dynamic analysis of a multi-link manipulator with flexible links-joints mounted on a mobile platform
[J].
基于ADAMS-Cable的多机吊装刚柔耦合动力学分析
[J].
Rigid-flexible coupling dynamic analysis for multi-crane lifting based on ADAMS-Cable
[J].DOI:10.3963/j.issn.1000-8969.2016.03.002 [本文引用: 1]
基于ADAMS/Cable模块的柔索驱动仿真研究
[J].
Research on simulation of cable drive based on ADAMS/Cable
[J].DOI:10.3969/j.issn.1671-6906.2014.06.001
基于ADAMS/Cable的起重机钢丝绳的仿真分析
[J].
Simulation analysis for the wire rope of the crane based on ADAMS/Cable
[J].DOI:10.3969/j.issn.1009-0134.2013.13.004 [本文引用: 1]
基于刚柔耦合动力学仿真的塔式起重机疲劳寿命分析
[D].
Fatigue life analysis of tower crane based on rigid-flexible coupling dynamics simulation
[D].
超长柔吊装臂架回转作业刚柔耦合动力学模型与分析
[J].
Rigid-flexible coupling dynamics model and analysis of ultra flexible hoisting boom in rotating operation
[J].DOI:10.11776/cjam.35.06.C043 [本文引用: 1]