对于信号滤波技术,卡尔曼滤波因其最优递推估计能力展现出独特优势. Akhlaghi等[13]提出的自适应方法改进了过程噪声协方差矩阵(
综上,卡尔曼滤波方法依然存在以下问题: 1) 在低信噪比条件下,滤波对信号前沿的噪声抑制较差; 2)滤波后信号平滑度较差,影响过零点位置估计; 3)滤波后信号失真严重,影响特征点判断; 4)可能存在明显的相位滞后问题. 这些问题将影响起振点位置和ToF估计准确性,进而降低覆盖物深度计算精度. 因此,本研究提出结合总变差和贝叶斯估计的自适应卡尔曼滤波方法(TV-BAKF),动态调整
1. 研究背景
1.1. 噪声信号起振点估计
在超声波检测冰雪水深度时,外界环境因素(包括风、温度波动和机械振动)以及覆盖物自身的介质特性都会影响回波信号的信噪比. 其中,风和温度不仅会改变波速,还会导致信号振幅变化和波形畸变;机械振动则会产生高频噪声,干扰原始信号并降低信噪比. 此外,覆盖物本身若具有松散多孔或表面粗糙的特性,也会减弱回波信号的能量,进一步降低信噪比,这种低信噪比环境会对信号起振点的准确识别和ToF的精确估计带来挑战. 现有方法(如小波去噪)虽能提升整体信噪比和平滑波形,但对起振点附近的噪声抑制效果有限,难以准确提取信号前沿波形特征,导致起振点估计误差较大,ToF精度较低.
1.2. 卡尔曼滤波算法降噪
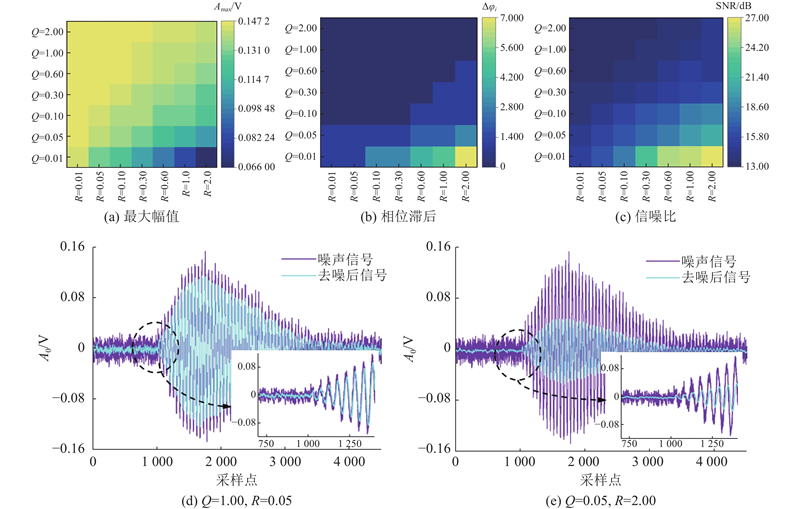
卡尔曼滤波通过动态融合预测和测量信息抑制噪声,其性能由过程噪声
图 1
图 1 不同Q、R组合的滤波结果影响(幅值、信噪比和相位滞后)
Fig.1 Effects of different Q,R value combinations on filtering results (amplitude, SNR, and phase delay)
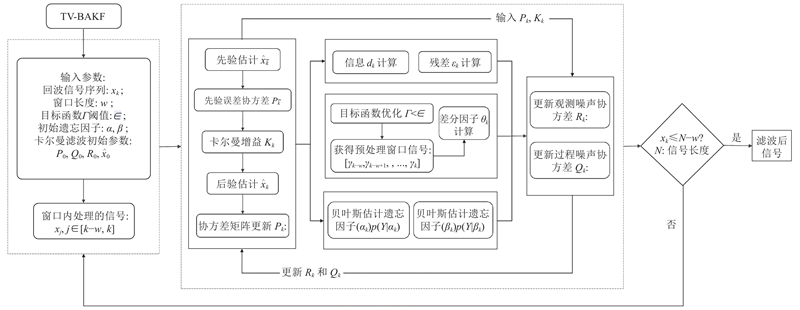
2. TV-BAKF方法
2.1. 卡尔曼滤波
卡尔曼滤波通过动态融合状态预测值与实测值,实现系统状态的最优估计. 其核心表达式如下:
式中:
式中:
2.2. 总变差法
总变差法(total variation denoising,TV)常用于去除信号中的噪声并平滑信号. 设有一维连续函数
对于一维离散信号的全变分,设某信号序列为
在一维信号降噪中,总变差法的目标是使得去噪后的信号
式中:
2.3. TV-BAKF
2.3.1. 基于残差和新息更新的AKF
对于一维信号的去噪,本研究采用改进的自适应卡尔曼滤波. 由于是对一维信号处理,因此卡尔曼滤波参数,如
式中:
式中:
由于
式中:
式中:
式中:
因此,
又由于
式中:
2.3.2. TV-BAKF算法
采用总变差(TV)与贝叶斯估计相结合的方法,是为了应对现有常见滤波算法在超声波回波信号处理中的局限性. 小波变换的时频局部化特导致其在信号突变处难以准确区分噪声和真实信号,从而产生周期跳跃误差;巴特沃斯滤波器陡峭的截止特性容易导致信号过度平滑,高斯滤波器则存在边缘模糊的问题,两者都会带来明显的相位偏移,且参数设置不当将导致波形过度平滑,影响ToF的估计. 相比之下,TV方法通过分析信号的局部梯度特征,能够动态获得噪声分布情况,为后续处理提供更准确的噪声评估依据.
在参数适应性方面,传统自适应卡尔曼滤波算法对初始参数敏感,不同的参数选择可能导致信号特征丢失或噪声残留的问题. 贝叶斯估计通过概率化的处理方式,可以根据实际观测数据动态调整参数更新的权重,使得滤波过程对初始设置的依赖性有所降低. TV方法与贝叶斯估计的结合,一方面通过梯度分析提供了更可靠的噪声评估,另一方面通过概率框架增强了参数调整的适应性.
本研究提出的TV-BAKF算法包含3个步骤.
1)采用高斯-牛顿法优化窗口内信号的
式中:
采用高斯-牛顿法求解预处理后的最终信号
解
式中:G为梯度矩阵.
2)求解差分因子
式中:
3)基于贝叶斯估计计算遗忘因子
式中:
对于后验分布,
若似然函数与Beta分布共轭,则后验分布仍持Beta分布形式,此时,有
式中:
对于每个事件步
以后验分布均值作为权重
对于
最终,将遗忘因子
图 2
3. 回波信号仿真与测试
3.1. 信号模拟试验
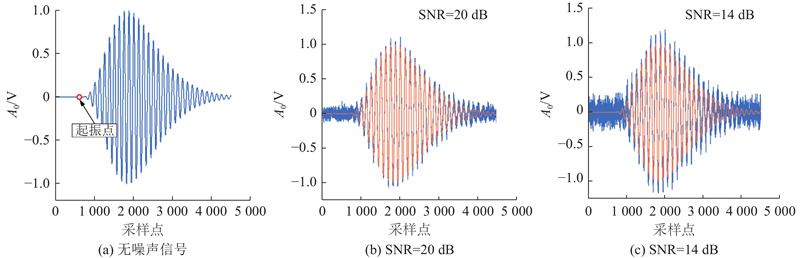
为了验证TV-BAKF方法在噪声回波信号估计中的准确性,基于MATLAB构建符合低频空气耦合探头窄带特性的混合指数模型噪声信号:
式中:
通过向基础信号逐级添加噪声,模拟实际冰雪水回波信号,结果如图3所示.
图 3
图 3 不同信噪比下的超声波窄带回波信号模拟
Fig.3 Modeling of ultrasonic narrow band echo signals across varying SNR values
3.2. 低温环境舱试验
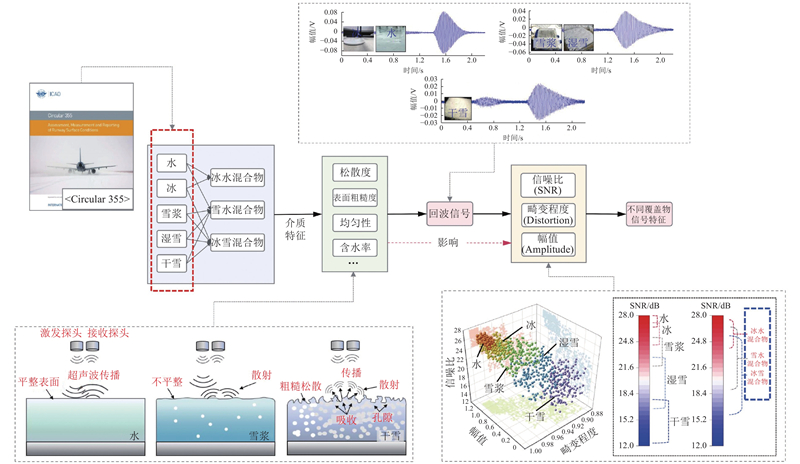
为了验证所提出的信号滤波方法提取冰雪覆盖物回波信号起振点的能力,在课题组自主研发的低温环境实验舱中开展了冰雪水超声波回波信号测试. 该实验舱配备了造雪设备、水冷却系统、风扇及温/湿度控制系统,可调节舱内温度和湿度,并通过控制造雪机进水与进气比例来改变雪的含水率. 结合温湿度控制与流动水雾化系统,实验舱成功制造出干雪、湿雪和雪浆等多种雪样. 课题组还通过中国北方实地雪样的光谱测试验证了模拟雪样的真实性,基于光谱分析,课题组研发的低温环境舱制造的雪和真实世界雪特性一致. 测试系统采用40 kHz空气探头、示波器、放大器和信号发生器,其中探头距离覆盖物为20 cm. 低温环境舱、各类覆盖物样本及试验装置如图4所示.
图 4
图 4 低温环境舱、各类覆盖物样本及试验装置图片
Fig.4 Low-temperature laboratory, covering material samples, and experimental setup images
由于用于计算污染物深度的ToF参数基于超声波在空气中的传播速度,而温湿度变化会影响波速,为了获得精确的计算结果,采用以下公式对不同环境条件下的波速进行修正[17]:
式中:
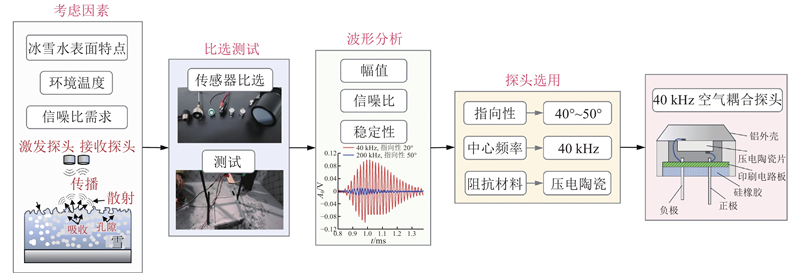
3.3. 探头比选
针对冰雪水介质表面的复杂反射特性(雪表面粗糙多孔、冰表面裂缝)、低温环境及高精度ToF测量对信噪比的要求,首先进行超声探头比选,如图5所示. 其中,t为时间. 通过低温环境箱试验,测试了不同频率、指向性和阻抗层材料的探头. 发现较高频率探头(200 kHz)信号因波长小于表面不平整度,导致强散射,回波幅值低(<0.1V)且信噪比较低;40 kHz波长(
图 5
4. 结果与讨论
4.1. 仿真试验结果分析
4.1.1. R、Q、P、K分析
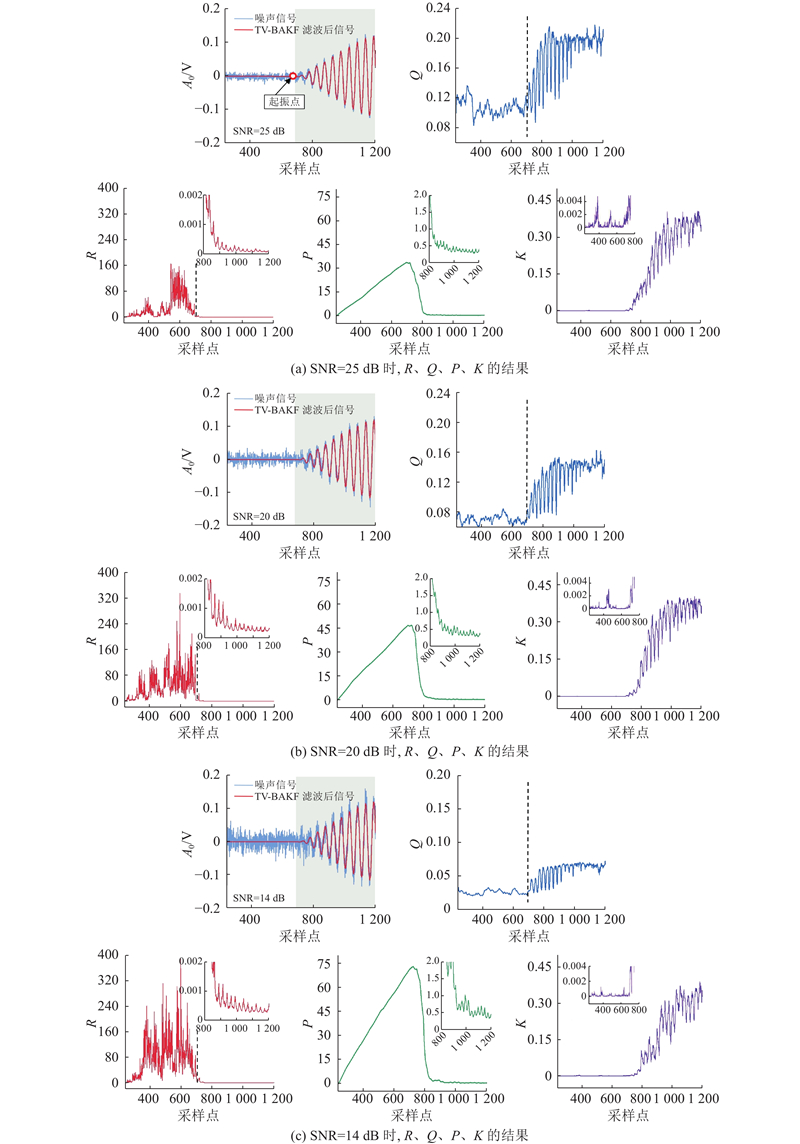
对R(观测噪声协方差)、Q(过程噪声协方差) 、P(误差协方差) 、K(卡尔曼增益系数)进行分析. TV-BAKF对模拟指数信号施加不同噪声功率后,滤波效果如图6所示. 结果表明,该方法在不同信噪比条件下均能有效平滑信号,显著减少毛刺干扰. 特别是信号前沿的前3个周期波形清晰可辨,即使在14 dB的低信噪比情况下,仍能准确提取信号前沿特征.
图 6
图 6 3种信噪比下卡尔曼滤波器关键参数的变化
Fig.6 Variations of Kalman filter key parameters under three signal-to-noise ratios
TV-BAKF通过总差分预处理技术能够获取信号的噪声分布特征并实现参数动态调整. 在信号处理过程中,Q和R会根据信号特征进行协同调节:在信噪比较低的零线及信号前沿段,Q自适应性降低使滤波器更信任预测结果,同时R相应增大以抑制测量噪声影响;在波包段则呈现相反趋势,Q增大而R自适应性减小以提高观测权重,这种自适应调节在起振点前后表现尤为明显(如黑色虚线标示),特别是在低信噪比区域(信噪比<20 dB)调节幅度明显. 实验结果表明,该机制使TV-BAKF在14~40 dB的信噪比范围内均能保持良好的滤波性能,有效抑制噪声干扰.
通过P的变化趋势可以看出,在信号零线段P明显增大,而在波包前沿段则显著下降,特别是在第3个周期位置P降至1.0以下,这表明系统状态估计精度明显提升. 与之相对应的是, K呈现出与P相反的变化规律:在高信噪比区域K维持在较低水平,说明此时滤波器更倾向于采用预测值;而在信号前3个周期之后,K明显增大,表明测量值的权重显著提高. 值得注意的是,在低信噪比条件下,K整体降低,这种自适应调整使滤波器更依赖系统状态估计值,从而确保在强噪声干扰下仍能保持滤波结果的稳定性.
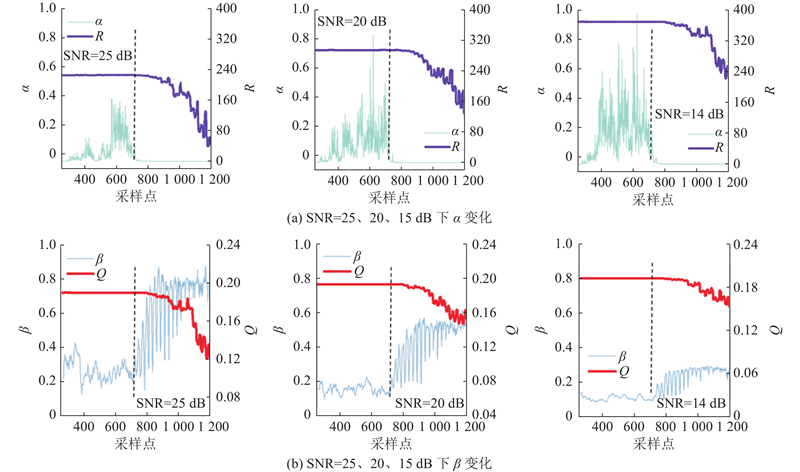
4.1.2. α 和 β
如图7所示展示了贝叶斯估计动态调整遗忘因子α 和 β的结果. 在信号零线位置,由于信号变化平缓且观测噪声占主导,α 和 β趋近于1.0,滤波器更信任预测值;而在波包段信号变化显著时,α 和 β明显减小,使滤波器更依赖当前观测数据. 信噪比的影响表现为:低信噪比时α 和 β趋近1.0(依赖历史信息),高信噪比时趋近0(信任当前观测).
图 7
图 7 3种信噪比下遗忘因子α和β
Fig.7 Forgetting factor value α and β under three SNR values
值得注意的是,α 的变化幅度明显大于β的. 这是因为α用于调节观测噪声协方差 R,由于观测噪声易受外部环境干扰,须扩展其调节区间以更好地权衡历史信息与实时观测数据. 因此,通过贝叶斯估计动态调整遗忘因子,卡尔曼滤波能够自适应地平衡历史信息和当前观测数据,从而更好地适应系统状态和噪声特性的变化.
4.1.3. 初始值敏感性
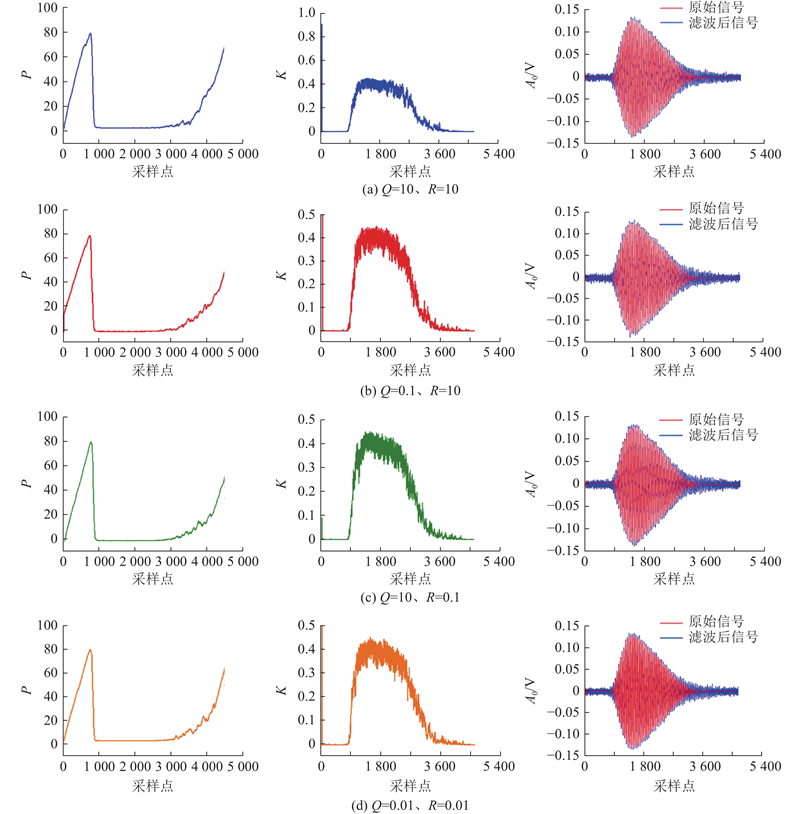
通过设置4种差异较大的初始参数组合(即Q=10, R=0.1; Q=0.1, R=10; Q=10, R=10; Q=0.01, R=0.01)对滤波结果进行比较分析,结果如图8所示. 可以看出,无论初始Q、R设定如何,TV-BAKF方法都能通过捕捉当前信号波形特征及噪声分布,动态调整Q、R至最优范围. 也可以看出,在4种Q、R参数组合下,卡尔曼增益在波包段的峰值均接近0.45,而P在零线噪声段的最高值均接近80,在波包段则均下降至接近0. 因此,分析其参数动态变化可见,在低信号幅值区段,Q均自适应地减小而R相应增大,以更好抑制测量噪声并保持稳定;在高信号能量区段,Q增大而R减小,以增强对信号动态变化的适应性. 由此可见,TV-BAKF方法对初始参数敏感性低,能够依据信号本身的动态特性和噪声水平进行实时调整,因而对初始参数的选择具有较高鲁棒性.
图 8
图 8 4种Q、R初参数组合下P和K变化及滤波效果
Fig.8 P and K values and filtering performance under four Q and R initial parameter combinations
4.1.4. 滤波效果评价
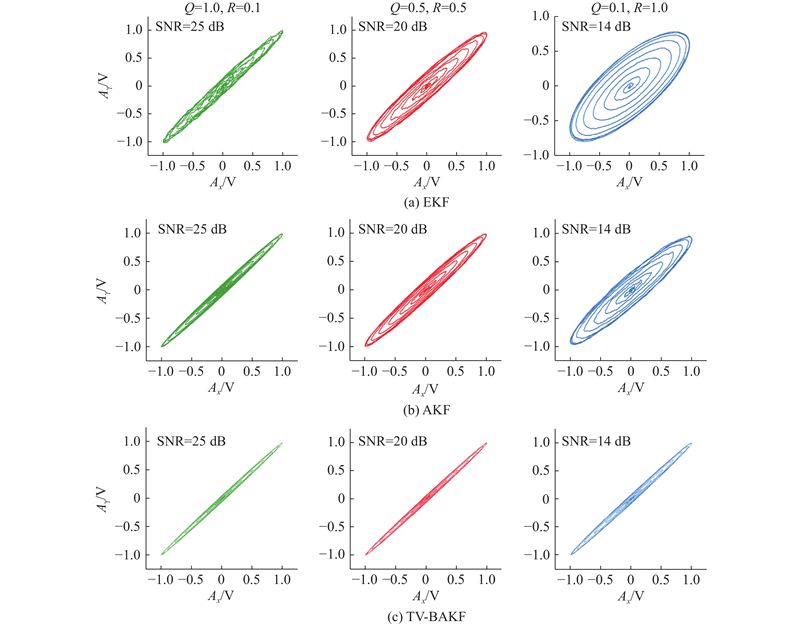
为了直观地比较传统卡尔曼滤波和本研究提出的优化卡尔曼滤波方法的滤波效果,图9展示了采用不同卡尔曼滤波方法所得的Lissajous图,该图能够直观评价滤波后信号保真能力,如相位滞后程度与波形平滑度. 在Lissajous图中,相位滞后现象严重,表现为椭圆曲线更宽,而椭圆的圆滑则表征信号平滑程度.
图 9
图 9 不同卡尔曼滤波方法(及Q-R组合)的Lissajous图
Fig.9 Lissajous diagrams of different Kalman filter methods with various Q and R combination
如图9所示为不同卡尔曼滤波方法(及Q、R组合)的Lissajous图,其中
进一步地,本研究对目前先进的滤波方法和TV-BAKF方法的滤波效果进行评估,并分别从均方误差(MSE)、平滑度(
式中:
如表1所示列举了5种滤波方法(改进小波变换[18]、改进的S-滤波[19]、UAKF[20]、VBAKF[15]以及TV-BAKF)的滤波效果. 5种滤波方法的对比分析显示,在信噪比较高(25 dB)时,改进小波变换的均方误差最小,表现最佳;然而在低信噪比(14 dB)下,其均方误差超过0.5,滤波性能下降. 改进S-G滤波在低信噪比(14 dB)下误差最大,达到约0.82,2种改进卡尔曼滤波方法(UAKF和VBAKF)的均方误差均超过0.4,而TV-BAKF方法的误差始终稳定在0.35以下,展现出其良好的低信噪比下抗噪能力. 从平滑度指标来看,UAKF在低信噪比下平滑效果最显著,VBAKF平滑度最高,但其相位保真度超过0.20 rad,存在明显相位滞后;相比之下,改进小波变换和TV-BAKF方法的相位保真度均低于0.15 rad. 在幅值保真度方面,UAKF和VBAKF在20 dB时低于0.90,在14 dB时进一步降至0.85以下,表明其过度平滑导致波形失真. 虽然改进小波变换在保真度上略优,但其低信噪比下的误差和平滑度表现较差. 综合来看,TV-BAKF在噪声抑制能力与信号特征保持之间实现了良好平衡.
表 1 5种滤波方法下的滤波效果评价
Tab.1
| SNR/dB | MSE | ||||
| 改进小波变换 | 25 | 0.013 | 4.34 | 0.065 | 0.975 |
| 20 | 0.078 | 8.42 | 0.084 | 0.943 | |
| 14 | 0.513 | 18.27 | 0.108 | 0.922 | |
| 改进S-G滤波 | 25 | 0.025 | 6.24 | 0.062 | 0.946 |
| 20 | 0.168 | 13.16 | 0.104 | 0.914 | |
| 14 | 0.821 | 22.03 | 0.171 | 0.881 | |
| UAKF | 25 | 0.022 | 3.19 | 0.082 | 0.928 |
| 20 | 0.102 | 8.13 | 0.151 | 0.877 | |
| 14 | 0.698 | 17.24 | 0.245 | 0.823 | |
| VBAKF | 25 | 0.015 | 2.14 | 0.052 | 0.938 |
| 20 | 0.092 | 5.32 | 0.234 | 0.897 | |
| 14 | 0.446 | 15.88 | 0.208 | 0.843 | |
| TV-BAKF | 25 | 0.015 | 2.77 | 0.042 | 0.984 |
| 20 | 0.063 | 6.53 | 0.094 | 0.947 | |
| 14 | 0.342 | 17.32 | 0.145 | 0.917 |
4.2. 低温环境舱试验分析
4.2.1. 覆盖物回波信号
根据ICAO《Circular 355》GRF要求,重点研究了水、冰、雪浆、湿雪和干雪5种污染物状态,同时对冰水、冰雪、水雪混合覆盖物进行了测试. 通过分析不同覆盖物的回波信号特征发现:水和冰的回波信号具有较高的幅值和信噪比,波形与标准指数模型吻合度好;湿雪和雪浆则表现出幅值降低,波形畸变、波形前沿畸变严重,及信号拖尾延长等特征;干雪由于多孔结构和粗糙表面,导致信号能量大幅衰减,信噪比显著下降. 混合覆盖物的信号特征介于其组成成分之间,其信噪比和幅值分布包含在水和干雪的区间范围内. 不同覆盖物(包括水/冰/雪浆/湿雪/干雪和混合覆盖物)的信噪比和波形特征研究流程如图10所示. 进一步分析表明,冰、水及冰水混合物的信号特征集中分布在高信噪比区域,而各类雪覆盖物则分散在低信噪比区域,其中干雪的信号最为离散. 基于研究低信噪比条件下ToF估计精度的核心目标,并响应GRF规范需求,本研究选取水、冰、雪浆、湿雪和干雪5种典型GRF覆盖物作为研究对象.
图 10
图 10 不同覆盖物(包括水/冰/雪浆/湿雪/干雪和混合覆盖物)的信噪比和波形特征研究流程
Fig.10 Sesearch process on SNR and waveform characteristics of different coverings (water, ice, slush, wet snow, dry snow and mixed covering)
4.2.2. 起振点估计
选取某次检测中的低信噪比回波信号进行分析. 首先通过深度测量和波形前沿分析确定信号前若干周期的起振点位置作为基准. 随后采用双阈值法,对比3种去噪方法(小波、AKF和TV-BAKF)处理后的起振点估计结果. 双阈值法通过设置2个电压阈值,获取信号与阈值交叉后的首个零交叉点作为特征点,进而估计起振点位置.
如图11所示展示了3种滤波方法的处理效果. 小波去噪在波包段效果较好,但信号前沿和零线位置的噪声滤除不足,可能导致双阈值法误判. AKF方法虽然使信号前沿更平滑,但过度依赖预测值导致幅值畸变,影响特征点判断. 相比之下,TV-BAKF通过总变差预处理和贝叶斯动态调整Q、R值,显著提升了零线与波包段的分割准确性,在保持波形平滑度的同时有效减少了相位滞后,展现出良好的信号前沿波形特征提取能力.
图 11
图 11 3种滤波方法的起振点估计结果
Fig.11 Estimation results of waveform onset point by three filtering methods
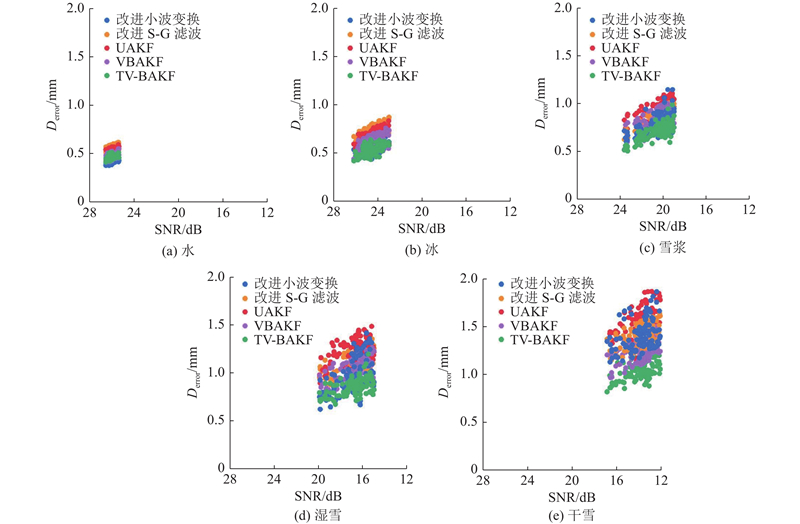
4.2.3. 误差分析
在4.1.4节已经通过仿真测试对比分析了改进小波变换、改进S-G滤波、AUKF、VBAKF和TV-BAKF方法的滤波效果. 接下来,利用上述5种滤波方法,对5种道面覆盖物的超声波回波信号进行滤波,采用双阈值方法估计起振点位置,并计算覆盖物深度. 如图12所示展示了5种道面覆盖物下,3种信号处理方法在不同信噪比时的深度误差(
图 12
图 12 5种滤波方法对于5种覆盖物的深度计算误差与SNR分布的散点图
Fig.12 Scatter plots of depth calculation error versus SNR for five coverings using five filtering methods
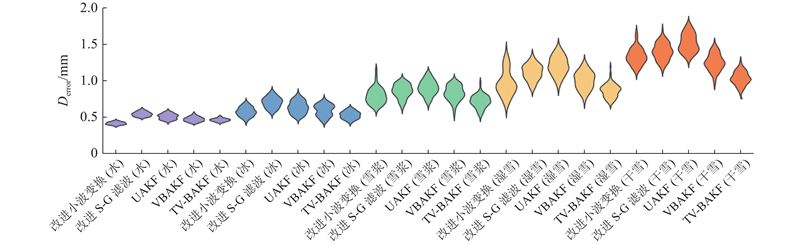
图 13
图 13 5种滤波方法下5种覆盖物深度计算误差小提琴图
Fig.13 Violin plots of depth errors for five surface coverings under five filtering methods
5. 结 论
提出结合总变差和贝叶斯估计的自适应卡尔曼滤波方法(TV-BAKF),旨在提升对道面覆盖物(水/冰/雪)回波信号的ToF估计精度.
(1) TV-BAKF方法利用总变差法检测滑动窗口信号内的噪声分布,结合贝叶斯估计计算差分因子以反映信号变化率与噪声水平的相对关系,并借助残差矩阵和创新矩阵构建的自适应调整机制,结合差分因子加权动态调整Q和R.
(2) TV-BAKF方法在处理低信噪比信号时表现出色,尤其是在信号的前沿位置和零线位置. 信号模拟实验表明,该方法能够准确提取低信噪比信号的波形,保持信号的平滑度,同时减少相位滞后,提高信号的起振点估计精度.
(3) TV-BAKF方法在处理较高信噪比(水、冰)覆盖物回波信号时,计算误差和小波及VBAKF方法差异较小;而对于松散且表面粗糙(干/湿雪)覆盖物回波信号,TV-BAKF相比其他方法仍能够对ToF进行准确估计,并能够将深度精度提升至1 mm以内.
本研究还须进一步优化TV-BAKF方法中滑动窗口尺寸的选择,以及其在非平稳噪声(如突发干扰)场景下的适应性表现. 针对现有不足,后续研究将重点优化滑动窗口的动态调整策略,在保证滤波精度的同时降低计算复杂度;同时,通过改进噪声协方差矩阵的更新机制,增强算法对极端噪声条件的鲁棒性,进一步提升滤波稳定性.
参考文献
A decision support model to assess the braking performance on snow and ice contaminated runways
[J].DOI:10.1016/j.coldregions.2015.06.002 [本文引用: 1]
An integrated analytical model for friction characteristics of aircraft tire on wet runway pavement
[J].DOI:10.1016/j.triboint.2023.108501 [本文引用: 1]
Effects of surface texture deterioration and wet surface conditions on asphalt runway skid resistance
[J].DOI:10.1016/j.triboint.2020.106589 [本文引用: 1]
Ultrasonic investigation of snow and ice parameters
[J].DOI:10.12693/APhysPolA.120.625 [本文引用: 1]
Road surface classification using automotive ultrasonic sensor
[J].DOI:10.1016/j.proeng.2016.11.119 [本文引用: 1]
Evaluation of ultrasonic snow depth sensors for U. S. snow measurements
[J].DOI:10.1175/2007JTECHA947.1 [本文引用: 1]
A study of a parametric method for the snow reflection coefficient estimation using air-coupled ultrasonic waves
[J].DOI:10.3390/s20154267 [本文引用: 1]
Onset detection of ultrasonic signals for the testing of concrete foundation piles by coupled continuous wavelet transform and machine learning algorithms
[J].DOI:10.1016/j.aei.2020.101034 [本文引用: 1]
A method to avoid the cycle-skip phenomenon in time-of-flight determination for ultrasonic flow measurement
[J].DOI:10.1631/jzus.A2000284 [本文引用: 1]
High-precision time-of-flight determination algorithm for ultrasonic flow measurement
[J].
Enhancing ultrasonic time-of-flight estimation using adaptive differential evolution and levenberg–marquardt algorithm
[J].
Improving the accuracy of time-difference measurement by reducing the impact of baseline shift
[J].DOI:10.1109/TIM.2015.2437635 [本文引用: 1]
Drift suppression method based on signal stability detection and adaptive Kalman filter for NMR sensor
[J].DOI:10.1016/j.dsp.2024.104812 [本文引用: 1]
Denoising algorithm of ground-airborne time-domain electromagnetic method based on Variational Bayesian-based adaptive Kalman filter (VBAKF)
[J].DOI:10.1016/j.jappgeo.2022.104674 [本文引用: 2]
Deep koopman Kalman filter for nonlinear model-free industrial process data denoising and its soft sensing application
[J].DOI:10.1109/JSEN.2024.3453326 [本文引用: 1]
Effects of environment on accuracy of ultrasonic sensor operates in millimetre range
[J].DOI:10.1016/j.pisc.2016.06.024 [本文引用: 2]
Optimal wavelet selection for signal denoising
[J].DOI:10.1109/ACCESS.2024.3377664 [本文引用: 1]
EWT-ASG: empirical wavelet transform with adaptive savitzky–golay filtering for TDLAS
[J].
State-of-charge estimation for lithium-ion batteries based on modified unscented Kalman filter using improved parameter identification
[J].DOI:10.1016/j.ijoes.2024.100574 [本文引用: 1]