宽体矿用自卸车是用于露天矿区运输的三轴重型非公路车辆. 露天矿区路面崎岖不平，常出现凹坑、石块 ^[1]，易使车辆发生横向偏移，影响横向稳定性，甚至引发侧滑、侧翻，导致安全事故. 得益于计算机技术的发展，越来越多的主动安全控制系统被应用于汽车. 这些控制系统能够根据车辆运动状态对车辆底盘进行控制，准确可靠的车辆状态信息是实现良好控制效果的必要条件. 质心侧偏角作为表征车辆运动状态的重要参数，是许多主动安全控制系统的关键输入^[2-3]. 由于技术和成本的限制，能够直接测量质心侧偏角的装置难以实现量产车应用^[4]，须借助估计方法对质心侧偏角进行观测.

在车辆质心侧偏角估计方面，基于车辆模型的估计方法较为常见，该方法可根据使用的模型粗略划分为运动学方法和动力学方法^[5]. 运动学方法使用运动学模型描述传感器测量值和质心侧偏角之间的运动学关系^[6]，通常采用积分方法^[7-8]或卡尔曼滤波方法进行计算^[9]. 运动学方法容易出现误差累积的现象，因此很少单独使用. 动力学方法利用车辆和轮胎的动力学模型来描述车辆运动状态，其准确性依赖于模型的精度. 已有多种数据处理技术被应用在动力学方法中，其中卡尔曼滤波及其改进算法较为常见^[10]. Wu等^[11]提出基于联邦-容积卡尔曼滤波的车辆行驶状态与路面附着系数估计方法，使用低成本传感器实现了较好的观测效果. Zhang等^[12]提出基于改进自适应无迹卡尔曼滤波的车辆行驶状态估计方法，克服了在噪声信息快速变化时自适应卡尔曼滤波估计不准确的问题. 李韶华等^[13]提出基于双径向基函数神经网络和扩展卡尔曼滤波(extended Kalman filter, EKF)的质心侧偏角与路面附着系数估计方法，该方法在满足实时性要求的同时具有较好的估计精度. Qi等^[14]为了解决在非高斯噪声情况下卡尔曼滤波估计效果不佳的问题，提出基于最大相关熵准则的EKF算法. 张年瑞^[15]提出利用奇异值分解替换Cholesky分解的改进无迹卡尔曼滤波算法，该算法能够较好适应非线性车辆模型.除了使用先进的数据处理技术，将多种方法融合的估计方法也可以有效提高估计精度和多工况适应能力. 陈建锋等^[16]通过设置横向加速度阈值，设计出动力学方法和运动学方法切换策略. 李小雨等^[17-18]使用运动几何方法，利用前、后轮胎侧偏角与质心侧偏角之间的运动几何关系来估计质心侧偏角，提出基于运动几何方法和运动学方法融合的质心侧偏角估计方法. Cheng等^[19]通过阻尼项和零点复位方法对积分估计方法进行校正，将结果与自适应平方根容积卡尔曼滤波估计结果进行自适应融合. Park^[20]提出交互式多模型卡尔曼滤波算法，该方法在常规动力学方法的基础上融合了GPS信号.

已有研究集中在观测乘用车的平坦路面行驶状态. 矿用车具有较大的质量、尺寸和转动惯量，运行在崎岖路面，使其动力学系统的强耦合、非线性特性突出. 现有估计方法多基于高度简化的模型，未考虑车辆的俯仰、侧倾以及悬架的运动，难以准确描述矿用车在崎岖路面行驶的运动状态. 本研究建立矿用车十七自由度动力学模型，设计基于EKF的车辆纵、横向速度估计器和车辆横向速度积分估计器，结合EKF估计器和积分估计器的特点，提出基于加权融合的质心侧偏角估计方法.

矿用车各轴通常采用非独立悬架，二、三轴采用平衡悬架结构. 在崎岖路面工况下，悬架挠度和悬架力变化幅度较大，须通过车桥和平衡悬架的运动计算轮胎垂向力，以便后续计算轮胎侧向力. 当两侧悬架挠度不一致使车桥发生相对车身的侧倾时，车轮会产生额外的横向偏移，因此在计算轮胎侧偏角时须考虑车桥侧倾运动的影响. 参考徐工XDR80TE矿用自卸车，车辆参数如表1所示.

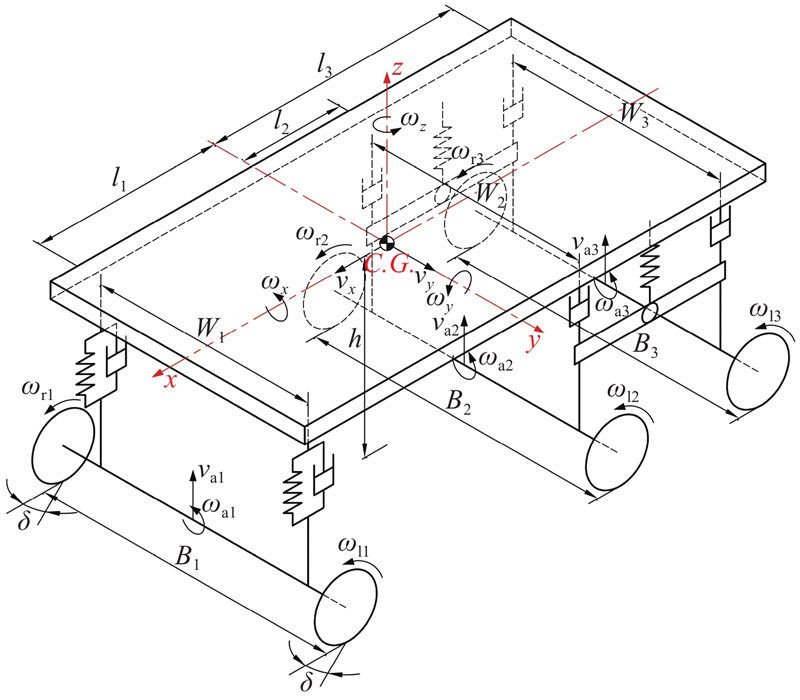
建立矿用车十七自由度动力学模型如图1所示，模型的17个自由度分别为车身的纵向、横向、侧倾、俯仰、横摆运动，3个车桥的垂向和侧倾运动以及6个车轮的旋转运动. 将车辆二、三轴平衡悬架的钢板弹簧简化为2个元件：可以绕平衡轴转动的刚性平衡梁和安装在平衡梁中间的弹簧. 根据研究对象的悬架特点，二、三轴的两侧安装有独立的减振器. 图1中，坐标系原点为车辆质心（C.G.），x轴正方向为车辆前方，y轴正方向为车辆左侧，z轴正方向为车辆上方，车辆从前向后各轴依次为一、二、三轴，v_x、v_y分别为车辆的纵、横向速度，ω_x、ω_y、ω_z分别为车辆的侧倾角速度、俯仰角速度和横摆角速度，v_aj、ω_aj分别为各车桥的垂向速度和侧倾角速度，ω_ij为车轮旋转角速度，δ为前轮转角，h为车辆质心高度，B_j为各轴的轮距，W_j为各轴两侧悬架的间距，l_j为车辆质心到各轴的纵向距离（下标i∈{l，r}分别代表左侧和右侧，j=1、2、3分别代表一、二、三轴）. B₂和B₃以及W₂和W₃的数值相等，为了便于表达须进行区分.

模型的横向运动和横摆动力学方程为

(1)$ \begin{split} m{a_y} =& m\left( {{{\dot v}_y}+{v_x}{\omega _z}} \right)= \\ & \left( {{F_{y{\text{l}}1}}+{F_{y{\text{r}}1}}} \right)\cos \delta +\left( {{F_{x{\text{l}}1}}+{F_{x{\text{r}}1}}} \right)\sin \delta + \\ & {F_{y{\text{l}}2}}+{F_{y{\text{r}}2}}+{F_{y{\text{l}}3}}+{F_{y{\text{r}}3}}, \end{split} $

(2)$ \begin{split} {I_z}{{\dot \omega }_z} =& {l_1}\left[ {\left( {{F_{y{\text{l}}1}}+{F_{y{\text{r}}1}}} \right)\cos \delta +\left( {{F_{x{\text{l}}1}}+{F_{x{\text{r}}1}}} \right)\sin \delta } \right] - \\ & {l_2}\left( {{F_{y{\text{l}}2}}+{F_{y{\text{r}}2}}} \right) - {l_3}\left( {{F_{y{\text{l}}3}}+{F_{y{\text{r}}3}}} \right)+ \\ & 0.5{B_1}[ {( {{F_{y{\text{l}}1}} - {F_{y{\text{r}}1}}} )\sin \delta +}\left. {\left( {{F_{x{\text{r}}1}} - {F_{x{\text{l}}1}}} \right)\cos \delta } \right]+ \\ & 0.5{B_2}\left( {{F_{x{\text{r}}2}} - {F_{x{\text{l}}2}}} \right)+ 0.5{B_3}\left( {{F_{x{\text{r}}3}} - {F_{x{\text{l}}3}}} \right). \end{split} $

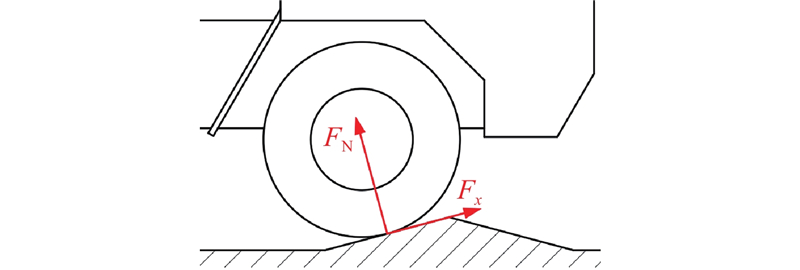
式中：m为整车质量，a_y为车辆横向加速度，I_z为整车横摆转动惯量，F_xij为轮胎纵向力，F_yij为轮胎侧向力. 如图2所示，地面对轮胎的法向力F_N垂直于地面，轮胎纵向力F_x与路面相切，在崎岖路面下，当轮胎所接触的地面与车辆坐标系xoy平面不平行时，F_x不与车辆坐标系x轴平行，且F_N在车辆坐标系x轴方向存在分量，导致车辆实际纵向合力与各轮胎纵向分力之和存在较大差异. 可以看出，将车辆的纵向运动描述为类似式(1)的形式是不准确的，因此仅列出纵向加速度方程：

(3)$ {a_x} = {\dot v_x} - {v_y}{\omega _z} . $

式中：a_x为车辆纵向加速度.

各车轮在车辆坐标系下的纵向速度表达式为

(4)$ \left. \begin{gathered} {v_{x{\text{l}}j}} = {v_x} - h{\omega _y} - \frac{{{B_j}}}{2}{\omega _z}, \\ {v_{x{\text{r}}j}} = {v_x} - h{\omega _y}+\frac{{{B_j}}}{2}{\omega _z}. \\ \end{gathered} \right\} $

车轮在车辆坐标系下的横向速度由2个部分叠加而成：1）不考虑车桥与车身之间的相对侧倾，由车身运动产生的车轮横向速度；2）车桥与车身发生相对侧倾，使车轮相对车身产生的横向速度. 各车轮在车辆坐标系下的横向速度表达式为

(5)$ {v_{yij}} = {v_{yij{\text{\_b}}}}+{v_{yij{\text{\_s}}}} . $

式中：v_{yij_b}为由车身运动产生的车轮横向速度，v_{yij_s}为车桥相对侧倾产生的车轮横向速度.

(6)$ \left. \begin{gathered} {v_{yi1\_{\text{b}}}} = {v_y}+h{\omega _x}+{l_1}{\omega _z}, \\ {v_{yi2\_{\text{b}}}} = {v_y}+h{\omega _x} - {l_2}{\omega _z}, \\ {v_{yi3\_{\text{b}}}} = {v_y}+h{\omega _x} - {l_3}{\omega _z}. \\ \end{gathered} \right\} $

以左侧车轮为例，

(7)$ \begin{split} {v_{y{\text{l}}j{\text{\_s}}}} &= {{\text{d}}\left( {{h_j}\sin {\theta _{{\text{a}}j{\text{\_r}}}}+\dfrac{{{B_j}}}{2}\cos {\theta _{{\text{a}}j{\text{\_r}}}}} \right)}/{{{\text{d}}t}} =\\ & {h_j}\left( {{\omega _{{\text{a}}j}} - {\omega _z}} \right)\cos {\theta _{{\text{a}}j{\text{\_r}}}} - \frac{{{B_j}}}{2}\left( {{\omega _{{\text{a}}j}} - {\omega _z}} \right)\sin {\theta _{{\mathrm{a}}j{\text{\_r}}}}. \end{split} $

式中：h_j为侧倾中心距地面的高度，θ_{aj_r}为车桥相对车身的侧倾角度. 同理，右侧车轮横向速度表达式为

(8)$ {v_{y{\text{r}}j{\text{\_s}}}} = {h_j}\left( {{\omega _{{\text{a}}j}} - {\omega _z}} \right)\cos {\theta _{{\text{a}}j{\text{\_r}}}}+\frac{{{B_j}}}{2}\left( {{\omega _{{\text{a}}j}} - {\omega _z}} \right)\sin {\theta _{{\text{a}}j{\text{\_r}}}}. $

在实际情况中，由于θ_{aj_r}的数值较小，可近似认为cos θ_{aj_r}=1，sin θ_{aj_r}=0，因此将v_{yij_s}简化为

(9)$ {v_{yij{\text{\_s}}}} = {h_j}\left( {{\omega _{{\text{a}}j}} - {\omega _z}} \right). $

各轮胎的侧偏角为

(10)$ \left. \begin{gathered} {\alpha _{{\text{l}}1}} = \frac{{{v_y}+h{\omega _x}+{l_1}{\omega _z}+{h_1}\left( {{\omega _{{\text{a}}1}} - {\omega _z}} \right)}}{{{v_x} - h{\omega _y} - {{{B_1}{\omega _z}} \mathord{\left/ {\vphantom {{{B_1}{\omega _z}} 2}} \right. } 2}}} - \delta , \\ {\alpha _{{\text{r}}1}} = \frac{{{v_y}+h{\omega _x}+{l_1}{\omega _z}+{h_1}\left( {{\omega _{{\text{a}}1}} - {\omega _z}} \right)}}{{{v_x} - h{\omega _y}+{{{B_1}{\omega _z}} \mathord{\left/ {\vphantom {{{B_1}{\omega _z}} 2}} \right. } 2}}} - \delta , \\ {\alpha _{{\text{l}}2}} = \frac{{{v_y}+h{\omega _x} - {l_2}{\omega _z}+{h_2}\left( {{\omega _{{\text{a}}2}} - {\omega _z}} \right)}}{{{v_x} - h{\omega _y} - {{{B_2}{\omega _z}} \mathord{\left/ {\vphantom {{{B_2}{\omega _z}} 2}} \right. } 2}}}, \\ {\alpha _{{\text{r}}2}} = \frac{{{v_y}+h{\omega _x} - {l_2}{\omega _z}+{h_2}\left( {{\omega _{{\text{a}}2}} - {\omega _z}} \right)}}{{{v_x} - h{\omega _y}+{{{B_2}{\omega _z}} \mathord{\left/ {\vphantom {{{B_2}{\omega _z}} 2}} \right. } 2}}}, \\ {\alpha _{{\text{l}}3}} = \frac{{{v_y}+h{\omega _x} - {l_3}{\omega _z}+{h_3}\left( {{\omega _{{\text{a}}3}} - {\omega _z}} \right)}}{{{v_x} - h{\omega _y} - {{{B_3}{\omega _z}} \mathord{\left/ {\vphantom {{{B_3}{\omega _z}} 2}} \right. } 2}}}, \\ {\alpha _{{\text{r}}3}} = \frac{{{v_y}+h{\omega _x} - {l_3}{\omega _z}+{h_3}\left( {{\omega _{{\text{a}}3}} - {\omega _z}} \right)}}{{{v_x} - h{\omega _y}+{{{B_3}{\omega _z}} \mathord{\left/ {\vphantom {{{B_3}{\omega _z}} 2}} \right. } 2}}}. \\ \end{gathered} \right\} $

车桥的运动微分方程为

(11)$ {m_{{\text{a}}j}}{\dot v_{{\text{a}}j}} = {F_{z{\text{l}}j}}+{F_{z{\text{r}}j}} - {F_{{\text{sl}}j}} - {F_{{\text{sr}}j}} - {m_{{\text{a}}j}}g, $

(12)$ \begin{split} {{\dot \omega }_{{\text{a}}j}}{I_{{\text{a}}j}} =& \frac{{{B_j}}}{2}\left( {{F_{z{\text{l}}j}} - {F_{z{\text{r}}j}}} \right)+\frac{{{W_j}}}{2}\left( {{F_{{\text{sr}}j}} - {F_{{\text{sl}}j}}} \right)+ \\ & R\left( {{F_{y{\text{r}}j}}+{F_{y{\text{l}}j}}} \right). \end{split} $

式中：R为车轮半径，m_aj为各轴非簧载质量，I_aj为各车桥的侧倾转动惯量，g为重力加速度，F_sij为各车轮对应的悬架力，F_zij为轮胎垂向力. 对于一轴，悬架力F_sl1和F_sr1等于弹力和阻尼力之和，表达式为

(13)$ {F_{{\text{s}}i1}} = {k_1}{z_{{\text{s}}i1}}+{c_1}{\dot z_{{\text{s}}i1}} . $

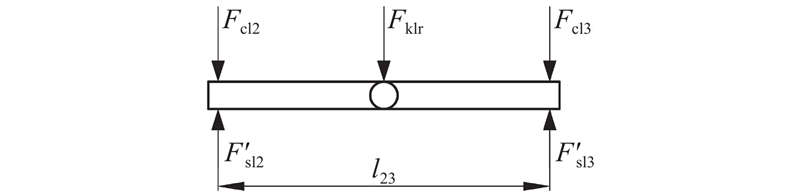
式中：z_si1为左前或右前悬架的挠度，k₁、c₁分别为前悬架的弹簧刚度和阻尼系数. 二、三轴须考虑平衡悬架的影响. 以左侧悬架为例，其平衡梁受力如图3所示. 忽略平衡梁自身的质量和转动惯量，则平衡梁的运动微分方程为

(14)$ {F'_{{\text{sl}}2}}+{F'_{{\text{sl}}3}} - {F_{{\text{klr}}}} - {F_{{\text{cl}}2}} - {F_{{\text{cl}}3}} = 0 \text{，} $

(15)$ \frac{{{l_{23}}}}{2}\left( {{F'_{{\text{sl}}3}}+{F_{{\text{cl}}2}} - {F'_{{\text{sl}}2}} - {F_{{\text{cl}}3}}} \right) = 0 . $

式中：F'_sl2和F'_sl3为作用于车桥的悬架力的反力，与F_sl2和F_sl3大小相等方向相反；F_klr为左侧平衡悬架弹力；F_cl2和F_cl3为左中、左后悬架阻尼力；l₂₃为二轴与三轴之间的轴距，即l₃和l₂之差. 平衡悬架弹簧挠度

(16)$ {z_{{\text{slr}}}} = \frac{{{z_{{\text{sl}}2}}+{z_{{\text{sl}}3}}}}{2}. $

式中：z_sl2，z_sl3为左侧二、三轴减振器的挠度. 联立式(14)~(16)得到

(17)$ \left. \begin{gathered} {F_{{\text{sl}}2}} = {F'_{{\text{sl}}2}} = {F_{{\text{klr}}}}+{F_{{\text{cl}}2}} = {k_{\text{r}}}\left( {\frac{{{z_{{\text{sl}}2}}+{z_{{\text{sl}}3}}}}{2}} \right)+{c_2}{{\dot z}_{{\text{sl}}2}}, \\ {F_{{\text{sl}}3}} = {F'_{{\text{sl}}3}} = {F_{{\text{klr}}}}+{F_{{\text{cl}}3}} = {k_{\text{r}}}\left( {\frac{{{z_{{\text{sl}}2}}+{z_{{\text{sl}}3}}}}{2}} \right)+{c_3}{{\dot z}_{{\text{sl}}3}}. \\ \end{gathered} \right\} $

式中：c₂和c₃为二、三轴悬架的阻尼系数，k_r为平衡悬架弹簧刚度. 右侧平衡悬架同理. 因此二、三轴的悬架力表达式为

(18)$ \left. \begin{gathered} {F_{{\text{s}}i2}} = {k_{\text{r}}}\left( {\frac{{{z_{{\text{s}}i2}}+{z_{{\text{s}}i3}}}}{2}} \right)+{c_2}{{\dot z}_{{\text{s}}i2}}, \\ {F_{{\text{s}}i3}} = {k_{\text{r}}}\left( {\frac{{{z_{{\text{s}}i2}}+{z_{{\text{s}}i3}}}}{2}} \right)+{c_3}{{\dot z}_{{\text{s}}i3}}. \\ \end{gathered} \right\} $

联立式(11)、(12)得到轮胎垂向力表达式为

(19)$ \left. \begin{gathered} {F_{z{\text{l}}j}} = \frac{{{m_{{\text{a}}j}}\left( {{{\dot v}_{{\text{a}}j}}+g} \right)+{F_{{\text{sl}}j}}+{F_{{\text{sr}}j}}}}{2}+ \\ {\text{ }}\frac{{{{\dot \omega }_{{\text{a}}j}}{I_{{\text{a}}j}} - R\left( {{F_{y{\text{r}}j}}+{F_{y{\text{l}}j}}} \right)+{{{W_j}\left( {{F_{{\text{sr}}j}} - {F_{{\text{sl}}j}}} \right)} / 2}}}{{{B_j}}}, \\ {F_{z{\text{r}}j}} = \frac{{{m_{{\text{a}}j}}\left( {{{\dot v}_{{\text{a}}j}}+g} \right)+{F_{{\text{sl}}j}}+{F_{{\text{sr}}j}}}}{2} - \\ {\text{ }}\frac{{{{\dot \omega }_{{\text{a}}j}}{I_{{\text{a}}j}} - R\left( {{F_{y{\text{r}}j}}+{F_{y{\text{l}}j}}} \right)+{{{W_j}\left( {{F_{{\text{sr}}j}} - {F_{{\text{sl}}j}}} \right)} / 2}}}{{{B_j}}}. \\ \end{gathered} \right\} $

车轮转动微分方程为

(20)$ \left. \begin{gathered} {I_{{\text{w1}}}}{{\dot \omega }_{i1}} = - {T_{{\text{b}}i1}} - {T_{{\text{f}}i1}} - {F_{xi1}}R, \\ {I_{{\text{w2}}}}{{\dot \omega }_{i2}} = {T_{{\text{d}}i2}} - {T_{{\text{b}}i2}} - {T_{{\text{f}}i2}} - {F_{xi2}}R, \\ {I_{{\text{w3}}}}{{\dot \omega }_{i3}} = {T_{{\text{d}}i3}} - {T_{{\text{b}}i3}} - {T_{{\text{f}}i3}} - {F_{xi3}}R. \\ \end{gathered} \right\} $

式中：I_wj为车轮转动惯量，T_bij为制动力矩，T_fij为车轮滚动阻力矩，T_dij为驱动力矩. 车轮滚动阻力矩T_fij的简化计算式为

(21)$ {T_{{\text{f}}ij}} = {F_{zij}}fR. $

式中：f为滚动阻力系数.

为了准确估计车辆在崎岖路面行驶时的轮胎侧向力，选用魔术公式轮胎模型，其侧向力表达式为

(22)$ \begin{split} {F_y} = & {D_y}\sin \left\{ {{C_y}\arctan \left[ {{B_y}{\alpha _y} - {E_y}\left( {{B_y}{\alpha _y} - } \right.} \right.} \right. \\ &\left. {\left. {\left. {\arctan \left( {{B_y}{\alpha _y}} \right)} \right)} \right]} \right\}+{S_v}. \end{split} $

式中：F_y为轮胎侧向力；α_y为侧向力组合自变量，α_y=α+S_h，S_h为水平偏移因子；B_y为刚度因子；C_y为形状因子；D_y为峰值因子；E_y为曲率因子；S_v为垂直偏移因子.

(23)$ \left. \begin{gathered} {C_y} = {a_0}, \\ {D_y} = {a_1}F_z^2+{a_2}{F_z}, \\ {B_y} = \frac{{{a_3}\sin \left[ {2\arctan \left( {{{{F_z}} / {{a_4}}}} \right)} \right]\left( {1 - {a_5}\left| \gamma \right|} \right)}}{{{C_y}{D_y}}}, \\ {E_y} = {a_6}{F_z}+{a_7}, \\ {S_h} = {a_8}\gamma +{a_9}{F_z}+{a_{10}}, \\ {S_v} = {a_{11}}{F_z}\gamma +{a_{12}}{F_z}+{a_{13}}. \\ \end{gathered} \right\} $

式中：γ为轮胎倾角，对于非独立悬架，轮胎倾角等同于车桥侧倾角度；a₀~a₁₃为轮胎侧向力特性参数，可通过拟合轮胎侧偏特性曲线得到. 研究对象使用的工程轮胎拟合参数如表2所示.

基于线性轮胎逆模型，将轮速转化为轮胎接地点速度在轮胎前进方向上的分速度v_tij，表达式为

(24)$ {v_{{\text{t}}ij}} = \left\{ \begin{gathered} {\omega _{ij}}R\left( {1 - {{{F_{xij}}} / {{C_x}}}} \right),\quad {F_{xij}} \geqslant 0; \\ \frac{{{\omega _{ij}}R}}{{1+{{{F_{xij}}} / {{C_x}}}}},\quad\quad\quad\;\;\; {F_{xij}} < 0. \\ \end{gathered} \right. $

式中：C_x为轮胎纵向刚度. 根据式(4)，v_tij与车辆纵向速度的关系式为

(25)$ \left. \begin{gathered} {v_{x{\text{tl}}1}} = \frac{{{v_{{\text{tl}}1}}}}{{\cos {\alpha _{ij}}}}\cos ({\alpha _{ij}}+\delta )+{\omega _z}\frac{{{B_1}}}{2}+{\omega _y}h, \\ {v_{x{\text{tr}}1}} = \frac{{{v_{{\text{tr}}1}}}}{{\cos {\alpha _{ij}}}}\cos ({\alpha _{ij}}+\delta ) - {\omega _z}\frac{{{B_1}}}{2}+{\omega _y}h, \\ {v_{x{\text{tl}}2}} = {v_{{\text{tl}}2}}+{\omega _z}\frac{{{B_2}}}{2}+{\omega _y}h, \\ {v_{x{\text{tr}}2}} = {v_{{\text{tr}}2}} - {\omega _z}\frac{{{B_2}}}{2}+{\omega _y}h, \\ {v_{x{\text{tl}}3}} = {v_{{\text{tl}}3}}+{\omega _z}\frac{{{B_3}}}{2}+{\omega _y}h, \\ {v_{x{\text{tr}}3}} = {v_{{\text{tr}}3}} - {\omega _z}\frac{{{B_3}}}{2}+{\omega _y}h. \\ \end{gathered} \right\} $

式中：v_xtij为根据对应车轮得到的车辆纵向速度. 在崎岖路面行驶过程中，轮胎垂直载荷变化幅度较大，可能发生个别轮胎垂向载荷较小导致滑转率快速增大的状况，使计算结果产生较大偏差. 为此采用最小轮速法，即选择数值最小的结果作为车辆纵向速度的初步估计值，表达式为

(26)$ {\hat v_{x\_{\text{whe}}}} = \min\; ({v_{x{\text{tl}}1}},{v_{x{\text{tr}}1}},{v_{x{\text{tl}}2}},{v_{x{\text{tr}}2}},{v_{x{\text{tl}}3}},{v_{x{\text{tr}}3}}). $

式中：$ {\hat v_{x\_{\text{whe}}}} $为基于轮速的纵向速度观测值.

根据车辆动力学模型建立离散化状态方程和测量方程：

(27)$ \left. \begin{gathered} {{\boldsymbol{x}}_k} = f\left( {{{\boldsymbol{x}}_{k - 1}},{{\boldsymbol{u}}_k}} \right)+{{\boldsymbol{w}}_k}, \\ {{\boldsymbol{y}}_k} = h\left( {{{\boldsymbol{x}}_k},{{\boldsymbol{u}}_k}} \right)+{{\boldsymbol{v}}_k}. \\ \end{gathered} \right\} $

式中：x_k−1为k−1时刻的状态向量，u_k为k时刻的输入向量，y_k为k时刻的测量向量，f(x_k−1,u_k)为状态转移方程，h(x_k,u_k)为测量方程，w_k为过程噪声，v_k为测量噪声，下角标k表示时刻. 选取的状态向量x、输入向量u以及观测向量y：

(28)$ {\boldsymbol{x}} = {\left[ {{v_x}{\text{, }}{a_x}{\text{, }}{v_y}{\text{, }}{{\dot \omega }_z}{\text{, }}{{\boldsymbol{F}}_{y{\text{v}}}}} \right]^{\text{T}}}, $

(29)$ {\boldsymbol{u}} = {\left[ {\delta {\text{, }}{F_{x{\text{l}}1}}{\text{, }}{F_{x{\text{r}}1}}{\text{, }}{F_{x{\text{l}}2}}{\text{, }}{F_{x{\text{r}}2}}{\text{, }}{F_{x{\text{l}}3}}{\text{, }}{F_{x{\text{r}}3}}} \right]^{\text{T}}}, $

(30)$ {\boldsymbol{y}} = {\left[ {{{\hat v}_{x\_{\text{whe}}}}{\text{, }}{a_x}{\text{, }}{a_y}{\text{, }}{{\dot \omega }_z}{\text{, }}{{\boldsymbol{F}}_{y{\text{v}}\_{\text{mag}}}}} \right]^{\text{T}}}, $

(31)$ {{\boldsymbol{F}}_{y{\text{v}}}} = {\left[ {{F_{y{\text{l}}1}}{\text{, }}{F_{y{\mathrm{r}}1}}{\text{, }}{F_{y{\text{l2}}}}{\text{, }}{F_{y{\mathrm{r}}2}}{\text{, }}{F_{y{\text{l3}}}}{\text{, }}{F_{y{\mathrm{r}}3}}} \right]^{\text{T}}}, $

(32)$ \begin{split} {{\boldsymbol{F}}_{y{\text{v\_mag}}}} =& \left[ {{{\hat F}_{y{\text{l}}1{\text{\_mag}}}}{\text{, }}{{\hat F}_{y{\mathrm{r}}1{\text{\_mag}}}}{\text{, }}{{\hat F}_{y{\text{l2\_mag}}}}{\text{, }}{{\hat F}_{y{\mathrm{r}}2{\text{\_mag}}}}} ,\right. \\ & {\left. {{\text{ }}{{\hat F}_{y{\text{l3\_mag}}}}{\text{, }}{{\hat F}_{y{\mathrm{r}}3{\text{\_mag}}}}} \right]^{\text{T}}}. \end{split} $

式中：$ {\hat F_{yij\_{\text{mag}}}} $为使用魔术公式轮胎模型计算得到的轮胎侧向力估计值，轮胎模型所需的垂向力和轮胎侧偏角使用十七自由度动力学模型公式计算. $ {\hat v_{x\_{\text{whe}}}} $和$ {\hat F_{yij\_{\text{mag}}}} $基于传感器数据计算得到的，其中包含传感器的噪声. 为了降低EKF的计算量，先将传感器数据进行计算处理，得到初步估计值$ {\hat v_{x\_{\text{whe}}}} $和$ {\hat F_{yij\_{\text{mag}}}} $，再将$ {\hat v_{x\_{\text{whe}}}} $和$ {\hat F_{yij\_{\text{mag}}}} $作为观测值与加速度、角速度信号一起输入EKF算法中. 将式(1)~(3)离散化，得到状态转移方程：

(33)$ \begin{split}& f\left( {{{\boldsymbol{x}}_{k - 1}},{{\boldsymbol{u}}_k}} \right) = \left[ {{v_{x,k - 1}}+T\left( {{a_{x,k - 1}}+{v_{y,k - 1}}{{\dot \omega }_{z,k - 1}}} \right),} \right.{a_{x,k - 1}}, \\&\quad {v_{y,k - 1}}+T\left\{ {\left[ {\left( {{F_{x{\text{l}}1,k}}+{F_{x{\text{r}}1,k}}} \right)\sin {\delta _k}} \right.} \right.+\left( {{F_{y{\text{l}}1,k - 1}}+} \right. \\&\quad \left. {{F_{y{\text{r}}1,k - 1}}} \right)\cos {\delta _k}+{F_{x{\text{l}}2,k}}+{F_{x{\text{r}}2,k}}+{F_{x{\text{l}}3,k}}+{{\left. {{F_{x{\text{r}}3,k}}} \right]} / m} - \\&\quad \left. {{v_{x,k - 1}}{{\dot \omega }_{z,k - 1}}} \right\}, {\dot \omega }_{z,k - 1}+T\left\{ {l_1}\left[ \left( F_{x{\text{l}}1,k}+ F_{x{\text{r}}1,k} \right)\sin \delta _k+ \right.\right. \\&\quad \left.\left( F_{y{\text{l}}1,k - 1}+ {{F_{y{\text{r}}1,k - 1}}} \right)\cos {\delta _k} \right] - {l_2}\left( {F_{y{\text{l}}2,k - 1}}+ {{F_{y{\text{r}}2,k - 1}}} \right) - \\&\quad {l_3}\left( {F_{y{\text{l}}3,k - 1}} + {{F_{y{\text{r}}3,k - 1}}} \right) + 0.5{B_1}\left[ {\left( {{F_{y{\text{l}}1,k - 1}} - {F_{y{\text{r}}1,k - 1}}} \right)\sin {\delta _k}+} \right. \\&\quad \left. \left( {{F_{x{\text{r}}1,k}} - F_{x{\text{l}}1,k}} \right)\cos {\delta _k} \right]+ 0.5{B_2}\left( {F_{x{\text{r}}2,k}} - {F_{x{\text{l}}2,k}} \right) + \\&\quad \left.\left. \left. 0.5{B_3}\left( {F_{x{\text{r}}3,k}} - {{F_{x{\text{l}}3,k}}} \right) \right\} / {{I_z}},{{\boldsymbol{F}}_{y{\text{v}},k - 1}} \right]^{\text{T}}\right..\\[-4pt] \end{split} $

式中：T为估计器的采样周期. 系统测量方程为

(34)$ \begin{split}& h\left( {{{\boldsymbol{x}}_k},{{\boldsymbol{u}}_k}} \right) = \left[ {{v_x},{a_{x,k}},\left\{ {\left[ {\left( {{F_{x{\text{l}}1,k}}+{F_{x{\text{r}}1,k}}} \right)\sin {\delta _k}+} \right.} \right.} \right. \\& \left. {\left( {{F_{y{\text{l}}1,k}}+} \right.{F_{y{\text{r}}1,k}}} \right)\cos {\delta _k}+{F_{x{\text{l}}2,k}}+{F_{x{\text{r}}2,k}}+{F_{x{\text{l}}3,k}}+ \\& \left. {{{\left. {{F_{x{\text{r}}3,k}}} \right]} / m} - {v_{x,k}}{{\dot \omega }_{z,k}}} \right\},{\left. {{{\dot \omega }_{z,k}},{{\boldsymbol{F}}_{y{\text{v}},k}}} \right]^{\text{T}}}. \end{split} $

EKF计算过程可分为预测和校正2个部分. 预测部分根据上一时刻的系统状态计算先验估计值并更新先验误差协方差矩阵，表达式为

(35)$ \hat {\boldsymbol{x}}_k^ - = f\left( {{{\hat {\boldsymbol{x}}}_{k - 1}},{{\boldsymbol{u}}_k}} \right) \text{，} $

(36)$ {\boldsymbol{P}}_k^ - = {{\boldsymbol{F}}_k}{{\boldsymbol{P}}_{k - 1}}{\boldsymbol{F}}_k^{\text{T}}+{\boldsymbol{Q}} . $

式中：$ \hat {\boldsymbol{x}}_k^ - $为k时刻先验估计值，$ {\hat {\boldsymbol{x}}_{k - 1}} $为k−1时刻最优估计值，$ {\boldsymbol{P}}_k^ - $为k时刻先验误差协方差矩阵，$ {{\boldsymbol{P}}_{k - 1}} $为k−1时刻误差协方差矩阵，$ {{\boldsymbol{F}}_k} $为式(33)对x求偏导得到的雅可比矩阵，Q为过程噪声协方差矩阵. 校正部分将预测值与测量值结合，得到当前时刻状态量最优估计值并更新误差协方差矩阵，表达式为

(37)$ {{\boldsymbol{K}}_k} = {\boldsymbol{P}}_k^ - {\boldsymbol{H}}_k^{\text{T}}{\left( {{{\boldsymbol{H}}_k}{\boldsymbol{P}}_k^ - {\boldsymbol{H}}_k^{\text{T}}+{\boldsymbol{R}}} \right)^{ - 1}} \text{，} $

(38)$ {\hat {\boldsymbol{x}}_k} = \hat {\boldsymbol{x}}_k^ - +{{\boldsymbol{K}}_k}\left[ {{{\boldsymbol{y}}_k} - h\left( {\hat {\boldsymbol{x}}_k^ - ,{{\boldsymbol{u}}_k}} \right)} \right] \text{，} $

(39)$ {{\boldsymbol{P}}_k} = \left( {{\boldsymbol{I}} - {{\boldsymbol{K}}_k}{{\boldsymbol{H}}_k}} \right){\boldsymbol{P}}_k^ - . $

式中：$ {{\boldsymbol{K}}_k} $为k时刻卡尔曼增益矩阵，$ {{\boldsymbol{H}}_k} $为式(34)对x求偏导得到的雅可比矩阵，R为测量噪声协方差矩阵，I为单位矩阵.

根据式(1)，在离散系统中车辆横向速度表达式为

(40)$ {v_{y,k}} = {v_{y,k - 1}}+T({a_{y,k}} - {v_{x,k}}{\omega _{z,k}}) . $

由于横向加速度和横摆角速度数据由传感器测得，在计算前须先使用一阶低通滤波去除高频噪声. 一阶低通滤波表达式^[21]为

(41)$ {Y_k} = c{X_k}+\left( {1 - c} \right){Y_{k - 1}} . $

式中：Y_k为滤波器在k时刻的输出，X_k为滤波器在k时刻的输入，c为滤波系数.

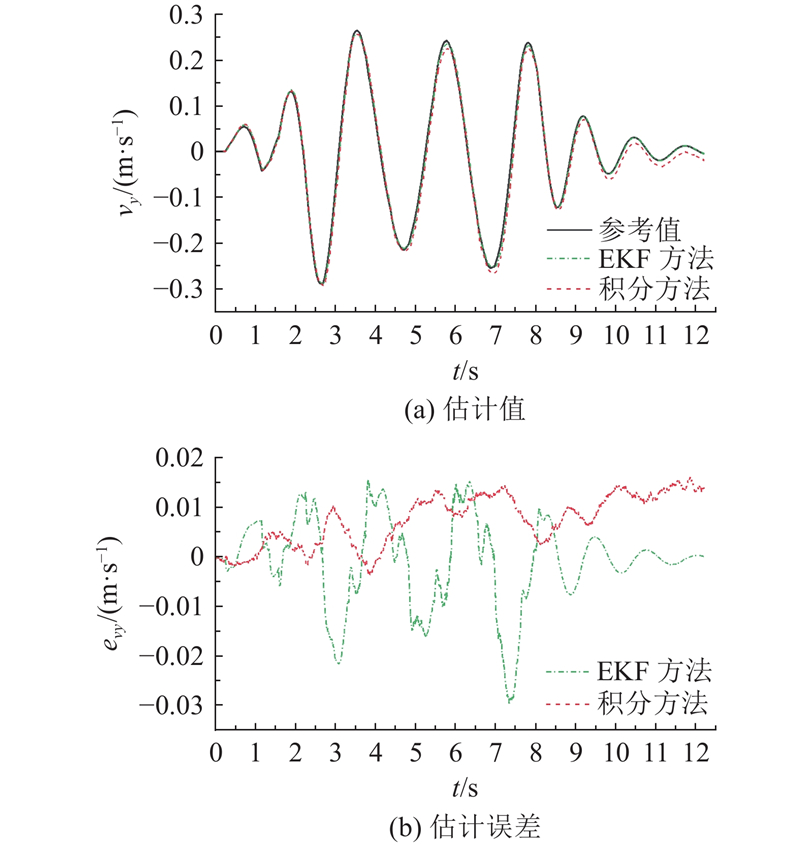
车辆通过扭曲路，速度为15 km/h，扭曲路左右交错布置6个高度为150 mm的正弦波形凸块，使用EKF方法和积分方法对车辆横向速度进行估计，仿真结果如图4所示. t=0.3~8.5 s，车辆进入扭曲路行驶，车辆运动状态变化率较大，这时EKF方法估计结果的误差波动幅度较大，其误差以零为中心上下波动；积分方法估计误差波动较小，但由积分产生的累计误差随时间逐渐增大. t=8.5~12 s，车辆驶出扭曲路段，车辆运动状态逐渐恢复平稳，这时EKF方法的估计误差逐渐收敛到零，积分方法的累积误差无法自行修正.

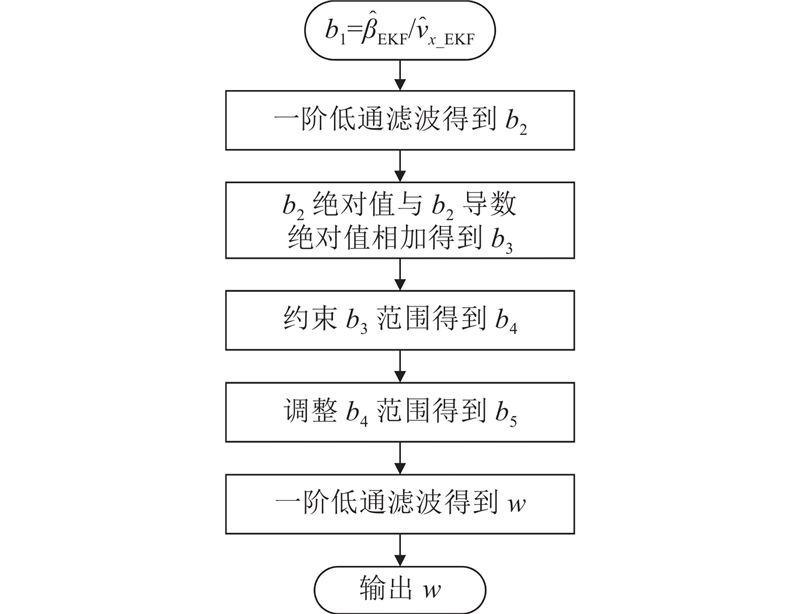
根据EKF方法和积分方法的特点，提出比例-微分融合权重系数计算方法，在此基础上对上述2种方法的估计结果进行加权融合. 当车辆颠簸较为剧烈时，融合权重系数w接近或等于1，使融合结果偏向或等于积分方法；当车辆运动状态平稳时，w接近或等于0，使融合结果偏向或等于EKF方法. 融合权重系数w的计算流程如图5所示. 图5中，b₁~b₅均为中间变量. 比例-微分融合权重系数计算方法选取质心侧偏角和车辆纵向速度作为车辆运动状态的评价参数，其中车辆纵向速度使用由EKF输出的纵向速度估计值$ {\hat v_{x\_{\text{EKF}}}} $，质心侧偏角是EKF输出的横向速度除以纵向速度得到的质心侧偏角初步估计值$ {\hat \beta _{{\text{EKF}}}} $. 为了得到反映车辆运动状态的权重系数，通过车辆运动状态参数提取表征车辆运动剧烈程度的变量，再通过范围约束和调整得到范围在0到1之间的融合权重系数w. 先将质心侧偏角除以车辆纵向速度得到b₁，再使用一阶低通滤波将b₁平滑处理得到b₂，方法同式(41). 车辆在崎岖地形行驶，处于不断摇晃的状态，b₂的数值在正负之间来回变化，此时稳定保持在较高数值范围的变量才能表征车辆的运动剧烈程度. 为此参考比例-微分控制器的思路，将b₂的绝对值与其变化率的绝对值各乘以系数并相加，得到较为稳定的数值. b₂的瞬时绝对值提供系统的当前状态， b₂的一阶导数的绝对值反映信号变化的趋势，车辆在持续颠簸时，二者的数值交替变化，将二者结合起来能够较好地反映车辆的运动剧烈程度，有效避免权重系数在车辆摆动过程中频繁波动，对瞬时干扰具有较强的鲁棒性. 中间变量b₃的表达式为

(42)$ {b_3} = {K_{\text{p}}}\left| {{b_2}} \right|+{K_{\text{d}}}\left| {{{\dot b}_2}} \right| . $

式中：K_p为比例系数，K_d为微分系数. 得到b₃之后，将其范围约束在[b_4min,1+b_4min]，得到b₄，表达式为

(43)$ {b_4} = \min \left[ {\max \left( {{b_3},{b_{4\min }}} \right),{b_{4\min }}+1} \right] . $

将b₄减去下限值b_4min，得到范围在0到1的中间变量b₅，使用一阶低通滤波平滑处理，得到权重系数w. 车辆横向速度融合估计结果为

(44)$ {\hat v_y} = w{\hat v_{y\_{\text{int}}}}+\left( {1 - w} \right){\hat v_{y\_{\text{EKF}}}}. $

式中：$ {\hat v_{y\_{\text{int}}}} $为积分方法横向速度估计值，$ {\hat v_{y\_{\text{EKF}}}} $为EKF方法横向速度估计值.与积分方法单独使用的情况不同，在使用融合方法过程中，为了避免积分方法估计值的累积误差持续增加，当w=0时，将积分重置为上一时刻的融合估计值. 积分计算所需的车辆纵向速度和横摆角速度使用EKF输出的估计值，其数值比一阶低通滤波结果更准确. 因此基于式(40)，融合方法中的积分方法估计值表达式为

(45)$ {\hat v_{y{\text{\_int}},k}} = \left\{ \begin{gathered} {{\hat v}_{y{\text{\_int}},k - 1}}+T({a_{y,k}} - {{\hat v}_{x{\text{\_EKF}},k}}{{\hat \omega }_{z{\text{\_EKF}},k}}),{\text{ 0 < }}w \leqslant 1; \\ {{\hat v}_{y,k - 1}}+T({a_{y,k}} - {{\hat v}_{x{\text{\_EKF}},k}}{{\hat \omega }_{z{\text{\_EKF}},k}}),\quad\;{\text{ }}w = 0. \\ \end{gathered} \right. $

式中：$ {\hat \omega _{z\_{\text{EKF}}}} $为EKF横摆角速度估计值. 车辆质心侧偏角融合估计结果为

(46)$ \hat \beta = \frac{{{{\hat v}_y}}}{{{{\hat v}_{x\_{\text{EKF}}}}}}. $

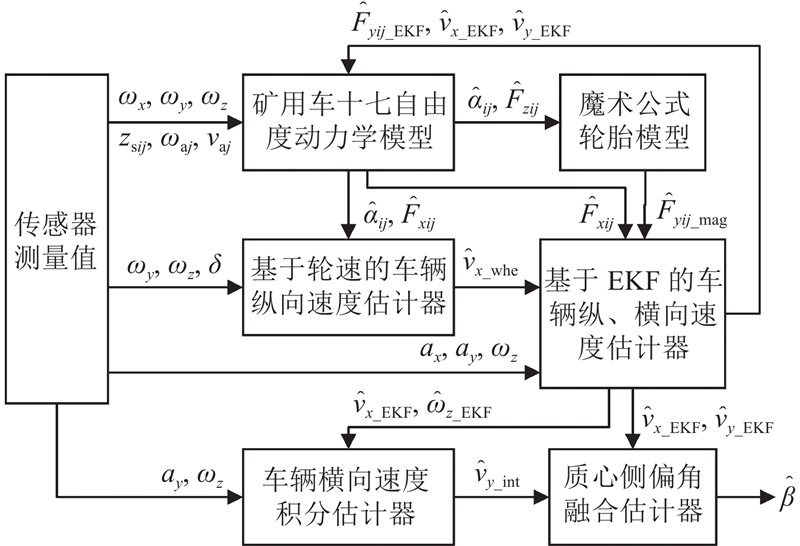
本研究所提质心侧偏角估计方法流程如图6所示. 为了确保EKF估计器信息形成闭环反馈，避免误差累积，使用车辆纵、横向速度和轮胎侧向力的EKF估计值作为矿用车十七自由度动力学模型在下一时刻的输入.

使用TruckSim和Simulink建立联合仿真平台，在TruckSim中建立参数相同的矿用车模型，设置多种工况进行仿真实验. 将TruckSim输出的加速度、角速度、悬架位移等数据作为估计器的输入，以TruckSim输出的车辆质心侧偏角数据作为参考值，验证本研究所提估计方法的准确性.

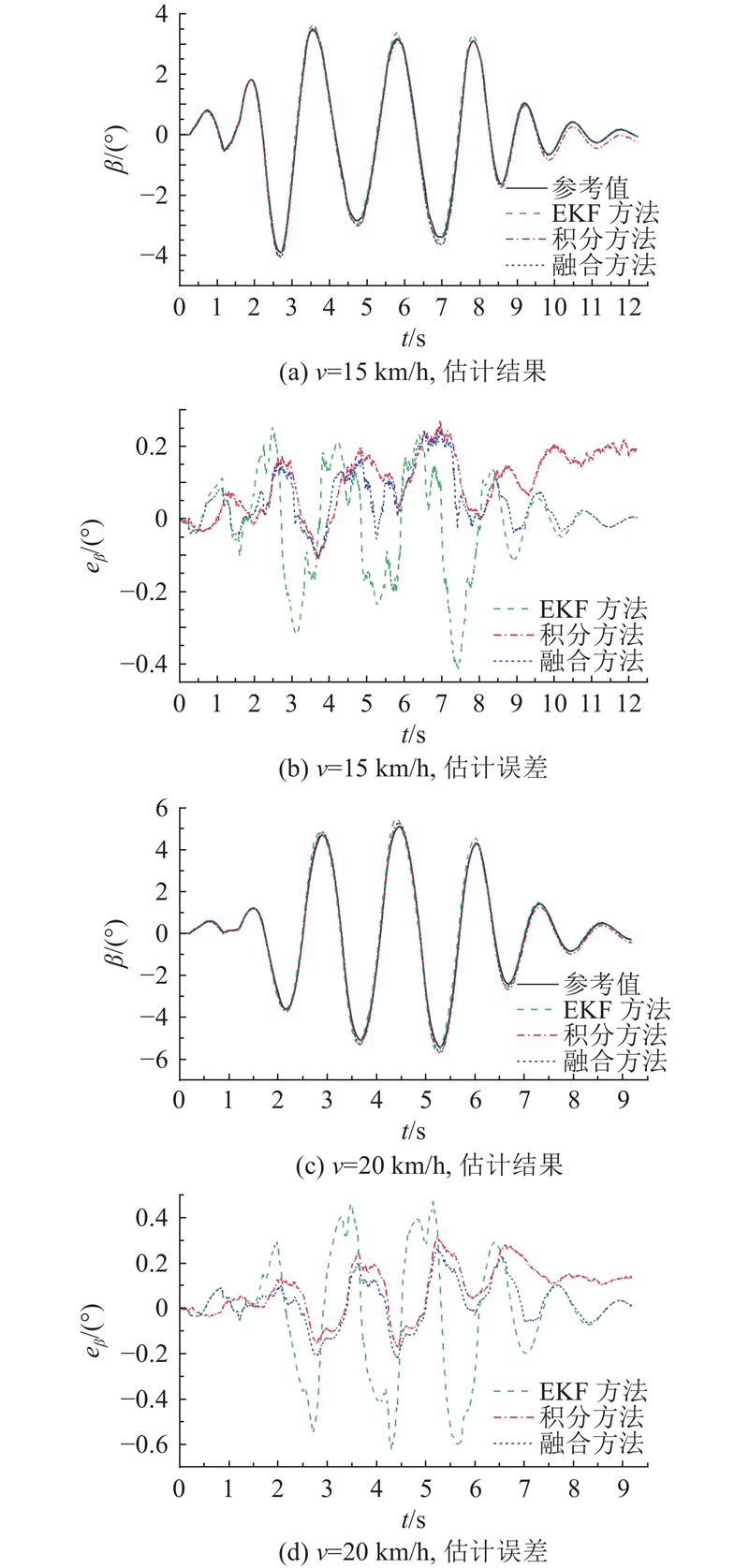
选择扭曲路进行仿真实验，扭曲路由左右交错分布的凸块组成，能够在一定程度上模拟崎岖路面对车辆稳定性的影响. 根据《汽车试验场特种道路设计与施工技术规程T/CECS G:T10-2018》，选取凸块高度H_s=150、200 mm的2种正弦波形扭曲路，为了使车辆对角悬架同时被压缩，异侧相邻两凸块纵向间距根据车辆轴距取4.5 m. 扭曲路后接平坦路面. 车辆分别以v=15、20 km/h匀速通过上述2种高度的扭曲路. 估计结果的均方根误差RMSE和最大误差ME如表3所示，H_s=150 mm扭曲路的仿真结果如图7所示，其中e_β为质心侧偏角估计误差. 由图7可知，当车辆在扭曲路行驶时，积分方法的估计精度优于EKF方法；当车辆离开扭曲路，车身晃动逐渐减小时，EKF方法的误差随之逐渐减小到零，积分方法的误差仍在无序地波动. 融合方法在车辆颠簸幅度较大时偏向于积分方法，在车辆恢复平稳时偏向EKF方法，使估计结果较为精确的同时避免了累积误差的产生. 由表3可知，与EKF方法相比，融合方法的均方根误差在H_s=150 mm扭曲路的2种车速工况下分别减小了36%和61%，在H_s=200 mm扭曲路的2种车速工况下分别减小了41%和56%；与积分方法相比，融合估计方法的均方根误差在H_s=150 mm扭曲路的2种车速工况下分别减小了34%和27%，在H_s=200 mm扭曲路的2种车速工况下分别减小了26%和27%.

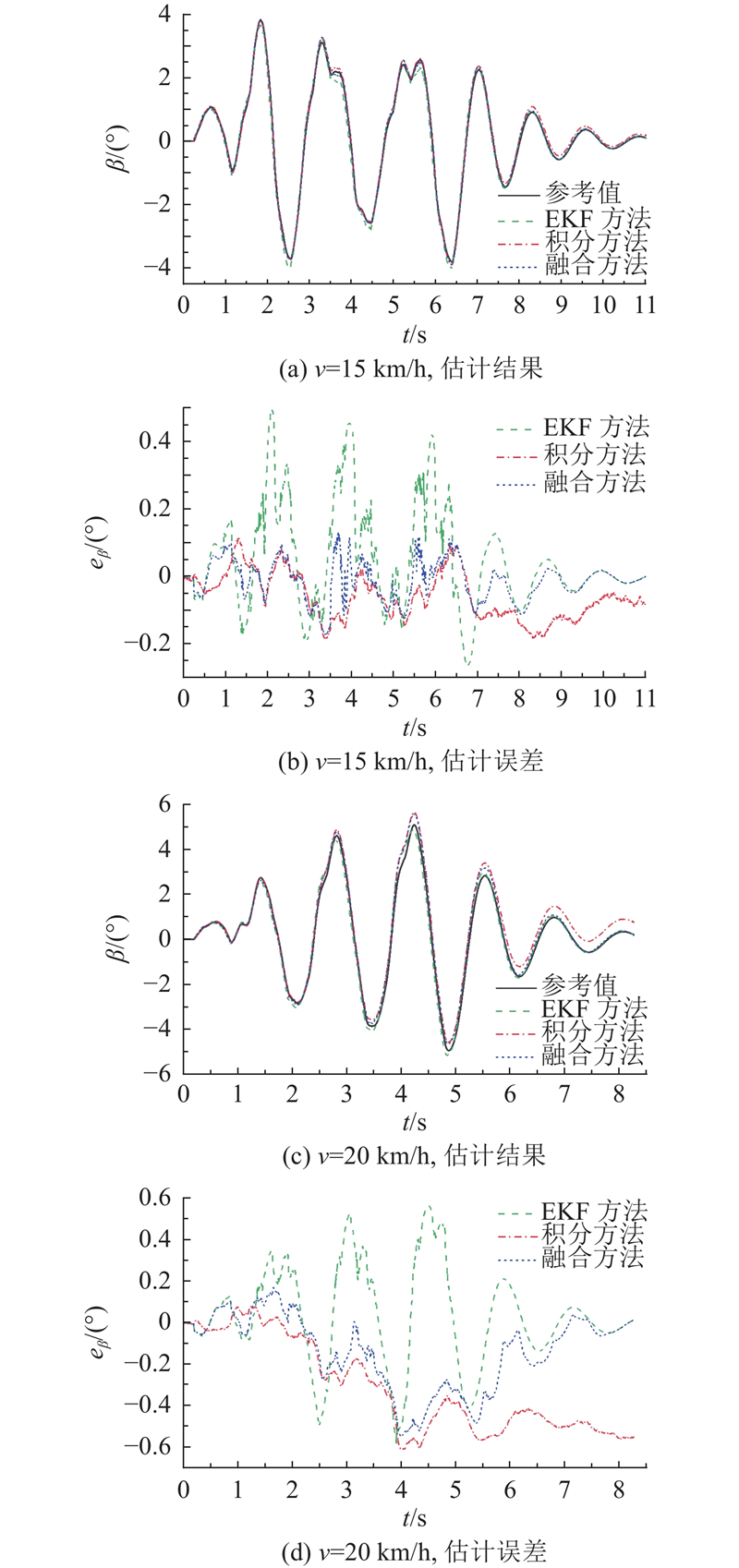
单边凸块路面可以模拟车辆单侧车轮受到落石或路面不平干扰的状况，在矿用车行驶过程中这样的干扰可能引起车辆侧倾和横摆，极易对汽车横向稳定性造成不良影响. 使用单边凸块路面进行仿真，进一步验证所述融合估计方法的效果. 设置H_s=180、140 mm的单边梯形凸块路面，车辆分别以v=15、20 km/h通过3个间隔为8 m的凸块，估计结果的均方根误差和最大误差如表4所示，其中H_s=180 mm单边凸块路面仿真结果如图8所示. 由图8可知，融合方法能够在EKF方法和积分方法之间进行合理的选择和切换，得到更加准确的估计结果. 其中当车速为20 km/h时，车辆出现剧烈颠簸，积分方法的误差累积较快，使融合方法结果出现一定程度的偏离. 但在车辆颠簸减小后，权重系数快速减小，融合估计误差跟随EKF方法逐渐收敛，同时融合方法中的积分器被重置，消除了累积误差. 由表4可知，与EKF方法相比，融合方法的均方根误差在H_s=180 mm单边凸块路面的2种车速工况下分别减小了62%和6%，在H_s=140 mm单边凸块路面的2种车速工况下分别减小了59%和15%；与积分方法相比，融合方法的均方根误差在H_s=180 mm单边凸块路面的2种车速工况下分别减小了34%和41%，在H_s=140 mm单边凸块路面的2种车速工况下分别减小了6%和19%.

为了准确描述矿用车在崎岖地形行驶工况下的运动状态，建立包含非独立悬架和平衡悬架的十七自由度动力学模型. 构建基于EKF的车辆纵、横向速度估计器和车辆横向速度积分估计器. 根据EKF方法和积分方法在不同运动状态下的估计效果，设计能够根据车辆运动状态调节权重系数的质心侧偏角融合估计器，融合EKF方法和积分方法的估计结果. 仿真结果表明，所提方法在车辆受路面不平影响发生较大幅度颠簸的情况下具有良好的估计效果，其估计精度与单独的EKF方法和积分方法相比有显著提升，实现了在崎岖路面下质心侧偏角的准确估计. 所提估计方法仅在TruckSim/Simulink联合仿真平台进行验证，后续将考虑通过硬件在环试验进行进一步性能验证.