针对上述问题,本文提出基于经验小波变换和长短时记忆网络(empirical wavelet transform and long short term memory, EWT-LSTM)的工业机器人关节异常检测方法. 构建实时数据采集平台,通过智能终端从可编程逻辑控制器(programmable logic controller, PLC)读取速度和电流信号,在终端数据库完成实时数据的动态存储、传输,实现不添加传感器的实时数据采集. 设计基于EWT-LSTM的关节异常检测算法,EWT是在小波变换的基础上通过经验模态分解(empirical mode decomposition, EMD)优化实现自适应分解的信号处理方法[19],LSTM是基于循环神经网络(recurrent neural network, RNN)优化梯度消失和梯度爆炸的长时序预测模型[20]. 通过EWT提取电流信号的特征分量,输入卷积神经网络(convolutional neural network, CNN)和注意力机制优化的双向LSTM模型,预测补全工业机器人当前关节的完整周期,解决了异常检测实时完整周期信号数据缺失导致的延迟问题. 度量预测补全的完整周期数据与标准周期数据的差异,实现实时关节的异常检测. 针对工业机器人制造企业出厂检测场景中关节伺服参数的异常问题,设计关节故障注入实验,以验证方法的准确性. 实验和工程应用的结果表明,该方法在实际工程场景中能够提供实时、准确、便捷的关节异常检测.
1. 基本原理
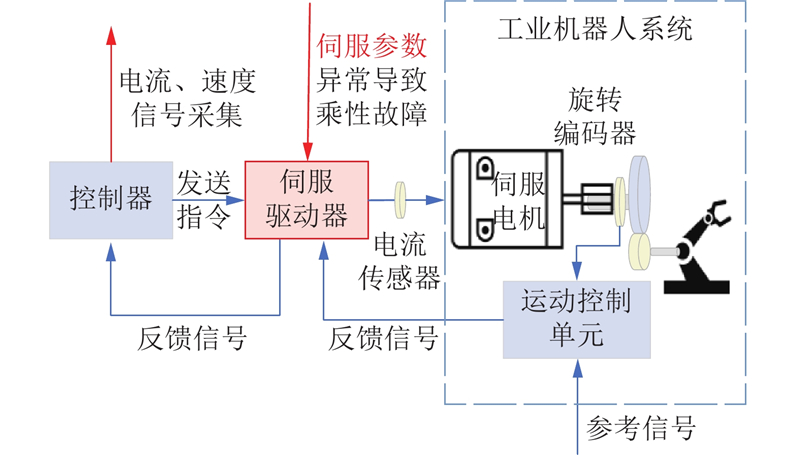
1.1. 工业机器人关节运动控制系统
图 1
目前能够通过工业机器人对应的PLC直接读取的工业机器人闭环控制回路中的反馈信号有关节位置、速度、加速度、角度、角速度、角加速度和电流信号. 针对工业机器人制造企业出厂检测关注的关节伺服参数异常所引起系统输出异常的乘性故障,由于关节电流信号与伺服电机输出扭矩成正比,电流信号能够很好地反映关节的健康状况和系统乘性故障. 关节异常检测可以转化为以电流信号为主的时间序列差异检测.
1.2. EWT-LSTM算法
在对生产测试区工业机器人针对关节伺服参数异常进行实时异常检测时,除了工业机器人恰好结束一个周期运动,其余处于运动周期中采集得到的实时周期是不完整的. 等待机器人完成完整的周期运动,会导致异常检测的延迟和效率的低下. 利用LSTM对时间序列数据的强大处理能力,预测并补全关节电流信号的时间序列,使其成为完整周期用于异常检测,以此大幅地降低等待机器人完成运动的延迟,提高异常检测的实时性.
在工业机器人关节电流信号中包含复杂的频率成分和噪声,对这些关节电流信号进行高准确率的预测极为困难. EWT同时克服了小波变换需要找到合适的小波基和EMD模态混叠的问题,能够自适应地分解出无模态混叠的反映时域特征的分量,这些特征分量较原信号更为光滑,为LSTM模型提供优化的特征输入.
EWT将信号的傅里叶谱在
细节系数
式中:
EWT后原始信号
选取EWT后能够反映时域特征的光滑分量作为LSTM模型的输入,可以显著降低预测难度,提高预测完整周期的准确率.
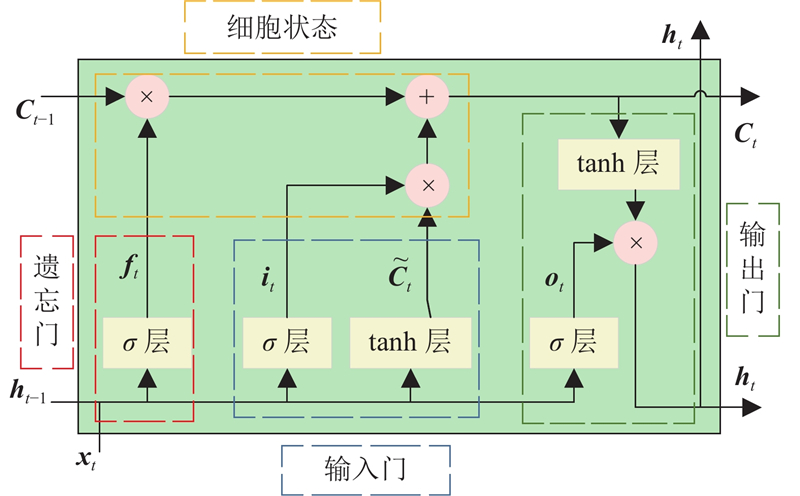
图 2
当接收上一步细胞传递的输出
式中:Wf为遗忘门权重,bf为遗忘门的偏置参数.
Sigmoid层的输入门确定需要更新的信息
式中:Wi、bi分别为输入门的权重与偏置,WC、bC分别为细胞状态的权重与偏置.
将旧细胞状态
Sigmoid层的输出门确定输出信息,将ot与通过tanh层处理的细胞状态相乘,得到当前步的输出
式中:Wo、bo分别为输出门的权重与偏置.
与其他时间序列预测方法相比,LSTM在处理长时间依赖和复杂非线性关系方面表现更优. 结合EWT和LSTM,可以实现高准确率的预测并补全工业机器人关节实时电流信号特征分量的完整周期,作为实时异常检测的基础.
2. 异常检测方法
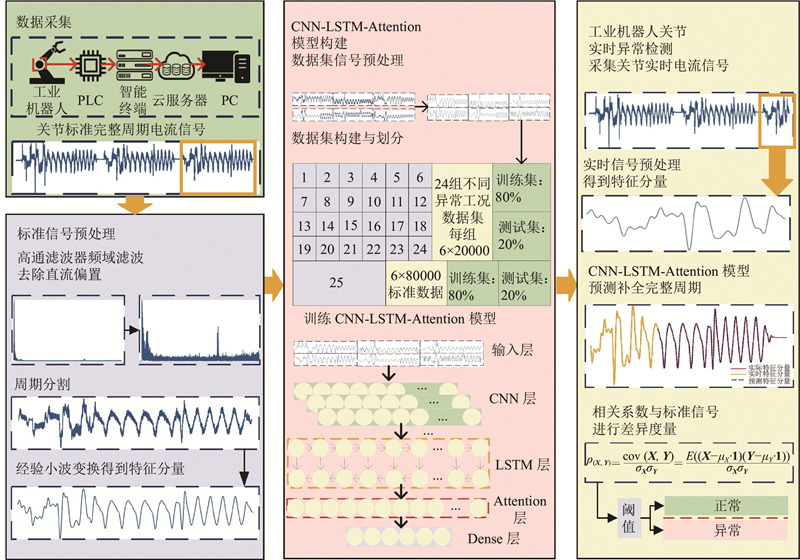
如图3所示,基于EWT-LSTM的工业机器人关节异常检测方法框架主要包含4个模块:数据采集、标准信号预处理、CNN-LSTM-Attention模型构建和实时关节异常检测. 通过工业机器人PLC-智能终端-云服务器一体化关节实时数据采集平台,采集存储工业机器人各关节的速度信号及伺服电机和伺服驱动器之间电流传感器采集到的电流信号. 对采集到的标准电流信号进行信号预处理,去除直流偏移后,根据各关节速度对信号进行周期分割,通过EWT对电流信号进行频带划分,提取反映时域特征的特征分量,生成用于异常检测的标准电流信号特征分量. 采集24组不同异常工况和1组标准工况的电流信号,经过滤波和EWT处理后,得到该工况下的电流信号特征分量时间序列,构建CNN-LSTM-Attention模型. 通过数据采集平台实时采集关节电流和速度信号,经过滤波、周期分割和EWT处理,得到实时电流特征分量序列. 当工业机器人处于运动周期中时,利用上述模型预测补全当前序列的最新完整周期,解决了因缺乏实时完整周期导致的异常检测延时问题. 将EWT分解得到的特征分量作为模型输入,提高了模型预测的准确率. 通过计算2个序列的相关系数,将实时特征分量与标准电流信号的特征分量进行差异度量,与关节设定阈值进行对比,高于阈值为正常,低于阈值为异常,得到实时的异常检测结果.
图 3
2.1. 数据采集
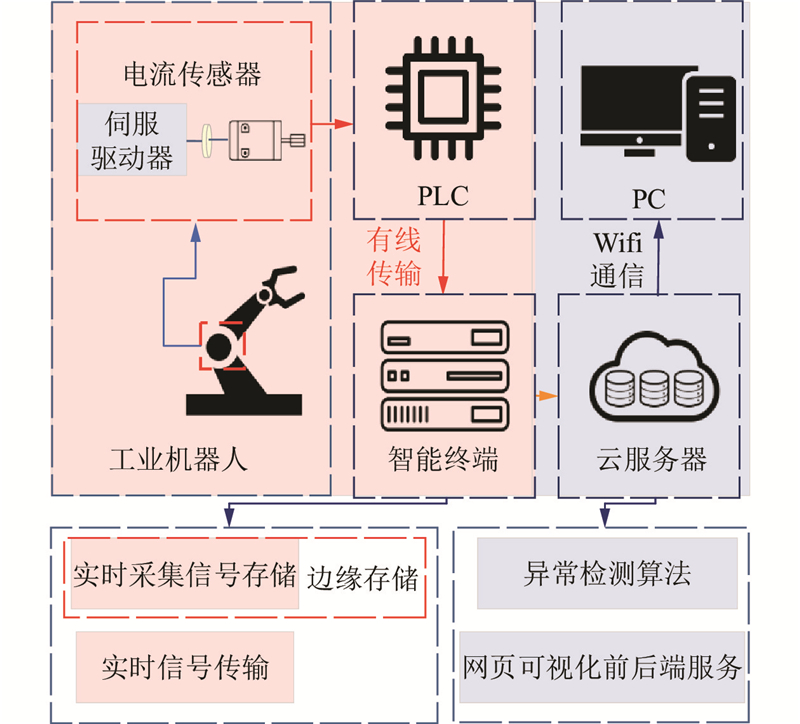
工业机器人的实时数据采集平台框架如图4所示. PLC通过有线连接,实时读取工业机器人闭环控制回路中的反馈信号,包括各关节的速度信号和电流信号.
图 4
图 4 工业机器人实时数据采集平台的框架
Fig.4 Framework of industrial robot real-time data collection platform
智能终端通过Docker部署influxDB和数据采集容器. 在数据采集容器中,通过flask和异步编程,运行的程序的功能是对工业机器人的关节电流信号进行实时采集、存储和传输. 实时采集和存储程序通过TCP通信,建立与PLC的Socket通信. 在250 Hz的采样频率下,生产线程机器人端采集打包50行数据为一个队列,消费线程将其存储至终端influxDB数据库,平均用时为0.15 s,确保在0.2 s的采样周期内不丢包不累积,实现实时数据的存储. 每台智能终端为4台机器人同时提供边缘存储服务,每秒需要存储的数据量为
云服务器端基于CentOS7系统,通过Docker部署了MySQL、异常检测算法、基于Spring Boot的网页后端和基于Vue3的网页前端容器. 用户在网页前端页面输入需要进行异常检测的工业机器人信息,如机器人序列号、机器人型号、动作类型、负载和速率等,后端将其写入MySQL设备的基本信息存储表中,在对应终端根据序列号创建独立的异步线程. 异常检测算法读取该信息表中的设备信息,查询该型号设备在该工况下的标准数据,在智能终端influxDB存储桶中查询实时数据进行实时异常检测,将检测结果与终端传输的实时数据一起在网页前端可视化,实现实时状态的监测.
该云边协同数据采集平台通过智能终端和influxDB实现工业机器人数据的实时采集和存储,在避免数据丢包和延迟的同时,减轻了云服务器负荷. 利用Docker容器化和异步技术的分布式架构,可以为多台机器人提供独立服务,互不干扰,提升系统稳定性和并发处理能力,能够同时管理和处理大量的工业机器人数据. 此外,云服务器利用强大的算力进行快速异常检测,通过网页前后端实现数据的实时传输和可视化,方便用户进行监控和管理. 该云边协同数据采集平台实现了无须额外添加传感器,对机器人关节的实时信号进行采集存储、实时状态监测和异常检测.
2.2. 标准信号的预处理
图 5
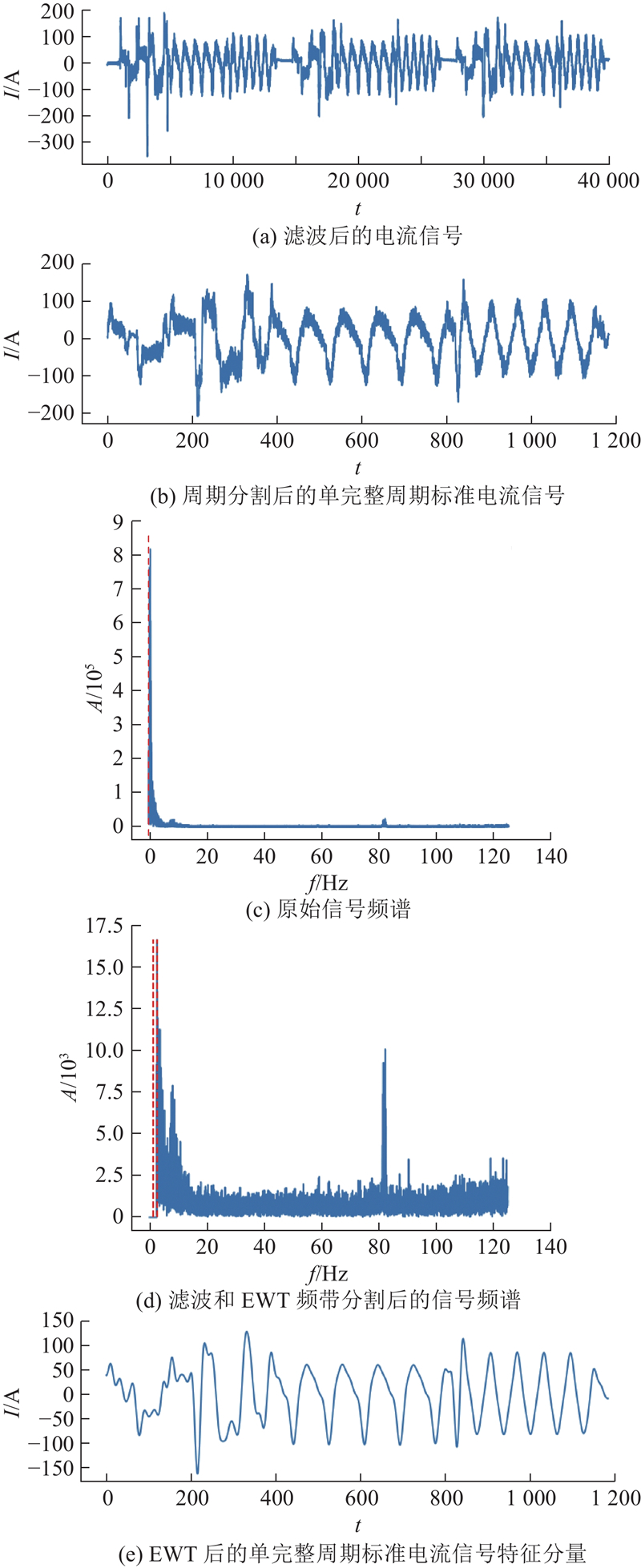
根据采集到的工业机器人各关节速度信号进行信号分割,以六关节速度绝对值之和为零作为机器人运动周期的开始和结束指标,确定标准电流信号的完整周期时间索引. 根据速度信号的时间索引,分割工业机器人6个关节的电流信号,得到各关节单完整周期标准电流信号的时间序列,如图5(a)、(b)所示.
为了提高后续异常检测算法中时序预测的准确性,采用EWT分解电流信号,获得光滑、反映信号时域特征的分量. 选择EWT分解得到的特征分量作为异常检测的基准. 首先需要获得完整周期标准信号的特征分量. 构建EWT信号分解模型的关键是通过检测局部极大值频带作为分割依据,确定分解信号特征分量的频带数量N. 如图5(c)~(e)所示,原始信号滤波后设定N=3进行频带划分,经过EWT分解可以得到电流信号的特征分量. 将标准电流信号经过EWT分解得到的特征分量存储在数据库中,作为在异常检测时与实时信号序列进行差异度量的基准.
2.3. 构建CNN-LSTM-Attention模型
在对周期运动的工业机器人进行异常检测时,除非正好处于运动周期的结束点,大部分时间段的实时数据都不完整,难以与标准时间序列进行对比. 为了实现实时异常检测,需要通过时间序列预测的方法补全不完整的周期. 针对不完整的实时周期电流信号,在经过滤波、信号分割和EWT分解后,对特征分量进行预测补全一个完整周期. 构建CNN-LSTM-Attention模型,用于特征分量时序的预测,模型架构如图6所示.
图 6
用于训练和测试模型的数据集来自后续实验中针对工业机器人关节伺服参数异常获取的24组实验组和1组对照组实验测得的不同工况数据,以提升模型的泛化能力. 实验组在6个关节上设置4组不同的异常伺服参数进行故障注入,对照组是6个关节伺服参数正常. 每组实验组的数据集包含20 000条6关节电流信号数据,对照组数据集包含80 000条6关节电流信号数据. 所有数据经过滤波和EWT分解得到特征分量后,转换为监督学习数据集,使用MinMaxScaler将数据缩放到[−1,1],以在模型训练中加速收敛. 6关节序列同时作为输入和输出特征,数据重塑为3D格式. 每个数据集按8∶2的比例分为训练集和测试集.
开发并构建CNN-LSTM-Attention模型,以预测和补全工业机器人实时异常检测时由于运动周期中断导致的不完整关节周期电流信号的特征分量,便于与完整周期标准特征分量进行差异度量. 如图6所示,模型主要包括CNN、双向LSTM和Attention 3部分,输入为工业机器人6个关节的电流信号特征分量.
输入数据进入由2层组成的CNN网络. 每层包含1个以ReLU为激活函数、128个大小为4的卷积核的卷积层和1个池化窗口为4的平均池化层. 卷积层提取局部特征,通过非线性激活函数增强模型的表达能力. 池化层减少特征图尺寸和计算量,降低过拟合风险. 2层CNN网络间通过填充层连接,以调整输入尺寸,保留边界信息. CNN层输出通过Dropout层,连接双向LSTM层. Dropout层通过随机丢弃神经元,减小依赖性和过拟合风险,提高泛化能力.
双向LSTM层采用32个LSTM单元,通过前向和后向处理输入序列,捕捉更多的全局信息,提升预测性能. LSTM层的隐藏层输出经过全连接层后输入Attention层,Attention层通过softmax函数归一化LSTM每个时间步的输出权重,衡量其对预测结果的重要性. 将训练得到的权重与LSTM隐藏层输出加权平均,输出最终的预测结果. 权重训练与加权平均和公式[27]如下:
式中:
表 1 CNN-LSTM-Attention模型的详细信息
Tab.1
| 层编号 | 描述 | 详细信息 | 输出尺寸 |
| Layer 1 | Input | Input_shape = (12,6) | 6×12 |
| Layer 2 | Conv1D | filters=128, kernel_size=1, activation=ReLU, padding='same' | 128×12 |
| Layer 3 | AveragePooling1D | pool_size=4 | 128×3 |
| Layer 4 | ZeroPadding1D | padding=(1, 0) | 128×4 |
| Layer 5 | Conv1D | filters=128, kernel_size=1, activation=ReLU, padding='same' | 128×4 |
| Layer 6 | AveragePooling1D | pool_size=4 | 128×1 |
| Layer 7 | Dropout | 0.2 | 128×1 |
| Layer 8 | Bidirectional | Units=32, return_sequences=True | 64×1 |
| Layer 9 | Dropout | 0.2 | 64×1 |
| Layer 10 | Permute | (2,1) | 1×64 |
| Layer 11 | Dense | layer_size = 64, activation='softmax' | 1×64 |
| Layer 12 | Permute | (2,1) | 64×1 |
| Layer 13 | Concatenate | [Layer 9, Layer 12] | 128×1 |
| Layer 14 | Flatten | — | 128 |
| Layer 15 | Dense | layer_size = 6, activation='sigmoid' | 6 |
采用基于TensorFlow框架的Keras库,建立混合深度神经网络模型,使用处理好的数据集进行训练. 训练在一台配备Intel i5-8250U CPU和2 GB NVIDIA GeForce MX150 GPU的笔记本电脑上进行. 选择Adam优化器和均方误差(mean squared error, MSE)作为优化器和损失函数. 训练参数设置如下:学习率为0.002,迭代次数(epochs)为100,批量大小(batch size)为100. 为了防止过拟合,设置终止函数监控验证集上的损失(val_loss). 若在5个连续轮次内验证集损失没有减少,则停止训练. 使用测试集,评估训练好的模型对关节预测的准确性.
2.4. 工业机器人关节实时异常检测
通过实时数据采集平台采集工业机器人各关节的速度和电流信号,并存储在智能终端的实时数据表中. 智能终端对电流信号进行滤波和信号分割得到实时周期,通过EWT分解得到实时周期电流信号的特征分量,以供云服务器上部署的异常检测算法使用. 异常检测算法对这些特征分量进行差分转化和MinMaxScaler缩放后,利用训练好的CNN-LSTM-Attention模型预测补全完整的实时周期. 将补全的实时特征分量与得到的标准电流信号特征分量进行差异度量,得到实时异常检测结果.
针对工业机器人关节电机电流信号的时间序列差异度量,常用的距离指标包括欧几里得距离、曼哈顿距离和动态时间规整距离等. 由于完整周期的电流信号序列较长,距离度量结果可能过大,选择2个时间序列绝对差的均方根作为差异度量指标[28],公式如下所示:
关节伺服参数异常表现为电流信号时域峰值异常,峰值差异可以作为时间序列信号异常检测的指标,用峰值差的绝对值与标准序列值作商得到的百分比表示[21].
皮尔逊相关系数作为描述2个变量的客观线性关联性程度的统计量,常用于2个时间序列X、Y的差异度量,公式如下所示:
皮尔逊相关系数是归一化后的相关系数,计算结果为[−1,1],其中−1表示负相关,0表示无关系,1表示正相关[29].
由于均方差依赖绝对距离,受大幅值噪点的影响较大,而峰值差异因作商受到零值附近值的干扰,选取反映两时序整体相似度且归一化的皮尔逊相关系数作为差异度量指标. 通过计算补全完整周期的电流信号特征分量和标准特征分量的相关系数,并与各关节异常阈值比较,完成关节实时异常检测.
3. 实验验证方案
工业机器人关节实时异常检测方法存在依赖振动、声音和视觉等外置传感器及基于完整周期对比导致延迟的问题. 为了验证该方法对上述问题的解决效果,设计如下实验验证方案.
3.1. 实验装置
图 7
图 7 工业机器人关节异常检测试验台的实物图
Fig.7 Physical picture of industrial robot joint abnormality detection test bench
表 2 工业机器人关节异常检测试验台的硬件架构
Tab.2
| 设备名称 | 型号配置 |
| 服务器 | CPU:Intel(R) Core(TM) i7- CPU @ 3.60 GHz 内存:23.86 GB 硬盘:1.13 TB 系统:CentOS7.4 |
| 智能终端 | 型号:NanoPi R6S 主控处理器:瑞芯微RK3588S 内存:8 GB 系统:Ubuntu 22.04 |
智能终端通过网线与机器人控制柜连接,终端LAN口IPv4静态路由设置为192.168.39.195,与IP为192.168.39.220的机器人通信,采集并动态保存实时速度和电流信号至智能终端的MySQL数据库. 智能终端WiFi的IPv4静态路由设置为192.168.77.195,通过路由器与IP为192.168.77.198的服务器通信. 服务器通过Docker部署MySQL、前后端及异常检测算法容器. 算法容器调用预处理后的实时数据进行异常检测,结果保存至服务器的MySQL数据库并显示在前端网页,通过电脑访问网页可以查看机器人实时可视化电流信号和异常检测结果.
3.2. 验证方案
根据工业机器人的出厂检测需求,统一应用出厂检测规定动作,单个运动周期包括6个关节的移动和转动,总时长为47.3 s,每个周期有5 s的停顿时间. 其他运动参数如下:机器人负载为20 kg,运动速率为额定最大速度的50%.
在该条件下,通过运维平台数据库服务采集标准工业机器人电流和速度信号,采集6 min、共90 000条数据作为标准工况数据集,另采集3个完整周期用于异常检测方法的验证. 将电流信号经过截止频率为0.01 Hz的傅里叶高通滤波器滤波,根据速度信号为0进行周期划分,得到一个完整周期的时间索引进行信号分割. 使用N = 3频带划分进行EWT分解,得到各关节电流信号的特征分量,保存至标准数据库中,供后续的异常检测调用.
表 3 工业机器人各关节的标准伺服参数
Tab.3
| 关节编号 | 伺服参数 | 关节编号 | 伺服参数 | |
| 1 | Kp = 40, Ti = 50 | 4 | Kp = 60, Ti = 30 | |
| 2 | Kp = 40, Ti = 50 | 5 | Kp = 50, Ti = 50 | |
| 3 | Kp = 70, Ti = 50 | 6 | Kp = 70, Ti = 20 |
实验组往6个关节分别修改4组伺服参数Kp以进行不同程度的故障注入,详细的伺服参数见表4. 每组另采集3个完整周期,用于异常检测方法的验证.
表 4 工业机器人各关节异常实验组的伺服参数设置
Tab.4
| 实验组编号 | 关节编号 | 伺服参数 |
| 1 | 1 | Kp = 10, Ti = 50 |
| 2 | 1 | Kp = 25, Ti = 50 |
| 3 | 1 | Kp = 55, Ti = 50 |
| 4 | 1 | Kp = 70, Ti = 50 |
| 5 | 2 | Kp = 10, Ti = 50 |
| 6 | 2 | Kp = 25, Ti = 50 |
| 7 | 2 | Kp = 55, Ti = 50 |
| 8 | 2 | Kp = 70, Ti = 50 |
| 9 | 3 | Kp = 10, Ti = 50 |
| 10 | 3 | Kp = 25, Ti = 50 |
| 11 | 3 | Kp = 40, Ti = 50 |
| 12 | 3 | Kp = 55, Ti = 50 |
| 13 | 4 | Kp = 10, Ti = 30 |
| 14 | 4 | Kp = 25, Ti = 30 |
| 15 | 4 | Kp = 40, Ti = 30 |
| 16 | 4 | Kp = 70, Ti = 30 |
| 17 | 5 | Kp = 10, Ti = 50 |
| 18 | 5 | Kp = 25, Ti = 50 |
| 19 | 5 | Kp = 60, Ti = 50 |
| 20 | 5 | Kp = 70, Ti = 50 |
| 21 | 6 | Kp = 10, Ti = 20 |
| 22 | 6 | Kp = 25, Ti = 20 |
| 23 | 6 | Kp = 40, Ti = 20 |
| 24 | 6 | Kp = 55, Ti = 20 |
实验通过1组标准伺服参数的对照组和24组各关节不同异常程度的实验组,验证异常检测方法对“正常-正常”和“正常-异常”检测的鲁棒性及对关节不同异常程度反应的一致性,从而验证异常检测方法的有效性.
4. 实验结果与分析
4.1. 标准信号的预处理
将实验采集到的工业机器人速度和电流信号输入提出的异常检测方法中,以验证该方法的有效性. 对采集到的对照组标准电流信号进行预处理. 先进行滤波,设计截止频率为0.01 Hz的高通滤波器,通过快速傅里叶变换去除电流信号中的低频直流偏移. 根据工业机器人1~6关节速度同时为0的时间索引,将电流信号分割为各关节的完整单周期标准电流信号.
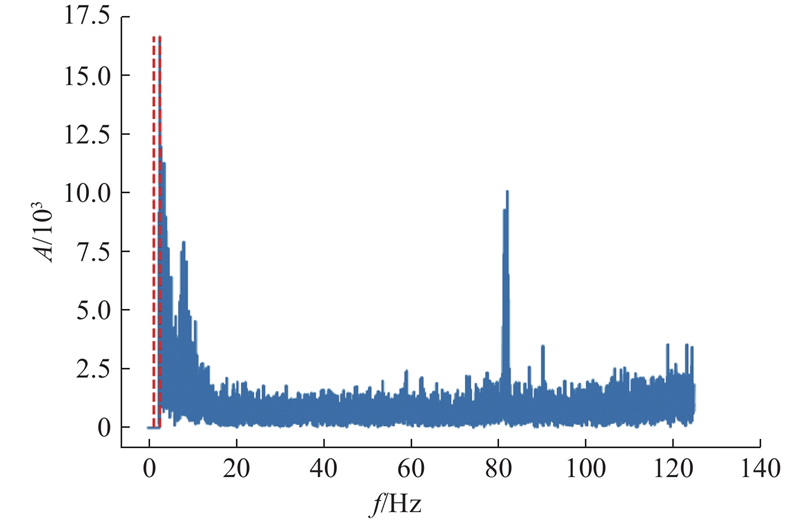
在EWT分解部分,采用N = 3的频带划分对预处理后的电流信号进行分解. 对照组的标准电流信号频带划分结果如图8所示,以关节1为例,其中虚线表示频带划分边界.
图 8
图 8 关节1标准信号的频域预处理
Fig.8 Frequency domain preprocessing of joint 1 standard signal
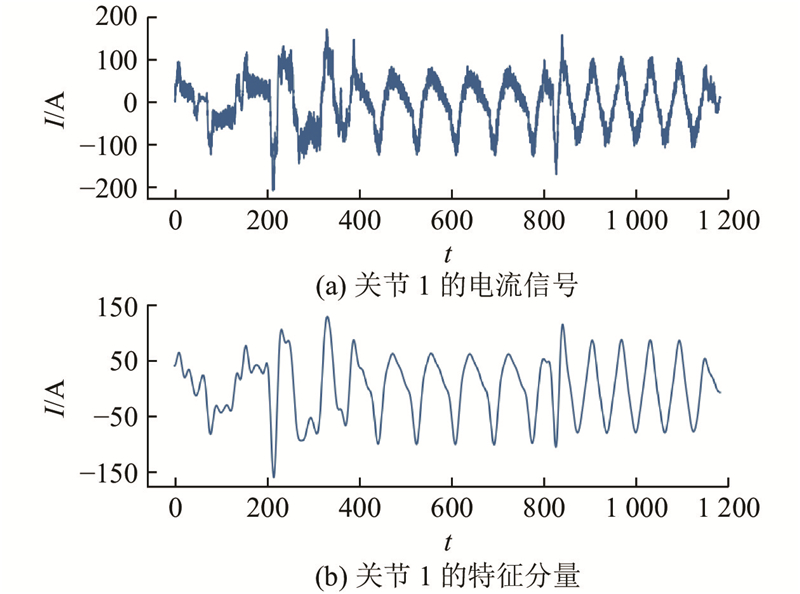
图 9
图 9 关节1标准信号特征分量的提取结果
Fig.9 Extraction result of characteristic component of joint 1 standard signal
通过EWT分解得到的各关节特征分量可以作为标准的完整单周期时间序列,用于后续异常检测中的差异度量.
4.2. CNN-LSTM-Attention模型的评估
为了评估提出模型的性能,采用平均绝对误差(mean absolute error, MAE)、均方根误差(root mean squared error, RMSE)和决定系数R2等统计指标[30]. MAE 是预测值与真实值之间的平均绝对误差,反映误差的实际值. RMSE 是误差平方的平均值的平方根,用于评估预测结果与真实值的偏差程度,常用作回归问题的损失函数. MAE和RMSE反映了预测值与真实值之间的差异,值越小表示预测精度越高. R2反映了模型对数据的拟合程度,R2越接近1,表示模型对数据的解释能力越强.
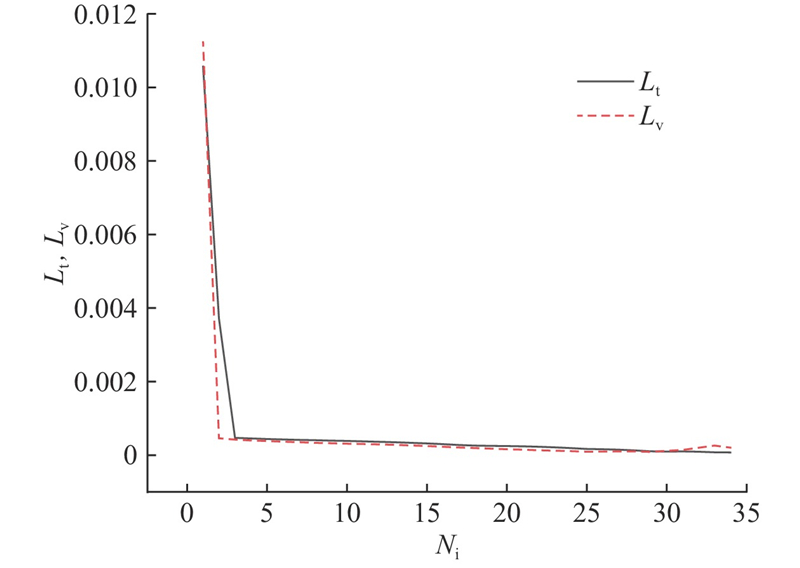
图10中,Lt为训练集损失,Lv为验证集损失,Ni为迭代次数.如图10所示,在模型训练的过程中,训练集和验证集的损失函数都在迅速下降后收敛到较小的值,并在第37个轮次时自动终止训练,防止过拟合. 当训练达到一定轮次时,训练集和验证集的损失差异较小,表明该模型在训练过程中几乎没有出现过拟合,因此该模型对于工业机器人关节电流信号特征分量之间的非线性关系有较好的学习能力,能够较好地提取训练集和验证集数据的有效特征. 在24个不同异常工况的异常数据集和1个标准工况的标准数据集上进行测试. 其中,MAE最小值为0.001 85,最大值为0.011 20,平均值为0.006 91;RMSE最小值为0.002 53,最大值为0.015 06,平均值为0.008 53;R2最小值为0.991 20,最大值为0.999 75,平均值为0.996 62. 该模型在25个不同数据集上均取得较高的精度,表明该模型具有良好的稳定性和泛化能力,适用于工业机器人关节电流信号特征分量时间序列的预测.
图 10
图 10 模型训练过程中的训练和验证损失
Fig.10 Training and validation loss during model training process
目前,用于时间序列预测的方法主要包括基于机器学习的随机森林(random forest, RF)、支持向量回归(support vector regression, SVR)以及基于深度学习的RNN、CNN和LSTM. 针对LSTM模型的优化方法还包括seq2seq、LSTM-Attention和seq2seq-Attention. 为了验证该模型的有效性、泛化能力和优越性,将上述8个模型的结构和参数调整至最佳预测性能,并在工业机器人关节电流信号的25个数据集上采用相同的输入进行预测,用相同的评估指标进行性能评估. 如表5所示为这些模型在25个数据集上6个关节的平均MAE、RMSE和R2结果,本文模型均优于其他8个模型,表明该模型在25个数据集上具有更高的预测精度. 该模型的优势主要在于其结合了CNN提取有效特征的能力、双向LSTM捕捉序列全局信息的优势以及Attention机制动态分配输入权重,以关注序列重要时刻和特征的特点,使得模型具有更好的预测精度. 模型引入Dropout组成多层结构,提升了泛化能力.
表 5 利用时序预测模型预测工业机器人关节信号的评估结果
Tab.5
| 模型 | MAE | RMSE | R2 |
| RF | |||
| SVR | |||
| RNN | |||
| CNN | |||
| LSTM | |||
| seq2seq | |||
| LSTM-Attention | |||
| seq2seq-Attention | |||
| CNN-LSTM-Attention |
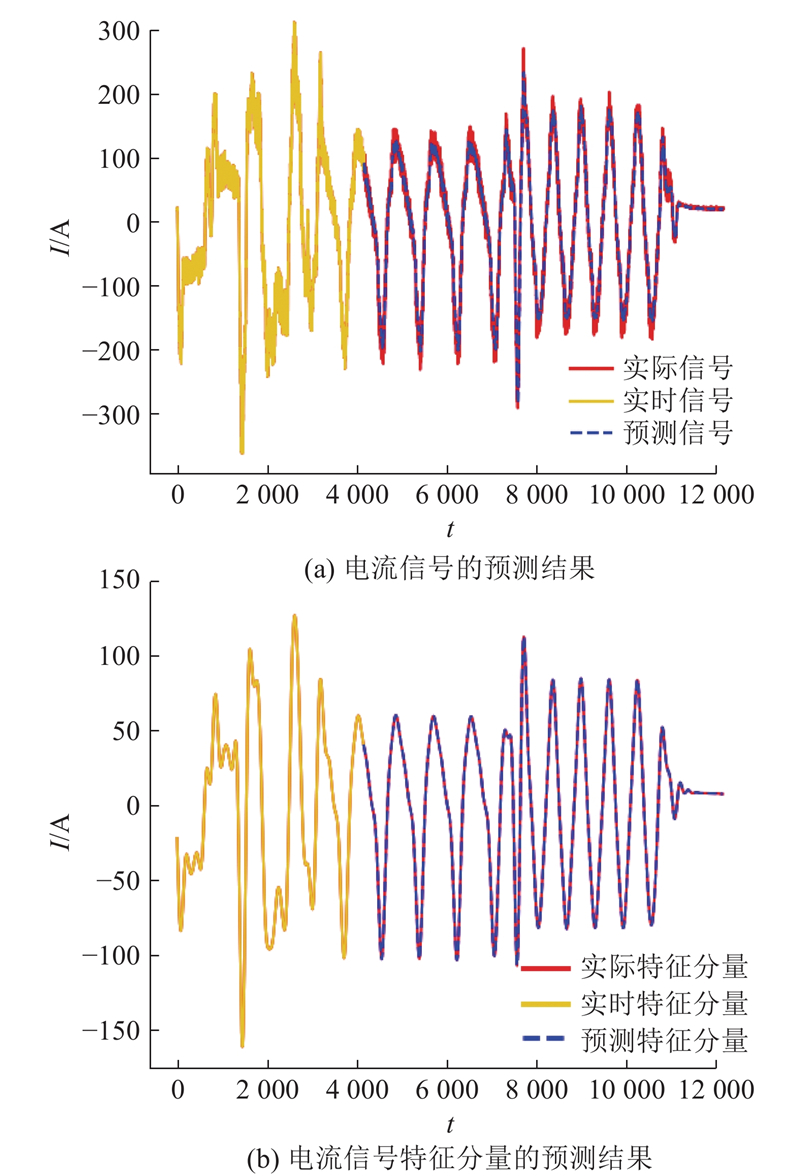
讨论将原始电流信号和EWT提取电流信号中的特征分量分别作为输入对模型预测精度的影响. 以关节1为例,相同数据集使用原始电流信号和EWT提取电流信号特征分量作为模型输入时的预测结果如图11所示. 当使用原始电流信号作为模型输入时,25个数据集上6个关节的平均预测MAE为
图 11
图 11 模型关节1不同输入预测结果的对比
Fig.11 Comparison of prediction result for different input of model joint 1
本文方法在预测前使用EWT提取平滑,能够反映时域特征的电流信号特征分量,显著提升了模型的预测精度. 这对于异常表现不明显的关节伺服参数异常差异度量的准确率提升尤为显著.
4.3. 工业机器人关节实时异常检测
工业机器人关节实时异常检测通过实时数据采集平台采集实时数据,并将其动态存储到智能终端的实时数据库中. 经过信号预处理,获取各关节的实时电流信号特征分量,由服务器上的异常检测算法调用. 通过CNN-LSTM-Attention模型补全实时特征分量的最新周期,计算实时周期与标准周期特征分量的相关系数,以度量相似度,进行异常检测.
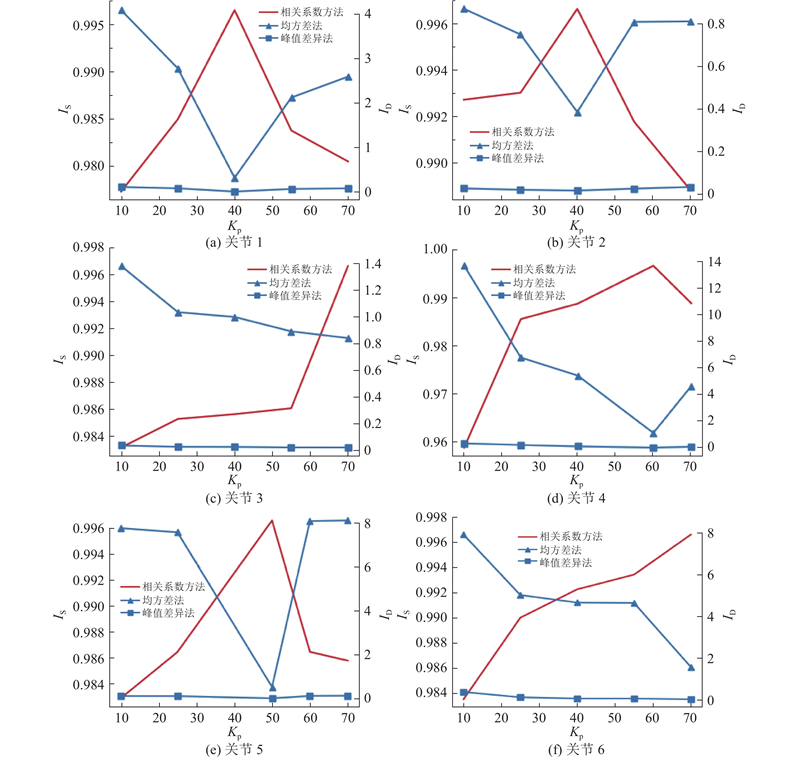
实验采集24组异常注入实验组和1组对照组各3个周期数据,开展异常检测方法的验证. 采用皮尔逊相关系数法进行差异度量,采用均方根差法和峰值差异法进行效果对比. 实验结果如图12所示,其中各关节标准伺服参数Kp分别为40、40、70、60、50和70. 图中,IS为相似度,ID为差异度. 当利用相关系数法、均方差法和峰值差异法检测6个关节的异常程度时,3种方法的结果与Kp的偏离程度有较好的一致性. 随着Kp的偏离,相关系数逐渐减小,均方差和峰值差异逐渐增大,能够反映关节的异常程度.
图 12
图 12 利用3种异常检测方法对工业机器人的6个关节进行异常检测得到的结果
Fig.12 Abnormal detection result of six joints of industrial robot obtained by three abnormal detection methods
对每组数据的3个周期进行异常检测并计算方差D,以验证算法的稳定性. 结果如表6所示,相关系数法和均方差法在同一条件下的连续周期方差较小,不同周期的结果波动小于不同伺服参数的结果波动,表明这2种方法对异常情况的反应是有效、准确的. 当存在接近0的较小峰值时,峰值差异法的结果波动较大,准确率较低.
表 6 工业机器人各关节3个周期异常检测结果的方差
Tab.6
| 关节编号 | D | ||
| 相关系数法 | 峰值差异法 | 均方差法 | |
| 1 | 1.12×10−7 | 3.65 | 6.21×10−4 |
| 2 | 8.35×10−9 | 108.30 | 1.19×10−6 |
| 3 | 3.77×10−9 | 3.10 | 1.97×10−2 |
| 4 | 5.94×10−7 | 14.24 | 1.00×10−1 |
| 5 | 1.28×10−8 | 1.62 | 9.96×10−3 |
| 6 | 3.29×10−8 | 5.26 | 1.39×10−3 |
针对3种方法,分别为6个关节设定最佳准确率的阈值进行异常检测,确定异常与否. 相关系数法的各关节阈值分别为0.986、0.993、0.986、0.989、0.987和0.993;均方差法的阈值分别为2.0、0.6、0.9、4.0、7.0和4.6;峰值差异法的阈值分别为0.050 0、0.014 0、0.021 5、0.080 0、0.110 0和0.050 0. 在对实验采集的25组数据、3个周期、6个关节进行450次异常检测的结果中,相关系数法的准确率为94.2%,均方差法为81.8%,峰值差异法为54.7%. 由于工业机器人关节之间存在耦合,单关节伺服参数异常会导致其他关节信号出现异常,均方差和峰值差异法因依赖绝对距离而受噪点的影响较大,存在较多的误判. 相关系数法着眼于2个时序的整体相似度,对不同幅值和噪点有较好的适应性,能够提供归一化结果. 其90%以上的准确率证明了相关系数法能够有效、稳定地检测关节异常. 采用的相关系数法能够为工业机器人关节提供较高准确率的异常检测.
5. 结 论
(1) 构建无侵入式传感器的工业机器人PLC-智能终端-云服务器一体化的云边协同数据采集平台,实现了边缘端实时速度和电流信号的采集、存储和传输,并在云服务器端进行实时状态监测和异常检测.
(2) 设计基于EWT-LSTM的工业机器人关节实时异常检测算法. 通过EWT分解得到关节时域特征分量,利用光滑的特征分量作为CNN-LSTM-Attention模型的输入,提高模型预测的准确性. 利用该模型,能够预测补全实时信号的最新周期特征分量,并与标准信号特征分量进行差异度量,实现实时异常检测.
(3) 通过对工业机器人6个关节进行4种不同程度的异常注入实验,验证了上述异常检测方法的有效性. 以相关系数作为差异度量指标,实验结果表明,该方法在定位关节异常方面具有较高的准确性和稳定性,且检测结果与关节异常程度具有良好的一致性.
参考文献
Predictive monitoring and control of the cold extrusion process
[J].DOI:10.1016/S0007-8506(07)62970-9 [本文引用: 1]
Early chatter detection in robotic milling under variable robot postures and cutting parameters
[J].DOI:10.1016/j.ymssp.2022.109860 [本文引用: 1]
Towards manufacturing robotics accuracy degradation assessment: a vision-based data-driven implementation
[J].DOI:10.1016/j.rcim.2020.102029 [本文引用: 1]
A non-intrusive approach for fault detection and diagnosis of water distribution systems based on image sensors, audio sensors and an inspection robot
[J].DOI:10.1016/j.enbuild.2021.110967 [本文引用: 1]
Unsupervised anomaly detection of industrial robots using sliding-window convolutional variational autoencoder
[J].DOI:10.1109/ACCESS.2020.2977892 [本文引用: 2]
S, ERDEM O. Robotically assisted active vibration control in milling: a feasibility study
[J].
Quick health assessment for industrial robot health degradation and the supporting advanced sensing development
[J].DOI:10.1016/j.jmsy.2018.04.004 [本文引用: 1]
Recursive least squares and adaptive Kalman filter-based state and parameter estimation for series arc fault detection on DC microgrids
[J].DOI:10.1109/JESTPE.2021.3135409 [本文引用: 1]
On intelligent risk analysis and critical decision of underwater robotic vehicle
[J].DOI:10.1016/j.oceaneng.2017.06.020 [本文引用: 1]
Fault diagnosis for industrial robots based on a combined approach of manifold learning, treelet transform and Naive Bayes
[J].DOI:10.1063/1.5118000 [本文引用: 1]
Multiscale local features learning based on BP neural network for rolling bearing intelligent fault diagnosis
[J].DOI:10.1016/j.measurement.2019.107419
Fault diagnosis of a reconfigurable crawling–rolling robot based on support vector machines
[J].
An improved empirical wavelet transform and its applications in rolling bearing fault diagnosis
[J].DOI:10.3390/app8122352 [本文引用: 2]
基于VMD-ISSA-LSTM的短时交通流预测研究
[J].
Research on short-term traffic flow prediction based on VMD-ISSA-LSTM
[J].
Empirical wavelet transform
[J].DOI:10.1109/TSP.2013.2265222 [本文引用: 1]
用SSA优化CNN-LSTM-SEnet预测模型实现风电机组故障预警
[J].DOI:10.3969/j.ISSN.1672-0792.2024.06.001 [本文引用: 1]
Wind turbine fault warning with SSA optimized CNN-LSTM-SEnet prediction model
[J].DOI:10.3969/j.ISSN.1672-0792.2024.06.001 [本文引用: 1]
盾构机刀盘主驱动电机异常检测与性能评估
[J].DOI:10.7652/xjtuxb202310013 [本文引用: 1]
Abnormal detection and performance evaluation of main drive motor of shield tunneling machine cutter head
[J].DOI:10.7652/xjtuxb202310013 [本文引用: 1]
基于EMD和相关系数法的列车滚动轴承故障诊断方法研究
[J].
Fault diagnosis method for train rolling bearing based on EMD and CCM
[J].
Precise cutterhead torque prediction for shield tunneling machines using a novel hybrid deep neural network
[J].DOI:10.1016/j.ymssp.2020.107386 [本文引用: 1]