管片拼装机是盾构机的关键部件,它将管片拼装到预定位置形成环形. 在盾构施工过程中,管片拼装是影响隧道施工速度和质量的关键因素. 现有的人工拼装方法拼装效率低,劳动强度大,危险性高[1-2]. 因此,亟须发展管片自动拼装技术. 管片拼装成功时相邻管片间距小于1 cm,对各机构的运动控制精度要求较高. 在管片拼装中平移运动会带动整个拼装机和管片一起做平移运动,因此在管片拼装过程中平移运动直接影响其他机构的精度和最后的管片拼装精度. 平移运动负载过大,因此非线性摩擦阻力过大,在平移运动过程中,液压缸会存在明显爬行现象,严重影响管片的控制和拼装精度,甚至造成安全隐患. 在管片自动拼装过程中,平移油缸的精确控制是管片拼装成功的重要保证.
精确控制方法有鲁棒控制、自适应控制、智能控制等,但考虑工程经济性及快速性和工程中工控机的配置,且大多先进控制算法需要精确的模型参数,但大型液压系统滞后大、摩擦扰动大,参数实时可变,很难精确建模. 闭环控制系统通常采用比例积分微分(proportion integration differentiation,PID)控制器. 通常,PID控制器增益参数是使用试错技术确定的,然而,在结构更为复杂的系统中,使用传统方法寻找PID增益参数是具有挑战性的. 因此,研究者将不同的方法结合起来开发PID控制器,包括分数阶PID (FOPID)[10-12]、二阶导数PID (PIDD2)[13-14]、智能PID(iPID)[15-17]、非线性校正PID[18]和神经网络PID[19-20]等.
本研究目的在于通过参数辨识得到的精确模型和设计的iPIDD2控制方法实现自动管片拼装机平移运动电液系统精确控制. 由于输入-输出信号的质量直接决定模型参数辨识的精确性,而输出信号含有大量外部干扰噪声. 通过设计的信号预处理方法,降低信号噪声,提高辨识结果的准确性. 为了更准确地辨识出模型的关键参数,采用带遗忘因子的偏差补偿递推最小二乘辨识算法. 针对在拼装过程中平移系统存在较大的摩擦,通过卡尔曼滤波和ESO (extended state observer)的方法补偿扰动,使得控制结果更精确. 为了实现平移系统的精确控制,设计iPIDD2方法,通过MATLAB/Simulink和AMESim联合仿真和全尺寸实验台测试验证上述方法的有效性.
1. 系统建模
1.1. 系统介绍
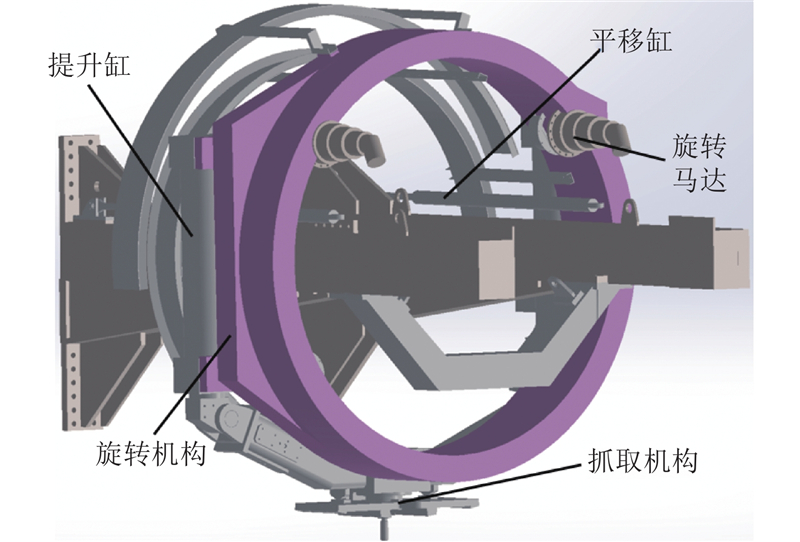
系统模型基于6 m级土压平衡盾构管片拼装机平移运动系统. 如图1所示,管片拼装机包括回转机构、提升机构、平移机构、摇摆机构和俯仰机构,实现6个自由度的无干涉拼装动作.
图 1
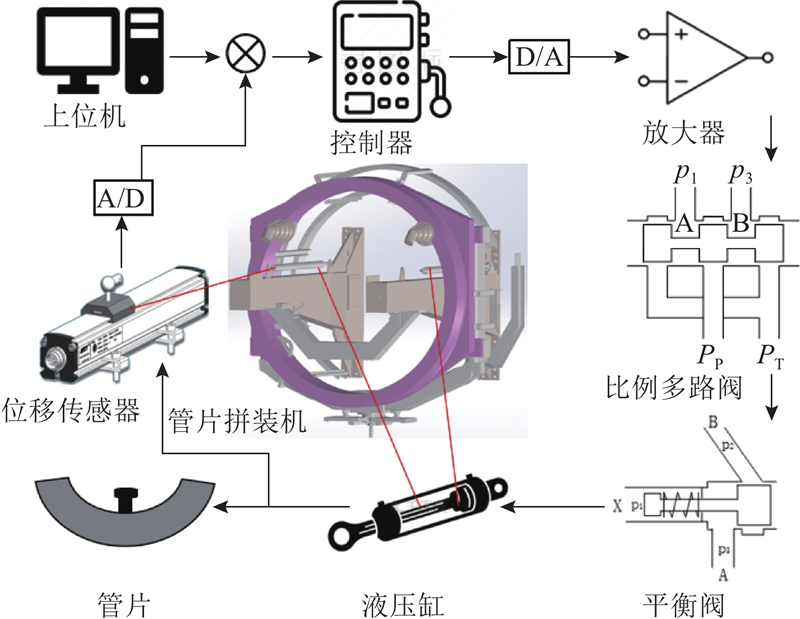
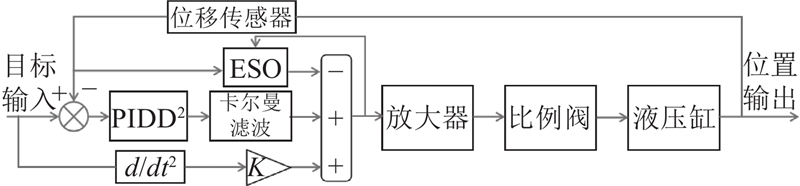
工作装置系统的基本液压回路如图2所示,液压系统主要包括液压缸、放大器、平衡阀、比例多路阀. 系统可以分为4部分:由计算机向控制器产生控制信号;电压控制信号由放大器转换成能够控制多路阀的电流信号;多路阀阀芯根据控制输出的电流信号移动;液压缸根据多路阀调节的油液压力进行伸缩. 此外,位移传感器为磁致伸缩位移传感器,被安装在油缸的侧面,将位移信号实时反馈给控制器.
图 2
图 2 平移机构电液系统原理图
Fig.2 Schematic diagram of electro-hydraulic system of translation mechanism
1.2. 平移机构电液比例系统模型
在进行建模之前,先假定管道中不会出现压力损失的情况,液压缸中所有工作腔中的压力都是均等的,并且体积弹性模量和油温为常数. 液压缸的内部泄露主要表现为层流动,向外并没有出现泄露.
1.2.1. 液压缸数学模型
按照负载和液压动力平衡方程可得
式中:
液压缸体积流量连续方程为
式中:
经过拉氏变换后得到
式中:
1.2.2. 比例调速阀数学模型
通过如下公式对从电液比例调速阀节流口流过的体积流量进行计算:
式中:Cd为阀的泄漏系数.
式中:
对其进行拉氏变换后得到
1.2.3. 比例阀控制液压缸数学模型
液压缸无杆腔输出位移如下:
式中:
当
系统的开环传递函数为
式中:
2. 参数辨识
2.1. 辨识信号预处理
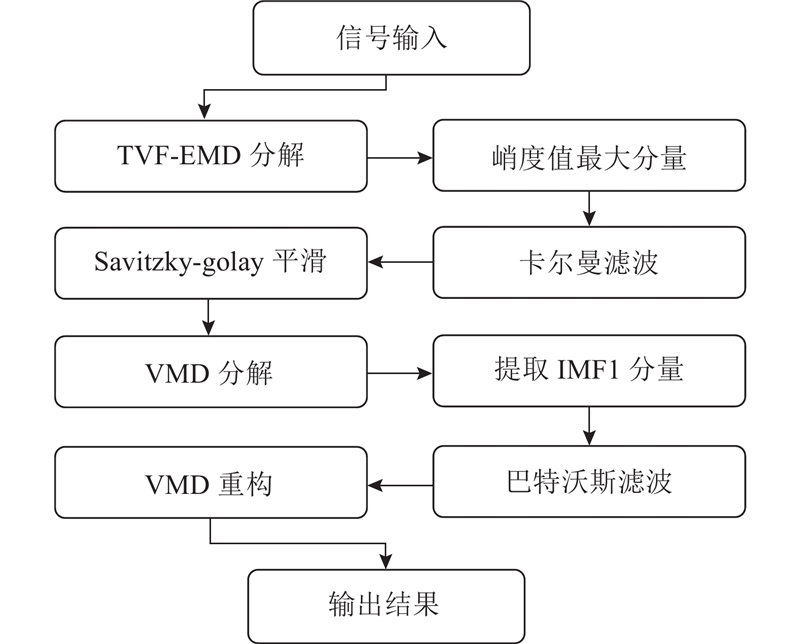
信号预处理是参数辨识不可或缺的前提,它直接影响到辨识结果. 如图3所示为本研究的信号预处理方法流程图.
图 3
时变滤波经验模态分解(time varying filtering-empirical mode decomposition, TVF-EMD)方法采用时变滤波器来解决模态混叠问题,以保持序列的时变性. 该方法充分利用瞬时幅值和瞬时频率,自适应地设计了局部截止频率,对给定序列进行时变滤波,并将其分为局部高频分量和局部低频分量,以得到固有模态函数(intrinsic mode function, IMF).
2.2. 带遗忘因子的偏差补偿递推最小二乘辨识算法
从上面的建模过程可以看出,数学模型中的参数几乎与拼装机的结构、运行状态和姿态有关. 由于难以获得准确的数值,模型中的关键参数都是估计出来的.
根据第1章中的模型,将系统模型定义为三阶,其离散差分方程为
式中:
写为最小二乘形式:
系统参数向量的估计误差准则函数表达式为
式中:
系统带遗忘因子得最小二乘估计为
通过矩阵推算及归纳,可得带遗忘因子的偏差补偿递推最小二乘估计:
式中:
3. 控制设计
3.1. PIDD2
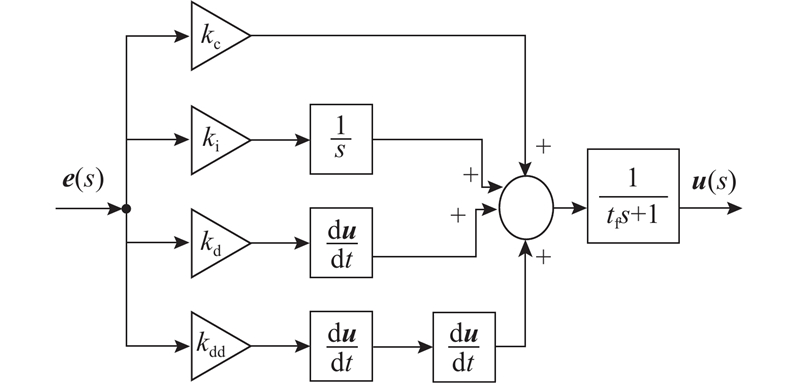
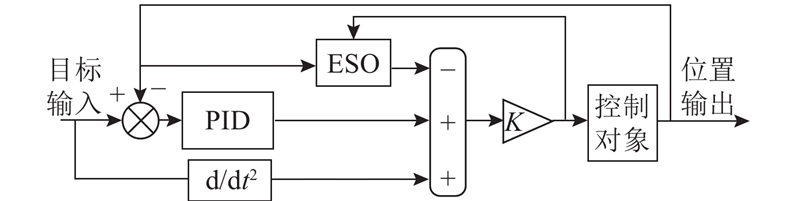
比例-积分-微分是经常用的控制方法,其原理简单,性能可靠,适用面广,为各领域的控制工程师所青睐. 为了获得极限性能,有时希望在比例、积分、微分之外,进一步提取并利用输出的二阶微分信息,这就是所谓的比例-积分-微分-二阶微分(PIDD2). 通过PIDD2 作为主控制器实现精确控制,如图4所示.
图 4
表达式如下:
式中:
3.2. iPID
iPID控制器为PID控制器,其中不考虑系统的未知部分建模过程,如图5所示. 它基于一个局部模型,通过系统的输入输出信息不断更新. 因此,未知的“复杂”数学模型被超局部模型所取代.
图 5
模型定义如下:
式中:
控制输入定义为
式中:
状态空间表达形式如下:
扩展状态观测器设计表达式如下:
式中:
观测器的状态误差可以定义为
式中:
稳定性证明参照文献[17], 文献通过自定义的Lyapunov方程证明了稳定性.
3.3. iPIDD2
如图6所示为iPIDD2控制算法示意图. 在iPID的基础上将PID模块换成PIDD2,为了减少其带来的增益过大和噪声,增加了卡尔曼滤波. iPID原有的ESO模块较好地减少了摩擦扰动和未知扰动.
图 6
由式(18)、(21)可得,控制输入定义为
iPIDD2控制器的主要优点概括如下: 1)不需要系统模型或任何关于系统的知识,可以方便地应用于各种高度非线性或时变的复杂系统;2)除了具有PID控制的所有优点外,由于消除了模型的未知部分,增益的整定是直接的;3)能提高控制器响应的快速性与鲁棒性;4)与许多其他无模型控制方法不同,iPIDD2控制不需要大数据集和复杂算法来建模系统行为.
4. 仿真研究
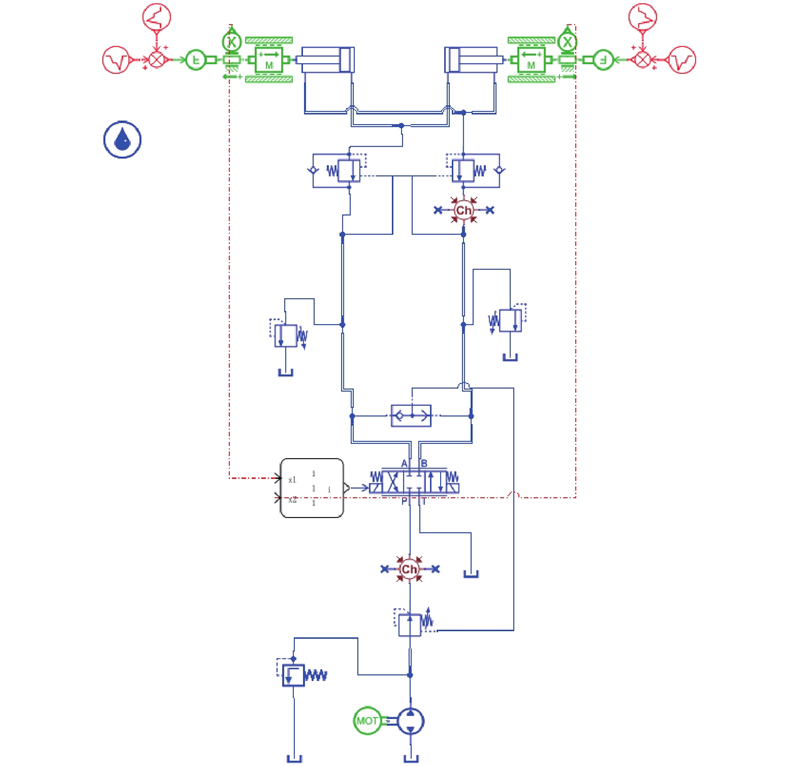
4.1. 液压系统AMESim模型
图 7
图 7 平移液压系统AMESim仿真模型
Fig.7 Simulation model of translation hydraulic system AMESim
表 1 平移系统仿真模型参数
Tab.1
| 参数 | 数值 |
| 活塞直径/mm | 80 |
| 杆直径/ mm | 50 |
| 油缸行程/ m | 2 |
| 负载/ kg | 11 000 |
| 黏性摩擦系数/ (N·m−1·s) | 3 000 |
| 库伦摩擦力/ N | 20 000 |
| 静摩擦力/ N | 22 000 |
4.2. 仿真控制
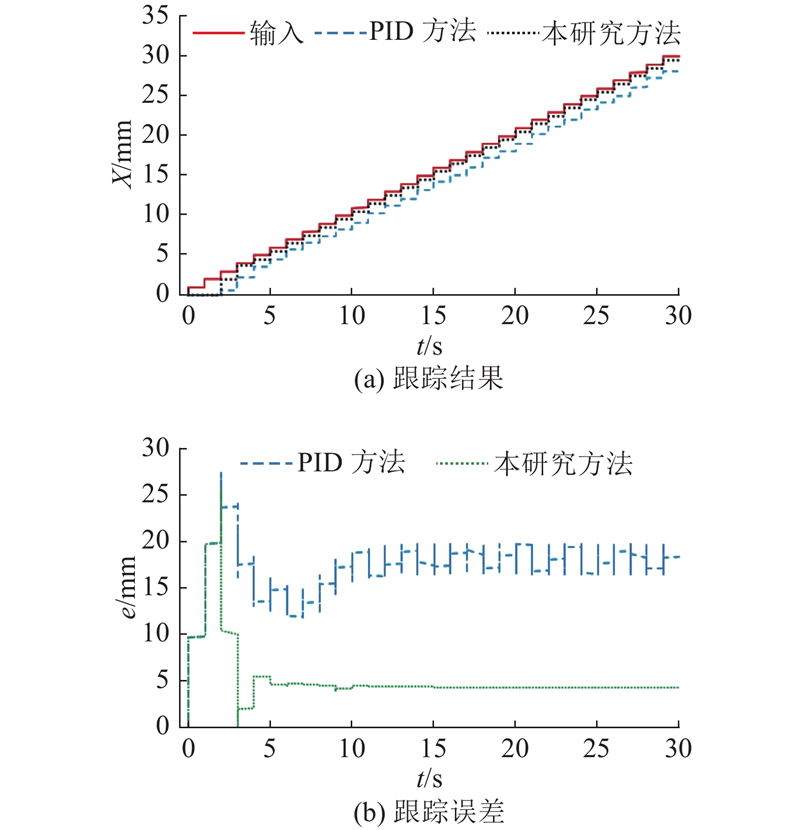
通过联合仿真,对平移运动精确控制进行仿真,验证本研究控制方法的有效性. 控制方法中kc=−0.2, ki=
图 8
图 8 本研究控制方法和PID控制方法的位移跟踪结果及跟踪误差
Fig.8 Displacement tracking results and tracking error of proposed control method and PID control method
5. 实验研究
图 9
表 2 智能管片拼装机全尺寸实验台参数
Tab.2
| 参数 | 数值 | 参数 | 数值 | |
| 转动范围/(°) | ±220 | 管片外径/m | 6 | |
| 举升行程/m | 0.8~1.2 | 轴向移动/(mm·s−1) | 80.0 (最大速度) | |
| 平移行程/m | 1.2~2.1 | 旋转移动/(r·min−1) | 0~1.5 | |
| 微调转角(α、β、γ)/(°) | ±2.5 | 提升移动/(mm·s−1) | 13.3 (最大速度) |
表 3 实验台传感器及参数
Tab.3
| 传感器 | 品牌型号 | 主要参数 |
| 深度相机 | Intel Realsense D435i | RGB 分辨率: 深度分辨率: |
| 控制器 | 西门子 S7-300 | 位内存: |
| 磁致伸缩位移传感器 | 北京特倍福 | 测量范围:TH25 ~7 650 mm,精度:0.02% |
| 拉线式位移传感器 | 北京特倍福 | 测量范围:0~1 000 mm,精度:±0.2%F.S. |
| 编码器 | 宜科 | 最大转速: |
智能拼装机利用识别和定位技术、运动学运动分解、轨迹规划、运动控制等技术替代人工实现管片自动拼装. 智能拼装大概流程如下:在管片拼装过程中,通过深度视觉获得待拼装管片和已拼装管片的位置;采用RGB-D(red, green, blue-depth)方法,在深度测距后通过坐标变换获得特征点相对于相机坐标系的坐标;通过陀螺仪和加速度计实时获取相机相对于世界坐标系的坐标;通过手眼标定实现对管片图像的识别和定位;通过Denavit-Hartenberg(D-H)法运动分解后,得到各执行机构须运动的位移;最后,通过拼装机各机构安装的位移传感器和控制算法实现对拼装机各机构的闭环精确控制,完成管片的自动拼装.
5.1. 信号预处理
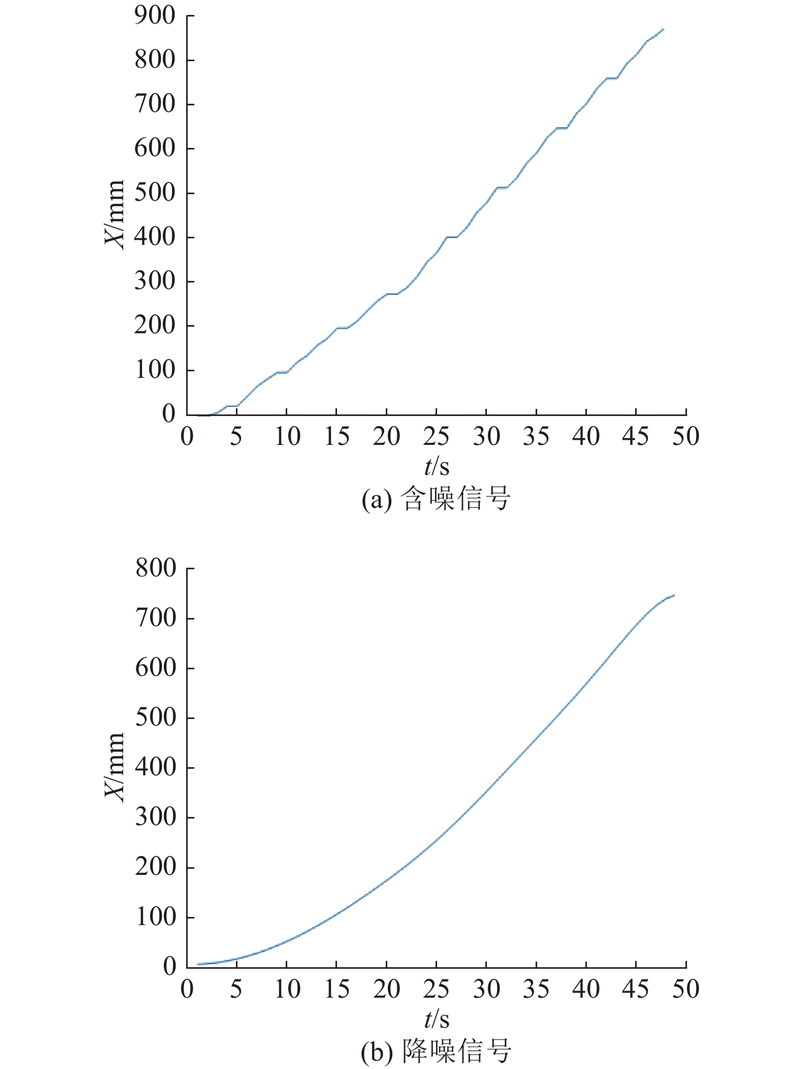
全尺寸实验台液压缸在空载情况下平稳运动一段位移,通过位移传感器采集到实验台平移液压缸的位移信号. 用本研究方法进行预处理,从而得到去噪后的信号,如图10所示. 从结果可以看出,降噪效果较好,为后续辨识的准确性提供了良好的条件.
图 10
图 10 平移油缸位移信号预处理
Fig.10 Preprocessing of translation cylinder displacement signal
5.2. 系统辨识
通过系统辨识获取AMESim仿真的一些关键参数. 为了防止实验台损坏和发生危险,实验测试前用辨识出的系统数学模型搭建Simulink用于预调参.
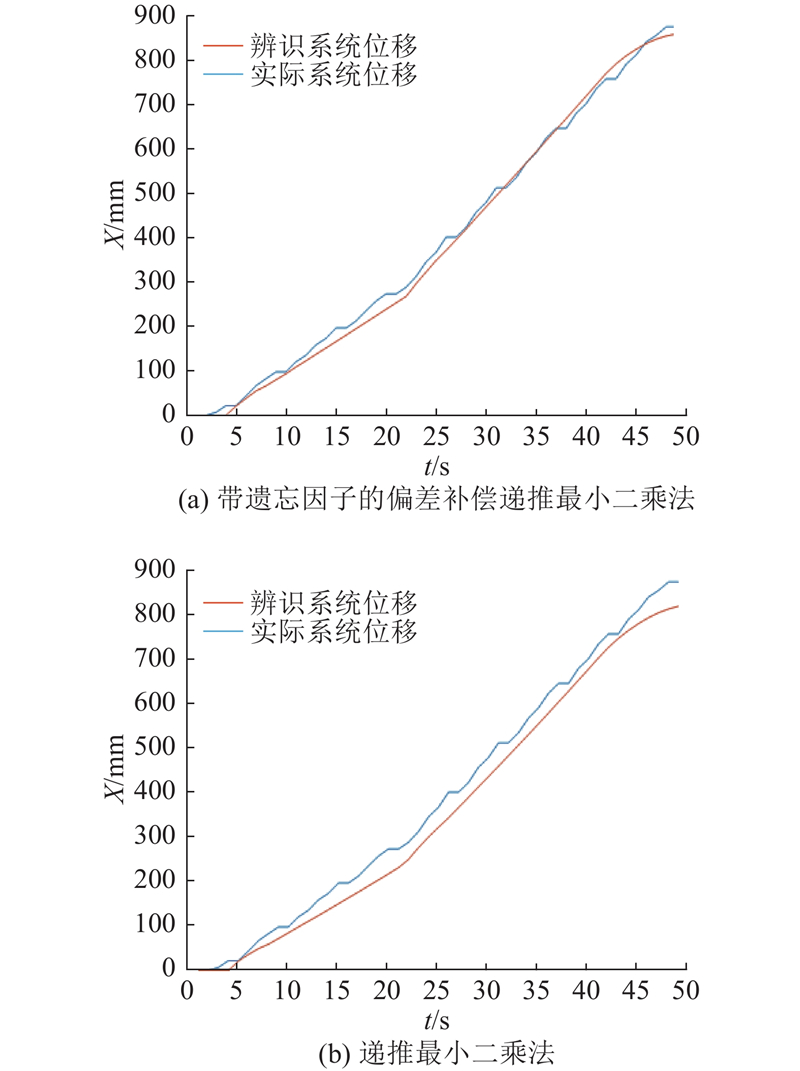
如图11所示为实验台平移液压系统不同方法系统辨识结果. 图中,蓝色实线为实际位移曲线,红色实线为辨识后的系统位移曲线. 带遗忘因子的偏差补偿递推最小二乘法辨识结果的RMSE为539.051,递推最小二乘法辨识结果的RMSE为506.203. 通过主观和客观分析可以看出,本研究估计方法比其他方法更准确,更加接近实际系统.
图 11
图 11 实验台平移液压系统不同方法的系统辨识结果
Fig.11 System identification results of different methods for translation hydraulic system of experimental bench
5.3. 平移运动精确控制
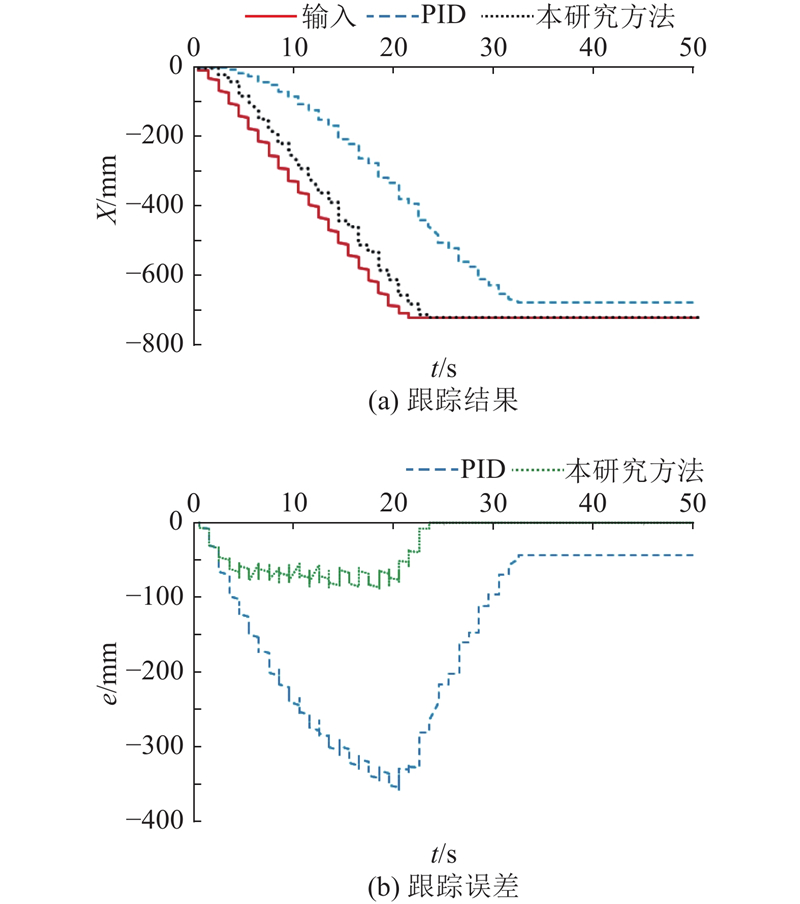
在管片抓取过程中,拼装机是空载的,因此下面是空载-大位移下拼装机平移液压缸的控制效果. 给定的信号按照实际的施工过程:先加速、再匀速、后减速的控制过程.
图 12
图 12 空载工况下本研究控制方法和PID控制方法的位移跟踪结果及跟踪误差
Fig.12 Displacement tracking results and displacement tracking error of proposed control method and PID control method obtained under no-load condition
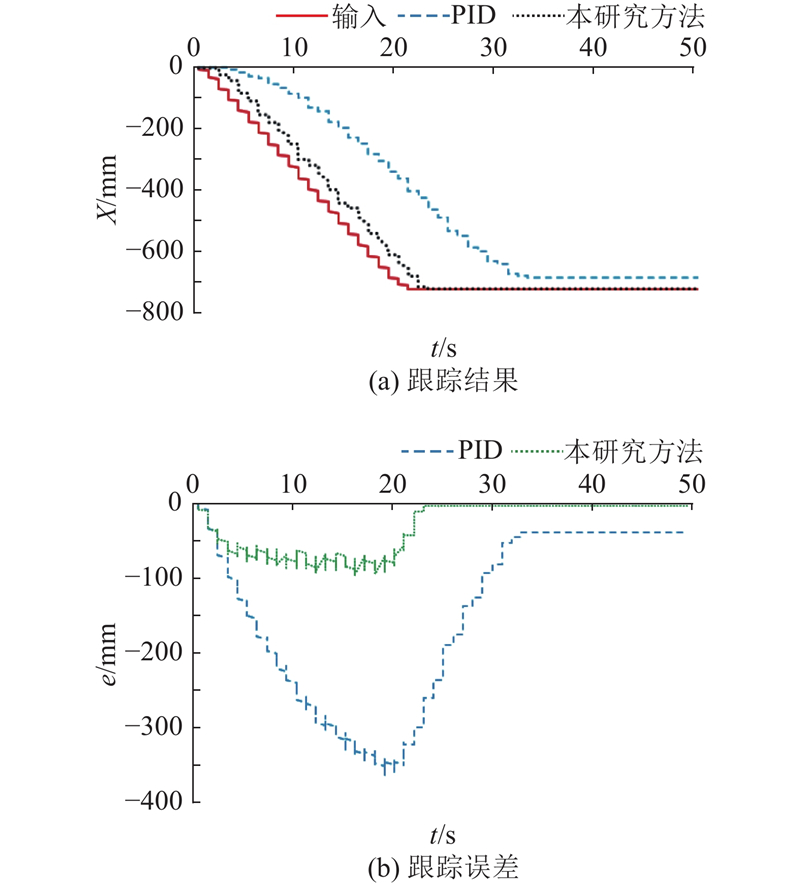
在管片拼装过程中,拼装机是负载的,因此下面是负载-大位移下拼装机平移液压缸的控制效果. 给定的信号按照实际的施工过程. 先加速,再匀速,后减速的控制过程.
图 13
图 13 负载工况下本研究控制方法和PID控制方法的位移跟踪结果及跟踪误差
Fig.13 Displacement tracking results and tracking error of proposed control method and PID control method under load condition
6. 结 语
设计iPIDD2控制方法,该方法集成了观测器,可实现对具有不确定参数和摩擦扰动的平移运动电液系统的精确控制. 采用理论分析、模型辨识、仿真优化和对比试验等一系列方法,重点分析基于PID和本研究算法的液压缸位移控制精度. 联合仿真结果表明,通过模型识别获得的平移机构传递函数具有较高的精度. 设计的控制算法兼顾了响应速度和控制精度,其控制性能优于PID算法的. 此外,还在空载、标准片(3 t)负载下进行了平移控制实验. 实验数据表明,与PID相比,本研究方法响应速度更快,稳态误差更小,最终误差小于3 mm. 本研究结果对提高摩擦扰动下自动管片拼装的拼装精度和效率具有积极意义.
本研究所提控制方法无法解决死区问题,同时控制精度有待进一步提高.
参考文献
Refined modeling method and analysis of an electromagnetic direct-drive hydrostatic actuation system
[J].
Master cylinder pressure estimation of the electro-hydraulic brake system based on modeling and fusion of the friction character and the pressure-position character
[J].
Automation of friction torque identification for vane-type semi-rotary pneumatic actuators
[J].
Establishment and experimental verification of a nonlinear position servo system model for a magnetically coupled rodless cylinder
[J].
Identification and compensation of non-linear friction for a electro-hydraulic system
[J].DOI:10.1016/j.mechmachtheory.2019.07.004 [本文引用: 1]
Constraint performance pressure tracking control with asymmetric continuous friction compensation for booster based brake-by-wire system
[J].
Research on adaptive friction compensation of digital hydraulic cylinder based on LuGre friction model
[J].
Actuation of an electrohydraulic manipulator with a novel feedforward compensation scheme and PID feedback in servo-proportional valves
[J].
Performance improvement of aircraft pitch angle control using a new reduced order fractionalized PID controller
[J].
Enhancing transient response performance of automatic voltage regulator system by using a novel control design strategy
[J].DOI:10.1007/s00202-023-01777-8 [本文引用: 1]
Decentralized load-frequency controller design for a single as well as multi-area power system
[J].DOI:10.1007/s40998-019-00246-y [本文引用: 1]
Intelligent PID control of an industrial electro-hydraulic system
[J].DOI:10.1016/j.isatra.2023.04.005 [本文引用: 1]
Intelligent-PID with PD feedforward trajectory tracking control of an autonomous underwater vehicle
[J].
Model-free controller design for nonlinear underactuated systems with uncertainties and disturbances by using extended state observer based chattering-free sliding mode control
[J].DOI:10.1109/ACCESS.2023.3234864 [本文引用: 2]
Research on stability of hydraulic system based on nonlinear PID control
[J].DOI:10.1515/nleng-2022-0222 [本文引用: 1]
Multi-motor cooperative control strategy for speed synchronous control of construction platform
[J].
Adaptive PI and RBFNN PID current decoupling controller for permanent magnet synchronous motor drives: hardware-validated results
[J].
自适应改进双树复小波变换的齿轮箱故障诊断
[J].
Gearbox fault diagnosis based on adaptive modified dual-tree complex wavelet transform
[J].
改进双树复小波变换和高阶累积量的齿轮箱信号降噪方法
[J].
Gearbox signal denoising method based on improved double tree complex wavelet transform and higher order cumulant
[J].