目标跟踪包括单目标与多目标跟踪,其中密集杂波环境下数据有效关联是多目标跟踪问题研究的关键. 数据关联的目的是实现相关波门内各候选回波与已知航迹的匹配. 经典的单一传感器数据关联方法主要包括最近邻域法[5]、概率密度数据关联(probability data association, PDA)[6]、联合概率数据关联[7-9]、多假设追踪[10-11]等. 其中,PDA适用于稀疏环境下单目标跟踪,通过对落入波门内的各个候选回波进行组合加权,得到一个等效回波,再利用该等效回波对目标状态进行更新. 当回波落入波门相交区域时,数据关联问题将变得复杂许多,须考虑各个回波的来源情况. 联合概率数据关联(joint probability data association, JPDA)通过计算各有效回波与其可能的源目标相关联的概率来解决多目标数据关联问题,再利用关联概率对当前点迹进行加权平均进而修正航迹,不过当目标较为密集或回波密度较大时,该算法计算量剧增,甚至会出现“组合爆炸”的问题. 为了表示有效回波与各目标跟踪门的复杂关系,Bar-Shalom引入确认矩阵的概念[12]. 进一步,为了提高JPDA算法的实时性,多种次优算法相继被提出. 改进思路主要集中在:1)对确认矩阵进行降维处理,如文献[7]先通过Cheap JPDA来计算关联概率,再通过阈值处理方法对聚概率矩阵进行重构,以降低优化算法复杂度;2)间接计算关联概率,如文献[13] 采用最大熵模糊聚类方法来间接计算目标与量测之间的关联概率,较好地解决了JPDA算法随着目标数、回波数的增加计算量呈指数趋势增长的组合问题.
多源数据融合[4]是多信源、多层次的处理过程. 按照融合系统结构来分,主要分为集中式、分布式、混合式. 按照融合的层级来分,又分为数据级融合、特征级融合、决策级融合. 按照处理方法来分,基本上可以概括为概率统计类、人工智能类. 在面向智能驾驶的多源数据关联与融合系统中,车侧或路侧各类传感器所提供的多源信息往往是不同时空、不同维度、不同数据结构的,因此,如何提高源自各传感器的量测数据关联的可靠程度,如何对时空上互补或冗余的信息进行多方位、多层次的优化处理,以提高信息的综合利用效率,都是非常值得研究与探讨的问题.
为了实现多源传感器量测数据的有效关联与车辆安全跟随,提出多目标车辆跟踪算法与纵向避撞预警策略. 针对多源传感器观测序列的时间异步、空间不同维度不同坐标系的问题,给出时间配准与空间融合方法;采用改进的JPDA多目标状态估计算法对目标轨迹进行滤波估计,降低计算复杂度,并采用序贯滤波设计,增强融合感知的鲁棒性;综合车辆跟驰过程中的诸多实际因素,设计威胁估计模型;通过实车试验对该算法的跟踪效果进行验证与探讨.
1. 多源异构传感器多目标观测模型
1.1. 数学建模
在多车道多目标车辆跟踪(multi-lane multi-vehicle tracking, ML-MVT)过程中,感兴趣目标(object of interest, OOI)是位于本车道与邻车道且离本车最近的前方目标车辆,这是由于其相对自车来说,危险系数较高,引发车辆追尾的隐患相对较大.
1.1.1. 状态方程
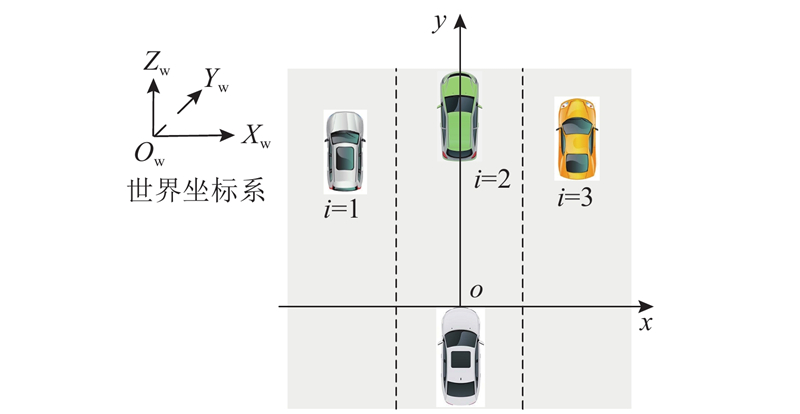
如图1所示为ML-MVT问题的坐标系建立. 假设雷达坐标系与世界坐标系的二维水平面平行,并忽略目标车辆的法向运动. 令第i个目标车辆k时刻的纵向距离为
图 1
图 1 多车道多目标车辆跟踪问题的坐标系建立
Fig.1 Coordinate system for multi-lane multi-vehicle tracking
式中:下标i表示第i个目标车辆,上标
1.1.2. 模型参数
采用毫米波雷达与单目视觉数据融合的技术方案. 在多目标观测模型中,下标
兼顾目标的机动特性与本地实时计算的需求,给出在线可调的匀速运动(tunable constant velocity, TCV)模型,即定义目标运动模型为匀速运动(constant velocity, CV)模型,并通过雷达量测数据动态校正传统CV模型中机动目标的速度. 假设过程噪声
式中:
1.2. 时间同步
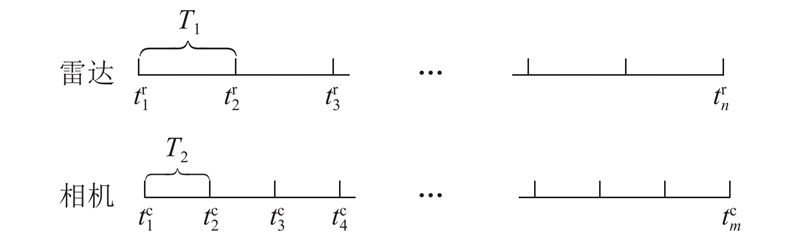
毫米波雷达采样周期约为60 ms,相机采样周期约为33 ms,两者的采样序列示意如图2所示,图中,
图 2
考虑到时间配准精度、实时性以及应用场景,选取内插外推的方法进行时间配准. 以x轴为例,将相机的采样序列配准至雷达的采样时刻上,时间配准公式如下:
式中:
1.3. 空间配准
前文假设雷达坐标系与世界坐标系的二维水平面是平行的,这样仅须建立相机像素坐标系与世界坐标系的映射关系.
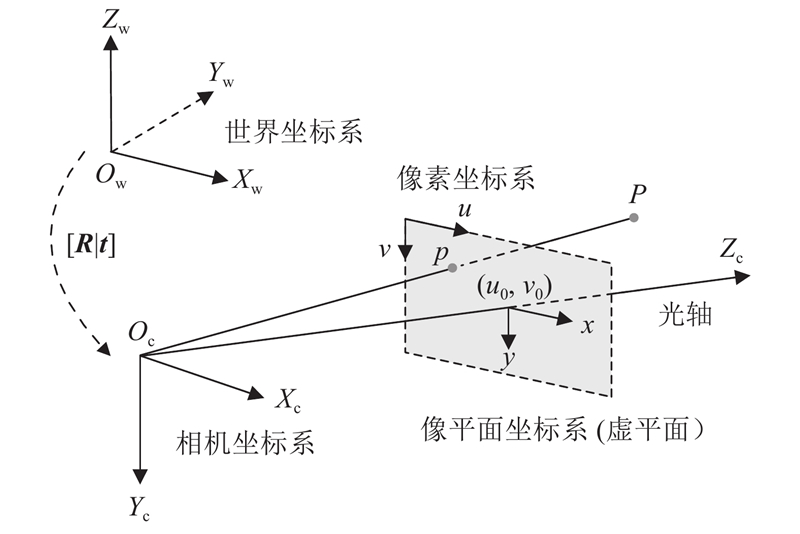
如图3所示,三维世界点P与其在像平面上投影点p的关系满足
图 3
图 3 相机像素坐标系与世界坐标系的映射关系
Fig.3 Relationship between camera pixel coordinate system and world coordinate system
式中:
2. 多源异构传感器融合估计
2.1. 数据关联
数据关联是将源自单个或多个传感器的量测数据与相应的确定轨迹进行关联的过程. 该过程主要分2步,首先是有效量测数据的筛选,接着是将当前有效量测数据匹配到最佳的目标序列上.
2.1.1. 定义
定义1 马氏距离(Mahalanobis distance).
马氏距离是由印度统计学家Mahalanobis提出的,用于计算2个未知样本集相似度. 为了弱化不同特征数据之间量纲的影响,定义模型预测与实际量测之间的马氏距离为
式中:
定义2 有效观测集.
式中:
定义3 观测确认矩阵.
定义1、2能够为判断量测是否落入目标的跟踪门内提供量化依据. 在某个采样周期内,将
式中:
定义4 目标关联概率.
对于量测落入跟踪门相交区域的情形,即某些量测可能源自于多个目标,这里定义目标关联概率,用以表示不确定性量测与其可能的源目标的关联程度.
假设如下:1)每个量测只能源自于一个目标或杂波;2)每个目标最多只能产生一个回波. 这样,式(7)表示的联合事件将被拆分成多个不相关的可行关联事件的组合.
定义目标关联概率为
式中:
2.1.2. 关联流程
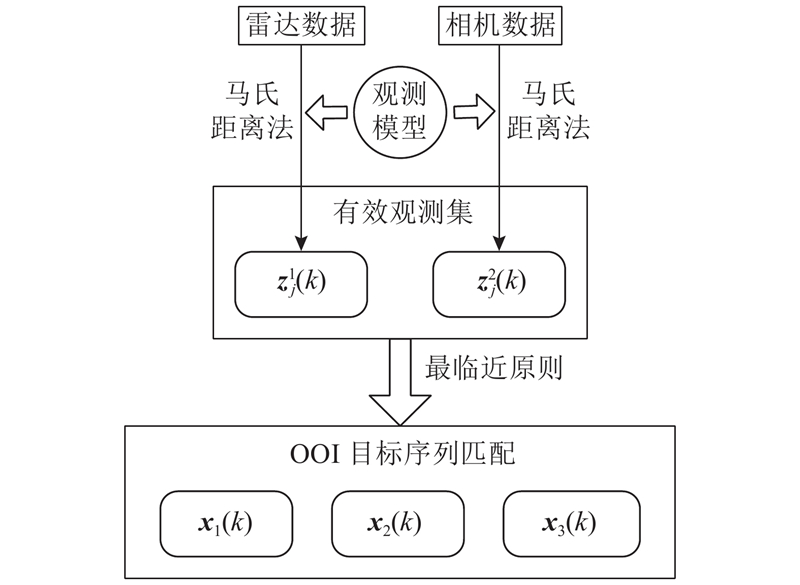
数据关联的流程如图4所示. 图中,
图 4
当有新的机动目标进入观测视野时,根据最临近原则,距离本车最近的目标所构成的威胁较为明显,从而更新OOI目标序列,否则维持当前OOI目标序列. 当机动目标超出雷达的观测范围或连续数个周期内皆无有效量测时,舍弃该目标.
2.2. 融合估计算法
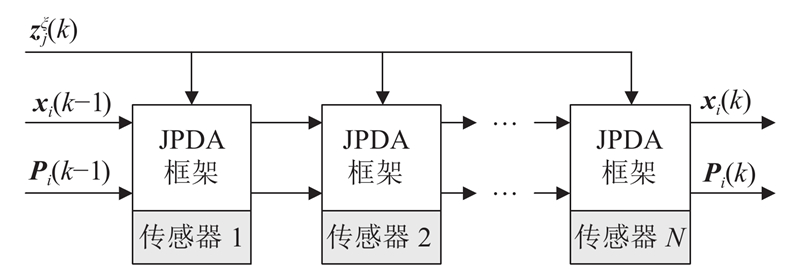
2.2.1. 单一传感器多目标状态估计
对于单一传感器,忽略标识符
1)时间更新过程.
式中:
2)关联概率更新过程.
根据式(6)所示的跟踪门规则生成确认矩阵,接着将其拆分成Lk个可行矩阵,再根据式(8)对关联概率进行更新.
3)量测更新过程.
式中:
2.2.2. 多源传感器数据融合
表 1 常用的数据融合方法比较
Tab.1
| 类别 | 融合方法 | 不确定性 | 融合层次 |
| 概率统计类 | 加权平均法 | — | 低层次 |
| 卡尔曼滤波法 | 高斯噪声 | 低层次 | |
| 贝叶斯估计法 | 高斯噪声 | 低层次 | |
| 产生式规则 | 置信因子 | 高层次 | |
| 人工智能类 | 模糊推理 | 隶属度 | 高层次 |
| 神经网络 | 学习误差 | 低或高 |
图 5
2.2.3. 算法改进
在JPDA数据关联过程中,对观测确认矩阵
由于关联概率较大的可行关联事件会在跟踪过程中起主导作用[7],设计一个参考阈值,用来忽略关联概率接近于0的事件,以实现对确认矩阵的稀疏化处理,进而减少可行联合事件的拆分次数. 对如式(7)所示的确认矩阵进行重构:
式中:
此外,考虑到传感器本身的局限性,为了避免有效目标短暂丢失、邻道车辆干扰、量测噪声等扰动因素的影响,在JPDA关联过程中增加有效目标的存续性判定策略. 判定策略如下:于某个跟踪目标i,
3. 纵向避撞预警策略
现役的纵向避撞预警模块容易受到横向扰动、目标关联可靠性、传感器局限性等因素的影响,虚警现象较明显. 此外,未能充分考虑不同驾驶群体的跟驰习惯[1] ,在友好性设计方面存在不足.
3.1. 威胁估计模型
基于前期研究成果[1],采用实际跟车车距、制动减速度、应急反应时间来量化驾驶群体的行为特征,并通过AI学习方法对不同驾驶群体的跟驰习惯进行学习以实现对TEM模型参数进行在线更新.
3.2. 分级预警策略
结合MSJPDA状态估计与TEM威胁估计模型,对追尾危险的发展态势进行评估与分级,并辅以相应的预警措施,更加符合人体工程学方法论,能够一定程度上改善驾乘体验. 分级预警策略如下. 比较MSJPDA状态估计结果
4. 仿真验证
图 6
表 2 雷达与相机的主要参数
Tab.2
| 传感器 | 参数 | 数值 | |
| 毫米波 雷达 | 型号 | 大陆ARS 408-21 | |
| 载波频率/ GHz | 77 | ||
| 长距模式 | 最大测距/m | 250 | |
| 量测精度/m | ±0.4 | ||
| 水平角/(°) | ±9 | ||
| 短距模式 | 最大测距/m | 70 | |
| 量测精度/m | ±0.1 | ||
| 水平角/(°) | ±45 | ||
| 速度范围/(km·h−1) | −400~200 (−表示远离目标;+表示靠近目标) | ||
| 通信方式 | CAN | ||
| 扫描周期/ms | ~60 | ||
| 相机 | 型号 | Logitech C310 | |
| 分辨率/像素 | 1 280×720 | ||
| 焦距/mm | 29.5 | ||
| 帧率/(帧·s−1) | 30 | ||
单目视觉测距原理是基于针孔成像模型采用相似三角变换得到相机与被测物之间的距离,这样图像坐标系下标识框的宽度或高度将直接影响世界坐标系下的距离信息. 考虑到毫米波雷达纵向测距能力的优越性,将雷达的纵向量测结果作为纵向“参考”,记为Lref,将基于YOLO框架的视觉检测结果,记为YOLO估计,将雷达与相机融合感知的结果,记为MSJPDA估计,并将MSJPDA估计与加权融合估计方法进行对比,令雷达与相机的融合权重分别为
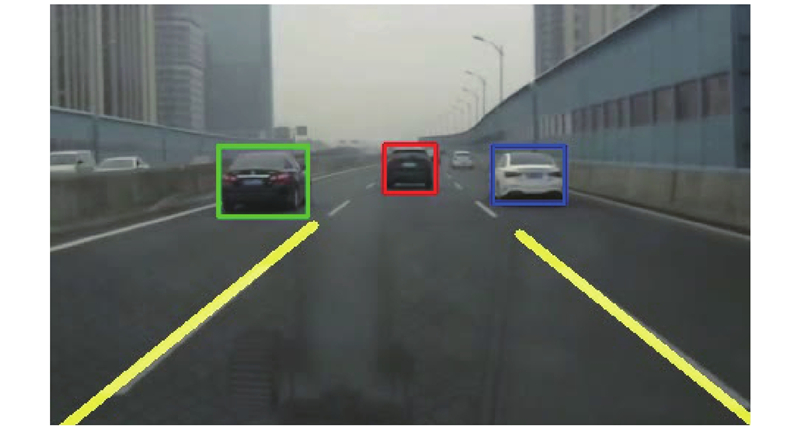
如图7所示为基于YOLO框架对多车道OOI车辆进行检测的结果. 先通过车道线识别技术对车道进行划分,再检测出相应车道内的OOI车辆.
图 7
图 7 多车道多目标车辆跟踪检测结果
Fig.7 Detection result of multi-lane multi-vehicle tracking
如图8所示为本车道内自车与OOI车辆的纵向相对运动估计. 图中,
图 8
图 8 本车道内自车与OOI车辆的纵向相对运动估计
Fig.8 Longitudinal inter-vehicle motion estimation between host vehicle and OOI vehicle in host-lane
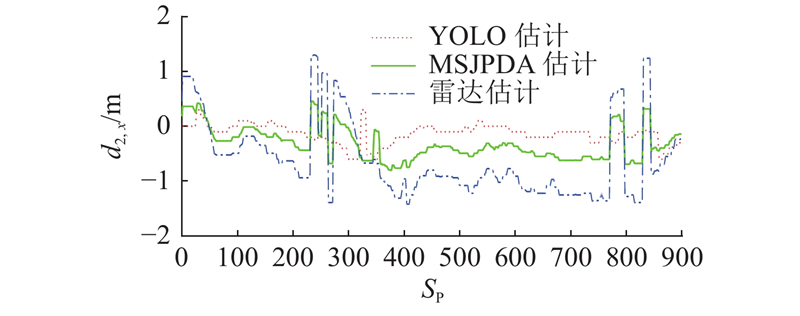
如图9所示为本车道内自车与OOI车辆的横向相对运动估计. 相对YOLO估计来说,雷达横向运动估计易受扰动因素影响,跟踪效果较差.
图 9
图 9 本车道内自车与OOI车辆的横向相对运动估计
Fig.9 Lateral inter-vehicle motion estimation between host vehicle and OOI vehicle in host-lane
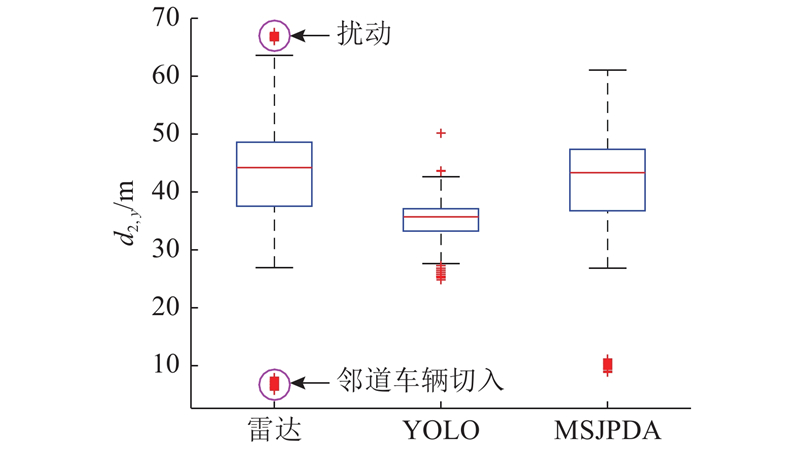
如图10所示为本车道内自车与OOI车辆的纵向车距分布,由于单目视觉测距的局限性,YOLO估计的箱线图分布较集中,而MSJPDA与雷达估计的箱线图能够较好体现出车间相对运动状况,且MSJPDA能够在一定程度上减少离群值.
图 10
图 10 本车道内自车与OOI车辆的纵向车距分布
Fig.10 Longitudinal inter-vehicle distance distribution between host vehicle and OOI vehicle in host-lane
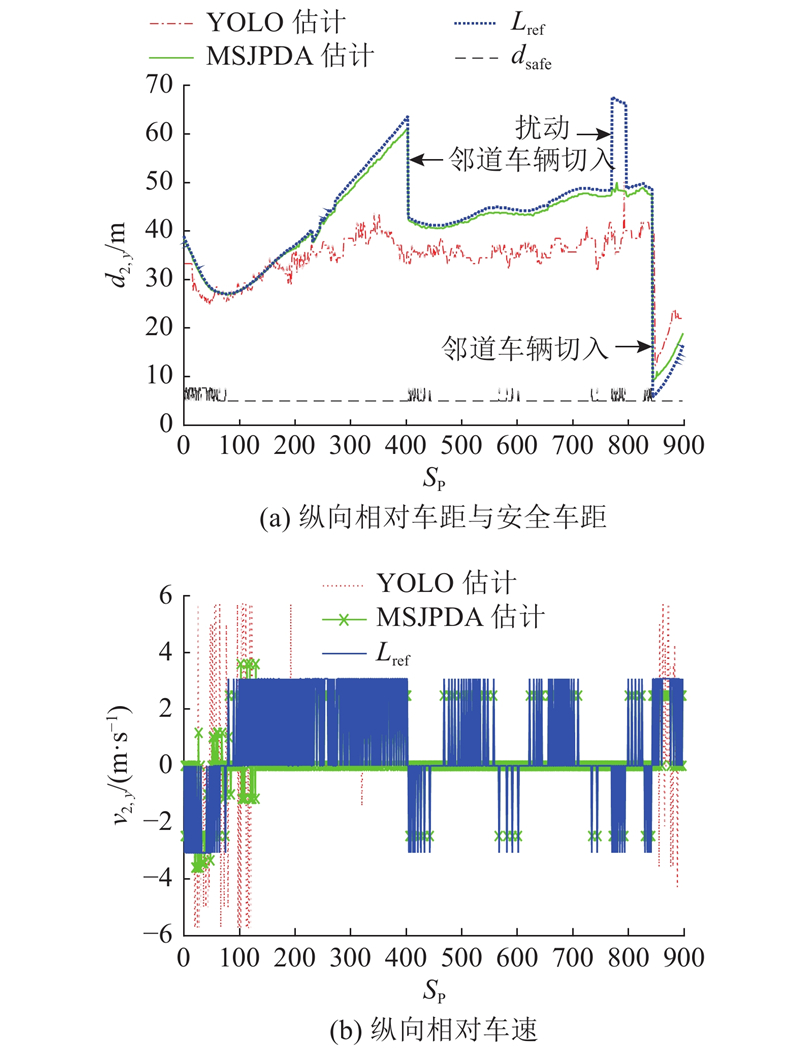
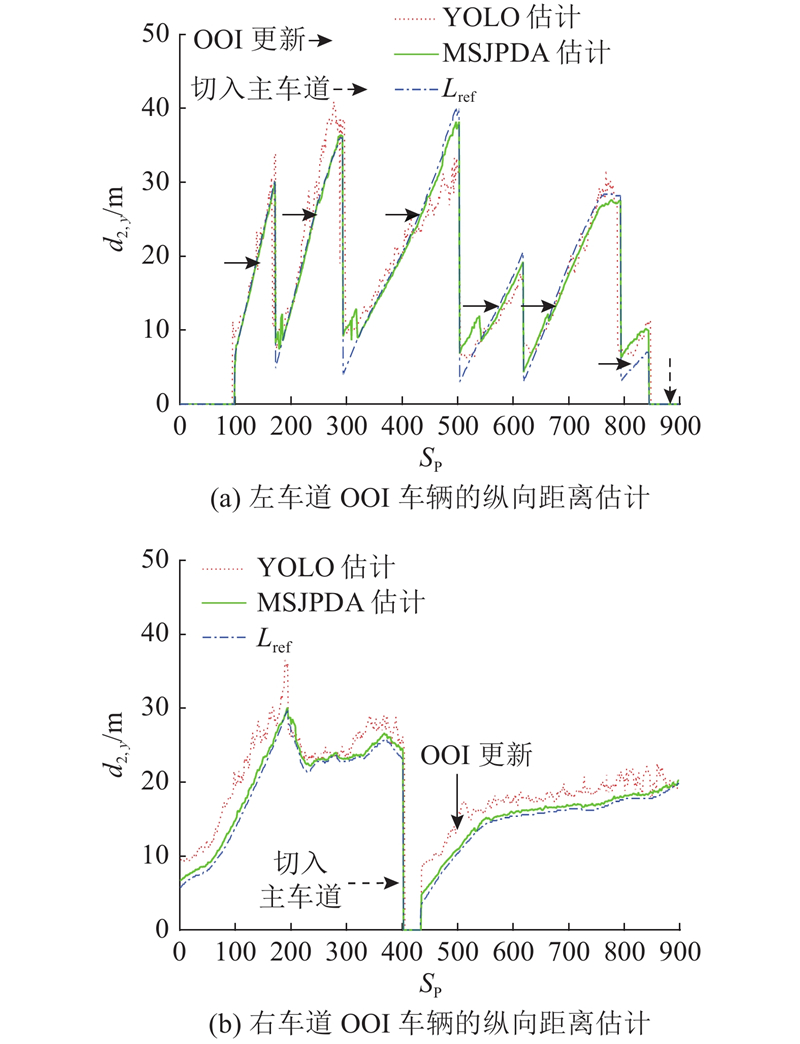
如图11所示为邻道OOI目标车辆运动估计的对比情况. 整体上来看,基于MSJPDA的滤波算法能够较好地实现多车道OOI目标车辆跟踪.
图 11
图 11 邻道OOI目标车辆纵向运动估计对比
Fig.11 Comparison of longitudinal inter-vehicle motion estimation between host vehicle and OOI vehicle in adjacent-lane
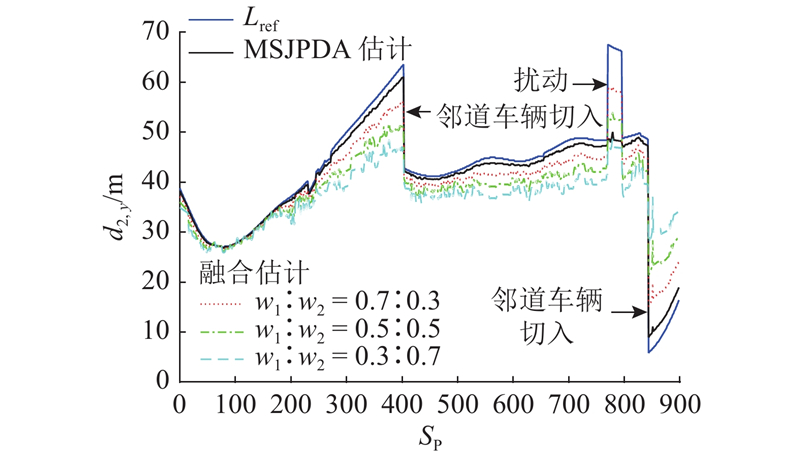
如图12所示为融合算法的对比情况. 相对加权融合估计来说,MSJPDA估计的跟踪效果更优、抗扰动性较强.
图 12
图 12 MSJPDA估计与加权融合估计算法对比
Fig.12 Comparison between MSJPDA estimation and weighted fusion estimation
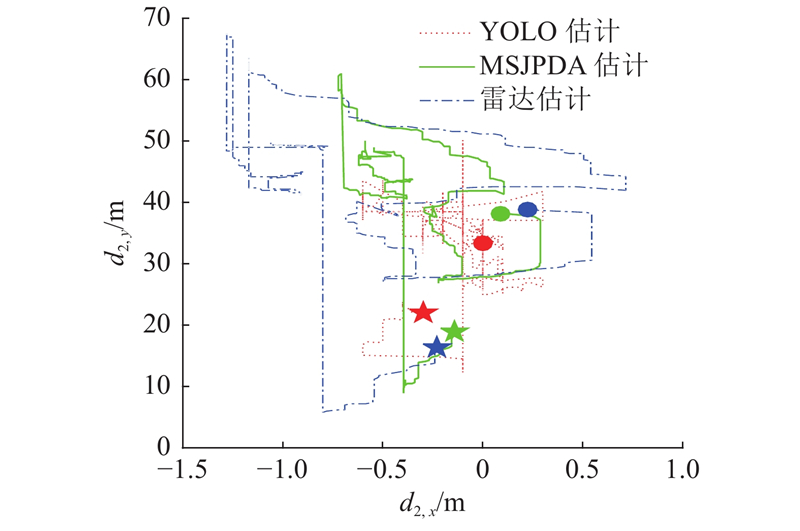
如图13所示为本车道内OOI车辆的运动轨迹估计. 图中,实心圆表示跟踪起始的相对位置,实心五角星表示跟踪结束的相对位置. 相对单一传感器估计效果而言,MSJPDA算法能够提升量测数据关联的可靠性,较好地兼顾了纵向、横向的跟踪性能,从而有望改善车辆纵向避撞预警模块的友好性.
图 13
5. 结 论
为了实现多源传感器量测数据的有效关联与车辆安全跟随,提出多源传感器多目标车辆跟踪算法与纵向避撞预警策略,主要结论如下.
(1)多源异构传感器的观测序列通常在时空上、数据结构上存在着较大差异,针对车辆纵向避撞的应用场景,对该问题进行数学描述,并给出时间配准与空间融合方法.
(2)关联概率较大的可行关联事件在跟踪过程中往往起着主导作用,通过设计一个参考阈值来忽略关联概率接近于0的事件,进而对确认矩阵进行稀疏化处理,以减少可行联合事件的拆分次数.
(3)MSJPDA序贯滤波提升了量测数据关联的可靠程度,充分发挥出单一传感器各自的性能优势,增强了融合感知的鲁棒性.
(4)考虑到不同驾驶群体跟驰习惯的差异性,后续将通过AI学习方法对TEM模型参数进行在线更新,以提升纵向避撞预警策略对驾驶群体的适应能力.
参考文献
基于BP神经网络的纵向避撞安全辅助算法
[J].
Safety assistance algorithm for longitudinal collision avoidance based on BP neural network
[J].
A novel multi-criteria discounting combination approach for multi-sensor fusion
[J].DOI:10.1109/JSEN.2019.2922769 [本文引用: 1]
Multi-sensor multi-target tracking using domain knowledge and clustering
[J].
多传感器信息融合研究进展与展望
[J].
Survey on the progress and prospect of multisensor information fusion
[J].
Track quality based multitarget tracking approach for global nearest-neighbor association
[J].DOI:10.1109/TAES.2012.6178056 [本文引用: 1]
An interacting multi-pattern probabilistic data association (IMP-PDA) algorithm for target tracking
[J].DOI:10.1109/9.940926 [本文引用: 1]
基于自适应聚概率矩阵的JPDA算法研究
[J].DOI:10.3969/j.issn.0258-2724.2017.02.018 [本文引用: 4]
Joint probabilistic data association algorithm based on adaptive cluster probability matrix
[J].DOI:10.3969/j.issn.0258-2724.2017.02.018 [本文引用: 4]
基于多传感器信息融合的车辆目标识别方法
[J].DOI:10.19562/j.chinasae.qcgc.2017.11.014 [本文引用: 1]
Vehicle target recognition based on multi-sensor information fusion
[J].DOI:10.19562/j.chinasae.qcgc.2017.11.014 [本文引用: 1]
杂波环境下基于全邻模糊聚类的联合概率数据互联算法
[J].DOI:10.11999/JEIT150849 [本文引用: 1]
Joint probabilistic data association algorithm based on all-neighbor fuzzy clustering in cluster
[J].DOI:10.11999/JEIT150849 [本文引用: 1]
Multiple hypothesis tracking for targets producing multiple measurements
[J].DOI:10.1109/TAES.2018.2796478 [本文引用: 1]
Online scheme for multiple camera multiple target tracking based on multiple hypothesis tracking
[J].DOI:10.1109/TCSVT.2016.2593619 [本文引用: 1]
Tracking in a cluttered environment with probabilistic data association
[J].
基于最大熵模糊聚类的快速多目标跟踪算法研究
[J].DOI:10.3969/j.issn.1000-2758.2017.04.011 [本文引用: 1]
A fast multi-target tracking algorithm based on maximum entropy fuzzy clustering
[J].DOI:10.3969/j.issn.1000-2758.2017.04.011 [本文引用: 1]
城市道路环境中驾驶人应激响应时间特性
[J].DOI:10.3969/j.issn.1001-7372.2013.06.019 [本文引用: 1]
Driver’s reaction time under city road conditions
[J].DOI:10.3969/j.issn.1001-7372.2013.06.019 [本文引用: 1]
路面附着系数识别方法发展现状综述
[J].
A review on the development status of road adhesion coefficient identification approach
[J].