智能车能利用不同类型的车载传感器,如激光雷达、毫米波雷达、摄像机[1-2]等,收集周边环境信息. 通过分析这些信息,智能车能区分可驾驶区域和障碍物,从而实现准确的环境感知[3]. 目标跟踪是自动驾驶系统环境感知的一项关键技术,其本质是动态系统的状态估计问题,通过传感器的噪声测量值估计动态目标的真实状态[4]. 卡尔曼滤波器[5](Kalman filter,KF)是用于传感器融合与目标跟踪的标准模型,过程噪声和测量噪声均假设为统计特性已知的高斯分布. KF可被视为更通用的贝叶斯滤波器[6]的特例. 随着系统模型越来越复杂,概率模型中的后验分布一般难以直接计算. 为了解决该问题,Beal[7]提出变分贝叶斯推断(variational Bayesian inference, VBI)方法,基于平均场理论近似求解隐变量的后验分布. Särkkä等[8]提出基于VBI的自适应卡尔曼滤波,可以对目标状态和噪声参数的联合后验分布进行近似计算. 沈忱等[9]提出基于层次贝叶斯结构的状态空间模型,将测量噪声的均值、方差和系统状态一起作为随机变量,并利用VBI进行解耦. 余东平等[10]提出基于VBI的多目标无源定位算法. Zhu等[11]应用学生t-分布作为测量噪声模型进行状态估计. Huang等[12]提出基于学生t-分布的分层高斯状态空间模型.
针对定位数据易受野值干扰而影响协同目标跟踪性能的问题,本研究提出适用于重尾非高斯定位噪声的协同目标跟踪方法,将定位噪声建模为多元学生t-分布,构建目标状态和未知定位噪声参数的联合概率推断模型. 应用变分贝叶斯推断原理将后验分布估计问题转化为最优化问题,以交替优化的方式实现变分后验分布参数的有效计算,降低野值对目标状态估计的影响.
1. 模型建立
1.1. 学生t-分布
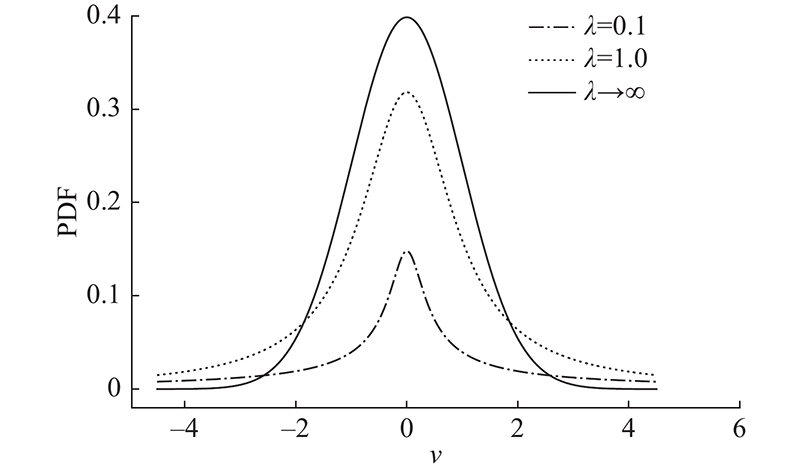
在参数估计问题上,学生t-分布具有重尾特性,在野值数据处理方面比高斯模型具有更好的鲁棒性. 因此,利用该分布刻画重尾非高斯定位噪声
式中:
学生t-分布的极大似然估计难以获得闭式解. 定义均值为
图 1
图 1
不同
Fig.1
Probability density function of Student’s t-distribution for different
1.2. 协同目标跟踪场景描述
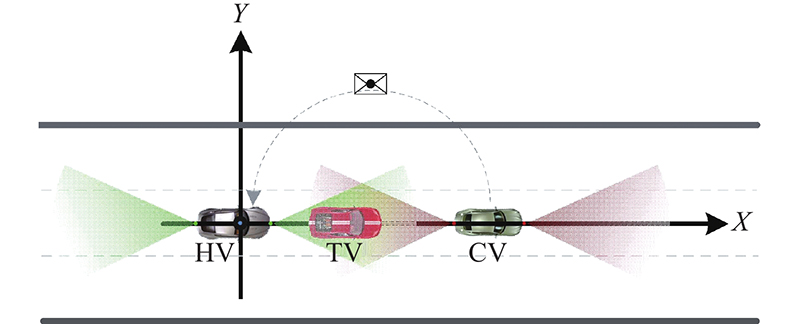
协同目标跟踪场景包括主车(host vehicle,HV)、协同车(cooperative vehicle,CV)和目标车(target vehicle,TV),其中,主车和协同车配备毫米波雷达、GPS定位系统和V2V通信设备等. 主车和协同车根据各自的车载传感器收集感知范围内的TV信息,CV将其对TV的测量数据和定位数据利用V2V通信设备发送给HV. HV融合本地感知数据与CV发送的数据,实现对TV状态的准确估计.
在跟踪过程中,假设系统状态转移方程服从如下线性模型:
式中:k为离散时刻,
另外,假设系统初始状态
定义如下系统测量方程:
式中:
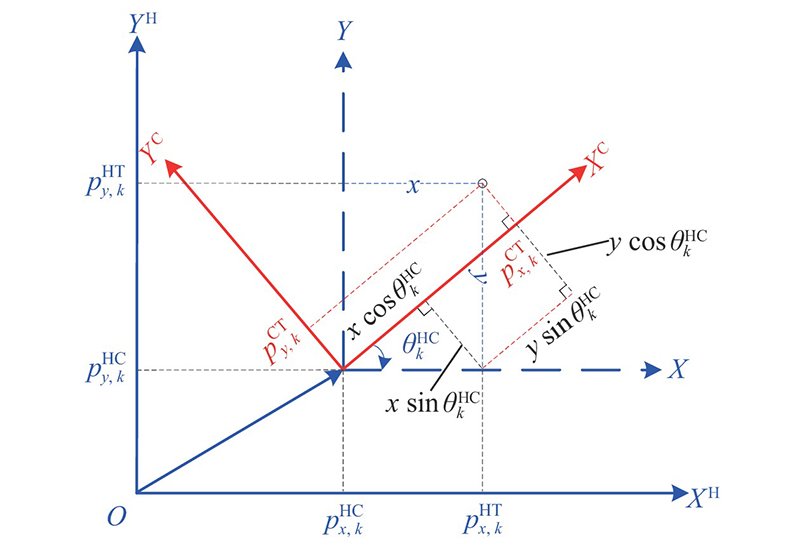
由于HV和CV基于各自车体坐标系感知TV状态,在测量方程中测量函数
图 2
图 2 平移与旋转坐标转换示意图
Fig.2 Illustration of translation and rotation of coordinate system
系统测量函数
式中:
测量噪声
为了增强跟踪算法对定位数据中野值的鲁棒性,采用重尾非高斯多元学生t-分布建模定位测量噪声
根据式(2),引入自举变量
假设精确度
式中:
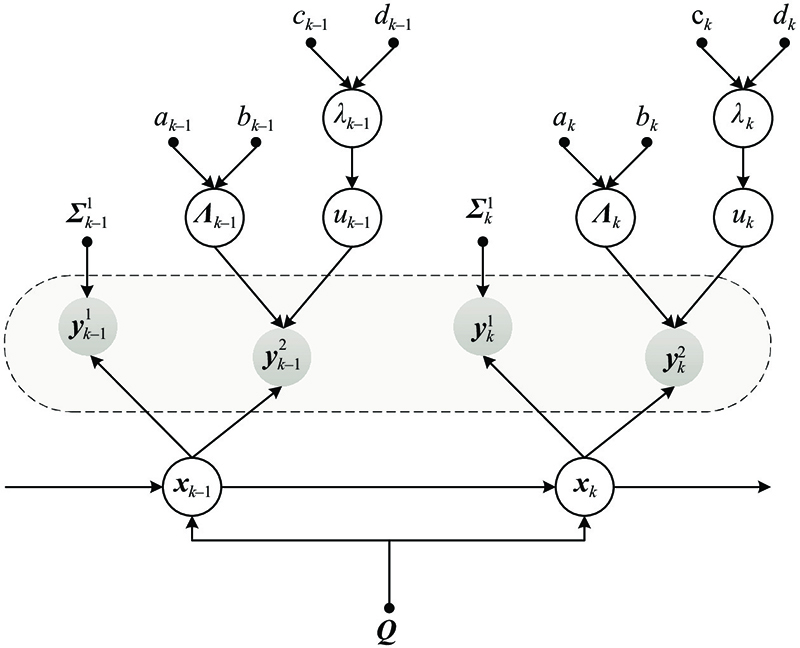
图 3
图 3 协同目标跟踪的概率图模型
Fig.3 Probabilistic graph model of cooperative target tracking
2. 变分贝叶斯推断原理
根据上述模型,选择状态变量
式中:
对数边缘似然函数
其中,
式中:
根据式(14),可以通过最小化式(16)来寻找
式中:
3. 变分贝叶斯推断推导变分参数
依据变分贝叶斯框架推导协同目标跟踪概率模型的变分后验分布. 由于测量函数
式中:
为了简便起见,将测量向量
经上述处理后,新的测量方程表示如下:
根据链式法则,利用分层高斯状态空间模型的条件独立性,将模型的联合概率分布函数表达为
根据如图3所示的概率图模型,式(21)中未知参数的似然函数为
3.1. 状态预测
未知参数
对于状态变量
式中:
对于每一个参数的后验分布,有
式中:
根据文献[11],定位测量噪声协方差的预测分布参数可以设置为
式中:
3.2. 变分迭代更新
根据变分贝叶斯推断原理推导系统状态和噪声参数的后验分布,式(21)中对数联合概率分布函数可以表示为
依据卡尔曼滤波,更新参数
式中:
3.2.1. 精确度 $ {{\boldsymbol{\varLambda}} _k} $
第r次变分迭代,变分分布
式中:
可以发现,
式中:
3.2.2. 自举变量 $ {u_k} $
第r次变分迭代,变分分布
可以发现,
3.2.3. 自由度 $ {\lambda _k} $
第r次变分迭代,变分分布
根据斯特林近似公式
可以发现,
3.3. 变分迭代终止条件
在变分迭代更新步骤中,须交替优化变分参数. 考虑到计算效率,提出如下终止条件.
条件1 如果2次相邻迭代,系统状态的变化量
式中:
条件2 如果变分迭代的次数达到设置的最大迭代次数
最终,本研究提出的协同目标跟踪算法变分贝叶斯-鲁棒协同跟踪(variational Bayesian-robust cooperative tracking, VB-RCT)算法流程如下.
算法:VB-RCT算法
输入:
初始化:
For
状态预测:式(25)、(27)
变分迭代更新:
For
更新状态:式(29) ~ (33)
更新变分参数:式(35)、(37)、(40)
变分迭代终止条件:式(41)、(42)
End for
End for
输出:
4. 仿真实验
为了验证VB-RCT算法的有效性与鲁棒性,对4种算法进行性能对比仿真实验.1)VB-RCT算法;2)非协同、仅依赖HV估计TV状态的单车跟踪(Kalman filter-single tracking,KF-ST)算法;3)基于扩展卡尔曼滤波,假定定位噪声协方差为固定值的协同跟踪(extend Kalman filter-cooperative tracking,EKF-CT)算法;4)定位噪声协方差建模为逆伽马分布的变分协同跟踪(variational Bayesian-cooperative tracking,VB-CT)[21]算法. 另外,对VB-RCT算法中相关参数的影响进行实验分析.
4.1. 模型基本参数设置
在线协同目标跟踪仿真场景如图4所示,假设TV和CV根据以下状态空间模型在二维空间中以恒定的速度运动:
图 4
式中:
式中:
变分贝叶斯迭代的终止条件参数设置为:
式中:
4.2. 跟踪性能
4.2.1. 算法对比分析
设置野值比率
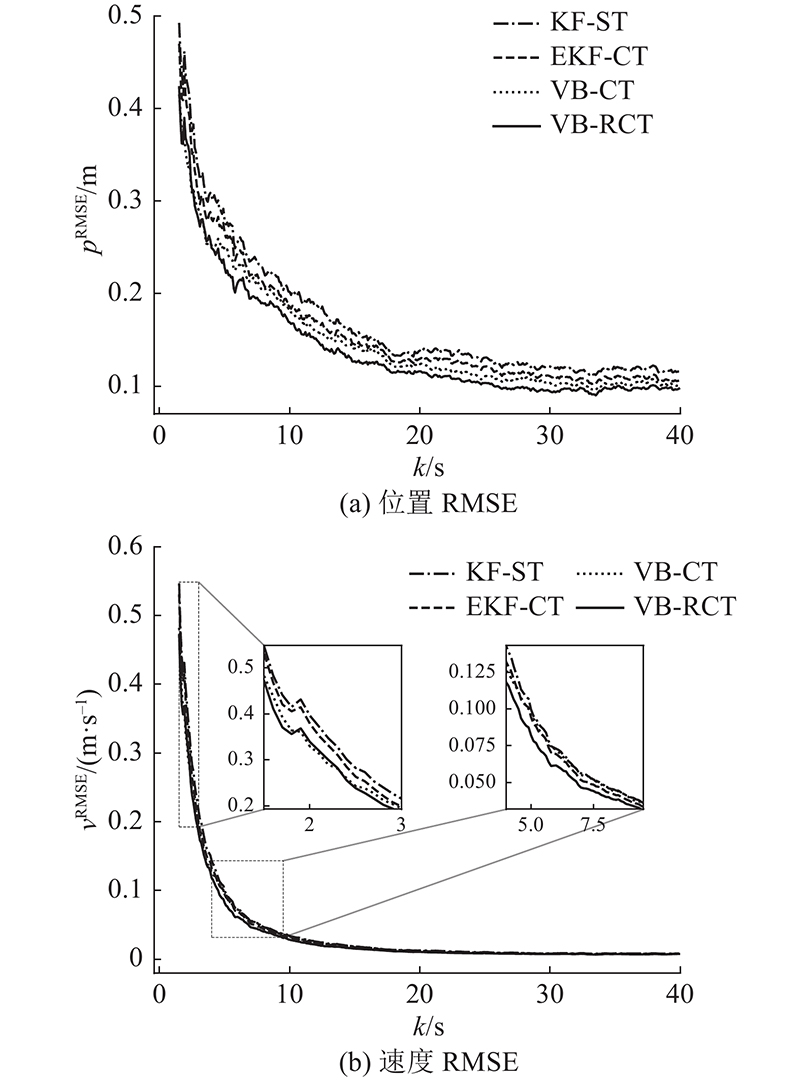
图 5
图 5 不同在线跟踪算法的误差对比
Fig.5 Error comparison of different online tracking algorithms
表 1 不同算法的跟踪误差性能分析
Tab.1
| 算法 | ARMSE | |||
| | | | | |
| KF-ST | 0.185 01 | − | 0.097 41 | − |
| EKF-CT | 0.171 99 | 7.0 | 0.093 06 | 4.5 |
| VB-CT | 0.160 40 | 13.3 | 0.087 43 | 10.2 |
| VB-RCT | 0.152 80 | 17.4 | 0.083 61 | 14.2 |
4.2.2. 系统环境参数分析
某一时刻的定位噪声是否为野值点与前、后时刻的数据无必然联系. 比较常见的是,当某个时刻噪声为野值点时,在该时刻的一个邻域内的数据是正常的,即野值点的出现是随机、孤立的. 基于
图 6
在上述实验中,野值定位噪声建模为固定异常程度参数值的学生t-分布,在野值比率
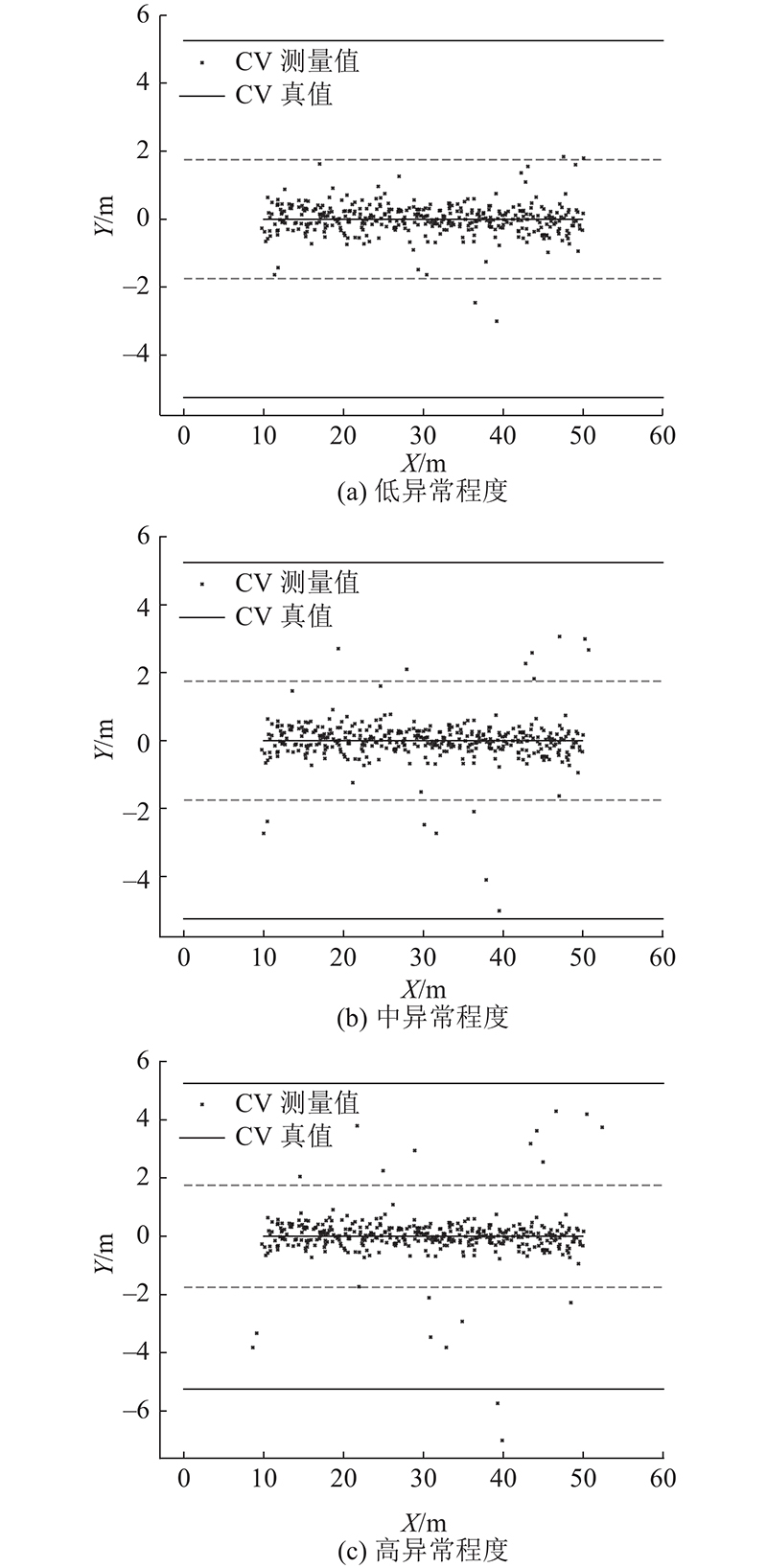
图 7
图 7 不同异常程度下,CV的非高斯分布定位噪声示意图
Fig.7 Schematic diagram of non-Gaussian distribution location noise of CV in different degrees of anomaly
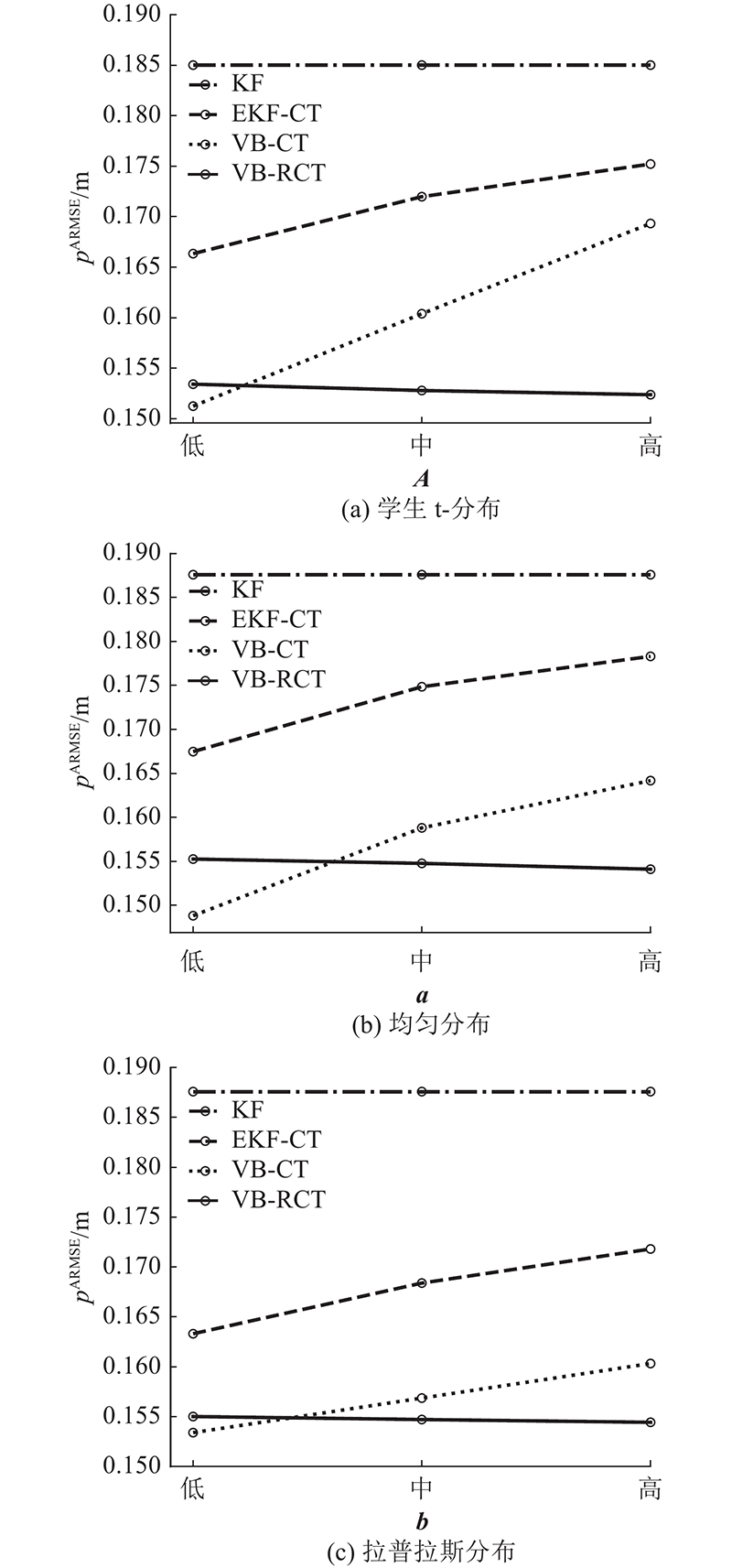
图 8
图 8 从不同分布采样野值数据时,不同算法的跟踪误差
Fig.8 Tracking errors of different algorithms when sampling outliers from different distributions
表 2 从不同分布采样野值数据时,不同算法的ARMSE
Tab.2
| 分布 | 异常程度 | pARMSE/m | |||
| KF | EKF-CT | VB-CT | VB-RCT | ||
| | | 0.185 01 | 0.166 35 | 0.151 25 | 0.153 42 |
| | 0.185 01 | 0.171 99 | 0.160 40 | 0.152 80 | |
| | 0.185 01 | 0.175 22 | 0.169 33 | 0.152 39 | |
| | | 0.187 60 | 0.167 49 | 0.148 83 | 0.155 28 |
| | 0.187 60 | 0.174 86 | 0.158 82 | 0.154 78 | |
| | 0.187 60 | 0.178 31 | 0.164 19 | 0.154 12 | |
| | | 0.187 60 | 0.163 32 | 0.153 40 | 0.155 02 |
| | 0.187 60 | 0.168 40 | 0.156 86 | 0.154 72 | |
| | 0.187 60 | 0.171 82 | 0.160 33 | 0.154 44 | |
4.2.3. 算法参数分析
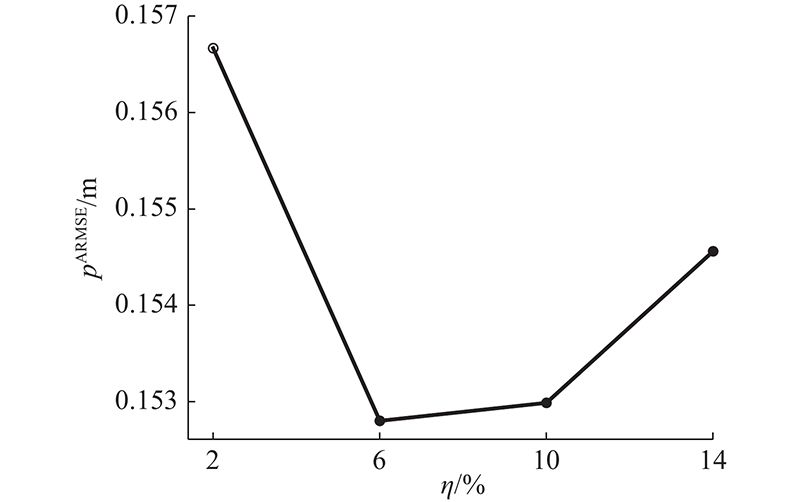
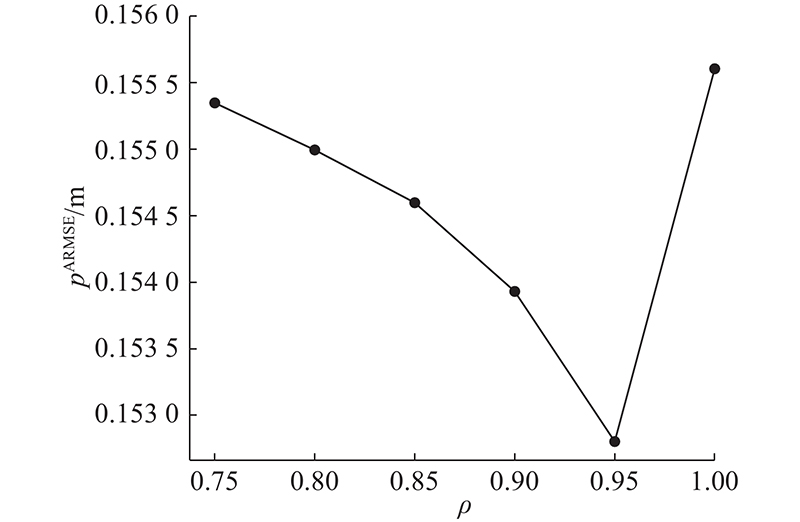
遗忘因子
图 9
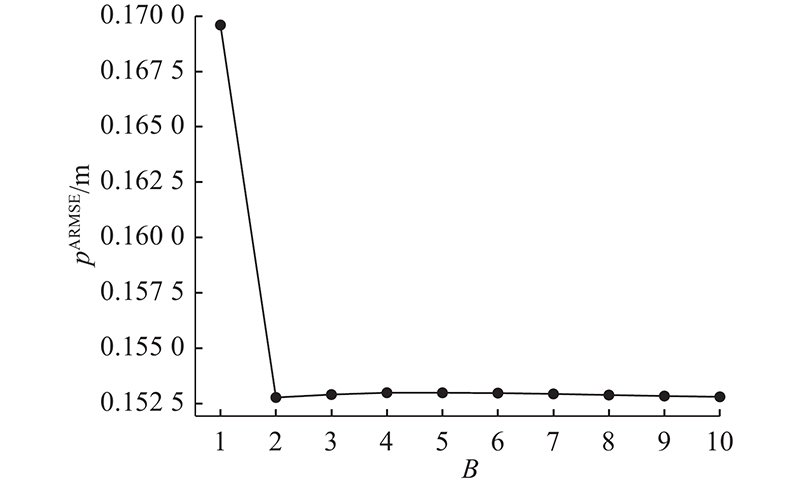
变分内循环中的迭代次数
图 10
图 10 跟踪误差随变分迭代次数的变化
Fig.10 Variation of tracking errors with number of variational iterations
5. 结 语
针对协同目标跟踪中定位数据统计特征未知且存在野值的问题,本研究提出一种鲁棒协同目标跟踪算法,将定位噪声建模为具有重尾的多元学生t-分布,建立目标状态与定位噪声参数的贝叶斯模型. 应用变分贝叶斯推断原理对变量进行解耦,以交替优化的方式实现后验分布的有效估计. 计算机仿真结果表明,与传统单车目标跟踪算法相比,提出的鲁棒跟踪算法能有效地提升目标跟踪的性能,位置和速度估计误差分别下降了17.4%和14.2%. 在未来工作中,将在真实环境下测试所提出方法的跟踪效果.
参考文献
基于深度学习的自动驾驶环境感知技术研究
[J].DOI:10.3969/j.issn.1674-957X.2021.04.089 [本文引用: 1]
Research on autonomous driving environment perception technology based on Deep Learning
[J].DOI:10.3969/j.issn.1674-957X.2021.04.089 [本文引用: 1]
No Blind Spots: full-surround multi-object tracking for autonomous vehicles using cameras and LiDARs
[J].DOI:10.1109/TIV.2019.2938110 [本文引用: 1]
Review of environment perception for intelligent vehicles
[J].
Performance loss and design method of Kalman filters for discrete-time linear systems with uncertainties
[J].DOI:10.1080/00207177008931830 [本文引用: 1]
A novel adaptive resampling for sequential Bayesian filtering to improve frequency estimation of time-varying signals
[J].DOI:10.1016/j.heliyon.2021.e06768 [本文引用: 1]
基于变分推断的一般噪声自适应卡尔曼滤波
[J].DOI:10.3969/j.issn.1001-506X.2014.08.03 [本文引用: 1]
Generalized noises adaptive Kalman filtering based on variational inference
[J].DOI:10.3969/j.issn.1001-506X.2014.08.03 [本文引用: 1]
基于变分贝叶斯推理的多目标无源定位算法
[J].
Variational Bayesian inference based multi-target device-free localization algorithm
[J].
A variational Bayesian approach to robust sensor fusion based on Student-t distribution
[J].DOI:10.1016/j.ins.2012.09.017 [本文引用: 2]
A novel robust student's t-based Kalman filter
[J].DOI:10.1109/TAES.2017.2651684 [本文引用: 1]
车载无线通信技术浅析
[J].DOI:10.3969/j.issn.1003-8639.2021.03.017 [本文引用: 1]
Discussion on vehicle wireless communication technology
[J].DOI:10.3969/j.issn.1003-8639.2021.03.017 [本文引用: 1]
Joint use of DSRC and C-V2X for V2X communications in the 5.9 GHz ITS band
[J].
Online optimum velocity calculation under V2X for smart new energy vehicles
[J].DOI:10.1177/0142331221997280 [本文引用: 1]
Robust data fusion of UAV navigation measurements with application to the landing system
[J].DOI:10.3390/rs12233849 [本文引用: 1]
非高斯噪声下的车载GPS信号定位算法
[J].
A Bayes filter algorithm with non-Gaussian noises based on location of vehicular GPS
[J].
基于T分布变分贝叶斯滤波的SINS/GPS组合导航
[J].
Variational Bayesian filtering based on Student-t distribution for SINS/GPS integrated navigation
[J].
Augmented extended Kalman filter with cooperative Bayesian filtering and multi-models fusion for precise vehicle localisations
[J].DOI:10.1049/iet-rsn.2020.0155 [本文引用: 1]
Multi-vehicle cooperative target tracking with time-varying localization uncertainty via recursive variational Bayesian inference
[J].