针对摩擦非线性的补偿,现阶段主要有2类解决方法:1)直接将摩擦视为外干扰,通过改进控制策略提高系统的抗干扰能力,从而抑制摩擦;2)通过基于摩擦模型的前馈补偿来消除摩擦环节对系统的影响. 对于第1类解决方法,人们提出的先进算法有状态反馈调节、自适应控制及鲁棒控制等. 自适应控制算法对于处理系统不确定性参数有很好的效果,但对于外干扰和未建模动态特性的抵御能力较差[6-7];鲁棒控制可以补偿具有已知上界函数的不确定动态特性[8],因此常用自适应鲁棒控制算法[9-12]结合两者特点来解决参数不确定性与外干扰共存的问題. 此外,神经网络被越来越多地应用于解决摩擦问题[13],但该类算法的控制精度依赖于较多的神经网络节点数和训练次数,不利于工程实现. 综上所述,该类方法无法精确地补偿摩擦非线性,且扰动增大会引起反馈增益加大,导致控制性能降低. 对于第2类解决方法,建立精确的数学模型能够更好地描述和预测摩擦过程,精准补偿摩擦非线性,已有的模型有静态模型(如Coulomb模型[14-15]、Stribeck模型[16-18])以及动态模型(如Dahl模型[19-20]、LuGre模型[21-23]). 其中,LuGre模型与真实的摩擦现象更接近,因此本文选择该模型来补偿机电作动系统的摩擦非线性.
LuGre模型的内部摩擦状态无法直接测量且摩擦系数通常未知,因此针对摩擦内部状态,本文设计非线性观测器进行观测. 针对摩擦系数、转动惯量及其他不确定性参数设计参数自适应律,引入鲁棒项克服系统的其他外干扰,实验结果证明了系统良好的跟踪性能与工程应用性能.
1. 系统建模
将永磁同步电机作为系统的伺服执行器,数学模型表示为
式中:J为系统负载折算到电机端的转动惯量,y为执行器角度输出变量,u为控制量,F为摩擦扭矩,TL为负载扭矩,f为其他外干扰变量.
LuGre摩擦模型如下:
式中:σ0为鬃毛刚度系数,σ1为阻尼摩擦系数,σ2为黏滞摩擦系数,这3个系数通常是未知的;z为内部摩擦状态变量,物理上不可测;
对于伺服执行器的二阶动力学模型(1)、LuGre摩擦模型(2)和(3),自适应鲁棒控制的目的是使得执行器的位置和速度能够渐近跟踪给定的有界参考信号,同时保证系统中的内部信号有界. 假定给定的信号是边界平滑且可微分的,可以将基于非线性观测器的自适应鲁棒控制表述为鲁棒的内部摩擦状态估计以及自适应位置和速度跟踪的控制方法.
2. 控制器设计
根据上述数学模型,定义系统位置与速度状态为
定义:
则式(5)转化为
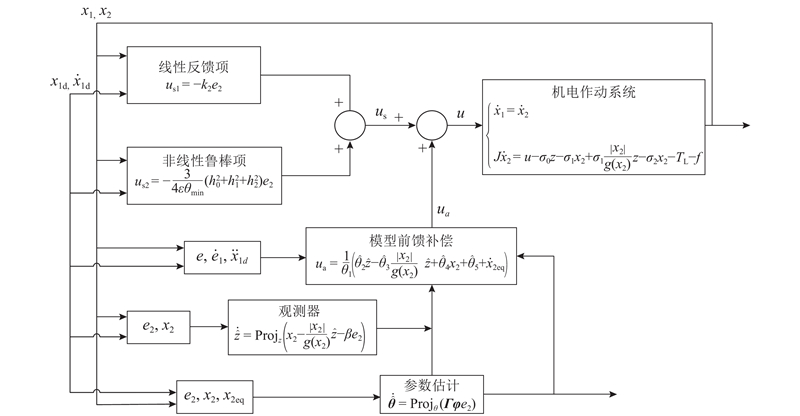
针对系统存在的非线性因素,采用反步设计的思想来设计控制器. 设计思路如图1所示.
图 1
1)设计虚拟控制量
将理想的位置状态设为
设
式中:
从式(8)可知,如果使e2趋于0,则e1必将趋向于0,此时控制器的跟踪性能将达到最好.
2)设计非线性观测器.
由于系统建模采用的LuGre模型中内部摩擦状态无法物理测量,设计非线性观测器,用以观测摩擦内部状态
3)设计实际控制量
根据式(11)可以设计控制量
式中:ua为前馈补偿项,
将式(12)代入式(11),可得
式中:
为了尽可能降低参数不确定性对控制性能的影响,设计参数回归器,用以估计系统参数. 在已知系统不确定性有界的前提下,设计参数自适应律为
不连续映射的表达式如下:
为了保证z稳定有界,修改式(10)为
上述设计满足如下性质.
4)设计非线性鲁棒项
在步骤3)中,
式中:
列出满足式(18)的
式中:
3. 稳定性证明
定理1 当系统的时变扰动对系统造成的影响不可忽略时,系统可以按照规定的状态对速度和位置进行跟踪,跟踪误差被限制在一个已知函数内,系统处于有界稳定状态,保证了系统的稳定性.
证明:对定理1所述的情况,定义如下的Lyapunov函数:
对式(21)进行求导,可得
求解式(22),可得
由以上证明过程可以得出,控制器具有以
定理2 若系统受到的时变扰动在系统所有的非线性因素中所占的比例很小,对系统造成的影响可以忽略不计,则此时控制器除了满足定理1的结论以外,还可以实现渐进稳定,即当
证明:当时变扰动的影响可以忽略,即满足定理2所述的情形时,建立的Lyapunov函数如下:
对式(24)进行求导,可得
由上述Lyapunov函数,根据Lyapunov稳定性定理可知,所设计的控制器能够获得渐进跟踪的性能.
4. 仿真结果
为了验证所提控制策略的有效性,使得系统输出跟踪期望位置曲线分别为低频正弦信号
对比3种控制器的跟踪性能,证明所设计控制器的有效性.
1)PID:比例-积分-微分控制器. 当位置曲线输入为阶跃信号
2)ARC:自适应鲁棒控制器. 当位置参考输入为阶跃信号
3)NOARC即提出的基于非线性观测器的自适应鲁棒控制器.
当位置参考输入为阶跃信号
工况1:跟踪阶跃位置曲线
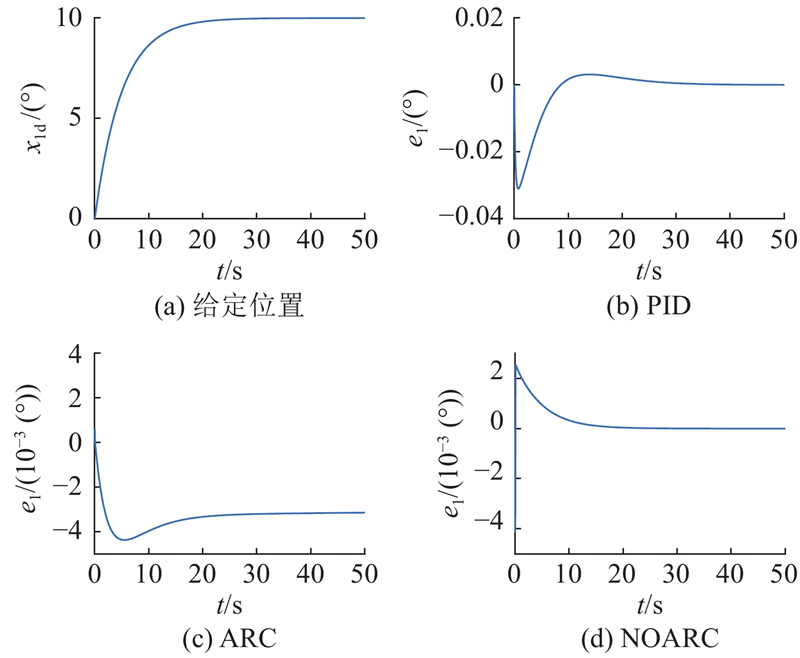
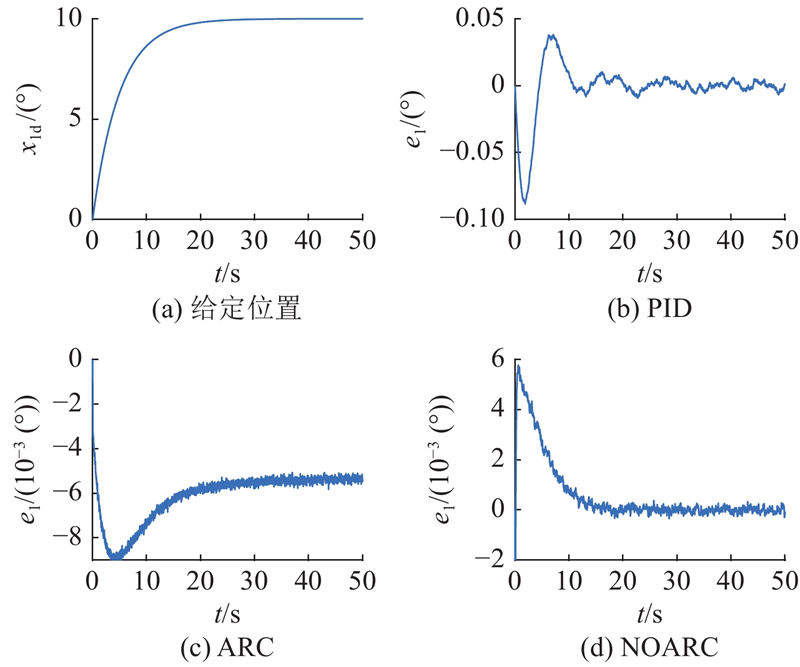
给定曲线及各控制器的跟踪误差如图2所示.
图 2
图 2 给定位置输入及各控制器跟踪误差
Fig.2 Input of given position and tracking error of each controller
选用以下3个性能指标,用于衡量每种控制算法的质量,即跟踪误差的最大值、平均值和标准差,定义如下.
3种控制器的性能指标比较如表1所示.
表 1 阶跃工况下的性能指标
Tab.1
| 指标 | Me | μ | σ |
| PID | 0.0031 | 0.0034 | 0.0071 |
| ARC | 0.0025 | 0.0016 | 5.2158×10−4 |
| NOARC | 6.0003×10−4 | 2.4833×10−4 | 5.1198×10−4 |
图 3
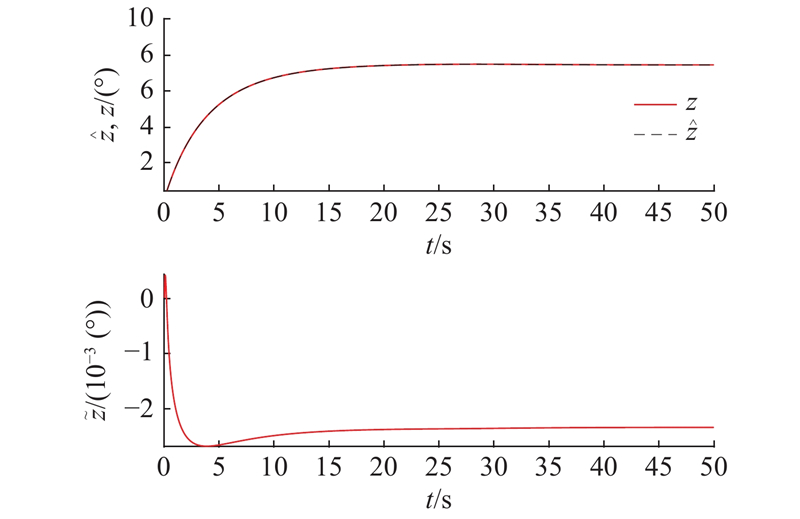
图 3 摩擦状态观测曲线和观测误差曲线
Fig.3 Friction state observation curve and observation error curve
图 4
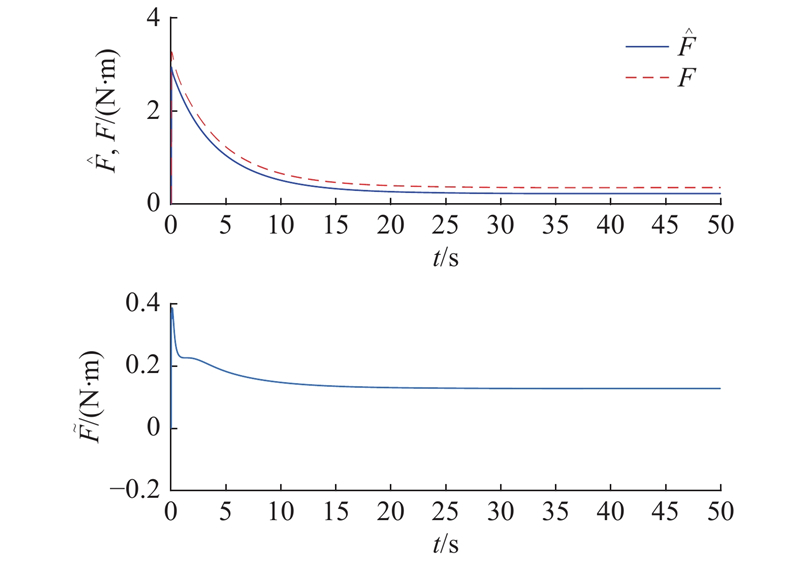
图 4 摩擦力观测曲线和观测误差曲线
Fig.4 Friction force observation curve and observation error curve
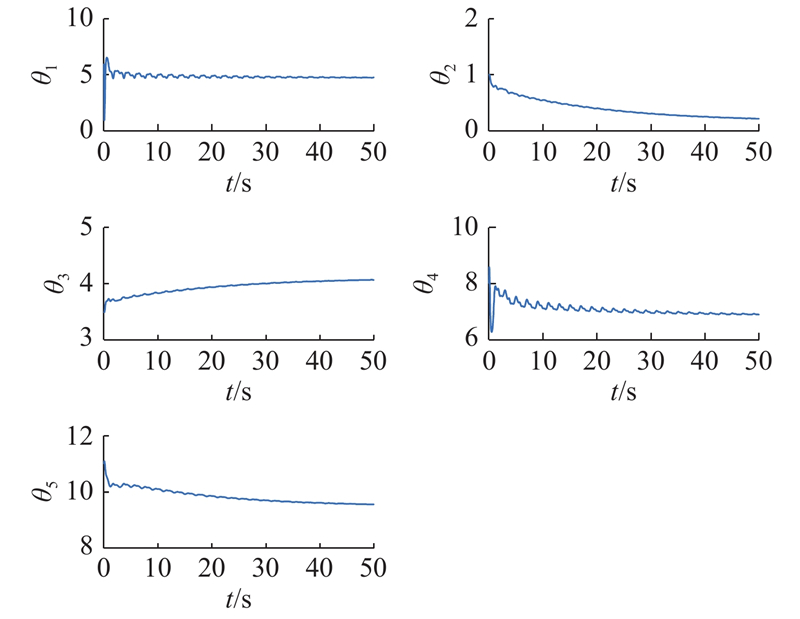
如图5所示为阶跃工况下NOARC的参数估计曲线. 模型中的5个参数均能够从估计值逐渐回归到真值,说明所设计的参数自适应律能够很好地发挥作用,控制器的性能良好.
图 5
工况2:跟踪低速低频正弦位置曲线
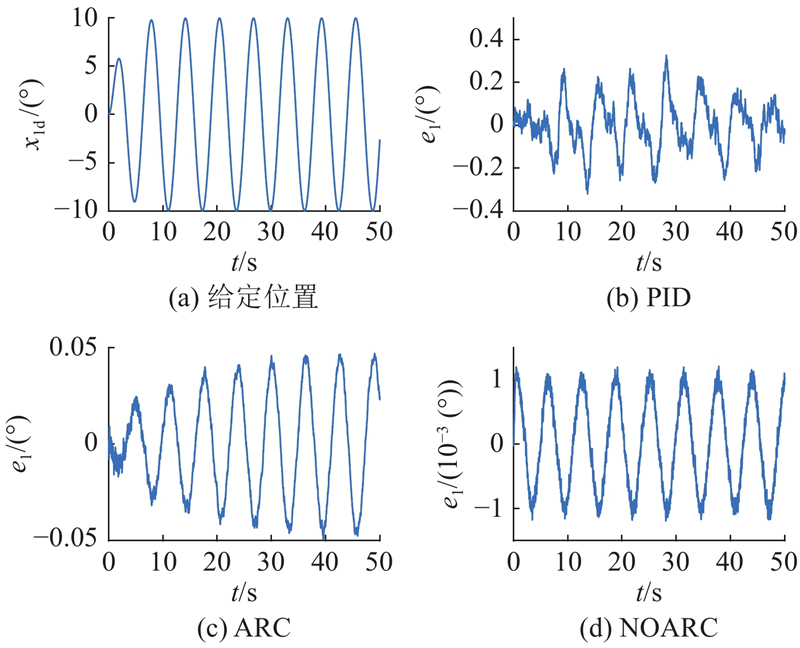
给定曲线及各控制器的跟踪误差如图6所示.
图 6
图 6 给定位置输入及各控制器跟踪误差
Fig.6 Input of given position and tracking error of each controller
表 2 低速低频工况下的性能指标
Tab.2
| 指标 | M | μ | σ |
| PID | 0.153 6 | 8.868 6×10−3 | 0.077 2 |
| ARC | 0.043 8 | 8.618 1×10−4 | 0.025 6 |
| NOARC | 0.010 1 | 1.638 5×10−4 | 0.006 9 |
图 7
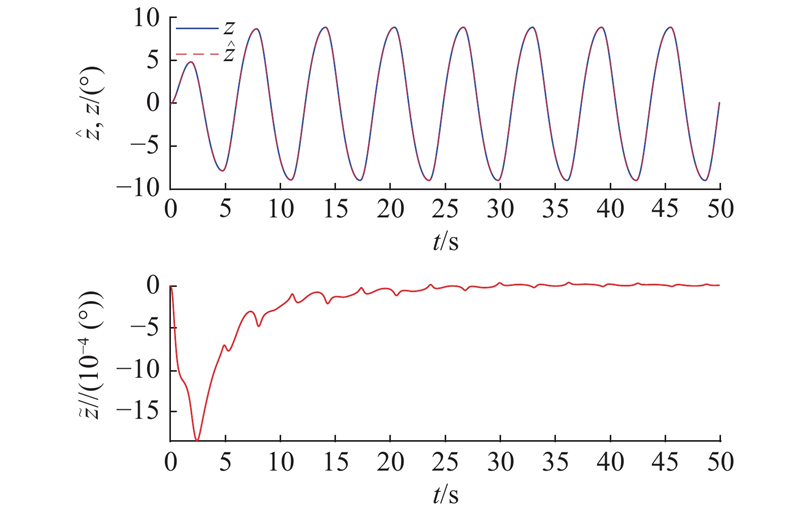
图 7 摩擦状态观测曲线和观测误差曲线
Fig.7 Friction state observation curve and observation error curve
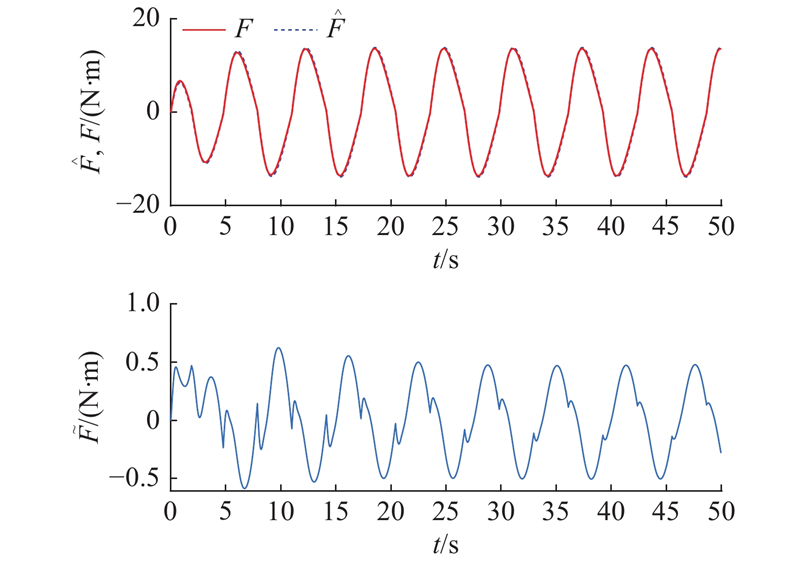
图 8
图 8 摩擦力观测曲线和观测误差曲线
Fig.8 Friction force observation curve and observation error curve
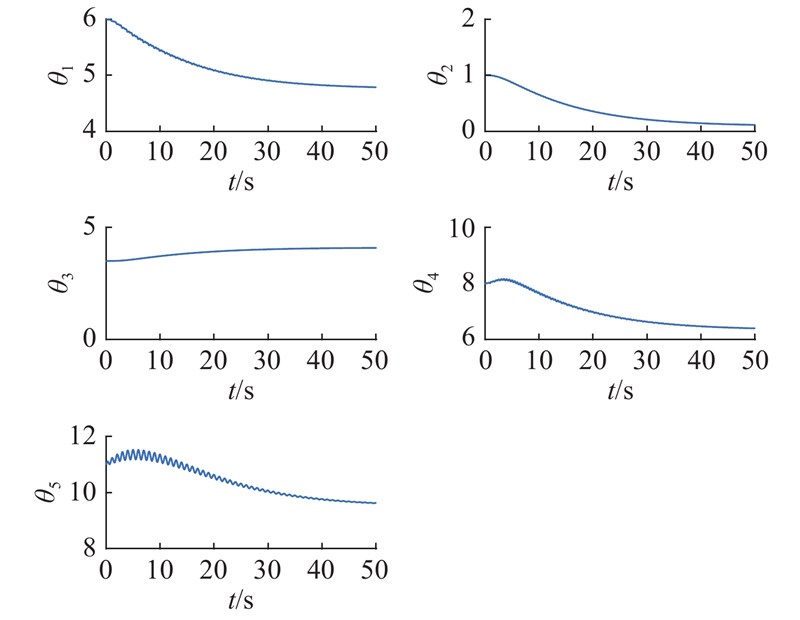
如图9所示为低频低速工况下NOARC的参数估计曲线. 可以看出,5个参数均能够从估计值逐渐回归到真值且振荡较小,参数自适应律和鲁棒项保证了系统的稳定性及不确定性参数估计的准确性.
图 9
5. 实验验证
实验验证平台的总装图及控制系统如图10、11所示. 实验系统的元器件表及电机参数见表3、4. 该平台包括1个基座、1个永磁同步电机运动系统(包括永磁同步电机Kollmorgen D063M-13-1310、电动驱动器Kollmorgen ServoStar 620、精度约为±13″的旋转编码器Heidenhain ERN180、惯量盘和联轴器)、电源以及测控系统. 测控系统包括1个监视软件和1个工控机,工控机装有实时操作系统RTU,使用C语言编写控制程序. 工控机内装有1个16位数字/模拟(D / A)转换卡Advantech PCI-1723(用于发送控制命令)和1个16位Heidenhain IK-220采集卡(用于采集光电编码器位置信息). 控制周期为0.5 ms. 系统速度由高精度位置信号的后向差产生. 采用截止频率为50 Hz的二阶Butterworth滤波器,衰减速度信号中的测量噪声.
图 10
图 10 机电伺服系统的实验平台总装图
Fig.10 Experimental platform diagram of electromechanical servo system
图 11
图 11 机电伺服实验平台的控制系统
Fig.11 Control system diagram of electromechanical servo experiment platform
表 3 机电伺服系统实验平台的元器件表
Tab.3
| 元器件名称 | 规格 |
| 执行电机 | kollmorgen伺服电机D063M-13-1310 |
| 旋转编码器 | 海德汉高安全性位置测量系统 |
| 扭矩传感器 | CD1140系列扭矩传感器 |
| 联轴器 | JB/ZQ4376-86 YL1型凸缘刚性联轴器 |
| 惯量盘 | 0.3 kg·m2 |
表 4 电机参数
Tab.4
| 参数 | 参数值 |
| 电机连续电流有效值 | 4.187 A |
| 电机直轴峰值电流有效值 | 1 A |
| 电机峰值电流有效值 | 14.5 A |
| 电机惯量 | 86.5 kg·cm2 |
| 电机转矩系数有效值 | 4.406 N·m/A |
| 电机最大速度 | 500 r/min |
| 电机最大电压有效值 | 240 V |
| 电机额定感应电压有效值 | 230 V |
为了验证所提控制策略的有效性,实验环节选择和仿真环节相同的3种控制器对比跟踪性能.
1)PID:比例-积分-微分控制器. 当位置曲线输入为阶跃信号
2)ARC:自适应鲁棒控制器. 当位置参考输入为阶跃信号
3)NOARC即提出的基于非线性观测器的自适应鲁棒控制器. 当位置参考输入为阶跃信号
工况1:跟踪阶跃位置曲线
图 12
图 12 给定阶跃位置输入及各控制器跟踪误差
Fig.12 Step position input and tracking error of each controller
工况2:跟踪低速低频正弦位置曲线
图 13
图 13 给定正弦位置输入及各控制器跟踪误差
Fig.13 Sinusoidal position input and tracking error of each controller
6. 结 语
本文设计基于非线性观测器的自适应鲁棒控制器,用以补偿机电作动系统的摩擦力矩及其他非线性. 利用LuGre模型对系统的摩擦非线性进行建模,针对模型的内部不可测量摩擦状态设计非线性观测器进行观测. 针对不确定参数,设计参数自适应律进行估计,针对参数补偿误差和外部扰动设计线性和非线性鲁棒项,利用李雅普诺夫函数证明所提的控制器有界稳定. 所设计的参数自适应律能够逼近未知的惯性和摩擦参数,补偿系统的参数不确定性及常值干扰. 线性鲁棒项可以提高系统的鲁棒性,保证系统的稳定性. 非线性鲁棒项可以克服部分外干扰对系统控制性能的影响. 实验结果表明,提出的NOARC与ARC相比跟踪精度提高了约50%,与PID相比跟踪精度提高了一个数量级,有效提升了机电作动系统的跟踪性能和鲁棒性.
参考文献
Numerical and experimental investigation on electromechanical aileron actuation system with joint clearance
[J].DOI:10.1007/s12206-019-0105-8 [本文引用: 1]
Research on improved control method of electromechanical actuation
[J].
小型飞机起落架收放机电作动器研究与开发
[J].
Research and development of electromechanical actuators for retracting and landing small aircraft landing gears
[J].
具有可参数化不确定性系统的对偶自适应模型预测控制
[J].DOI:10.7641/CTA.2018.80324 [本文引用: 1]
Dual adaptive model predictive control with parametric uncertainty system
[J].DOI:10.7641/CTA.2018.80324 [本文引用: 1]
伺服驱动系统无模型自适应控制
[J].
Model-free adaptive control of servo drive system
[J].
Robust control approach for handling matched and/or unmatched uncertainties in port-controlled Hamiltonian systems
[J].DOI:10.1049/iet-csr.2019.0019 [本文引用: 1]
Adaptive robust control of DC motors with extended state observer
[J].DOI:10.1109/TIE.2013.2281165 [本文引用: 1]
High-order sliding-mode observer based output feedback adaptive robust control of a launching platform with backstepping
[J].DOI:10.1080/00207179.2016.1147604
Adaptive control of hydraulic actuators with LuGre model-based friction compensation
[J].
机电伺服系统鲁棒自适应重复控制
[J].
Robust adaptive repetitive control of electromechanical servo systems
[J].
To stick or to slip: a reset PID control perspective on positioning systems with friction
[J].
数字液压缸反馈螺杆库伦摩擦仿真研究
[J].
Coulomb friction simulation study on feedback screw of digital hydraulic cylinder
[J].
Stribeck parameters estimation of a diaphragm valve using quasi Newton method
[J].DOI:10.1016/j.ifacol.2019.06.066 [本文引用: 1]
Identification and compensation of non-linear friction for a electro-hydraulic system
[J].
Stable PID control strategy to remove limit cycle due to Stribeck friction on DC servo motor
[J].DOI:10.15866/ireaco.v11i4.14883 [本文引用: 1]
磁流变阻尼器Dahl模型的参数化建模
[J].DOI:10.3969/j.issn.1674-957X.2020.06.051 [本文引用: 1]
Parametric modeling of the Dahl model of magnetorheological dampers
[J].DOI:10.3969/j.issn.1674-957X.2020.06.051 [本文引用: 1]
Minor loops of the Dahl and LuGre models
[J].
Inclusion of the dwell time effect in the LuGre friction model
[J].
基于改进LuGre摩擦模型的双旋弹丸固定舵翼滚转位置鲁棒自适应控制算法
[J].DOI:10.3969/j.issn.1000-1093.2019.12.005
Robust adaptive control algorithm for rolling position of fixed rudder wing of double-rotating projectile based on improved LuGre friction model
[J].DOI:10.3969/j.issn.1000-1093.2019.12.005
High-accuracy robust adaptive motion control of a torque-controlled motor servo system with friction compensation based on neural network
[J].
A new model for control of systems with friction
[J].DOI:10.1109/9.376053 [本文引用: 1]